Abstract
Empirical validation and verification procedures require the sophisticated development of research methodology. Therefore, researchers and practitioners in human–machine interaction and the automotive domain have developed standardized test protocols for user studies. These protocols are used to evaluate human–machine interfaces (HMI) for driver distraction or automated driving. A system or HMI is validated in regard to certain criteria that it can either pass or fail. One important aspect is the number of participants to include in the study and the respective number of potential failures concerning the pass/fail criteria of the test protocol. By applying binomial tests, the present work provides recommendations on how many participants should be included in a user study. It sheds light on the degree to which inferences from a sample with specific pass/fail ratios to a population is permitted. The calculations take into account different sample sizes and different numbers of observations within a sample that fail the criterion of interest. The analyses show that required sample sizes increase to high numbers with a rising degree of controllability that is assumed for a population. The required sample sizes for a specific controllability verification (e.g., 85%) also increase if there are observed cases of fails in regard to the safety criteria. In conclusion, the present work outlines potential sample sizes and valid inferences about populations and the number of observed failures in a user study.
1. Introduction
Level 2 driving automation technology [1] is already widely available to consumers, and the first Level 3 system obtained legal permission in March 2021 in Japan [2]. Moreover, the United Nations Economic Commission for Europe is also working towards regulations and standards for Level 3 vehicles [3]. It is likely that there will be different systems created by different manufacturers on the market in the next few years. A vehicle’s human–machine interface (HMI) must thus communicate the responsibilities of the system and the driver to the latter. The design of an automated vehicle HMI will eventually undergo testing procedures to ensure safety and usability. Compared to the evaluation of HMIs in manual driving focusing on driver distraction [4,5], a commonly agreed upon methodological framework for validation and verification does not yet exist. Deliverables on the investigation methodology of consortia projects can serve as a basis to build upon such a commonly agreed upon framework. For example, the Response Code of Practice [6] was first published in 2006 and was just recently been updated in the L3 Pilot project [7]. These reports combine a large body of research on driving automation systems and human–machine interfaces. Similarly, Naujoks et al. [8] proposed an approach on how to evaluate automated vehicle HMIs regarding the five criteria that are contained in the automated vehicles policy published by NHTSA [9]. Therein, the authors outline an appropriate design for user studies regarding driving scenarios, metrics, instructions, etc. One important aspect here is the number of participants that is required for user testing. The authors describe one approach that requires a sample size of N = 20, assuming that every participant meets the validation criterion. However, there might be additional considerations that are necessary to determine the sample size for a study to ensure the generalizability of the findings to a population. The objective of this work is to provide researchers and practitioners with a recommendation for how many participants to sample for validation procedures. Here, we will derive the number of required participants for different controllability levels. Moreover, researchers can face results in hindsight, where one or more participant might fail a test criterion. This work can also act as a guide for the interpretation of such outcomes. It supports researchers with indications of the controllability level that is permitted in such instances.
Thus, the present work describes an approach on how to recruit an appropriate sample size for user testing in human factor validation studies.
Before further describing the procedure, we want to emphasize that the use of G-Power is not applicable to calculate the adequate sample size in this instance. The reason for this is as follows: In the present case, researchers want to show that no difference between populations exist or that trials with a certain system come from a population in which (at least) x% of all trials are controllable. To show that, the researchers hope for a non-significant null hypothesis (H0) test in order to be able to keep the H0 of controllability. Since no H1 is formulated (or to be exact: an unspecific H1 is formulated), there is no defined effect size, and power analysis is not possible. However, it is possible to determine the smallest number of events (hits) associated with a test probability p that is larger than alpha 0.05 beforehand.
The code of practice for the validation of advanced driver assistance systems (ADAS) suggests that 20 out of 20 participants in the sample drawn have to meet a criterion to infer a controllability level of 85% in the population [6]. One example of a controllable event in a study on driving automation is a successful and safe take-over of the driving task when the driving automation system issues a request to do so (see, e.g., [10,11,12,13]). In contrast, crashes with a stationary object, exceedance of highway speeds, or crashing into a highway barrier are examples of uncontrollable events. ISO [14] (ISO 26262) lies the foundation for this approach by defining controllability levels (e.g., 85, 95, and 99%). This norm defines the required sample size (without uncontrollable events) for inferring a certain controllability level under an error probability that is <5%. Similar approaches are in effect today for evaluating HMIs for driver distraction. For example, NHTSA [4] suggests including a sample size of N = 24 participants of which at least n = 21 must meet the criteria for gaze metrics. Therefore, they argue that 85% of the sample must meet the criterion. Taking into account ISO 26262, it becomes obvious that this does not equal a level of 85% in the population but a considerably lower level. However, at first glance, many researchers might wonder why a 20/20 criterion is applied to ensure a controllability level of 85% in a user population. The present work will first provide background information about the origin of this rule and apply this logic to further examples of testing in the human factors area.
Prior considerations about sample size and composition are indispensable for human factor researchers when showing that a certain level of controllability can be met in the population. The aforementioned code of practice still represents the state of the art for user testing in driving simulators or test tracks. The 20/20 criterion for ensuring a 85% controllability level has been adopted in recent methodological frameworks for evaluating automated vehicles and HMIs [13,15]. However, it might be the case that one or more participants fail a criterion and that the researcher does not have a convincing argument to exclude the respective participant from the sample. Researchers might also have to interpret their obtained results regarding the level of controllability given a specific number of observed errors. Regarding these issues, researchers can first find advice in Weitzel and Winner [16], who have proposed a formula to calculate the number of required participants in a study based on the level of confidence and respective level of controllability (i.e., number of uncontrollable events). The authors, however, neither provide a comprehensive and transparent derivation of their solution nor provide an overview of the relationship between sample sizes, the number of errors, and the respective error probabilities.
Therefore, this work aims at a comprehensive description of the relationship between the number of participants in a study, the error probability or the confidence level, and the number of uncontrollable events that might occur in a study. We support researchers and practitioners working on (automated vehicle) HMI evaluation by providing a recommendation for sample size and controllability a priori. Moreover, the present work is helpful for the interpretation of the number of uncontrollable events by considering the sample size a posteriori. First, we transparently derive the commonly applied 20/20 criterion using binomial tests. With these, we calculate the relationship between error probability by sample size for different controllability levels (i.e., 85, 90, 95 and 99%). The following section outlines the procedure.
2. Materials and Methods
To determine adequate sample sizes for the validation and verification experiments, we calculated binomial probability density functions. To be more specific, we first calculated the error probabilities for zero uncontrollable events for each combination of level of controllability and the respective sample size. The resulting error probabilities were then analyzed to find the first value that drops below the statistical significance threshold of 0.05. This respective sample size was then considered as sufficient for the controllability inference of interest.
To determine acceptable sample sizes with observations that include uncontrollable events (i.e., from 1 up to 7), we varied the number of uncontrollable observations and calculated the error probability by using binomial probability density functions (see Algorithm 1). We accumulated the probabilities and determined the first value for each number of events that drops below the statistical threshold of 0.05, starting with zero. Thus, we can provide a range of potential sample sizes for each number of observed uncontrollable events.
| Algorithm 1. Calculation of error probabilities |
| %Loop through sample sizes from 1 up to 150 |
| for ii=1:350 |
| %set a container variable for results of binomial test |
| %set a variable to accumulate these results |
| cont=zeros(150,1); |
| container=[]; |
| %container=zeros(150,1); |
| b=0; |
| %For each sample size: Loop from 1 up the the respective size |
| %and calculate a binomial test each |
| for i=1:ii |
| %Calculate test: subtract i-1 for X |
| a=binopdf(i-1,ii,contr); |
| %accumulate the results |
| b=b+a; |
| %Save the accumulated result in the container. |
| container=[container;1-b]; |
| end |
| %Find the relevant sample size that drops below 0.05 |
| rel=find(container<.05); |
| if isempty(rel)==0 |
| rel=rel(1); |
| probability=container(rel); |
| err=ii-rel; |
| else |
| probability=container(end); |
| err=0; |
| end |
| %save variables of interest |
| errors=[errors;err]; |
| prob=[prob; probability]; |
| size=[size; ii]; |
| end |
Algorithm 1 shows the Matlab code for automated calculation of error probabilities and sample sizes for one specific level of controllability (variable “contr”). Note that the loop for sample sizes was increased for the populations of 95 and 99%.
3. Results
Figure 1 shows the error probabilities for the four populations of interest where the increasing sample sizes include no uncontrollable events. The plot also includes a horizontal line that depicts the 5% error probability. The first sample size that drops below this threshold can be considered as statistically significant. The graph also shows that the number of required participants increases as the percentage in the population increases or of the researchers want to find support for a higher level of controllability. Moreover, the number does not increase in a linear pattern.
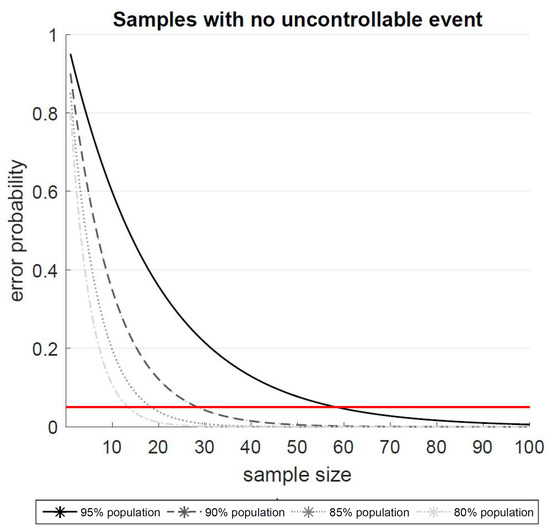
Figure 1.
Error probabilities for the four populations (80, 85, 90, and 95%) by sample sizes with no uncontrollable events.
This is reflected in the increasing distances between the curves. The exact values for the sample sizes are reported in Table 1. A closer observation of the error probabilities for the 85% population with no uncontrollable event revealed that the first sample size whose error probability drops below the threshold of 0.05 is a sample size of n = 19 (p = 0.0454), while the sample size of n = 18 is still above the threshold (p = 0.0510). The sample size of n = 20 revealed an error probability of p = 0.0396 (see Table 1).

Table 1.
Minimum and maximum required sample size with error probabilities for 0 up to 7 uncontrollable events for five different populations.
Based on the binomial tests that were described prior, we calculated the error probabilities for the different populations (i.e., 80, 85, 90, and 95% controllability) with increasing steps starting from one considering up to seven observed uncontrollable events. We reported both the first sample size for a respective number of observed errors and the last, which includes the respective error probabilities. The results are shown in Table 1.
The number of required participants also increases for each observation that does not meet a criterion. In the 85% population, for almost every ten participants that are included starting from 20, there can be one additional uncontrollable event. While a sample size of 20/20 is sufficient for a controllability verification of 85%, one observation with an error increases the sample size to n = 30, and another event increases it to n = 40. In comparison, the intervals of the 80% population are smaller, with a range of about seven participants per uncontrollable event. The intervals for the 90% population have an average range of 15, and the 95% population has a range between 25 and 30 participants per uncontrollable event, both of which are larger. In addition, Table 1 reports the results of the 99% (c1) population. The number of required participants in the 99% case without an error turned out to be even higher than the seven events in the 95% population. The intervals showed that approximately 150 additional participants would be necessary for each uncontrollable event observed in the sample.
4. Discussion
When setting up validation and verification studies for human–machine interfaces in automated driving, researchers need to determine the appropriate sample size in advance. Additionally, they have to define certain criteria that need to be met and to define the number of participants that have to meet each criterion in the user test. Based on the observations obtained in the study, they can draw inferences about for example levels of controllability in a population. However, to date, there is no comprehensive overview of the required number of participants and inferential assumptions from a sample to a population. To provide a recommendation to researchers and practitioners in the validation and verification of automated vehicle HMIs for appropriate sampling and interpretation of the obtained results, the present paper applied binomial tests with different populations, numbers of uncontrollable events, and sample sizes.
The first goal of this work was to transparently derive the 20/20 criterion. The investigation of the currently available sources for validation and verification [6,14] revealed that a sample size of 19 is already sufficient to infer a controllability level of 85%. The error probability of a sample size of 19 fell just below the threshold of statistical significance, while the sample size of 20 yielded an even smaller error probability. Nevertheless, this work suggests that experimental procedures for validation and verification might collect n = 19 participants and infer a controllability level of 85% if there are no uncontrollable events.
The second goal was to investigate the required sample size depending on different controllability levels and numbers of uncontrollable events that may occur in a study. Regarding the controllability level, the results showed that the required number of participants for populations with lower levels of controllability (e.g., 80, 85%) require a reasonable sample size of less than 50 participants, even if up to two uncontrollable events occur in the sample. Therefore, empirical tests for these instances can be performed well in validation procedures. However, to verify higher levels of controllability (e.g., above 90%), empirical studies would require an enormous number of participants. This becomes even more obvious with the additional example of the 99% population. In experimental procedures, samples with more than 60 participants require a high amount of effort to recruit participants to and to complete the study. With numbers of more than 100 participants, which is still much less 1000, validation and verification studies are impossible to conduct. Therefore, different methodological approaches such as heuristic expert assessments are necessary in these instances. Such heuristic evaluations should be based on the guidelines that are available for the topic of interest [17,18]. Regarding observations of uncontrollable events in a user study, the respective size of the sample for a verification of a certain population also increases. While the increase is quite moderate in the 80% and 85% population, the additional number of required participants per observed event at higher levels ranges between 15 and 30. Thus, if one aims to verify a high degree of controllability and plans to do so with a small number of uncontrollable events, the sample size would be unreasonably large.
Applying these obtained results to empirical experiments, we refer to Naujoks and colleagues [12]. In these studies, sample sizes were 21 or 22, respectively. At this point we can treat the data as if the results had been obtained in independent validation studies, while in fact the study employed a within-subject design. One might define a criterion that no driver may put his/her hands to the steering wheel later than 7 s after the take-over request has been issued. The data in the publication shows that when the take-over request was accompanied by an auditory warning, all of the participants passed the criterion, and evidence for 85% controllability was provided. In contrast, with mere visual warnings, a significant portion of the sample failed this criterion with a 95% percentile, even beyond 20 s. Thus, there is no support for 85% controllability nor for 80% (see Table 1), but there is support for a considerably lower controllability level that we have not calculated here.
From these observations, we suggest that a sample size of 59 could be a suitable and reasonable sample size for the verification and validation of automated vehicle HMIs. The advantage compared to a sample size of n = 30, where only one participant can fail a criterion, is that with twice the number of participants, four times the number of participants can fail a criterion. On average, for every ten participants that are included in a sample, one of these might fail a criterion, still permitting an inference to the 85% controllability level. This is especially important since there might be participants in a sample that fail a criterion due to a variety of reasons that are not directly obvious; thus, the researcher cannot exclude him/her from the sample. One example for this might be that the participant misunderstands certain questions that are relevant to the criterion of interest in the validation study [8]. Another possibility is that he/she cannot articulate the relevant aspect during the interview specifically enough even though he/she has the correct understanding of the HMI. This could be the naming and interaction of one sub-function (e.g., longitudinal vehicle control) in combination with another sub-function (e.g., traffic-sign detection). These examples would not permit the exclusion of the participant from the obtained sample but would lead to a rejection of the validation procedure regarding the 85% controllability level. Therefore, a larger sample size would provide a certain buffer against these rare but still possible events. At this point, we want to explicitly address the issue of additional sampling during the experimental procedure. The present work suggests not adding an additional ten participants to the sample if the intermediate results showed that the test did not meet the a priori defined criteria. We want to highlight that these numbers are meant to be considered by researchers in the design process of a study where they decide upon the sample size and the acceptable number of observed uncontrollable events.
Regarding the procedure for the distraction verification of HMIs, NHTSA [4] describes that 21 out of 24 participants must meet their criteria for glance behavior. This implies that three participants do not have to meet the test criteria. Table 1 shows that not even a verification of 80% controllability in the population is ensured here since the interval for three events ranges from 37 to 43. Thus, the assumptions about the population must be decreased by a significant amount, most likely to around 70%. Therefore, the distraction guidelines permit a sample percentage of 15% to fail their criteria, which translates to at least twice the amount in the population.
The present work also comes with certain limitations. One shortcoming of the present work is that it treats each participant as a controllable or uncontrollable event. However, it might be the case that the validation and verification procedures as described in NHTSA [4] (driver distraction) or [9] (automated vehicles) include multiple criteria per participant (i.e., 3 and 5). A conservative approach would be that if a participant does not meet one criterion, this specific participant is counted as a failure on the participant level. However, since this particular participant actually meets all of the other criteria, another option is to regard all of the criteria as separate and independent observations. Thus, the necessary sample size is higher (due to the observed event) and provides the opportunity to observe a certain number of errors while still permitting a valid inference to the population of interest, such as the 85% population (see Table 1). In other words, we suggest that each of the five criteria in NHTSA [9] is treated as a separate test and is investigated whether a sufficiently high number of participants meet the test criteria (and none or only a small number fail the criteria). In case of a sample size of N = 45 participants, each criterion might include two participants that fail in each criterion. However, the system or HMI still passes the test in this example.
Furthermore, the present binomial tests assumed single-tailed testing since the hypotheses in validation and verification testing only make sense if they are directed. Under the premise of single-tailed testing, the 85% population inference would require a ratio of 19/19, as described above. However, under a two-tailed premise, a ratio of 19/19 would not be sufficient to infer to this population but rather 20/20. Therefore, the ISO most likely assumed a two-tailed binomial test in their suggestion for the 20/20 criterion. In the end, researchers must decide by themselves whether to adhere to a one- or two-tailed test. However, in verification and validation, the procedures of directed hypotheses certainly make more sense compared to undirected hypotheses.
5. Conclusions
This work provides a transparent derivation of the common 20/20 criterion for validation and verification. It provides recommendations for researchers and practitioners when planning and interpreting their empirical studies. It also shows that empirical evidence for verification procedures quickly approaches its limits when inferring from the obtained results of the population. Thus, studies including 60 participants or less yield the possibility of verifying controllability levels of up to 90%, depending on the number of uncontrollable events that occur in the sample.
Author Contributions
Conceptualization, Y.F. and F.N.; methodology, Y.F.; formal analysis, Y.F.; writing—original draft preparation, Y.F.; writing—review and editing, Y.F. and F.N.; visualization, Y.F.; supervision, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Acknowledgments
The authors would like to thank Rainer Scheuchenpflug for his statistical advice, feedback on the first draft, and review of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- SAE. Taxonomy and Definitions for Terms Related to On-Road Motor Vehicle Automated Driving Systems, 2018 (J3016R). Available online: https://www.sae.org/standards/content/j3016_201609/ (accessed on 30 October 2019).
- The Japan Times. Honda to Start Offering World’s First Level-3 Autonomous Car Friday. Available online: https://www.japantimes.co.jp/news/2021/03/04/business/honda-cars-automakers-autonomous-driving/ (accessed on 17 May 2021).
- United Nations Economic Commission for Europe. Uniform Provisions Concerning the Approval of Vehicles with Regard to Automated Lane Keeping Systems: ALKS. 2020. Available online: https://unece.org/fileadmin/DAM/trans/doc/2020/wp29grva/GRVA-06-02r1e.pdf (accessed on 14 May 2021).
- NHTSA. Visual-Manual NHTSA Driver Distraction Guidelines for In-Vehicle Electronic Devices; National Highway Traffic Safety Administration (NHTSA), Department of Transportation (DOT): Washington, DC, USA, 2012. Available online: https://www.nhtsa.gov/sites/nhtsa.gov/files/distraction_npfg-02162012.pdf (accessed on 30 September 2020).
- AAM. Statement of Principles, Criteria and Verification Procedures on Driver Interactions with Advanced in Vehicle Information and Communication Systems; Alliance of Automobile Manufactures: Washington, DC, USA, 2006. [Google Scholar]
- RESPONSE Consortium. Code of Practice for the Design and Evaluation of ADAS: RESPONSE 3: A PReVENT Project. 2006. Available online: https://www.acea.auto/files/20090831_Code_of_Practice_ADAS.pdf (accessed on 14 May 2021).
- L3 Pilot Driving Automation Consortium. Deliverable D2.3: Code of Practice for the Development of Automated Driving Functions. 2021. Available online: https://l3pilot.eu/fileadmin/user_upload/Downloads/Deliverables/Update_26072021/L3Pilot-SP2-D2.3-Code_of_Practice_for_the_Development_of_Automated_Driving_Functions-v1.1_for_website.pdf (accessed on 23 April 2021).
- Naujoks, F.; Hergeth, S.; Wiedemann, K.; Schömig, N.; Forster, Y.; Keinath, A. Test procedure for evaluating the human–machine interface of vehicles with automated driving systems. Traffic Inj. Prev. 2019, 20, S146–S151. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- NHTSA. Federal Automated Vehicles Policy. Accelerating the Next Revolution in Roadway Safety, NHTSA, US DOT. 2016. Available online: https://www.nhtsa.gov/sites/nhtsa.gov/files/documents/13069a-ads2.0_090617_v9a_tag.pdf (accessed on 5 July 2017).
- Gold, C.; Damböck, D.; Lorenz, L.; Bengler, K. “Take Over!” How Long Does It Take to Get the Driver back into the Loop? In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; 2013. Available online: https://mediatum.ub.tum.de/doc/1308108/file.pdf (accessed on 14 May 2021).
- Forster, Y.; Naujoks, F.; Neukum, A.; Huestegge, L. Driver compliance to take-over requests with different auditory outputs in conditional automation. Accid. Anal. Prev. 2017, 109, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Naujoks, F.; Mai, C.; Neukum, A. The effect of urgency take-over requests during highly automated driving under distraction conditions. Adv. Hum. Asp. Transp. 2014, 7, 431. [Google Scholar]
- Wood, M.; Robbel, P.; Maass, M.; Rdboud, D.; Meijs, M.; Harb, M.; Reach, J.; Robinson, K.; Wittmann, D.; Srivastava, T.; et al. Safety First for Automated Driving. Whitepaper. 2019. Available online: https://www.daimler.com/documents/innovation/other/safety-first-for-automated-driving.pdf (accessed on 14 May 2021).
- ISO. Road Vehicles—Functional Safety, 2011, (26262). Available online: https://www.iso.org/standard/43464.html (accessed on 11 September 2019).
- Wolter, S.; Dominioni, G.C.; Hergeth, S.; Tango, F.; Whitehouse, S.; Naujoks, F. Human–Vehicle Integration in the Code of Practice for Automated Driving. Information 2020, 11, 284. [Google Scholar] [CrossRef]
- Weitzel, A.; Winner, H. Ansatz zur Kontrollierbarkeitsbewertung von Fahrerassistenzsystemen vor dem Hintergrund der ISO 26262. In Proceedings of the Workshop Fahrerassistenzsysteme, FAS 2012, Walting im Altmühltal, Germany, 26–28 September 2012; pp. 15–25. [Google Scholar]
- Naujoks, F.; Wiedemann, K.; Schömig, N.; Hergeth, S.; Keinath, A. Towards guidelines and verification methods for automated vehicle HMIs. Transp. Res. Part F Traffic Psychol. Behav. 2019, 60, 121–136. [Google Scholar] [CrossRef]
- Biondi, F.N.; Getty, D.; McCarty, M.M.; Goethe, R.M.; Cooper, G.E.; Strayer, D.L. The Challenge of Advanced Driver Assistance Systems Assessment: A Scale for the Assessment of the Human–Machine Interface of Advanced Driver Assistance Technology. Transp. Res. Rec 2018, 2672, 113–122. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).