Evaluation of Tree-Based Ensemble Machine Learning Models in Predicting Stock Price Direction of Movement
Abstract
1. Introduction
2. Experimental Design
2.1. Data and Features
2.2. Data Normalization
2.3. Feature Extraction
2.4. Machine Learning Algorithms
2.4.1. Base Classifier
2.4.2. Random Forest Classifier
2.4.3. AdaBoost Classifier
2.4.4. XGBoost Classifier
2.4.5. Bagging Classifier
2.4.6. Extra Trees Classifier
2.4.7. Voting Classifier
2.5. Evaluation Metric
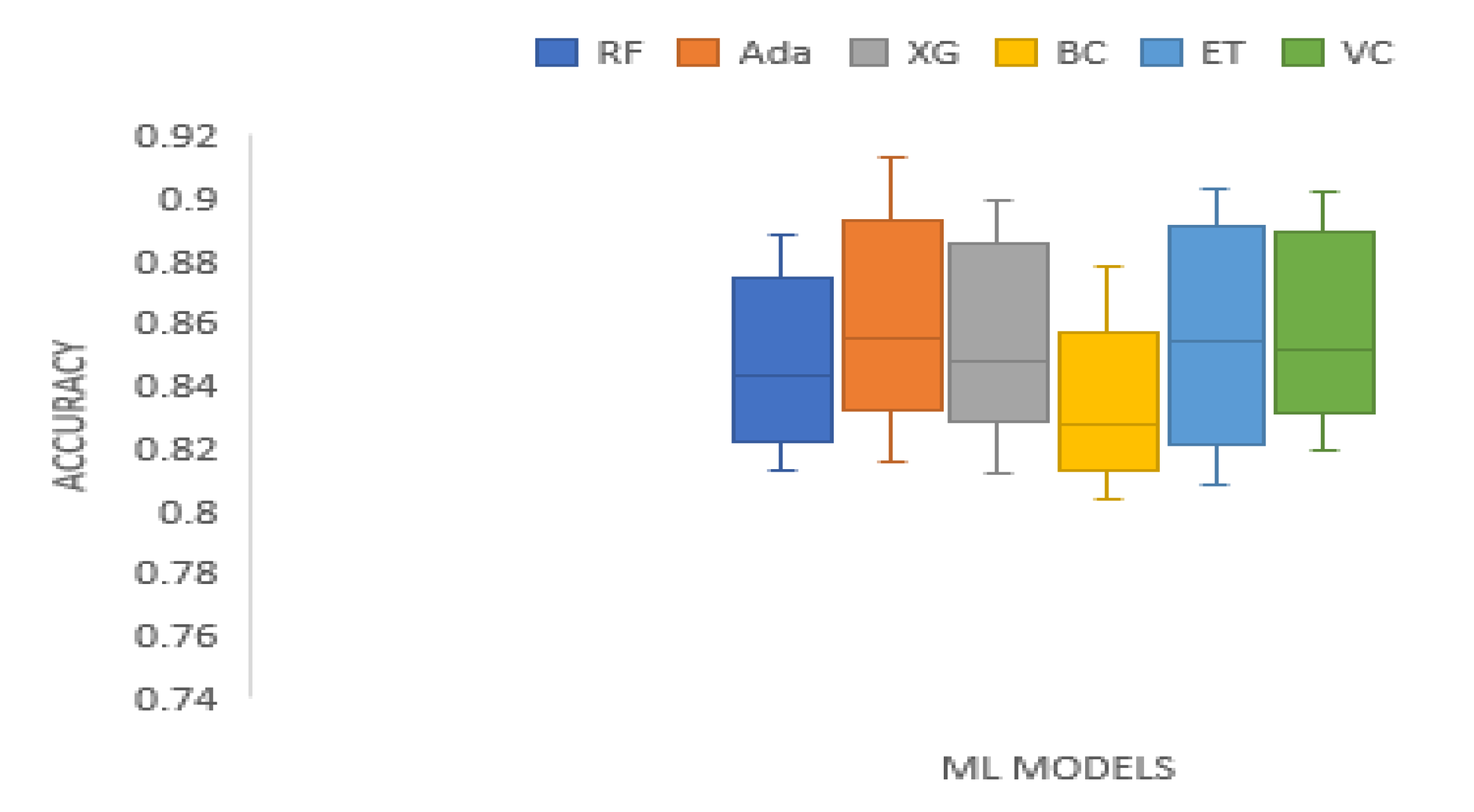
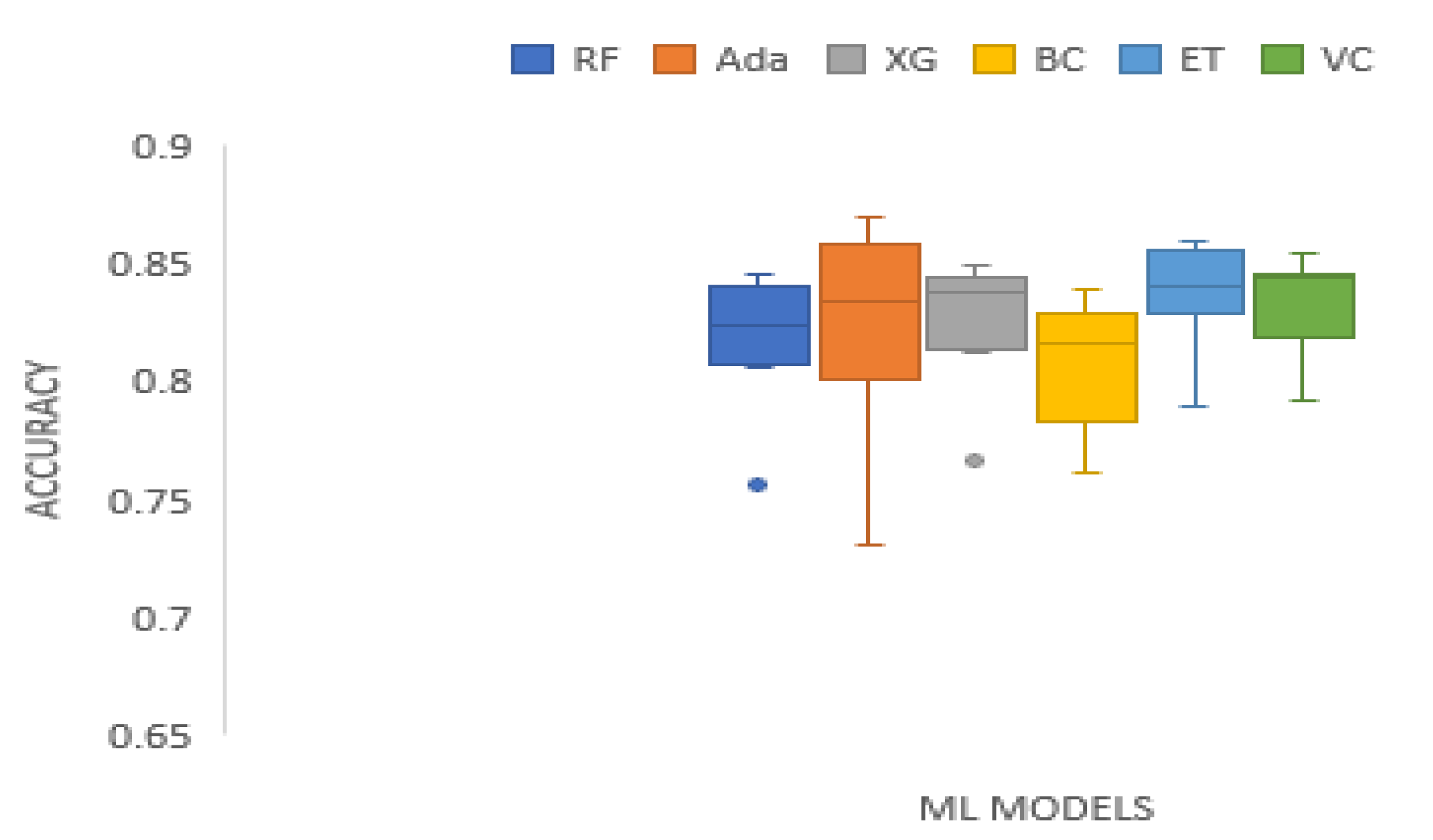
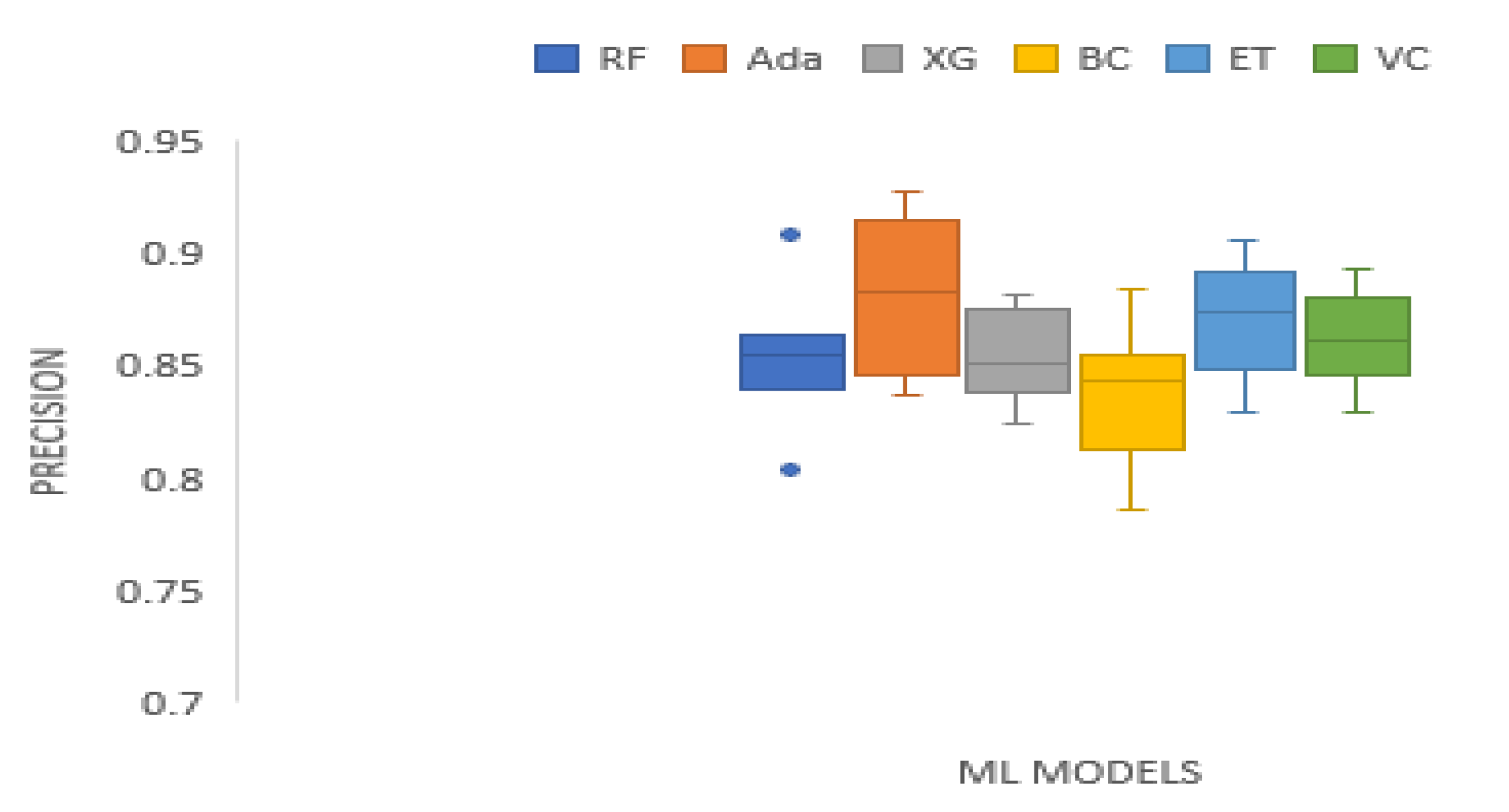
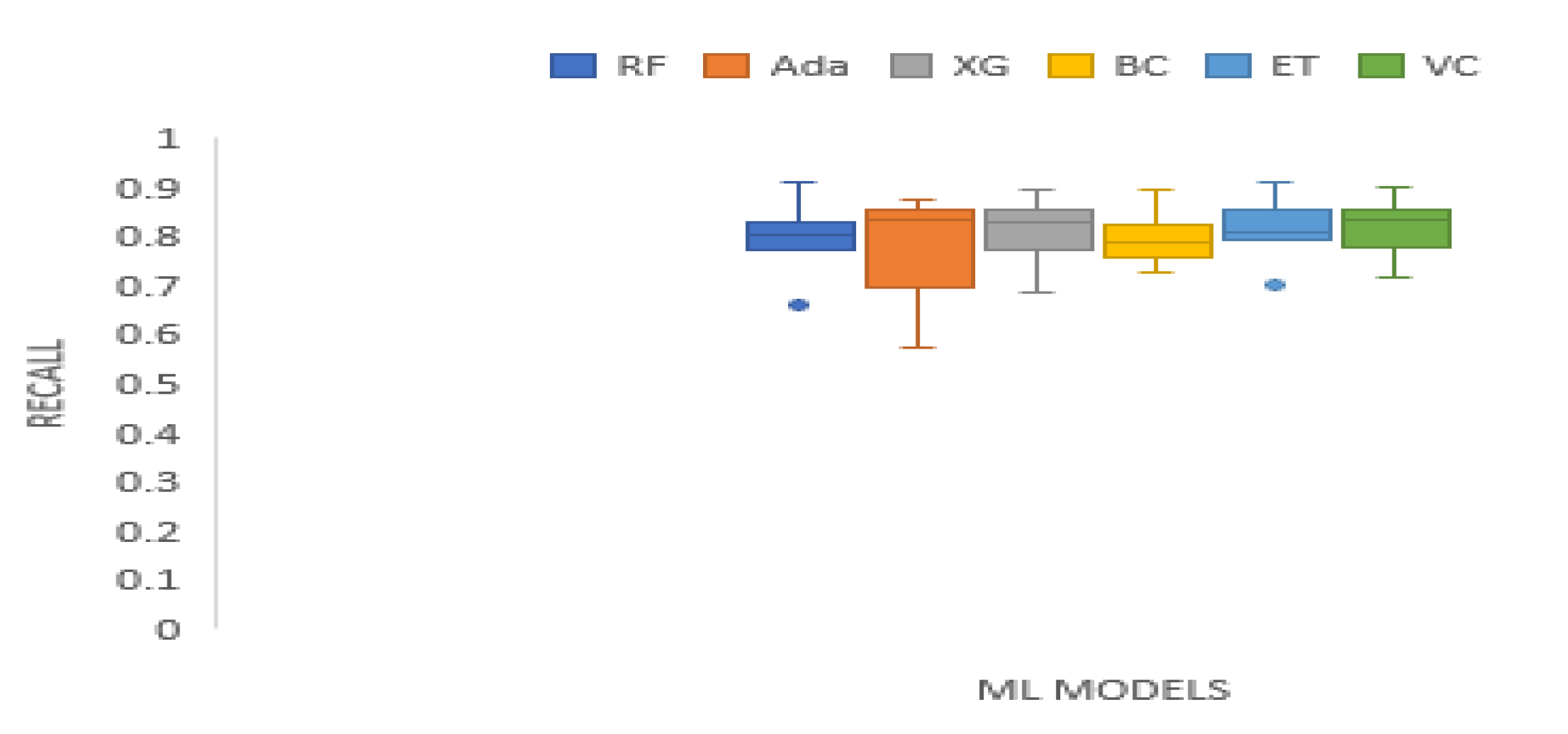
3. Results and Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Overlap Studies Indicators | Description |
|---|---|
| Bollinger Bands (BBANDS) | Describes the different highs and lows of a financial instrument in a particular duration. |
| Weighted Moving Average (WMA) | Moving average that assign a greater weight to more recent data points than past data points |
| Exponential Moving Average (EMA) | Weighted moving average that puts greater weight and importance on current data points, however, the rate of decrease between a price and its preceding price is not consistent. |
| Double Exponential Moving Average (DEMA) | It is based on EMA and attempts to provide a smoothed average with less lag than EMA. |
| Kaufman Adaptive Moving Average (KAMA) | Moving average designed to be responsive to market trends and volatility. |
| MESA Adaptive Moving Average (MAMA) | Adjusts to movement in price based on the rate of change of phase as determined by the Hilbert transform discriminator. |
| Midpoint Price over period (MIDPRICE) | Average of the highest close minus lowest close within the look back period |
| Parabolic SAR (SAR) | Heights potential reversals in the direction of market price of securities. |
| Simple Moving Average (SMA) | Arithmetic moving average computed by averaging prices over a given time period. |
| Triple Exponential Moving Average (T3) | It is a triple smoothed combination of the DEMA and EMA |
| Triple Exponential Moving Average (TEMA) | An indicator used for smoothing price fluctuations and filtering out volatility. Provides a moving average having less lag than the classical exponential moving average. |
| Triangular Moving Average (TRIMA) | Moving average that is double smoothed (averaged twice) |
| Volume Indicator | Description |
|---|---|
| Chaikin A/D Line (ADL) | Estimates the Advance/Decline of the market. |
| Chaikin A/D Oscillator (ADOSC) | Indicator of another indicator. It is created through application of MACD to the Chaikin A/D Line |
| On Balance Volume (OBV) | Uses volume flow to forecast changes in price of stock |
| Price Transform Indicator | Description |
|---|---|
| Median Price (MEDPRICE) | Measures the mid-point of each day’s high and low prices. |
| Typical Price (TYPPRICE) | Measures the average of each day’s price. |
| Weighted Close Price (WCLPRICE) | Average of each day’s price with extra weight given to the closing price. |
| Momentum Indicators | Description |
|---|---|
| Average Directional Movement Index (ADX) | Measures how strong or weak (strength of) a trend is over time |
| Average Directional Movement Index Rating (ADXR) | Estimates momentum change in ADX. |
| Absolute Price Oscillator (APO) | Computes the differences between two moving averages |
| Aroon | Used to find changes in trends in the price of an asset |
| Aroon Oscillator (AROONOSC) | Used to estimate the strength of a trend |
| Balance of Power (BOP) | Measures the strength of buyers and sellers in moving stock prices to the extremes |
| Commodity Channel Index (CCI) | Determine the price level now relative to an average price level over a period of time |
| Chande Momentum Oscillator (CMO) | Estimated by computing the difference between the sum of recent gains and the sum of recent losses |
| Directional Movement Index (DMI) | Indicate the direction of movement of the price of an asset |
| Moving Average Convergence/Divergence (MACD) | Uses moving averages to estimate the momentum of a security asset |
| Money Flow Index (MFI) | Utilize price and volume to identify buying and selling pressures |
| Minus Directional Indicator (MINUS_DI) | Component of ADX and it is used to identify presence of downtrend. |
| Momentum (MOM) | Measurement of price changes of a financial instrument over a period of time |
| Plus Directional Indicator (PLUS_DI) | Component of ADX and it is used to identify presence of uptrend. |
| Log Return | The log return for a period of time is the addition of the log returns of partitions of that period of time. It makes the assumption that returns are compounded continuously rather than across sub-periods |
| Percentage Price Oscillator (PPO) | Computes the difference between two moving averages as a percentage of the bigger moving average |
| Rate of change (ROC) | Measure of percentage change between the current price with respect to a at closing price n periods ago. |
| Relative Strength Index (RSI) | Determines the strength of current price in relation to preceding price |
| Stochastic (STOCH) | Measures momentum by comparing closing of a security with earlier trading range over a specific period of time |
| Stochastic Relative Strength Index (STOCHRSI) | Used to estimate whether a security is overbought or oversold. It measures RSI over its own high/low range over a specified period. |
| Ultimate Oscillator (ULTOSC) | Estimates the price momentum of a security asset across different time frames. |
| Williams’ %R (WILLR) | Indicates the position of the last closing price relative to the highest and lowest price over a time period. |
References
- Fischer, T.; Krauss, C. Deep learning with long short-term memory networks for financial market predictions. Eur. J. Oper. Res. 2018, 270, 654–669. [Google Scholar] [CrossRef]
- Cootner, P. The Random Character of Stock Market Prices; M.I.T. Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Fama, E.F.; Fisher, L.; Jensen, M.C.; Roll, R. The adjustment of stock prices to new information. Int. Econ. Rev. 1969, 10, 1–21. [Google Scholar] [CrossRef]
- Malkiel, B.G.; Fama, E.F. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Fama, E.F. The behavior of stock-market prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Jensen, M.C. Some anomalous evidence regarding market efficiency. J. Financ. Econ. 1978, 6, 95–101. [Google Scholar] [CrossRef]
- Bollen, J.; Mao, H.; Zeng, X. Twitter mood predicts the stock market. J. Comput. Sci. 2011, 2, 1–8. [Google Scholar] [CrossRef]
- Ballings, M.; Van den Poel, D.; Hespeels, N.; Gryp, R. Evaluating multiple classifiers for stock price direction prediction. Expert Syst. Appl. 2015, 42, 7046–7056. [Google Scholar] [CrossRef]
- Chong, E.; Han, C.; Park, F.C. Deep learning networks for stock market analysis and prediction: Methodology, data representations, and case studies. Expert Syst. Appl. 2017, 83, 187–205. [Google Scholar] [CrossRef]
- Nofsinger, J.R. Social mood and financial economics. J. Behav. Financ. 2005, 6, 144–160. [Google Scholar] [CrossRef]
- Smith, V.L. Constructivist and ecological rationality in economics. Am. Econ. Rev. 2003, 93, 465–508. [Google Scholar] [CrossRef]
- Avery, C.N.; Chevalier, J.A.; Zeckhauser, R.J. The CAPS prediction system and stock market returns. Rev. Financ. 2016, 20, 1363–1381. [Google Scholar] [CrossRef]
- Hsu, M.-W.; Lessmann, S.; Sung, M.-C.; Ma, T.; Johnson, J.E. Bridging the di- vide in financial market forecasting: Machine learners vs. financial economists. Expert Syst. Appl. 2016, 61, 215–234. [Google Scholar] [CrossRef]
- Weng, B.; Ahmed, M.A.; Megahed, F.M. Stock market one-day ahead movement prediction using disparate data sources. Expert Syst. Appl. 2017, 79, 153–163. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, L. Stock market prediction of s&p 500 via combination of improved bco approach and bp neural network. Expert Syst. Appl. 2009, 36, 8849–8854. [Google Scholar]
- Patel, J.; Shah, S.; Thakkar, P.; Kotecha, K. Predicting stock market index using fusion of machine learning techniques. Expert Syst. Appl. 2015, 42, 2162–2172. [Google Scholar] [CrossRef]
- Geva, T.; Zahavi, J. Empirical evaluation of an automated intraday stock recommendation system incorporating both market data and textual news. Decis. Support Syst. 2014, 57, 212–223. [Google Scholar] [CrossRef]
- Guresen, E.; Kayakutlu, G.; Daim, T.U. Using artificial neural network models in stock market index prediction. Expert Syst. Appl. 2011, 38, 10389–10397. [Google Scholar] [CrossRef]
- Meesad, P.; Rasel, R.I. Predicting stock market price using support vector regression. In Proceedings of the 2013 International Conference on Informatics, Electronics and Vision (ICIEV), Dhaka, Bangladesh, 17–18 May 2013; pp. 1–6. [Google Scholar]
- Wang, J.-Z.; Wang, J.-J.; Zhang, Z.-G.; Guo, S.-P. Forecasting stock indices with back propagation neural network. Expert Syst. Appl. 2011, 38, 14346–14355. [Google Scholar] [CrossRef]
- Schumaker, R.P.; Chen, H. Textual analysis of stock market prediction us- ing breaking financial news: The azfin text system. ACM Trans. Inf. Syst. 2009, 27, 12. [Google Scholar] [CrossRef]
- Barak, S.; Modarres, M. Developing an approach to evaluate stocks by fore- casting effective features with data mining methods. Expert Syst. Appl. 2015, 42, 1325–1339. [Google Scholar] [CrossRef]
- Booth, A.; Gerding, E.; Mcgroarty, F. Automated trading with performance weighted random forests and seasonality. Expert Syst. Appl. 2014, 41, 3651–3661. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, B.; Abraham, A. Flexible neural trees ensemble for stock index modeling. Neurocomputing 2007, 70, 697–703. [Google Scholar] [CrossRef]
- Hassan, M.R.; Nath, B.; Kirley, M. A fusion model of hmm, ann and ga for stock market forecasting. Expert Syst. Appl. 2007, 33, 171–180. [Google Scholar] [CrossRef]
- Rather, A.M.; Agarwal, A.; Sastry, V. Recurrent neural network and a hybrid model for prediction of stock returns. Expert Syst. Appl. 2015, 42, 3234–3241. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Qian, B.; Rasheed, K. Stock market prediction with multiple classifiers. Appl. Intell. 2007, 26, 25–33. [Google Scholar] [CrossRef]
- Xiao, Y.; Xiao, J.; Lu, F.; Wang, S. Ensemble ANNs-PSO-GA approach for day-ahead stock E-exchange prices forecasting. Int. J. Comput. Intell. Syst. 2014, 7, 272–290. [Google Scholar] [CrossRef]
- Mohamad, I.B.; Usman, D. Standardization and Its Effects on K-Means Clustering Algorithm. Res. J. Appl. Sci. Eng. Technol. 2013, 6, 3299–3303. [Google Scholar] [CrossRef]
- Lin, X.; Yang, Z.; Song, Y. Short-term stock price prediction based on echo state networks. Expert Syst. Appl. 2009, 36, 7313–7317. [Google Scholar] [CrossRef]
- Tsai, C.-F.; Hsiao, Y.-C. Combining multiple feature selection methods for stock prediction: Union, intersection, and multi-intersection approaches. Decis. Support Syst. 2010, 50, 258–269. [Google Scholar] [CrossRef]
- Torlay, L.; Perrone-Bertolotti, M.; Thomas, E. Machine learning–XGBoost analysis of language networks to classify patients with epilepsy. Brain Inform. 2017, 4, 159–169. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Document Analysis and Recognition, Proceedings of the Third International Conference, Montreal, QC, Canada, 14–16 August 1995; IEEE: New York, NY, USA, 1995; Volume 1, pp. 278–282. [Google Scholar]
- Ho, T.K. The random subspace method for constructing decision forests. Intell. IEEE Trans. Pattern Anal. Mach. 1998, 20, 832–844. [Google Scholar]
- Amit, Y.; Geman, D. Shape quantization and recognition with randomized trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Boinee, P.; De Angelis, A.; Foresti, G.L. Meta random forests. Int. J. Comput. Intell. 2005, 2, 138–147. [Google Scholar]
- Zhou, Y.; Qiu, G. Random forest for label ranking. Expert Syst. Appl. 2018, 112, 99–109. [Google Scholar] [CrossRef]
- Tan, Z.; Yan, Z.; Zhu, G. Stock selection with random forest: An exploitation of excess return in the Chinese stock market. Heliyon 2019, 5, e02310. [Google Scholar] [CrossRef]
- Chen, M.; Wang, X.; Feng, B.; Liu, W. Structured random forest for label distribution learning. Neurocomputing 2018, 320, 171–182. [Google Scholar] [CrossRef]
- Wongvibulsin, S.; Wu, K.C.; Zeger, S.L. Clinical risk prediction with random forests for survival, longitudinal, and multivariate (RF-SLAM) data analysis. BMC Med Res. Methodol. 2020, 20, 1. [Google Scholar] [CrossRef]
- Seifert, S. Application of random forest-based approaches to surface-enhanced Raman scattering data. Sci. Rep. 2020, 10, 5436. [Google Scholar] [CrossRef] [PubMed]
- Freund, Y.; Schapire, R. Experiments with a new boosting algorithm. In Machine Learning: Proceedings of the Thirteenth International Conference (ICML ’96); Morgan Kaufmann Publishers Inc.: Bari, Italy, 1996; pp. 148–156. [Google Scholar]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A 723 statistical view of boosting. Ann. Stat. 2000, 28, 337–374. [Google Scholar] [CrossRef]
- Wang, J.; Tang, S. Time series classification based on Arima and AdaBoost, 2019 International Conference on Computer Science Communication and Network Security (CSCNS2019). MATEC Web Conf. 2020, 309, 03024. [Google Scholar] [CrossRef][Green Version]
- Chang, V.; Li, T.; Zeng, Z. Towards an improved AdaBoost algorithmic method for computational financial analysis. J. Parallel Distrib. Comput. 2019, 134, 219–232. [Google Scholar] [CrossRef]
- Suganya, E.; Rajan, C. An AdaBoost-modified classifier using stochastic diffusion search model for data optimization in Internet of Things. Soft Comput. 2019, 1–11. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting hard rock pillar stability using GBDT, XGBoost, and LightGBM Algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Li, W.; Yin, Y.; Quan, X.; Zhang, H. Gene expression value prediction based on XGBoost algorithm. Front. Genet. 2019, 10, 1077. [Google Scholar] [CrossRef]
- Sharma, A.; Verbeke, W.J.M.I. Improving Diagnosis of Depression with XGBOOST Machine Learning Model and a Large Biomarkers Dutch Dataset (n = 11,081). Front. Big Data 2020, 3, 15. [Google Scholar] [CrossRef]
- Zareapoora, M.; Shamsolmoali, P. Application of Credit Card Fraud Detection: Based on Bagging Ensemble Classifier. Int. Conf. Intell. Comput. Commun. Converg. Procedia Comput. Sci. 2015, 48, 679–686. [Google Scholar] [CrossRef]
- Yaman, E.; Subasi, A. Comparison of Bagging and Boosting Ensemble Machine Learning Methods for Automated EMG Signal Classification. Biomed Res. Int. 2019, 2019, 13. [Google Scholar] [CrossRef] [PubMed]
- Roshan, S.E.; Asadi, S. Improvement of Bagging performance for classification of imbalanced datasets using evolutionary multi-objective optimization. Eng. Appl. Artif. Intell. 2020, 87, 103319. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Zafari, A.; Zurita-Milla, R.; Izquierdo-Verdiguier, E. Land Cover Classification Using Extremely Randomized Trees: A Kernel Perspective. IEEE Geosci. Remote Sens. Lett. 2019, 1–5. [Google Scholar] [CrossRef]
- Sharma, J.; Giri, C.; Granmo, O.C.; Goodwin, M. Multi-layer intrusion detection system with ExtraTrees feature selection, extreme learning machine ensemble, and softmax aggregation. EURASIP J. Info. Secur. 2019, 2019, 15. [Google Scholar] [CrossRef]
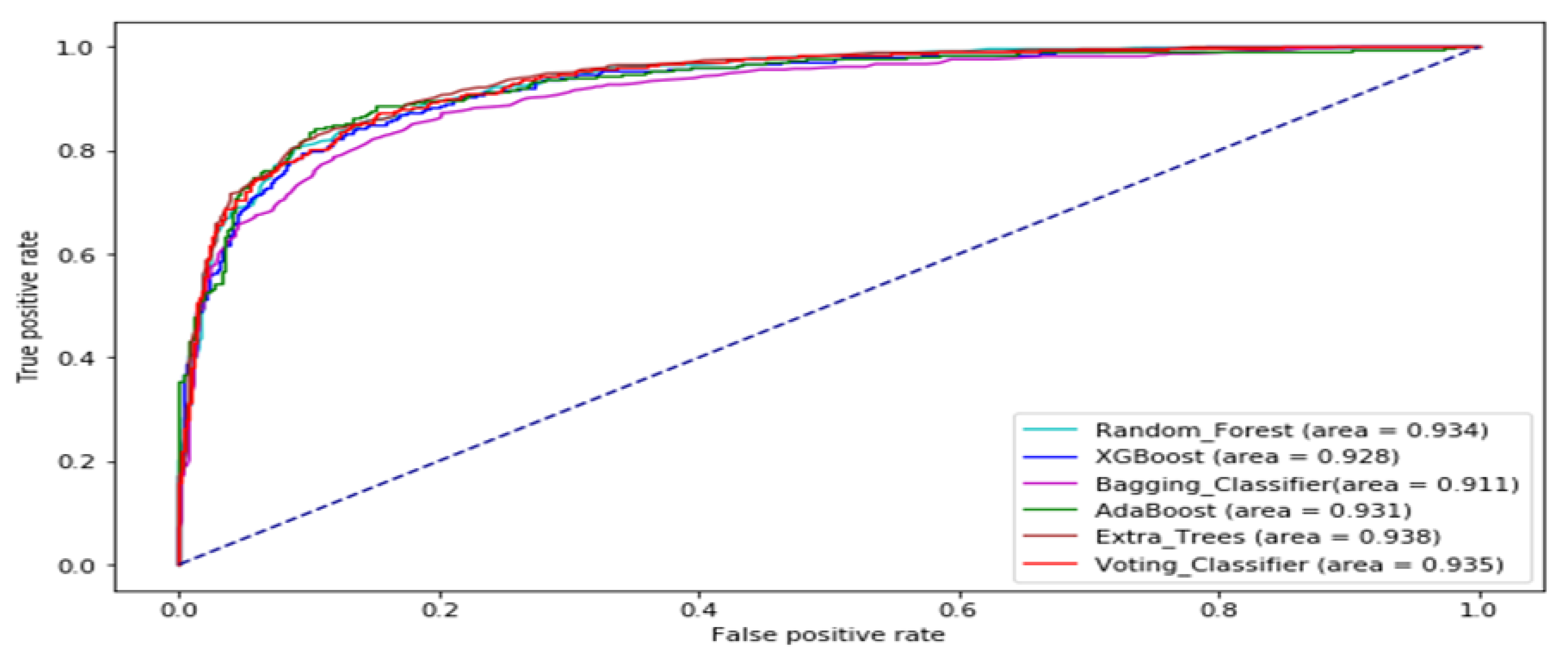
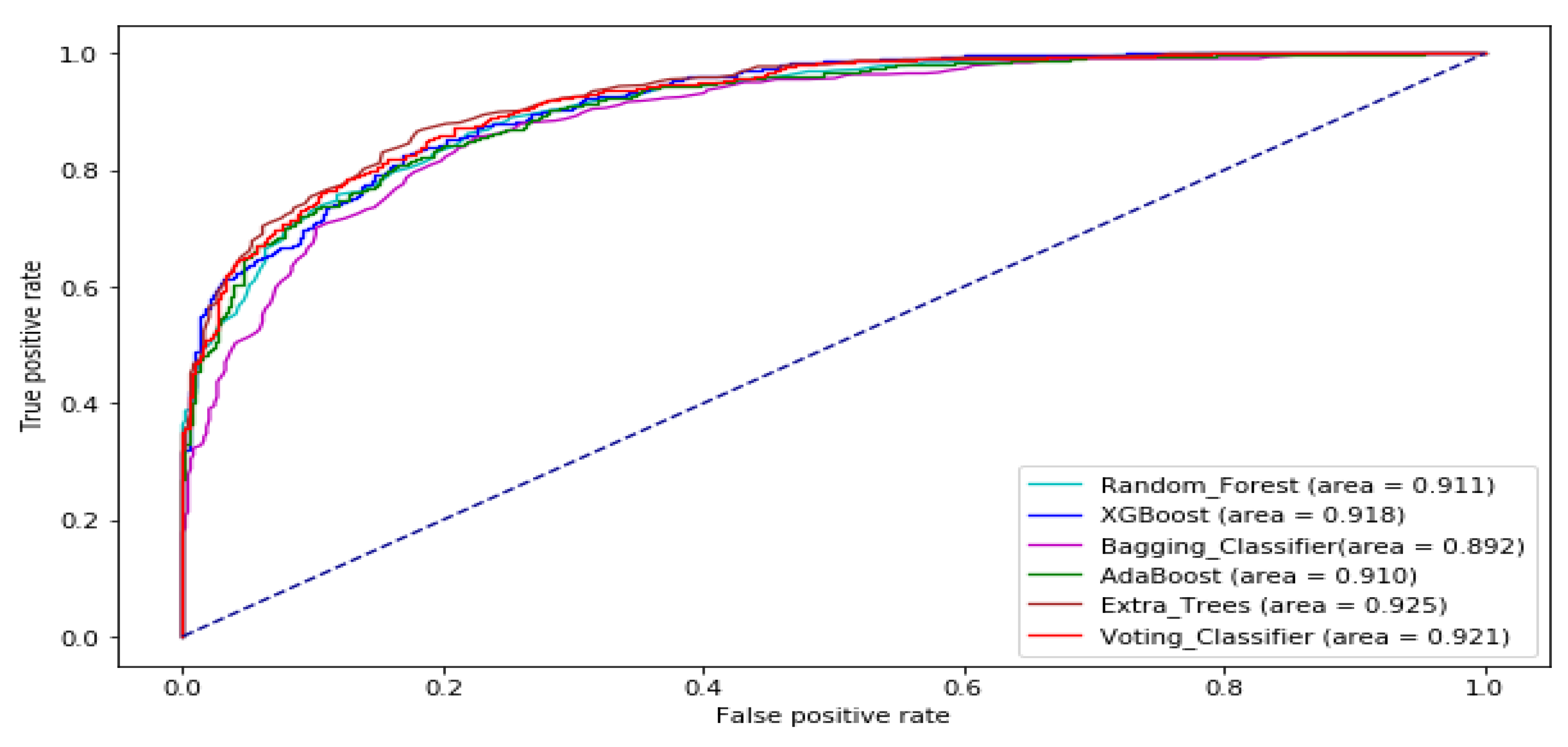
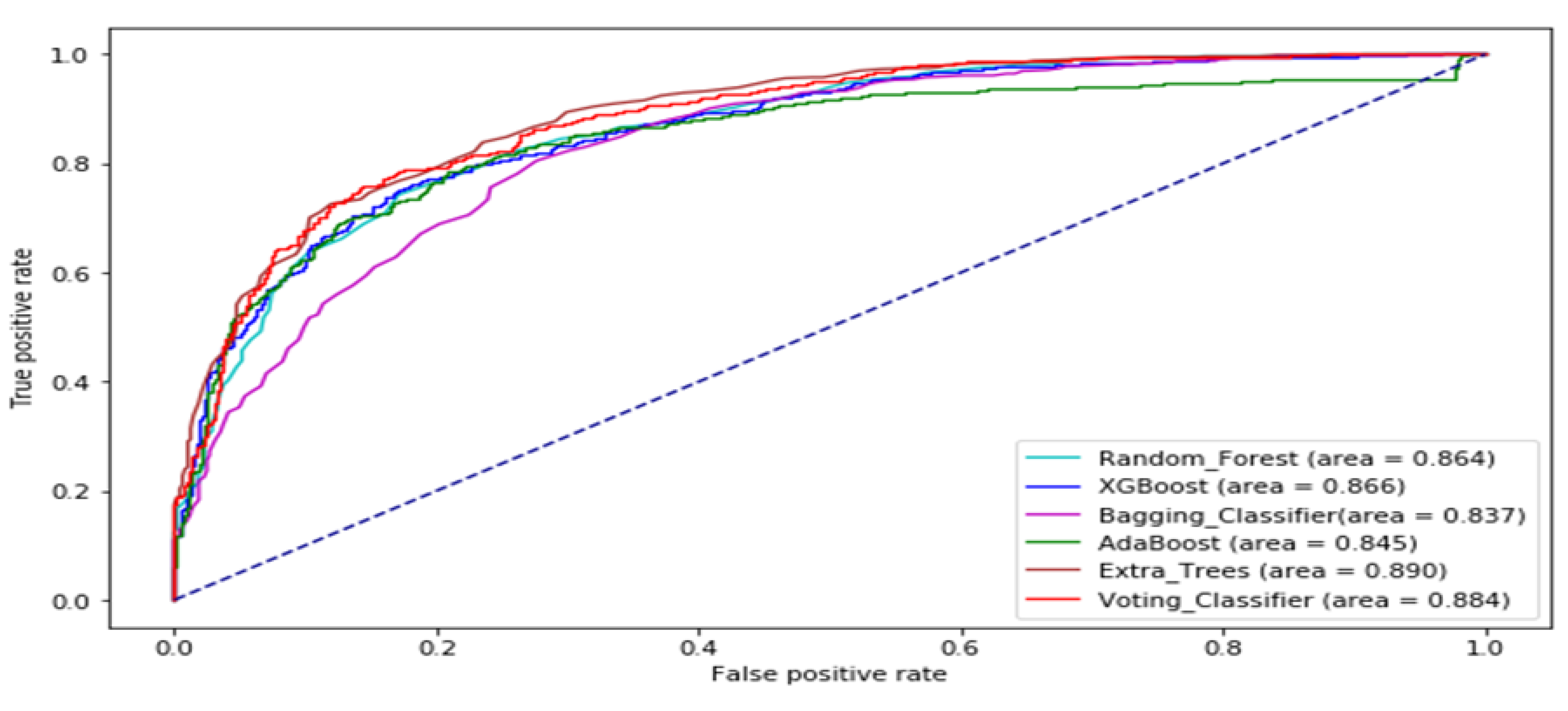
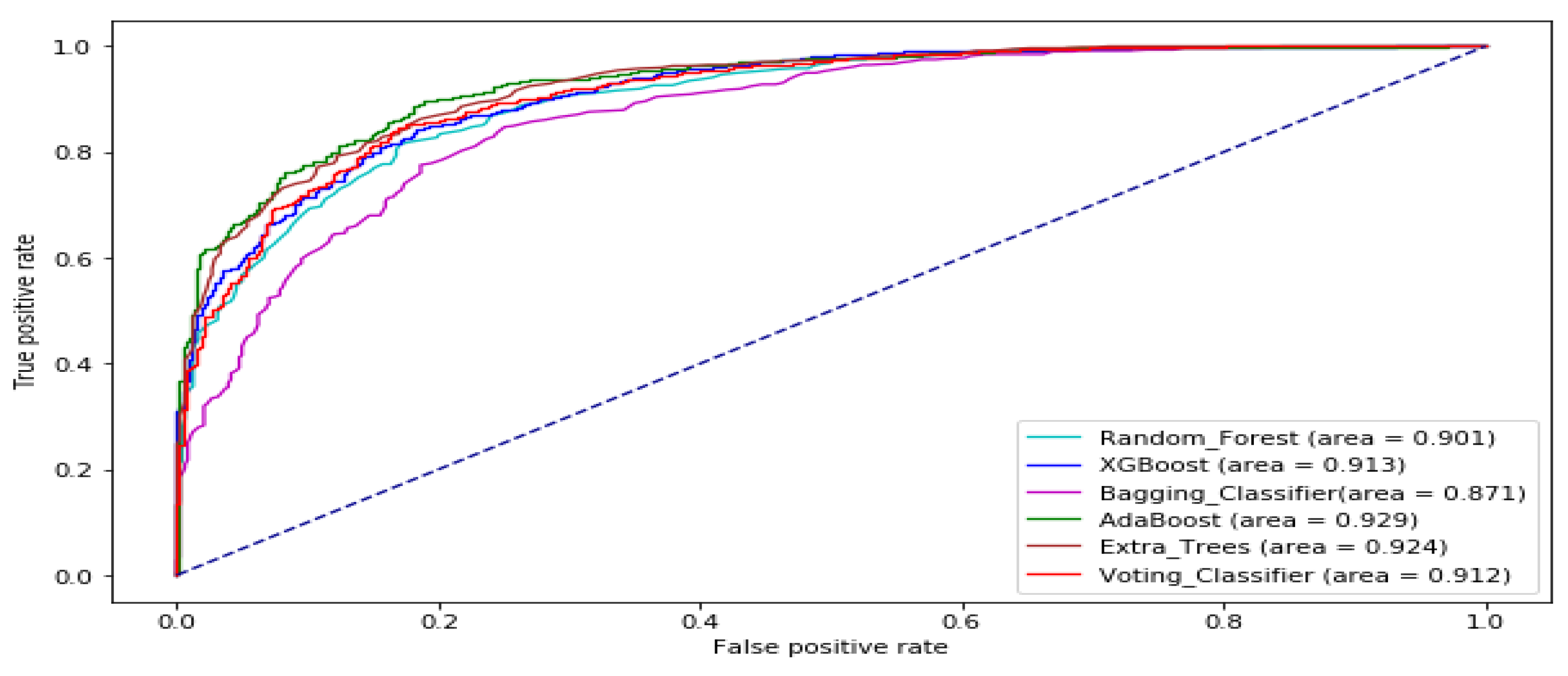
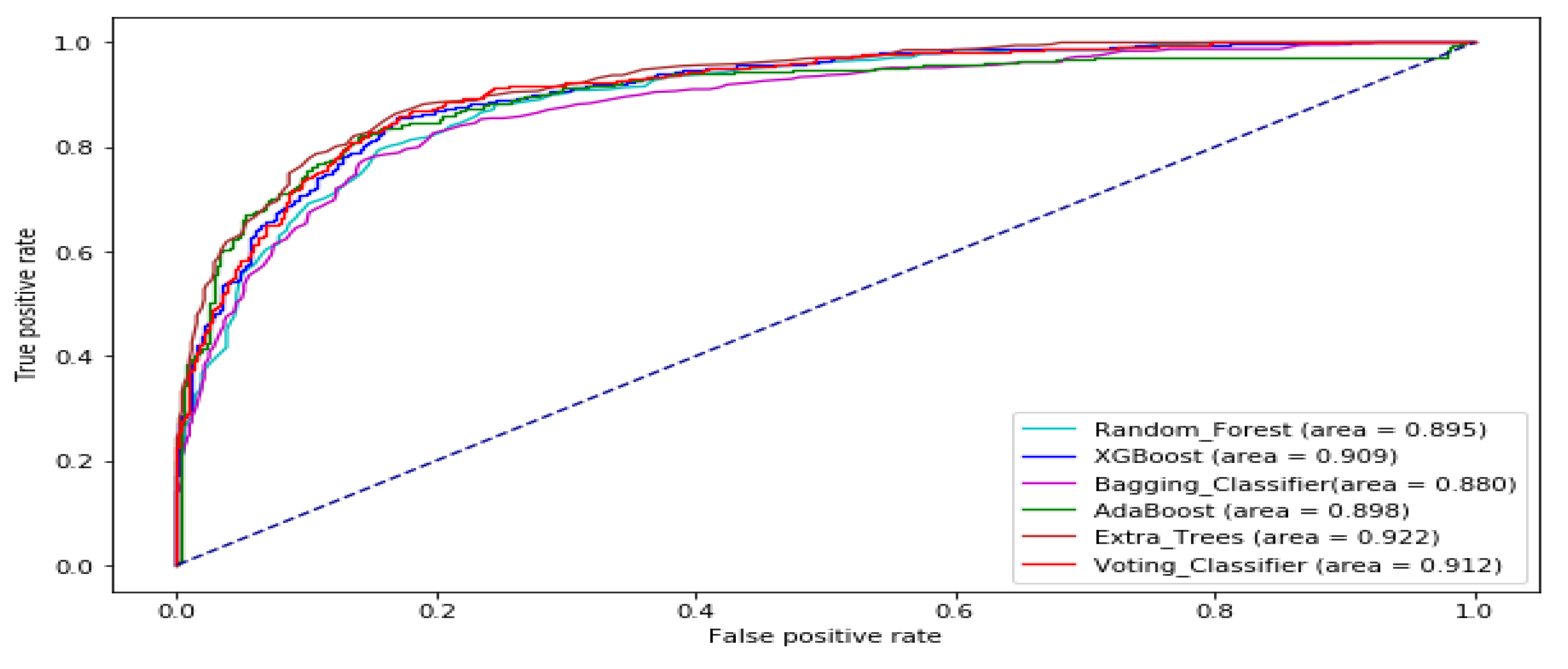
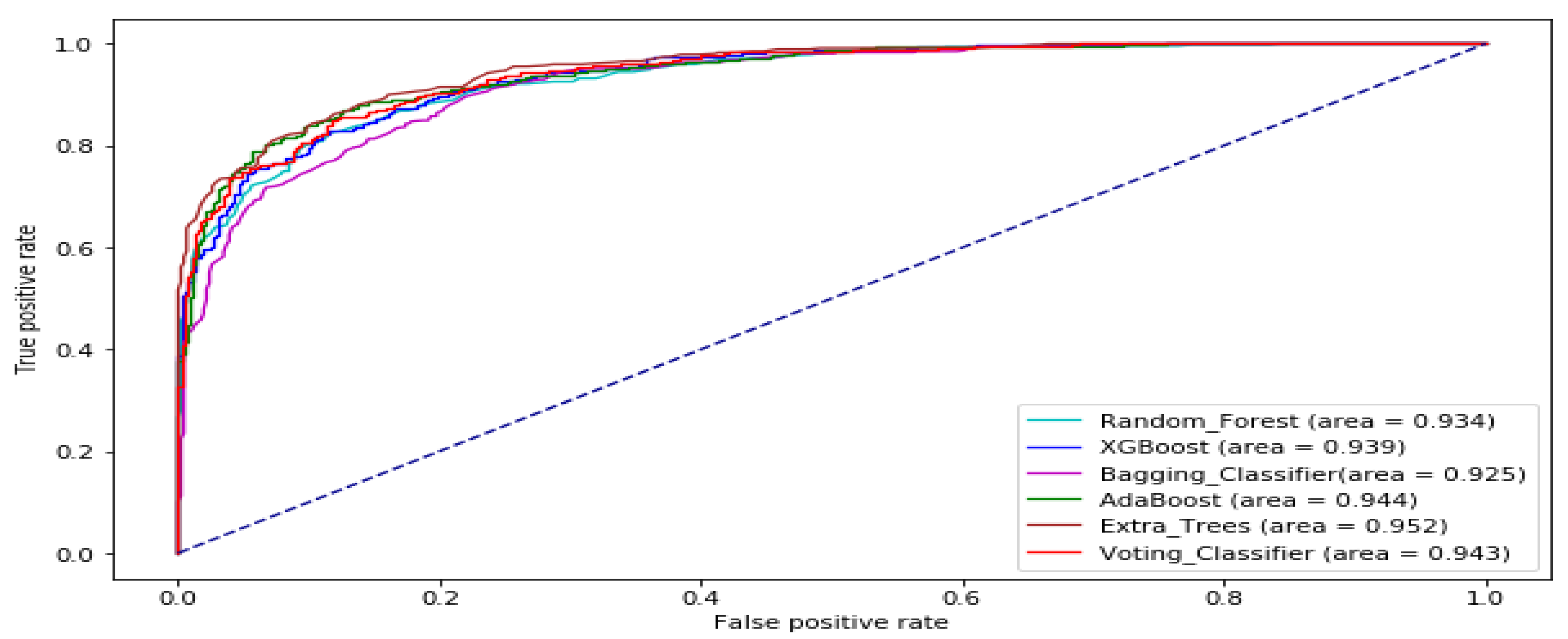
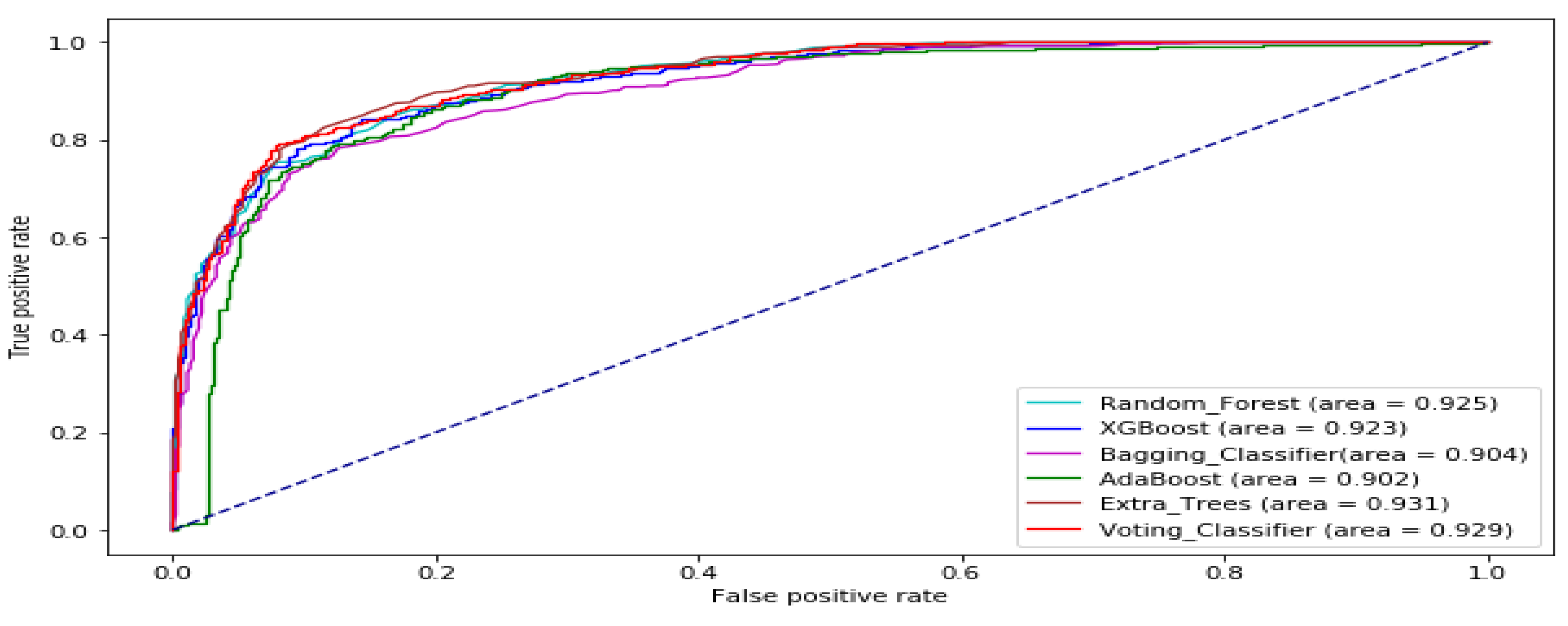
| Data Set | Stock Market | Time Frame | Number of Sample |
|---|---|---|---|
| BAC | NYSE | 2005-01-01 to 2019-12-30 | 3774 |
| DOWJONES | INDEXDJX | 2005-01-01 to 2019-12-30 | 3774 |
| TATASTEEL | NSE | 2005-01-01 to 2019-12-30 | 3279 |
| HCLTECH | NSE | 2005-01-01 to 2019-12-30 | 3477 |
| KMX | NYSE | 2005-01-01 to 2019-12-30 | 3774 |
| MSFT | NASDAQ | 2005-01-01 to 2019-12-30 | 3774 |
| S&P_500 | INDEXSP | 2005-01-01 to 2019-12-30 | 3774 |
| XOM | NYSE | 2005-01-01 to 2019-12-30 | 3774 |
| Data Sets | RF | Ada | XG | BC | ET | VC |
|---|---|---|---|---|---|---|
| BAC | 0.8345 | 0.8452 | 0.8392 | 0.8277 | 0.8329 | 0.8444 |
| XOM | 0.8181 | 0.8157 | 0.8249 | 0.8034 | 0.8170 | 0.8269 |
| S&P 500 | 0.8766 | 0.9004 | 0.8909 | 0.8607 | 0.8972 | 0.8960 |
| MSFT | 0.8388 | 0.8476 | 0.8478 | 0.8234 | 0.8531 | 0.8503 |
| DJIA | 0.8884 | 0.9127 | 0.8991 | 0.8781 | 0.9027 | 0.9019 |
| KMX | 0.8483 | 0.8626 | 0.8480 | 0.8273 | 0.8551 | 0.8519 |
| TATASTEEL | 0.8679 | 0.8720 | 0.8679 | 0.8472 | 0.8716 | 0.8674 |
| HCLTECH | 0.8131 | 0.8282 | 0.8122 | 0.8092 | 0.8087 | 0.8191 |
| Mean | 0.8482 | 0.8606 | 0.8538 | 0.8346 | 0.8547 | 0.8572 |
| Data Sets | RF | Ada | XG | BC | ET | VC |
|---|---|---|---|---|---|---|
| BAC | 0.8306 | 0.8435 | 0.8417 | 0.8306 | 0.8463 | 0.8463 |
| XOM | 0.8463 | 0.8639 | 0.8454 | 0.8222 | 0.8574 | 0.8463 |
| S&P 500 | 0.8139 | 0.7926 | 0.8213 | 0.8120 | 0.8287 | 0.8287 |
| MSFT | 0.7565 | 0.7306 | 0.7667 | 0.7620 | 0.7889 | 0.7917 |
| DJIA | 0.8055 | 0.8278 | 0.8120 | 0.7731 | 0.8306 | 0.8148 |
| KMX | 0.8185 | 0.8361 | 0.8407 | 0.8138 | 0.8361 | 0.8426 |
| TATASTEEL | 0.8412 | 0.8702 | 0.8498 | 0.8391 | 0.8594 | 0.8552 |
| HCLTECH | 0.8375 | 0.8335 | 0.8355 | 0.8184 | 0.8527 | 0.8456 |
| Mean | 0.8188 | 0.8248 | 0.8266 | 0.8089 | 0.8375 | 0.8344 |
| Data Sets | RF | Ada | XG | BC | ET | VC |
|---|---|---|---|---|---|---|
| BAC | 0.8392 | 0.8372 | 0.8378 | 0.8469 | 0.8429 | 0.8491 |
| XOM | 0.9085 | 0.8959 | 0.8822 | 0.8841 | 0.9057 | 0.8934 |
| S&P 500 | 0.8421 | 0.9277 | 0.8592 | 0.8311 | 0.8664 | 0.8612 |
| MSFT | 0.8640 | 0.9021 | 0.8626 | 0.7855 | 0.8929 | 0.8822 |
| DJIA | 0.8630 | 0.9185 | 0.8803 | 0.8398 | 0.8891 | 0.8767 |
| KMX | 0.8457 | 0.8448 | 0.8389 | 0.8469 | 0.8687 | 0.8442 |
| TATASTEEL | 0.8033 | 0.8695 | 0.8242 | 0.8073 | 0.8298 | 0.8297 |
| HCLTECH | 0.8629 | 0.8470 | 0.8438 | 0.8577 | 0.8796 | 0.8623 |
| Mean | 0.8536 | 0.8803 | 0.8536 | 0.8374 | 0.8719 | 0.8624 |
| Data Set | RF | Ada | XG | BC | ET | VC |
|---|---|---|---|---|---|---|
| BAC | 0.8255 | 0.8600 | 0.8545 | 0.8145 | 0.8582 | 0.8491 |
| XOM | 0.7764 | 0.8291 | 0.8036 | 0.7491 | 0.8036 | 0.7927 |
| S&P 500 | 0.8122 | 0.6734 | 0.8054 | 0.8240 | 0.8122 | 0.8190 |
| MSFT | 0.6622 | 0.5731 | 0.6857 | 0.7815 | 0.7008 | 0.7176 |
| DJIA | 0.7705 | 0.7554 | 0.7638 | 0.7286 | 0.7923 | 0.7739 |
| KMX | 0.7943 | 0.8372 | 0.8569 | 0.7818 | 0.8050 | 0.8533 |
| TATASTEEL | 0.9089 | 0.8750 | 0.8940 | 0.8962 | 0.9089 | 0.8983 |
| HCLTECH | 0.8324 | 0.8454 | 0.8547 | 0.7970 | 0.8436 | 0.8510 |
| Mean | 0.7978 | 0.7811 | 0.81488 | 0.7966 | 0.8156 | 0.8194 |
| Data Set | RF | Ada | XG | BC | ET | VC |
|---|---|---|---|---|---|---|
| BAC | 0.8323 | 0.8484 | 0.8461 | 0.8304 | 0.8505 | 0.8491 |
| XOM | 0.8373 | 0.8612 | 0.8411 | 0.8110 | 0.8516 | 0.8401 |
| S&P 500 | 0.8269 | 0.7804 | 0.8314 | 0.8275 | 0.8384 | 0.8395 |
| MSFT | 0.7498 | 0.7009 | 0.7640 | 0.7834 | 0.7853 | 0.7915 |
| DJIA | 0.8142 | 0.8290 | 0.8179 | 0.7803 | 0.8379 | 0.8221 |
| KMX | 0.8192 | 0.8410 | 0.8478 | 0.8130 | 0.8357 | 0.8488 |
| TATASTEEL | 0.8529 | 0.8722 | 0.8577 | 0.8494 | 0.8675 | 0.8627 |
| HCLTECH | 0.8474 | 0.8462 | 0.8492 | 0.8263 | 0.8612 | 0.8566 |
| Mean | 0.8225 | 0.8224 | 0.8319 | 0.8152 | 0.8410 | 0.8388 |
| Data Set | RF | Ada | XG | BC | ET | VC |
|---|---|---|---|---|---|---|
| AC | 0.8358 | 0.8264 | 0.8283 | 0.8472 | 0.8340 | 0.8440 |
| XOM | 0.9189 | 0.9000 | 0.8887 | 0.8981 | 0.9132 | 0.9019 |
| S&P 500 | 0.8160 | 0.9366 | 0.8405 | 0.7975 | 0.8487 | 0.8405 |
| MSFT | 0.8722 | 0.9237 | 0.8660 | 0.7381 | 0.8969 | 0.8825 |
| DJIA | 0.8489 | 0.9172 | 0.8716 | 0.8282 | 0.8778 | 0.8654 |
| KMX | 0.8445 | 0.8349 | 0.8234 | 0.8484 | 0.8695 | 0.8311 |
| TATASTEEL | 0.7717 | 0.8652 | 0.8043 | 0.7804 | 0.8087 | 0.8109 |
| HCLTECH | 0.8436 | 0.8194 | 0.8128 | 0.8436 | 0.8634 | 0.8392 |
| Mean | 0.8440 | 0.8779 | 0.8420 | 0.8227 | 0.8640 | 0.8519 |
| DataSet | RF | Ada | XG | BC | ET | VC |
|---|---|---|---|---|---|---|
| BAC | 0.9143 | 0.9230 | 0.9241 | 0.9081 | 0.9280 | 0.9231 |
| XOM | 0.9340 | 0.9314 | 0.9283 | 0.9112 | 0.9378 | 0.9351 |
| S&P 500 | 0.9109 | 0.9099 | 0.9176 | 0.8921 | 0.9250 | 0.9207 |
| MSFT | 0.8638 | 0.8451 | 0.8656 | 0.8366 | 0.8898 | 0.8838 |
| DJIA | 0.9014 | 0.9294 | 0.9133 | 0.8706 | 0.9243 | 0.9123 |
| KMX | 0.8950 | 0.8979 | 0.9087 | 0.8802 | 0.9219 | 0.9116 |
| TATASTEEL | 0.9335 | 0.9436 | 0.9392 | 0.9245 | 0.9515 | 0.9428 |
| HCLTECH | 0.9254 | 0.9023 | 0.9232 | 0.9042 | 0.9306 | 0.9293 |
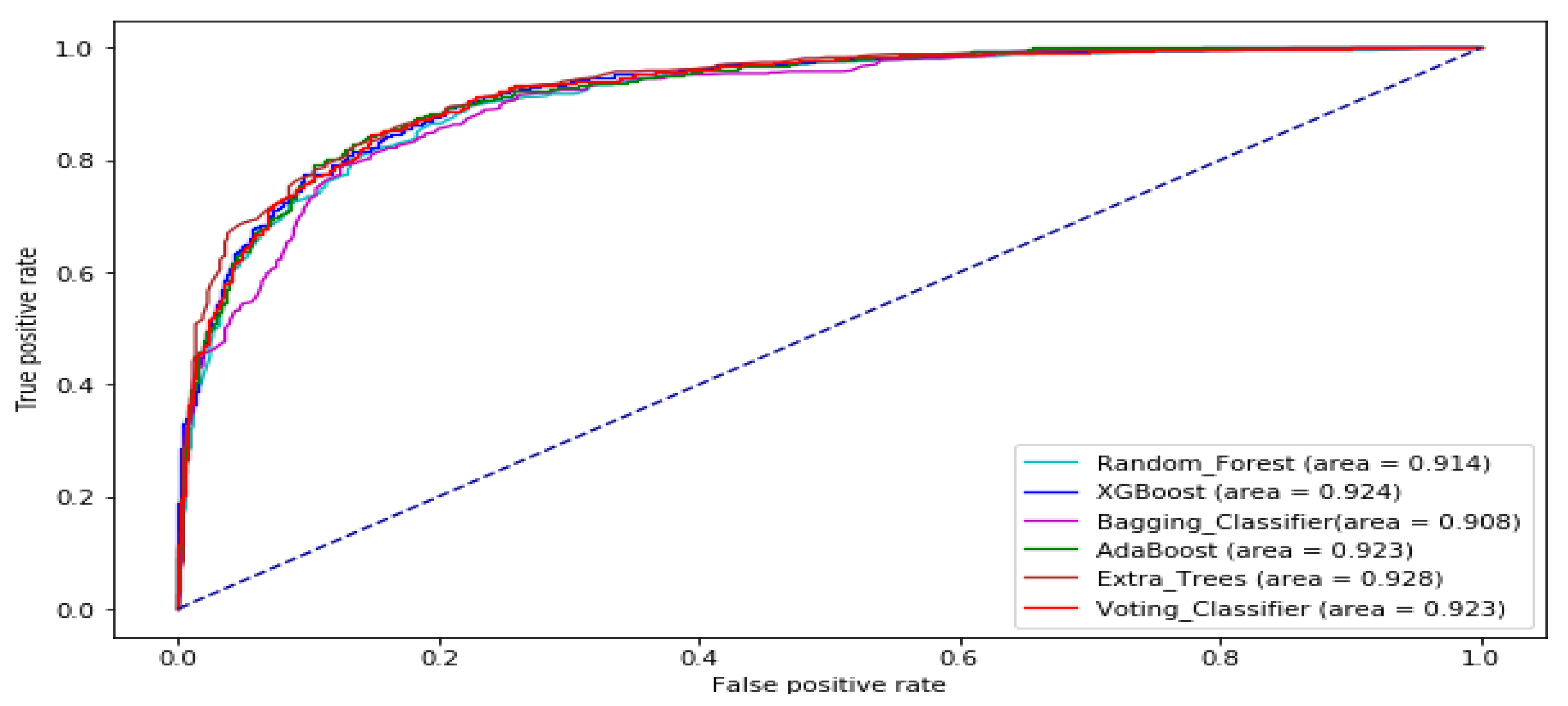
| Mean | 0.9098 | 0.9103 | 0.9150 | 0.8909 | 0.9261 | 0.9198 |
| Measure | W | p | Ranks | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.5496 | 21.9821 | 0.0005 | Technique | RF | Ada | XG | BC | ET | VC |
| Mean Rank | 2.9375 | 5.1250 | 3.4375 | 1.125 | 4.0000 | 4.3750 |
| Measure | W | p | Ranks | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Accuracy | 0.5821 | 23.2857 | 0.0003 | Technique | RF | Ada | XG | BC | ET | VC |
| Mean Rank | 2.5000 | 3.5625 | 3.3750 | 1.4375 | 5.1875 | 4.9375 |
| Measure | W | p | Ranks | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Precision | 0.3554 | 14.2143 | 0.0143 | Technique | RF | Ada | XG | BC | ET | VC |
| Mean Rank | 3.2500 | 4.2500 | 2.1250 | 2.5000 | 5.1250 | 3.7500 |
| Measure | W | p | Ranks | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Recall | 0.1746 | 6.9821 | 0.2220 | Technique | RF | Ada | XG | BC | ET | VC |
| Mean Rank | 2.8750 | 3.1250 | 3.8125 | 2.5000 | 4.3125 | 4.3750 |
| Measure | W | p | Ranks | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
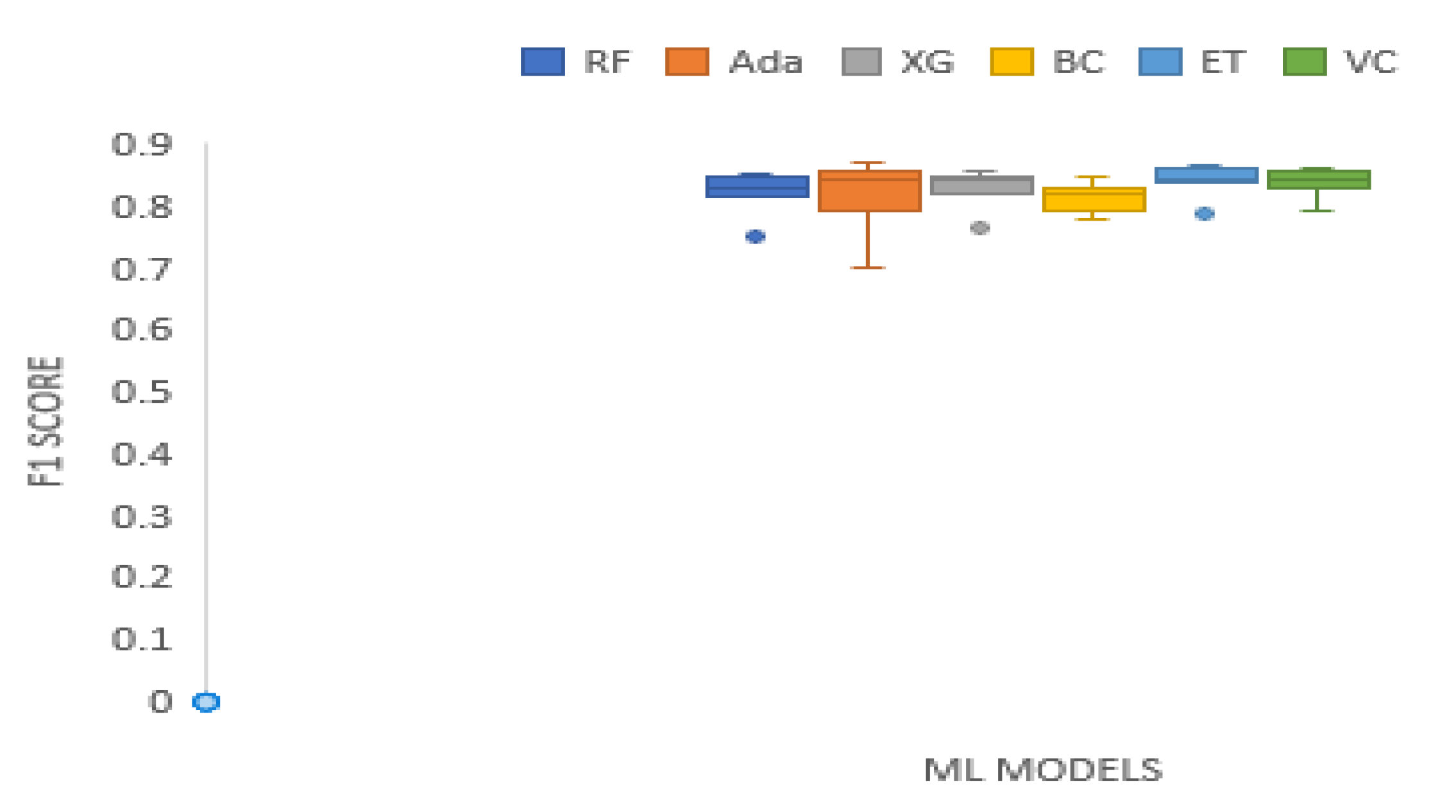
| F1 Score | 0.5696 | 22.7857 | 0.0004 | Technique | RF | Ada | XG | BC | ET | VC |
| Mean Rank | 2.1250 | 3.6250 | 3.6250 | 1.6250 | 5.1250 | 4.8750 |
| Measure | W | p | Ranks | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
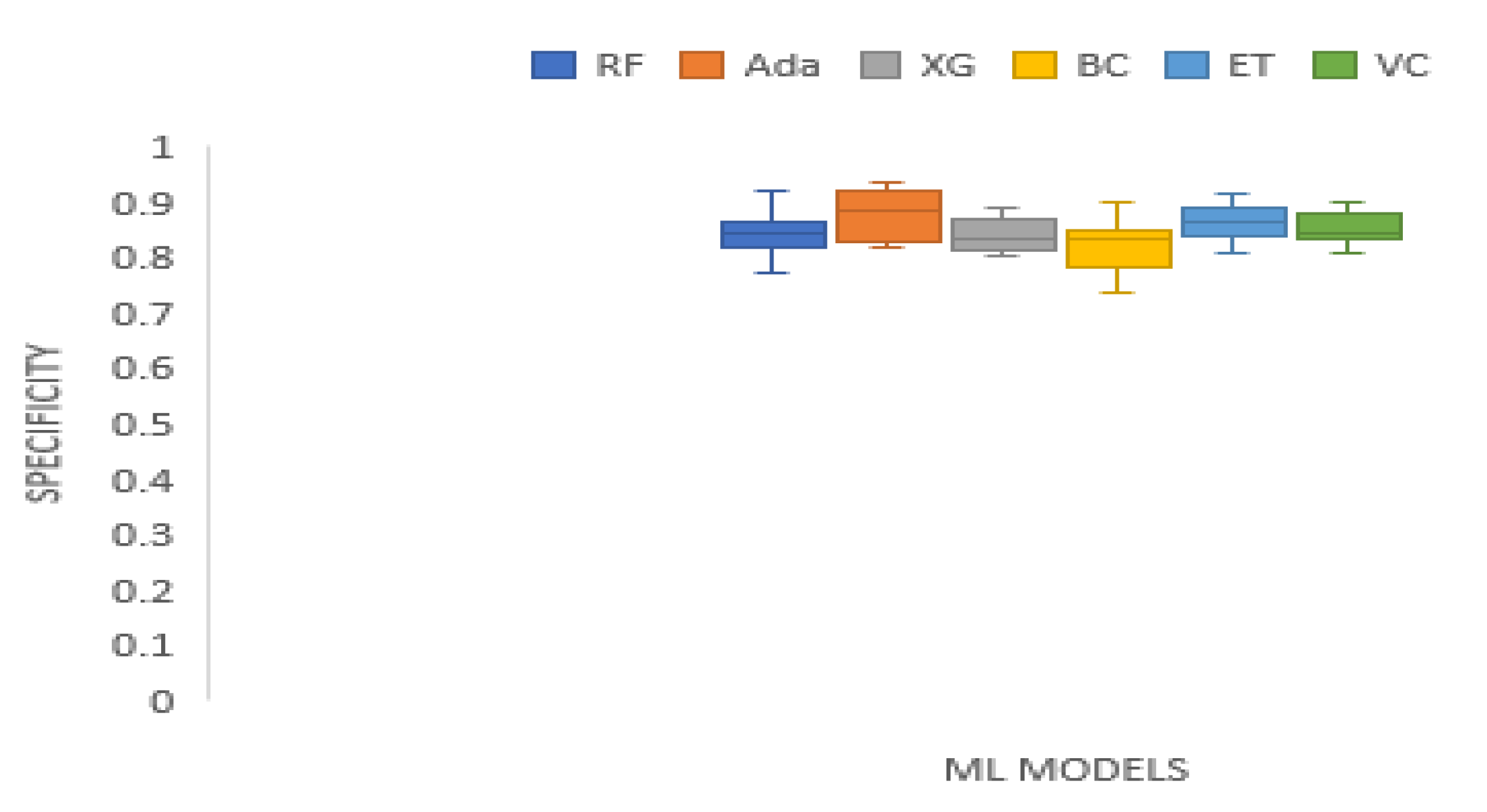
| Specificity | 0.2598 | 10.3929 | 0.0648 | Technique | RF | Ada | XG | BC | ET | VC |
| Mean Rank | 3.3125 | 4.1250 | 2.1875 | 2.8125 | 4.8750 | 3.6875 |
| Measure | W | p | Ranks | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
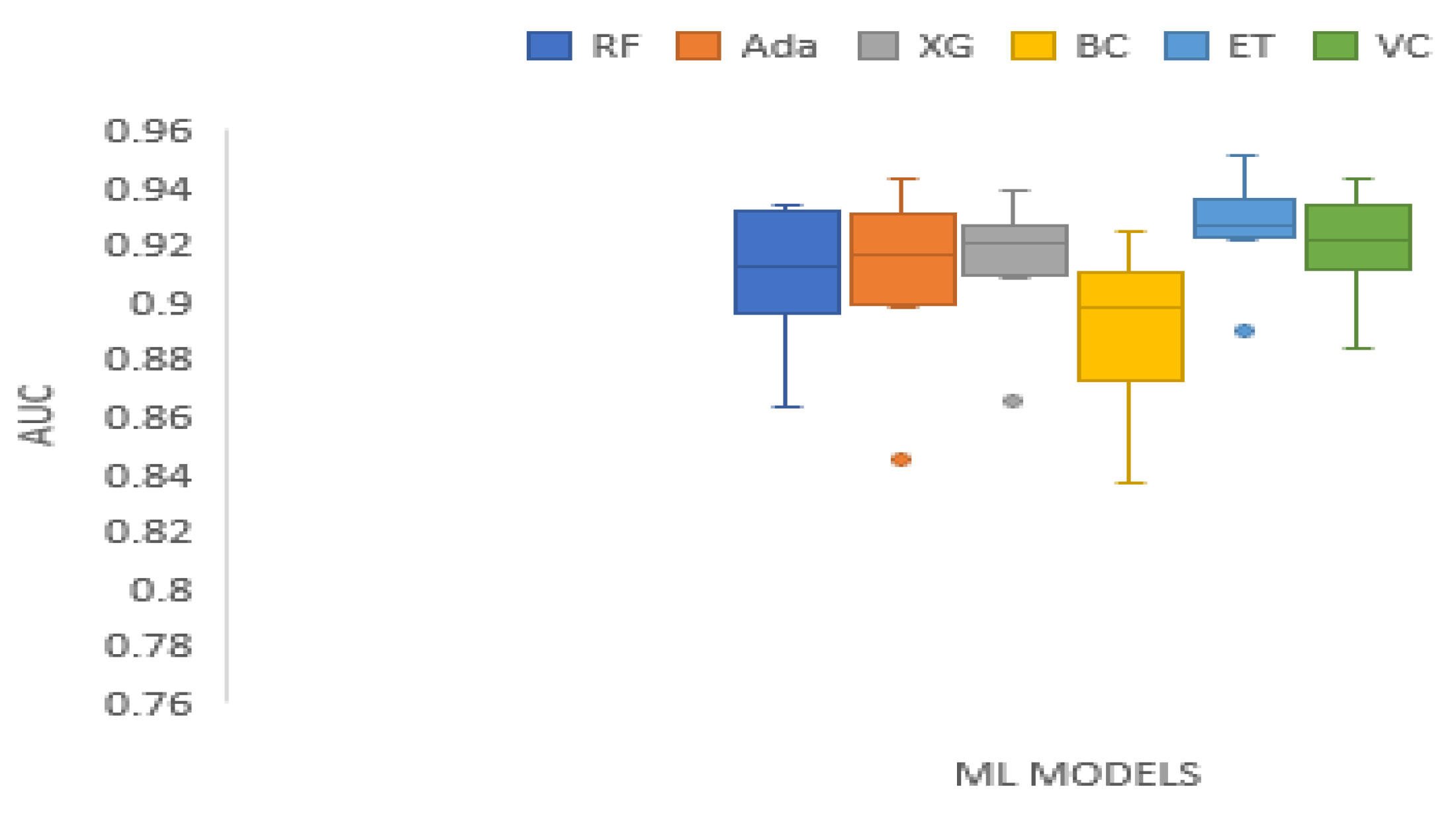
| AUC | 0.7429 | 29.7143 | 0.0000 | Technique | RF | Ada | XG | BC | ET | VC |
| Mean Rank | 2.7500 | 3.1250 | 3.6250 | 1.1250 | 5.8750 | 4.5000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ampomah, E.K.; Qin, Z.; Nyame, G. Evaluation of Tree-Based Ensemble Machine Learning Models in Predicting Stock Price Direction of Movement. Information 2020, 11, 332. https://doi.org/10.3390/info11060332
Ampomah EK, Qin Z, Nyame G. Evaluation of Tree-Based Ensemble Machine Learning Models in Predicting Stock Price Direction of Movement. Information. 2020; 11(6):332. https://doi.org/10.3390/info11060332
Chicago/Turabian StyleAmpomah, Ernest Kwame, Zhiguang Qin, and Gabriel Nyame. 2020. "Evaluation of Tree-Based Ensemble Machine Learning Models in Predicting Stock Price Direction of Movement" Information 11, no. 6: 332. https://doi.org/10.3390/info11060332
APA StyleAmpomah, E. K., Qin, Z., & Nyame, G. (2020). Evaluation of Tree-Based Ensemble Machine Learning Models in Predicting Stock Price Direction of Movement. Information, 11(6), 332. https://doi.org/10.3390/info11060332





