Signal Timing Optimization Model Based on Bus Priority

Abstract

This paper focuses on the optimization problem of a signal timing design based on the concept of bus priority. This optimization problem is formulated in the form of a bi-level programming model that minimizes average passenger delay at intersections and vehicle delay in lanes simultaneously. A solution framework that implements the differential evolution (DE) algorithm is developed to efficiently solve the model. A case study based on a real-world intersection in Beijing, China, is implemented to test the efficiency and applicability of the proposed modeling and computing methods. The experiment’s result shows that the optimization model can not only significantly improve the priority capacity of the buses at the intersection but also reduce the adverse impact of bus-priority approaches on the private vehicles for the intersections.

1. Introduction

Traffic congestion is already one of the greatest issues in many cities [1,2] of China, where it is no longer feasible to continue to increase capacity in the form of new roads or lanes to accommodate the ever-rising travel demand due to the limited land resources. With a higher capacity for moving people than private cars, public transit vehicles have been widely recognized as a more efficient way for trips in megalopolis. However, the uncertainty of the travel time of buses that may be caused by the uncertainty of dwell time for passenger loading and unloading, the delay of traffic signal control at an intersection, and the delay of traffic congestion along the bus routes will affect the service level of public transit systems [3]. Hence, implementing the strategy of “bus priority” would be an effective solution to relieve traffic congestion and improve mobility, in which reducing the bus delay at intersection is a very important factor.

In some traditional signal timing methods, the length of the cycle is determined to minimize the total delay of vehicles, and the green split is decided according to the ratio of traffic volumes in different phases, during which buses and private vehicles are regarded as the same. However, considering the capacity of bus is much larger than that of private vehicle, the traditional method is rather unfair for the phase that contains more bus traffic and cannot reflect a people-oriented traffic management philosophy [4,5,6]. Moreover, it cannot reduce the delay of public transport vehicles at intersections and ensure the implementation of a “bus priority” strategy by using these traditional timing schemes. Therefore, the signal timing design problem based on bus priority has become a research hotspot in the field of urban traffic management.

In order to ensure bus priority, a bus lane is usually set on the approaches of intersections to make sure that the running of buses is not affected by private vehicles. Due to the difference of the operation characteristics between public transport vehicles and private vehicles, the saturation of bus lanes and common lanes will be different, which may lead to an unequal saturation of each phase at the intersection. Thus, the signal timing of such intersections is different from that of ordinary intersections, in which the running characteristics of traffic flows in two types of lanes should be considered at the same time. Therefore, the purpose of this paper is to present a new mathematical framework for the signal timing optimization model of intersections equipped with bus lanes in terms of bus priority.

2. Literature Review

Many studies have been conducted on the signal control optimization of single intersections. Since delay of vehicles is a comprehensive indicator that involves many factors, many studies are based on it. Furth et al. [7] divided intersection delay into three scenarios, such as no priority, absolute priority, and conditional priority situations. The result showed that absolute priority increased delays significantly compared with no priority. Zhang et al. [5] established a signal planning model with average people delay as the target, and green time was decided by the passenger quantity and the saturation of phases. Richardson [8] used perceived, budgeted delay to evaluate the justification of bus priority signal intersections. By analyzing the evaluation index of the bus priority scheme at an intersection, Zheng [9] proposed matter element analysis to select the bus priority schemes which contribute to selecting and evaluating the bus priority signal scheme. In addition, many researchers have developed new procedures to study delay at independent intersections. Wu [10] researched the implementation of bus priority signals and proposed two pre-signal bus priority ways without detectors: only social vehicles were controlled by pre-signals, while buses had priority; both social vehicles and buses were controlled by pre-signals. They also gave the signal timing and compared the delay for the two schemes.

As the direct beneficiary of a bus priority strategy, the status of the bus traffic can directly reflect the effectiveness of the signal control method. In many previous studies, therefore, the bus traffic-related parameters are given more consideration when modelling the signal control problem. Mirchandani et al. [11] analyzed the schedule status of buses, the passenger counts in buses, and real-time optimization of the phasing that considers all the vehicles in the network. Based on these parameters, they proposed a bus priority model and changed signals to integrate traffic signal control and bus priority. Jacobson et al. [12] put forward a model of delays at signalized intersections under a bus preemption scheme. Experiments have shown that proper signal cycle and bus operation speed benefit bus preemption. Dion [13] developed an optimization algorithm that minimizes the number of parking times and the distribution of delays, considering the impacts of transit vehicles.

In addition to adjusting the departure time and frequency of buses, the influence of the bus priority strategy on other participants in the traffic system may also determine the application results. Sun et al. [14] presented a bus priority signal control algorithm based on frequency and demand intensity, considering the impact of bus priority on social vehicles. Based on transit priority control theory, Yang et al. [15] developed methods for transit priority signals at signalized intersections and proposed the optimal system. The linear programming model and examples were used to demonstrate the way to design transit priority signals in a fixed cycle. Zhou and Gan [16] proposed a queue jumper lane at intersections to increase transit bus priority. It is worth mentioning that this study used the VISSIM microscopic model to simulate and evaluate effects such as bus delay and general vehicle operations. These studies promote the implementation of a bus priority strategy and improve the traffic efficiency of single point signalized intersections.

As urban infrastructure construction progresses, the distances between intersections become shorter and shorter. Signal control optimization of a single intersection cannot satisfy the demand of urban traffic management. The signal control of different intersections should be considered in a more comprehensive way, and hence, the coordinated signal control is developed. Liu [17] proposed a two-layer bus priority control model under a coordination in which the upper layer was the overall coordinated control and the lower layer was the intersection control. Aiming at the comprehensive benefits of social traffic and buses, Wang [18] established a two-layer optimization model, in which the upper layer was progression control and the lower layer was bus priority control. The model was applied to evaluate the effect of arterial signal progression and bus delay. Liu et al. [6] analyzed vehicle queuing at intersections, signal timing, and bus operation conditions to build a hardware system and specific methods to the transit signal priority. Guan et al. [19] explored bus priority within a traffic signal control strategy and developed the control strategy of bus departure intervals and traffic flow on the road which was set as a bus detector. The optimal strategy was to minimize the total delay time of the passengers.

In view of the effectiveness of coordinated signal control, the network-based signal control is also proposed. However, since too many factors are involved in the area of signal control, most related studies are limited to theoretical analysis, with few practical applications conducted. Zhang et al. [20] suggested the whole traffic system to evaluate the implementation effect of the bus priority measure. The evaluation index covered the four aspects of social economy, traffic function, environmental influence, and resource utilization, and these four aspects are given through calculation. Salter et al. [21] put forward a computer simulation model to calculate the average delay, queue lengths, passenger delay, and bus travel time to evaluate the effects of bus-priority schemes. Chang et al. [22] applied the INTEGRATION simulation package to the Columbia Pike Corridor in Arlington, Virginia, and evaluated the influence of bus signal priority strategy on bus service reliability. Khasnabis et al. [23] presented the NETSIM simulation model to evaluate the bus priority strategies in intersections.

However, most of these studies focused on the benefits of vehicles, meaning that the traditional way of optimizing signal timing is to take the maximum benefits of all vehicles, including buses and private vehicles, as the optimization goal. That would be rather unreasonable since the capacity of a bus is typically 15 to 20 times the capacity of a private vehicle and the delay of buses would have a much higher effect than the delay of private cars. In these studies, the concept of a people-oriented priority strategy was not fully considered in the signal timing process.

Based on that, this paper attempts to propose a bi-level optimization model, in which passenger delay is explicitly considered in the process of signal timing optimization, aiming to improve the priority capacity of the buses at the intersection and reduce the loss of other private vehicle traffic benefits caused by the bus priority measures. Then the numerical calculation and simulation based on a real case are conducted to demonstrate the performance and applicability of the proposed model.

The signal timing optimization method needs to be implemented through a signal control systems. Many signal control systems have been developed to cover different application scenarios. Such systems can be classified into three main types, signal control, coordination control, and area control system, according to the object of application. The control mechanism of such systems also varies, including fixed-time control, actuated control, and adaptive control [24]. The microprocessor optimized vehicle actuation (MOVA) system is an advanced vehicle actuated controller, which is suitable for optimizing single signalized junctions at the microscale. A coordinated signal control system commonly includes the split cycle offset optimization technique (SCOOT), which is a vehicle actuated systems for optimizing multiple linked signalized junctions at the city scale or within certain zones of a city, and the Sydney coordinated adaptive traffic system (SCATS), which works on a combination of coordinated vehicle actuation and fixed time plans [25]. In area signal control systems, the traffic network study tool (TRANSYT) and the signal optimization program (SIGOP) are two common fixed time control design systems, which calculate the timings offline using historical, measured traffic data. The signal timing optimization method proposed in this paper, which can optimize the signal time cycle based on vehicle flow approaching a single junction, works significantly better for high traffic flow and is focused on increasing junction capacity. Therefore, the optimization process and characteristic of the proposed method similar to MOVA systems and can be utilized in isolated junctions or independently in several junctions in a city.

The remainder of this paper is organized as follows: Section 3 presents the basic framework of this specific signal timing design problem by giving the representation of the objective functions, in which the related parameters and constraints are elaborated. The bi-level optimization model of signal timing is proposed in Section 4. In Section 5, a solution framework based on the differential evolution (DE) algorithm is proposed. A case study based on a real-world intersection of Beijing is carried out in Section 6 to demonstrate the performance and applicability of the proposed model, in in which the results of two signal timing plans are compared by using the VISSIM simulation. Finally, in Section 7, a summary concludes this paper.

3. The Basic Outline of Optimization Signal Timing

3.1. Assumptions and Notations

In this study, the following assumptions are made:

• Only two modes of traffic (bus and private car) are contained in the network and mixed traffic influence is not considered.
• The travel demand is known and remains fixed during the analysis period.
• The traffic signal control details and the intersection configuration are known.

To facilitate the presentation and analysis of the signal timing optimization model, all definitions and notations used throughout this work are described in

Table 1. Notation Definitions.

Symbol	Definition
$C$	cycle length
$C_{\min }$	minimum cycle time
$C_{\max }$	maximum cycle time
$L$	total loss time of phases $i$
$n$	number of phases
$t_i$	green time of Phase $i$
${\lambda }_i$	green time ratio of Phase $i$
$f$	conversion factor
$m^s$	number of private vehicle lanes
$m^b$	number of bus lanes
$q_{ij}^s$	arrival rate of private vehicles in Phase $i$
$q_{ij}^b$	arrival rate of buses in Phase $i$
$s_{ij}^s$	saturate flow rate of private vehicle lane in Phase $i$
$s_{ij}^b$	saturate flow rate of bus lane in Phase $i$
$x_{ij}^s$	saturation of private vehicle lane in Phase $i$
$x_{ij}^b$	saturation of bus lane in Phase $i$
$y_{ij}^s$	flow ratio of private vehicle lane in Phase $i$
$y_{ij}^b$	flow ratio of bus lane in Phase $i$
$p_s$	average passenger capacity of private vehicle in Phase $i$
$p_b$	average passenger capacity of bus in Phase $i$
$y_{i\max }^s$	the biggest flow ratio of private vehicle lane in Phase $i$
$y_{i\max }^b$	the biggest flow ratio of bus lane in Phase $i$
$d_{ij}^s$	average delay of every private vehicle in Phase $i$
$d_{ij}^b$	average delay of every bus in Phase $i$
$D_{ps}$	total passenger delay of private vehicles in one cycle
$D_{pb}$	total passenger delay of buses in one cycle
$D_s$	total vehicle delay in private vehicle lane
$D_b$	total vehicle delay in bus lane
$D$	total passenger delay in one cycle
$D_G$	average running delay of all vehicles
$D_P$	average passenger delay
$b$	width of intersection
$v$	average walk speed to cross the intersection
$k$	compensation coefficient

.

3.2. The Objective Function of Signal Timing Optimization

3.2.1. The Representation of Total Passenger Delay

According to Webster’s computational formula of delay [26], the average delay of every bus at the intersection is:

$$d=\frac{C{(1-\lambda )}^2}{2(1-\lambda x)}+\frac{{(x)}^2}{2q(1-x)}$$

(1)

(1) the total passenger delay of private vehicles in one cycle.

Based on the above, the average delay of every private vehicle in Phase $i$ is:

$$d_{ij}^s=\frac{C{(1-{\lambda }_i)}^2}{2(1-{\lambda }_i{x}_{ij}^s)}+\frac{{(x_{ij}^s)}^2}{2q_{ij}^s(1-x_{ij}^s)}$$

(2)

Therefore, the total passenger delay of private vehicles in one cycle is:

$$D_{ps}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^s}{d}_{ij}^s{q}_{ij}^s{P}_s}}$$

(3)

(2) the total passenger delay of buses in one cycle.

Similarly, the average delay of every bus in Phase $i$ is:

$$d_{ij}^b=\frac{C{(1-{\lambda }_i)}^2}{2(1-{\lambda }_i{x}_{ij}^b)}+\frac{{(x_{ij}^b)}^2}{2q_{ij}^b(1-x_{ij}^b)}$$

(4)

Therefore, the total passenger delay of buses in one cycle is:

$$D_{pb}={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^b}{d}_{ij}^b{q}_{ij}^b{P}_b}}$$

(5)

(3) the total passenger delay.

Thus, the total passenger delay at the intersection in one cycle is:

$$D=D_{ps}+D_{pb}$$

(6)

3.2.2. The representation of total vehicle delay

(1) The total vehicle delay of private vehicle lane; for private vehicle lane:

$$y_{ij}^s=\frac{q_{ij}^s}{s_{ij}^s}$$

(7)

$$x_{ij}^s=\frac{q_{ij}^s}{{\lambda }_i{s}_{ij}^s}=\frac{y_{ij}^s}{{\lambda }_i}$$

(8)

$${\lambda }_i\approx \frac{t_i}{C}$$

(9)

According to Formulas (2), (7), (8), and (9), the total vehicle delay in private vehicle lane is:

$$D_s={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^s}{d}_{ij}^s}}{q}_{ij}^s={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^s}\left\{\left[\frac{C{(1-\frac{t_i}{C})}^2}{2(1-y_{ij}^s)}+\frac{{\left(C\frac{y_{ij}^s}{t_i}\right)}^2}{2q_{ij}^s(1-C\frac{y_{ij}^s}{t_i})}\right]\times q_{ij}^s\right\}}}$$

(10)

(2) The total vehicle delay of bus lane; for bus lane:

$$y_{ij}^b=\frac{q_{ij}^b}{s_{ij}^b}=\frac{q_{ij}^b}{\frac{s_{ij}^s}{f}}=\frac{f{q}_{ij}^b}{s_{ij}^s}$$

(11)

$$x_{ij}^b=\frac{q_{ij}^b}{{\lambda }_i{s}_{ij}^b}=\frac{f{q}_{ij}^b}{{\lambda }_i{s}_{ij}^s}=\frac{y_{ij}^b}{{\lambda }_i}$$

(12)

According to Formulas (4), (11), and (12), the total vehicle delay in a bus lane is:

$$D_b={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^b}{d}_{ij}^b}}{q}_{ij}^b={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^b}\left\{\left[\frac{C{(1-\frac{t_i}{C})}^2}{2(1-y_{ij}^b)}+\frac{{\left(C\frac{y_{ij}^b}{t_i}\right)}^2}{2q_{ij}^b(1-C\frac{y_{ij}^b}{t_i})}\right]\times q_{ij}^b\right\}}}$$

(13)

3.3. The Constraints of Signal Timing Optimization

While determining constraint conditions, the first thing to consider is the constraint of the maximum degree of saturation. Reasonable timing not only satisfies the restriction of the degree of saturation of general lanes but also takes that of bus lanes into account in order to avoid a traffic jam in some approaches caused by too high a degree of saturation of bus lanes. The model formulates that the degree of saturation of lanes of private vehicles is no more than 0.9, and that of bus lanes is no more than 0.8. The constraints of signal timing optimization are specifically as follows.

3.3.1. The Constraints of Timing Optimization for Private Vehicle Lane

For private vehicle lane:

$$Max[\frac{y_{i1}^s}{{\lambda }_i},\frac{y_{i2}^s}{{\lambda }_i}\dots \frac{y_{i{m}^s}^s}{{\lambda }_i}]\le 0.9$$

(14)

Then it can be obtained as follows according to Formulas (7)–(9):

$$\frac{y_{i\max }^s}{\frac{t_i}{C}}\le 0.9$$

(15)

Therefore, the constraint of green time in every phase is

$$t_i\ge \frac{C{y}_{i\max }^s}{0.9}$$

(16)

3.3.2. The constraints of timing optimization for bus lane

Similarly, for bus lanes, it can be obtained as follows according to Formulas (11) and (12):

$$\frac{y_{i\max }^b}{\frac{t_i}{C}}\le 0.8$$

(17)

Thus, for phases which contain bus lanes, the constraint of green time still needs to accord with the following formula:

$$t_i\ge \frac{C{y}_{i\max }^b}{0.8}$$

(18)

3.3.3. The Constraints of Green Time

The sum of the green time for all the phases at the intersection should meet the requirement as follows:

$${\displaystyle \sum _{i=1}^n{t}_i}=C-L$$

(19)

Then, in consideration of the actual security situation at the intersection, the shortest green time of every phase should not be less than a minimum $t_i^{\min }$. Hence, the timing of every phase must meet the following requirement:

$$t_i^{\min }\le t_i\le C-L-(n-1)t_i^{\min }$$

(20)

4. Bi-Level Optimization Model of Signal Timing

4.1. The Fundamentals of Bi-Level Programming Theory

Bi-level programming is a two-level system of planning and management. The decision-making process of the bi-level programming system is as follows: the upper layer gives certain information to the lower layer, under which the lower layer makes a response (decision making) according to its own interests or preferences, and then the upper layer makes a decision in line with the overall interests according to these responses.

The general form of bi-level programming model is as follows:

$$\begin{array}{l}\underset{x}{\min } F(x,y)\\ s.t. G(x,y)\le 0\end{array}$$

(21)

where y is the function of the upper-level decision variable $x$, that is $y=y(x)$. This function is called reaction function, which can be obtained by the following formula.

$$\begin{array}{l}\underset{y}{\min } f(x,y)\\ s.t. g(x,y)\le 0\end{array}$$

(22)

4.2. Bi-Level Model Formulation of Signal Timing Optimization

The signal timing optimization for intersections paved with bus lanes, which should consider the traffic benefits of both buses and private vehicles simultaneously, is a multi-objective optimization problem. Such a timing optimization problem can be described by a bi-level programming model, the optimization objectives of which are the minimum average running delay of all vehicles in lanes and the minimum passengers delay at intersections, in order to achieve bus priority.

4.2.1. Upper-Level Formulation

The upper-level model aims at improving the traffic capacity of buses at an intersection and reducing the running delay of private vehicles caused by the timing optimization scheme. Therefore, the upper-level formulation is expressed as follows, the objective function of which is to minimize the average running delay of all vehicles including buses and private vehicles.

$$\min D_G=\min \left\{\frac{D_s+D_b}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^s}{q}_{ij}^s+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^b}{q}_{ij}^b}}}}}\right\}$$

(23)

$$s.t.\{\begin{array}{l}{\displaystyle \sum _{i=1}^n{t}_i}=C-L\\ t_i\ge \frac{C{y}_{i\max }^s}{0.9}\\ t_i\ge \frac{C{y}_{i\max }^b}{0.8}\\ t_i^{\min }\le t_i\le C-L-(n-1)t_i^{\min }\\ q_{ij}^s\ge 0\\ q_{ij}^b\ge 0\end{array}$$

4.2.2. Lower-Level Formulation

The lower-level model is articulated in accordance with the concept of intersection bus priority, the aim of which is to reduce bus delay at an intersection. Considering the high capacity of a bus, the lower-level model is formulated to minimize the average passenger delay at intersection.

$$\min D_p=\min \left\{\frac{D_{ps}+D_{pb}}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^s}{P}_s{q}_{ij}^s+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^b}{P}_b{q}_{ij}^b}}}}}\right\}$$

(24)

$$s.t.\{\begin{array}{l}{x}_i^s(C)=\max \left\{\frac{y_{i1}^s}{{\lambda }_i},\frac{y_{i2}^s}{{\lambda }_i}\dots \frac{y_{i{m}^s}^s}{{\lambda }_i}\right\}\\ x_i^b(C)=\max \left\{\frac{y_{i1}^b}{{\lambda }_i},\frac{y_{i2}^b}{{\lambda }_i}\dots \frac{y_{i{m}^b}^b}{{\lambda }_i}\right\}\\ C_{\min }\le C\le C_{\max }\\ C_{\min }={\displaystyle \sum (5+\frac{b}{v})}\\ C_{\max }=\frac{1.5\left[(1.4+k)\varphi +6\right]}{1-y}\\ x_i^s(C)\le 0.9,x_i^b(C)\le 0.8\\ {\lambda }_i\ge 0\\ q_{ij}^s\ge 0,q_{ij}^b\ge 0\end{array}$$

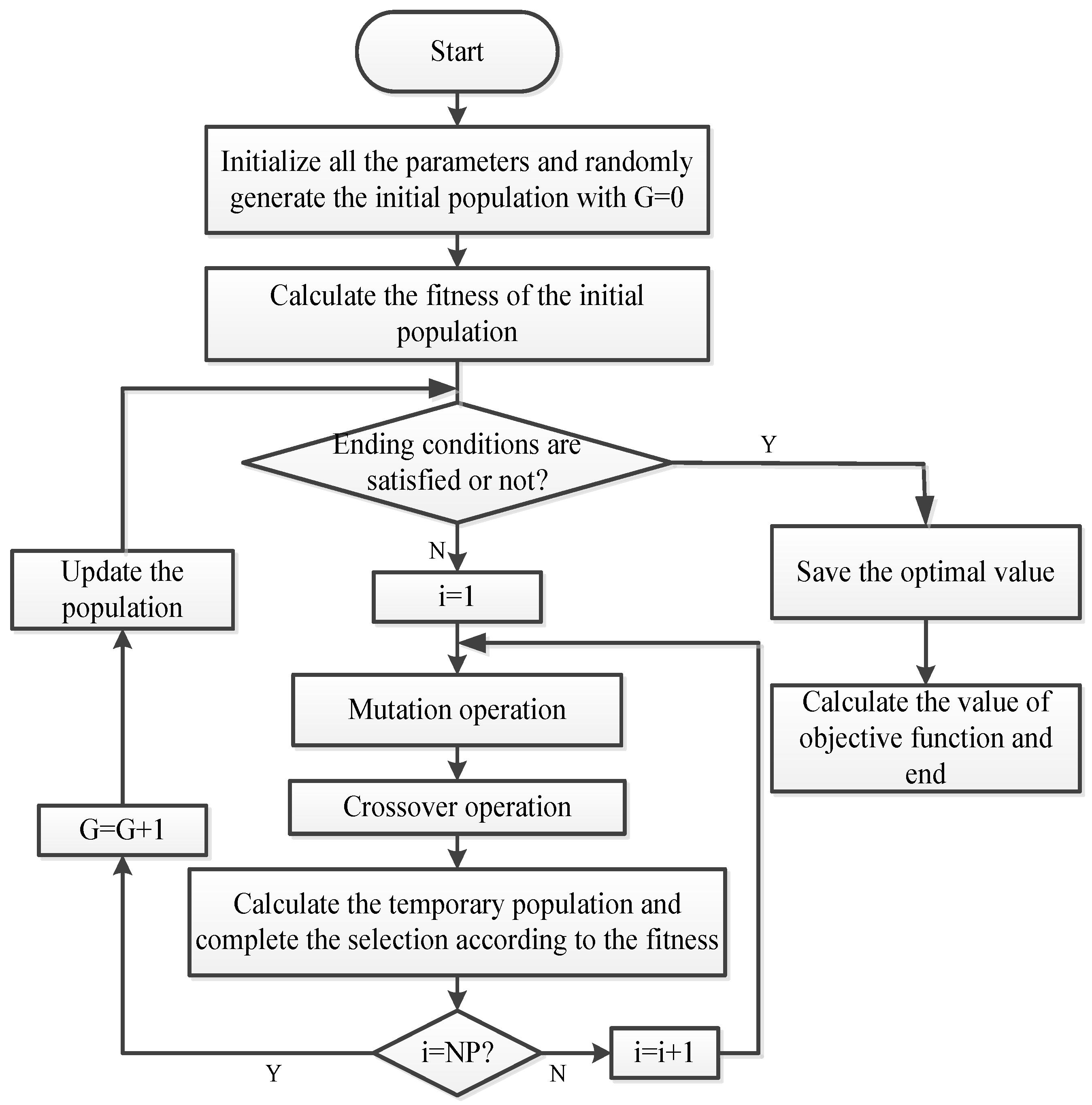
5. Solution Algorithm

5.1. Differential Evolution Algorithm

The differential evolution (DE) algorithm is a population-based algorithm, proposed by Storn [27]. As a stochastic and parallel-searched algorithm, the DE algorithm is regarded as an effective and robust method for global optimization by using three classic operators, crossover, mutation, and selection, to evolve from a randomly generated initial population to a final individual solution. The DE algorithm uses mutation and crossover operators to generate the trial vectors and a selection operator to determine whether the newly generated vectors can survive the next generation. The main advantages of the algorithm are its simple structure, local searching properties, few control parameters, and fast convergence [28]. Therefore, the DE algorithm is regarded as one of the best evolutionary algorithms and is widely used to solve diverse combinatorial optimization problems.

5.2. Application of DE Algorithm on Bi-Level Model

The bi-level model of timing signal optimization presented in this paper is an NP(Non-deterministic Polynomial)-hard problem which is difficult to solve and its solution domain and objective function vary with the change of feature vectors. The traditional deterministic methods cannot guarantee the global optimum. Due to its global search capability independent of gradient information, the DE algorithm can obtain a better solution and has better performance than other population-based evolutionary algorithms. Hence, the DE algorithm is applied to solve this bi-level optimization problem. The detailed procedure of the DE algorithm can be described as follows:

(i) Parameters initialization

The main parameters are population size $N$, length of the chromosome $D$, the mutation factor $F$, the crossover rate CR, and the maximum generations number $G$. The mutation factor F is selected in [0, 2]; the crossover rate CR is selected in [0, 1].

(ii) Population initialization

The initial population is randomly generated within the boundary by the following formulation:

$$x_{ij}^0=x_j^{\min }+rand\times (x_j^{\max }-x_j^{\min })$$

(25)

where $i=1,2,\dots N, j=1,2,\dots ,D,$ $x_j^{\min }$, and $x_j^{\max }$ are respectively the minimum and maximum limits of $j$th dimension, and rand is a uniform random number between [0, 1].

(iii) Mutation

For each target vector $x_i^G$ in generation G, the mutant vector $v_i^{G+1}$ is produced by

$$v_i^{G+1}=x_{r_1}^G+F(x_{r_2}^G-x_{r_3}^G)$$

(26)

where $F$ is a scaling factor affecting on difference vector $(x_{r_2}^G-x_{r_3}^G)$ used to control the amplification of the differential variation; $G$ is the current generation number; $i,r_1,r_2,r_3$ are randomly chosen and must be different from each other ($r_1\ne r_2\ne r_3\ne i$).

(iv) Crossover

The trail vector $u_{ij}^{G+1}$ is produced by mixing the target vectors $x_i^G$ with the mutated vectors $v_i^{G+1}$ according to the following rules:

$$u_{ij}^{G+1}=\{\begin{array}{ll}{v}_{ij}^{G+1}& \mathrm{if} rand(j)\le CR \mathrm{and} j=randn(t))\\ x_{ij}^G& \mathrm{otherwise}\end{array}$$

(27)

where $j=1,2,\dots ,D$; $rand(j)\in [0,1]$ is a random number;$CR\in [0,1]$ is the crossover constant; $randn(t)\in [1,2,\dots ,D]$ is a randomly selected integer to ensure that the trail vector gets at least one parameter from the mutated vector.

(v) Selection

The performances of the child vector $u_i^{G+1}$ and its parents $x_i^G$ are compared and the better one is selected in the next generation by the following formulation:

$$x_i^{G+1}=\{\begin{array}{ll}{u}_i^{G+1}& \mathrm{if} f\left(u_i^{G+1}\right)\le f\left(x_i^G\right)\\ x_i^G& \mathrm{otherwise}\end{array}$$

(28)

where $f(u_i^{G+1})$ is the fitness of the child vector $u_i^{G+1}$; $f(x_i^G)$ is the fitness of the parent $x_i^G$.

(vi) The determination of the weight coefficient

The weight coefficient of the objective function is determined by the entropy weight method, which is expressed as:

$$H_{\mathrm{u}}=(-\ln \mathrm{n}{)}^{-1}{\displaystyle \sum _{\mathrm{e}=1}^{\mathrm{n}}{p}_{ue} \ln p_{\mathrm{ue}}}$$

(29)

$$w_u=1-H_u/{\displaystyle \sum _{u=1}^m(1-H_u)}$$

(30)

where $H_u$ are the entropy values; $p_{ue}=r_{ue}/{\displaystyle {\sum }_{e=1}^n{r}_{ue},r_{ue}\in \left[0,1\right]}$; $w_u$ is the weight coefficient of the $u$th indicator $f_u$ of the objective function; and ${\displaystyle {\sum }_{u=1}^{\mathrm{m}}{w}_u=1}$.

(vii) The calculation of the objective function

The value of the objective function is calculated by

$$f(x)={\displaystyle \sum _{u=1}^m{w}_u{f}_u}$$

(31)

In this bi-level model, the optimization problem of the upper-level model is defined as $\min f(x)$ and can be solved with the algorithm mentioned above, which is also applicable for the lower-level sub-problem. The flowchart of the DE-based solution approach is illustrated in Figure 1.

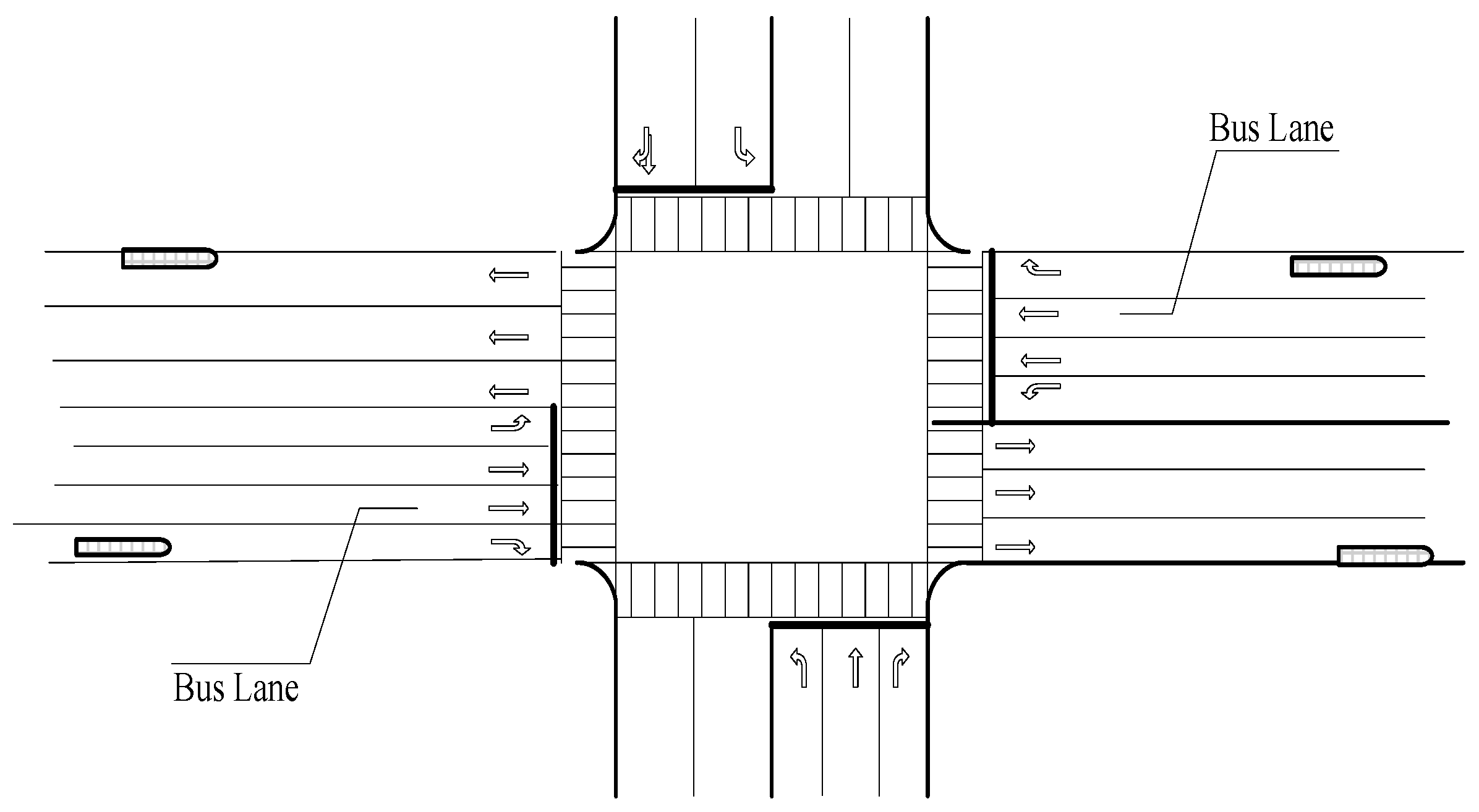
6. Case Study

6.1. Basic Data

This paper takes the actual four-phase intersection as an example, which is the intersection of Chaoyang Road and Zhengzhi Road in Beijing. This intersection is a typical crossing. The flow of buses is mainly distributed along the east–west approach; hence, through lanes for buses are set up. The intersection is as shown in Figure 2. The length of cycle is $C=146s$, $L=19s$. It is hypothesized that the saturation flow rate of lanes, $s_{ij}^s$, is uniformly $1600pcu/h$, and the conversion factor of buses is translated into the equivalent of cars $f=2,P_S=1,P_b=30$. Its four phases are: east-bound through–right lane and west-bound through–right lane; east-bound left turn and west-bound left turn; south-bound through–right lane and north-bound through–right lane; and south-bound left turn and north-bound left turn. For convenience, through lane and right turn are hypothesized to share the same phase, which means that it is forbidden to turn right during red time.

The data on the traffic volume per hour of each direction at this intersection was collected during the peak time, which are presented in matrix form. The flow data of private vehicles in approaches are as follows, which have been converted into cars.

$$q_{ij}^s=\left[\begin{array}{l}\begin{array}{cc}380& 292\end{array}\\ \begin{array}{cc}252& 168\end{array}\\ \begin{array}{cc}216& 284\end{array}\\ \begin{array}{cc}172& 112\end{array}\end{array}\right]s_{ij}^s=\left[\begin{array}{l}\begin{array}{cc}1600& 1600\end{array}\\ \begin{array}{cc}1600& 1600\end{array}\\ \begin{array}{cc}1600& 1600\end{array}\\ \begin{array}{cc}1600& 1600\end{array}\end{array}\right]y_{ij}^s=\left[\begin{array}{l}\begin{array}{cc}0.237& 0.182\end{array}\\ \begin{array}{cc}0.158& 0.105\end{array}\\ \begin{array}{cc}0.135& 0.177\end{array}\\ \begin{array}{cc}0.107& 0.07\end{array}\end{array}\right]$$

When $i=1$ and 2, $j=1$ refers to the western approach, and $j=2$ refers to the eastern one. When $i=3$ and 4, $j=1$ means the northern approach, and $j=2$ means the southern one.

For east- and west-bound through bus lanes, the flow ratio data of lanes computed based on Formula (11) are as follows:

$$q_{ij}^b=[\begin{array}{cc}168& 140\end{array}] s_{1j}^s=[\begin{array}{cc}1600& 1600\end{array}] y_{1j}^b=[\begin{array}{cc}0.21& 0.175\end{array}]$$

where $q_{11}^b$ stands for the flow of buses in the western bus lane, and $q_{12}^b$ stands for that in the eastern bus lane. The meanings of $s_{1j}^s$ and $y_{1j}^b$ are represented in a similar way.

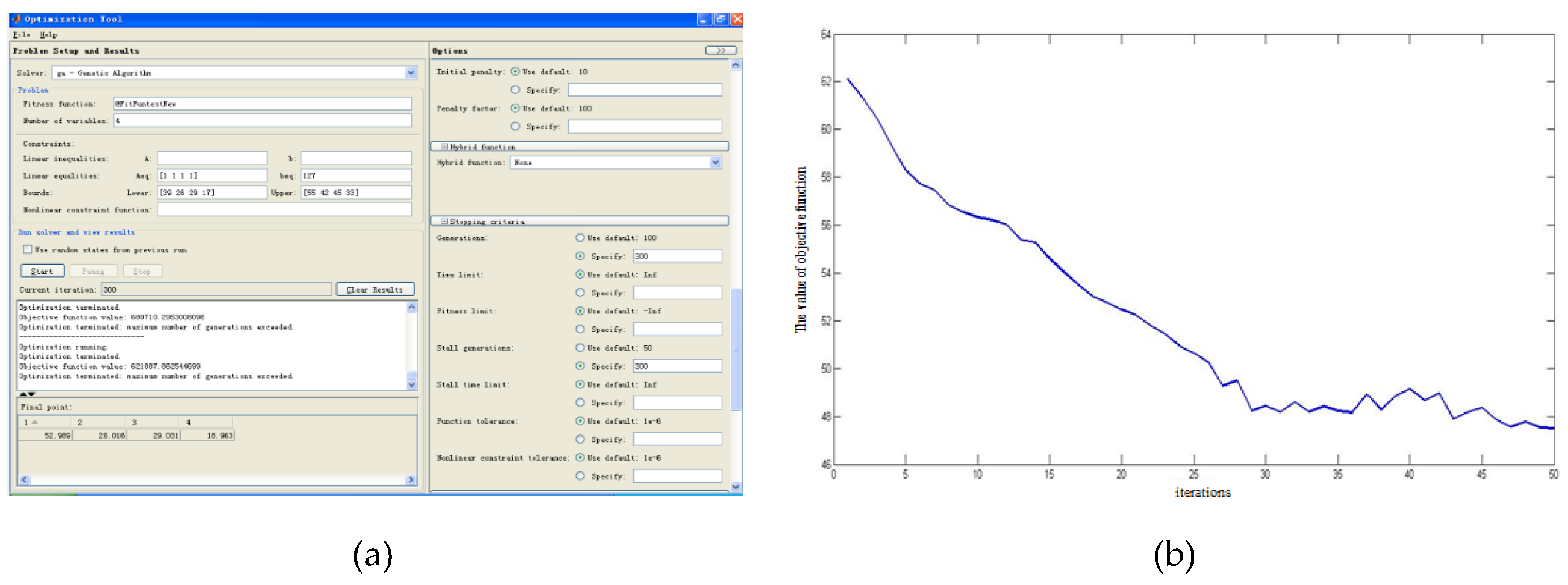
6.2. The Numerical Results

According to the model formulation proposed above and the data collected from the case, the upper-level model can be expressed as follows:

$$\begin{array}{l}\min D_G=\min \{\frac{D_s+D_b}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^s}{q}_{ij}^s+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^b}{q}_{ij}^b}}}}}\}\\ =\frac{{\displaystyle \sum _{i=1}^4{\displaystyle \sum _{j=1}^2\left\{\left[\frac{C{(1-\frac{t_i}{C})}^2}{2(1-y_{ij}^s)}+\frac{{\left(C\frac{y_{ij}^s}{t_i}\right)}^2}{2q_{ij}^s(1-C\frac{y_{ij}^s}{t_i})}\right]\times q_{ij}^s\right\}}}+{\displaystyle \sum _{j=1}^2\left\{\left[\frac{C{(1-\frac{t_1}{C})}^2}{2(1-y_{1j}^b)}+\frac{{\left(C\frac{y_{1j}^b}{t_1}\right)}^2}{2q_{1j}^b(1-C\frac{y_{1j}^b}{t_1})}\right]\times q_{1j}^b\right\}}}{{\displaystyle \sum _{i=1}^4{\displaystyle \sum _{j=1}^2{q}_{ij}^s+{\displaystyle \sum _{j=1}^2{q}_{1j}^b}}}}\end{array}$$

$$s.t.\{\begin{array}{l}{\displaystyle \sum _{i=1}^n{t}_i}=C-L\\ t_i\ge \frac{C{y}_{i\max }^s}{0.9}\\ t_i\ge \frac{C{y}_{i\max }^b}{0.8}\\ 10\le t_i\le C-L-10(n-1)\\ q_{ij}^s\ge 0\\ q_{ij}^b\ge 0\end{array}$$

The lower-level model is expressed as:

$$\begin{array}{l}\min D_p=\min \{\frac{D_{ps}+D_{pb}}{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^s}{P}_s{q}_{ij}^s+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m^b}{P}_b{q}_{ij}^b}}}}}\}\\ =\frac{{\displaystyle \sum _{i=1}^4{\displaystyle \sum _{j=1}^2\left\{\left[\frac{C{(1-{\lambda }_i)}^2}{2(1-{\lambda }_i{x}_{ij}^s)}+\frac{{\left(x_{ij}^s\right)}^2}{2q_{ij}^s(1-x_{ij}^s)}\right]\times q_{ij}^s\times P_s\right\}}}+{\displaystyle \sum _{j=1}^2\left\{\left[\frac{C{(1-{\lambda }_1)}^2}{2(1-{\lambda }_1{x}_{1j}^b)}+\frac{{\left(x_{1j}^b\right)}^2}{2q_{1j}^b(1-x_{1j}^s)}\right]\times q_{1j}^b\times P_b\right\}}}{{\displaystyle \sum _{i=1}^4{\displaystyle \sum _{j=1}^2{P}_s{q}_{ij}^s+{\displaystyle \sum _{j=1}^{2_i}{P}_b{q}_{1j}^b}}}}\end{array}$$

$$\{\begin{array}{l}{x}_i^s(C)=\frac{y_{i\max }^s}{{\lambda }_i}\\ x_1^b(C)=\frac{y_{1\max }^b}{{\lambda }_1}\\ 30\le C\le 120\\ x_i^s(C)\le 0.9,x_1^b(C)\le 0.8\\ {\lambda }_i\ge 0\\ q_{ij}^s\ge 0,q_{1j}^b\ge 0\end{array}$$

The DE algorithm procedure, which is proposed for solving the bi-level model of timing optimization, is coded by MATLAB and implemented on a computer with a 2.2 GHz CPU. The performance of the DE algorithm depends heavily on the settings of control parameters, which include population size, probabilities of crossover and mutation, and maximum iterations. In order to improve the quality and efficiency of solution procedure, the control parameters should be calibrated through aforehand sensitivity analysis. Here, some control parameters are found to be: population size 300, crossover possibility 0.7, mutation possibility 0.1, the number of iterations 50, and chromosome length 4 (namely four variables of $t_1,t_2,t_3,t_4$). The results of the iteration are shown in Figure 3, and the specific calculation results are shown in

Table 2. The calculated results of the example.

Variables	$t_1(s)$	$t_2(s)$	$t_3(s)$	$t_4(s)$	${\lambda }_1$	${\lambda }_2$	${\lambda }_3$
Results	41	21	24	17	0.360	0.184	0.211
Variables	${\lambda }_4$	$x_1(C)$	$x_2(C)$	$x_3(C)$	$x_4(C)$	$X_1(C)$
Results	0.149	0.731	0.859	0.839	0.718	0.750

.

6.3. Simulation and Result Discussion

Two different signal timing schemes are obtained by the traditional and optimization model respectively, which are simulated via VISSIM simulation software. In order to simulate the practical traffic condition more precisely, some global and local parameters of road traffic model, which are predefined in VISSIM, are recalibrated based on field data. Considering the intersection in the case is in the urban area, the Wiedemann 74 model, which is more suitable for urban traffic, is selected as the car following model, with some parameters adjusted, including reducing vehicle following distance and average residence distance, defining vehicle overtaking from the left, etc. The recalibrated parameters are shown in

Table 3. Changes in traffic behavior parameters.

Traffic Behavior	Parameters	Default Value	Modified Value
Car following	Average stand still	2.00(m)	1.50(m)
	Additive part of safety	2.00	1.50
	Multiplication part of safety	3.00	2.50
Lane changing	General Behavior	Free lane selection	Free lane selection
Lateral change	Desired Position	Middle of lane	Middle of lane
	Consider next turn direction	Not marked	Marked
	Overtake on same lane	Not marked	Marked (Left)
Signal Control	Decision-making model	Continuous inspection	Continuous inspection
	Reduction factor	0.60	0.70
Mesoscopic	Reaction time	1.20(s)	1.30(s)

, while the other parameters not mentioned here use the default value.

To verify the validity and reliability of the simulation model, the simulated results were compared with the field data, based on some key indicators, such as link traffic volume, vehicle queue length and delay, as shown in

Table 4. The comparison of observed data and simulated results.

Direction	Observed Data			Simulated Results			GEH Value	Error of Delay	Error of Queue Length
	Traffic Volume (pcu/h)	Delay (s)	Queue Length (m)	Traffic Volume (pcu/h)	Delay (s)	Queue Length (m)
West	840	37.4	78	930	39.8	81	3.03	6.42%	3.85%
East	565	26.1	60	525	24.6	58	1.71	−5.75%	−3.33%
North	504	19.7	54	565	20.8	56	2.64	5.58%	3.70%
South	384	24.3	42	455	25.5	40	3.47	4.94%	−4.76%

. As can be seen, the errors of indicators were all within 10%, which indicates the accuracy of the simulation model was satisfied. In addition, the road traffic volume was also evaluated using “GEH Statistic” [29], and corresponding values were all less than 5.0, which further verified the effectiveness of the model.

According to the evaluation indices about traffic efficiency as shown in

Table 5. Evaluation indices of traffic efficiency.

Index	Evaluated Objects and Content
Travel time	Average travel time of buses
	Average travel time of private vehicles
Delay	Average running delay of vehicles
	Average passenger delay at the intersection

, a comparison of simulation results of the two timing schemes was made, and the performances are plotted in

Table 6. Comparison of the two timing schemes.

Timing Scheme	Average Travel Time of Buses[s]	Average Travel Time of Private Vehicles[s]	Average Running Delay of Vehicles[s]	Average Passenger Delay at the Intersection[s]
Timing scheme of traditional model	56.01	53.57	49.85	46.29
Timing scheme of optimal model	53.18	55.99	47.53	41.01
Ratio enhancement	−5.1%	+4.5%	−4.6%	−11.4%

, which can verify the advantage of the optimization model.

According to the Table 6, the main conclusions could be drawn as follows:

(1)

Compared with the traditional timing model, the application of the optimization model reduces the total running delay of vehicles in lanes. The result shows that the optimization scheme can improve the overall traffic benefit by improving the traffic capacity of buses and reducing the adverse impact on private vehicles of bus-priority approaches.

(2)

Compared with the traditional timing model, the application of optimization model can reduce the average passenger delay at the intersection substantially. The result shows that the optimization scheme can decrease the overall traffic delay of passengers by improving the priority capacity of buses at the intersection, which reflects the people-oriented priority strategy in the optimization process.

7. Conclusions

This paper combined the concept of bus priority with the traditional way of a signal timing optimization problem. To solve this problem, a new methodology was proposed in which the passenger delay was explicitly considered in the process of signal timing optimization. The optimization problem modeled in the form of a bi-level optimization program aimed to minimize the average passenger delay at intersection and vehicle delay in lane simultaneously. Then the model was solved with the DE algorithm and applied to a real case of Beijing city. The application results showed that the optimization model can not only improve the priority capacity of the buses at the intersection but also reduce the loss of other private vehicle traffic benefits caused by the bus priority measures, which reflect the people-oriented priority strategy in the optimization process. By using the optimization model, the signal timing scheme can be adjusted in real time simply according to the change of traffic flow on bus lanes and ordinary lanes. Hence, the approach presented is a practical, effective, and feasible way to alleviate the traffic congestion, which can be used as a tool to help transport managers make bus priority policies while considering a network perspective.

However, caution should be taken while directly referring to this conclusion. First of all, the optimization model, which considered the intersection as an isolated entity, may not work well for connected signal system where several consecutive signals are connected. Secondly, the optimization model only considers updating signal timing scheme based on the traffic data collected in a fixed period of time, such as peak time, which may not be deployable for the near-real-time traffic data. Finally, in order to improve the quality and efficiency of the proposed solution algorithm, the sensitivity analysis was conducted to set the values of control parameters inherent in this algorithm. However, the robustness analysis of this solution algorithm is not considered in this study. For future studies, the robustness analysis of the DE-based solution algorithm can be conducted by comparing with some other optimization algorithms such as a genetic algorithm or ANN-based optimization. Several extensions may be considered. From modeling viewpoint, one may consider incorporating more traffic participants, such as micro-bus, taxi, into overall vehicular volumes in the modeling process to better optimize signal timing in dimensions. Another research area is that given the low cost and effectiveness of the signal timing optimization model utilized in the present study and the rapid spread of data networks, a systematic signal timing methodology integrating all signalized intersections may be developed in further research. These are the focus of our ongoing research.