Algorithmic Improvements of the KSU-STEM Method Verified on a Fund Portfolio Selection
Abstract
1. Introduction
2. Investment Decision-Making Situation
3. Decision-Making Theory Approaches for a Portfolio Selection
3.1. Review of Interactive Multiple Objective Programming Methods
3.2. STEM and KSU-STEM
3.2.1. STEM Algorithm
3.2.2. KSU-STEM Algorithm
3.2.3. STEM vs. KSU-STEM
- The first KSU-STEM positive is a possibility of determination of the weights of objectives by the DM. On the other side, this fact can also be a disadvantage for the DMs who are not able to determine the weights. As there are many supportive tools for weight estimation, this will reflect a minority of cases.
- Moreover, a calculation of STEM weights may not potentially work properly if the objective values are negative.
- In the original form of the STEM approach, the distances are not standardized, which can distort the result. On the contrary, KSU-STEM applies a relative standardized distance, which makes the result more reliable.
- KSU-STEM works better with a combination of minimizing and maximizing objective functions. Any transformation of the objective character is not required.
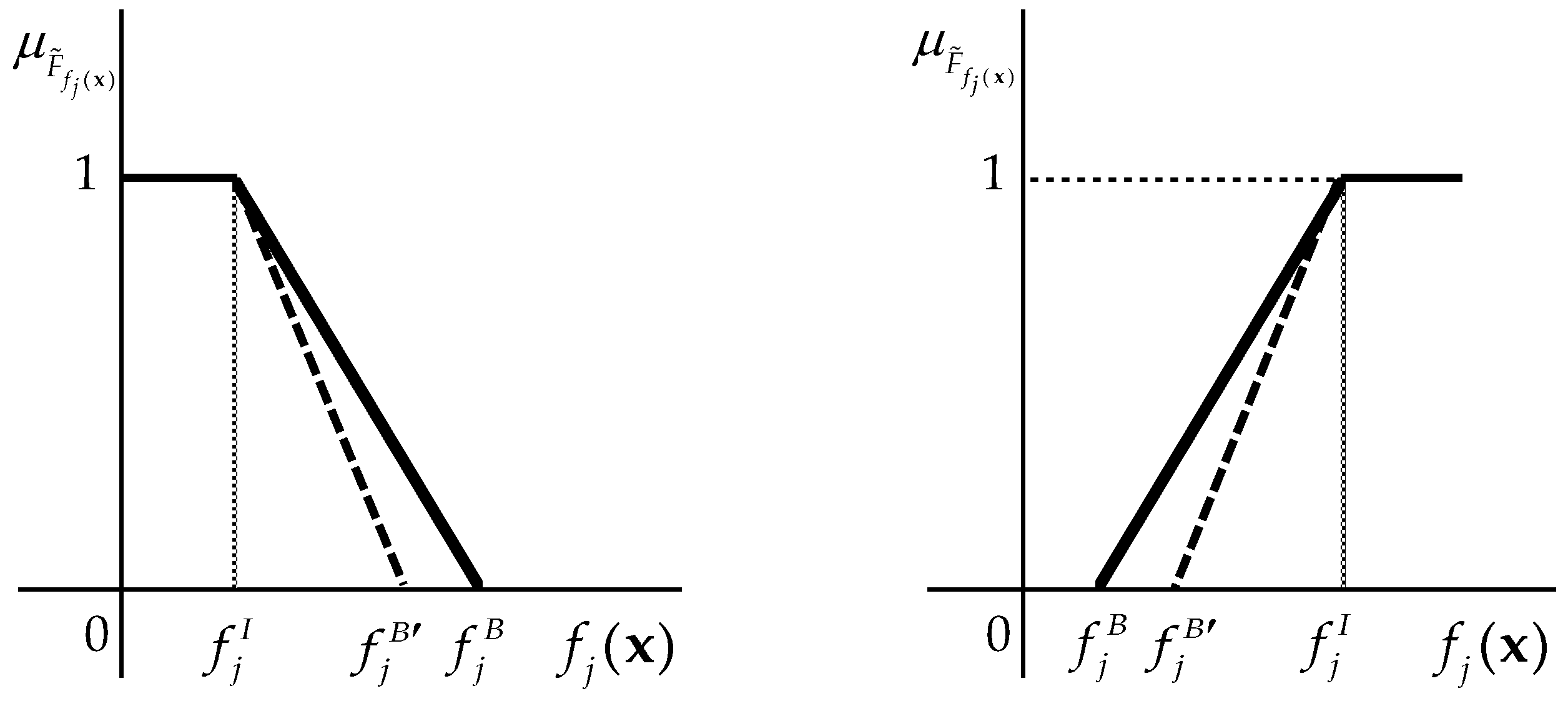
- The ideal value is determined via the same approach. However, KSU-STEM determines the basal value at an unnecessarily pessimistic level. This aspect can be considered as a minor drawback of KSU-STEM. This shortcoming is eliminated in the revised KSU-STEM described below.
- On the other side, these two extreme values of the objectives are artificially used to represent the normalization of their values. STEM uses only the ideal value in this process.
- Both methods zero the weights of satisfactory objectives. KSU-STEM, compared to STEM, recalculates the weights of other objectives, which is actually necessary action. This fact must also be duly examined (see more below).
4. Improvements of the KSU-STEM Algorithm
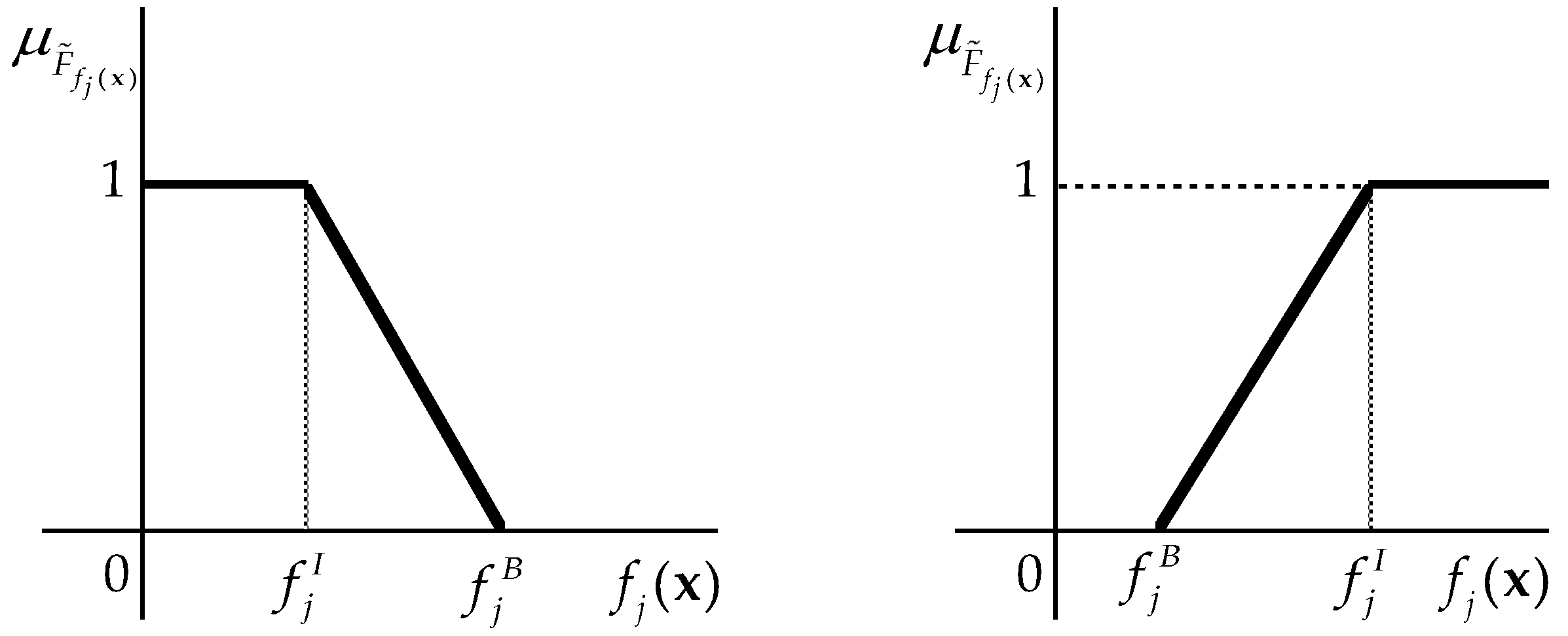
4.1. Step 2: Basal and Ideal Value of the Objectives
4.2. Step 3: Fuzzy Goal Construction
4.3. Step 4: Weight Recalculation
4.3.1. Special Case of Single Unsatisfactory Objective
4.3.2. Necessity of the Weight Recalculation?
4.3.3. Fuzzy Goal Modification
5. Selecting a Portfolio of CONSEQ Funds via Improved KSU-STEM
Discussion
6. Conclusions
Funding
Conflicts of Interest
Appendix A
References
- Le Bon, G. The Crowd: Study of the Popular Mind; Macmillan: New York, NY, USA, 1896. [Google Scholar]
- Graham, B.; Dodd, D. Security Analysis; McGraw-Hill Education: Columbus, OH, USA, 2008. [Google Scholar]
- Murphy, J.J. Technical Analysis of the Financial Markets: A Comprehensive Guide to Trading Methods and Applications, 1st ed.; New York Institute of Finance: New York, NY, USA, 1999. [Google Scholar]
- Markowitz, H.M. Portfolio Selection: Efficient Diversification of Investments, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1959. [Google Scholar]
- Benayoun, R.; De Montgolfier, J.; Tergny, J.; Laritchev, O. Linear programming with multiple objective functions: Step method (STEM). Math. Prog. 1971, 1, 366–375. [Google Scholar] [CrossRef]
- Geoffrion, A.M.; Dayer, J.S.; Feinberg, A. An interactive approach for multicriterion optimization with an application to the operation an academic department. Manag. Sci. 1972, 19, 357–367. [Google Scholar] [CrossRef]
- Teghem, J.; Dufrane, D.; Thauvoye, M.; Kunsch, P. STRANGE: An interactive method for multi-objective linear programming under uncertainty. Eur. J. Oper. Res. 1986, 26, 65–82. [Google Scholar] [CrossRef]
- Sakawa, M. Fuzzy Sets and Interactive Multiobjective Optimization, 1st ed.; Plenum Press: New York, NY, USA, 1993. [Google Scholar]
- Liang, T.-F. Distribution planning decisions using interactive fuzzy multi-objective linear programming. Fuzzy Sets Syst. 2006, 157, 1303–1316. [Google Scholar] [CrossRef]
- Leung, Y. Hierarchical programming with fuzzy objective and constraints. In Optimization Models Using Fuzzy Sets and Possibility Theory, 1st ed.; Kacprzyk, J., Orlovski, S.A., Eds.; D. Reidel: Dordrecht, The Netherlands, 1987; pp. 245–257. [Google Scholar]
- Fund Glossary—SRRI. Available online: http://fundglossary.erste-am.com/srri/ (accessed on 1 March 2020).
- CONSEQ Fund’ List. Available online: https://www.conseq.cz/investment/mutual-funds?lang=en-cz (accessed on 1 March 2020).
- Fiala, P. Models and Methods of Decision Making (in Czech), 2nd ed.; Oeconomica: Prague, Czech Republic, 2013. [Google Scholar]
- Zionts, S.; Wallenius, J. An interactive programming method for solving the multiple criteria problem. Manag. Sci. 1976, 22, 652–663. [Google Scholar] [CrossRef]
- Mietinen, K. Nonlinear Multiobjective Optimization, 1st ed.; Kluwer Academic Publishers: Boston, MA, USA, 1999. [Google Scholar]
- Lai, Y.J.; Hwang, C.L. Fuzzy Multiple Objective Decision Making: Methods and Applications; Springer: Berlin, Germany, 1996. [Google Scholar]
- Wierzbicki, A.P.; Makowski, M.; Wessels, J. Decision Support. Methodology with Environmental Applications, 1st ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Mietinen, K.; Mäkelä, M.M. Interactive bundle-based method for nondifferentiable multiobjective optimization: NIMBUS. Optimization 1995, 34, 231–246. [Google Scholar] [CrossRef]
- Greco, S.; Mousseau, V.; Slovinski, R. Ordinal regression revisited: Multiple criteria ranking with a set of additive value functions. Eur. J. Oper. Res. 2008, 191, 416–436. [Google Scholar] [CrossRef]
- Balibek, E.; Köksalan, M. A visual interactive approach for scenario-based stochastic multi-objective problems and an application. J. Oper. Res. Soc. 2012, 63, 1773–1787. [Google Scholar] [CrossRef]
- Köksalan, M.; Şakar, C.T. An interactive approach to stochastic programming-based portfolio optimization. Ann. Oper. Res. 2016, 245, 47–66. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Huang, G.H.; Wang, S.; Li, W.; Guan, P.B. A risk-based interactive multi-stage stochastic programming approach for water resources planning under dual uncertainties. Adv. Water Resour. 2016, 94, 217–230. [Google Scholar] [CrossRef]
- Adeyefa, A.S.; Luhandjula, M.K. Multiobjective stochastic linear programming: An overview. Am. J. Oper. Res. 2011, 1, 203–213. [Google Scholar] [CrossRef][Green Version]
- Abo-Sinna, M.A.; Amer, A.H.; El Sayed, H.H. An interactive algorithm for decomposing the parametric space in fuzzy multiobjective dynamic programming problem. Appl. Math. Comput. 2006, 174, 684–699. [Google Scholar] [CrossRef]
- Abd El-Wahed, W.F.; Lee, S.M. Interactive fuzzy goal programming for multi-objective transportation problems. Omega Int. J. Manag. Sci. 2006, 34, 158–166. [Google Scholar] [CrossRef]
- Arora, S.R.; Gupta, R. Interactive fuzzy goal programming approach for bilevel programming problem. Eur. J. Oper. Res. 2008, 194, 368–376. [Google Scholar] [CrossRef]
- Eschenauer, H.A.; Osyczka, A.; Schäfer, E. Interactive multicriteria optimization in design process. In Multicriteria Design Optimization Procedures and Applications, 1st ed.; Eschenauer, H., Koski, J., Osyczka, A., Eds.; Springer: Berlin, Germany, 1990; pp. 71–114. [Google Scholar]
- Vanderpooten, D.; Vincke, P. Description and analysis of some representative interactive multicriteria procedures. Math. Comput. Model. 1989, 12, 1221–1238. [Google Scholar] [CrossRef]
- Brožová, H.; Houška, M.; Šubrt, T. Models for Multi-Criteria Decision Making (in Czech), 2nd ed.; Czech University of Life Sciences Prague: Prague, Czech Republic, 2014. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making—Methods and Applications, A State-of-the Art Survey, 1st ed.; Springer: New York, NY, USA, 1981. [Google Scholar]
- Bellman, R.E.; Zadeh, L.A. Decision making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Borovička, A. KSU-STEM approach and its possible algorithmic revisions verified in a portfolio selection process. In Proceedings of the European Simulation and Modelling Conference (ESM 2019), Palma de Mallorca, Spain, 28–30 October 2019; EUROSIS-ETI Publication: Ostend, Belgium, 2019. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Talašová, J. Fuzzy Methods for Multi-Criteria Evaluation and Decision Making (in Czech), 1st ed.; Palacký University Olomouc: Olomouc, Czech Republic, 2003. [Google Scholar]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Gupta, M.; Bhattacharjee, D. Multi objective problem in fuzzy environment where resources are triangular fuzzy number. Eur. J. Sci. Res. 2010, 46, 99–106. [Google Scholar]
- Mohamed, R.H. The relationship between goal programming and fuzzy programming. Fuzzy Sets Syst. 1997, 89, 215–222. [Google Scholar] [CrossRef]
| Fund | Return [%] | Risk [Point] | Cost [%] |
|---|---|---|---|
| Active Invest Dynamic | 0.2083 | 5 | 5 |
| Active Invest Conservative | 0.0697 | 3 | 2.5 |
| Active Invest Balanced | 0.1310 | 4 | 4 |
| Conseq Private Invest Dynamic Portfolio | 0.2809 | 5 | 3 |
| Conseq Private Invest Conservative Portfolio | 0.1112 | 3 | 3 |
| Conseq Private Invest Balanced Portfolio | 0.2032 | 4 | 4 |
| Conseq Invest New Europe Equity A | 0.5914 | 5 | 5 |
| Conseq Invest New Europe Equity B | 0.6236 | 5 | 5 |
| Conseq Invest New Europe Equity D | −0.1009 | 5 | 5 |
| Conseq Opportunity OPFKI | 0.8215 | 7 | 5 |
| Conseq Invest Bond A | 0.0970 | 2 | 2.5 |
| Conseq Invest New Europe Bond A | 0.1042 | 4 | 2.5 |
| Conseq Corporate Bond A | 0.1319 | 2 | 2.5 |
| Conseq Invest Bond B | 0.1211 | 2 | 5 |
| Conseq Invest Bond D | −0.0206 | 2 | 5 |
| Conseq Invest New Europe Bond D | −0.2577 | 4 | 5 |
| Conseq Invest Conservative A | 0.0931 | 2 | 5 |
| Conseq Invest Conservative D | −0.0084 | 2 | 5 |
| Conseq Real Estate | 0.3137 | 2 | 5 |
| Conseq Real Estate Fund | 0.2699 | 6 | 3.5 |
| Approach | Return | Risk | Cost |
|---|---|---|---|
| KSU-STEM | −0.136 | 5.9 | 5 |
| Improved approach | 0.029 | 4.3 | 4.3 |
| Model (22) | Return | Risk | Cost |
|---|---|---|---|
| Original | 0.252 | 2.45 | 3.977 |
| With | 0.17 | 3.083 | 3.744 |
| Objective | Score | Weight |
|---|---|---|
| Return | 6 | 0.353 |
| Risk | 9 | 0.529 |
| Cost | 2 | 0.118 |
| Objective | Basal | Ideal |
|---|---|---|
| Return | 0.029 | 0.429 |
| Risk | 4.3 | 2 |
| Cost | 4.3 | 2.5 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borovička, A. Algorithmic Improvements of the KSU-STEM Method Verified on a Fund Portfolio Selection. Information 2020, 11, 262. https://doi.org/10.3390/info11050262
Borovička A. Algorithmic Improvements of the KSU-STEM Method Verified on a Fund Portfolio Selection. Information. 2020; 11(5):262. https://doi.org/10.3390/info11050262
Chicago/Turabian StyleBorovička, Adam. 2020. "Algorithmic Improvements of the KSU-STEM Method Verified on a Fund Portfolio Selection" Information 11, no. 5: 262. https://doi.org/10.3390/info11050262
APA StyleBorovička, A. (2020). Algorithmic Improvements of the KSU-STEM Method Verified on a Fund Portfolio Selection. Information, 11(5), 262. https://doi.org/10.3390/info11050262




