Logic-Based Technologies for Intelligent Systems: State of the Art and Perspectives
Abstract
1. Introduction
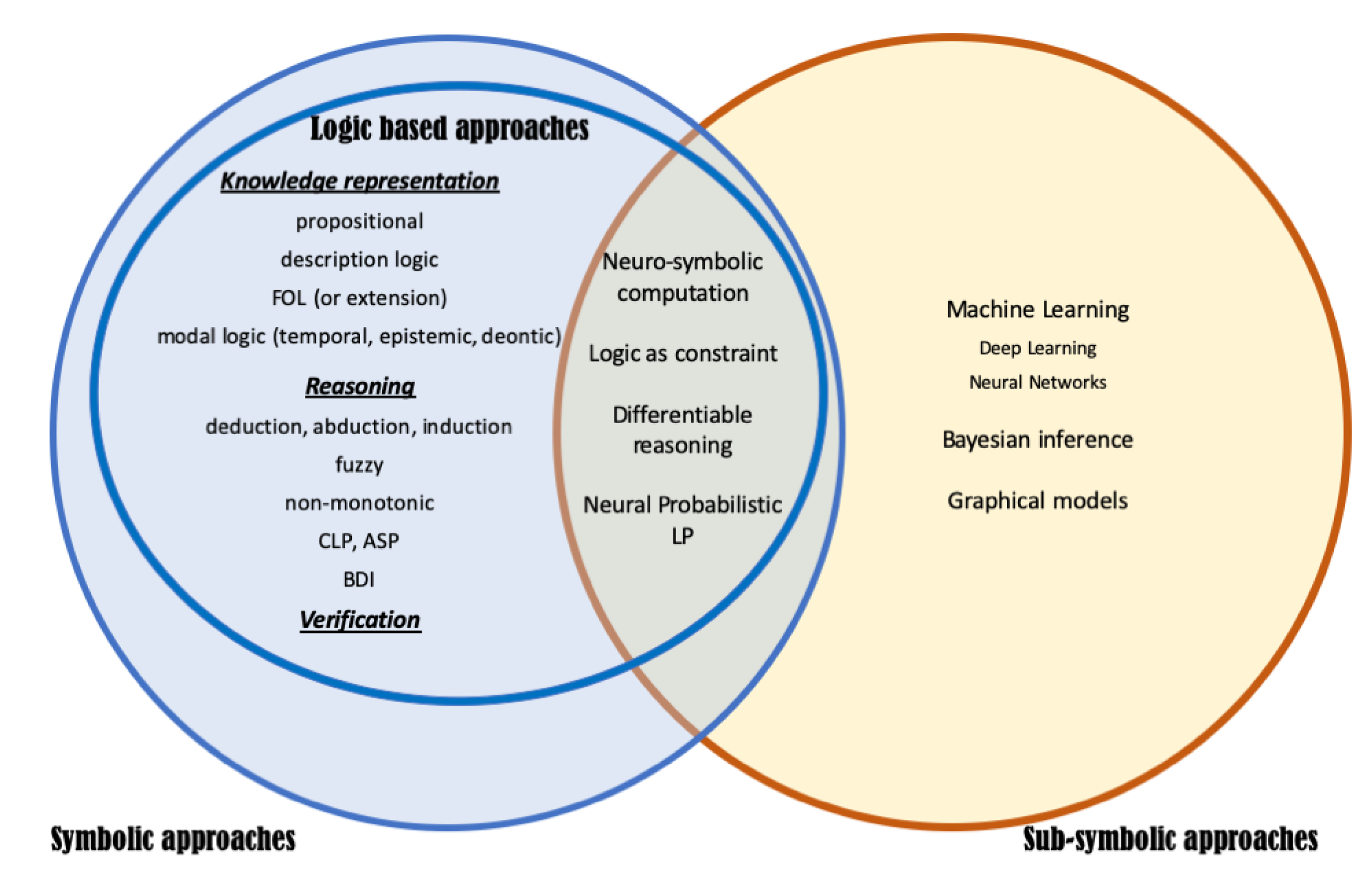
2. State of the Art: 60 Years in a Nutshell
2.1. The Premise: Computational Logic
2.2. Knowledge Representation
2.3. Reasoning Approaches and Techniques
2.4. Verification and Model-Checking
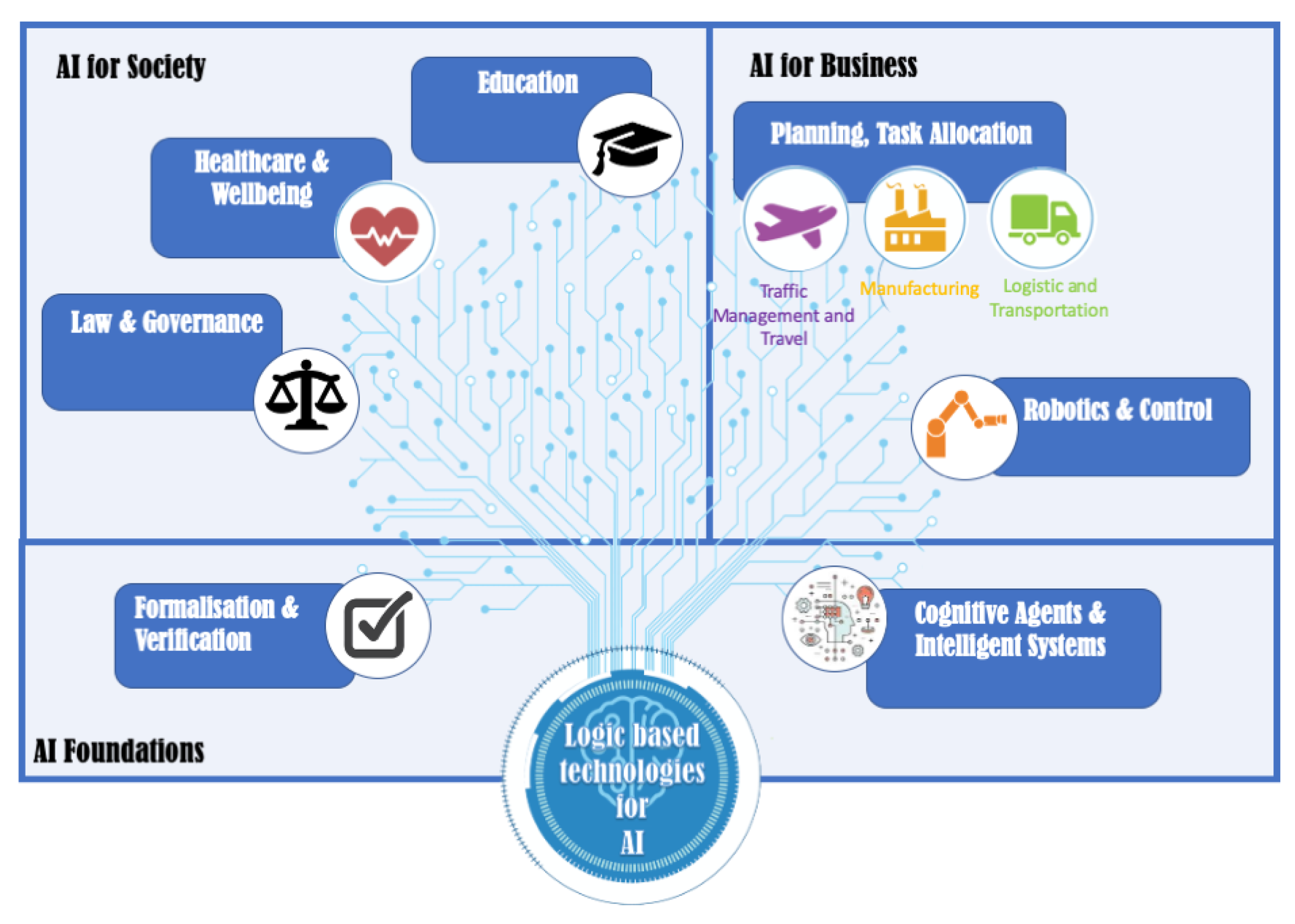
3. Logic-Based AI: Application Areas
3.1. Ai Foundations
3.1.1. Formalization and Verification of Computational Systems
3.1.2. Cognitive Agents and Intelligent Systems
3.2. AI for Society
3.2.1. Healthcare and Wellbeing
3.2.2. Law and Governance
3.2.3. Education
3.3. AI for Business: Automation and Robotics
3.3.1. Planning and Task Allocation
3.3.2. Robotics and Control
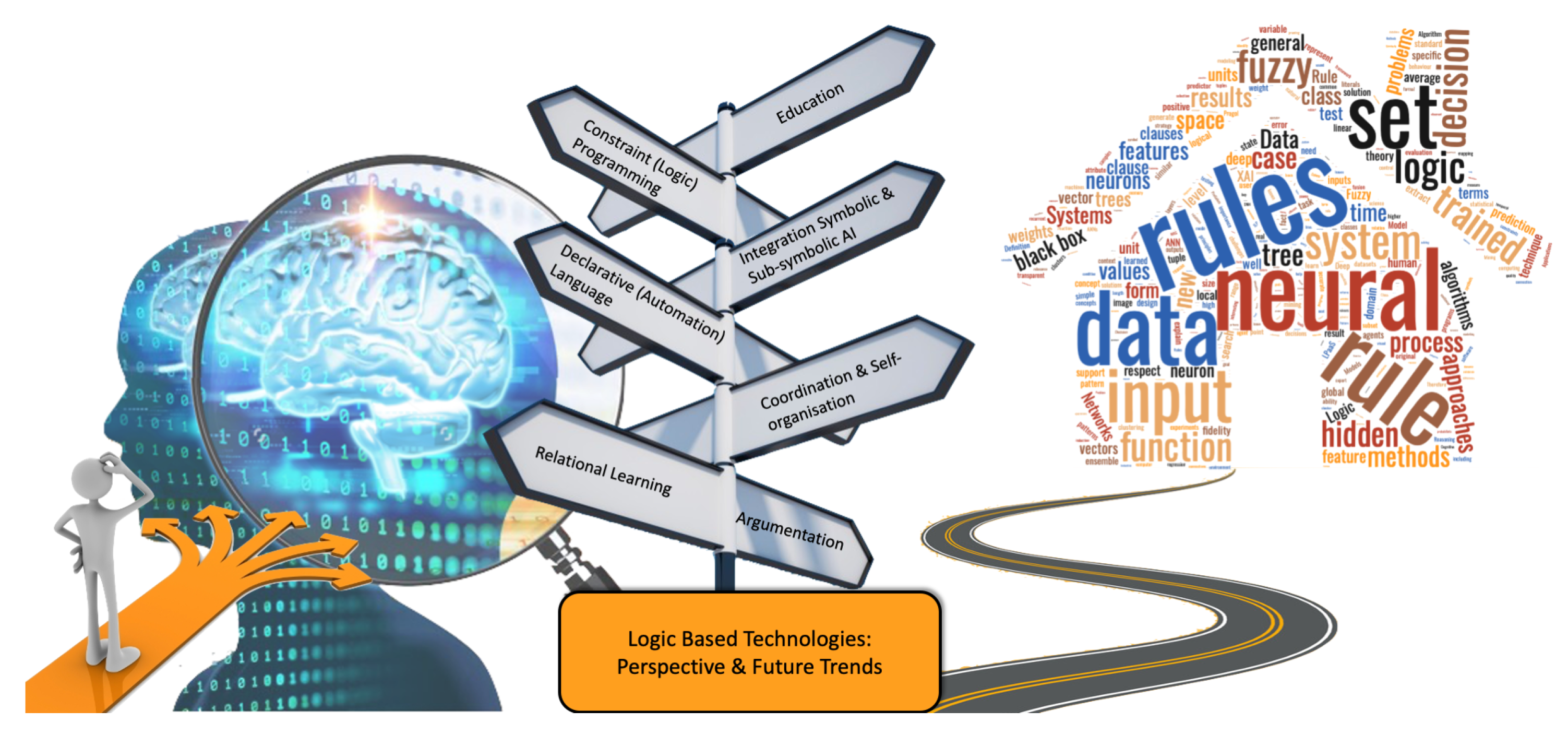
4. Perspective and Future Trends
4.1. Integration of Symbolic and Sub-Symbolic AI
- sub-symbolic AI is opaque, meaning that human beings struggle in understanding the functioning and behavior of sub-symbolically intelligent systems; instead, symbolic AI is more transparent, as it is both human- and machine-interpretable at the same time
- sub-symbolic AI can improve itself automatically by consuming data, but it is difficult to extend and re-use outside the contexts it was designed for; conversely, symbolic AI is flexible and extensible, but requires humans to manually provide symbolic knowledge
- sub-symbolic AI is adequate for fuzzy problems where some (minimal) degree of error or uncertainty can be tolerated; whereas symbolic AI calls for precise data and queries provided by human beings, yet provides exact, crisp results as its outcome.
4.1.1. Techniques and Approaches: Hybrid Models for Intelligent Systems
4.1.2. Application Scenarios: Explainable, Responsible, and Ethical AI
4.2. Relational Learning
Inductive Logic Programming
4.3. Constraint (Logic) Programming
- will (C)LP ever reach full declarativeness? In other words, will it ever be possible to write CLP programs containing custom, user-defined domains and constraints?
- can sub-symbolic AI play a role in the development of more efficient or more expressive CLP solvers?
4.4. Argumentation
Argumentation Mining
4.5. Coordination and Self-Organization
4.6. Education
4.7. Declarative Languages
- what is favoring adoption of non-logic declarative technologies?
- what is preventing a wider adoption of logic-based declarative technologies in these areas?
- can computational logic and logic programming contribute in overcoming the current shortcomings of non-logic declarative technologies?
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gunning, D. Explainable Artificial Intelligence (XAI); Funding Program DARPA–BAA–16–53; Defense Advanced Research Projects Agency (DARPA): Arlington, VA, USA, 2016. [Google Scholar]
- Gallier, J.H. Logic for Computer Science: Foundations of Automatic Theorem Proving; Harper & Row Publishers, Inc.: New York, NY, USA, 1985. [Google Scholar]
- Boyer, R.S.; Moore, J.S. A Computational Logic; Academic Press Professional, Inc.: Cambridge, MA, USA, 1988. [Google Scholar]
- Levesque, H.J. A logic of implicit and explicit belief. In Proceedings of the 4th AAAI Conference on Artificial Intelligence (AAAI ’84); Number 5 in AAAI’84, Palo Alto, CA, USA, 6–10 August 1984; AAAI Press: Austin, TX, USA, 1984; pp. 198–202. [Google Scholar]
- Omicini, A.; Denti, E.; Natali, A. Agent Coordination and Control through Logic Theories. In Topics in Artificial Intelligence, Proceedings of the 4th Congress of the Italian Association for Artificial Intelligence (AI*IA’95), Florence, Italy, 11–13 October 1995; Gori, M., Soda, G., Eds.; LNAI; Springer: Berlin/Heidelberg, Germany, 1995; Volume 992, pp. 439–450. [Google Scholar] [CrossRef]
- Bordini, R.H.; Braubach, L.; Dastani, M.; Seghrouchni, A.E.F.; Gomez-Sanz, J.J.; Leite, J.; O’Hare, G.; Pokahr, A.; Ricci, A. A survey of programming languages and platforms for multi-agent systems. Informatica 2006, 30, 33–44. [Google Scholar]
- Green, C.C.; Raphael, B. The use of theorem-proving techniques in question-answering systems. In Proceedings of the 23rd ACM National Conference, Las Vegas, NV, USA, 27–29 August 1968; pp. 169–181. [Google Scholar] [CrossRef]
- Baader, F. Basic description logics. In The Description Logic Handbook: Theory, Implementation, and Applications; Cambridge University Press: Cambridge, MA, USA, 2003; pp. 43–95. [Google Scholar]
- Cimiano, P. Ontology Learning and Population from Text; Springer: New York, NY, USA, 2006. [Google Scholar]
- Sowa, J.F. (Ed.) Principles of Semantic Networks: Explorations in the Representation of Knowledge; Morgan Kaufmann Series in Representation and Reasoning; Morgan Kaufmann Pub.: Burlington, MA, USA, 1991. [Google Scholar]
- Artale, A.; Franconi, E.; Wolter, F.; Zakharyaschev, M. A Temporal Description Logic for Reasoning over Conceptual Schemas and Queries. In Proceedings of the European Workshop on Logics in Artificial Intelligence (JELIA 2002), Cosenza, Italy, 23–26 September 2002; Springer: Cham, Switzerland, 2002; pp. 98–110. [Google Scholar] [CrossRef]
- Horrocks, I. OWL: A Description Logic Based Ontology Language. In Principles and Practice of Constraint Programming (CP 2005); Van Beek, P., Ed.; Extended Abstract; Springer: Cham, Switzerland, 2005; pp. 5–8. [Google Scholar] [CrossRef]
- Van Engers, T.; Boer, A.; Breuker, J.; Valente, A.; Winkels, R. Ontologies in the legal domain. In Digital Government; Springer: Cham, Switzerland, 2008; pp. 233–261. [Google Scholar]
- Valente, A. Types and roles of legal ontologies. In Law and the Semantic Web; Benjamins, V.R., Casanovas, P., Breuker, J., Gangemi, A., Eds.; Springer: Cham, Switzerland, 2005; pp. 65–76. [Google Scholar] [CrossRef]
- Cohen, W.W.; Hirsh, H. Learning the CLASSIC description logic: Theoretical and experimental results. In Principles of Knowledge Representation and Reasoning; Elsevier: Amsterdam, The Netherlands, 1994; pp. 121–133. [Google Scholar]
- Moller, R.; Haarslev, V. Description logic systems. In The Description Logic Handbook: Theory, Implementation, and Applications; Cambridge University Press: Cambridge, MA, USA, 2003; pp. 282–305. [Google Scholar]
- Yang, G.; Kifer, M.; Zhao, C. Flora-2: A Rule-Based Knowledge Representation and Inference Infrastructure for the Semantic Web. In Lecture Notes in Computer Science, Proceedings of the OTM Confederated International Conferences On the Move to Meaningful Internet Systems, Catania, Italy, 3–7 November 2003; Meersman, R., Tari, Z.S.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2888, pp. 671–688. [Google Scholar]
- Mccarthy, J.; Shannon, C. Automata Studies. J. Symb. Log. 1958, 23, 59–60. [Google Scholar] [CrossRef]
- Lieberman, H.; Liu, H.; Singh, P.; Barry, B. Beating common sense into interactive applications. AI Mag. 2004, 25, 63. [Google Scholar]
- Trinh, T.H.; Le, Q.V. A Simple Method for Commonsense Reasoning. arXiv 2018, arXiv:1806.02847. [Google Scholar]
- Liu, H.; Singh, P. ConceptNet—A practical commonsense reasoning tool-kit. BT Technol. J. 2004, 22, 211–226. [Google Scholar] [CrossRef]
- Liu, H.; Lieberman, H.; Selker, T. GOOSE: A goal-oriented search engine with commonsense. In Lecture Notes in Computer Science, Proceedings of the International Conference on Adaptive Hypermedia and Adaptive Web-Based Systems, Malaga, Spain, 29–30 May 2002; De Bra, P., Brusilovsky, P.C.R., Eds.; Springer: Cham, Switzerland, 2002; Volume 2347, pp. 253–263. [Google Scholar]
- Shapiro, S.C. SNePS: A logic for natural language understanding and commonsense reasoning. In Natural Language Processing and Knowledge Representation: Language for Knowledge and Knowledge for Language; MIT Press: Cambridge, MA, USA, 2000; pp. 175–195. [Google Scholar]
- Lenat, D.B. CYC: A large-scale investment in knowledge infrastructure. Commun. ACM 1995, 38, 33–38. [Google Scholar] [CrossRef]
- Robinson, J.A. A machine-oriented logic based on the resolution principle. J. ACM 1965, 12, 23–41. [Google Scholar] [CrossRef]
- Montali, M.; Torroni, P.; Chesani, F.; Mello, P.; Alberti, M.; Lamma, E. Abductive logic programming as an effective technology for the static verification of declarative business processes. Fundam. Informaticae 2010, 102, 325–361. [Google Scholar] [CrossRef]
- Kowalski, R. Predicate logic as programming language. In Proceedings of the IFIP Congress, Stockholm, Sweden, 5–10 August 1974; pp. 569–574. [Google Scholar]
- Colmerauer, A. Theoretical model of Prolog II. In Logic Programming and its Applications; van Canegham, M., Warren, D.H., Eds.; Ablex Publishing Corporation: New York, NY, USA, 1986; pp. 3–31. [Google Scholar]
- Dawson, S.; Ramakrishnan, C.R.; Warren, D.S. Practical Program Analysis Using General Purpose Logic Programming Systems—A Case Study. In Proceedings of the ACM SIGPLAN 1996 Conference on Programming Language Design and Implementation, Philadelphia, PA, USA, 21–24 May 1996; PLDI ’96. Association for Computing Machinery: New York, NY, USA, 1996; pp. 117–126. [Google Scholar] [CrossRef]
- Yen, J.; Langari, R. Fuzzy Logic: Intelligence, Control, and Information; Prentice Hall Press: Upper Saddle River, NJ, USA, 1999; Volume 1. [Google Scholar]
- Goyal, S.; Grover, S. Applying fuzzy grey relational analysis for ranking the advanced manufacturing systems. Grey Syst. Theory Appl. 2012, 2, 284–298. [Google Scholar] [CrossRef]
- Gebser, M.; Kaminski, R.; Kaufmann, B.; Schaub, T. Clingo = ASP + Control: Preliminary Report. In Proceedings of the Technical Communications of the 30th International Conference on Logic Programming (ICLP’14), Vienna, Austria, 19–22 July 2014. [Google Scholar]
- Eiter, T.; Faber, W.; Leone, N.; Pfeifer, G. Declarative problem-solving using the DLV system. In Logic-Based Artificial Intelligence; Springer: Boston, MA, USA, 2000; pp. 79–103. [Google Scholar] [CrossRef]
- Jaffar, J.; Lassez, J.L. Constraint logic programming. In Proceedings of the 14th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, Munich, Germany, 21–23 January 1987; pp. 111–119. [Google Scholar] [CrossRef]
- Rossi, F. Constraint (Logic) Programming: A Survey on Research and Applications. In New Trends in Constraints; Apt, K.R., Monfroy, E., Kakas, A.C., Rossi, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 40–74. [Google Scholar]
- Rossi, F.; Van Beek, P.; Walsh, T. Constraint programming. Found. Artif. Intell. 2008, 3, 181–211. [Google Scholar]
- Simonis, H. The CHIP system and its applications. In Lecture Notes in Computer Science, Proceedings of the International Conference on Principles and Practice of Constraint Programming, Cassis, France, 19–22 September 1995; Montanari, U., Rossi, F., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; Volume 976, pp. 643–646. [Google Scholar]
- Cplex, I.L.O.G. 11.0 User’s Manual; ILOG SA: Gentilly, France, 2007; p. 32. [Google Scholar]
- Aggoun, A.; Beldiceanu, N. Extending CHIP in order to solve complex scheduling and placement problems. Math. Comput. Model. 1993, 17, 57–73. [Google Scholar] [CrossRef]
- Colmerauer, A. An introduction to Prolog III. In Computational Logic; Springer: Cham, Switzerland, 1990; pp. 37–79. [Google Scholar]
- Benhamou, F.; Touraïvane, T. Prolog IV: Langage et algorithmes. In Proceedings of the JFPLC’95, IVèmes Journées Francophones de Programmation en Logique & Journée d’étude Programmation par Contraintes et Applications Industrielles, Dijon, France, 17–19 May 1995; pp. 51–64. [Google Scholar]
- Jaffar, J.; Michaylov, S.; Stuckey, P.J.; Yap, R.H.C. The CLP(R) language and system. ACM Trans. Program. Lang. Syst. 1992, 14, 339–395. [Google Scholar] [CrossRef]
- Codognet, P.; Diaz, D. Compiling constraints in clp (FD). J. Log. Program. 1996, 27, 185–226. [Google Scholar] [CrossRef]
- Minsky, M. A Framework for Representing Knowledge Representation. In The Psychology of Computer Vision; Mc Graw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Reiter, R. A logic for default reasoning. Artif. Intell. 1980, 13, 81–132. [Google Scholar] [CrossRef]
- Pollock, J.L. Defeasible reasoning. Cogn. Sci. 1987, 11, 481–518. [Google Scholar] [CrossRef]
- Bondarenko, A.; Dung, P.M.; Kowalski, R.A.; Toni, F. An abstract, argumentation-theoretic approach to default reasoning. Artif. Intell. 1997, 93, 63–101. [Google Scholar] [CrossRef]
- Rao, A.S. AgentSpeak(L): BDI Agents Speak Out in a Logical Computable Language. In Lecture Notes in Computer Science, Agents Breaking Away, Proceedings of the 7th European Workshop on Modelling Autonomous Agents in a Multi-Agent World, Eindhoven, The Netherlands, 22–25 January 1996; de Velde, W.V., Perram, J.W., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1038, pp. 42–55. [Google Scholar] [CrossRef]
- Lee, J.; Durfee, E.H. Structured circuit semantics for reactive plan execution systems. In Proceedings of the 12th National Conference on Artificial Intelligence, Seattle, WA, USA, 31 July–4 August 1994; Hayes-Roth, B., Korf, R.E., Eds.; AAAI Press/The MIT Press: Cambridge, MA, USA, 1994; Volume 2, pp. 1232–1237. [Google Scholar]
- Huber, M.J. JAM: A BDI-theoretic mobile agent architecture. In Proceedings of the Third Annual Conference on Autonomous Agents, Seattle, WA, USA, 1–5 May 1999; pp. 236–243. [Google Scholar]
- Howden, N.; Rönnquist, R.; Hodgson, A.; Lucas, A. Intelligent agents-summary of an agent infrastructure. In Proceedings of the 5th International Conference on Autonomous Agents, Montreal, Canada, 28 May–1 June 2001. [Google Scholar]
- d’Inverno, M.; Kinney, D.; Luck, M. Interaction protocols in Agentis. In Proceedings of the International Conference on Multi Agent Systems (Cat. No. 98EX160), Paris, France, 3–7 July 1998; pp. 112–119. [Google Scholar]
- Grumberg, O.; Veith, H. 25 Years of Model Checking: History, Achievements, Perspectives; Springer: Cham, Switzerland, 2008; Volume 5000. [Google Scholar]
- Castillo, O.; Cervantes, L.; Soria, J.; Sanchez, M.; Castro, J.R. A generalized type-2 fuzzy granular approach with applications to aerospace. Inf. Sci. 2016, 354, 165–177. [Google Scholar] [CrossRef]
- Ooi, M.E.; Sayuti, M.; Sarhan, A.A.D. Fuzzy logic-based approach to investigate the novel uses of nano suspended lubrication in precise machining of aerospace AL tempered grade 6061. J. Clean. Prod. 2015, 89, 286–295. [Google Scholar] [CrossRef]
- Jaffar, J.; Maher, M.J. Constraint Logic Programming: A Survey. J. Logic Program. 1994, 19/20, 503–581. [Google Scholar] [CrossRef]
- Carlsson, M.; Mildner, P. SICStus Prolog—The first 25 years. Theory Pract. Log. Program. 2012, 12, 35–66. [Google Scholar] [CrossRef]
- Leitão, P.; Karnouskos, S.; Ribeiro, L.; Lee, J.; Strasser, T.I.; Colombo, A.W. Smart Agents in Industrial Cyber-Physical Systems. Proc. IEEE 2016, 104, 1086–1101. [Google Scholar] [CrossRef]
- Torres, A.; Nieto, J.J. Fuzzy logic in medicine and bioinformatics. BioMed Res. Int. 2006, 2006, 7. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Keller, J.; Popescu, M.; Bondugula, R. Applications of Fuzzy Logic in Bioinformatics; World Scientific: Singapore, 2008; Volume 9. [Google Scholar]
- Kwiatkowska, M.Z.; Norman, G.; Parker, D. PRISM: Probabilistic Symbolic Model Checker. In Lecture Notes in Computer Science, Proceedings of the Computer Performance Evaluation, Modelling Techniques and Tools 12th International Conference, TOOLS 2002, London, UK, 14–17 April 2002; Field, T., Harrison, P.G., Bradley, J.T., Harder, U., Eds.; Springer: Cham, Switzerland, 2002; Volume 2324, pp. 200–204. [Google Scholar] [CrossRef]
- Pasareanu, C.S.; Visser, W.; Bushnell, D.H.; Geldenhuys, J.; Mehlitz, P.C.; Rungta, N. Symbolic PathFinder: Integrating symbolic execution with model checking for Java bytecode analysis. Autom. Softw. Eng. 2013, 20, 391–425. [Google Scholar] [CrossRef]
- Wu, H. Industrial Applications of Probabilistic Model Checking- A Model-based Approach for Embedded Networked Systems and Concurrent Data Structures. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 4 July 2017. [Google Scholar]
- Winikoff, M. JACKTM Intelligent Agents: An Industrial Strength Platform. In Multi-Agent Programming: Languages, Platforms and Applications; Bordini, R.H., Dastani, M., Dix, J., Fallah-Seghrouchni, A.E., Eds.; Springer: Cham, Switzerland, 2005; Volume 15, pp. 175–193. [Google Scholar]
- Holzmann, G.J. The Model Checker SPIN. IEEE Trans. Softw. Eng. 1997, 23, 279–295. [Google Scholar] [CrossRef]
- Alam, K.M.; El Saddik, A. C2PS: A digital twin architecture reference model for the cloud-based cyber-physical systems. IEEE Access 2017, 5, 2050–2062. [Google Scholar] [CrossRef]
- Mbuli, J.; Trentesaux, D.; Clarhaut, J.; Branger, G. Decision support in condition-based maintenance of a fleet of cyber-physical systems: A fuzzy logic approach. In Proceedings of the Intelligent Systems Conference (IntelliSys), London, UK, 7–8 September 2017; pp. 82–89. [Google Scholar]
- Goztepe, K. Designing fuzzy rule based expert system for cyber security. Int. J. Inf. Secur. Sci. 2012, 1, 13–19. [Google Scholar]
- Linda, O.; Manic, M.; Vollmer, T.; Wright, J. Fuzzy logic based anomaly detection for embedded network security cyber sensor. In Proceedings of the IEEE Symposium on Computational Intelligence in Cyber Security (CICS), Paris, France, 11–15 April 2011; pp. 202–209. [Google Scholar]
- Kacprzyk, J.; Yager, R.R.; Zadrożny, S. A fuzzy logic based approach to linguistic summaries of databases. Int. J. Appl. Math. Comput. Sci. 2000, 10, 813–834. [Google Scholar]
- Kacprzyk, J.; Zadrożny, S.; Ziołkowski, A. FQUERY III+: A “human-consistent” database querying system based on fuzzy logic with linguistic quantifiers. Inf. Syst. 1989, 14, 443–453. [Google Scholar] [CrossRef]
- Liu, K.F.R.; Lai, J.H. Decision-support for environmental impact assessment: A hybrid approach using fuzzy logic and fuzzy analytic network process. Expert Syst. Appl. 2009, 36, 5119–5136. [Google Scholar] [CrossRef]
- Adriaenssens, V.; De Baets, B.; Goethals, P.L.M.; De Pauw, N. Fuzzy rule-based models for decision support in ecosystem management. Sci. Total Environ. 2004, 319, 1–12. [Google Scholar] [CrossRef]
- Gómez, S.A.; Chesñevar, C.I.; Simari, G.R. ONTOarg: A decision support framework for ontology integration based on argumentation. Expert Syst. Appl. 2013, 40, 1858–1870. [Google Scholar] [CrossRef]
- Suganthi, L.; Iniyan, S.; Samuel, A.A. Applications of fuzzy logic in renewable energy systems—A review. Renew. Sustain. Energy Rev. 2015, 48, 585–607. [Google Scholar] [CrossRef]
- Bojadziev, G. Fuzzy Logic for Business, Finance, and Management; World Scientific: Singapore, 2007; Volume 23. [Google Scholar]
- Gil-Lafuente, A.M. Fuzzy Logic in Financial Analysis; Springer: Cham, Switzerland, 2005. [Google Scholar]
- Prakken, H. Logical Tools for Modelling Legal Argument: A Study of Defeasible Reasoning in Law; Springer Science & Business Media: Berlin, Germany, 2013; Volume 32. [Google Scholar]
- Costa, A.; De Gloria, A.; Faraboschi, P.; Pagni, A.; Rizzotto, G. Hardware solutions for fuzzy control. Proc. IEEE 1995, 83, 422–434. [Google Scholar] [CrossRef]
- Bolognani, S.; Zigliotto, M. Hardware and software effective configurations for multi-input fuzzy logic controllers. IEEE Trans. Fuzzy Syst. 1998, 6, 173–179. [Google Scholar] [CrossRef]
- Croatti, A.; Montagna, S.; Ricci, A.; Gamberini, E.; Albarello, V.; Agnoletti, V. BDI personal medical assistant agents: The case of trauma tracking and alerting. Artif. Intell. Med. 2019, 96, 187–197. [Google Scholar] [CrossRef]
- Abbod, M.F.; von Keyserlingk, D.G.; Linkens, D.A.; Mahfouf, M. Survey of utilisation of fuzzy technology in medicine and healthcare. Fuzzy Sets Syst. 2001, 120, 331–349. [Google Scholar] [CrossRef]
- Yuan, B.; Herbert, J. Fuzzy CARA—A Fuzzy-Based Context Reasoning System For Pervasive Healthcare. Procedia Comput. Sci. 2012, 10, 357–365. [Google Scholar] [CrossRef][Green Version]
- Gupta, Y.; Saini, A.; Saxena, A.K. A new fuzzy logic based ranking function for efficient information retrieval system. Expert Syst. Appl. 2015, 42, 1223–1234. [Google Scholar] [CrossRef]
- Horng, Y.J.; Chen, S.M.; Chang, Y.C.; Lee, C.H. A new method for fuzzy information retrieval based on fuzzy hierarchical clustering and fuzzy inference techniques. IEEE Trans. Fuzzy Syst. 2005, 13, 216–228. [Google Scholar] [CrossRef]
- Azadegan, A.; Porobic, L.; Ghazinoory, S.; Samouei, P.; Kheirkhah, A.S. Fuzzy logic in manufacturing: A review of literature and a specialized application. Int. J. Prod. Econ. 2011, 132, 258–270. [Google Scholar] [CrossRef]
- Lin, J.L.; Lin, C.L. The use of grey-fuzzy logic for the optimization of the manufacturing process. J. Mater. Process. Technol. 2005, 160, 9–14. [Google Scholar] [CrossRef]
- Kohan, A.; Yamamoto, M.; Artho, C.; Yamagata, Y.; Ma, L.; Hagiya, M.; Tanabe, Y. Java Pathfinder on Android Devices. ACM SIGSOFT Softw. Eng. Notes 2016, 41, 1–5. [Google Scholar] [CrossRef]
- Martinelli, F.; Mercaldo, F.; Nardone, V. Identifying Insecure Features in Android Applications using Model Checking. In Proceedings of the 4th International Conference on Information Systems Security and Privacy (ICISSP 2018), Funchal, Madeira, Portugal, 22–24 January 2018; Mori, P., Furnell, S., Camp, O., Eds.; SciTePress: Setubal, Portugal, 2018; pp. 589–596. [Google Scholar] [CrossRef]
- Sezer, S.; Atalay, A.E. Dynamic modeling and fuzzy logic control of vibrations of a railway vehicle for different track irregularities. Simul. Model. Pract. Theory 2011, 19, 1873–1894. [Google Scholar] [CrossRef]
- Skarlatos, D.; Karakasis, K.; Trochidis, A. Railway wheel fault diagnosis using a fuzzy-logic method. Appl. Acoust. 2004, 65, 951–966. [Google Scholar] [CrossRef]
- Ghosh, S.; Razouqi, Q.; Schumacher, H.J.; Celmins, A. A survey of recent advances in fuzzy logic in telecommunications networks and new challenges. IEEE Trans. Fuzzy Syst. 1998, 6, 443–447. [Google Scholar] [CrossRef]
- Catania, V.; Ficili, G.; Palazzo, S.; Panno, D. Using fuzzy logic in ATM source traffic control: Lessons and perspectives. IEEE Commun. Mag. 1996, 34, 70–74. [Google Scholar] [CrossRef]
- Sarkar, A.; Sahoo, G.; Sahoo, U.C. Application of fuzzy logic in transport planning. Int. J. Soft Comput. 2012, 3, 1. [Google Scholar] [CrossRef]
- Quddus, M.A.; Noland, R.B.; Ochieng, W.Y. A high accuracy fuzzy logic based map matching algorithm for road transport. J. Intell. Transp. Syst. 2006, 10, 103–115. [Google Scholar] [CrossRef]
- Donini, F.M.; Mongiello, M.; Ruta, M.; Totaro, R. A Model Checking-based Method for Verifying Web Application Design. Electron. Notes Theor. Comput. Sci. 2006, 151, 19–32. [Google Scholar] [CrossRef]
- Artzi, S.; Kiezun, A.; Dolby, J.; Tip, F.; Dig, D.; Paradkar, A.M.; Ernst, M.D. Finding Bugs in Web Applications Using Dynamic Test Generation and Explicit-State Model Checking. IEEE Trans. Softw. Eng. 2010, 36, 474–494. [Google Scholar] [CrossRef]
- Tran, V.X.; Tsuji, H. QoS based ranking for web services: Fuzzy approaches. In Proceedings of the 4th International Conference on Next Generation Web Services Practices, Seoul, Korea, 20–22 October 2008; pp. 77–82. [Google Scholar]
- Chao, K.M.; Younas, M.; Lo, C.C.; Tan, T.H. Fuzzy matchmaking for web services. In Proceedings of the 19th International Conference on Advanced Information Networking and Applications (AINA’05) Volume 1 (AINA papers), Taipei, Taiwan, 28–30 March 2005; Volume 2, pp. 721–726. [Google Scholar]
- Omicini, A. SODA: Societies and Infrastructures in the Analysis and Design of Agent-based Systems. In Agent-Oriented Software Engineering, Proceedings of the 1st International Workshop (AOSE 2000), Limerick, Ireland, 10 June 2000; Ciancarini, P., Wooldridge, M.J., Eds.; Revised Papers; Lecture Notes in Computer Science; Revised Papers; Springer: Berlin/Heidelberg, Germany, 2001; Volume 1957, pp. 185–193. [Google Scholar] [CrossRef]
- Ciancarini, P. Distributed Programming with Logic Tuple Spaces. New Gener. Comput. 1994, 12, 251–283. [Google Scholar] [CrossRef]
- Omicini, A.; Zambonelli, F. Coordination for Internet Application Development. Auton. Agents Multi-Agent Syst. 1999, 2, 251–269. [Google Scholar] [CrossRef]
- Omicini, A.; Denti, E. From Tuple Spaces to Tuple Centres. Sci. Comput. Program. 2001, 41, 277–294. [Google Scholar] [CrossRef]
- Jensen, A.S.; Dignum, V.; Villadsen, J. The AORTA Architecture: Integrating Organizational Reasoning in Jason. In Engineering Multi-Agent Systems; Dalpiaz, F., Dix, J., van Riemsdijk, M.B., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2014; Volume 8758, pp. 127–145. [Google Scholar]
- Dung, P.M. On the Acceptability of Arguments and Its Fundamental Role in Nonmonotonic Reasoning, Logic Programming and N-person Games. Artif. Intell. 1995, 77, 321–357. [Google Scholar] [CrossRef]
- Gaggl, S.A.; Linsbichler, T.; Maratea, M.; Woltran, S. Summary Report of the Second International Competition on Computational Models of Argumentation. AI Mag. 2018, 39, 77–79. [Google Scholar] [CrossRef]
- Nardini, E.; Omicini, A.; Viroli, M. Description Spaces with Fuzziness. In Proceedings of the 26th Annual ACM Symposium on Applied Computing (SAC 2011), TaiChung, Taiwan, 21–25 March 2011; Palakal, M.J., Hung, C.C., Chu, W., Wong, W.E., Eds.; Volume II: Artificial Intelligence & Agents, Information Systems, and Software Development. 2011; pp. 869–876. [Google Scholar] [CrossRef]
- Nardini, E.; Viroli, M.; Panzavolta, E. Coordination in open and dynamic environments with TuCSoN semantic tuple centres. In Proceedings of the 2010 ACM Symposium on Applied Computing (SAC), Sierre, Switzerland, 22–26 March 2010; Shin, S.Y., Ossowski, S., Schumacher, M., Palakal, M.J., Hung, C., Eds.; ACM: Sierre, Switzerland, 2010; pp. 2037–2044. [Google Scholar] [CrossRef]
- Hollan, J.; Hutchins, E.; Kirsh, D. Distributed Cognition: Toward a New Foundation for Human-Computer Interaction Research. ACM Trans. Comput.-Hum. Interact. (TOCHI) 2000, 7, 174–196. [Google Scholar] [CrossRef]
- Hendler, J. Agents and the Semantic Web. IEEE Intell. Syst. 2001, 16, 30–37. [Google Scholar] [CrossRef]
- Anderson, J.R.; Lebiere, C. The Newell Test for a Theory of Cognition. Behav. Brain Sci. 2003, 26, 587–601. [Google Scholar] [CrossRef]
- Sun, R. (Ed.) The CLARION Cognitive Architecture: Extending Cognitive Modeling to Socia Simulation. In Cognition and Multi-Agent Interaction: From Cognitive Modeling to Social Simulation; Cambridge University Press: Cambridge, UK, 2005; pp. 79–100. [Google Scholar] [CrossRef]
- Franklin, S.; Madl, T.; D’Mello, S.; Snaider, J. LIDA: A Systems-level Architecture for Cognition, Emotion, and Learning. IEEE Trans. Auton. Ment. Dev. 2014, 6, 19–41. [Google Scholar] [CrossRef]
- Bie, T.D.; Cristianini, N. Convex methods for transduction. In Advances in Neural Information Processing Systems; Thrun, S., Saul, L.K., Schölkopf, B., Eds.; MIT Press: Cambridge, MA, USA, 2004; pp. 73–80. [Google Scholar]
- Berners-Lee, T.; Hendler, J.; Lassila, O. The semantic web. Sci. Am. 2001, 284, 34–43. [Google Scholar] [CrossRef]
- Abidi, S.S.R. Healthcare Knowledge Management: The Art of the Possible. In Knowledge Management for Health Care Procedures; Riaño, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–20. [Google Scholar]
- Ossowski, S. Agreement Technologies; Law, Governance and Technology Series; Springer: Amsterdam, The Netherlands, 2012; Volume 8. [Google Scholar] [CrossRef]
- Garcia, A.J.; Simari, G.R. Defeasible logic programming: An argumentative approach. Theory Pract. Log. Program. 2004, 4, 95–138. [Google Scholar] [CrossRef]
- Modgil, S.; Prakken, H. The ASPIC+ framework for structured argumentation: A tutorial. Argum. Comput. 2014, 5, 31–62. [Google Scholar] [CrossRef]
- Dung, P.M.; Kowalski, R.A.; Toni, F. Assumption-based argumentation. In Argumentation in Artificial Intelligence; Springer: Amsterdam, The Netherlands, 2009; pp. 199–218. [Google Scholar]
- Solarte-Vasquez, M.C.; Järv, N.; Nyman-Metcalf, K. Usability factors in transactional design and smart contracting. In The Future of Law and eTechnologies; Kerikmäe, T., Rull, A., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 149–176. [Google Scholar] [CrossRef]
- Kerikmae, T.; Hoffmann, T.; Chochia, A. Legal technology for law firms: Determining roadmaps for innovation. Croat. Int. Relations Rev. 2018, 24, 91–112. [Google Scholar] [CrossRef]
- Prakken, H.; Sartor, G. Law and logic: A review from an argumentation perspective. Artif. Intell. 2015, 227, 214–245. [Google Scholar] [CrossRef]
- Guangzuo, C.; Fei, C.; Hu, C.; Shufang, L. OntoEdu: A case study of ontology-based education grid system for e-learning. In Proceedings of the GCCCE Global Chinese Conference on Computers in Education, Hong Kong, China, 23–27 May 2004; pp. 1–9. [Google Scholar]
- Sancho, P.; Martínez, I.; Fernández-Manjón, B. Semantic Web Technologies Applied to e-learning Personalization in <e-aula>. J. Univers. Comput. Sci. 2005, 11, 1470–1481. [Google Scholar]
- Almohammadi, K.; Hagras, H. An adaptive fuzzy logic based system for improved knowledge delivery within intelligent E-Learning platforms. In Proceedings of the IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2013), Hyderabad, India, 7–10 July 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Chrysafiadi, K.; Virvou, M. PeRSIVA: An empirical evaluation method of a student model of an intelligent e-learning environment for computer programming. Comput. Educ. 2013, 68, 322–333. [Google Scholar] [CrossRef]
- Gong, T.; Cai, Z. An immune agent for web-based AI course. Int. J. E-Learn. 2006, 5, 493–506. [Google Scholar]
- Yacef, K. The Logic-ITA in the classroom: A medium scale experiment. Int. J. Artif. Intell. Educ. 2005, 15, 41–62. [Google Scholar]
- Pedro, F.; Subosa, M.; Rivas, A.; Valverde, P. Artificial Intelligence in Education: Challenges and Opportunities for Sustainable Development; Technical Report Number ED-2019/WS/8, January 2019; UNESCO: Paris, France, 2019; Available online: https://unesdoc.unesco.org/ark:/48223/pf0000366994 (accessed on 21 March 2020).
- Tuomi, I. The Impact of Artificial Intelligence on Learning, Teaching, and Education; Technical Report, JRC Working Paper; Joint Research Centre (Seville site): Seville, Spain, 2018. [Google Scholar]
- Baheti, R.; Gill, H. Cyber-physical systems. Impact Control Technol. 2011, 12, 161–166. [Google Scholar]
- Akbarinia, R.; Martins, V.; Pacitti, E.; Valduriez, P. Design and implementation of Atlas P2P architecture. Glob. Data Manag. 2006, 8, 98. [Google Scholar]
- Simonis, H. Building Industrial Applications with Constraint Programming. In Constraints in Computational Logics, Proceedings of the Theory and Applications International Summer School (CCL ’99), Gif-sur-Yvette, France, 5–8 September 1999; Goos, G., Hartmanis, J., van Leeuwen, J., Comon, H., Marché, C.M., Treinen, R., Eds.; Revised Lecture; Springer: Cham, Switzerland, 2001; pp. 271–309. [Google Scholar] [CrossRef]
- Simonis, H.; Charlier, P.; Kay, P. Constraint handling in an integrated transportation problem. IEEE Intell. Syst. Their Appl. 2000, 15, 26–32. [Google Scholar] [CrossRef]
- Baues, G.; Kay, P.; Charlier, P. Constraint based resource allocation for airline crew management. Proc. ATTIS 1994, 94. [Google Scholar]
- Wallace, M. Practical applications of constraint programming. Constraints 1996, 1, 139–168. [Google Scholar] [CrossRef]
- Simonis, H. Application development with the CHIP system. In Lecture Notes in Computer Science, Proceedings of the Constraint Databases and Applications, Friedrichshafen, Germany, 8–9 September 1996; Kuper, G.W.M., Ed.; Springer: Berlin/Heidelberg, Germany, 1996; Volume 1034, pp. 1–21. [Google Scholar]
- Bistarelli, S. Soft Constraint Solving and Programming: A General Framework. Ph.D. Thesis, Computer Science Department, University of Pisa, Pisa, Italy, 1 March 2001. [Google Scholar]
- Ferrein, A.; Lakemeyer, G. Logic-based robot control in highly dynamic domains. Robot. Auton. Syst. 2008, 56, 980–991. [Google Scholar] [CrossRef]
- Lytras, M.D. Knowledge Management Strategies: A Handbook of Applied Technologies: A Handbook of Applied Technologies; IGI Global: Hershey, PA, USA, 2008; Volume 5. [Google Scholar]
- Chilwal, B.; Mishra, P.K. A Survey of Fuzzy Logic Inference System and Other Computing Techniques for Agricultural Diseases. In Proceedings of the International Conference on Intelligent Computing and Smart Communication, New Tehri, Uttarakhand, India, 20–21 April 2019; Singh Tomar, G., Chaudhari, N.S., Barbosa, J.L.V., Aghwariya, M.K., Eds.; Springer: Cham, Switzerland, 2020; pp. 1–6. [Google Scholar]
- Rastogi, A.; Arora, R.; Sharma, S. Leaf disease detection and grading using computer vision technology & fuzzy logic. In Proceedings of the 2nd International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 19–20 February 2015; pp. 500–505. [Google Scholar]
- Patil, P.; Kulkarni, U.; Desai, B.L.; Benagi, V.I.; Naragund, V.B. Fuzzy logic based irrigation control system using wireless sensor network for precision agriculture. In Proceedings of the 3rd National Conference on Agro-Informatics and Precision Agriculture (AIPA), Hyderabad, India, 1–3 August 2012; pp. 262–269. [Google Scholar]
- Zhu, A.; Yang, S.X. A fuzzy logic approach to reactive navigation of behavior-based mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’04), New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 5045–5050. [Google Scholar]
- Center, B.; Verma, B.P. Fuzzy logic for biological and agricultural systems. In Artificial Intelligence for Biology and Agriculture; Springer: Cham, Switzerland, 1998; Volume 12, pp. 213–225. [Google Scholar]
- Tahmasebi, P.; Hezarkhani, A. A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation. Comput. Geosci. 2012, 42, 18–27. [Google Scholar] [CrossRef]
- Finucane, C.; Jing, G.; Kress-Gazit, H. LTLMoP: Experimenting with language, temporal logic and robot control. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1988–1993. [Google Scholar]
- Fainekos, G.E.; Girard, A.; Kress-Gazit, H.; Pappas, G.J. Temporal logic motion planning for dynamic robots. Automatica 2009, 45, 343–352. [Google Scholar] [CrossRef]
- Kloetzer, M.; Belta, C. Temporal Logic Planning and Control of Robotic Swarms by Hierarchical Abstractions. IEEE Trans. Robot. 2007, 23, 320–330. [Google Scholar] [CrossRef]
- Smolensky, P. Connectionist AI, symbolic AI, and the brain. Artif. Intell. Rev. 1987, 1, 95–109. [Google Scholar] [CrossRef]
- Sun, R. Artificial Intelligence: Connectionist and Symbolic Approaches. In International Encyclopedia of the Social and Behavioral Sciences; Pergamon: Izmir, Turkey; Elsevier: Amsterdam, The Netherlands, 2001; pp. 783–789. [Google Scholar]
- Hendler, J. Avoiding Another AI Winter. IEEE Intell. Syst. 2008, 23, 2–4. [Google Scholar] [CrossRef]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education: London, UK, 2003. [Google Scholar]
- Hoehndorf, R.; Queralt-Rosinach, N. Data science and symbolic AI: Synergies, challenges and opportunities. Data Sci. 2017, 1, 27–38. [Google Scholar] [CrossRef]
- Calegari, R.; Ciatto, G.; Dellaluce, J.; Omicini, A. Interpretable Narrative Explanation for ML Predictors with LP: A Case Study for XAI. In Proceedings of the WOA 2019—20th Workshop “From Objects to Agents”, CEUR Workshop Proceedings, Parma, Italy, 26–28 June 2019. [Google Scholar]
- Calegari, R.; Ciatto, G.; Mariani, S.; Denti, E.; Omicini, A. LPaaS as Micro-intelligence: Enhancing IoT with Symbolic Reasoning. Big Data Cogn. Comput. 2018, 2, 23. [Google Scholar] [CrossRef]
- Besold, T.R.; d’Avila Garcez, A.S.; Bader, S.; Bowman, H.; Domingos, P.M.; Hitzler, P.; Kühnberger, K.; Lamb, L.C.; Lowd, D.; Lima, P.M.V.; et al. Neural-Symbolic Learning and Reasoning: A Survey and Interpretation. CoRR 2017, abs/1711.03902. [Google Scholar]
- Medsker, L.R. Hybrid Intelligent Systems; Springer Science & Business Media: Cham, Switzerland, 2012. [Google Scholar]
- Corchado, E.; Kurzynski, M.; Wozniak, M. Hybrid Artificial Intelligent Systems, Proceedings of the 6th International Conference, HAIS 2011, Wroclaw, Poland, 23–25 May 2011; Springer: Cham, Switzerland, 2011; Volume 667. [Google Scholar]
- Nauck, D.; Klawonn, F.; Kruse, R. Foundations of Neuro-Fuzzy Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1997. [Google Scholar]
- Sahoo, S.; Panda, S.K.; Pratihar, D.K.; Mukhopadhyay, S. Prediction of Step Length Using Neuro-Fuzzy Approach Suitable for Prosthesis Control. IEEE Trans. Instrum. Meas. 2020, 1, 1. [Google Scholar] [CrossRef]
- Sohani, M.; Makki, B.; Sadati, N.; Kermani, K.K.; Riazati, A. A Neuro-Fuzzy approach to diagnosis of neonatal jaundice. In Proceedings of the 1st Bio-Inspired Models of Network, Information and Computing Systems, Madonna di Campiglio, Italy, 11–13 December 2006; pp. 1–4. [Google Scholar]
- Wu, Y.; Zhang, B.; Lu, J.; Du, L.; Du, K.L. Fuzzy Logic and Neuro-fuzzy Systems: A Systematic Introduction. Int. J. Artif. Intell. Expert Syst. 2011, 2, 2011–2047. [Google Scholar]
- Garcez, A.S.D.; Lamb, L.C.; Gabbay, D.M. Neural-Symbolic Cognitive Reasoning; Springer Publishing Company, Inc.: Cham, Switzerland, 2008. [Google Scholar]
- Garcez, A.D.; Gori, M.; Lamb, L.C.; Serafini, L.; Spranger, M.; Tran, S.N. Neural-symbolic computing: An effective methodology for principled integration of machine learning and reasoning. J. Appl. Logics IfCoLoG J. Logics Their Appl. 2019, 6, 611. [Google Scholar]
- Makki, B.; Hosseini, M.N. Some refinements of the standard autoassociative neural network. Neural Comput. Appl. 2013, 22, 1461–1475. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Garcez, A.D.; Besold, T.R.; De Raedt, L.; Földiak, P.; Hitzler, P.; Icard, T.; Kühnberger, K.U.; Lamb, L.C.; Miikkulainen, R.; Silver, D.L. Neural-symbolic learning and reasoning: Contributions and challenges. In Proceedings of the AAAI Spring Symposium Series, Stanford University, Palo Alto, CA, USA, 23–25 March 2015. [Google Scholar]
- Pinkas, G. Symmetric neural networks and propositional logic satisfiability. Neural Comput. 1991, 3, 282–291. [Google Scholar] [CrossRef]
- Guidotti, R.; Monreale, A.; Turini, F.; Pedreschi, D.; Giannotti, F. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. (CSUR) 2019, 51, 1–42. [Google Scholar] [CrossRef]
- Andrews, R.; Diederich, J.; Tickle, A.B. Survey and critique of techniques for extracting rules from trained artificial neural networks. Knowl.-Based Syst. 1995, 8, 373–389. [Google Scholar] [CrossRef]
- d’Avila Garcez, A.S.; Broda, K.; Gabbay, D.M. Symbolic knowledge extraction from trained neural networks: A sound approach. Artif. Intell. 2001, 125, 155–207. [Google Scholar] [CrossRef]
- Bologna, G.; Hayashi, Y. A Comparison Study on Rule Extraction from Neural Network Ensembles, Boosted Shallow Trees, and SVMs. Appl. Comput. Intell. Soft Comput. 2018, 2018, 20. [Google Scholar] [CrossRef]
- Bologna, G.; Hayashi, Y. A rule extraction study on a neural network trained by deep learning. In Proceedings of the IEEE International Joint Conference on Neural Networks (IJCNN 2016), Vancouver, BC, Canada, 24–29 July 2016; pp. 668–675. [Google Scholar] [CrossRef]
- Frosst, N.; Hinton, G.E. Distilling a Neural Network Into a Soft Decision Tree. In Proceedings of the First International Workshop on Comprehensibility and Explanation in AI and ML 2017 Co-Located with 16th International Conference of the Italian Association for Artificial Intelligence (AI*IA 2017), CEUR Workshop Proceedings, Bari, Italy, 14–17 November 2017; Besold, T.R., Kutz, O., Eds.; 2017; Volume 2071. [Google Scholar]
- Johansson, U.; Niklasson, L. Evolving decision trees using oracle guides. In Proceedings of the IEEE Symposium on Computational Intelligence and Data Mining, CIDM 2009, Part of the IEEE Symposium Series on Computational Intelligence, Nashville, TN, USA, 30 March–2 April 2009; pp. 238–244. [Google Scholar] [CrossRef]
- Krishnan, R.; Sivakumar, G.; Bhattacharya, P. Extracting decision trees from trained neural networks. Pattern Recognit. 1999, 32, 1999–2009. [Google Scholar] [CrossRef]
- Hruschka, E.R.; Ebecken, N.F.F. Extracting rules from multilayer perceptrons in classification problems: A clustering-based approach. Neurocomputing 2006, 70, 384–397. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y.; Chen, S.F. Extracting symbolic rules from trained neural network ensembles. AI Commun. 2003, 16, 3–15. [Google Scholar]
- Craven, M.W.; Shavlik, J.W. Extracting Tree-Structured Representations of Trained Networks. In Proceedings of the 8th International Conference on Neural Information Processing Systems (NIPS’95), Denver, CO, USA, 27–30 November 1995; Touretzky, D.S., Mozer, M., Hasselmo, M.E., Eds.; MIT Press: Cambridge, MA, USA, 1995; pp. 24–30. [Google Scholar]
- Augasta, M.G.; Kathirvalavakumar, T. Reverse Engineering the Neural Networks for Rule Extraction in Classification Problems. Neural Process. Lett. 2012, 35, 131–150. [Google Scholar] [CrossRef]
- Sato, M.; Tsukimoto, H. Rule extraction from neural networks via decision tree induction. In Proceedings of the IJCNN’01, International Joint Conference on Neural Networks, Proceedings (Cat. No.01CH37222), Washington, DC, USA, 15–19 July 2001; Volume 3, pp. 1870–1875. [Google Scholar] [CrossRef]
- Kahramanli, H.; Allahverdi, N. Rule extraction from trained adaptive neural networks using artificial immune systems. Expert Syst. Appl. 2009, 36, 1513–1522. [Google Scholar] [CrossRef]
- Arrieta, A.B.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; García, S.; Gil-López, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion 2020, 58, 82–115. [Google Scholar] [CrossRef]
- Došilović, F.K.; Brčić, M.; Hlupić, N. Explainable artificial intelligence: A survey. In Proceedings of the 41st International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 21–25 May 2018; pp. 210–215. [Google Scholar]
- Muggleton, S. Inverse entailment and Progol. New Gener. Comput. 1995, 13, 245–286. [Google Scholar] [CrossRef]
- Muggleton, S.; Buntine, W. Machine invention of first-order predicates by inverting resolution. In Machine Learning Proceedings 1988; Elsevier: Amsterdam, The Netherlands, 1988; pp. 339–352. [Google Scholar]
- Muggleton, S.; Santos, J.; Tamaddoni-Nezhad, A. ProGolem: A system based on relative minimal generalisation. In Lecture Notes in Computer Science, Proceedings of the International Conference on Inductive Logic Programming, Leuven, Belgium, 2–4 July 2009; De Raedt, L., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5989, pp. 131–148. [Google Scholar]
- Bordini, R.H.; Hübner, J.F.; Wooldridge, M. Programming Multi-Agent Systems in AgentSpeak Using Jason; Wiley Series in Agent Technology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007; Volume 8. [Google Scholar] [CrossRef]
- Mochales, R.; Moens, M.F. Argumentation mining. Artif. Intell. Law 2011, 19, 1–22. [Google Scholar] [CrossRef]
- Denti, E.; Natali, A.; Omicini, A. Programmable Coordination Media. In Coordination Languages and Models, Proceedings of the 2nd International Conference (COORDINATION’97), Berlin, Germany, 1–3 September 1997; Garlan, D., Le Métayer, D., Eds.; LNCS; Springer: Berlin, Germany, 1997; Volume 1282, pp. 274–288. [Google Scholar] [CrossRef]
- De Angelis, F.L.; Di Marzo Serugendo, G. Logic Fragments: Coordinating Entities with Logic Programs. In Leveraging Applications of Formal Methods, Verification and Validation: Foundational Techniques; Margaria, T., Steffen, B., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 589–604. [Google Scholar]
- Gardelli, L.; Viroli, M.; Omicini, A. Combining Simulation and Formal Tools for Developing Self-Organizing MAS. In Multi-Agent Systems: Simulation and Applications; Uhrmacher, A.M., Weyns, D., Eds.; Computational Analysis, Synthesis, and Design of Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2009; Chapter 5; pp. 133–165. [Google Scholar]
- Calegari, R.; Denti, E.; Mariani, S.; Omicini, A. Logic Programming as a Service. Theory Pract. Log. Program. 2018, 18, 846–873. [Google Scholar] [CrossRef]
- Goranko, V.; Montanari, A.; Sciavicco, G. A road map of interval temporal logics and duration calculi. J. Appl. Non-Class. Logics 2004, 14, 9–54. [Google Scholar] [CrossRef]
- Hölldobler, S.; Lutz, C.; Wansing, H. Logics in Artificial Intelligence; Springer: Cham, Switzerland, 2008; Volume 5293. [Google Scholar]
- Della Monica, D.; Goranko, V.; Montanari, A.; Sciavicco, G. Interval temporal logics: A journey. Bull. EATCS 2013, 3, 105. [Google Scholar]
- Larus, J.R.; Rajwar, R. Transactional memory. Synth. Lect. Comput. Archit. 2007, 1, 1–226. [Google Scholar]
- Jacobsen, D.A.; Senocak, I. Multi-level parallelism for incompressible flow computations on GPU clusters. Parallel Comput. 2013, 39, 1–20. [Google Scholar] [CrossRef]
| FOL | DL | BDI | TL | FL | PL | DR | CLP | |
|---|---|---|---|---|---|---|---|---|
| Formalization & Verification | ✓ | ✓ | ||||||
| Cognitive Agents | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| Healthcare & Wellbeing | ✓ | ✓ | ✓ | |||||
| Law & Governance | ✓ | ✓ | ||||||
| Education | ✓ | ✓ | ✓ | |||||
| Planning & Task Allocation | ✓ | ✓ | ✓ | ✓ | ||||
| Robotics & Control | ✓ | ✓ | ✓ | ✓ |
| FOL | DL | BDI | TL | FL | PL | DR | CLP | |
|---|---|---|---|---|---|---|---|---|
| Aerospace | [54,55] | [56] | ||||||
| Analytics | [57] | [58] | ||||||
| Bioinformatics | [57] | [12,17] | [59,60] | [61] | [56] | |||
| BPM | [57] | [17] | ||||||
| Constructions | [56] | |||||||
| Critical systems | [62,63] | |||||||
| CPS | [17] | [58,64] | [65] | [66,67] | [61] | |||
| Cybersecurity | [68,69] | [61] | ||||||
| Databases | [12] | [70,71] | ||||||
| Decision support | [72,73] | [74] | ||||||
| Energy | [24] | [58] | [65] | [75] | [61] | [56] | ||
| Finance | [24] | [76,77] | [56] | |||||
| Government & Legal | [78] | |||||||
| Hardware | [24] | [79,80] | [56] | |||||
| Healthcare | [58,81] | [65] | [82,83] | |||||
| Information retrieval | [12] | [84,85] | ||||||
| Logistic | [57] | [24] | [58,64] | [65] | [56] | |||
| Manufacturing | [58,64] | [65] | [86,87] | |||||
| Mechanics | [56] | |||||||
| Mobile applications | [88,89] | |||||||
| Railways | [63] | [90,91] | ||||||
| Telecommunications | [57] | [92,93] | [61] | [56] | ||||
| Transports | [58] | [94,95] | ||||||
| Web services | [12,17] | [96,97] | [98,99] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calegari, R.; Ciatto, G.; Denti, E.; Omicini, A. Logic-Based Technologies for Intelligent Systems: State of the Art and Perspectives. Information 2020, 11, 167. https://doi.org/10.3390/info11030167
Calegari R, Ciatto G, Denti E, Omicini A. Logic-Based Technologies for Intelligent Systems: State of the Art and Perspectives. Information. 2020; 11(3):167. https://doi.org/10.3390/info11030167
Chicago/Turabian StyleCalegari, Roberta, Giovanni Ciatto, Enrico Denti, and Andrea Omicini. 2020. "Logic-Based Technologies for Intelligent Systems: State of the Art and Perspectives" Information 11, no. 3: 167. https://doi.org/10.3390/info11030167
APA StyleCalegari, R., Ciatto, G., Denti, E., & Omicini, A. (2020). Logic-Based Technologies for Intelligent Systems: State of the Art and Perspectives. Information, 11(3), 167. https://doi.org/10.3390/info11030167








