1.1. Signal Detection Theory in Perception: A Primer
Signal detection theory (SDT) has been widely used in studies of human visual and auditory perception since its introduction by [
1] Green and Swets. A textbook by [
2] Macmillan and Creelman provides a nice introduction to what has become a rather developed field. An important aspect of the theory from the point of view of this paper is that it provides a role for a mental concept, namely, attention, which was previously taken to be entirely subjective. Signal detection theory (SDT) provides ways of conceptualizing the role of attention both in processing sensory information and in how decisions about what is sensed are reached. SDT points towards methods of identifying the effects of attention which can also be applied in studies of animals, making attention an objective concept at some cost to its phenomenology.
Intuition suggests that paying more attention should enhance performance; indeed, it has been taken as a defining characteristic in Psychology that items selected by attention will be processed better, and rejected items worse, than neutral items (e.g., Posner et al. [
3]). To explain this role for attention in SDT terms requires at least an elementary exposition of SDT, which the reader may skip if this material is already familiar. The essential idea is that stimulation (auditory, visual, tactile) can be represented as activity on a single internal dimension termed ‘strength’. Strength represents the evidence accumulated by the senses towards a categorical decision, such as that I see a butterfly—evidence that may rely on one dimension (e.g., sound level) or on numerous dimensions (color, motion, size) which are presumed to be integrated into one evidential signal. The perceiver in an experimental trial is assumed to orient towards a signal or stimulus, denoted by S, and answer ‘Yes’ when interrogated about its presence if the strength of the evidence (denoted z) elicited by S exceeds a criterion level, denoted c. The perceiver has a forced-choice decision between Yes and No, not being allowed to report ‘uncertain’.
Averaged over trials, one can compute the ‘hit rate’ or probability P (z > c S) that the subject reports ‘Yes’ given that the signal or stimulus was present, the ‘false alarm rate’ P (z > c no S), the ‘miss rate’ P (z < c S) and the ‘correct rejection’ P (z < c no S). Accuracy, the proportion of correct trials, Pc, is then P (z > c S) Ps + P (z < c no S) (1-Ps), where Ps is the probability of a stimulus being presented. These definitions apply to binary trials, when there are two possible signals or stimulus conditions, and two possible responses. In general, there are four classes of events: a hit {S1, R1}, a false alarm {S1, R2}, a miss {S1, R2}, and a correct rejection {S2, R2}.
These binary definitions apply to ‘Yes, No’ experiments, in which S2 is null and R2 is ‘No’, as well as to discrimination experiments in which S1 and S2 are distinct stimuli and R1 and R2 the corresponding identifiers. For example, subjects might discriminate between a square and a triangle, or between a high and a low tone. Since the mathematics are the same, P (z < c S1), P (z < c S2), P (z < c S1) and P (z < c S2) are still termed ‘hits’, ‘false alarms’, ‘misses’, and correct rejections, even though these terms are logical only for the detection experiment. In a search experiment, S1 might be the target (say, an apple) and S2 a set of distractors (a bowl of many other fruits), but again the mathematics are the same.
These four probabilities, P (z > c S) and so on, can be modeled if the internal strength variable is assumed to be corrupted by Gaussian noise, N, with mean 0 and variance 1.0. Other probability distributions are possible, as when light is detected and a Poisson counting variable is required, but only for the Gaussian are the mean and variance mathematically independent, which simplifies matters. Strengths on discrimination trials are either S + N, with mean S, or N, with mean 0, while strengths on discrimination trials are either S1 + N or S2 + N, with means S1, S2. When signals are constant, the corresponding variances all equal 1.0, the noise variance. The hit rate is then Phit = P (z > c S + N), the false alarm rate is Pfa = P (z > c N), and detectability, d’ = z (Phit)-z (Pfa), where z(p) is the inverse normal score, z, associated with probability p, such that z (0.5) = 0, z (0.1) = −1.28, and z (0.9) = + 1.28. The criterion, c = −[z (Phit)−z (Pfa)]/2; this defines c as mathematically independent of d’, i.e., values of one do not constrain the value of the other. A ‘conservative’ value of c, that is c > 0, implies that the subject reports ‘No’ more often than Yes; a ‘liberal’ criterion, c < 0, implies the opposite; and a balanced criterion, c = 0, implies no bias either way (Other definitions of the criterion, such as β, are not independent of d’ and will not be considered further here, although they have their specialized uses [
2]).
Note that d’ in an unbiased estimate of S, that is, d’ tends to S, since the mean strength on signal trials is S—much greater than that on noise trials (d’ is an estimate given a finite number of trials; its uncertainty is given in [
4]). For example, if Phit = 0.9 and Pfa = 0.1, the detectability score d’ = 1.28–−1.28 = 2.46. As the perceiver makes more hits and fewer false alarms, detectability (d’) increases. Conversely, if Phit = Pfa, so that d’ = 0, the subject operates at chance, reporting ‘Yes’ equally often whether the stimulus is present or not. Usually, 0 < d’ < 4.0; negative d’s are possible but represent aberrant responding (saying No for Yes and vice versa), whereas d’ > 4 indicates so few erroneous trials as to make estimation suspect.
As the response probabilities are conditional, Ps, the probability of the stimulus, does not enter into the measurement of d’. It therefore becomes an empirical matter whether varying Ps increases, decreases or leaves detectability unchanged. An increase in d’ with Ps may imply an increase in the preparation or ‘set’ for a stimulus, which is one aspect of paying attention. In ‘signal known exactly’ experiments, clear versions of S are presented, along with temporal cues to indicate onset and offset of S, so that the perceiver knows what the target is and when it can occur. In contrast, in ‘oddity’ experiments, the signal is an unexpected deviation from a standard, one whose timing or nature cannot be anticipated. Differences in d’ between signals known exactly and unprepared signals provide evidence that attention to the signal improves sensitivity (e.g., [
5] Santhi and Reeves, 2003).
Crime provides a real-world example of SDT. Suppose the world contains dishonest (S1) and honest (S2) individuals, and the response of society is to lock them up (R1) or set them free (R2). Noise (N) is the uncertainty of the evidence, and the criterion (c) is the amount of evidence needed to convict. Different bodies collect evidence (police) and make Yes/No decisions (jury). Improvements in policing increase d’, while changes in laws alter c. The analogy to perception is useful. The sensorium (ear, eye) collects the evidence on which the decision is made (in cortex). Detectability measures the sensory efficiency, and the criterion measures the deciding element. As long as the latter does not interfere with the former, the evidence will not be biased by the desire to obtain one or other answer (as when the judge and jury are segregated from the police to avoid corruption.) Distinguishing a sensory stage from a subsequent decision stage helps to provide a rational account in SDT terms of sensation (the first stage alone), perception (sensation plus a correct decision leading to a hit) and hallucination (sensation plus a wrong decision generating a false alarm or a miss in the case of a negative hallucination).
1.2. The Role of Selective Attention
Selective attention is defined here as resources devoted to collecting evidence about a particular target stimulus, S, and rejecting other possible stimuli as noise (N) [
6] Fine and Reeves, 2018, tabulate 19 other ways in which attention has been defined and operationalized in psychology and neuroscience). Given a limited time for collection, increasing resources (i.e., increasing attention) will increase d’ by increasing signal strength, S; decreasing resources by attending elsewhere will attenuate the stimulus (e.g., Carrasco et al. [
7]). This definition includes all-or-none selection, which occur if the stimulus is either selected fully or rejected completely ([
8] Palmer, 1995), as well as graded selection (for an example in hearing, see Reeves and Scharf [
9]). In the following paper, the term ‘focusing’ is used for concentrating attention on a stimulus or subset of stimuli, the task set for the subject being to ‘monitor’ those stimuli. The expected sequence in a selective attention experiment is that, when asked to monitor a subset of stimuli, the subject focuses attention on them, and sensitivity (d’) improves.
Altering c does not change the amount of evidence and so is not equivalent to selective attention as defined. Since the overall proportion of correct trials, Pc, can go up based on either better evidence or a more optimal criterion, finding an increase in Pc is not necessarily evidence of more attention, despite claims to the contrary. Careful experimenters often choose an experimental design in which the criterion is balanced (c = 0) in every condition, so that any change in accuracy implies a change in d’ and therefore an effect on processing. For example, in a discrimination experiment, S1 and S2 may be presented in successive halves of each trial, and the subject is asked to pick which interval contains S1. So long as any bias towards one or other interval is constant across conditions, changes in accuracy imply changes in d’, so such methods are termed ‘criterion-free’. Demonstrating an effect of selective attention is easiest if a criterion-free method can be employed; if not, rating methods, not discussed here, may also be used [
10] (Egan, 1957.)
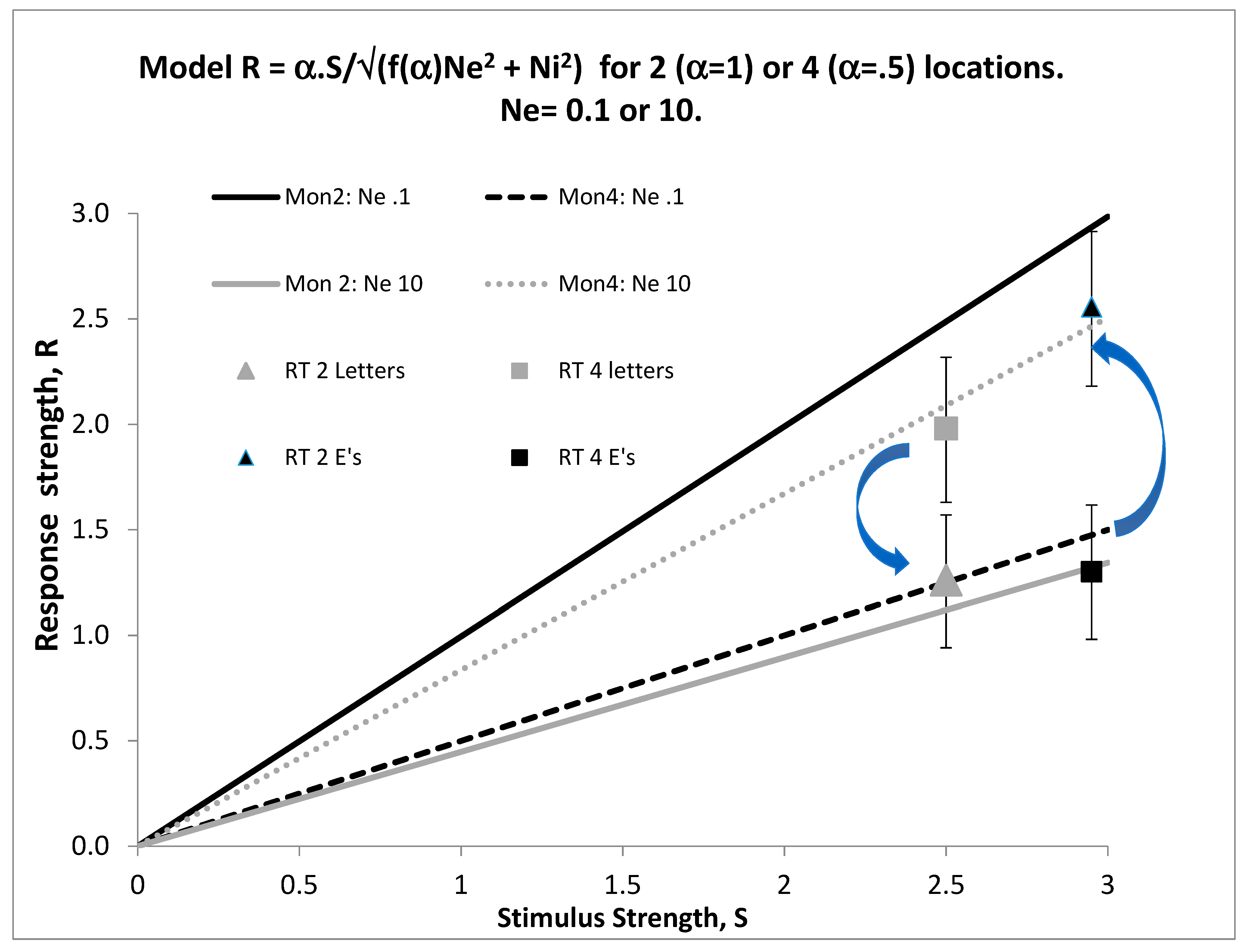
We now need one more concept from signal detection theory, that of the signal/noise ratio, S/N. As signal strength diminishes or noise increases, detectability must deteriorate, so d’ = S/N. This can be fleshed out by defining the transduction function f(.) of the sensory organ. Signal strength increases monotonically with stimulus energy, E, that is, S = f(E), where f(0) = 0, so that no signal is obtained when the stimulus is off. If S = bE or S = blog(E), for some constant b, the sensory transducer is linear or is Weberian, two cases which (perhaps surprisingly) cover wide ranges of stimulation in hearing, vision, and touch, though obviously do not accommodate color or harmony. The sources of noise (N) are external (environmental), Ne, or internal (neural) Ni. If both sources are Gaussian, N = √(Ne
2 + Ni
2 − 2rNeNi), where r is the correlation between Ni and Ne. If external and internal noise sources are independent, r = 0 and N = √(Ne
2 + Ni
2). In this case, d’ = f(E)/√(Ne
2 + Ni
2), and Ni can be measured by first removing all external noise, so Ne = 0, and then applying various amounts of external noise to find the level which doubles d’; this gives Ni in units of stimulus energy [
11], thereby providing a behavioral measure of random neural activity in the sensory transducer.
Given signal detection, that is, d’ = S/N, selective attention can increase detectability by increasing S or decreasing N, or both. One way in which attention can decrease noise is by ‘noise exclusion’, that is, by reducing Ne by filtering out Ne components distant from the signal [
12,
13]. Attention (α) can increase S by increasing the efficiency of transduction [
7]. Either S = f(αE) or S = αf(E), depending on whether attention accesses the sensory input before transduction, as by orienting the eyes for better vision or the head for better sound, or after transduction, as might be in the brain. These mechanisms are not exclusive; attention can both increase S and reduce N.
This ends the primer on elementary signal detection theory. Readers who wish to follow up can read Macmillan and Creelman [
2], which is a lucid exposition for experimentalists, or Egan [
10] for a deeper mathematical treatment. What is common to every idea mentioned so far is that increasing attention must
improve performance, either by filtering out noise (e.g., Palmer [
8]), or decreasing uncertainty about the signal (Lu and Dosher, [
12,
13]), or directly enhancing the signal (Carrasco et al. [
7]). Foreknowledge of the signal (‘attention’ to it) permits the subject to improve detectability by creating optimal filters to enhance S, decrease N, or both ([
1], Green and Swets, p. 162).
Indeed, evidence that selective attention enhances performance has been often secured. For example, an auditory ‘signal’ tone presented at an expected frequency is detected more reliably than a ‘probe’ tone presented at an unexpected frequency ([
14] Greenberg and Larkin, 1968; [
9] Reeves and Scharf); line segments shown at an expected orientation (‘signals’) are detected more accurately than line segments (‘probes’) presented at an unexpected orientation ([
15] Kurylo, Reeves, and Scharf); and letters whose locations are cued in advance are reported more accurately than uncued letters ([
16] Eriksen and Yeh; [
17] Skelton and Eriksen.) Attentional enhancement is not restricted to location in frequency space or visual space; attended objects may be processed more precisely than un-attended ones ([
18] Egly, Driver, and Rafal), even when the locations of attended and unattended objects are identical ([
19] Blaser et al.).
A focus on signal detection rather than on broader organismic factors is surely justified when subjects are in the same mental state in every experimental condition, and are not distracted, indifferent, lethargic, unclear about the task, overly aroused, or otherwise abnormal. The great advantage of STD in these situations is that the experimenter is required develop methods consistent with the theory and show that d’, not just the criterion, changes with attentive state. In our research ([
6], Fine and Reeves), we employed criterion-free behavioral methods so that changes in accuracy would reflect changes in sensitivity, not changes in the criterion.
Critically, the generalization that attention improves performance presupposes
validity: that is, attention can be paid to the signal rather than to irrelevant or competing locations or features, the task instructions and cues are never misleading, and the stimuli and task are known in advance and well-practiced. Validity permits the subject to process the target signal optimally, i.e., as well as possible given the inevitable noise. Attention to the wrong location (e.g., [
14] Greenberg and Larkin) or the wrong spatial frequency band ([
20] Yeshurun and Carrasco) or to signals not known exactly [
1] causes perceptual decisions to be based on the outputs of less-than-optimal filters, impairing sensitivity.