Machine Vibration Monitoring for Diagnostics through Hypothesis Testing
Abstract
:1. Introduction
- (a)
- Operational evaluation,
- (b)
- Data acquisition and cleansing,
- (c)
- Signal processing: features selection, extraction, and metrics,
- (d)
- Pattern processing: statistical model development and validation,
- (e)
- Situation assessment,
- (f)
- Decision making.
- Level 1: Detection—indication of the presence of damage, possibly at a given confidence
- Level 2: Localization—knowledge about the damage location
- Level 3: Classification—knowledge about the damage type
- Level 4: Assessment—damage size
- Level 5: Consequence—actual degree of safety and remaining useful life
1.1. Features
- Damage consistency,
- Damage sensitivity and noise-rejection ability,
- Low sensitivity to unmonitored confounding factors.
1.2. Pattern Recognition
1.3. Methodology
1.4. The Experimental Setup and the Dataset
2. The Methods
2.1. Statistics and Probability: An Introduction to Hypothesis Testing
The probability is the limiting value of the relative frequency of a given attribute within a considered collective. The probabilities of all the attributes within the collective form its distribution.
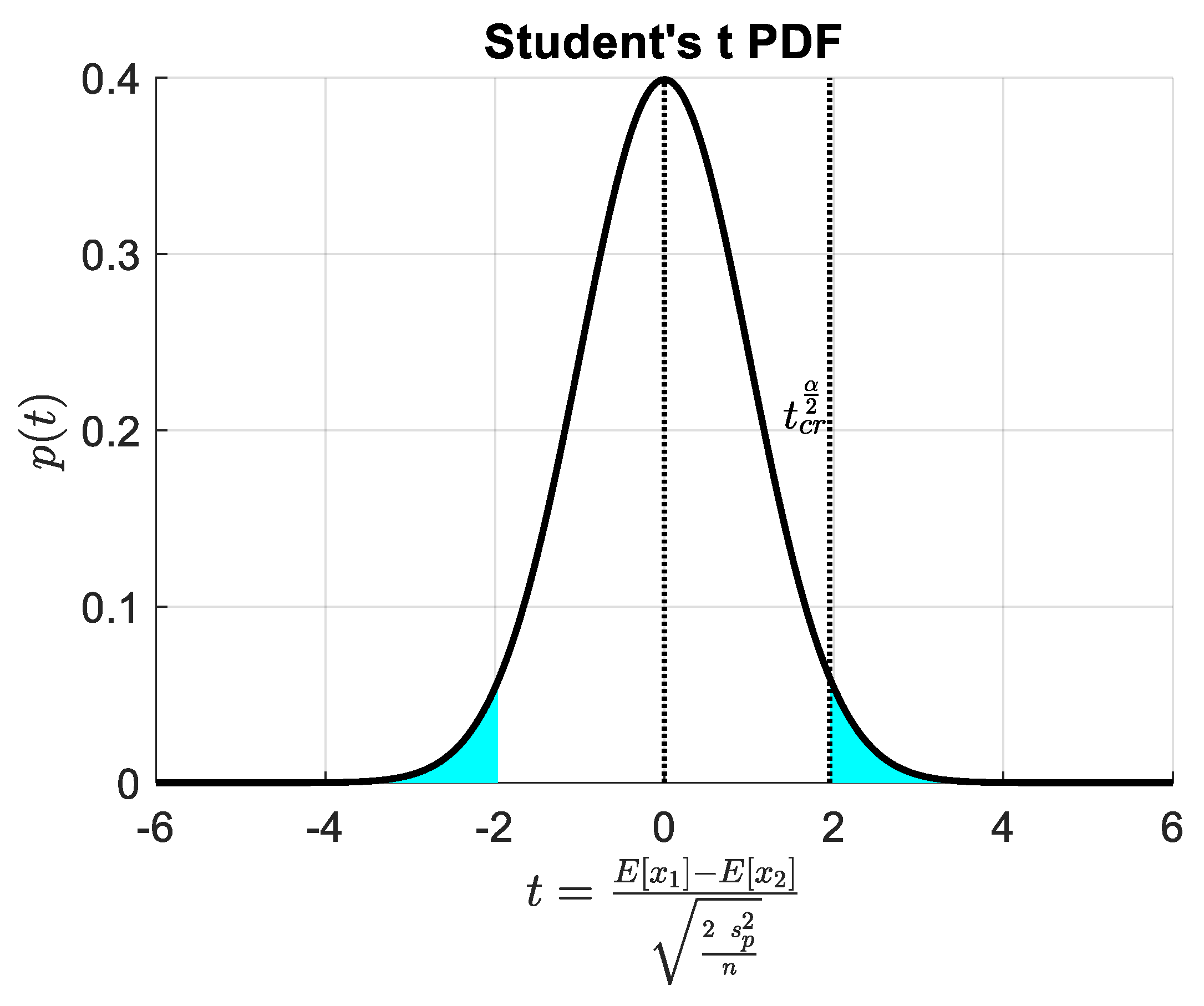
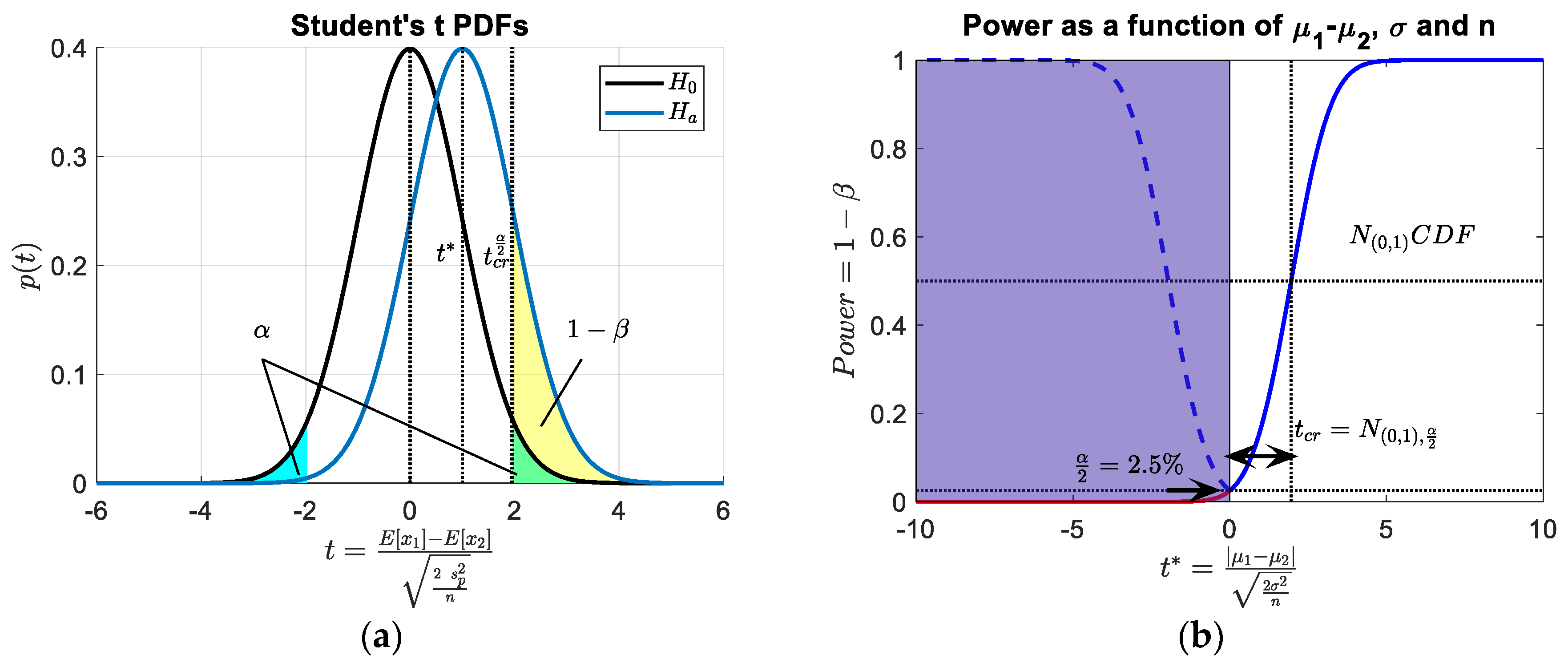
2.1.1. Hypothesis Testing of the Difference between Two Population Means
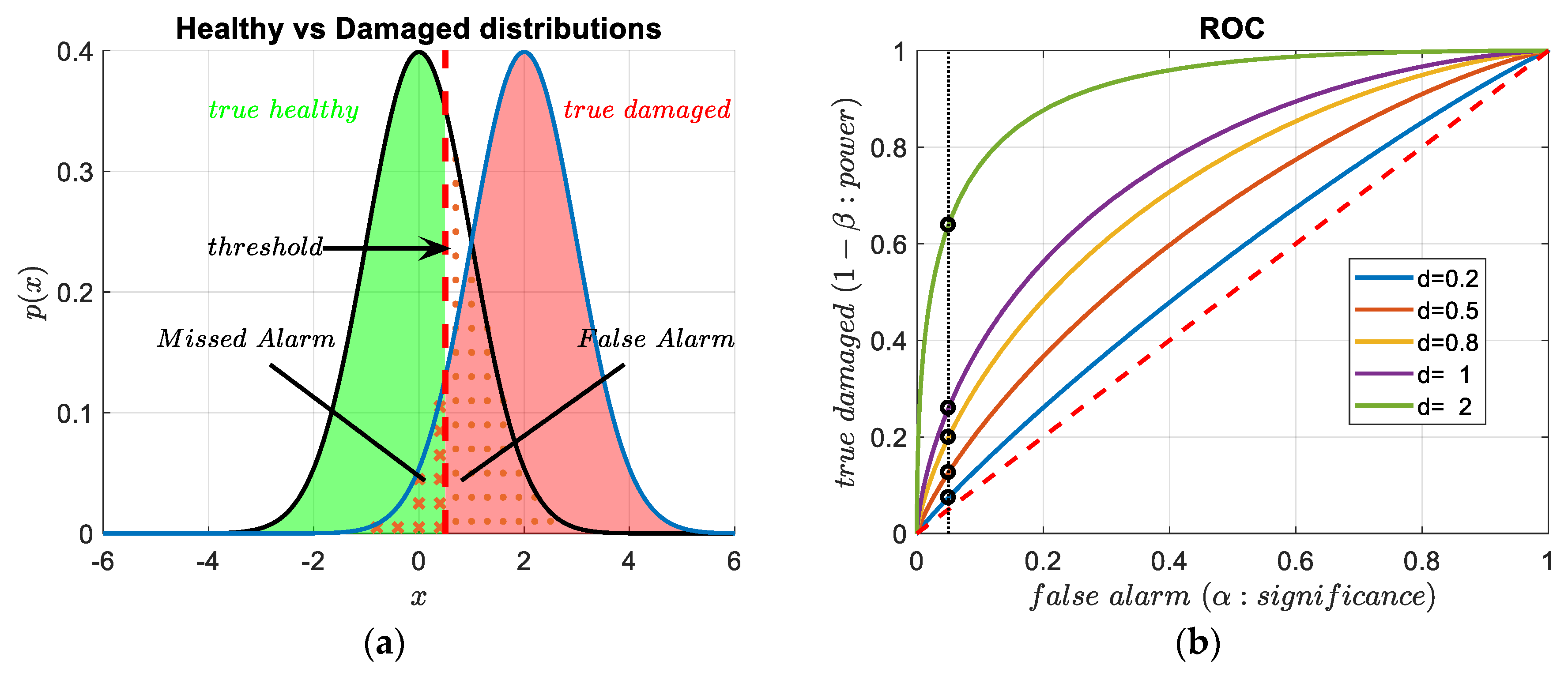
2.1.2. Diagnostics, Hypothesis Testing and Errors
- (a)
- In the training phase, the labelled samples are used to build a classifier, namely a function which divides the feature (variable) space into groups. This separation is then found in terms of distributions. When a single feature is used to investigate the machine, the classifier function corresponds to the selection of a threshold. It is relevant to point out that this feature-space partitioning can also be obtained in an unsupervised way (i.e., without exploiting the labels). This takes the name of clustering.
- (b)
- In a second phase, the new observations are assigned to the corresponding class (i.e., classified) according the classifier function. Each new unlabelled data point is then treated individually.
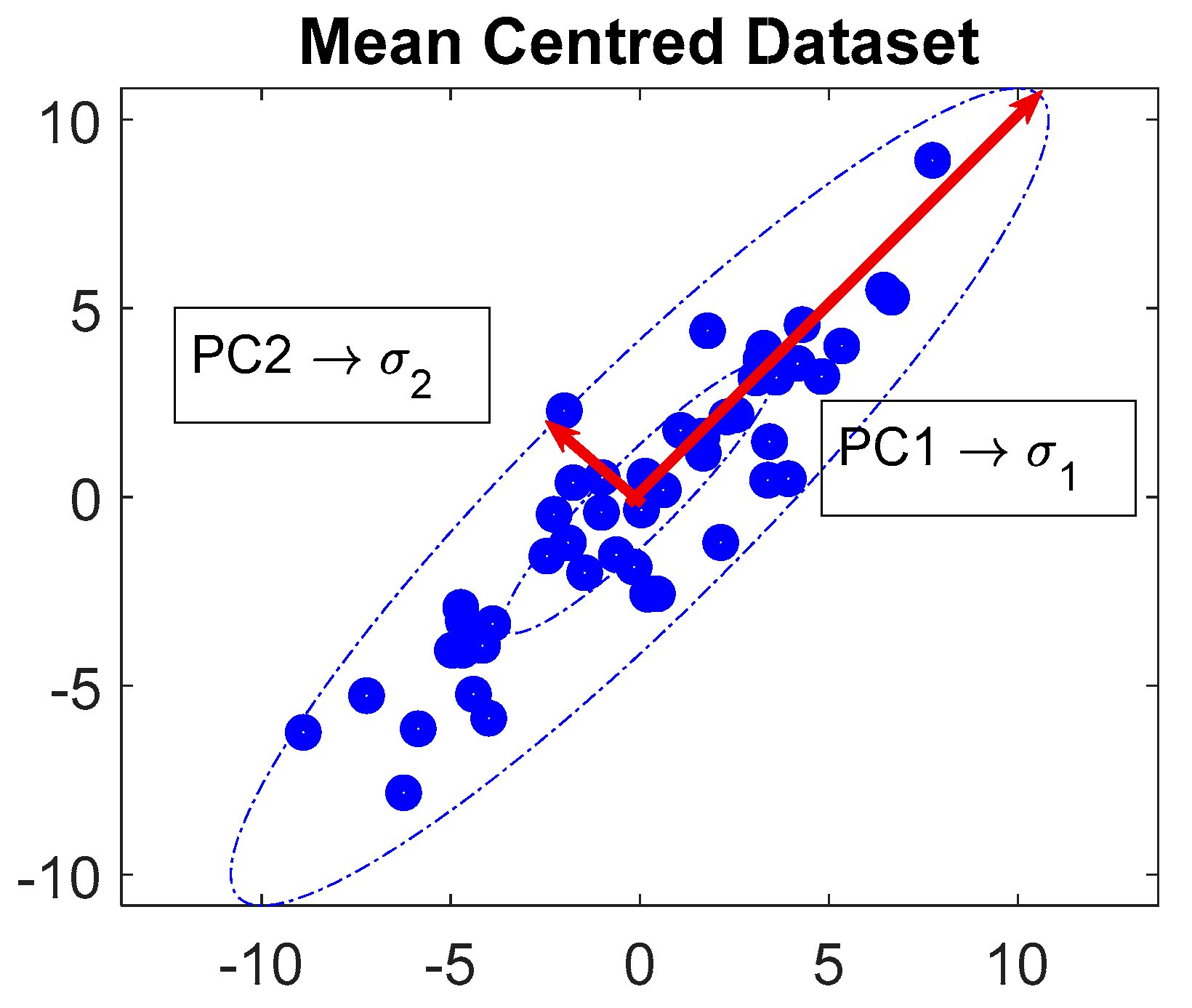
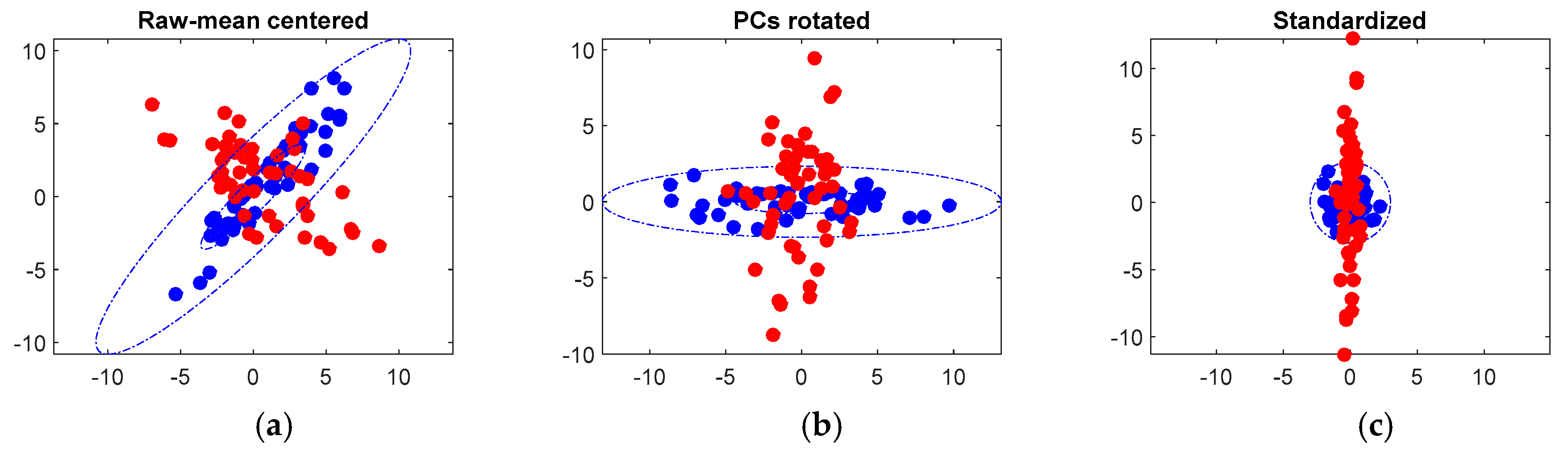
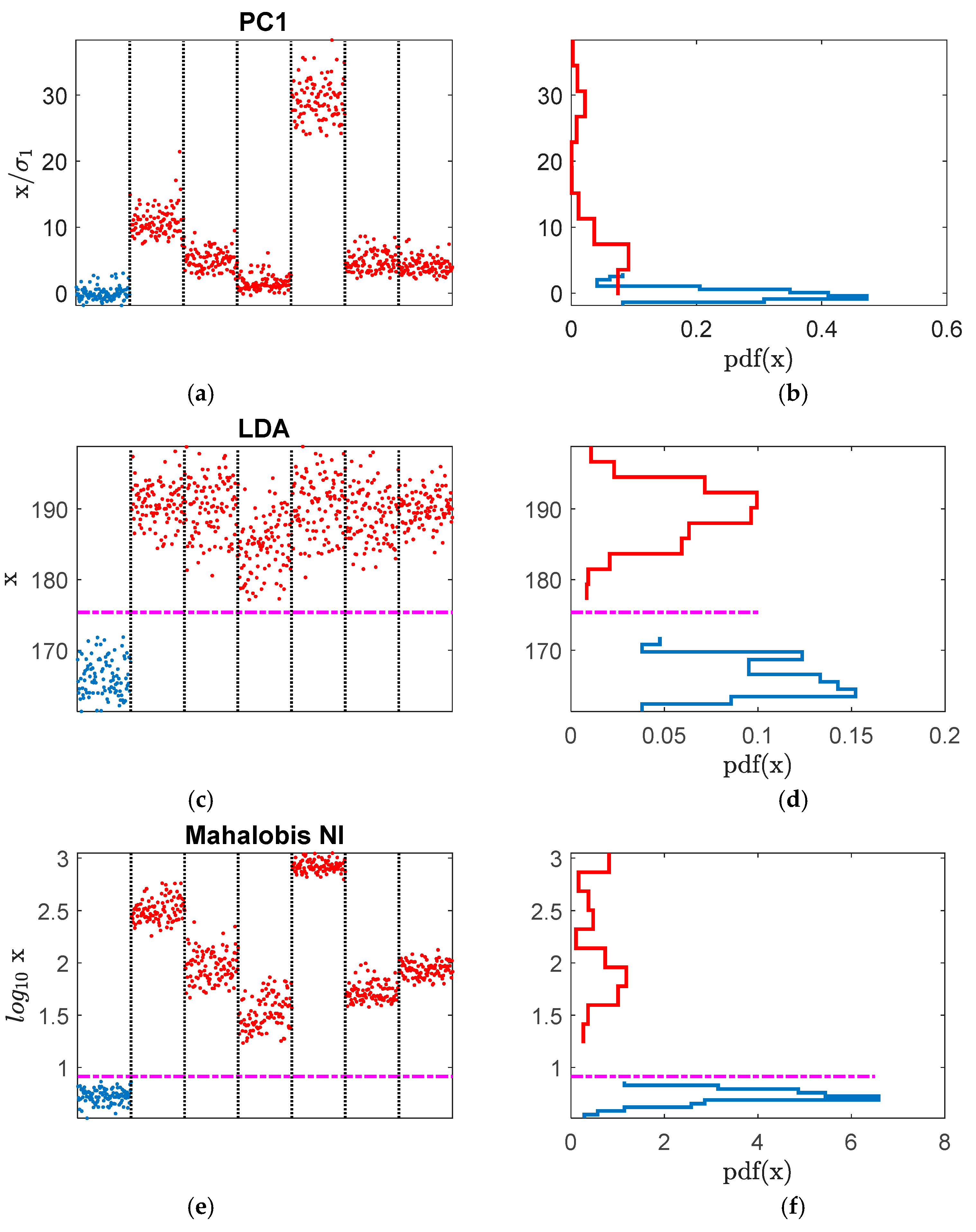
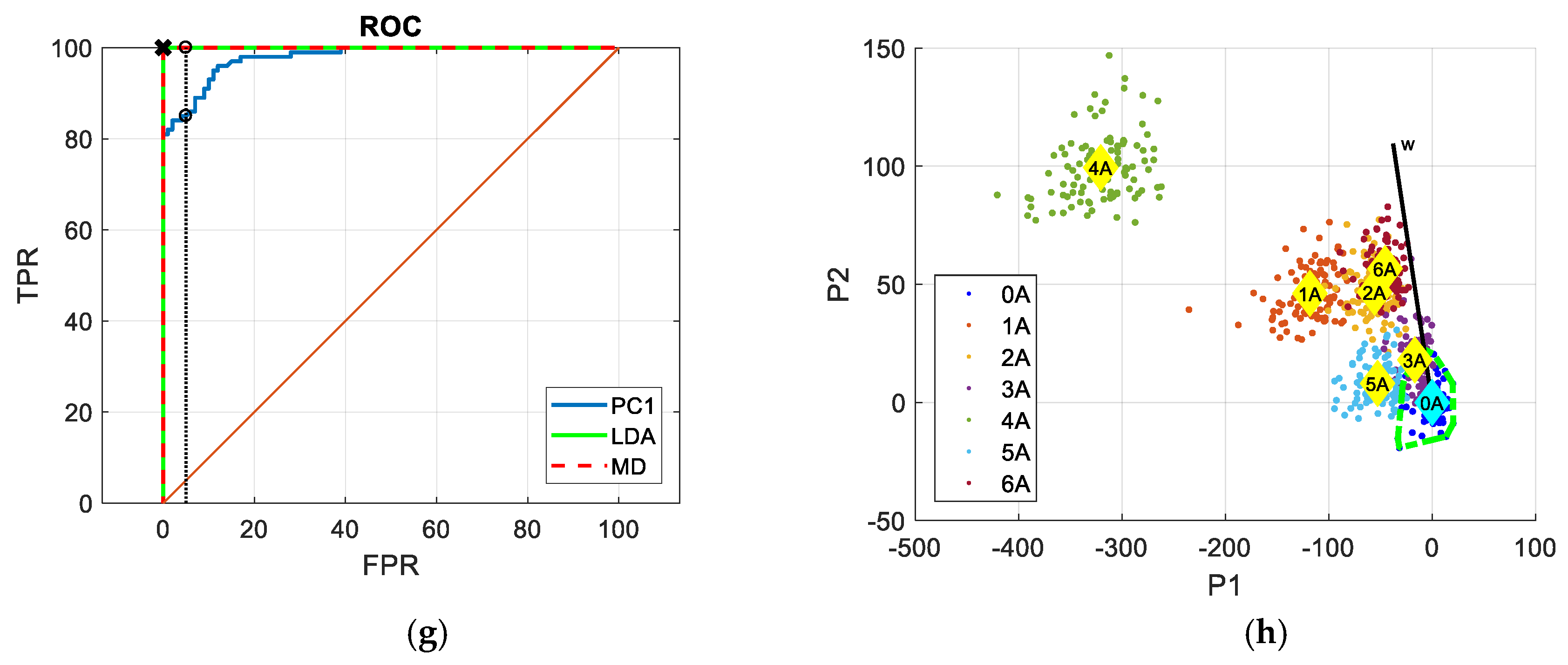
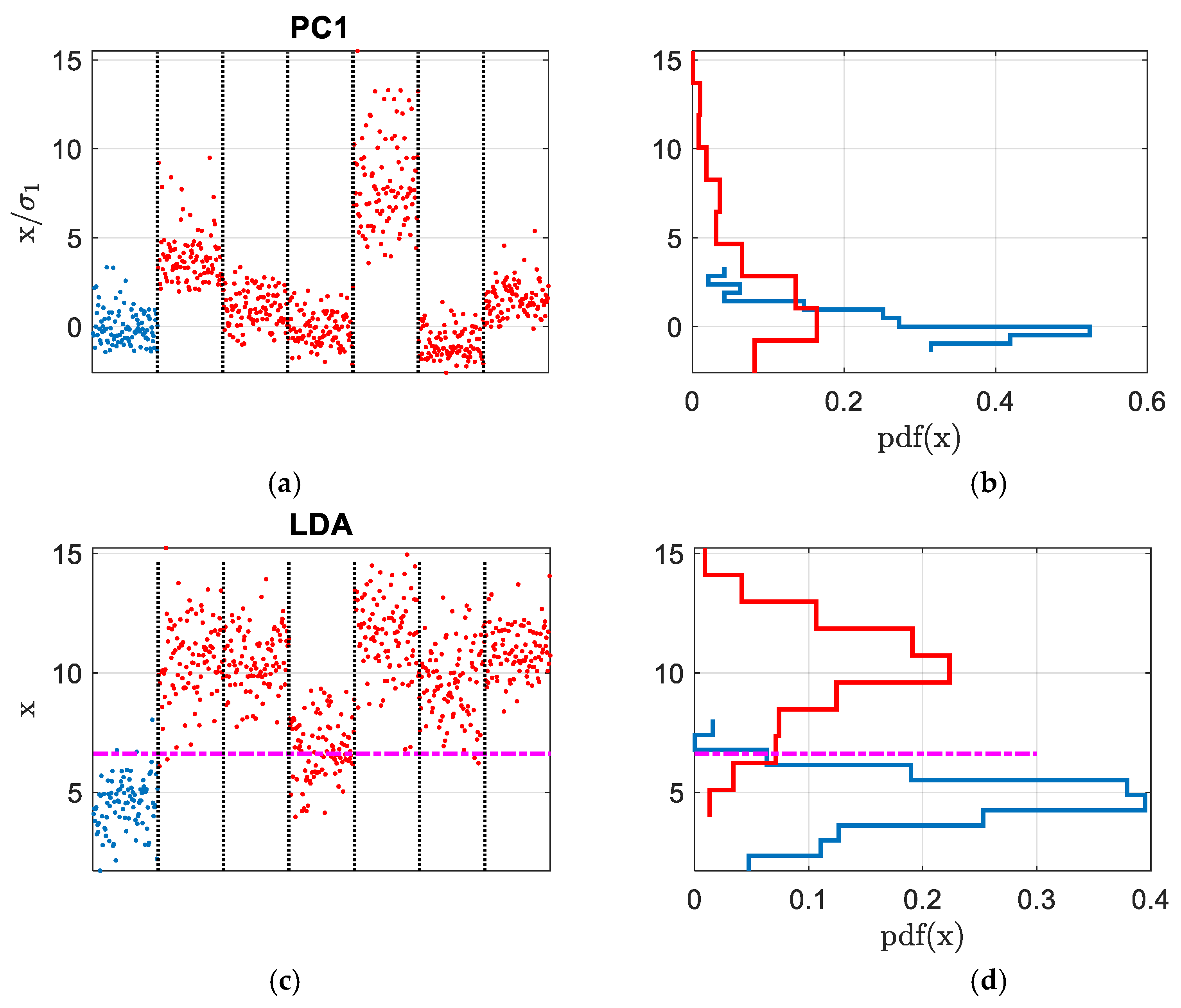
2.2. Principal Component Analysis (PCA)
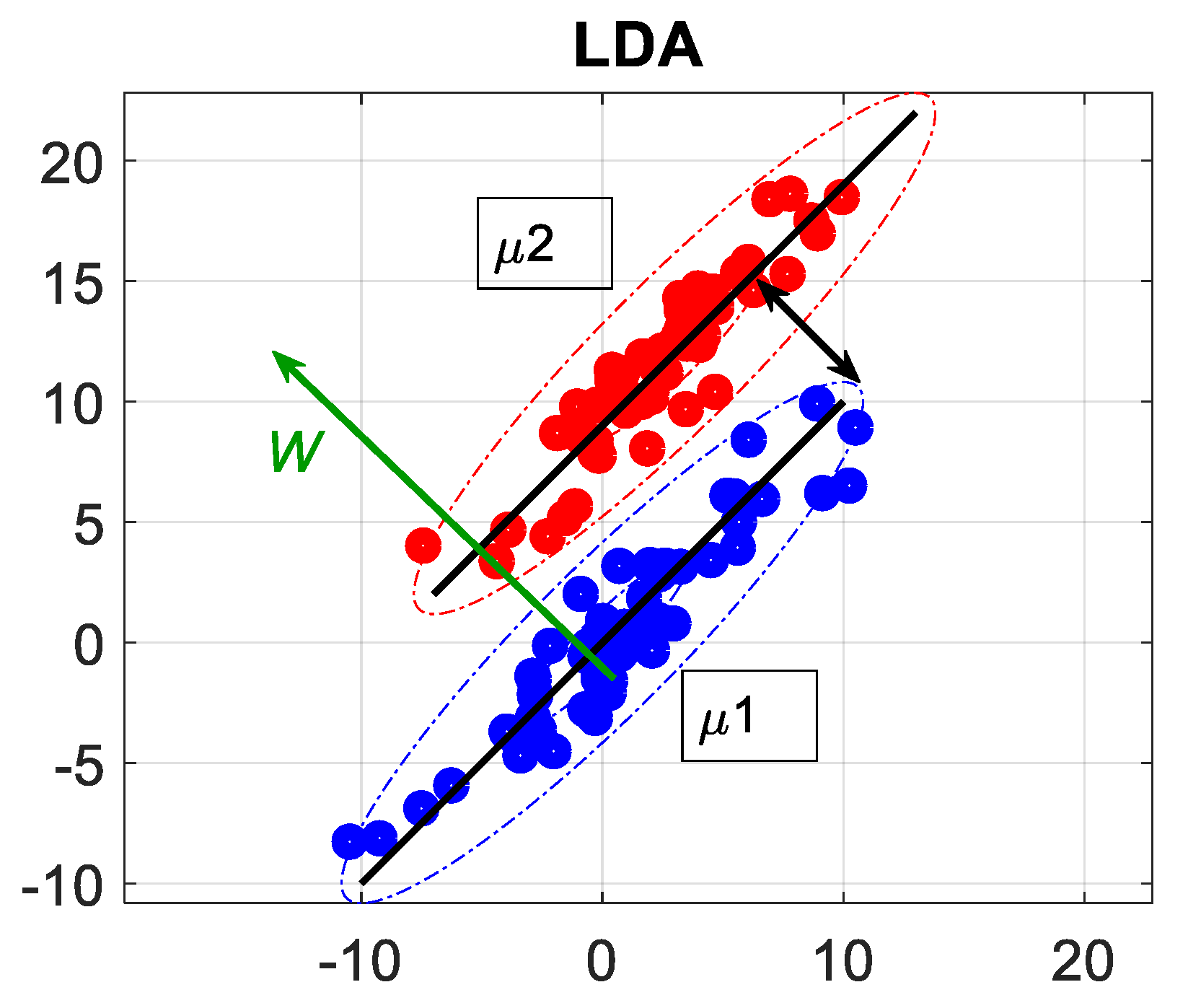
2.3. Linear Discriminant Analysis (LDA)
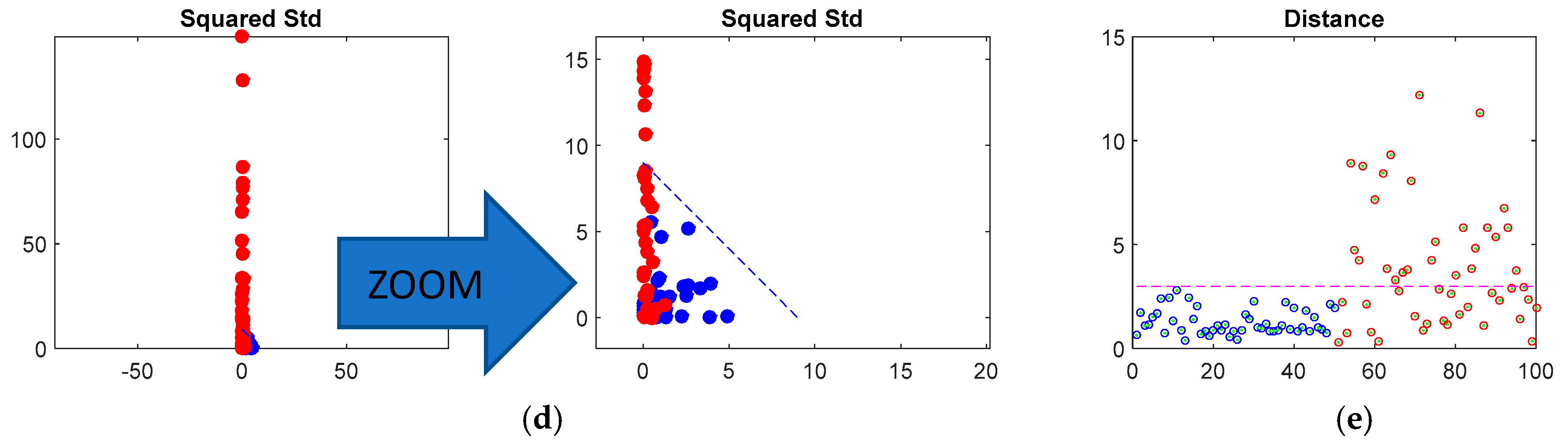
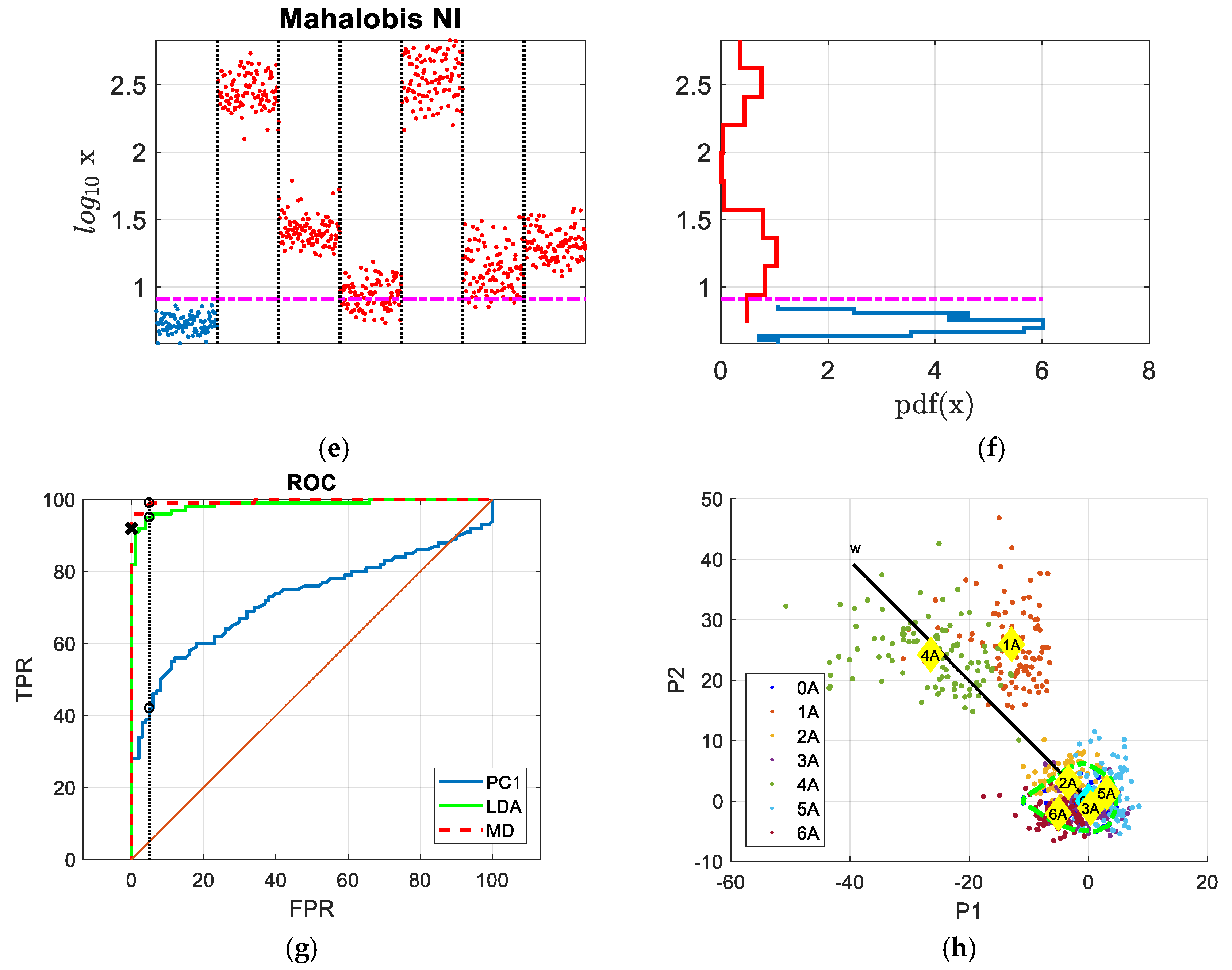
2.4. Mahalanobis Distance Novelty Detection
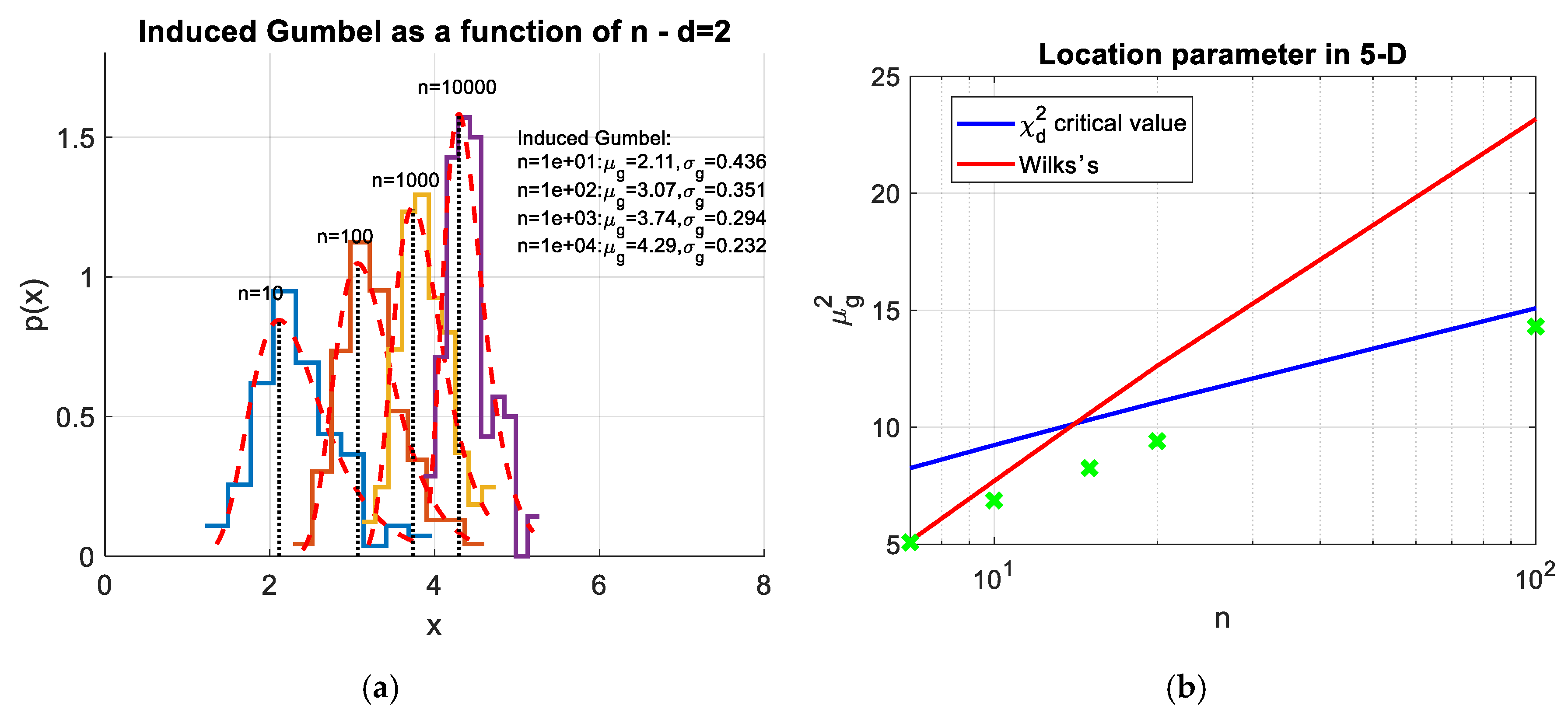
2.4.1. Hypothesis Testing of Outliers
- Draw a sample of observations randomly generated from a -dimensional standard normal distribution,
- Compute the deviation of each observation in terms of distance from the centroid i.e., the NI,
- Save the maximum deviation and repeat the draw for times.
2.4.2. The Curse of Dimensionality
2.4.3. Mahalanobis Distance and Confounding Influences
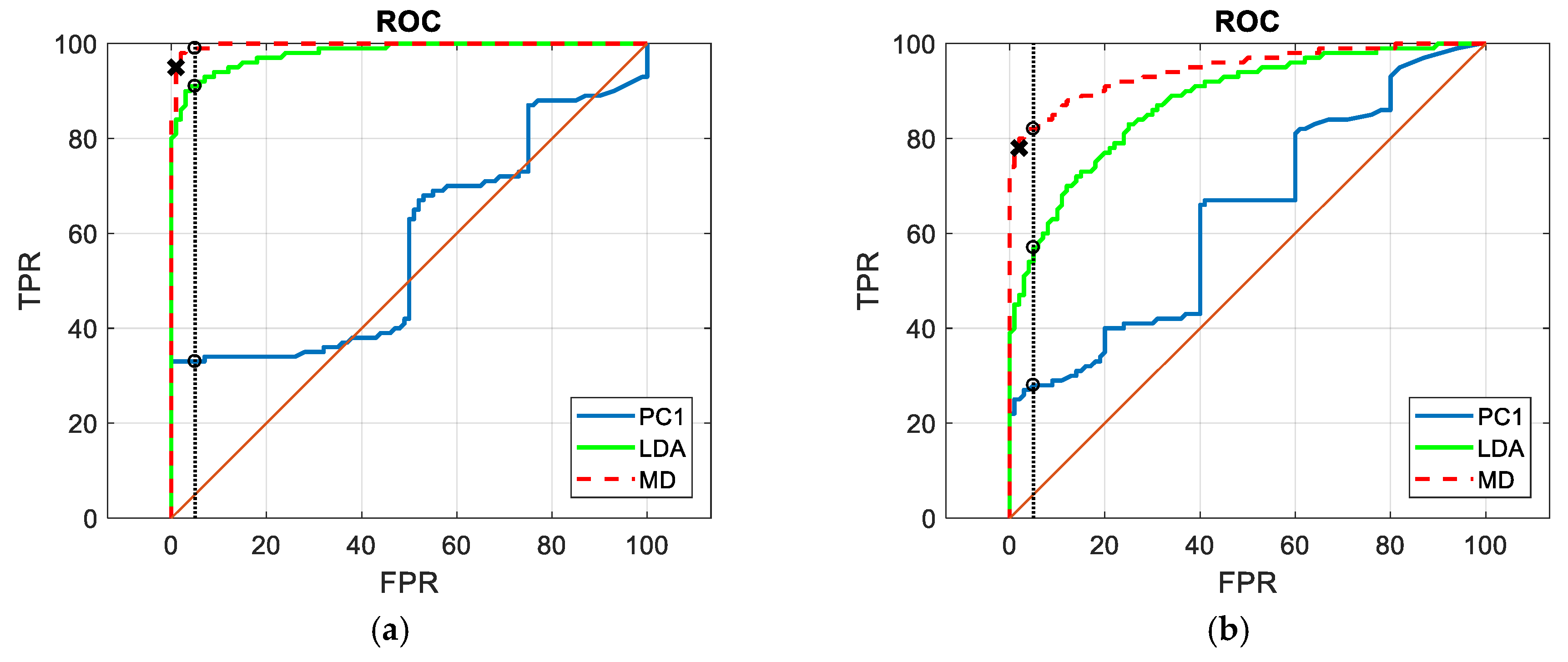
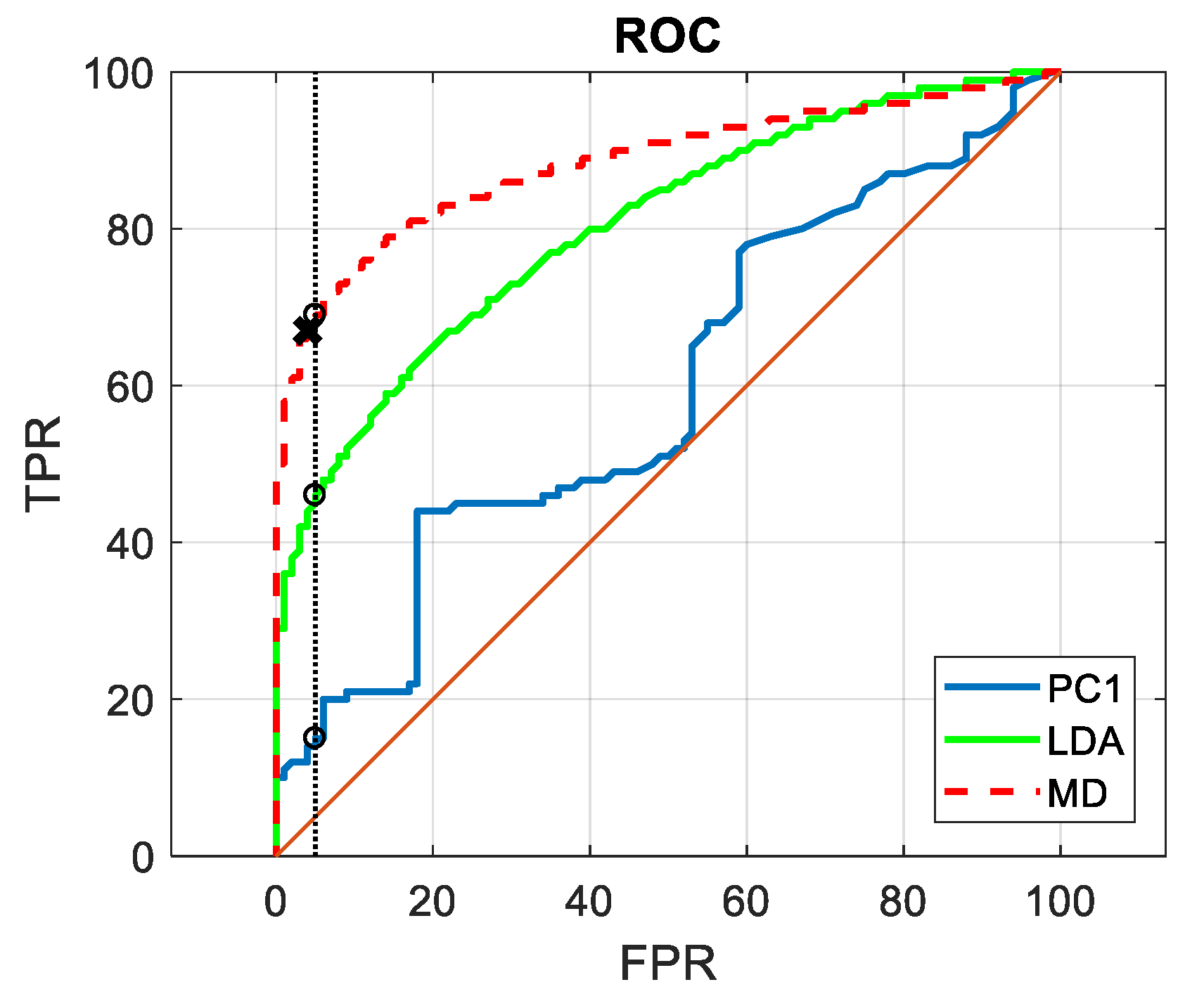
3. The Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Farrar, C.R.; Doebling, S.W. Damage Detection and Evaluation II. In Modal Analysis and Testing; Silva, J.M.M., Maia, N.M.M., Eds.; NATO Science Series (Series E: Applied Sciences); Springer: Dordrecht, The Netherlands, 1999; ISBN 978-0-7923-5894-7. [Google Scholar]
- Rytter, A. Vibration Based Inspection of Civil Engineering Structures. Ph.D. Thesis, University of Aalborg, Aalborg, Denmark, May 1993. [Google Scholar]
- Worden, K.; Dulieu-Barton, J.M. An overview of intelligent fault detection in systems and structures. Struct. Health Monit. 2004, 3, 85–98. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Worden, K. A comparison of linear approaches to filter out environmental effects in structural health monitoring. Mech. Syst. Signal Process. 2018, 105, 1–15. [Google Scholar] [CrossRef]
- Jardine, A.K.S.; Lin, D.; Banjevic, D. A review of machinery diagnostics and prognostics implementing condition-based maintenance. Mech. Syst. Signal Process. 2006, 20, 1483–1510. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, J. Fault Diagnosis for Rolling Element Bearings Based on Feature Space Reconstruction and Multiscale Permutation Entropy. Entropy 2019, 21, 519. [Google Scholar] [CrossRef]
- You, L.; Fan, W.; Li, Z.; Liang, Y.; Fang, M.; Wang, J. A Fault Diagnosis Model for Rotating Machinery Using VWC and MSFLA-SVM Based on Vibration Signal Analysis. Shock Vib. 2019, 2019, 1908485. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Antoni, J.; Griffaton, J.; Andréc, H.; Avendaño-Valencia, L.D.; Bonnardot, F.; Cardona-Morales, O.; Castellanos-Dominguez, G.; Paolo Daga, A.; Leclère, Q.; Vicuña, C.M.; et al. Feedback on the Surveillance 8 challenge: Vibration-based diagnosis of a Safran aircraft engine. Mech. Syst. Signal. Process. 2017, 97, 112–144. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. Unsupervised noise cancellation for vibration signals: Part I and II—Evaluation of adaptive algorithms. Mech. Syst. Signal Process. 2004, 18, 89–117. [Google Scholar] [CrossRef]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]
- Daga, A.P.; Fasana, A.; Marchesiello, S.; Garibaldi, L. The Politecnico di Torino rolling bearing test rig: Description and analysis of open access data. Mech. Syst. Signal Process. 2019, 120, 252–273. [Google Scholar] [CrossRef]
- Sikora, M.; Szczyrba, K.; Wróbel, Ł.; Michalak, M. Monitoring and maintenance of a gantry based on a wireless system for measurement and analysis of the vibration level. Eksploat. Niezawodn. 2019, 21, 341. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis; Springer: New York, NY, USA, 2002. [Google Scholar]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
- Worden, K.; Manson, G.; Fieller, N.R.J. Damage detection using outlier analysis. J. Sound Vib. 2000, 229, 647–667. [Google Scholar] [CrossRef]
- Von Mises, R. Probability, Statistics, and Truth, 2nd rev. English ed.; Dover Publications: New York, NY, USA, 1981; ISBN 0-486-24214-5. [Google Scholar]
- Holman, J.P.; Gajda, W.J. Experimental Methods for Engineers; McGraw-Hill: New York, NY, USA, 2011; ISBN 10: 0073529303. [Google Scholar]
- Daniel, W.W.; Cross, C.L. Biostatistics: A Foundation for Analysis in the Health Sciences; Wiley: Hoboken, NJ, USA, 2012; ISBN 13: 978-1118302798. [Google Scholar]
- Howell, D.C. Fundamental Statistics for the Behavioral Sciences, 8th ed.; Cengage Learning: Boston, MA, USA, 2013; ISBN 13: 978-1285076911. [Google Scholar]
- Yan, A.M.; Kerschen, G.; De Boe, P.; Golinval, J.C. Structural damage diagnosis under varying environmental conditions—Part I: A linear analysis. Mech. Syst. Signal Process. 2005, 19, 847–864. [Google Scholar] [CrossRef]
- Penny, K.I. Appropriate critical values when testing for a single multivariate outlier by using the Mahalanobis distance. J. Royal Stat. Soc. Series C (Appl. Stat.) 1996, 45, 73–81. [Google Scholar] [CrossRef]
- Worden, K.; Allen, D.W.; Sohn, H.; Farrar, C.R. Damage detection in mechanical structures using extreme value statistics. SPIE 2002. [Google Scholar] [CrossRef]
- Toshkova, D.; Lieven, N.; Morrish, P.; Hutchinson, P. Applying Extreme Value Theory for Alarm and Warning Levels Setting under Variable Operating Conditions. Available online: https://www.ndt.net/events/EWSHM2016/app/content/Paper/293_Filcheva_Rev4.pdf (accessed on 5 June 2019).
- Takahashi, R. Normalizing constants of a distribution which belongs to the domain of attraction of the Gumbel distribution. Stat. Probab. Lett. 1987, 5, 197–200. [Google Scholar] [CrossRef]
- Gupta, P.L.; Gupta, R.D. Sample size determination in estimating a covariance matrix. Comput. Stat. Data Anal. 1987, 5, 185–192. [Google Scholar] [CrossRef]
- Yan, A.M.; Kerschen, G.; De Boe, P.; Golinval, J.C. Structural damage diagnosis under varying environmental conditions—Part II: Local PCA for non-linear cases. Mech. Syst. Signal Process. 2005, 19, 865–880. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Worden, K. New Trends in Vibration Based Structural Health Monitoring; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; ISBN 978-3-7091-0399-9. [Google Scholar]
- Arnaiz-González, Á.; Fernández-Valdivielso, A.; Bustillo, A.; López de Lacalle, L.N. Using artificial neural networks for the prediction of dimensional error on inclined surfaces manufactured by ball-end milling. Int. J. Adv. Manufact. Technol. 2016, 83, 847–859. [Google Scholar] [CrossRef]

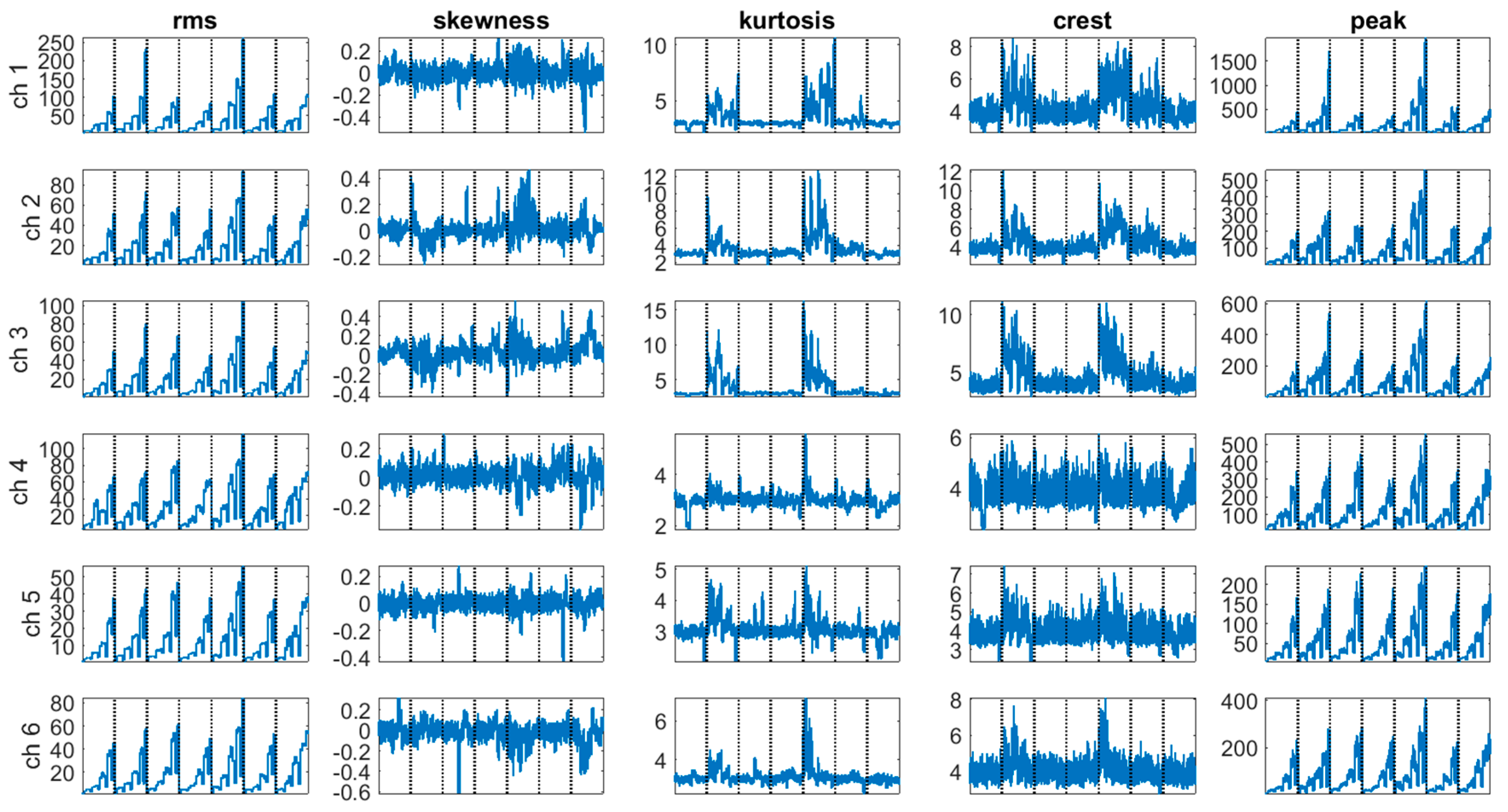



| Moments | Name | Formulation |
|---|---|---|
| Order 1—raw moment: Location | Mean Value | |
| Order 2—central moment: Dispersion | Variance | |
| Order 3—standardized moment: Symmetry | Skewness | |
| Order 4—standardized moment: “Tailedness” | Kurtosis |
| Level Indicators | Name | Formulation |
|---|---|---|
| Root Mean Square | RMS | |
| Peak value | Peak | |
| Crest factor | Crest |
| Code | 0A | 1A | 2A | 3A | 4A | 5A | 6A |
|---|---|---|---|---|---|---|---|
| Damage type | none | Inner Ring | Inner Ring | Inner Ring | Rolling Element | Rolling Element | Rolling Element |
| Damage size [µm] | - | 450 | 250 | 150 | 450 | 250 | 150 |
| Label | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [dHz] | 9 | 9 | 9 | 9 | 18 | 18 | 18 | 18 | 28 | 28 | 28 | 28 | 37 | 37 | 37 | 47 | 47 |
| [kN] | 0 | 1 | 1.4 | 1.8 | 0 | 1 | 1.4 | 1.8 | 0 | 1 | 1.4 | 1.8 | 0 | 1 | 1.4 | 0 | 1 |
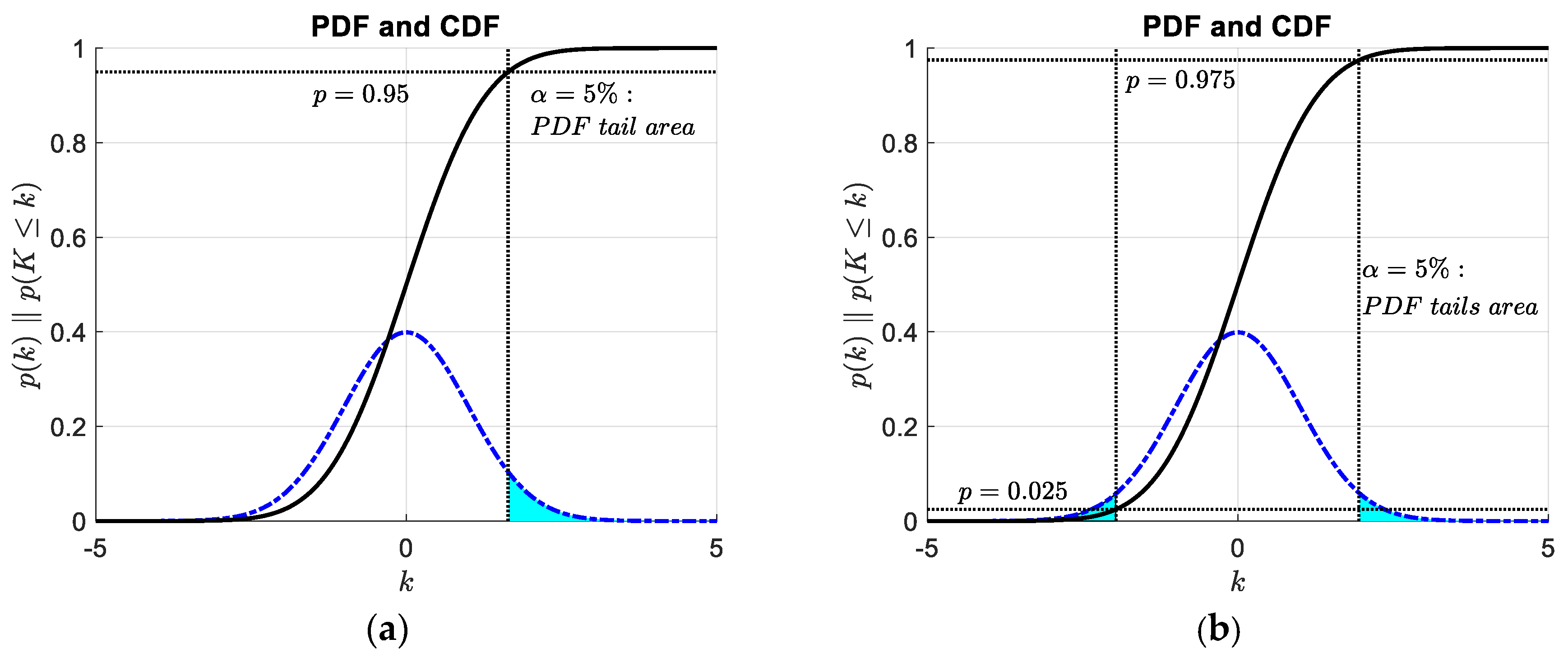
| Standard Interval | Inside to Outside Ratio | |
|---|---|---|
| Tails | Confidence Interval |
|---|---|
| For a right tail event, it can be stated as | |
| For a left tail event, it is | |
| For a double tail event (on a symmetric distribution), it becomes |
| Distribution of the Population: | Statistical Summary of the Sample: |
|---|---|
| Normal distributions with given variance or Generic distributions (also non-normal) assuming , thanks to CLT | |
| Normal distributions with unknown variance |
| Effect Size | |
|---|---|
| Small | |
| Medium | |
| Large |
| True Health Condition: | |||
|---|---|---|---|
| Healthy (H0) | Damaged | ||
| CBM Actions | accept : Healthy | No Alarm— true healthy | Missed Alarm— type II error |
| reject : Damaged | False Alarm— type I error | Alarm— true damaged | |
| Scatter Matrices | Optimization of the Separation Index |
|---|---|
| Between class scatter matrix: | |
| Within class scatter matrix: |
| True Class | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0A | 1A | 2A | 3A | 4A | 5A | 6A | ||
| Classified | Healthy | 95 | 9 | 52 | 64 | 0 | 32 | 26 |
| Damaged | 5 | 91 | 48 | 36 | 100 | 68 | 74 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daga, A.P.; Garibaldi, L. Machine Vibration Monitoring for Diagnostics through Hypothesis Testing. Information 2019, 10, 204. https://doi.org/10.3390/info10060204
Daga AP, Garibaldi L. Machine Vibration Monitoring for Diagnostics through Hypothesis Testing. Information. 2019; 10(6):204. https://doi.org/10.3390/info10060204
Chicago/Turabian StyleDaga, Alessandro Paolo, and Luigi Garibaldi. 2019. "Machine Vibration Monitoring for Diagnostics through Hypothesis Testing" Information 10, no. 6: 204. https://doi.org/10.3390/info10060204
APA StyleDaga, A. P., & Garibaldi, L. (2019). Machine Vibration Monitoring for Diagnostics through Hypothesis Testing. Information, 10(6), 204. https://doi.org/10.3390/info10060204





