An Efficient Image Reconstruction Framework Using Total Variation Regularization with Lp-Quasinorm and Group Gradient Sparsity
Abstract
1. Introduction
2. Prerequisite Knowledge
2.1. L1- and L2-Norm Modeling in TV Regularization
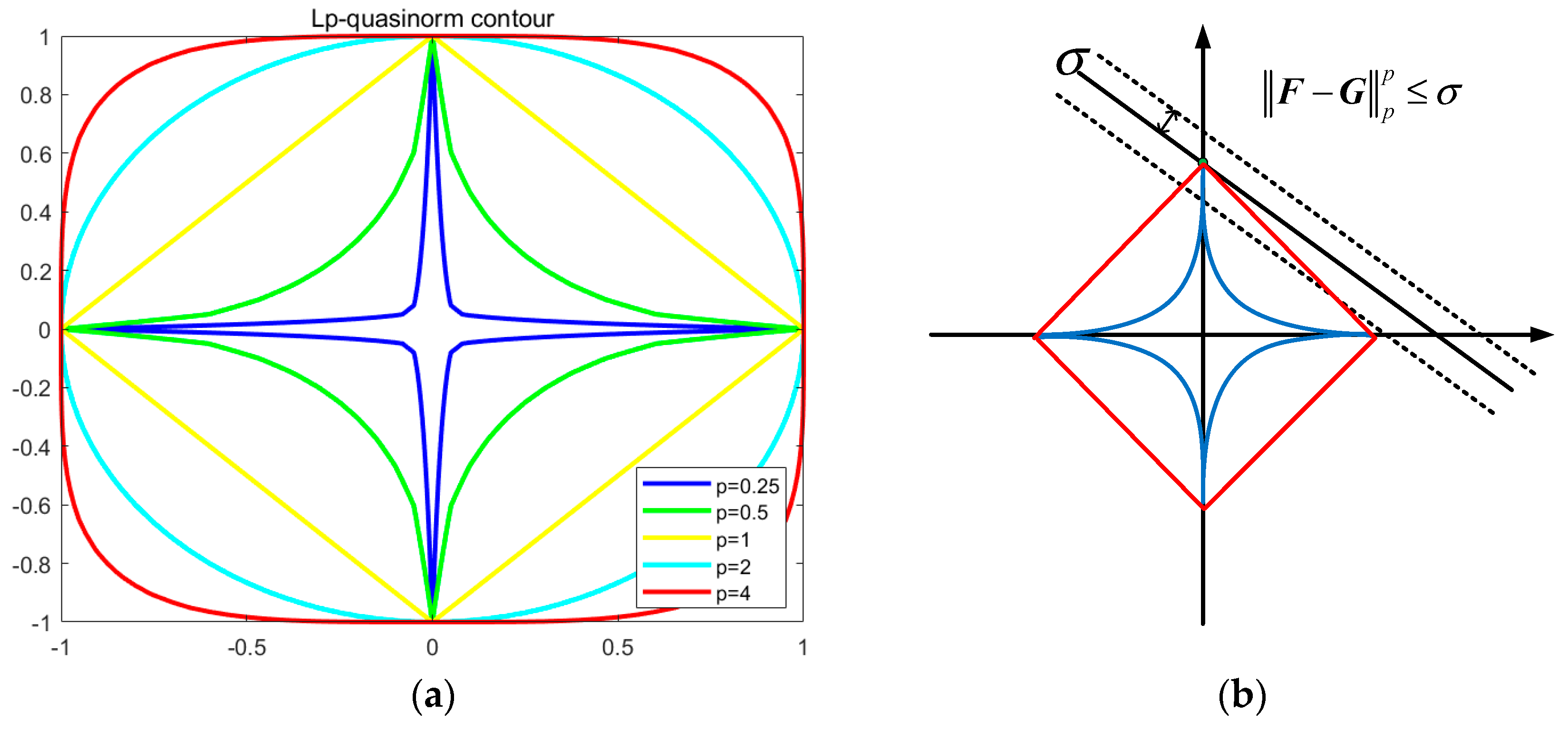
2.2. Lp-Quasinorm
2.3. OGS_L1 Model
2.4. MM Algorithm
3. Propose Model and Solution
3.1. Subproblem Solving
| Algorithm 1: Pseudocode GGS_Lp for image reconstruction |
| Input: |
| Output: |
| Initialize: |
| 1: Set as 1; |
| 2: while do |
| 3: Update using Equation (16); |
| 4: Update using Equation (17); |
| 5: while do |
| 6: Update using Equation (18); |
| 7: ; |
| 8: ; |
| 9: end while |
| 10: Update using Equation (20); |
| 11: ; |
| 12: end while |
| 13: Returnas. |
3.2. Fast ADMM Solver with Restart
| Algorithm 2: Pseudocode GGS_LP_Fast for image reconstruction |
| Input: |
| Output: |
| Initialize: |
| 1: Set as 1; |
| 2: while do |
| 3: Update using Equation (16); |
| 4: Update using Equation (21); |
| 5: while do |
| 6: Update using Equation (21); |
| 7: ; |
| 8: ; |
| 9: end while |
| 10: Update using Equations (22) and (23); |
| 11: if then |
| 12: Update using Equation (25), |
| 13: else Update using Equation (26), |
| 14: end if |
| 15: ; |
| 16: end while |
| 17: Returnas. |
4. Numerical Experiments
4.1. Evaluation Criteria and Running Environment
4.2. Parameter Sensitivity Analysis
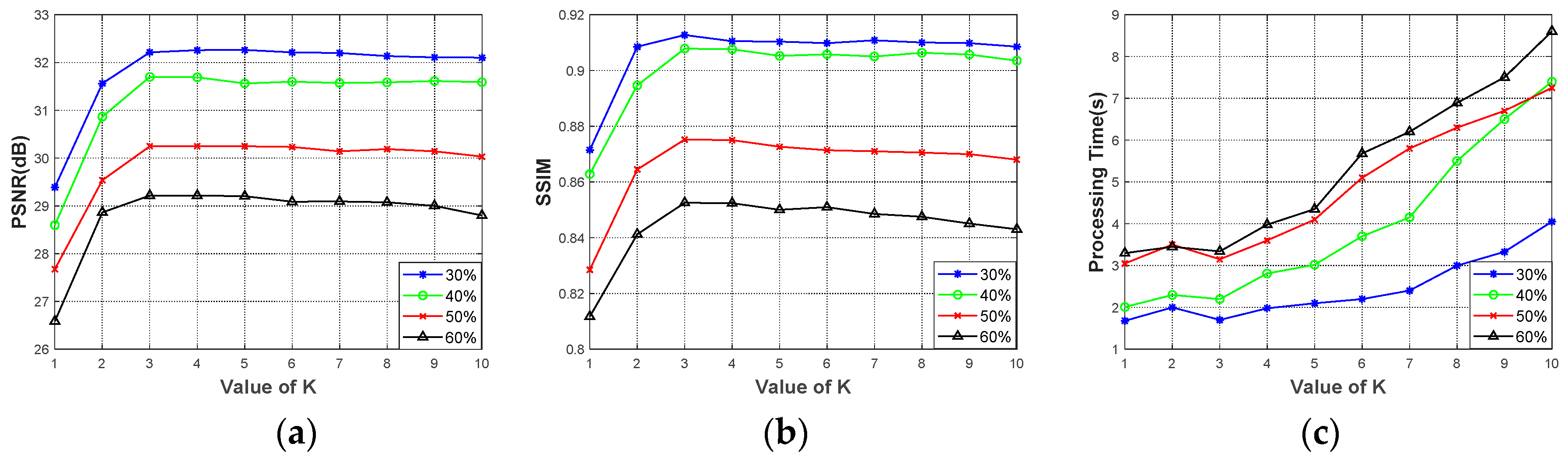
4.2.1. Number of Inner Iteration Steps
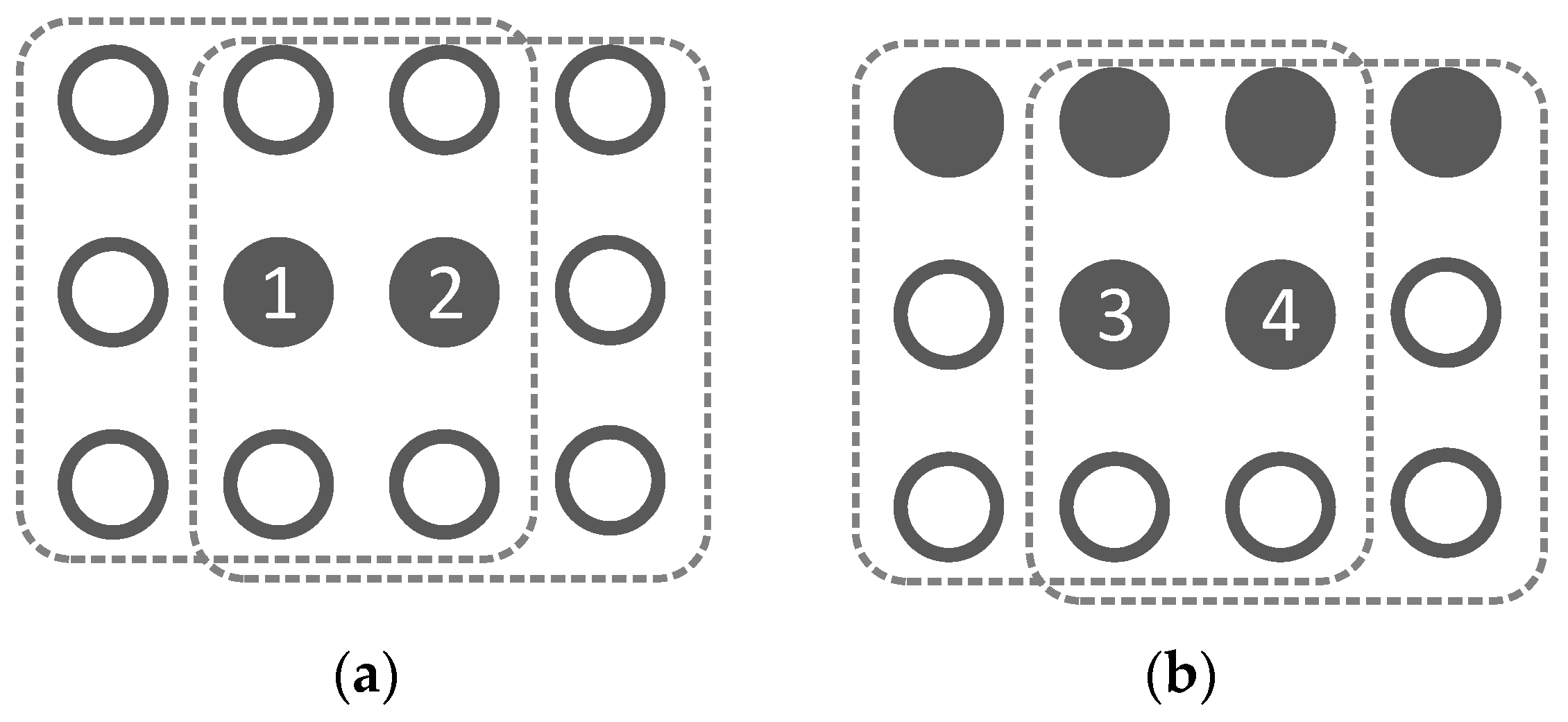
4.2.2. Group Gradient Parameter K
4.2.3. Regularization Parameter and Quasinorm
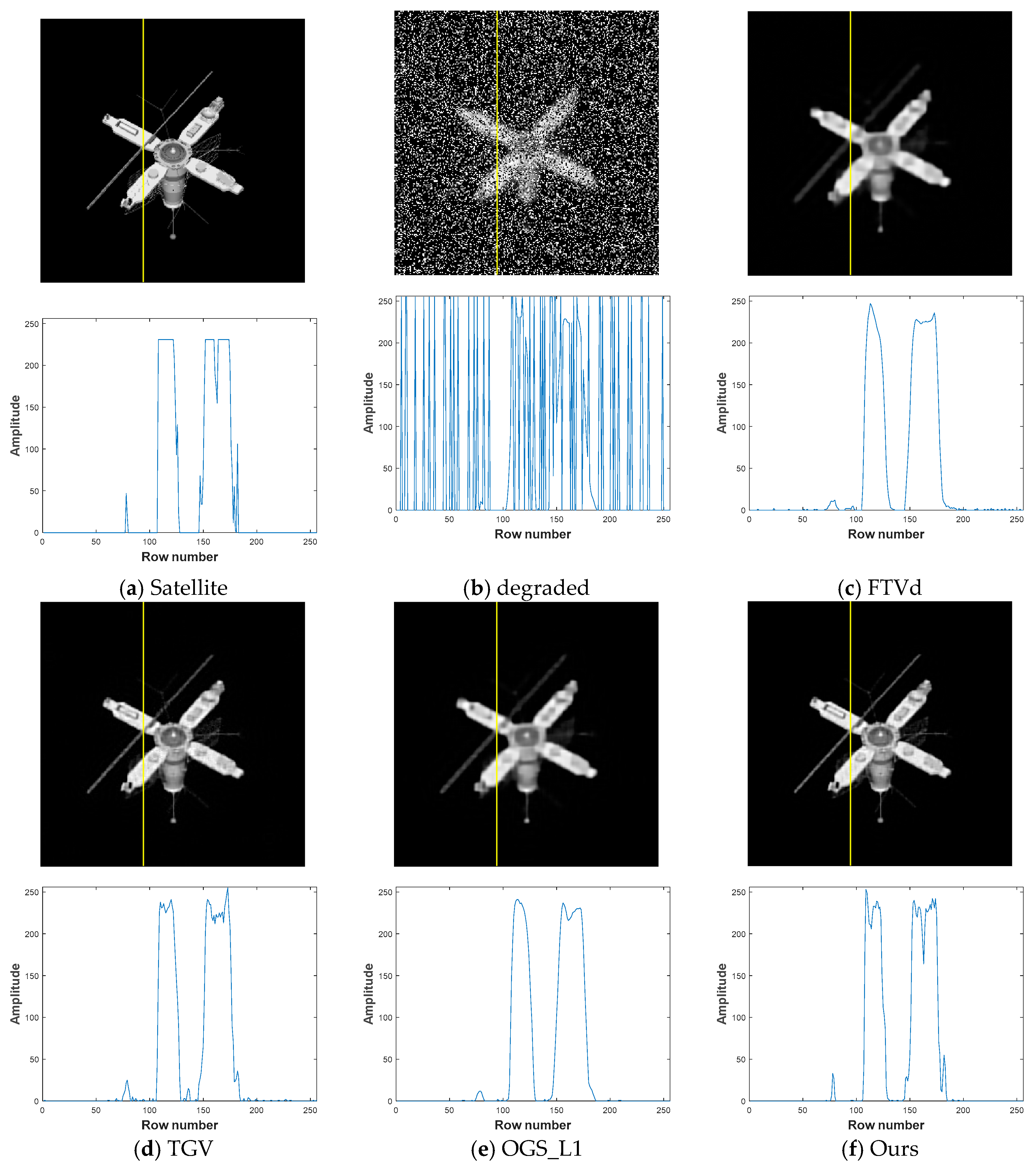
4.2.4. Comparative Testing of Image Reconstruction Effectiveness between Several Algorithms
- With the addition of blurring and different levels of noise in various images, the proposed models in this study are superior to other excellent models for image reconstruction in terms of PSNR and SSIM. This indicates that the proposed models have good deblurring and denoising performance, while allowing the reconstructed images to be more similar to the original images.
- When the proposed models are employed to reconstruct the eight images, the PSNR values are higher than those of the TGV model by 0.204–2.177 dB, and the superiority of the proposed models is more evident at higher levels of noise. For example, PSNR of the proposed models (28.081 dB) is 2.177 dB higher than that of the TGV model (25.904 dB) for the image of Lena at a noise level of 60%, and the PSNR difference becomes 2.174 dB for the image of the boat at the same noise level (26.797 dB vs. 24.623 dB).
- Compared with OGS_L1, the proposed models increase the Lp-quasinorm shrinkage and improve the ability to characterize image gradient sparsity. When recovering the eight images, the proposed models have PSNR values that are 0.328–1.964 dB higher than those of the OGS_L1 model. For the butterfly image at the noise level of 60%, PSNR of the proposed models (26.077 dB) is 1.964 dB higher than that of the OGS_L1 model (24.113 dB).
4.2.5. Comparison of Image Reconstruction Time for Several Algorithms
- The GGS_Lp model and its accelerated restart version GGS_LP_Fast, both proposed in this study, lead to similar PSNR values when the two models are used to reconstruct images, but their PSNR values are all greater than those of the FTVd, TGV, and OGS_L1 models.
- As a classic algorithm, FTVd is still advantageous in terms of computational speed. TGV and OGS_L1 give better image reconstruction results than FTVd, but they are more time-consuming. In this study, neighborhood gradient information is thoroughly considered, and the Lp-quasinorm is introduced as a regularization constraint, which leads to a greater computational complexity and thereby greater time consumption for image reconstruction compared with the FTVd model. By contrast, the GGS_LP_Fast model increases computational efficiency to a great extent, and its performance is especially prominent for images with a high level of noise.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gonzalez, R.C. Digital Image Processing; Prentice Hall: Upper Saddle River, NJ, USA, 2016. [Google Scholar]
- Karayiannis, N.B.; Venetsanopoulos, A.N. Regularization theory in image restoration—The stabilizing functional approach. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1155–1179. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer Science & Business Media: Berlin, Germany, 1995. [Google Scholar]
- Chen, Y.; Peng, Z.; Gholami, A.; Yan, J. Seismic signal sparse time-frequency analysis by Lp-quasinorm constraint. arXiv, 2018; arXiv:1801.05082. [Google Scholar]
- Lin, F.; Yu, F.; Chen, Y.; Li, M.; Peng, Z. Seismic signal denoising using total generalized variation with overlapping group sparsity in the accelerated ADMM framework. J. Geophys. Eng. 2019. [Google Scholar] [CrossRef]
- Mousavi Kahaki, S.M.; Nordin, M.J.; Ashtari, A.H.; Zahra, S.J. Invariant Feature Matching for Image Registration Application Based on New Dissimilarity of Spatial Features. PLoS ONE 2016, 11, e0149710. [Google Scholar] [CrossRef] [PubMed]
- Kahaki, S.M.M.; Nordin, M.J.; Ashtari, A.H.; Zahra, S.J. Deformation invariant image matching based on dissimilarity of spatial features. Neurocomputing 2016, 175, 1009–1018. [Google Scholar] [CrossRef]
- Phillips, D.L. A Technique for the Numerical Solution of Certain Integral Equations of the First Kind. J. ACM 1962, 9, 84–97. [Google Scholar] [CrossRef]
- Tihonov, A.N. Solution of incorrectly formulated problems and the regularization method. Sov. Math. 1963, 4, 1035–1038. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Lassen, A.L. Implementation and Evaluation of a Splitting Method for Total Variation Deblurring; Technical University of Denmark: Lyngby, Denmark, 2011. [Google Scholar]
- Guo, X.; Li, F.; Ng, M.K. A fast ℓ 1-TV algorithm for image restoration. SIAM J. Sci. Comput. 2009, 31, 2322–2341. [Google Scholar] [CrossRef]
- Chambolle, A. An algorithm for total variation minimization and applications. J. Math. Imaging Vis. 2004, 20, 89–97. [Google Scholar]
- Salvadeo, D.H.P.; Mascarenhas, N.D.A.; Levada, A.L.M. Nonlocal Markovian models for image denoising. J. Electron. Imaging 2016, 25, 013003. [Google Scholar] [CrossRef]
- Chan, T.; Esedoglu, S.; Park, F.; Yip, A. Recent developments in total variation image restoration. Math. Models Comput. Vis. 2005, 17, 1–18. [Google Scholar]
- Yang, J.; Zhang, Y.; Yin, W. An efficient TVL1 algorithm for deblurring multichannel images corrupted by impulsive noise. SIAM J. Sci. Comput. 2009, 31, 2842–2865. [Google Scholar] [CrossRef]
- Huang, G.; Jiang, H.; Matthews, K.; Wilford, P. Lensless Imaging by Compressive Sensing. In Proceedings of the IEEE International Conference on Image Processing, Melbourne, Australia, 15–18 September 2013; pp. 2101–2105. [Google Scholar]
- Chen, Y.; Peng, Z.; Cheng, Z.; Tian, L. Seismic signal time-frequency analysis based on multi-directional window using greedy strategy. J. Appl. Geophys. 2017, 143, 116–128. [Google Scholar] [CrossRef]
- Lu, T.; Li, S.; Fang, L.; Ma, Y.; Benediktsson, J.A. Spectral–spatial adaptive sparse representation for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2016, 54, 373–385. [Google Scholar] [CrossRef]
- Zhao, W.; Lu, H. Medical Image Fusion and Denoising with Alternating Sequential Filter and Adaptive Fractional Order Total Variation. IEEE Trans. Instrum. Meas. 2017, 66, 2283–2294. [Google Scholar] [CrossRef]
- Wu, L.; Chen, Y.; Jin, J.; Du, H.; Qiu, B. Four-directional fractional-order total variation regularization for image denoising. J. Electron. Imaging 2017, 26, 053003. [Google Scholar] [CrossRef]
- Bredies, K. Symmetric tensor fields of bounded deformation. Annali di Matematica Pura ed Applicata 2013, 192, 815–851. [Google Scholar] [CrossRef]
- Bredies, K.; Holler, M. Regularization of linear inverse problems with total generalized variation. J. Inverse Ill-Posed Probl. 2014, 22, 871–913. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imaging Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Knoll, F.; Bredies, K.; Pock, T.; Stollberger, R. Second order total generalized variation (TGV) for MRI. Magn. Reson. Med. 2011, 65, 480–491. [Google Scholar] [CrossRef]
- Kong, D.; Peng, Z. Seismic random noise attenuation using shearlet and total generalized variation. J. Geophys. Eng. 2015, 12, 1024–1035. [Google Scholar] [CrossRef]
- Zhang, X.; Burger, M.; Bresson, X.; Osher, S. Bregmanized nonlocal regularization for deconvolution and sparse reconstruction. SIAM J. Imaging Sci. 2010, 3, 253–276. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, T.F. Wavelet inpainting by nonlocal total variation. Inverse Probl. Imaging 2017, 4, 191–210. [Google Scholar]
- Ren, Z.; He, C.; Zhang, Q. Fractional order total variation regularization for image super-resolution. Signal Process. 2013, 93, 2408–2421. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Yin, W.; Zhang, Y. A new alternating minimization algorithm for total variation image reconstruction. SIAM J. Imaging Sci. 2008, 1, 248–272. [Google Scholar] [CrossRef]
- Sakurai, M.; Kiriyama, S.; Goto, T.; Hirano, S. Fast algorithm for total variation minimization. In Proceedings of the 2011 18th IEEE International Conference on Image Processing (ICIP), Brussels, Belgium, 11–14 September 2011; pp. 1461–1464. [Google Scholar]
- Selesnick, I.; Farshchian, M. Sparse signal approximation via nonseparable regularization. IEEE Trans. Signal Process. 2017, 65, 2561–2575. [Google Scholar] [CrossRef]
- Selesnick, I.W.; Chen, P.-Y. Total variation denoising with overlapping group sparsity. In Proceedings of the Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; pp. 5696–5700. [Google Scholar]
- Liu, G.; Huang, T.Z.; Liu, J.; Lv, X.-G. Total variation with overlapping group sparsity for image deblurring under impulse noise. PLoS ONE 2015, 10, e0122562. [Google Scholar] [CrossRef]
- Liu, J.; Huang, T.Z.; Liu, G.; Wang, S.; Lv, X.G. Total variation with overlapping group sparsity for speckle noise reduction. Neurocomputing 2016, 216, 502–513. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Pro. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef]
- Woodworth, J.; Chartrand, R. Compressed sensing recovery via nonconvex shrinkage penalties. Inverse Probl. 2016, 32, 75004–75028. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006; pp. 29–76. [Google Scholar]
- De Vieilleville, F.; Weiss, P.; Lobjois, V.; Kouame, D. Alternating direction method of multipliers applied to 3D light sheet fluorescence microscopy image deblurring using GPU hardware. In Proceedings of the International Conference of the IEEE Engineering in Medicine & Biology Society, Boston, MA, USA, 30 August–3 September 2011; p. 4872. [Google Scholar]
- Chen, P.Y.; Selesnick, I.W. Translation-invariant shrinkage/thresholding of group sparse signals. Signal Process. 2014, 94, 476–489. [Google Scholar] [CrossRef]
- Kahaki, S.M.M.; Arshad, H.; Nordin, M.J.; Ismail, W. Geometric feature descriptor and dissimilarity-based registration of remotely sensed imagery. PLoS ONE 2018, 13, e0200676. [Google Scholar] [CrossRef] [PubMed]
- Eybposh, M.H.; Turani, Z.; Mehregan, D.; Nasiriavanaki, M. Cluster-based filtering framework for speckle reduction in OCT images. Biomed. Opt. Express 2018, 9, 6359–6373. [Google Scholar] [CrossRef]
- Adabi, S.; Rashedi, E.; Clayton, A.; Mohebbi-Kalkhoran, H.; Chen, X.W.; Conforto, S.; Nasiriavanaki, M. Learnable despeckling framework for optical coherence tomography images. J. Biomed. Opt. 2018, 23, 016013. [Google Scholar] [CrossRef] [PubMed]
- Nikolova, M. A variational approach to remove outliers and impulse noise. J. Math. Imaging Vis. 2004, 20, 99–120. [Google Scholar] [CrossRef]
- Zheng, L.; Maleki, A.; Weng, H.; Wang, X.; Long, T. Does ℓp-minimization outperform ℓ1-minimization? IEEE Trans. Inf. Theory 2017, 63, 6896–6935. [Google Scholar] [CrossRef]
- Liu, C.; Shi, Z.; Hou, T.Y. On the Uniqueness of Sparse Time-Frequency Representation of Multiscale Data. Multiscale Model. Simul. 2015, 13, 790–811. [Google Scholar] [CrossRef]
- Liu, J.; Huang, T.Z.; Selesnick, I.W.; Lv, X.G.; Chen, P.Y. Image restoration using total variation with overlapping group sparsity. Inf. Sci. 2015, 295, 232–246. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends® Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Goldstein, T.; O’Donoghue, B.; Setzer, S.; Baraniuk, R. Fast alternating direction optimization methods. SIAM J. Imaging Sci. 2014, 7, 1588–1623. [Google Scholar] [CrossRef]
- Emory University Image Database. Available online: http://www.mathcs.emory.edu/~nagy/RestoreTools/ (accessed on 15 March 2018).
- CVG-UGR (Computer Vision Group, University of Granada) Image Database. Available online: http://decsai.ugr.es/cvg/dbimagenes/index.php (accessed on 15 March 2018).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]





| Noise Level | Lena | Butterfly | Boat | Plane | Seabird | Fish | House | Satellite |
|---|---|---|---|---|---|---|---|---|
| 30 | 0.65 | 0.45 | 0.55 | 0.55 | 0.50 | 0.65 | 0.70 | 0.75 |
| 40 | 0.65 | 0.45 | 0.55 | 0.55 | 0.50 | 0.65 | 0.70 | 0.75 |
| 50 | 0.65 | 0.45 | 0.55 | 0.55 | 0.50 | 0.65 | 0.70 | 0.75 |
| 60 | 0.65 | 0.50 | 0.55 | 0.55 | 0.50 | 0.65 | 0.70 | 0.75 |
| Images | Noise Level | FTVd | FrTV | TGV | OGS_L1 | Ours | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | ||
| Lena | 30 | 27.121 | 0.813 | 28.742 | 0.854 | 29.108 | 0.863 | 29.443 | 0.875 | 29.825 | 0.889 |
| 40 | 25.270 | 0.750 | 26.341 | 0.773 | 28.589 | 0.842 | 28.750 | 0.857 | 29.551 | 0.878 | |
| 50 | 23.843 | 0.654 | 24.508 | 0.760 | 27.673 | 0.810 | 27.899 | 0.832 | 28.899 | 0.859 | |
| 60 | 21.861 | 0.592 | 22.823 | 0.611 | 25.904 | 0.672 | 26.444 | 0.794 | 28.081 | 0.831 | |
| Butterfly | 30 | 26.592 | 0.813 | 27.214 | 0.824 | 27.852 | 0.854 | 27.902 | 0.859 | 28.416 | 0.875 |
| 40 | 26.013 | 0.782 | 26.378 | 0.803 | 27.078 | 0.829 | 26.996 | 0.827 | 27.732 | 0.837 | |
| 50 | 25.433 | 0.761 | 26.015 | 0.791 | 26.429 | 0.794 | 26.527 | 0.770 | 26.917 | 0.817 | |
| 60 | 24.731 | 0.730 | 24.909 | 0.741 | 25.041 | 0.752 | 24.113 | 0.721 | 26.077 | 0.771 | |
| Boat | 30 | 27.543 | 0.860 | 28.040 | 0.865 | 29.028 | 0.881 | 28.938 | 0.880 | 29.266 | 0.883 |
| 40 | 27.251 | 0.851 | 27.638 | 0.862 | 28.182 | 0.863 | 28.077 | 0.861 | 28.756 | 0.868 | |
| 50 | 25.703 | 0.820 | 26.325 | 0.826 | 26.733 | 0.842 | 26.594 | 0.827 | 27.997 | 0.860 | |
| 60 | 23.902 | 0.731 | 24.233 | 0.760 | 24.623 | 0.781 | 24.923 | 0.782 | 26.797 | 0.828 | |
| Plane | 30 | 30.245 | 0.772 | 30.551 | 0.833 | 31.649 | 0.891 | 32.751 | 0.907 | 33.281 | 0.913 |
| 40 | 29.869 | 0.872 | 30.538 | 0.851 | 31.362 | 0.883 | 32.092 | 0.891 | 32.837 | 0.919 | |
| 50 | 29.072 | 0.851 | 29.556 | 0.862 | 31.126 | 0.881 | 31.371 | 0.883 | 32.121 | 0.890 | |
| 60 | 28.167 | 0.803 | 28.299 | 0.841 | 29.495 | 0.712 | 29.732 | 0.877 | 31.479 | 0.885 | |
| Seabird | 30 | 29.377 | 0.872 | 29.750 | 0.882 | 31.344 | 0.891 | 31.843 | 0.910 | 32.214 | 0.913 |
| 40 | 28.500 | 0.863 | 28.951 | 0.868 | 30.530 | 0.880 | 30.811 | 0.889 | 31.700 | 0.908 | |
| 50 | 27.636 | 0.829 | 28.073 | 0.844 | 29.156 | 0.855 | 29.418 | 0.864 | 30.249 | 0.875 | |
| 60 | 26.594 | 0.812 | 27.010 | 0.803 | 27.881 | 0.852 | 27.938 | 0.840 | 29.215 | 0.853 | |
| Fish | 30 | 23.111 | 0.693 | 23.752 | 0.730 | 24.554 | 0.772 | 24.350 | 0.764 | 24.758 | 0.788 |
| 40 | 22.850 | 0.661 | 23.032 | 0.700 | 23.310 | 0.682 | 23.547 | 0.737 | 24.150 | 0.755 | |
| 50 | 21.896 | 0.623 | 22.649 | 0.681 | 22.881 | 0.692 | 22.572 | 0.685 | 23.585 | 0.726 | |
| 60 | 20.933 | 0.572 | 21.051 | 0.581 | 21.113 | 0.583 | 21.109 | 0.601 | 22.458 | 0.675 | |
| House | 30 | 26.558 | 0.771 | 26.791 | 0.773 | 28.322 | 0.832 | 28.283 | 0.833 | 28.659 | 0.847 |
| 40 | 26.151 | 0.750 | 26.573 | 0.760 | 27.972 | 0.821 | 27.501 | 0.806 | 28.246 | 0.822 | |
| 50 | 24.959 | 0.693 | 25.100 | 0.701 | 25.510 | 0.722 | 25.764 | 0.724 | 26.868 | 0.778 | |
| 60 | 24.110 | 0.670 | 24.212 | 0.674 | 24.727 | 0.684 | 24.315 | 0.673 | 25.692 | 0.726 | |
| Satellite | 30 | 28.372 | 0.934 | 29.190 | 0.942 | 30.930 | 0.963 | 31.751 | 0.967 | 32.732 | 0.977 |
| 40 | 28.074 | 0.931 | 28.635 | 0.911 | 30.745 | 0.952 | 30.296 | 0.962 | 32.362 | 0.974 | |
| 50 | 27.403 | 0.921 | 27.682 | 0.923 | 29.874 | 0.951 | 30.095 | 0.951 | 31.397 | 0.954 | |
| 60 | 26.245 | 0.901 | 26.453 | 0.909 | 28.152 | 0.931 | 28.289 | 0.942 | 29.845 | 0.949 | |
| Images | Noise Level | FTVd | TGV | OGS_L1 | GGS_LP | GGS_LP_Fast | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | Time | PSNR | Time | PSNR | Time | PSNR | Time | PSNR | Time | ||
| Lena | 30 | 27.121 | 1.02 | 29.108 | 5.12 | 29.443 | 1.72 | 29.825 | 2.56 | 29.920 | 1.14 |
| 60 | 21.861 | 1.98 | 25.904 | 8.34 | 26.444 | 3.10 | 28.081 | 3.45 | 27.913 | 2.10 | |
| Butterfly | 30 | 26.592 | 1.33 | 27.852 | 6.01 | 27.902 | 0.96 | 28.416 | 2.06 | 28.573 | 1.25 |
| 60 | 24.731 | 1.88 | 25.041 | 9.26 | 24.113 | 2.82 | 26.077 | 2.95 | 25.827 | 1.83 | |
| Boat | 30 | 27.543 | 0.83 | 29.028 | 4.98 | 28.938 | 2.25 | 29.266 | 1.48 | 29.586 | 1.61 |
| 60 | 23.902 | 1.95 | 24.623 | 9.30 | 24.923 | 2.46 | 26.797 | 3.04 | 26.688 | 2.17 | |
| Plane | 30 | 30.245 | 0.72 | 31.649 | 3.47 | 32.751 | 1.25 | 33.281 | 2.28 | 32.909 | 1.59 |
| 60 | 28.167 | 1.84 | 29.495 | 5.92 | 29.732 | 3.93 | 31.479 | 4.09 | 31.387 | 2.82 | |
| Seabird | 30 | 29.377 | 1.56 | 31.344 | 5.64 | 31.843 | 2.40 | 32.214 | 1.70 | 32.528 | 1.87 |
| 60 | 26.594 | 2.35 | 27.881 | 9.76 | 27.938 | 3.73 | 29.215 | 3.84 | 29.183 | 2.29 | |
| Fish | 30 | 23.111 | 0.92 | 24.554 | 6.23 | 24.350 | 1.53 | 24.758 | 1.36 | 24.833 | 1.17 |
| 60 | 20.933 | 1.90 | 21.113 | 10.85 | 21.109 | 3.07 | 22.458 | 2.59 | 22.386 | 1.87 | |
| House | 30 | 26.558 | 1.15 | 28.322 | 6.24 | 28.283 | 1.36 | 28.659 | 1.59 | 28.884 | 1.62 |
| 60 | 24.110 | 2.38 | 24.727 | 11.23 | 24.315 | 2.37 | 25.692 | 3.34 | 25.585 | 2.29 | |
| Satellite | 30 | 28.372 | 0.76 | 30.930 | 3.69 | 31.751 | 1.39 | 32.732 | 1.67 | 32.799 | 1.14 |
| 60 | 26.245 | 1.88 | 28.152 | 7.86 | 28.289 | 2.85 | 29.845 | 1.70 | 30.013 | 1.60 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, F.; Chen, Y.; Wang, L.; Chen, Y.; Zhu, W.; Yu, F. An Efficient Image Reconstruction Framework Using Total Variation Regularization with Lp-Quasinorm and Group Gradient Sparsity. Information 2019, 10, 115. https://doi.org/10.3390/info10030115
Lin F, Chen Y, Wang L, Chen Y, Zhu W, Yu F. An Efficient Image Reconstruction Framework Using Total Variation Regularization with Lp-Quasinorm and Group Gradient Sparsity. Information. 2019; 10(3):115. https://doi.org/10.3390/info10030115
Chicago/Turabian StyleLin, Fan, Yingpin Chen, Lingzhi Wang, Yuqun Chen, Wei Zhu, and Fei Yu. 2019. "An Efficient Image Reconstruction Framework Using Total Variation Regularization with Lp-Quasinorm and Group Gradient Sparsity" Information 10, no. 3: 115. https://doi.org/10.3390/info10030115
APA StyleLin, F., Chen, Y., Wang, L., Chen, Y., Zhu, W., & Yu, F. (2019). An Efficient Image Reconstruction Framework Using Total Variation Regularization with Lp-Quasinorm and Group Gradient Sparsity. Information, 10(3), 115. https://doi.org/10.3390/info10030115




