Development of a New Adaptive Backstepping Control Design for a Non-Strict and Under-Actuated System Based on a PSO Tuner

Abstract

In this work, a new adaptive block-backstepping control design algorithm was developed for an under-actuated model (represented by a ball–arc system) to enhance the transient and steady-state behaviors and to improve the robustness characteristics of the controlled system against parameter variation (load change and model uncertainty). For this system, the main mission of the proposed controller is to simultaneously hold the ball at the top of the arc and retain the cart at the required position. The stability of a controlled system based on the proposed adaptive controller was analyzed, and its globally asymptotic stability was proven based on the Lyapunov theorem. A comparative study of adaptive and non-adaptive block-backstepping controllers was conducted in relation to the transient, steady-state, and robustness characteristics. The effectiveness of the controller was verified via simulation within a MATLAB/SIMULINK environment. The simulated results show that the proposed adaptive control strategy could successfully stabilize the under-actuated ball–arc system, regardless of both the regulation problem and the tracking problem. This provides a better dynamic performance and a better load rejection capability, and it performs well in solving the uncertainty problem in the model parameter.

1. Introduction

Over the past 50 years, adaptive control was a fertile ground for active research in control design. This area of control design was reinforced by a proof of global stability, which led to the enhancement of transient performance and system tracking and, additionally, to the success of both theoretical and practical developments. The breakthrough and rapid growth achieved by adaptive control are due to its ability to cope with plant uncertainties during the operation time of the systems. Some adaptive control methodologies apply certain algorithms to acquire the system model, which, in turn, is utilized in synthesizing the adaptive controller. Other adaptive approaches combine the process of estimating unknown parameters and control law in order to design an adaptive controller. The salient feature of the adaptive controller is that it adjusts its constituting parameters instantaneously during the operation of the controlled system in order to maintain the desired performance values under the effects of the uncertainties [1].

In the early 1990s, a new approach, called “backstepping”, emerged as a tool for designing adaptive controllers. Backstepping is a recursive approach based on the Lyapunov method and strictly tailored to the class of feedback systems. It was shown that this approach could guarantee both global and local asymptotic convergence for regulation and tracking properties. The main advantage of the backstepping approach is that it follows a systematic or step-by-step procedure in order to obtain the design of the stabilizing controller. In other words, synthesizing the feedback control laws based on the Lyapunov functions is performed systematically. The other advantage of this control design scheme is that it has the adaptability that allows it to avoid eliminating helpful nonlinearities. Meanwhile, it achieves the required objectives of stabilization, regulation, and tracking [2,3].

Recently, the backstopping control design method for uncertain nonlinear systems attracted many researchers and, consequently, many theoretical improvements, and their applications based on backstepping were presented. For example, Bang et al. [4] designed a backstepping-based control algorithm to address the general stabilization problem, and also employed the disturbance observer to compensate for input-matched disturbances and uncertainties. Rudra et al. [5] combined two control strategies in order to solve the Furuta pendulum stabilization problem in the presence of external disturbances. One control design was based on the adaptive backstepping approach, and the other design was based on the sliding mode control methodology. However, the above backstepping algorithms are often too complicated to be effectively implemented for under-actuated systems. Therefore, the authors proposed a block-backstepping control algorithm to solve the stabilization problem for a generalized nonlinear under-actuated mechanical system [6]. Humaidi et al. proposed a block-backstepping control algorithm, which was devoted to track and balance the control of a ball–arc system [7]. The proposed controller was enhanced by adding an integral term to enhance both the robustness and steady-state characteristics of the overall system. However, the controller could not deal with unknown disturbances. Cheng approached the adaptive decentralized control problem with a perturbation estimation scheme for a class of nonlinear systems via the backstepping approach, where the dynamic equations of the plant are in the non-strict feedback form [8]. This technique depends on the transformation of the dynamic model to a strict feedback form by means of state transformation. Then, the decentralized adaptive backstepping algorithm is applied. Li and Yang focused on the adaptive decentralized control problem for a class of interconnected nonlinear systems, in which the interconnections are assumed to be unknown and completely nonlinear [9]. The adaptive law was established by introducing a smooth switching function. The stability of the closed-loop system based on the adaptive decentralized controller was analyzed using the graph theory and Lyapunov method. This study proved that all states of a closed-loop system are globally bounded and that the tracking errors converge to a compact set. Li and Yang considered the adaptive decentralized fault-tolerant tracking control problem for a class of uncertain interconnected nonlinear systems with unknown and strong interconnections, which were addressed using the graph theory [10]. A neural-network-based adaptive decentralized fault-tolerant control was employed to achieve tracking performance and to compensate for the system uncertainties and actuator faults. This study proved that the semi-globally bounded signals are exponentially convergent to a compact set, based on the Lyapunov method. Uk and Lee et al. proposed the formation control of quad-rotors based on the backstepping control approach with the state transformation technique [11]. The work employed the state transformation technique to develop reference attitude angles, without the need for small-angle assumptions or the simplification of system dynamics, both of which are commonly used. A Lyapunov-based stability analysis showed that an asymptotical convergence of the quad-rotor formation system error can be reached by the proposed formation controller.

Throughout the development of the adaptive backstepping control design, different design parameters emerged, which have to be set. However, their setting should satisfy the stabilization of the designed controller, and it was also shown that these design parameters have an impact on the controlled system performance. A trial-and-error procedure for selecting their values is exhaustive, and it does not lead to an optimal solution in terms of the best performance. In other words, the optimization problem represents the design parameters of a control algorithm. As such, a modern optimization technique is required to find their optimal values in an automatic manner.

In this work, the particle swarm optimization (PSO) algorithm is suggested as an optimal tuner. PSO is an evolutionary computation technique that was proposed by Kennedy and Eberhart in 1995 [12]. This algorithm was inspired by the behavior of organisms, such as bird flocking and fish schooling. Generally, this optimization technique is famous, and it is commonly used as an optimized tuner, since it is easily executed, quickly convergent, and computationally efficient, and it has the ability to find a local and global solution [13].

It was shown that the PSO algorithm could effectively address the tuning problem of the design parameters of block-backstepping control for a wide range of engineering applications. Fazillah et al. presented a backstepping control design of an under-actuated system, represented by X4-AUV [14]. The PSO algorithm was suggested to tune and find the optimal values of the backstepping controller design parameters. Basri proposed an optimal backstepping controller for an autonomous quad-rotor unmanned aerial vehicle [15]. The design of the backstepping controller was firstly established based on a conventional setting of design parameters; then, a PSO was invoked to find the optimal values of these design parameters. Rozali et al. designed a backstepping controller for an electro-hydraulic actuator (EHA) system [16]. Two optimization techniques were employed—gravitational search algorithm (GSA) and particle swarm optimization (PSO) techniques—for optimizing the design parameters of a backstepping controller, so as to improve the performance of the EHA system controlled by a backstepping controller. The simulated results verified that GSA provides a better performance than PSO in terms of tracking error. Wai and Chuang focused on the design of the backstepping particle swam optimization control (BSPSOC) for the online levitating, balancing, and propulsive positioning of a magnetic levitation (maglev) transportation system, which consisted of a propulsive linear induction motor (LIM) and levitating electromagnetic system [17]. The PSO technique was utilized to solve the chattering effort in backstepping control design and ensure the stability of the controlled system, without the need for strict constraints. Recently, advanced optimization techniques were presented to tackle different problems in control strategies, such as the tuning of design parameters or the improvement of controller performances [18,19,20,21,22].

In the present work, the PSO is suggested to compute the optimal values of design parameters, which appear throughout the design of an adaptive block-backstepping controller for a ball–arc system.

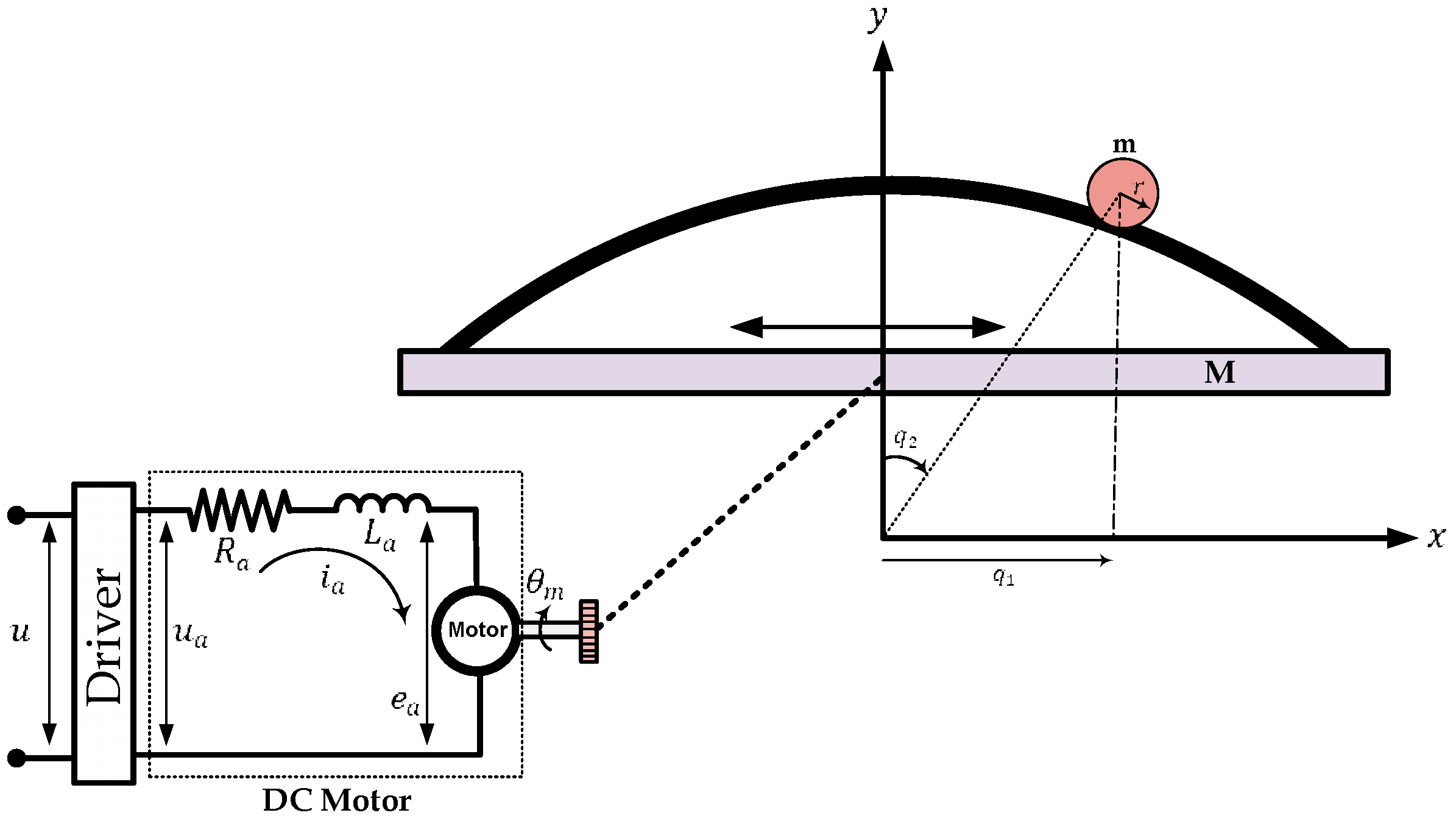
The motivation behind the present work was that the under-actuated model, represented by the ball–arc system, is not in a strict-feedback form, and it is characterized by high complexity. Moreover, the effect of unknown disturbances and the uncertainty of the model causes system instability. Therefore, an adaptive backstepping design and control of such systems is a challenging problem, the solution of which was the aim of the work. The following points can summarize the contributions of this work:

• The main contribution of the work is the development of a novel adaptive block-backstepping design for solving the control problem of non-strict under-actuated systems under unknown disturbance and an uncertainty in parameters. Throughout the development of this new adaptive control design, the following minor tasks were addressed:
  • The non-strict form system was transformed into a reduced-order strict feedback form based on the zero-dynamics equation.
  • To improve the performance of the controller, a parameter term was added to the initial regulated variables.
  • Control and adaptive laws were developed to estabilish adaptive block-backstepping control, so as to cope with unknown disturbance and parameter uncertainty.
  • The global asymptotic stability (GAS) of the proposed adaptive block-backstepping controlled system was analyzed, and the convergence of all states to the desired trajectory was proven.
• Instead of relying on the trial-and-error procedure to set the design parameters of the adaptive block-backstepping control algorithm, a modern optimization technique based on a PSO tuner was utilized to find the optimal design parameters of the adaptive controller to further enhance the performance of the proposed controller.

This paper is arranged in the following order: Section 2 presents the modeling of the under-actuated system, represented by a ball–arc system. A novel adaptive block-backstepping design algorithm is developed in Section 3. The stability analysis based on the Lyapunov method is presented in Section 4 to prove the asymptotic convergence of all states to their corresponding desired states. The optimization of block-backstepping controller parameters is introduced in Section 5 to find the optimal values of the design parameter, so as to improve the closed-system dynamic. The simulated results are presented in Section 6. In Section 7, conclusions based on the simulated results are drawn.

2. Ball–Arc System Model

The ball–arc system is an Under-actuated Mechanical System (UMS) with two Degree of Freedoms (DOFs) which was proposed as a case study to demonstrate the basic concepts of modern control theory. This system can be described by a ball that rolls on the top of an arc. The arc sits on a cart driven by a motor, as depicted in Figure 1 [7,23]. The parameter $M$ represents the total mass of the cart and arc, $m$ denotes the ball mass, $R$ is the radius of the arc, $r$ is radius of the moving ball, $R_a$ represents the armature resistance of the direct current (DC) motor, $k_m$ defines the motor constant, and the control voltage is denoted by $u$.

The ball–arc system dynamic model with disturbance can be rewritten as follows [7]:

$$\begin{array}{c}{\dot{q}}_1=p_1,\\ {\dot{p}}_1=\frac{1}{\beta \left(q\right)}·(m_{12}·m_{22}·p_2^2·\sin q_2-m_{12}^2·g·\sin q_2·\cos q_2+m_{22}\hfill \\ ·\left(\frac{k_m}{R_a·R_1}u-\frac{k_m^2}{R_a·R_1^2}{p}_1\right)-(m·{\left(R+r\right)}^2·{\cos }^2{q}_2-m_{22})·F);\hfill \end{array}$$

$${\dot{q}}_2=p_2,$$

(1)

$$\begin{array}{c}{\dot{p}}_2=\frac{1}{\beta }·(m_{11}·m_{12}·g·\sin q_2-m_{12}^2·p_2^2·\sin q_2·\cos q_2-m_{12}·\cos q_2\hfill \\ ·\left(\frac{k_m}{R_a·R_1}·u-\frac{k_m}{R_a·R_1^2}·p_1\right)-\left(m_{12}-m_{11}·\left(R+r\right)\right)·F·\cos q_2)\hfill \end{array}$$

where

$$m_{11}=M+m,m_{12}=m·\left(R+r\right),$$

$$m_{22}=m·{\left(R+r\right)}^2+I·{\left(\frac{R+r}{r}\right)}^2,$$

(2)

$$\beta \left(q\right)=m_{11}·I{\left(\frac{R+r}{r}\right)}^2+M·m{\left(R+r\right)}^2+m_{12}^2·{\sin }^2{q}_2>0,$$

where $q_1$, $p_1$, $q_2$, and $p_2$ represent the mass center displacement of the cart, the velocity of the cart, the angular displacement (between the vertical line through the center of the arc and the line passing through the ball center), and the angular velocity of the ball, respectively.

3. Proposed Adaptive Block-Backstepping Algorithm for the Ball–Arc System

In this section, the unknown disturbance is applied to the center of the ball. As a result, the novel adaptive block-backstepping scheme was developed to design the control law. Here, the estimation error can be written as follows:

$$\tilde{F}=\widehat{F}-F$$

(3)

where $\tilde{F}$ represents the estimation error of disturbance, $\widehat{F}$ is the estimation of disturbance, and F is assumed to be a constant disturbance. The time derivative of Equation (3) is formulated as

$$\dot{\tilde{F}}=\dot{\widehat{F}}$$

(4)

The adaptive block-backstepping scheme was designed based on the selection of a suitable regulated variable.

Theorem 1.

Consider an under-actuated system with the non-strict form, as described by Equation (1). There exists a nonlinear controller and adaptation law based on a block-backstepping control design, which can cope with uncertainty in the parameters of the system.

Proof. 

The proposed design procedure is depicted in the following steps:

Step 1: Firstly, the regulated variable is introduced as

$$z_1=q_2+k_1·e+k_2·\left(m_{12}·\cos q_2\dot{e}+m_{22}·p_2\right),$$

(5)

$$e=q_1-q_{1d},$$

(6)

$$\dot{e}=p_1-{\dot{q}}_{1d},$$

(7)

where $e$ denotes the error (between the actual and desired cart displacements), $q_{1d}$ is the desired cart displacement, and $k_1$ and $k_2$ are design constants. The time derivative of regulated variable $z_1$ can be calculated as

$${\dot{z}}_1=p_2+k_1·\dot{e}+k_2\left(-m_{12}·p_2·\sin q_2·\dot{e}+m_{12}·\cos q_2·\ddot{e}+m_{22}·{\dot{p}}_2\right)$$

(8)

After a sequence of substitutions, the above equation can be arranged to become

$$\begin{array}{l}{\dot{z}}_1=p_2+(k_1-k_2{m}_{12}{p}_2\sin q_2)\dot{e}+\frac{k_2{m}_{11}{m}_{12}{m}_{22}g\sin q_2}{\beta }-\frac{0.5k_2{m}_{12}^{3}g\sin 2q_2\cos q_2}{\beta }-\\ k_2{m}_{12}\cos q_2{\ddot{q}}_{1d}+\frac{k_2(m_{22}{m}_{11}(R+r)\cos q_2-m_{12}m{(R+r)}^2{\cos }^3{q}_2)}{\beta }(\widehat{F}-\tilde{F}),\end{array}$$

(9)

The stabilizing function is selected as follows:

$$\begin{array}{c}\alpha =-(k_1-k_2·m_{12}·p_2·\sin q_2)\dot{e}-c_1·z_1-\frac{k_2·m_{11}·m_{12}·m_{22}·g·\sin q_2}{\beta }+\\ \frac{0.5·k_2·m_{12}^3·g·\sin 2q_2·\cos q_2}{\beta }+k_2·m_{12}·\cos q_2·{\ddot{q}}_{1d}-\frac{k_2·(m_{22}·m_{11}·(R+r)·\cos q_2-m_{12}·m·{(R+r)}^2·{\cos }^3{q}_2)}{\beta },\end{array}$$

(10)

where $c_1$ is a design constant of a positive value. The corresponding error variable is calculated as

$$z_2=p_2-\alpha .$$

(11)

As a result, the time derivative of $z_1$ is given by

$${\dot{z}}_1=z_2-c_1·z_1+\frac{{\gamma }_4+{\gamma }_5}{\beta }\widehat{F}.$$

(12)

Step 2: The time derivative of variable $z_2$ is computed as

$${\dot{z}}_2={\dot{p}}_2-\dot{\alpha }.$$

(13)

After a long calculation, Equation (13) can be expressed as follows:

$${\dot{z}}_2=\psi ·u+c_1·\left(z_2-c_1·z_1\right)+\varphi +{\zeta }_1·\tilde{F}+{\zeta }_2·\dot{\widehat{F}},$$

(14)

where

$$\begin{array}{l}\psi =\frac{k_m}{R_a·R_1·\beta }\left(\left(k_1-k_2·m_{12}·p_2·\sin q_2\right)·m_{22}-\left(1-k_2·m_{12}·\dot{e}·\sin q_2\right)·m_{12}·\cos q_2\right),\\ {\zeta }_1=\frac{1}{\beta }(\left(1-k_2·m_{12}·\dot{e}·\sin q_2\right)\left(m_{12}-m_{11}·\left(R+r\right)\right)·\cos q_2\\ +\left(k_1-k_2·m_{12}·p_2·\sin q_2\right)\left(m·{\left(R+r\right)}^2·{\cos }^2{q}_2-m_{22}\right))+c_1\frac{\left({\gamma }_4+{\gamma }_5\right)}{\beta },\\ {\zeta }_2=-\frac{\left({\gamma }_4+{\gamma }_5\right)}{\beta },\\ \begin{array}{l}\varphi =\frac{\left({\gamma }_2+{\gamma }_3\right)·\dot{\beta }\left(q\right)-\left({\dot{\gamma }}_2+{\dot{\gamma }}_3\right)·\beta \left(q\right)}{\beta {\left(q\right)}^2}\\ +\frac{\left(1-k_2·m_{12}· \dot{e}·\sin q_2\right)}{\beta }(m_{11}·m_{12}·g·\sin q_2-m_{12}^2·p_2^2·\sin q_2·\cos q_2\\ +\frac{m_{12}· \cos q_2· k_m^2}{R_a· R_1^2}{p}_1-\left( m_{12}-m_{11}· \left(R+r\right)\right)· \widehat{F}· \cos q_2)\\ +\frac{\left(k_1-k_2· m_{12}· p_2· \sin q_2\right)}{\beta }(m_{12}·m_{22}·p_2^2·\sin q_2-m_{12}^2·g·\sin q_2·\cos q_2\\ -\frac{k_m^2·m_{22}}{R_a·R_1^2} p_1-\left( m·{\left(R+r\right)}^2·{\cos }^2{q}_2-m_{22}\right)·\widehat{F}-\beta \left(q\right)·{\ddot{q}}_{1d})-k_2·m_{12}·p_2^2·\dot{e}\\ ·\cos q_2+k_2·m_{12}·p_2·\sin q_2·{\ddot{q}}_{1d}-k_2·m_{12}·\cos q_2·{\stackrel{⃛}{q}}_{1d}\\ +\frac{\left({\gamma }_4+{\gamma }_5\right)·\dot{\beta }\left(q\right)-\left({\dot{\gamma }}_4+{\dot{\gamma }}_5\right)·\beta \left(q\right)}{\beta {\left(q\right)}^2}\widehat{F}\end{array}\\ {\gamma }_1=\left(k_1-k_2·m_{12}·p_2·\sin q_2\right)·\dot{e},\\ {\gamma }_2=-k_2·m_{11}·m_{12}·m_{22}·g·\sin q_2,\\ {\gamma }_3=0.5·k_2·m_{12}^3·g·\sin 2q_2·\cos q_2,\\ {\gamma }_4=-k_2·m_{22}·m_{11}·\left(R+r\right)·\cos q_2,\\ {\gamma }_5=k_2·m_{12}·m·{\left(R+r\right)}^2·{\cos }^3{q}_2,\\ {\dot{\gamma }}_1=\left(k_1-k_2·m_{12}·p_2·\sin q_2\right)·\ddot{e}-k_2·m_{12}·p_2^2·\cos q_2·\dot{e}-k_2·m_{12}·\dot{p_2}·\sin q_2·\dot{e}\\ {\dot{\gamma }}_2=-k_2·m_{11}·m_{12}·m_{22}·g·p_2·\cos q_2,\\ {\dot{\gamma }}_3=-0.5·k_2·m_{12}^3·g·\sin 2q_2·\sin q_2·p_2+k_2·m_{12}^3·g·p_2·\cos 2q_2·\cos q_2,\\ {\dot{\gamma }}_4=k_2·m_{22}·m_{11}·\left(R+r\right)p_2·\sin q_2,\\ {\dot{\gamma }}_5=-0.5·k_2·m_{12}·m·{\left(R+r\right)}^2·p_2·\sin 2q_2·\cos q_2,\\ \dot{\beta }\left(q\right)=m_{12}^2·\sin 2q_2\end{array}$$

The nonlinear controller $u$ can be expressed as

$$u={\psi }^{-1}·\left(-\varphi -c_1·\left(z_2-c_1{z}_1\right)-{\zeta }_2·\dot{\widehat{F}}-z_1-c_2·z_2\right).$$

(15)

Furthermore, the adaptation law can be obtained as follows:

$$\dot{\widehat{F}}=c_3\left(-z_1\frac{\left({\gamma }_4+{\gamma }_5\right)}{\beta }-z_2·{\zeta }_1\right),$$

(16)

where ψ is invertible, $c_2$ is the positive design constant, and $c_3$ is the rate of adaptation. □

4. Stability Analysis

In this section, the stability analysis is presented to prove the globally asymptotic stable signals and to guarantee the convergence of errors on their corresponding equilibriums.

Theorem 2.

Consider the under-actuated and non-strict system in Equation (1). The developed nonlinear controller and adaptive law based on the backstepping control design in Equation (15) and Equation (16), respectively, asymptotically stabilize all states to their corresponding desired trajectories.

Proof. 

Here, the following Lyapunov function was chosen to analyze the stability of the system:

$$V=\frac{1}{2}{z}_1^2+\frac{1}{2}{z}_2^2+\frac{1}{2c_3}{\tilde{F}}^2.$$

(17)

The time derivative of Equation (17) is calculated as

$$\dot{V}=z_1·{\dot{z}}_1+z_2·{\dot{z}}_2+\frac{1}{c_3}\tilde{F}·\dot{\widehat{F}}$$

(18)

Equation (18) is substituted for Equations (12), (14), (15), and (16). Then, Equation (18) can be expressed as

$$\begin{array}{c}\dot{V}=z_1·z_2-c_1·z_1^2+z_2·\left(\psi ·u+c_1·\left(z_2-c_1·z_1\right)+\varphi +{\zeta }_2·\dot{\widehat{F}}\right)\hfill \\ +\left(z_1\frac{\left({\gamma }_4+{\gamma }_5\right)}{\beta }+z_2·{\zeta }_1+\frac{1}{c_3}·\dot{\widehat{F}}\right)·\tilde{F}\hfill \end{array}$$

$$\dot{V}=-c_1{z}_1^2-c_2{z}_2^2\le 0.$$

(19)

It is clear that V is a positive definite, and $\dot{V}$ is a semi-negative definite for all $t\ge 0$, and this initially indicates that $V$ will converge to a finite limit, as $t\to \infty$. Integrating both sides of Equation (20) yields

$$V\left(t\right)-V\left(0\right)\le \underset{0}{\overset{t}{{\displaystyle \int }}}-c_1·z_1^2-c_2·z_2^{2}d\tau$$

(20)

Let $N\left(t\right)=-c_1{z}_1^2-c_2{z}_2^2$. Then, Equation (20) can be expressed as

$$\underset{0}{\overset{t}{{\displaystyle \int }}}N\left(t\right)d\tau \le (V\left(0\right)-V\left(t\right))<\infty$$

(21)

From Equation (21), it follows that, when $t\to \infty$, the integral ${{\displaystyle \int }}_0^{t}N\left(t\right)d\tau$ approaches a finite limit. The time derivative of $N\left(t\right)$ is easily computed as

$$\dot{N}\left(t\right)=-2c_1·z_1·{\dot{z}}_1-2c_2·z_2·{\dot{z}}_2$$

(22)

Since $\dot{N}\left(t\right)$ is bounded, $N\left(t\right)$ is uniformly continuous. The application of Barbalat’s lemma leads to $\underset{t\to \infty }{\lim }N\left(t\right)=0$ being ensured, which immediately implies that $z_1$ and $z_2$ converge on zero, as $t\to \infty .$ Moreover, the same procedure in Reference [8] for the zero dynamic of the ball–arc system was applied to guarantee the global asymptotic stability of the overall system. Hence, the proposed control law achieves the design objective. □

5. Optimization of the Design Parameters for the Block-Backstepping Controllers

Throughout the design of the adaptive block-backstepping control algorithm, one issue arises, which is represented by selecting the values of design parameters for the backstepping control algorithm. In most backstepping control-based applications, the setting of these design parameters is based on a trial-and-error procedure. However, this conventional procedure is cumbersome, and it does not give the optimal setting of these design parameters. As such, a particle swarm optimization (PSO) algorithm was adopted for autonomous tuning and to find optimal values of these parameters in terms of a better performance of the adaptive controller.

The problem of PSO can be defined as

$$\underset{x\in S}{\mathrm{Optimize}}f\left(x\right),$$

(23)

where “optimize” stands for a min of $f:R^n\to R$, denoted as the objective function, and $S\subseteq R^n$ is the feasible set of all admissible choices of $x$. The fitness function (objective function f) is used to evaluate the cost of each particle during the search for choosing the best value with the minimum cost, and it was chosen as>

$$f=e^{[\mu ·({(q_i-q_{i}d)}^2+{(p_i-{\dot{q}}_{i}d)}^2)]}-1,i=1,2,$$

(24)

where $\mu >0$ is a constant coefficient. The expression of fitness was selected so as to enhance the transient and steady-state performance of the controlled system in terms of minimum steady-state errors. It was shown that the candidate formula below gives a good optimization search, and, in turn, it leads to good dynamic performance.

The design parameters of an adaptive block-backstepping controller are ($c_1,c_2,c_3,k_1,k_2).$ Therefore, the feasible set $S$ is a subset of $R^n$; hence, $x={\left[c_1,c_2,c_3,k_1,k_2\right]}^T$ is the vector of variables of dimension $n=5$, and $f$ is a function of n real values $f\left(c_1,c_2,c_3,k_1,k_2\right)$.

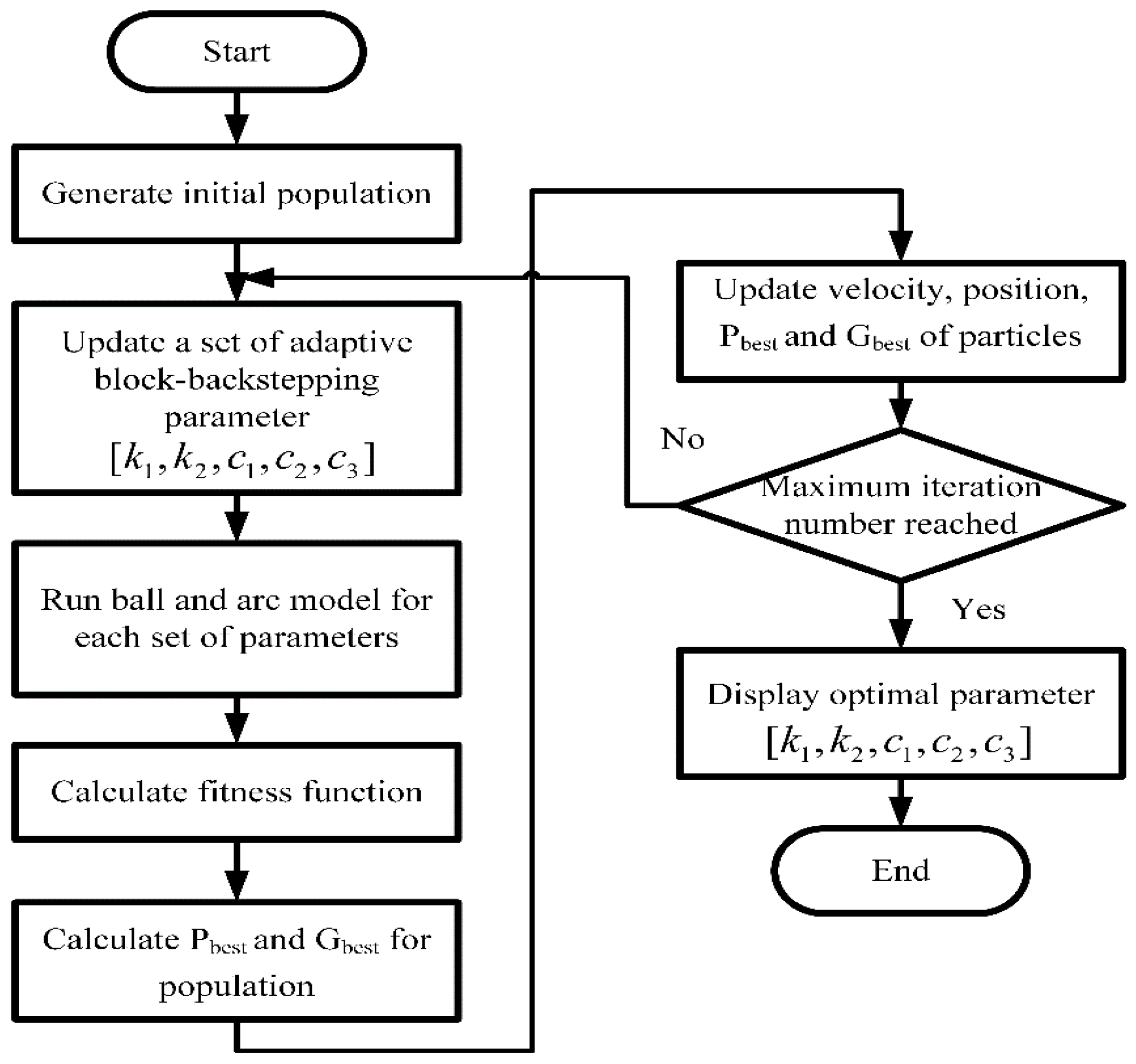
The algorithm of the PSO-based adaptive block-backstepping control of the ball–arc system is illustrated in Figure 2.

In the present optimization problem, the searching ranges for the backstepping parameters are limited, and the optimization process is repeated ten times. When the fitness function reaches its minimum value, the variance of error tends to zero, and the optimal design parameters are reached, which in turn gives an enhanced dynamic performance of the adaptive controlled systems.

Each particle in the population is updated in each iteration, according to two “best” values. The first best value is the best result (fitness), which was found previously by the same particle, and it is indicated as $P_{best}$. Another “best” value that is followed by the PSO is obtained so far by any particle in the population. This is the global best value, and it is called $G_{best}$. In finding these two best values, each particle can update its velocity according to the following iterative equation [24,25]:

$$V_i^{k+1}=w·V_i^k+c_{11}·rand·\left(P_{best}-X_i^k\right)+c_{22}·rand·\left(G_{best}-X_i^k\right),$$

(25)

where weight factors $w$, $c_{11},$ and $c_{22}$ are called the inertia factor, self-confidence factor, and swarm confidence factor, respectively. The range of 1–2 was found to be most appropriate for $c_{11}$ and $c_{22}$.

However, the random values used in the PSO algorithms are to prevent the stagnation of the PSO algorithm, i.e., these random values enable the particles to jump out of the local optimum and search for the global optimum. The uniform distribution in the range of [0, 1] is often used in most PSO applications. However, the random values define the weights of two distances to update the particle velocity. Therefore, a small range of random values has little effect on the new particle velocity; hence, this could not help the updated velocity to escape from the local optima [26,27]. Therefore, it is necessary to extend the range of random values in order to improve the global optimization ability of the PSO algorithm. In the present application of optimization, the “rand” indicated in Equation (25) is a random function, which generates random real values between 1 and 5.

The inertia weight $w$ is governed by the following equation:

$$w=w_{max}-\left(w_{max}-w_{min}\right)·k/k_{max},$$

(26)

where $k$ is the current number of iterations, $k_{max}$ is the maximum number of iterations, and $w_{max}$ and $w_{min}$ are the maximum and minimum weights, respectively. The appropriate value of $w_{min}$ is 0.4, while that for $w_{max}$ is 0.9. The benefit of using this parameter is to balance the exploration and exploitation in PSO. The updated position for each particle is described by

$$X_{\mathrm{i}}^{k+1}=X_i^k+V_i^{k+1},$$

(27)

where $X_i$ indicates the current particle, and $V_i$ defines the particle velocity.

In this study, the values assigned to the parameters of the PSO algorithm are listed in

Table 1. The set values of the particle swarm optimization (PSO) parameters.

Parameter	Value
The dimension of the search space	$5$
Population Size	$20$
Maximum number of iterations	$100$
Self-confidence factor $c_{11}$	$2$
Swarm confidence factor $c_{22}$	$2$
The maximum value of weight factor $w_{max}$	$0.9$
The minimum value of weight factor $w_{min}$	$0.4$

.

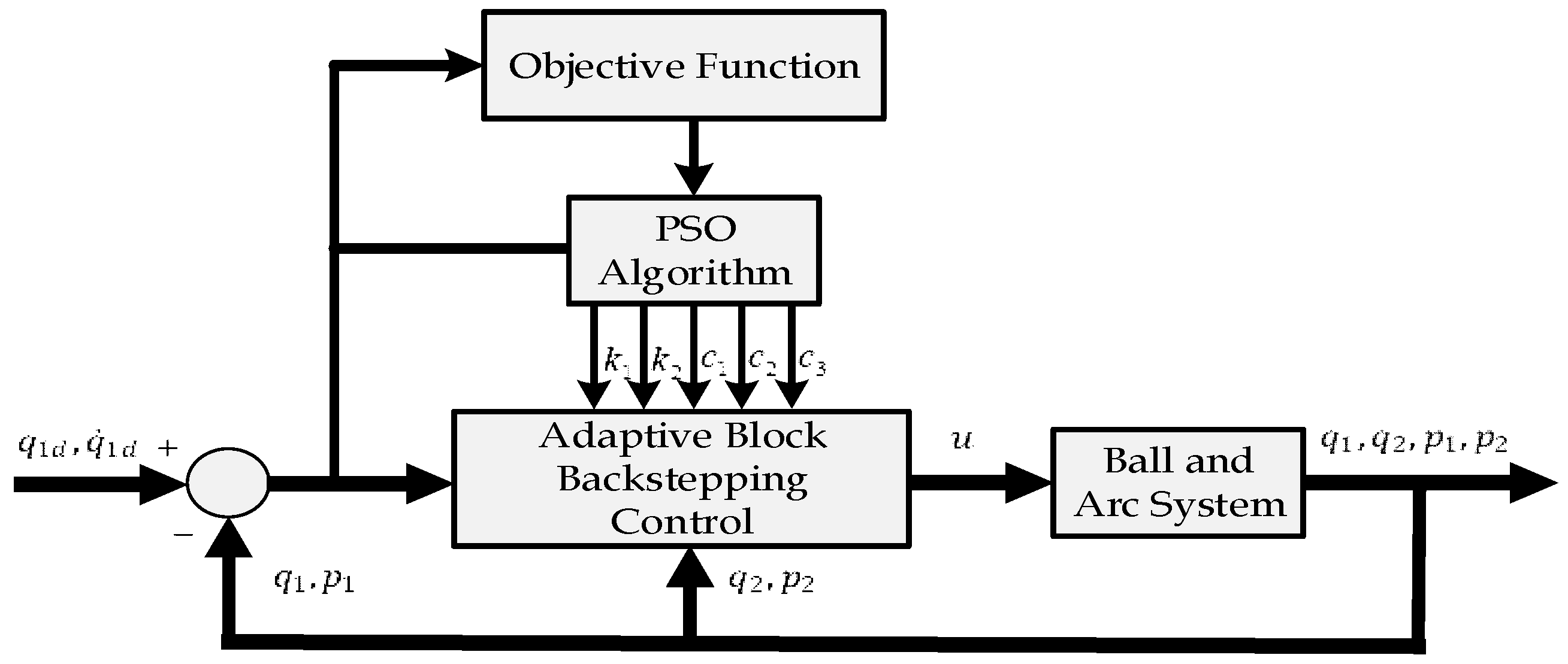
The block diagram of the closed-loop system with the PSO tuner is shown in Figure 3. Based on an objective function, the PSO algorithm could find the optimal values of the design parameters ($c_1,c_2,c_3,k_1,k_2)$. These parameters are fed to the adaptive law, described by Equation (16). Then, the estimated $\widehat{F}$, resulting from the adaptive law, is given to the nonlinear controller, described by Equation (15). This nonlinear control law is responsible for compensating the uncertainty in the parameters.

For the purpose of comparison with the classical block-backstepping control, the nonlinear control action of the classical block-backstepping is described by the following Equation [7]:

$$u={\psi }^{-1}\left(-\left(1-c_3^2+{\lambda }_1\right)·z_3-\left(c_3+c_4\right)·z_4+{\lambda }_2·c_3·{\chi }_1-\varphi \right),$$

(28)

where

$$\begin{array}{l}\psi =\frac{k_m}{\beta \left(q\right)·R_1·R_a}·\left(\left(k_3-k_4·m_{12}·p_2·\sin q_2\right)·m_{22}-\left(1-k_4·m_{12}·\dot{e}·\sin q_2\right)·m_{12}·\cos q_2\right),\\ \begin{array}{l}\varphi =\frac{\left({\gamma }_2+{\gamma }_3\right)·\dot{\beta }\left(q\right)-\left({\dot{\gamma }}_2+{\dot{\gamma }}_3\right)·\beta \left(q\right)}{\beta {\left(q\right)}^2}-k_4·m_{12}·\dot{e}·p_2^2·\cos q_2+\frac{\left(k_3-k_4·m_{12}·p_2·\sin q_2\right)}{\beta \left(q\right)}\\ ·\left(-\beta \left(q\right)·{\ddot{q}}_{1d}-g·\cos q_2·\sin q_2·m_{12}^2+m_{22}·\sin q_2·m_{12}·p_2^2-\frac{k_m^2·m_{22}·p_1}{R_1^2·R_a}\right)\\ +\frac{\left(1-\dot{e}·k_4{m}_{12}·\sin q_1\right)}{\beta \left(q\right)}(g·m_{11}·m_{12}·\sin q_2-m_{12}^2·p_2^2·\cos q_2·\sin q_2\\ +\frac{k_m^2·m_{12}·p_1·\cos q_2}{R_1^2·R_a})+{\ddot{q}}_{1d}·k_4·m_{12}·p_2·\sin q_2-{\stackrel{⃛}{q}}_{1d}·k_4·m_{12}·\cos q_2,\\ \end{array}\\ {\gamma }_2=-k_4·m_{11}·m_{12}·m_{22}·g·\sin q_2,\\ {\gamma }_3=0.5·k_4·m_{12}^3·g·\sin 2q_2·\cos q_2,\\ {\dot{\gamma }}_2=-k_4·m_{11}·m_{12}·m_{22}·g·p_2·\cos q_2,\\ {\dot{\gamma }}_3=-0.5·k_4·m_{12}^3·g·p_2·\sin 2q_2·\sin q_2+k_4·m_{12}^3·g·p_2·\cos 2q_2·\cos q_2,\\ \dot{\beta }\left(q\right)=m_{12}^2·\sin 2q_2\end{array}$$

Since, in the next computer simulation section, a comparison of the adaptive block-backstepping control with the classical block-backstepping control is intended, it is worth mentioning that the PSO tuner is utilized for tuning the design parameters of both the classical and adaptive controllers.

Table 2. Optimal design constants of both schemes of the block-backstepping controllers.

Design Constants for the Adaptive Block-Backstepping Controller	Value	Design Constants for the Block-Backstepping Controller	Value
$k_1$	$1.5$	$k_3$	$0.0214$
$k_2$	$39.0883$	$k_4$	$18$
$c_1$	$9.5138$	$c_3$	$1.855$
$c_2$	$14.5013$	$c_4$	$82.8141$
$c_3$	$0.01$	${\lambda }_1$	$56.7862$

lists the optimal values for an adaptive backstepping controller ($c_1,c_2,c_3,k_1,k_2)$ and those for the classical block-backstepping controller $\left(k_3,k_4,c_3,c_4,{\lambda }_1\right)$.

One can consult Reference [28] for a detailed description of the program for establishing the upcoming scenarios of the simulation.

6. Simulation Results

In this section, the effectiveness of the proposed adaptive controller via the simulated results within the MATLAB environment is provided. A performance comparison study of this new adaptive block-backstepping controller with the classical block-backstepping controller, referred to in Reference [7], is performed and discussed through simulation. The model parameter values of the ball–arc system are listed in

Table 3. The numerical values of the ball–arc system parameters [7].

Parameter Description	Symbol	Value (unit)
Total mass of cart and arc assembly	$M$	$2.0 \mathrm{kg}$
Ball mass	$m$	$5\times {10}^{-2} \mathrm{kg}$
Gravitational acceleration	$g$	$9.81 \mathrm{m}/{\mathrm{s}}^2$
Ball moment of inertia	$I$	$2.88\times {10}^{-6} \mathrm{kg}·{\mathrm{m}}^2$
The arc radius	$R$	$8\times {10}^{-2}\mathrm{m}$
The ball radius	$r$	$1.2\times {10}^{-2} \mathrm{m}$
Armature resistance of motor	$R_a$	$1.6979 \mathsf{\Omega }$
The radius of the pinion	$R_1$	$8\times {10}^{-2} \mathrm{m}$
The motor constant	$k_m$	$5.34\times {10}^{-2} \mathrm{N}·\mathrm{m}/\mathrm{A}$
Maximum allowable voltage (control input)	$u_{max}$	$24 \mathrm{V}$

.

The resultant optimal values of the design parameters, which appeared throughout the design of both the classical and adaptive block-backstepping controllers, are listed in Table 3. The initial values of variables $q_1$, $p_1$, $q_2$, and $p_2$, which are used to initialize the simulation for both the adaptive and conventional block-backstepping controllers, were set as follows:

$${\left[q_1\left(0\right)p_1\left(0\right)q_2\left(0\right)p_2\left(0\right)\right]}^T={\left[000.5230\right]}^T.$$

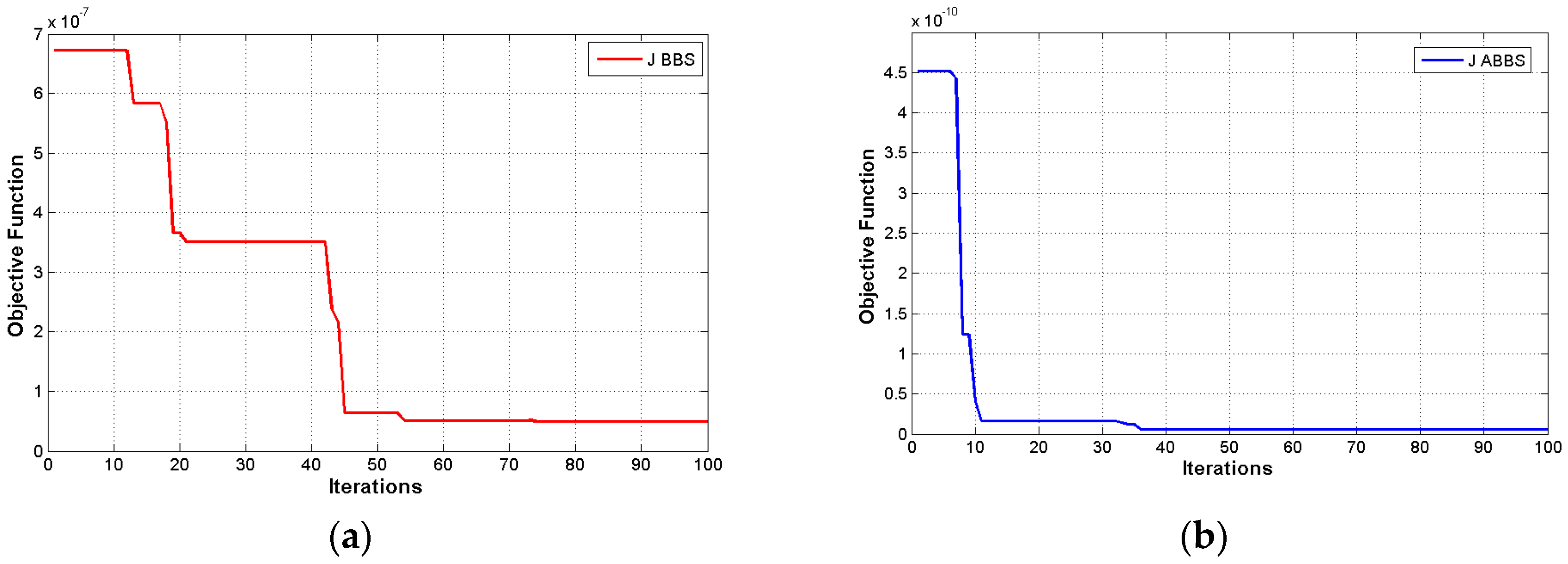
The simulation results were launched by showing the behavior of the fitness function concerning the optimization iterations, as illustrated in Figure 4. The final value of the fitness function indicates the reaching of the optimal set of optimized parameters. The behavior of the fitness functions throughout the optimization process of the design parameters for the adaptive and classical controllers are described in Figure 4a and Figure 4b, respectively.

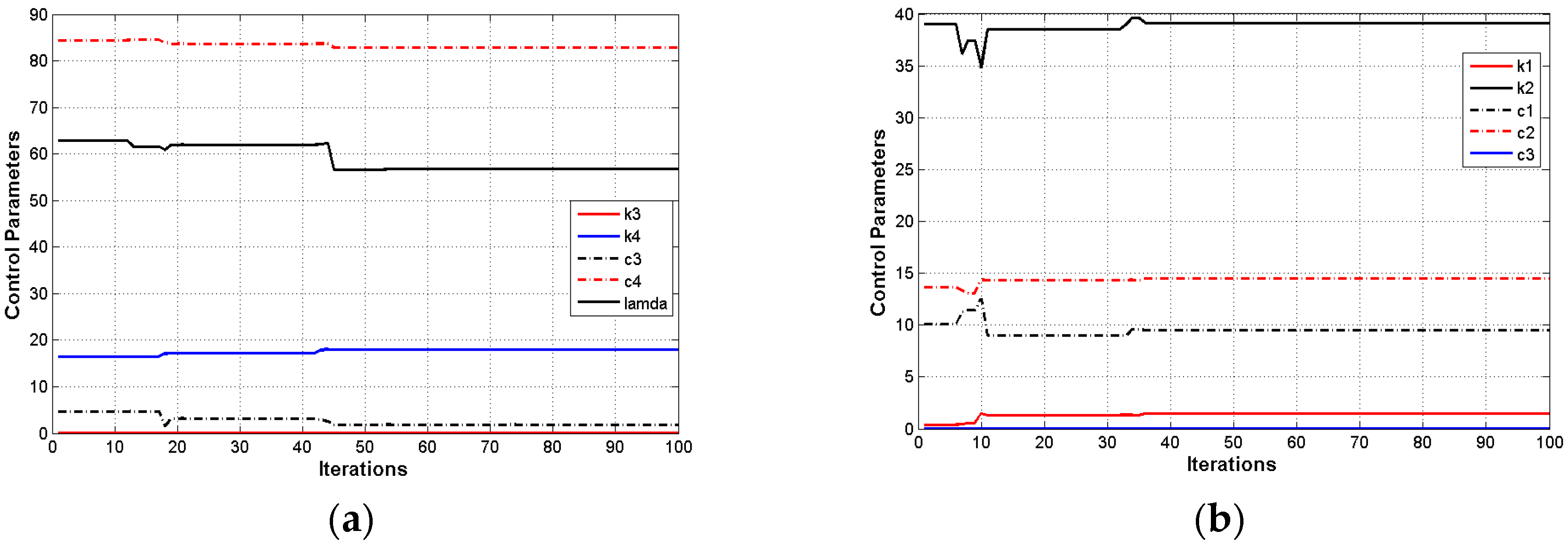
The behavior of the design parameters concerning the iteration of the optimization process is given in Figure 5. Figure 5a shows the behavior of the design parameters $k_1$, $k_2$, $c_1$, $c_2$, and $c_3$, associated with the adaptive block-backstepping controller, while the behavior of the design parameters $k_3$, $k_4$, $c_3$, $c_4$, and ${\lambda }_1,$ belonging to the conventional block-backstepping controller, are depicted in Figure 5b.

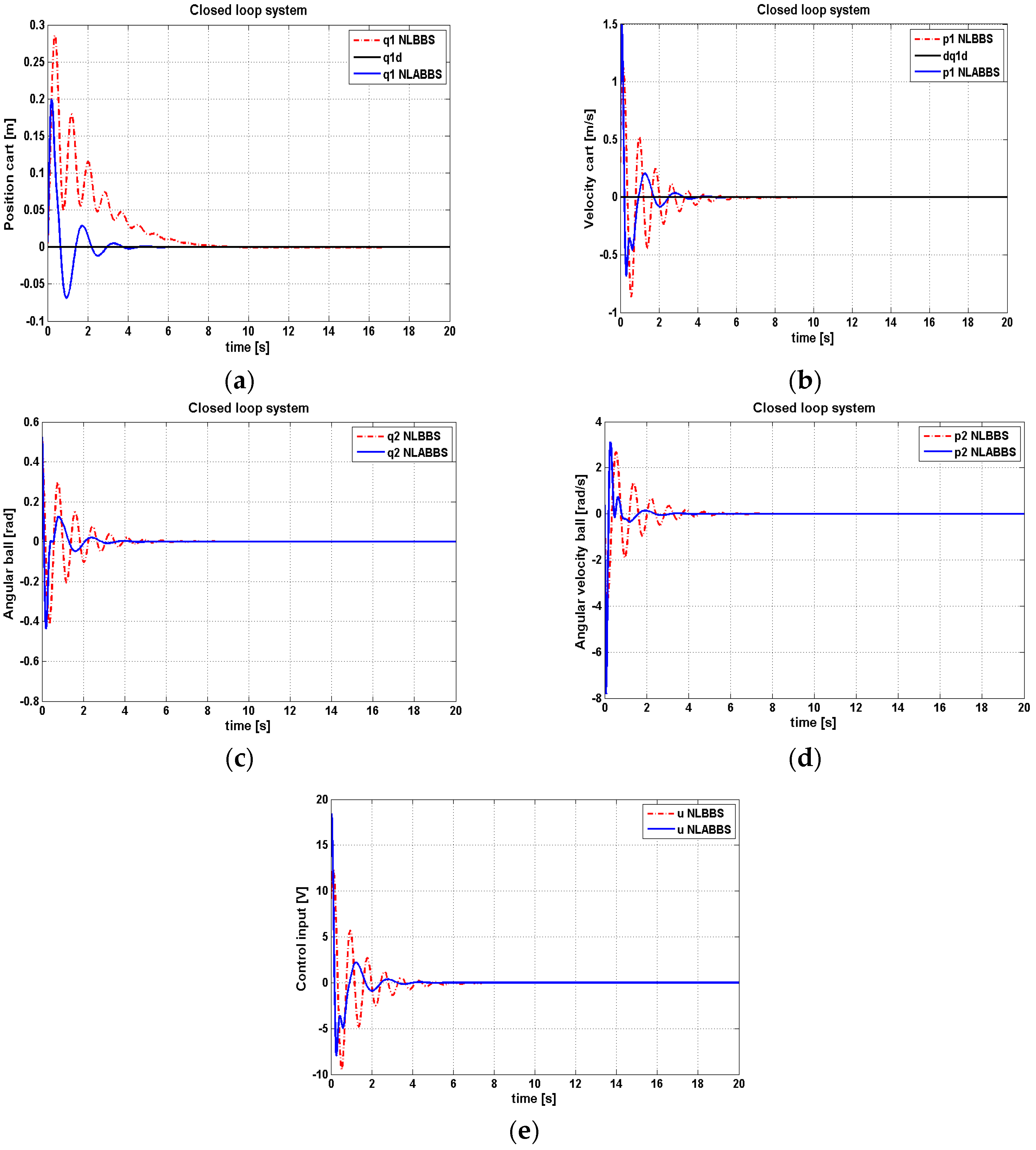
Figure 6 shows the dynamic responses of the cart position, cart velocity, ball position, and ball velocity, resulting from the conventional and adaptive block-backstepping controllers, so as to balance and stabilize the ball at the top of the arc and simultaneously return the cart to its starting point. The corresponding control signals due to both controllers are shown in Figure 6e. The performance of Nonlinear Block-Backstepping controller (NLBBS) and Nonlinear Adaptive Block-Backstepping controller (NLABBS) is reported in

Table 4. Report of the dynamic performances of the adaptive and conventional block-backstepping controllers.

Controller Type	State Variable	RMSE	Max Peak	Settling Time (s)
NLBBS	$q_1$	$0.050657$	$0.286$	$8$
	$q_2$	$0.068186$	$0.4$	$4$
NLABBS	$q_1$	$0.023856$	$0.2$	$4$
	$q_2$	$0.048037$	$0.42$	$3$

. The performance evaluation is based on Root Mean Square Error (RMSE), maximum peak, and settling time. It is evident from the table that the adaptive block-backstepping has better dynamic characteristics than the conventional controller.

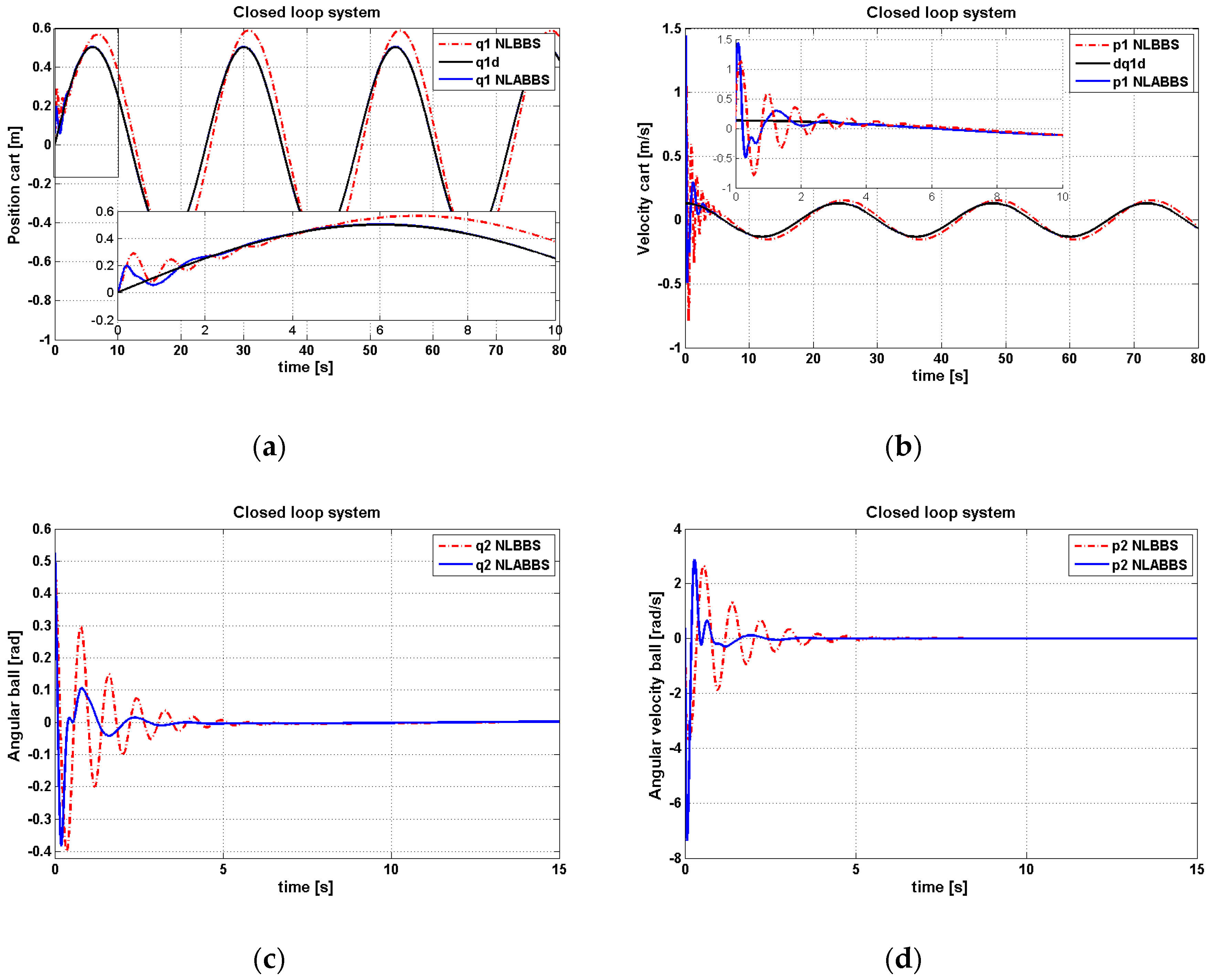
The next scenario presents the tracking performance of the ball–arc system based on both of the backstepping controllers, with the same initial conditions. With these particular initial states, Figure 7a,b show that the adaptive controller outperforms the classical one in terms of the tracking errors and transient responses for both the cart linear position and velocity.

Additionally, it is clear from Figure 7a,b that the dynamic tracking performance of the ball angular position and velocity with an adaptive controller is better than that for a conventional one. Thus, one can conclude that the adaptive block-backstepping controller better enhances the tracking performance than a classical block-backstepping controller.

A numerical evaluation of the tracking dynamic performance, resulting from both of the control strategies, is reported in

Table 5. Tracking performance of the ball–arc system based on the controllers.

Type of Controller	State Variable	RMSE	Max Peak	Settling Time (s)
NLBBS	$q_1$	$0.091774$	$0.28$	$5$
	$q_2$	$0.033624$	$0.4$	$5$
NLABBS	$q_1$	$0.010164$	$0.2$	$4$
	$q_2$	$0.021891$	$0.39$	$3$

. The transient and steady-state parameters of the tracking responses of both controllers listed in the table indicate that the adaptive controller has a better tracking performance than the non-adaptive controller.

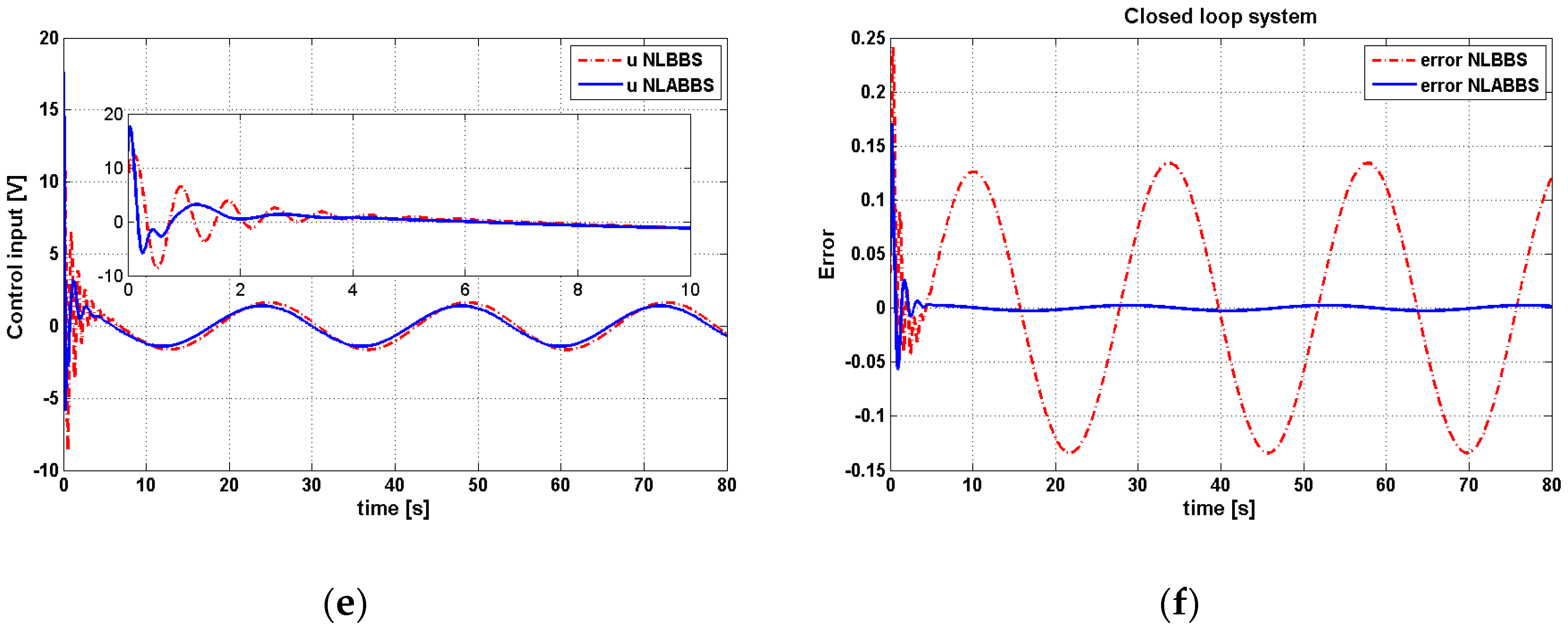
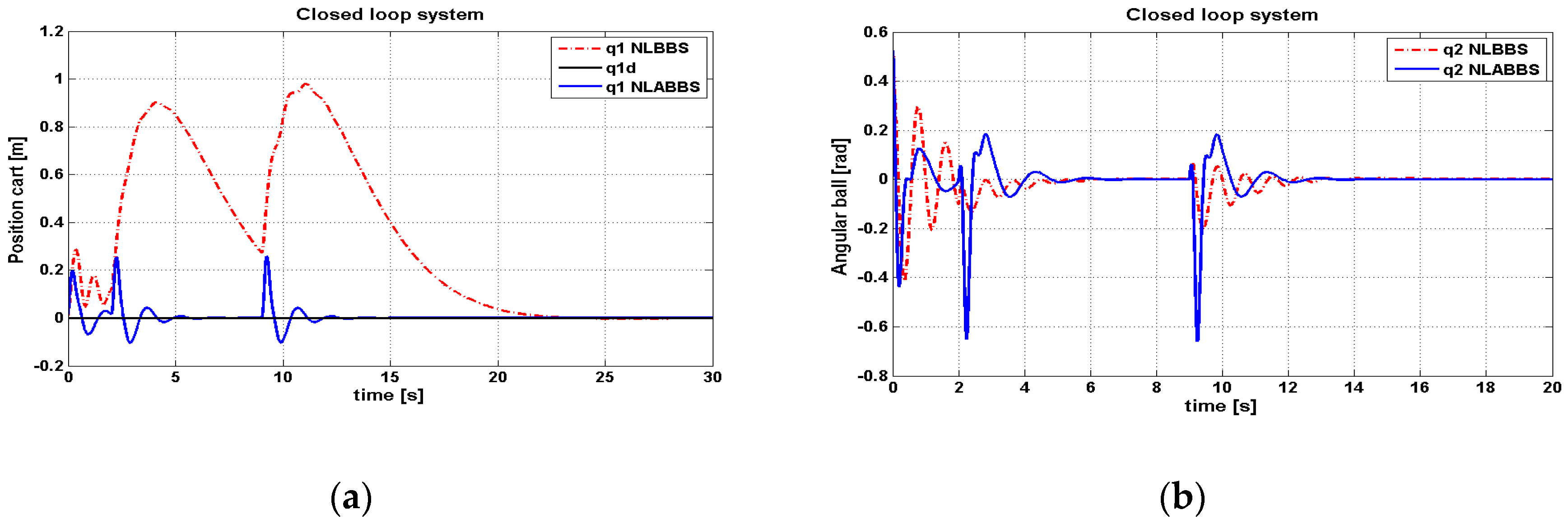
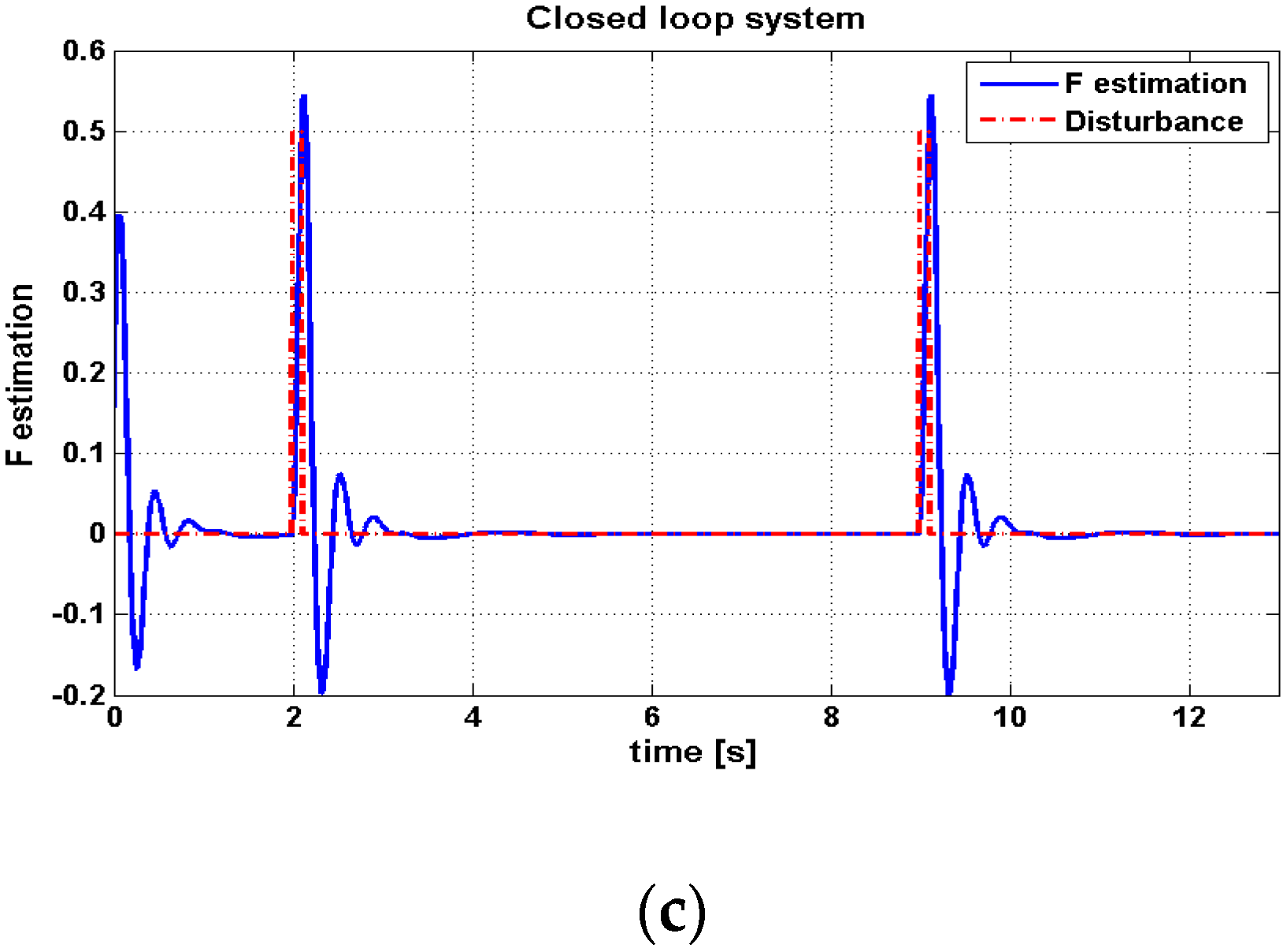
Next, the disturbance rejection capability was investigated by exerting a pulse-shaped disturbance of height value 0.5 N during periods of 2–2.1 and 9–9.1 s. The effect of the applied disturbance on the dynamic response of the controlled system, with the adaptive and non-adaptive controller, is shown in Figure 8. It is clear from this figure that the adaptive block-backstepping controller has better robustness characteristics than the other controller, because the adaptive block-backstepping could better keep the dynamic performance of the nonlinear-controlled system unchanged in the presence of parameter variation (disturbance) than a non-adaptive controller.

Table 6. Dynamic performance of the ball–arc system based on the controllers with disturbance.

Controller Type	State Variable	RMSE	Max Peak
NLBBS	$q_1$	$0.473639$	$0.99$
	$q_2$	$0.061268$	$0.352$
NLABBS	$q_1$	$0.03946$	$0.26$
	$q_2$	$0.080977$	$0.67$

gives a numerical report of the controlled ball–arc system performance with both of the controllers under disturbance application.

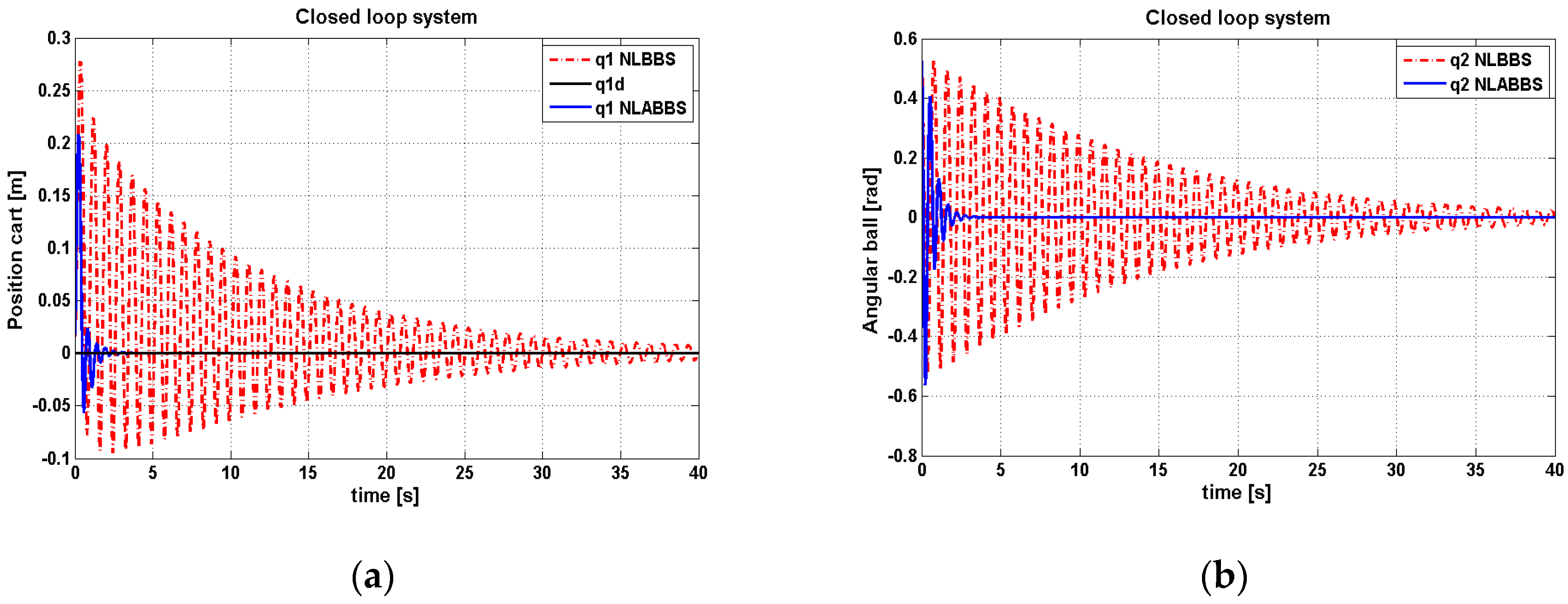
The performance examination of both controllers against uncertainty in the model parameters is clarified in Figure 9. For this system, the uncertainty changes can be assumed by first changing the cart weight from its nominal value to a value of 3 kg, or by replacing the sliding ball with another one, which has a weight value of 0.1 kg.

Table 7. Dynamic performance reports of the ball–arc system based on the two controllers.

Controller Type	State Variable	RMSE	Max Peak	Settling Time (s)
NLBBS	$q_1$	$0.054593$	$0.28$	$30$
	$q_2$	$0.16394$	$0.53$	$30$
NLABBS	$q_1$	$0.015151$	$0.21$	$4$
	$q_2$	$0.048748$	$0.57$	$3$

shows a numerical report concerning the performance of the controlled ball–arc system under model uncertainty.

7. Conclusions

This paper presented the development of a new adaptive algorithm based on a block-backstepping control design for ball–arc systems. The effectiveness of this control scheme was verified through a simulation on the MATLAB platform. A comparison study of the proposed adaptive controller and the non-adaptive controller was made. The PSO algorithm was included to optimize the design parameters of the proposed controller in order to enhance its performance.

The simulated results showed that the proposed adaptive controller gives better transient and steady-state characteristics than the non-adaptive one in both regulation and tracking cases. Additionally, the proposed adaptive controller has better robustness characteristics when the system is subjected to disturbance or suffers uncertainty in model parameters. Therefore, the newly proposed control scheme could successfully enhance the dynamic performance of the controlled system and improve its robustness against system parameter variation.