Analysis of Data Persistence in Collaborative Content Creation Systems: The Wikipedia Case
Abstract
:1. Introduction
Contribution and Main Results
- How accurately does the popularity of Wikipedia pages fit a power law distribution?
- How are update statistics distributed?
- Are update events related to the popularity distribution? (Are the most updated contents also the most requested?)
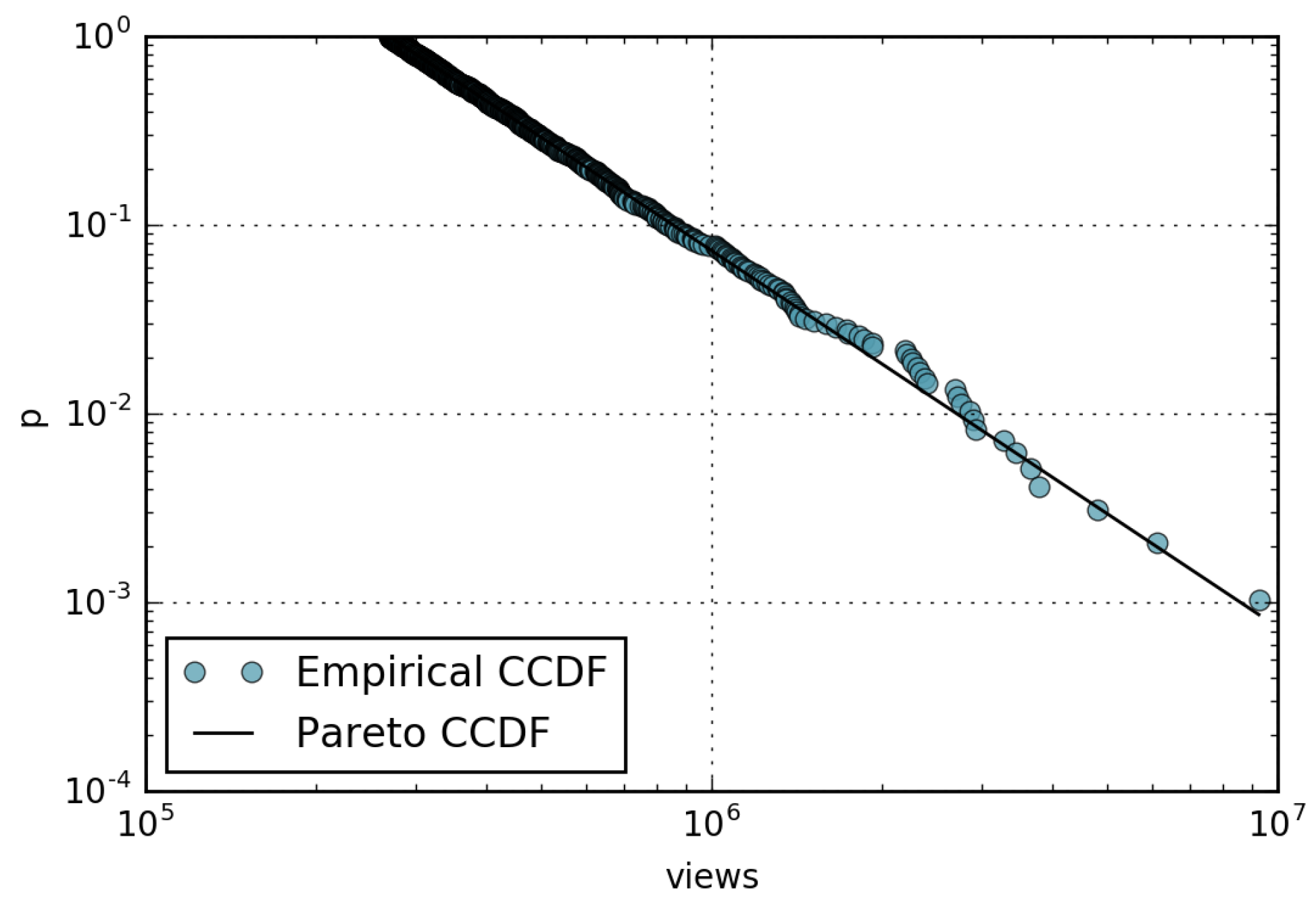
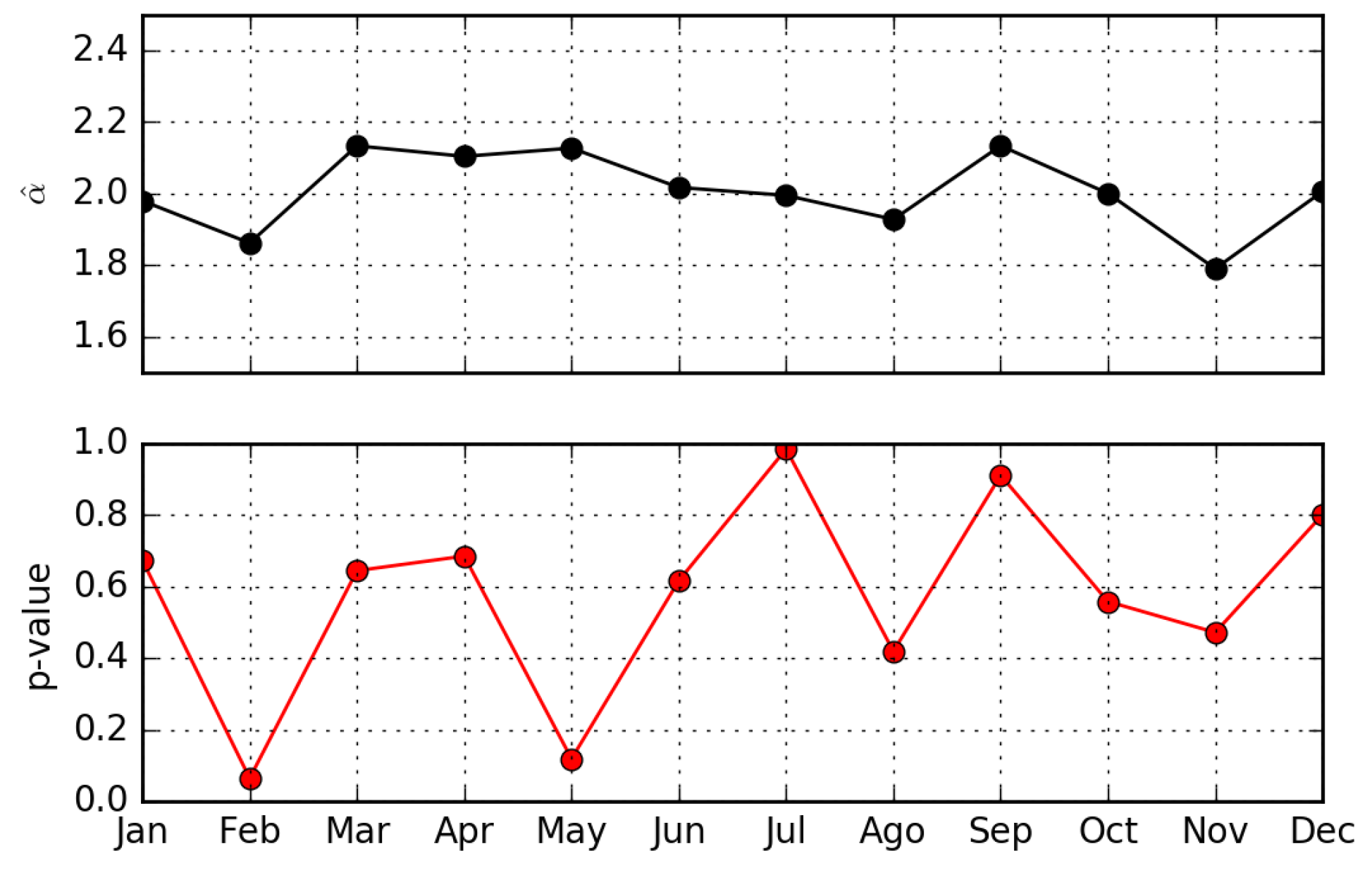
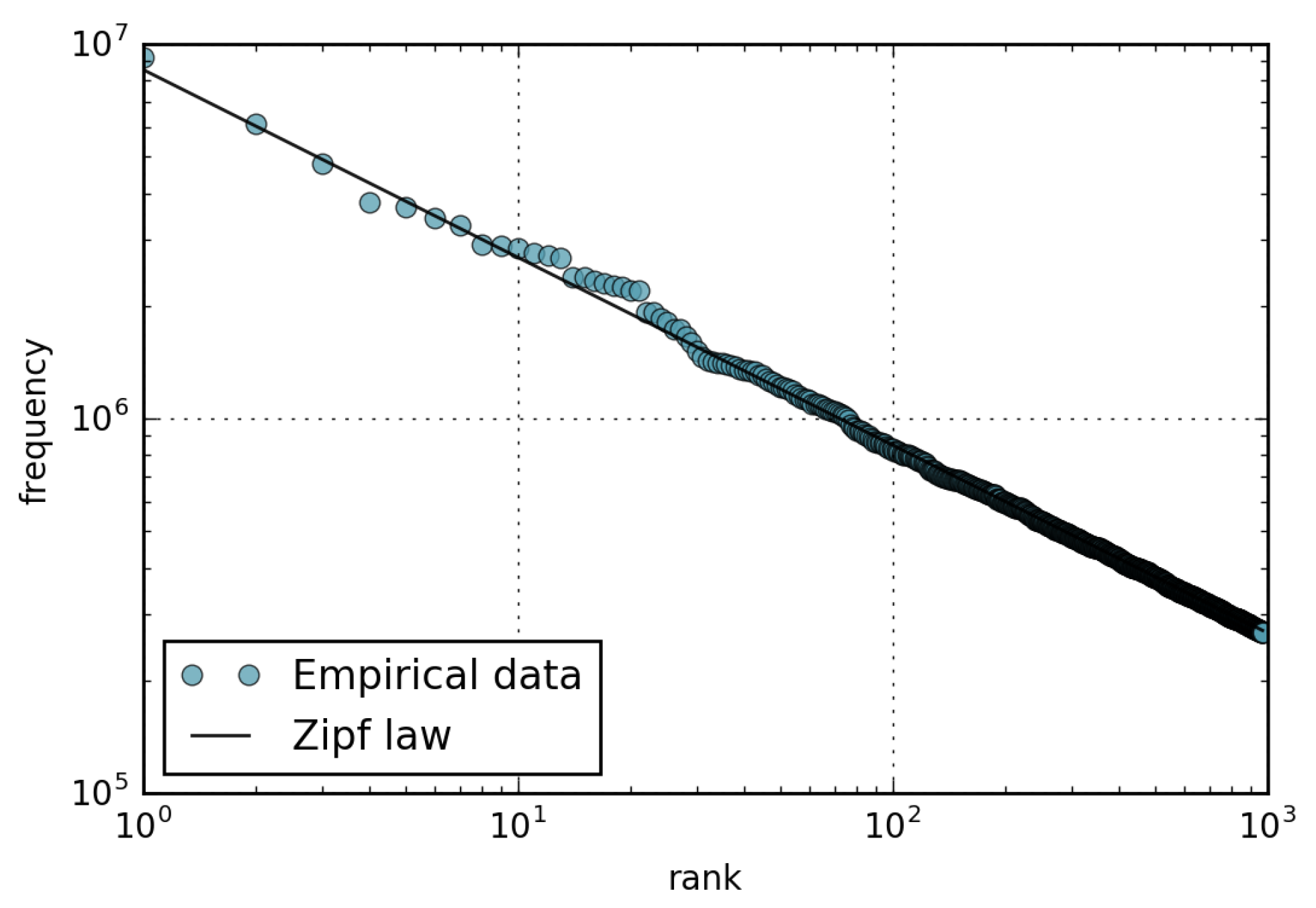
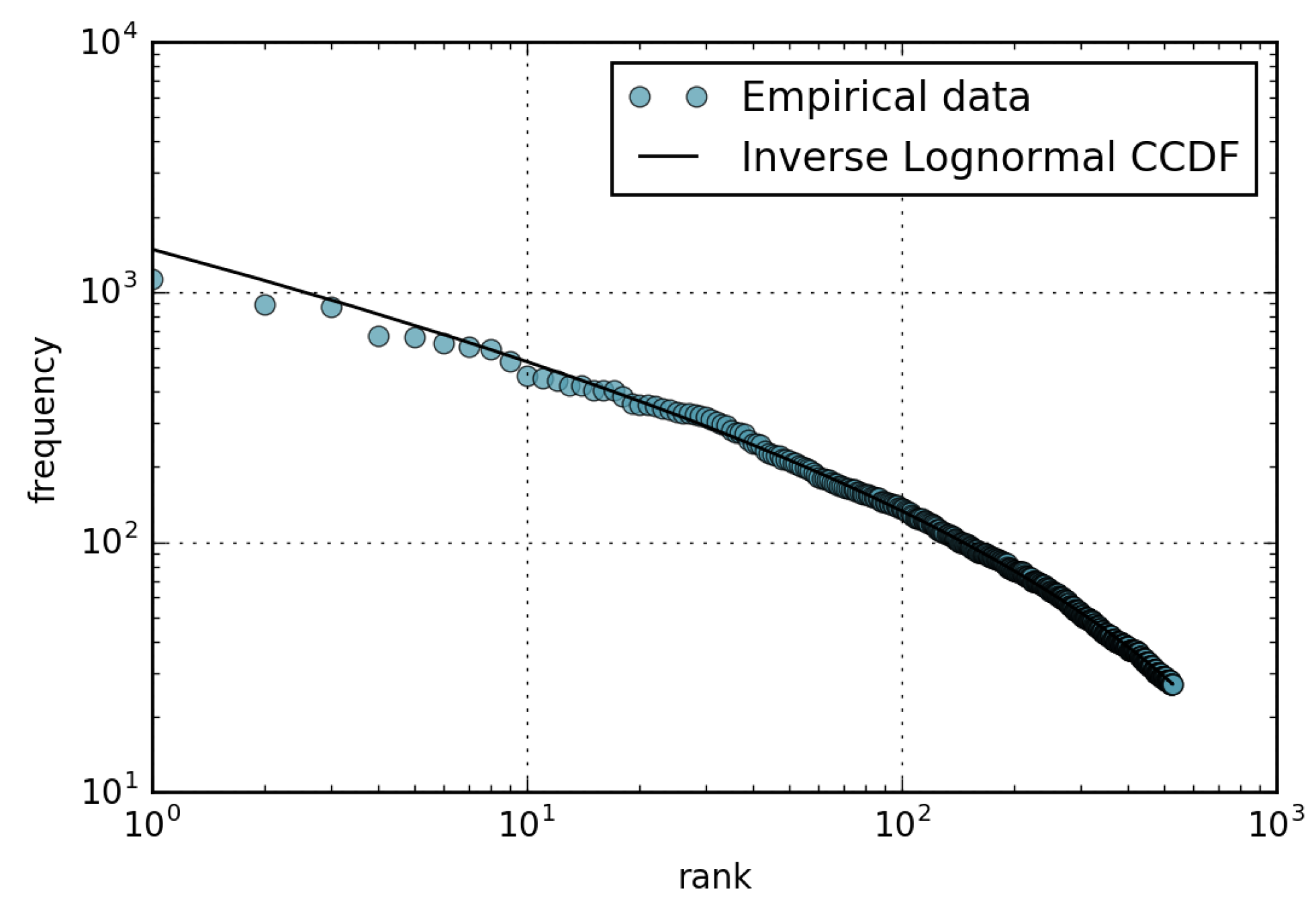
- The amount of views received by a page is well described by the Pareto distribution with shape parameter ; consequently, the rank-frequency behavior can be approximated by a Zipf distribution with parameter .
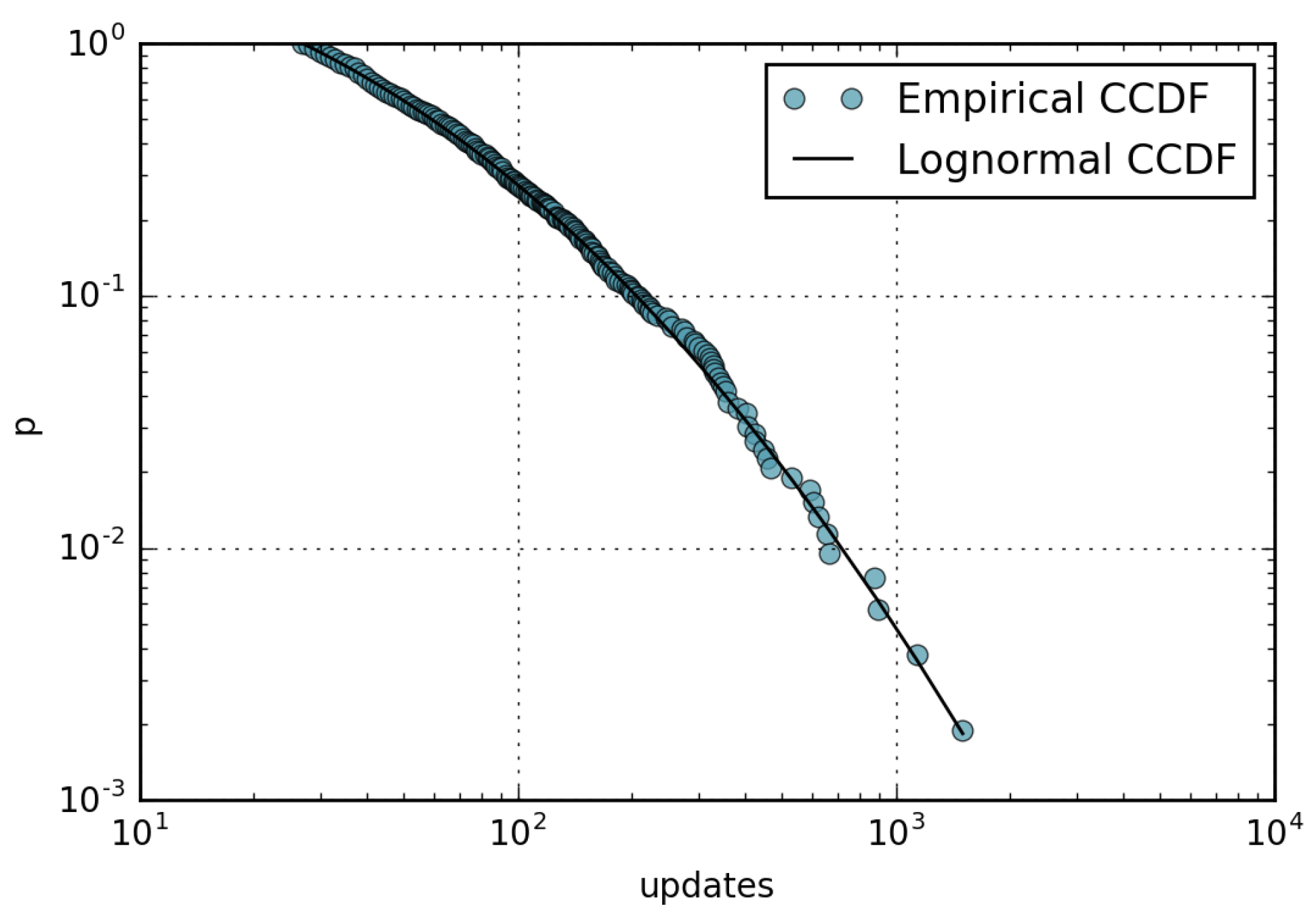
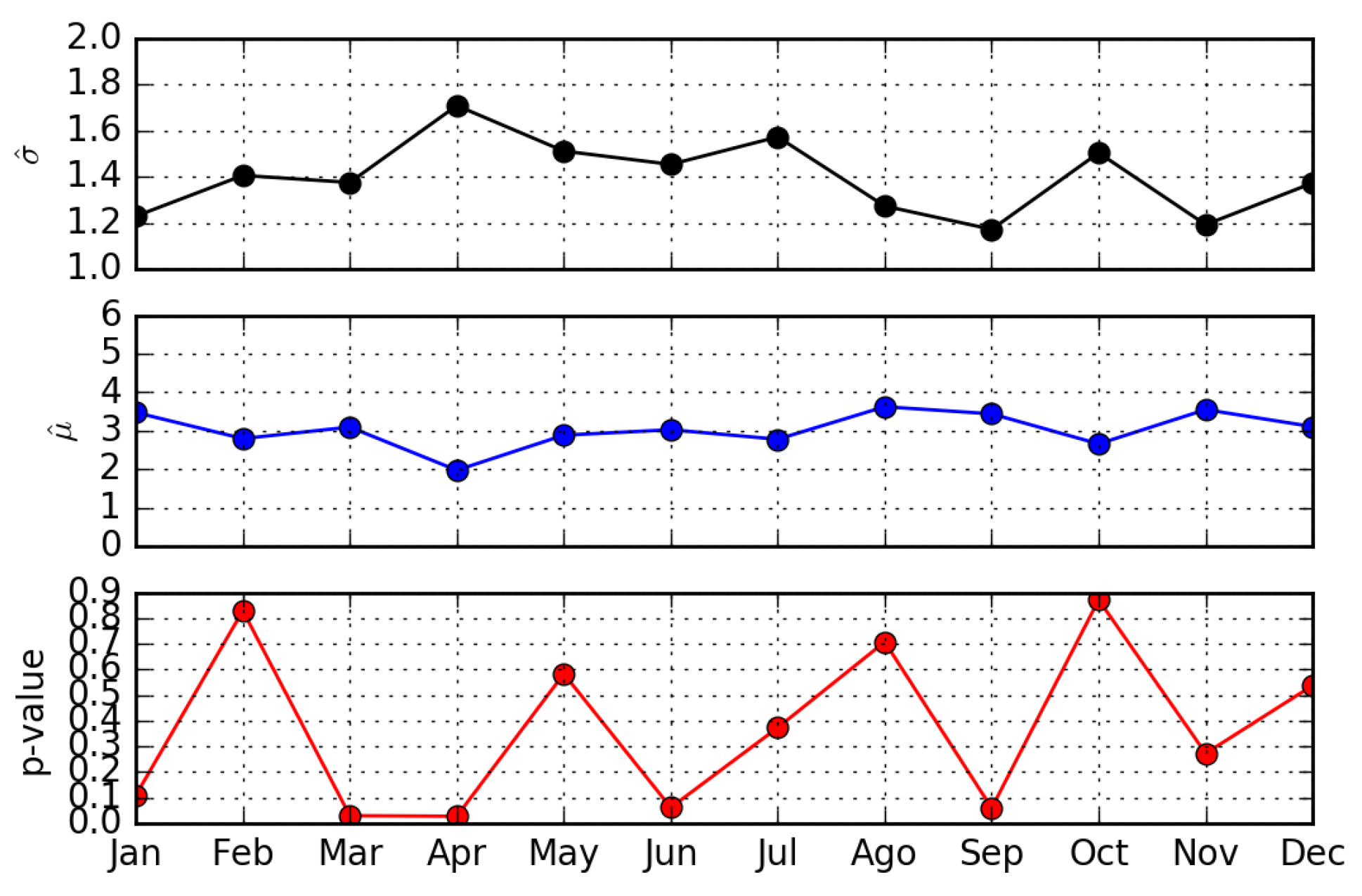
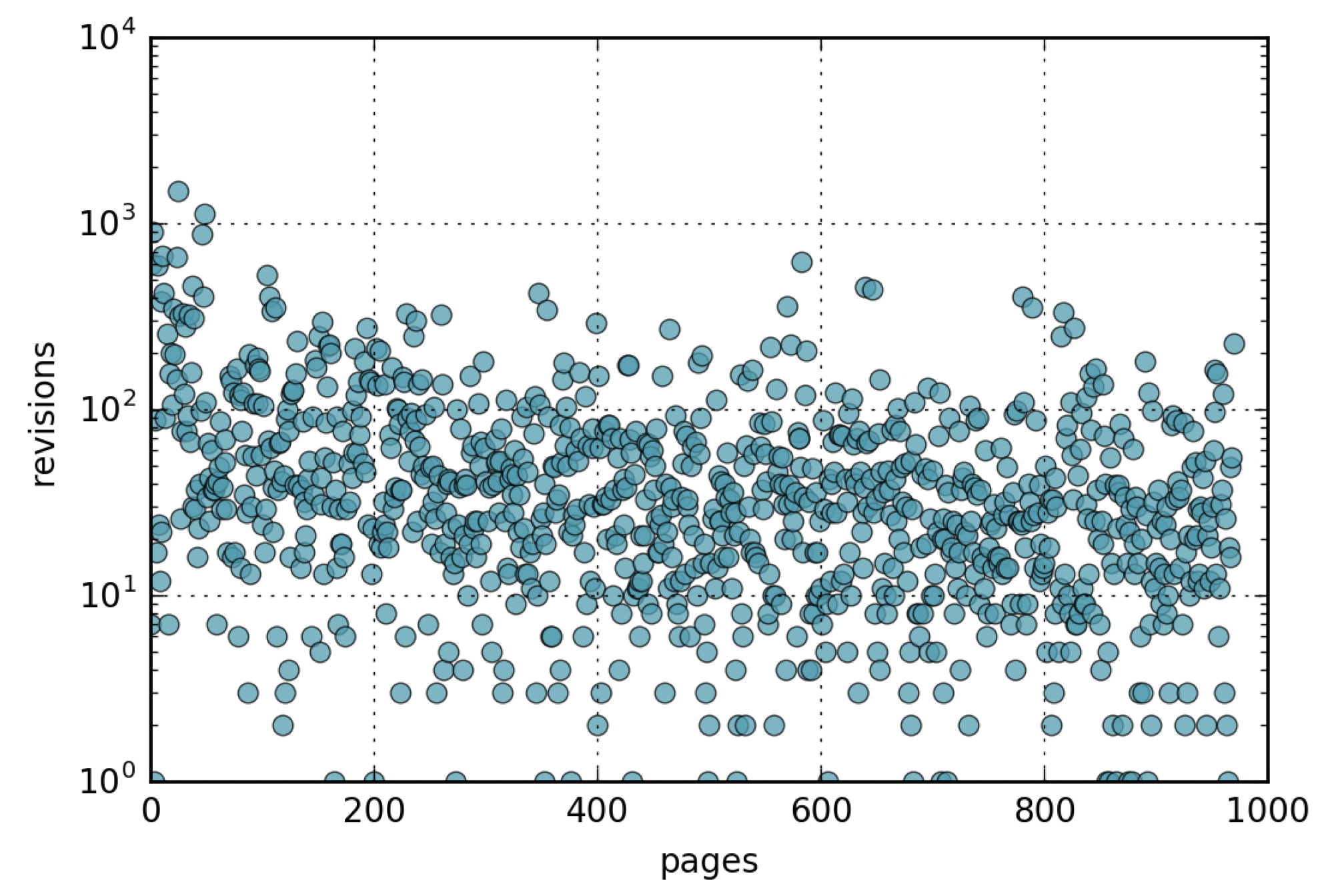
- The number of page updates is distributed according to a lognormal distribution with parameters and .
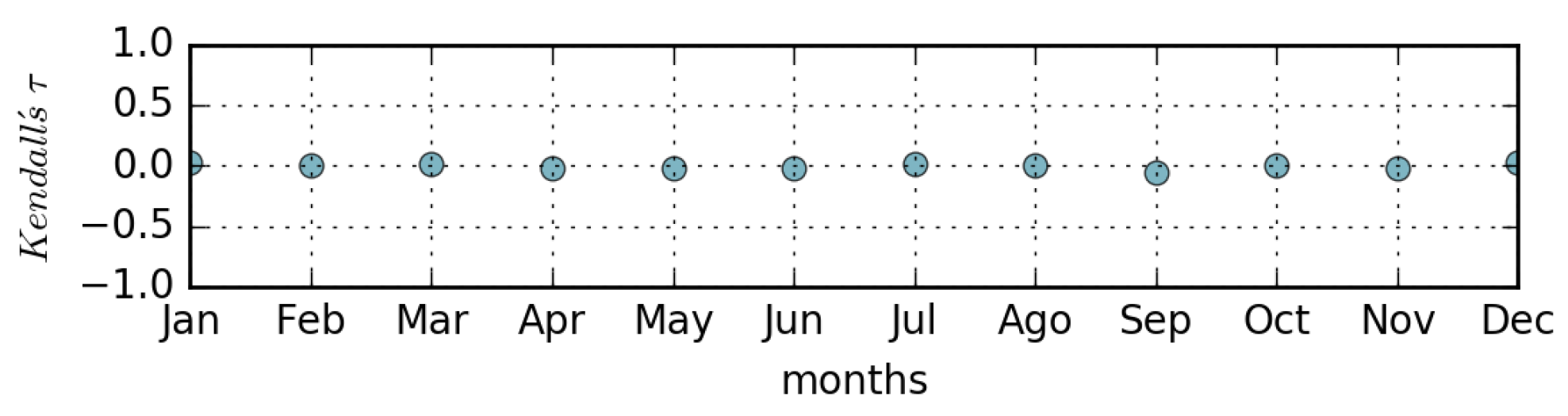
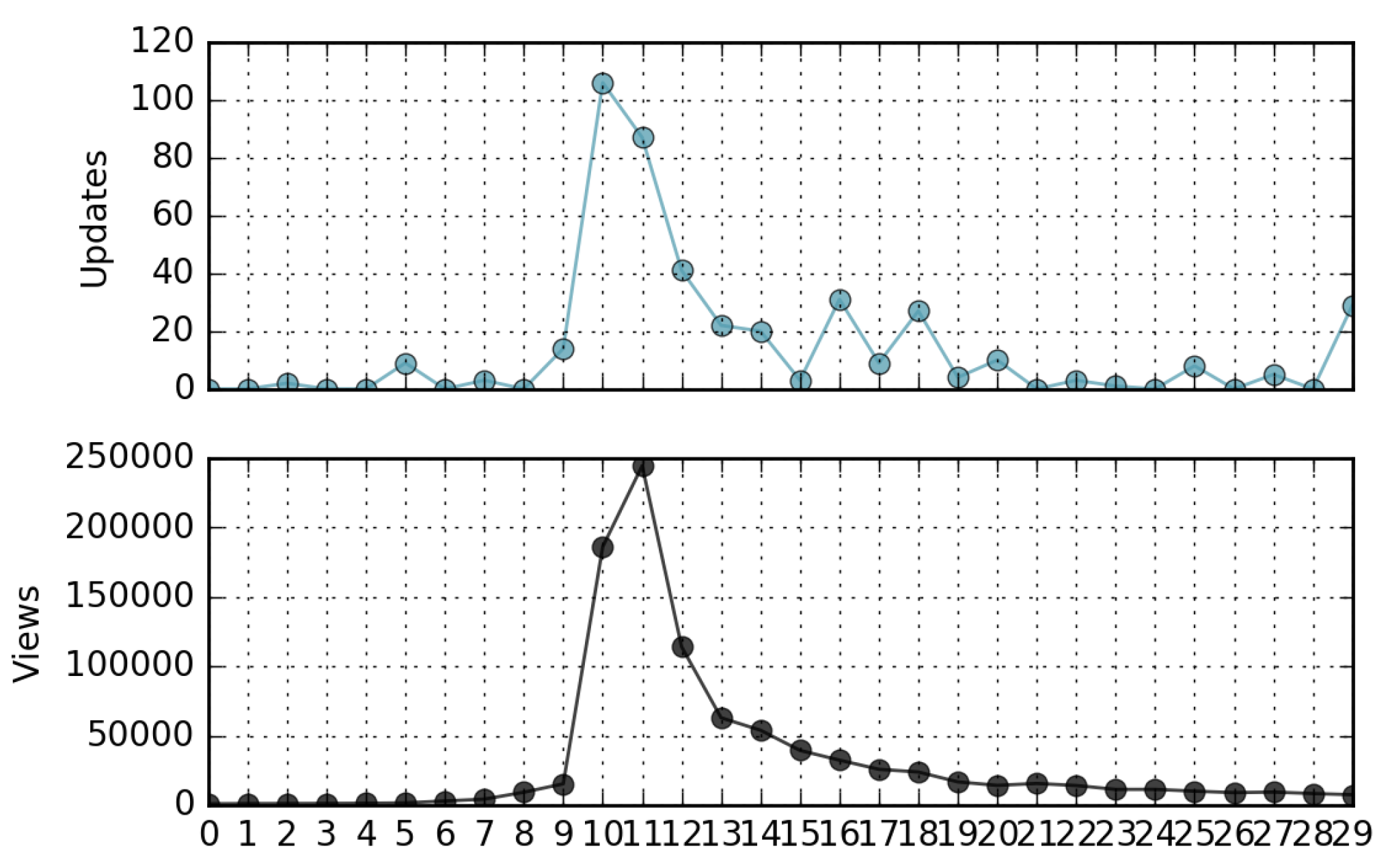
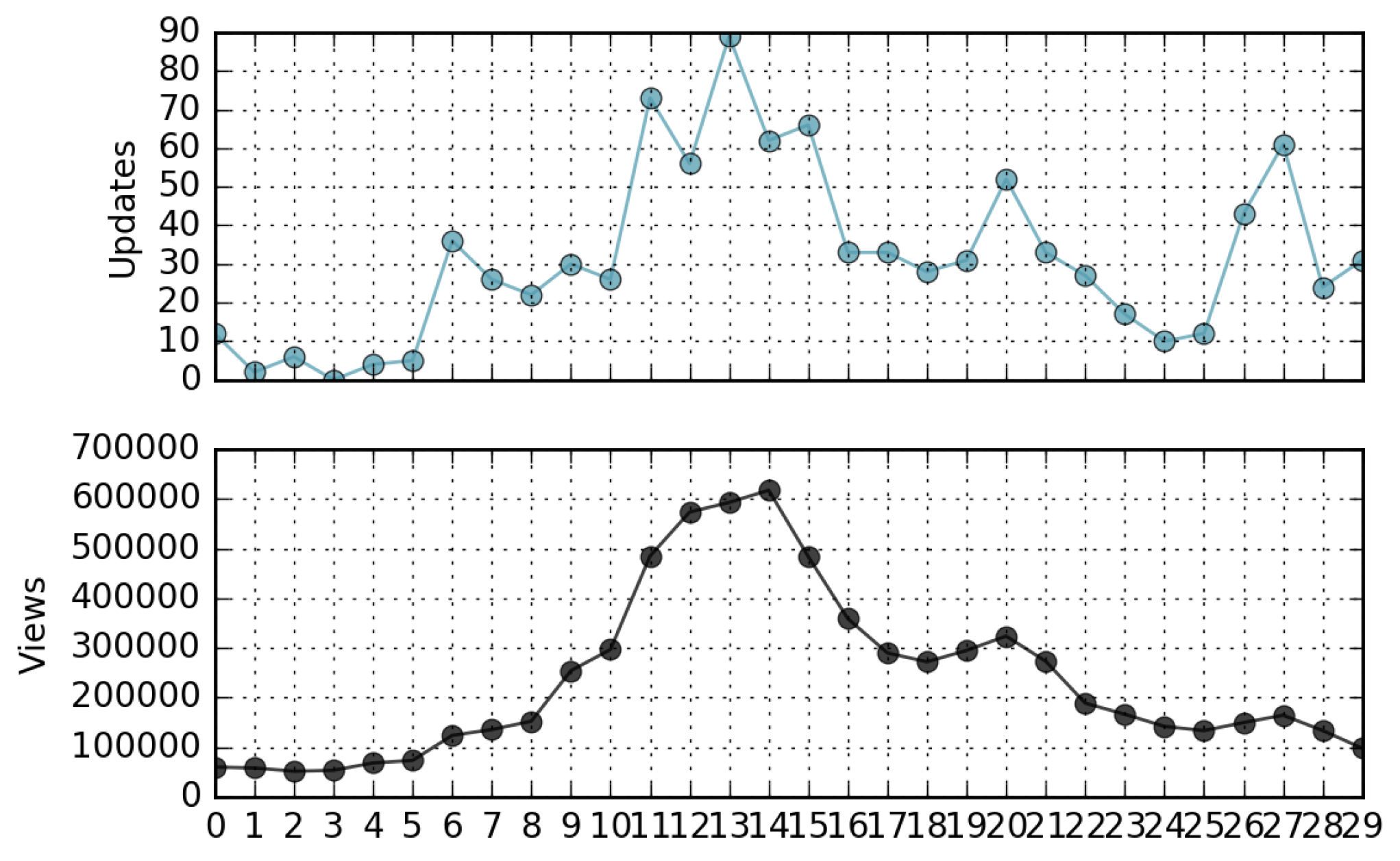
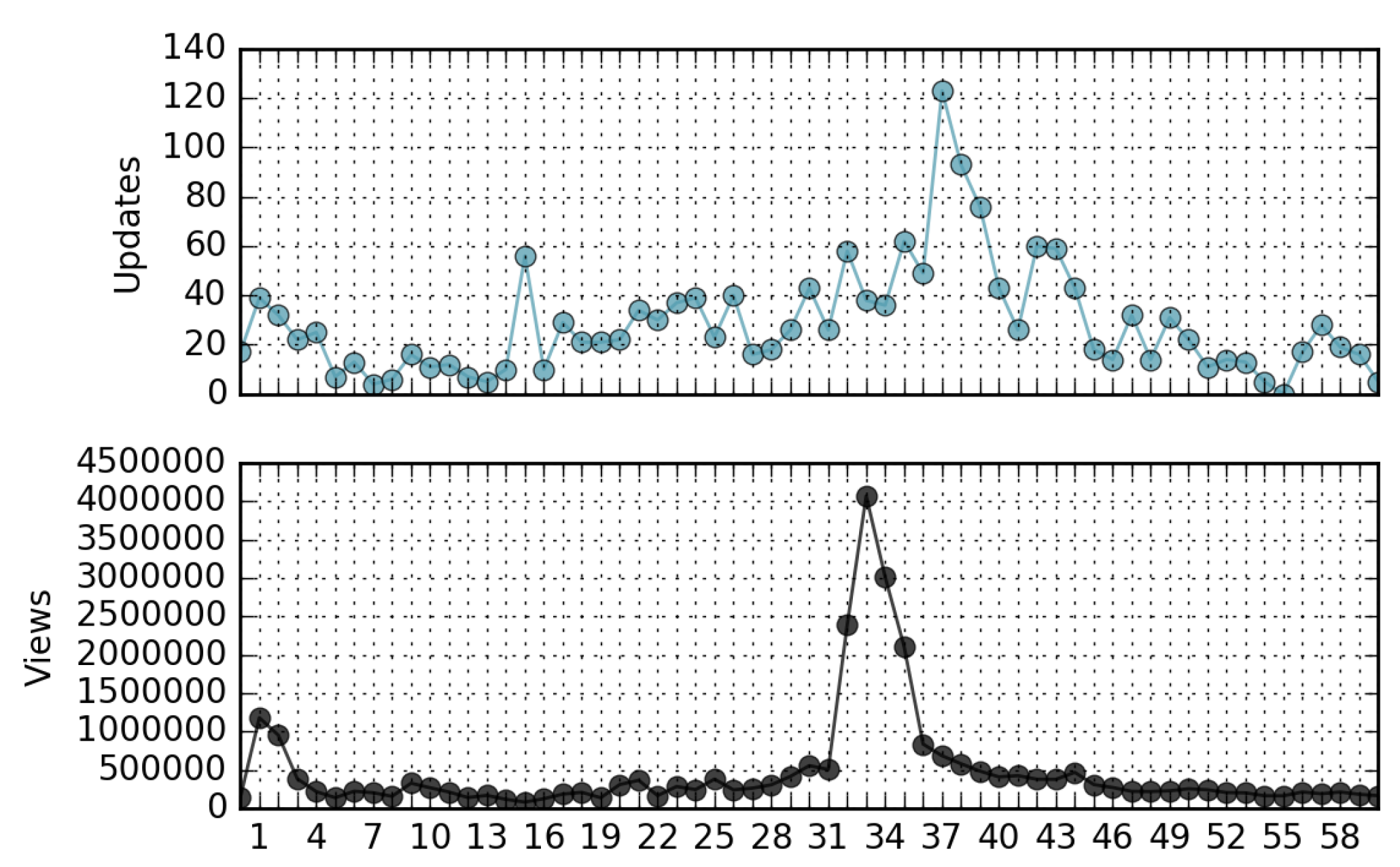
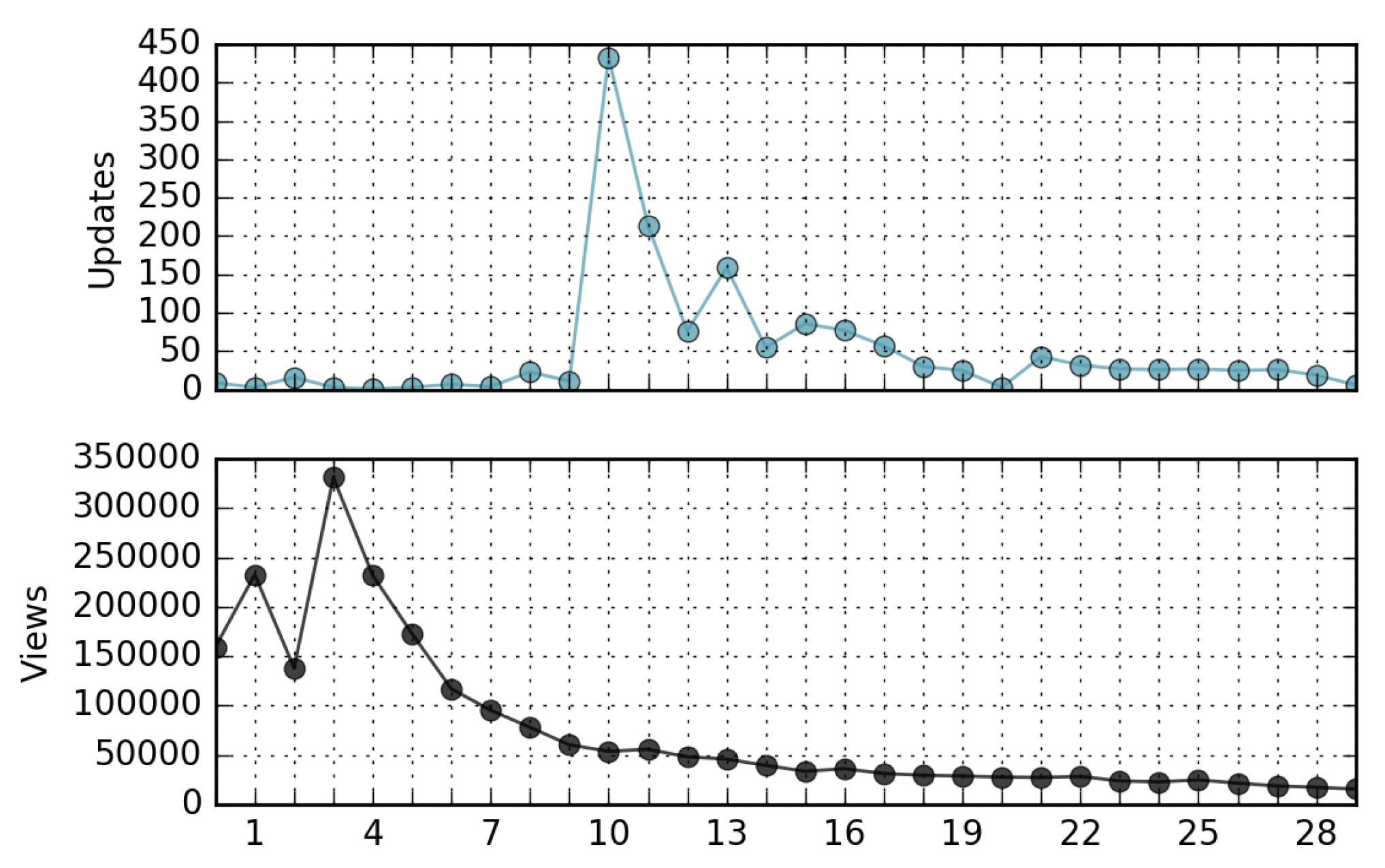
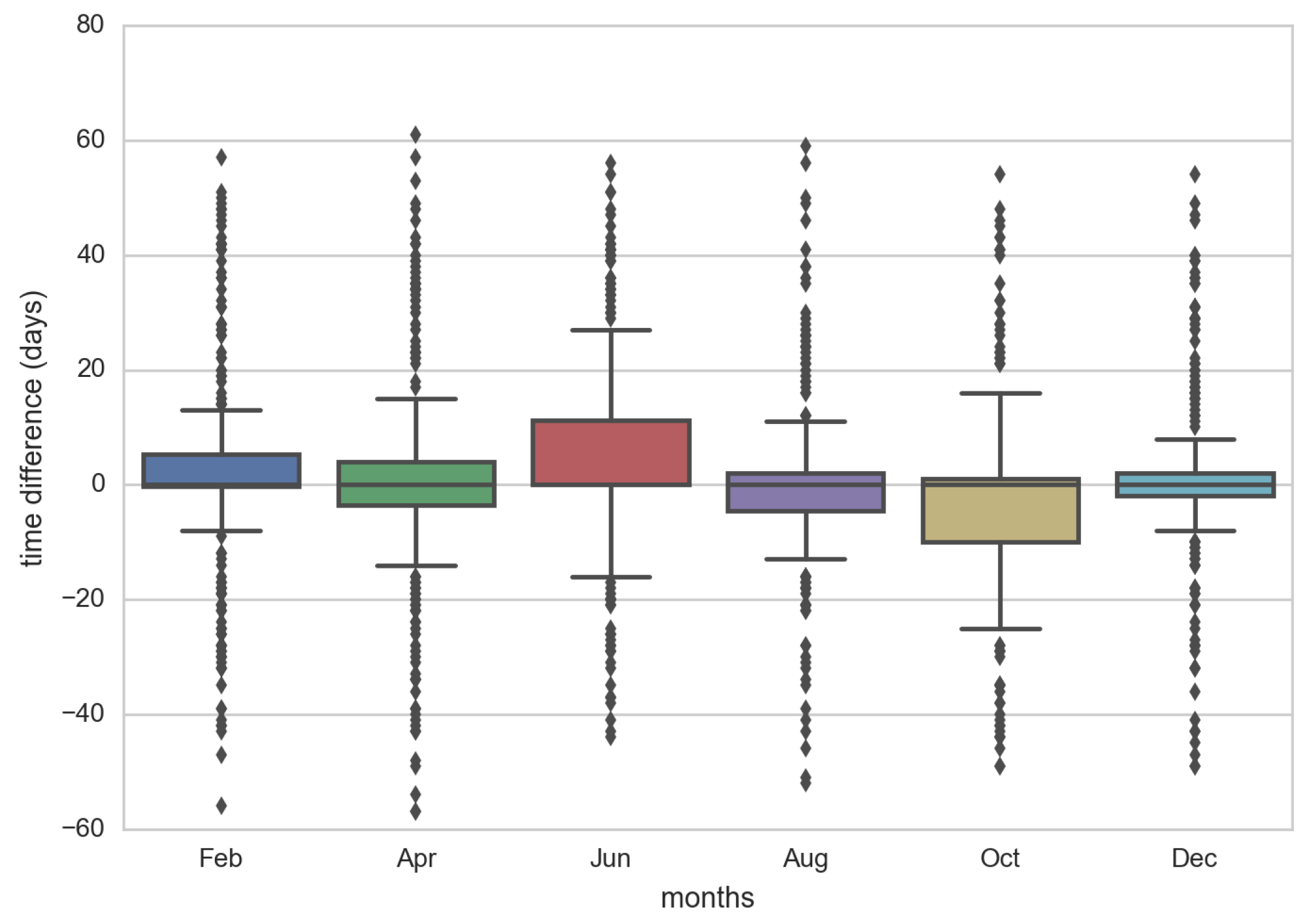
- The correlation coefficient between the ranking of page views and the ranking of page updates in a relatively long time period is negligible. In other words, in general, not only is the most viewed page not the most updated, but there is a lack of similarity in the ordering of the pages when ranked by views and updates (Kendall’s Tau∼0). However, in many cases the peaks of views-per-day can be directly associated with corresponding peaks of updates-per-day.
2. Related Work
2.1. Content Update Statistics
2.2. Wikipedia-Related Studies
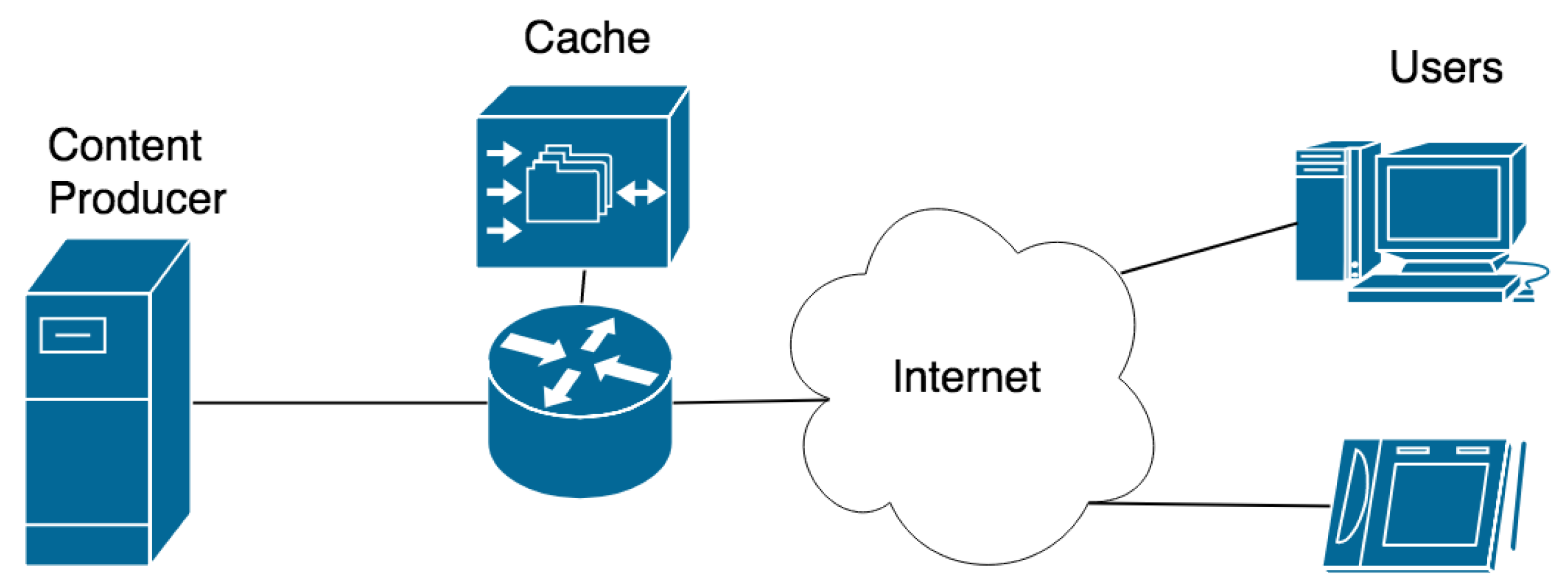
2.3. In-Network Caching
3. Methodology and Background
3.1. Background
3.2. Contribution and Methodology
3.3. Approach
4. Empirical Models
4.1. Wikipedia Views
4.2. Wikipedia Updates
4.3. Relationship Between Views and Updates
5. In-Network Caching Simulation
5.1. Simulation Scenario
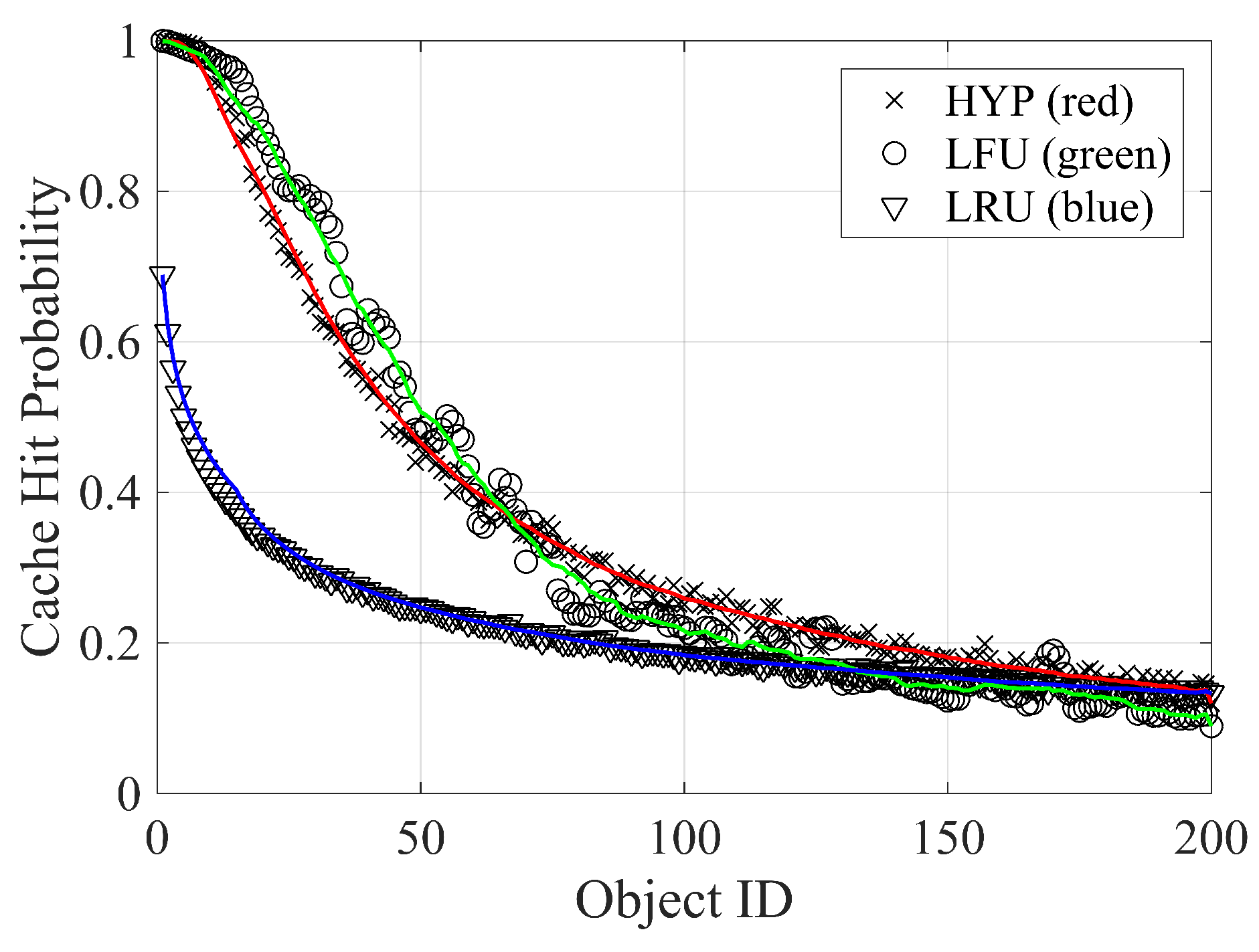
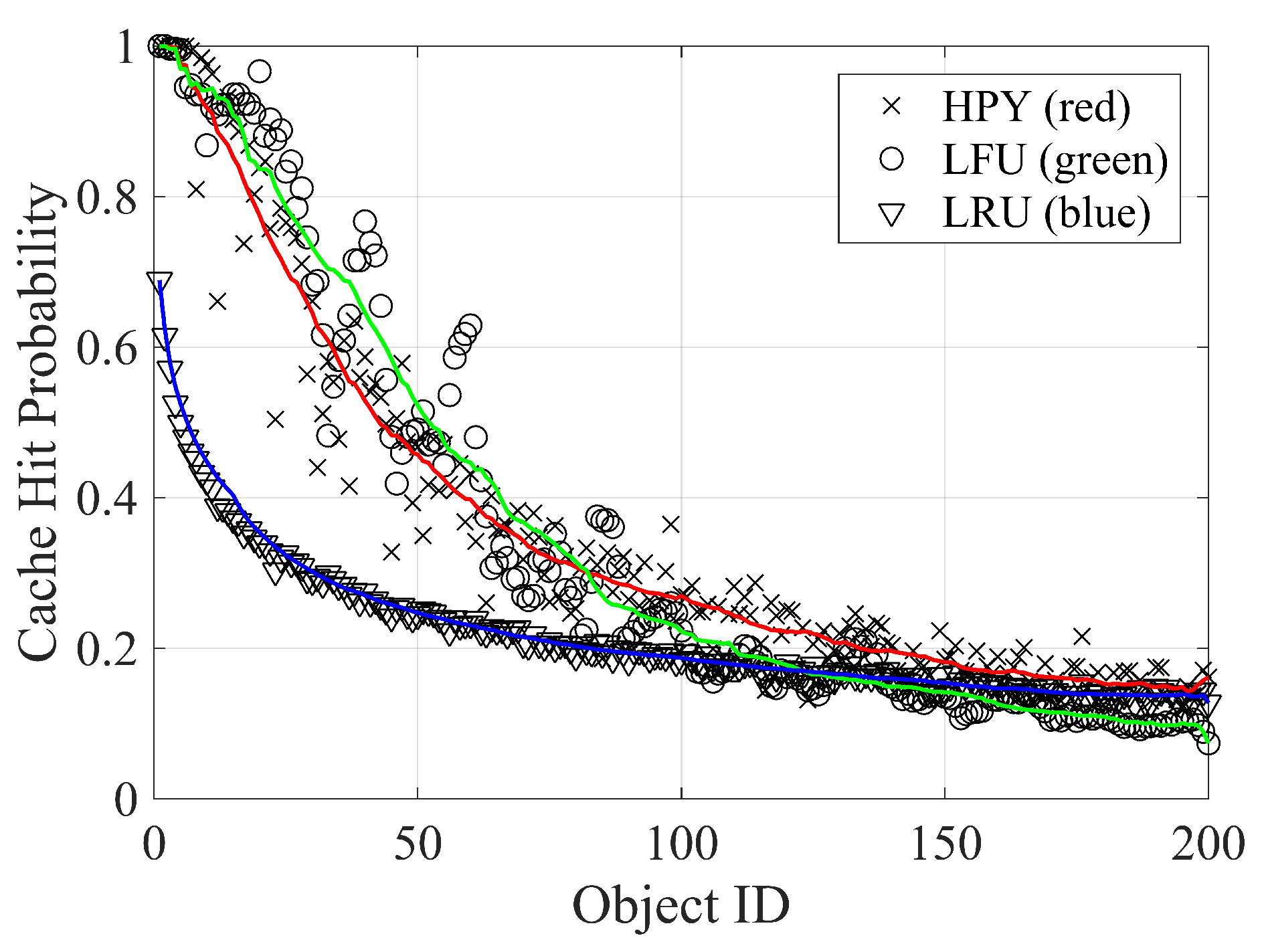
5.2. Caching Replacement Policies
- The least recently used (LRU) replacement strategy uses the time of access to replace items. In a typical implementation, items are stored in a memory stack. When requested, an item is added or moved to the top of the stack, and if necessary, the last item of the stack is removed to comply with the storage limit.
- The least frequently used (LFU) replacement strategy keeps the most popular items in the cache, i.e., the items that receive most views. A simple implementation of the policy records the number of hits for each item in the cache and replaces the item with the lowest value. This strategy suffers from problems: (i) a bad estimation of the popularity of newly inserted items and (ii) the persistence of popular items in a dynamic environment, i.e., when the request’s ranking changes over time.
- Hyperbolic caching (HYP) has been recently proposed to solve some LFU issues [50]. The HYP strategy replaces the item with the lowest ratio between the number of hits and the amount of time in the cache memory : .
5.3. Performance Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Breslau, L.; Cao, P.; Fan, L.; Phillips, G.; Shenker, S. Web caching and Zipf-like distributions: Evidence and implications. In Proceedings of the IEEE International Conference on Computer Communications 1999 (INFOCOM’99), New York, NY, USA, 21–25 March 1999; pp. 126–134. [Google Scholar]
- Cho, J.; Garcia Molina, H. Estimating frequency of change. ACM Trans. Internet Technol. 2003, 3, 256–290. [Google Scholar] [CrossRef]
- Wu, H.; Li, J.; Zhi, J.; Ren, Y.; Li, L. Design and evaluation of probabilistic caching in information-centric networking. IEEE Access 2018, 6, 32754–32768. [Google Scholar] [CrossRef]
- Detti, A.; Bracciale, L.; Loreti, P.; Melazzi, N.B. Modeling LRU cache with invalidation. Comput. Netw. 2018, 134, 55–65. [Google Scholar] [CrossRef]
- Bracciale, L.; Loreti, P.; Detti, A.; Paolillo, R.; Melazzi, N.B. Lightweight Named Object: An ICN-based Abstraction for IoT Device Programming and Management. IEEE Internet Things J. 2019, 6, 5029–5039. [Google Scholar] [CrossRef]
- Bastug, E.; Bennis, M.; Debbah, M. Living on the edge: The role of proactive caching in 5G wireless networks. IEEE Commun. Mag. 2014, 52, 82–89. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Qian, Y.; Hao, Y.; Li, Y.; Song, J. Data-driven computing and caching in 5G networks: Architecture and delay analysis. IEEE Wirel. Commun. 2018, 25, 70–75. [Google Scholar] [CrossRef]
- Ibrahimi, K.; Serbouti, Y. Prediction of the content popularity in the 5G network: Auto-regressive, moving-average and exponential smoothing approaches. In Proceedings of the 2017 International Conference on Wireless Networks and Mobile Communications, Rabat, Morocco, 1–4 November 2017; pp. 1–7. [Google Scholar]
- Jiang, W.; Feng, G.; Qin, S.; Liu, Y. Multi-Agent Reinforcement Learning Based Cooperative Content Caching for Mobile Edge Networks. IEEE Access 2019, 7, 61856–61867. [Google Scholar] [CrossRef]
- Garg, N.; Bhatia, V.; Bharath, B.; Sellathurai, M.; Ratnarajah, T. Online Learning Models for Content Popularity Prediction In Wireless Edge Caching. arXiv 2019, arXiv:1901.06476. [Google Scholar]
- Li, X.; Cline, D.B.; Loguinov, D. Temporal update dynamics under blind sampling. IEEE/ACM Trans. Netw. 2017, 25, 363–376. [Google Scholar] [CrossRef]
- Sun, Y.; Uysal-Biyikoglu, E.; Yates, R.D.; Koksal, C.E.; Shroff, N.B. Update or wait: How to keep your data fresh. IEEE Trans. Inf. Theory 2017, 63, 7492–7508. [Google Scholar] [CrossRef]
- Kayaaslan, E.; Cambazoglu, B.B.; Aykanat, C. Document replication strategies for geographically distributed web search engines. Inf. Process. Manag. 2013, 49, 51–66. [Google Scholar] [CrossRef] [Green Version]
- Trattner, C.; Kusmierczyk, T.; Nørvåg, K. Investigating and predicting online food recipe upload behavior. Inf. Process. Manag. 2019, 56, 654–673. [Google Scholar] [CrossRef]
- Li, X.; de Rijke, M. Characterizing and predicting downloads in academic search. Inf. Process. Manag. 2019, 56, 394–407. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Goslin, K.; Hofmann, M. A Wikipedia powered state-based approach to automatic search query enhancement. Inf. Process. Manag. 2018, 54, 726–739. [Google Scholar] [CrossRef]
- Ryu, P.M.; Jang, M.G.; Kim, H.K. Open domain question answering using Wikipedia-based knowledge model. Inf. Process. Manag. 2014, 50, 683–692. [Google Scholar] [CrossRef]
- Hasslinger, G.; Kunbaz, M.; Hasslinger, F.; Bauschert, T. Web caching evaluation from wikipedia request statistics. In Proceedings of the 15th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt), Paris, France, 15–19 May 2017; pp. 1–6. [Google Scholar]
- Cheng, X.; Dale, C.; Liu, J. Statistics and Social Network of YouTube Videos. In Proceedings of the 16th Interntional Workshop on Quality of Service, Enschede, The Netherlands, 2–4 June 2008; pp. 229–238. [Google Scholar]
- Gill, P.; Arlitt, M.; Li, Z.; Mahanti, A. Youtube Traffic Characterization: A View from the Edge. In Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement, San Diego, CA, USA, 24–26 October 2007; pp. 15–28. [Google Scholar]
- Mitzenmacher, M. A brief history of generative models for power law and lognormal distributions. Internet Math. 2004, 1, 226–251. [Google Scholar] [CrossRef]
- Cao, G. Proactive power-aware cache management for mobile computing systems. IEEE Trans. Comput. 2002, 51, 608–621. [Google Scholar]
- Detti, A.; Bracciale, L.; Loreti, P.; Rossi, G.; Melazzi, N.B. A cluster-based scalable router for information centric networks. Comput. Netw. 2018, 142, 24–32. [Google Scholar] [CrossRef]
- Detti, A.; Orru, M.; Paolillo, R.; Rossi, G.; Loreti, P.; Bracciale, L.; Melazzi, N.B. Application of information centric networking to nosql databases: The spatio-temporal use case. In Proceedings of the 2017 IEEE International Symposium on Local and Metropolitan Area Networks (LANMAN), Osaka, Japan, 12–14 June 2017; pp. 1–6. [Google Scholar]
- Bracciale, L.; Loreti, P.; Bianchi, G. Human time-scale duty cycle for opportunistic wifi based mobile networks. In Proceedings of the 24th Tyrrhenian International Workshop on Digital Communications-Green ICT (TIWDC), Genoa, Italy, 23–25 September 2013; pp. 1–6. [Google Scholar]
- Lam, S.T.K.; Riedl, J. Is Wikipedia growing a longer tail? In Proceedings of the ACM 2009 International Conference on Supporting Group Work, Sanibel Island, FL, USA, 10–13 May 2009; pp. 105–114. [Google Scholar]
- Ihm, S.; Pai, V.S. Towards understanding modern web traffic. In Proceedings of the 2011 ACM SIGCOMM Internet Measurement Conference, Berlin, Germany, 2–4 November 2011; pp. 295–312. [Google Scholar]
- Hoiles, W.; Aprem, A.; Krishnamurthy, V. Engagement and Popularity Dynamics of YouTube Videos and Sensitivity to Meta-Data. IEEE Trans. Knowl. Data Eng. 2017, 29, 1426–1437. [Google Scholar] [CrossRef]
- Park, M.; Naaman, M.; Berger, J. A data-driven study of view duration on youtube. In Proceedings of the Tenth International AAAI Conference on Web and Social Media, Cologne, Germany, 17–20 May 2016. [Google Scholar]
- Ponzetto, S.; Strube, M. Wikirelate! computing semantic relatedness using wikipedia. In Proceedings of the Twenty-First National Conference on Artificial Intelligence and the Eighteenth Innovative Applications Artificial Intelligence Conference, Boston, MA, USA, 16–20 July 2006. [Google Scholar]
- Witten, I.; Milne, D. An effective, low-cost measure of semantic relatedness obtained from Wikipedia links. In Proceedings of the AAAI Workshop on Wikipedia and Artificial Intelligence: An Evolving Synergy, Chicago, IL, USA, 13–17 July 2008; pp. 25–30. [Google Scholar]
- Gabrilovich, E.; Markovitch, S. Computing semantic relatedness using wikipedia-based explicit semantic analysis. In Proceedings of the Twentieth International Joint Conference on Artificial Intelligence (IJcAI), Hyderabad, India, 6–12 January 2007; pp. 1606–1611. [Google Scholar]
- Suh, B.; Chi, E.H.; Pendleton, B.A.; Kittur, A. Us vs. Them: Understanding Social Dynamics in Wikipedia with Revert Graph Visualizations. In Proceedings of the 2007 IEEE Symposium on Visual Analytics Science and Technology, Sacramento, CA, USA, 30 October–1 November 2007; pp. 163–170. [Google Scholar]
- Iba, T.; Nemoto, K.; Peters, B.; Gloor, P.A. Analyzing the Creative Editing Behavior of Wikipedia Editors: Through Dynamic Social Network Analysis. Procedia-Soc. Behav. Sci. 2010, 2, 6441–6456. [Google Scholar] [Green Version]
- Suh, B.; Chi, E.H.; Kittur, A.; Pendleton, B.A. Lifting the Veil: Improving Accountability and Social Transparency in Wikipedia with Wikidashboard. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Florence, Italy, 5–10 April 2008; pp. 1037–1040. [Google Scholar]
- Masucci, A.P.; Kalampokis, A.; Eguíluz, V.M.; Hernández-García, E. Wikipedia information flow analysis reveals the scale-free architecture of the semantic space. PLoS ONE 2011, 6, e17333. [Google Scholar] [CrossRef] [PubMed]
- Singer, P.; Lemmerich, F.; West, R.; Zia, L.; Wulczyn, E.; Strohmaier, M.; Leskovec, J. Why we read wikipedia. In Proceedings of the 26th International Conference on World Wide Web. International World Wide Web Conferences Steering Committee, Perth, Australia, 3–7 April 2017; pp. 1591–1600. [Google Scholar]
- Kämpf, M.; Tessenow, E.; Kenett, D.Y.; Kantelhardt, J.W. The detection of emerging trends using Wikipedia traffic data and context networks. PLoS ONE 2015, 10, e0141892. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, J.; Müller-Birn, C.; Laniado, D.; Lalmas, M.; Kaltenbrunner, A. Reader preferences and behavior on Wikipedia. In Proceedings of the 25th ACM Conference on Hypertext and Social Media, Santiago, Chile, 1–4 September 2014; pp. 88–97. [Google Scholar]
- Warncke-Wang, M.; Ranjan, V.; Terveen, L.; Hecht, B. Misalignment between supply and demand of quality content in peer production communities. In Proceedings of the Ninth International AAAI Conference on Web and Social Media, Palo Alto, CL, USA, 26–29 May 2015. [Google Scholar]
- Capiluppi, A.; Pimentel, A.C.D.; Boldyreff, C. Patterns of creation and usage of Wikipedia content. In Proceedings of the 2012 14th IEEE International Symposium on Web Systems Evolution (WSE), Trento, Italy, 28 September 2012; pp. 85–89. [Google Scholar]
- ten Thij, M.; Volkovich, Y.; Laniado, D.; Kaltenbrunner, A. Modeling page-view dynamics on Wikipedia. arXiv 2012, arXiv:1212.5943. [Google Scholar]
- Ratkiewicz, J.; Menczer, F.; Fortunato, S.; Flammini, A.; Vespignani, A. Traffic in social media ii: Modeling bursty popularity. In Proceedings of the 2010 IEEE Second International Conference on Social Computing, Minneapolis, MN, USA, 20–22 August 2010; pp. 393–400. [Google Scholar]
- Wilkinson, D.M.; Huberman, B.A. Cooperation and quality in wikipedia. In Proceedings of the 2007 International Symposium on Wikis, Montreal, QC, Canada, 21–23 October 2007; pp. 157–164. [Google Scholar]
- Urdaneta, G.; Pierre, G.; Van Steen, M. Wikipedia workload analysis for decentralized hosting. Comput. Netw. 2009, 53, 1830–1845. [Google Scholar] [CrossRef] [Green Version]
- Ali, W.; Shamsuddin, S.M.; Ismail, A.S. A survey of web caching and prefetching. Int. J. Adv. Soft Comput. Appl. 2011, 3, 18–44. [Google Scholar]
- Giatsoglou, N.; Ntontin, K.; Kartsakli, E.; Antonopoulos, A.; Verikoukis, C. D2D-aware device caching in mmWave-cellular networks. IEEE J. Sel. Areas Commun. 2017, 35, 2025–2037. [Google Scholar] [CrossRef]
- Loreti, P.; Bracciale, L. Optimized Neighbor Discovery for Opportunistic Networks of Energy Constrained IoT Devices. IEEE Trans. Wirel. Commun. 2019. [Google Scholar] [CrossRef]
- Blankstein, A.; Sen, S.; Freedman, M.J. Hyperbolic caching: Flexible caching for web applications. In Proceedings of the 2017 USENIX Annual Technical Conference, Santa Clara, CA, USA, 12–14 July 2017; pp. 499–511. [Google Scholar]
- Hasslinger, G.; Ntougias, K.; Hasslinger, F.; Hohlfeld, O. Performance evaluation for new web caching strategies combining LRU with score based object selection. Comput. Netw. 2017, 125, 172–186. [Google Scholar] [CrossRef]
- Balamash, A.; Krunz, M. An overview of web caching replacement algorithms. IEEE Commun. Surv. Tutor. 2004, 6, 44–56. [Google Scholar] [CrossRef]
- Fofack, N.C.; Nain, P.; Neglia, G.; Towsley, D. Analysis of TTL-based cache networks. In Proceedings of the 6th International ICST Conference on Performance Evaluation Methodologies and Tools, Cargese, France, 9–12 October 2012; pp. 1–10. [Google Scholar]
- Sornette, D. Critical Phenomena In Natural Sciences: Chaos, Fractals, Selforganization and Disorder: Concepts and Tools; Springer Science Business Media: New York, NY, USA, 2006. [Google Scholar]
- Newman, M.E. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005, 46, 323–351. [Google Scholar] [CrossRef]
- Sobkowicz, P.; Thelwall, M.; Buckley, K.; Paltoglou, G.; Sobkowicz, A. Lognormal distributions of user post lengths in Internet discussions-a consequence of the Weber-Fechner law? EPJ Data Sci. 2013, 2, 2. [Google Scholar] [CrossRef]
- Reed, W.J.; Jorgensen, M. The double Pareto-lognormal distribution-a new parametric model for size distributions. Commun. Stat.-Theory Methods 2004, 33, 1733–1753. [Google Scholar] [CrossRef]
- Alstott, J.; Bullmore, E.; Plenz, D. Powerlaw: A Python package for analysis of heavy-tailed distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef] [PubMed]
- Tsvetkova, M.; García-Gavilanes, R.; Floridi, L.; Yasseri, T. Even good bots fight: The case of Wikipedia. PLoS ONE 2017, 12, e0171774. [Google Scholar] [CrossRef] [PubMed]
- Steiner, T. Bots vs. wikipedians, anons vs. logged-ins. In Proceedings of the 23rd International Conference on World Wide Web, Seoul, Korea, 7–11 April 2014; pp. 547–548. [Google Scholar]
- Poularakis, K.; Iosifidis, G.; Sourlas, V.; Tassiulas, L. Exploiting Caching and Multicast for 5G Wireless Networks. IEEE Trans. Wirel. Commun. 2016, 15, 2995–3007. [Google Scholar] [CrossRef]
- Wang, W.; Sun, Y.; Guo, Y.; Kaafar, D.; Jin, J.; Li, J.; Li, Z. CRCache: Exploiting the correlation between content popularity and network topology information for ICN caching. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 3191–3196. [Google Scholar]
- Almeida, V.; Bestavros, A.; Crovella, M.; De Oliveira, A. Characterizing reference locality in the WWW. In Proceedings of the Fourth International Conference on Parallel and Distributed Information Systems, Miami Beach, FL, USA, 18–20 December 1996; pp. 92–103. [Google Scholar]
| Considered | Total | |
|---|---|---|
| Jan | 97.20% | 627M |
| Feb | 100.00% | 596M |
| Mar | 43.31% | 545M |
| Apr | 91.94% | 499M |
| May | 100.00% | 488M |
| Jun | 99.12% | 508M |
| Jul | 100.00% | 516M |
| Aug | 100.00% | 549M |
| Sep | 100.00% | 486M |
| Oct | 98.14% | 538M |
| Nov | 100.00% | 658M |
| Dec | 68.30% | 597M |
| Considered | Total | |
|---|---|---|
| Jan | 93.59% | 69K |
| Feb | 91.21% | 59K |
| Mar | 90.73% | 66K |
| Apr | 91.25% | 66K |
| May | 91.40% | 71K |
| Jun | 91.45% | 70K |
| Jul | 91.23% | 72K |
| Aug | 92.13% | 73K |
| Sep | 91.26% | 53K |
| Oct | 90.87% | 62K |
| Nov | 91.18% | 70K |
| Dec | 90.90% | 69K |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bracciale, L.; Loreti, P.; Detti, A.; Blefari Melazzi, N. Analysis of Data Persistence in Collaborative Content Creation Systems: The Wikipedia Case. Information 2019, 10, 330. https://doi.org/10.3390/info10110330
Bracciale L, Loreti P, Detti A, Blefari Melazzi N. Analysis of Data Persistence in Collaborative Content Creation Systems: The Wikipedia Case. Information. 2019; 10(11):330. https://doi.org/10.3390/info10110330
Chicago/Turabian StyleBracciale, Lorenzo, Pierpaolo Loreti, Andrea Detti, and Nicola Blefari Melazzi. 2019. "Analysis of Data Persistence in Collaborative Content Creation Systems: The Wikipedia Case" Information 10, no. 11: 330. https://doi.org/10.3390/info10110330
APA StyleBracciale, L., Loreti, P., Detti, A., & Blefari Melazzi, N. (2019). Analysis of Data Persistence in Collaborative Content Creation Systems: The Wikipedia Case. Information, 10(11), 330. https://doi.org/10.3390/info10110330







