Hybrid Optimization Algorithm for Bayesian Network Structure Learning
Abstract
:1. Introduction
2. Bayesian Network Structure Learning Overview
2.1. Bayesian Network and Structure Model
2.2. Main Structure Learning Method
3. Hybrid Optimization Artificial Bee Colony Algorithm for Bayesian Network Structure Learning
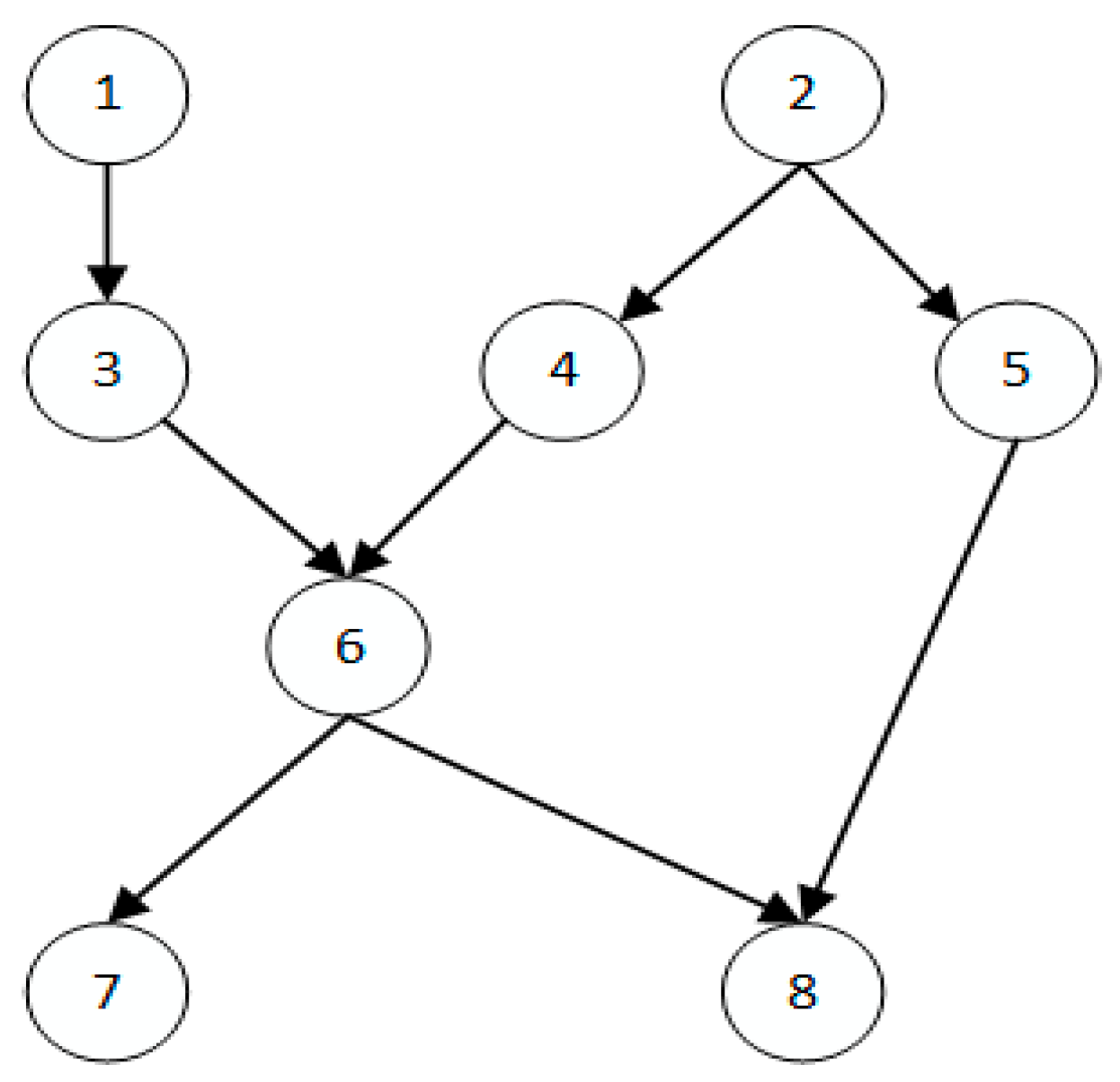
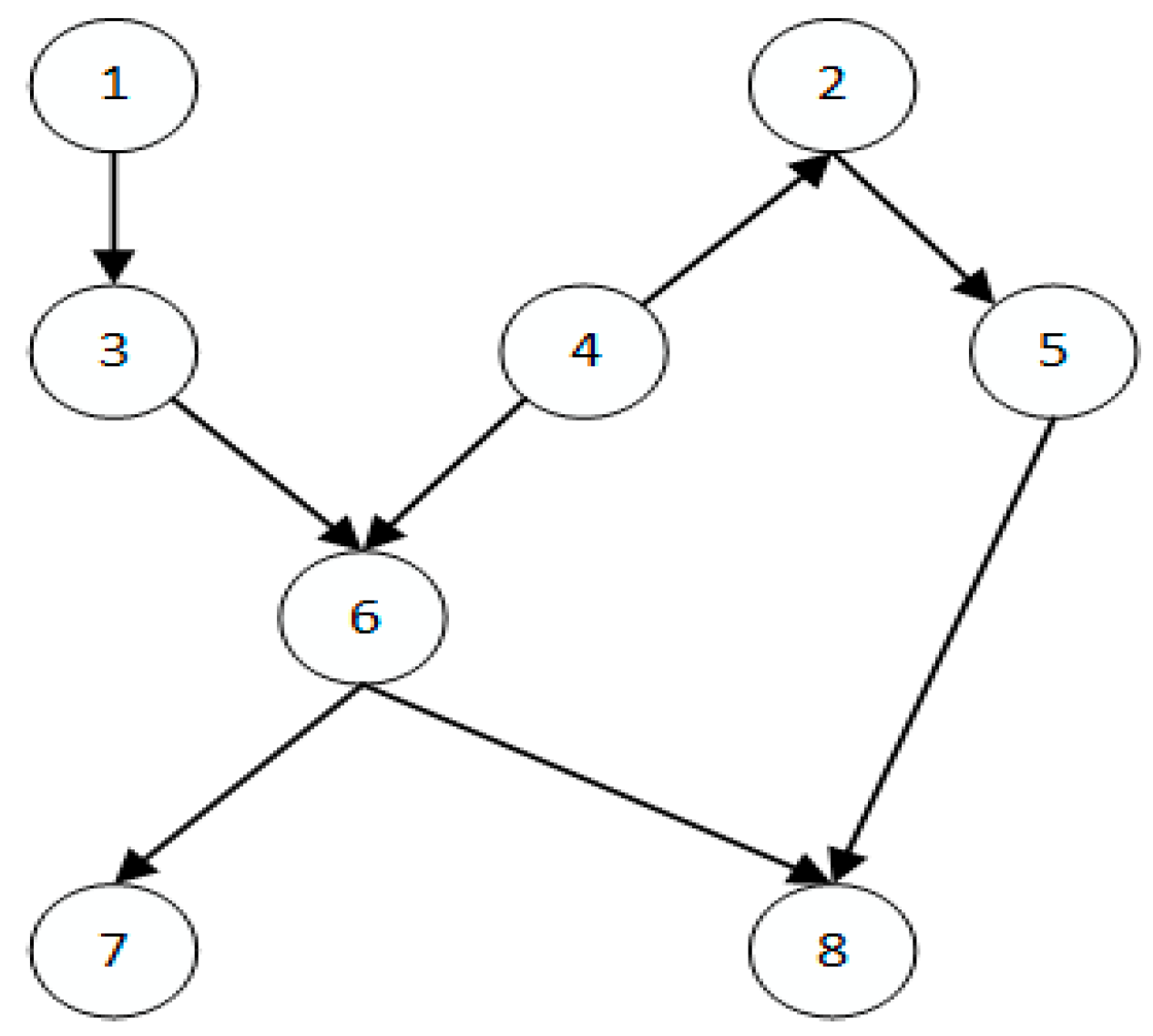
3.1. Problem Abstraction
3.2. Algorithm Description
3.2.1. Initialization Phase
3.2.2. Fitness Function
3.2.3. Employed Foragers
| Algorithm 1. Bswap Mutation |
| Input: food source Xi |
| Output: food source after mutation operation M(Xi) |
| 1 Select two random values in [1, D], u, v; |
| 2 If Xiu(t) = Xiv(t), then Xiu(t) = (Xiu(t) + 1) mod 2; |
| Otherwise, Xiu(t) = (Xiu(t) + 1) mod 2, Xiv(t) = (Xiv(t) + 1) mod 2 |
3.2.4. Followers
3.2.5. Scouter
3.2.6. Structure Correction
3.3. Algorithm Flow
| Algorithm 2. CMABC-BNL |
| Input: Training data D Output: Optimal food source (structure)
|
3.4. Algorithm Complexity Analysis
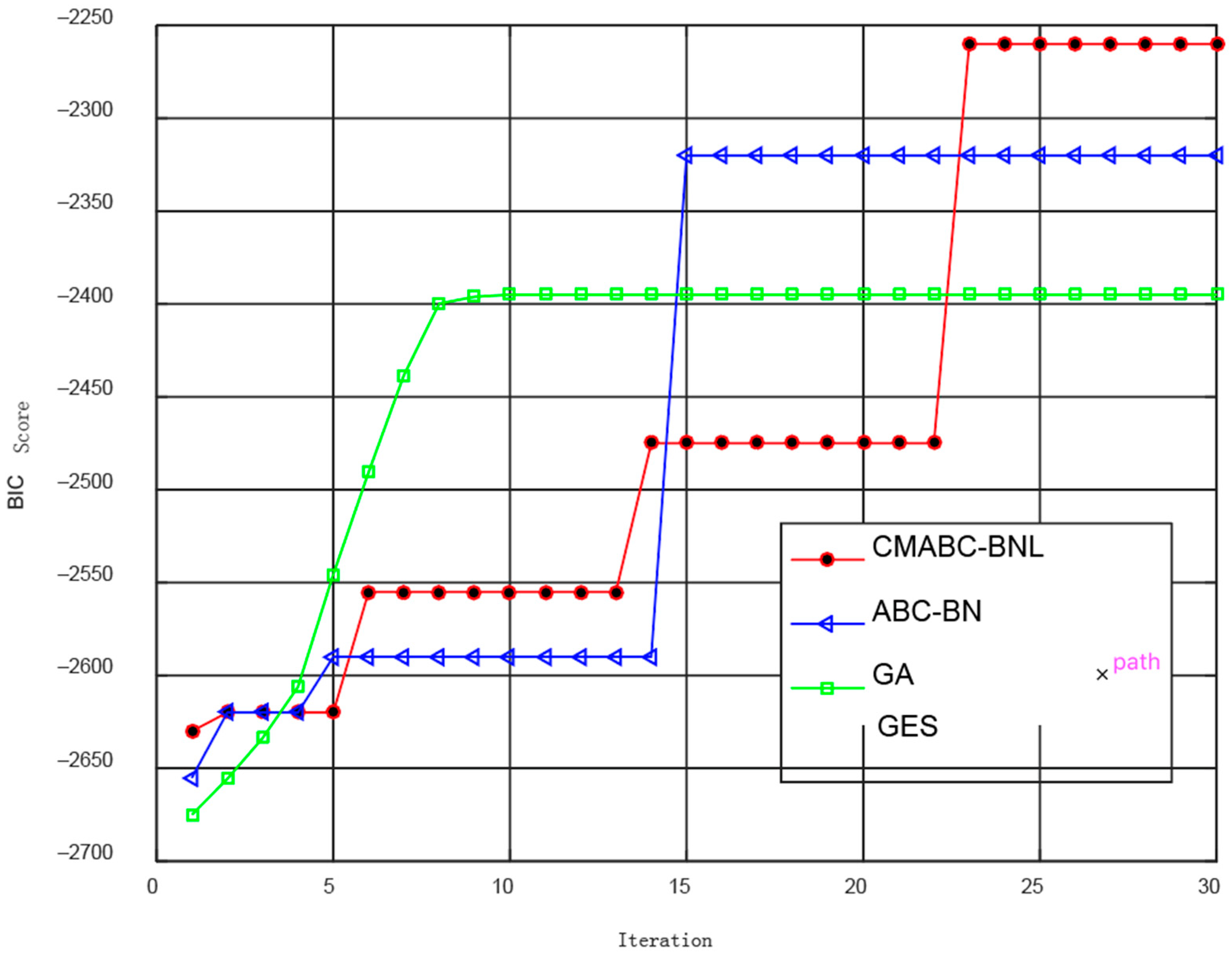
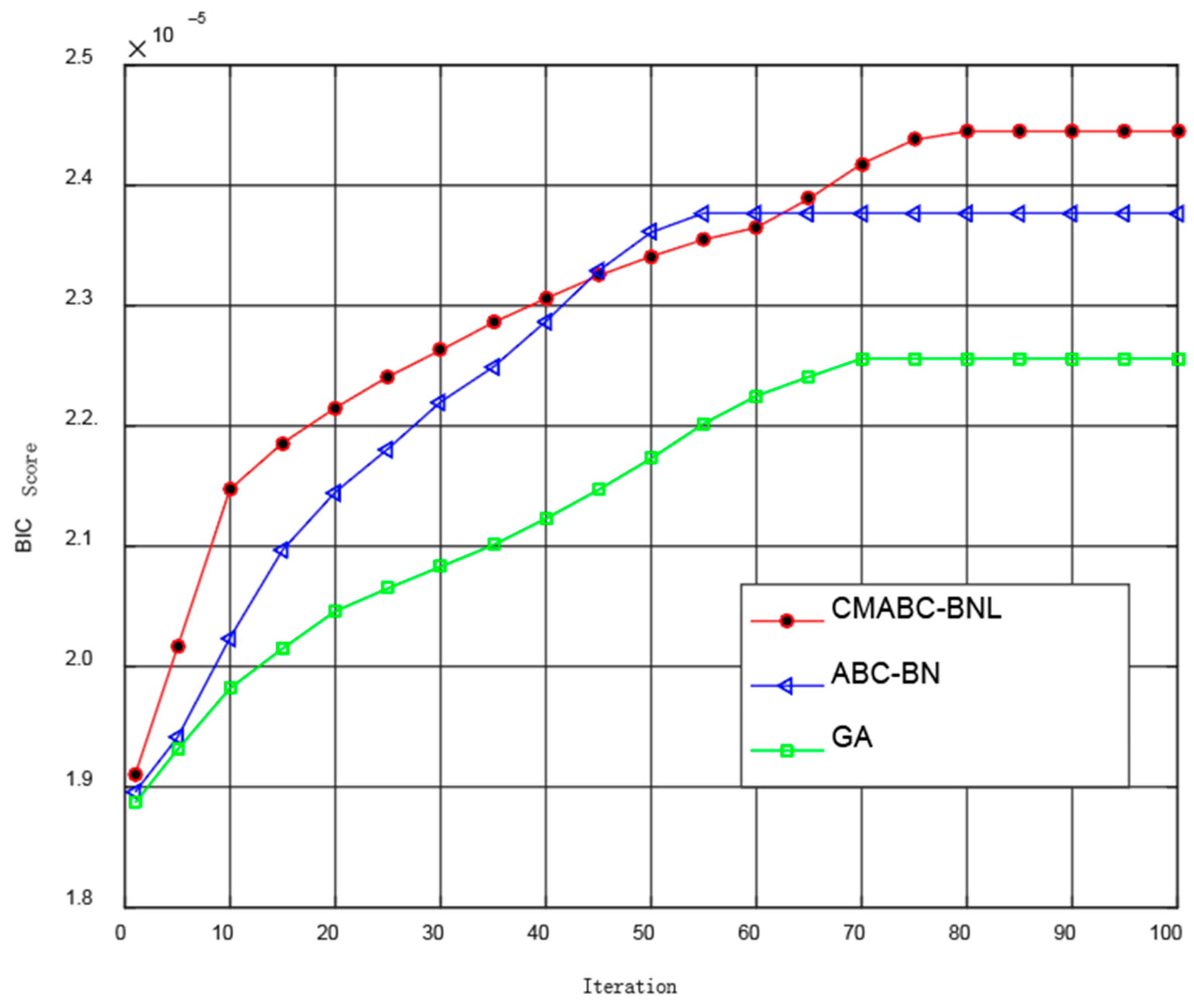
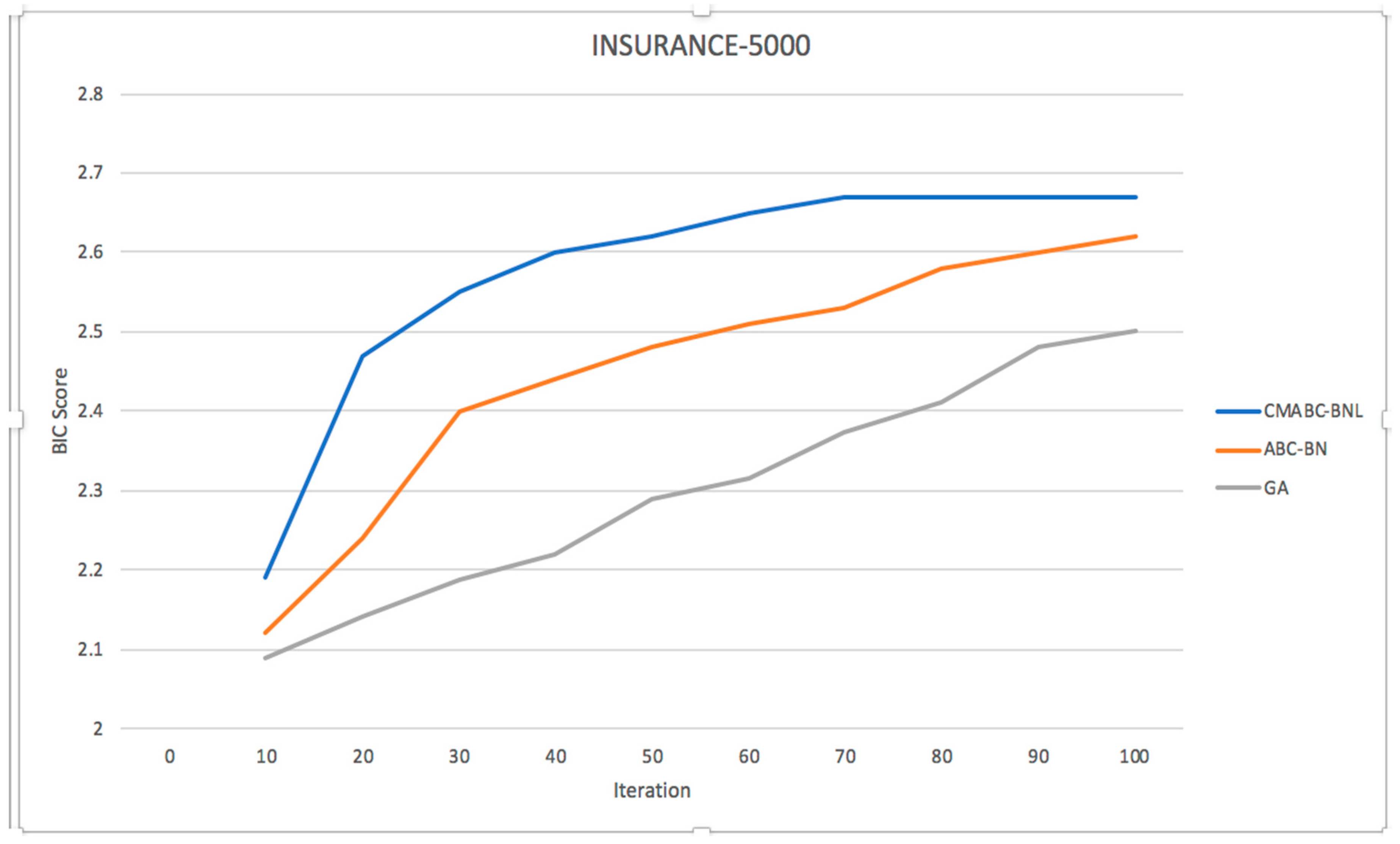
3.5. Simulation Experiment and Result Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Friedman, N.; Dan, G.; Goldszmidt, M. Bayesian Network Classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef] [Green Version]
- Taheri, S.; Mammadov, M. Structure Learning of Bayesian Networks using Global Optimization with Applications in Data Classification. Optim. Lett. 2015, 9, 931–948. [Google Scholar] [CrossRef]
- Pearl, J. Probabilistic reasoning in intelligent systems: Networks of plausible inference. J. Philos. 1988, 88, 434–437. [Google Scholar]
- Chickering, D.M.; Dan, G.; Heckerman, D. Learning Bayesian Networks is NP-Hard. Networks 1994, 112, 121–130. [Google Scholar]
- Pinto, P.C.; Runkler, T.A. Using a local discovery ant algorithm for Bayesian network structure learning. IEEE Trans. Evol. Comput. 2009, 13, 767–779. [Google Scholar] [CrossRef]
- Balasubramanian, A.; Levine, B.; Venkataramani, A. DTN routing as a resource allocation problem. ACM Sigcomm Comput. Commun. Rev. 2007, 37, 373–384. [Google Scholar] [CrossRef] [Green Version]
- Geng, H.J.; Shi, X.G.; Wang, Z.L.; Yin, X.; Yin, S.P. Energy-efficient Intra-domain Routing Algorithm Based on Directed Acyclic Graph. Comput. Sci. 2018, 45, 112–116. [Google Scholar]
- Lauritzen, S.L.; Spiegelhalter, D.J. Local Computations with Probabilities on Graphical Structures and their Application to Expert Systems. J. R. Stat. Soc. 1988, 50, 157–224. [Google Scholar] [CrossRef]
- Robinson, R.W. Counting unlabeled acyclic digraphs. In Proceedings of the Fifth Australian Conference on Combinatorial Mathematics V, Melbourne, Australia, 24–26 August 1976; Springer: Berlin/Heidelberg, Germany, 1977; pp. 28–43. [Google Scholar]
- Schellenberger, J.; Que, R.; Fleming, R.M.; Thiele, I.; Orth, J.D.; Feist, A.M.; Zielinski, D.C.; Bordbar, A.; Lewis, N.E.; Rahmanian, S. Quantitative prediction of cellular metabolism with constraint-based models: The COBRA Toolbox v2.0. Nat. Protoc. 2011, 6, 1290–1307. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; van Beek, P. Metaheuristics for Score-and-Search Bayesian Network Structure Learning. In Proceedings of the 30th Canadian Conference on Artificial Intelligence, Canadian AI 2017, Edmonton, AB, Canada, 16–19 May 2017. [Google Scholar]
- Campos, L.M.D. A Scoring Function for Learning Bayesian Networks based on Mutual Information and Conditional Independence Tests. J. Mach. Learn. Res. 2006, 7, 2149–2187. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. Autom. Control. IEEE Trans. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Anděl, J.; Perez, M.G.; Negrao, A.I. Estimating the dimension of a linear model. Ann. Stat. 1981, 17, 514–525. [Google Scholar]
- Kirkpatrick, S. Optimization by simulated annealing: Quantitative studies. J. Stat. Phys. 1984, 34, 975–986. [Google Scholar] [CrossRef]
- Heckerman, D.; Dan, G.; Chickering, D.M. Learning Bayesian Networks: The Combination of Knowledge and Statistical Data. Mach. Learn. 1995, 20, 197–243. [Google Scholar] [CrossRef]
- An, N.; Teng, Y.; Zhu, M.M. Bayesian network structure learning method based on causal effect. J. Comput. Appl. 2018, 35, 95–99. [Google Scholar]
- Cao, J. Bayesian Network Structure Learning and Application Research. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10358-1017065349.htm (accessed on 22 September 2019). (In Chinese).
- Gao, X.G.; Ye, S.M.; Di, R.H.; Kou, Z.C. Bayesian network structure learning based on fusion prior method. Syst. Eng. Electron. 2018, 40, 790–796. [Google Scholar]
- Yu, Y.Q.; Chen, X.X.; Yin, J. Structure Learning Method of Bayesian Network with Hybrid Particle Swarm Optimization Algorithm. Small Microcomput. Syst. 2018, 39, 2060–2066. [Google Scholar]
- Du, Z.F.; Liu, G.Z.; Zhao, X.H. Ensemble learning artificial bee colony algorithm. J. Xidian Univ. (Natural Science Edition) 2019, 46, 124–131. (In Chinese) [Google Scholar]
- Larranaga, P.; Poza, M.; Yurramendi, Y.; Murga, R.H.; Kuijpers, C.M.H. Structure learning of Bayesian networks by genetic algorithms: A performance analysis of control parameters. IEEE Trans. Pattern Anal. Mach. Intell. 1996, 18, 912–926. [Google Scholar] [CrossRef]
- Bernoulli Process. Available online: https://link.springer.com/referenceworkentry/10.1007%2F978-1-4020-6754-9_1682 (accessed on 22 September 2019).
- Shen, X.; Zou, D.X.; Zhang, X. Stochastic adaptive differential evolution algorithm. Electron. Technol. 2018, 2, 51–55. [Google Scholar]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Tasgetiren, M.F.; Pan, Q.K.; Suganthan, P.N.; Liang, Y.C.; Chua, T.J. Metaheuristics for Common due Date Total Earliness and Tardiness Single Machine Scheduling Problem; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
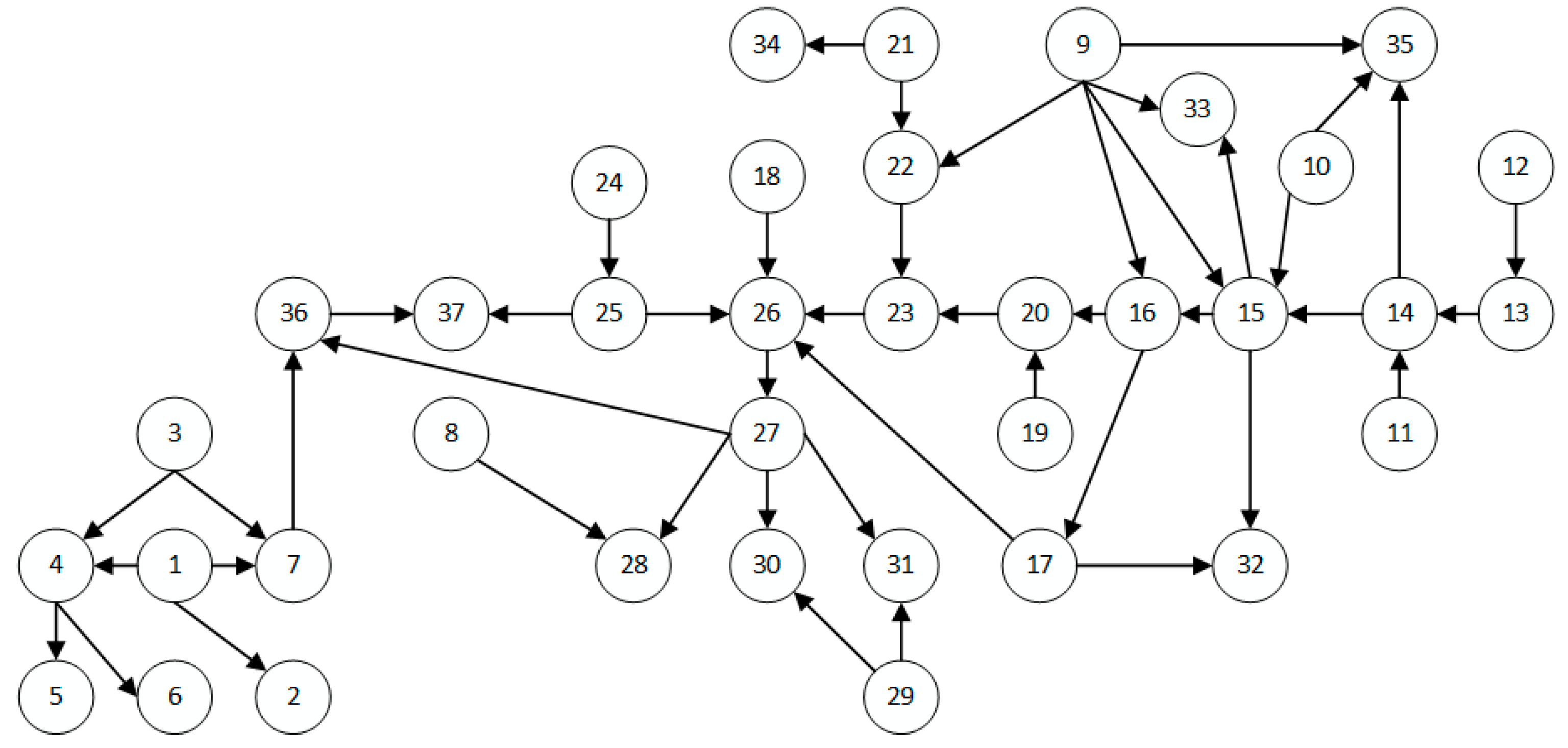
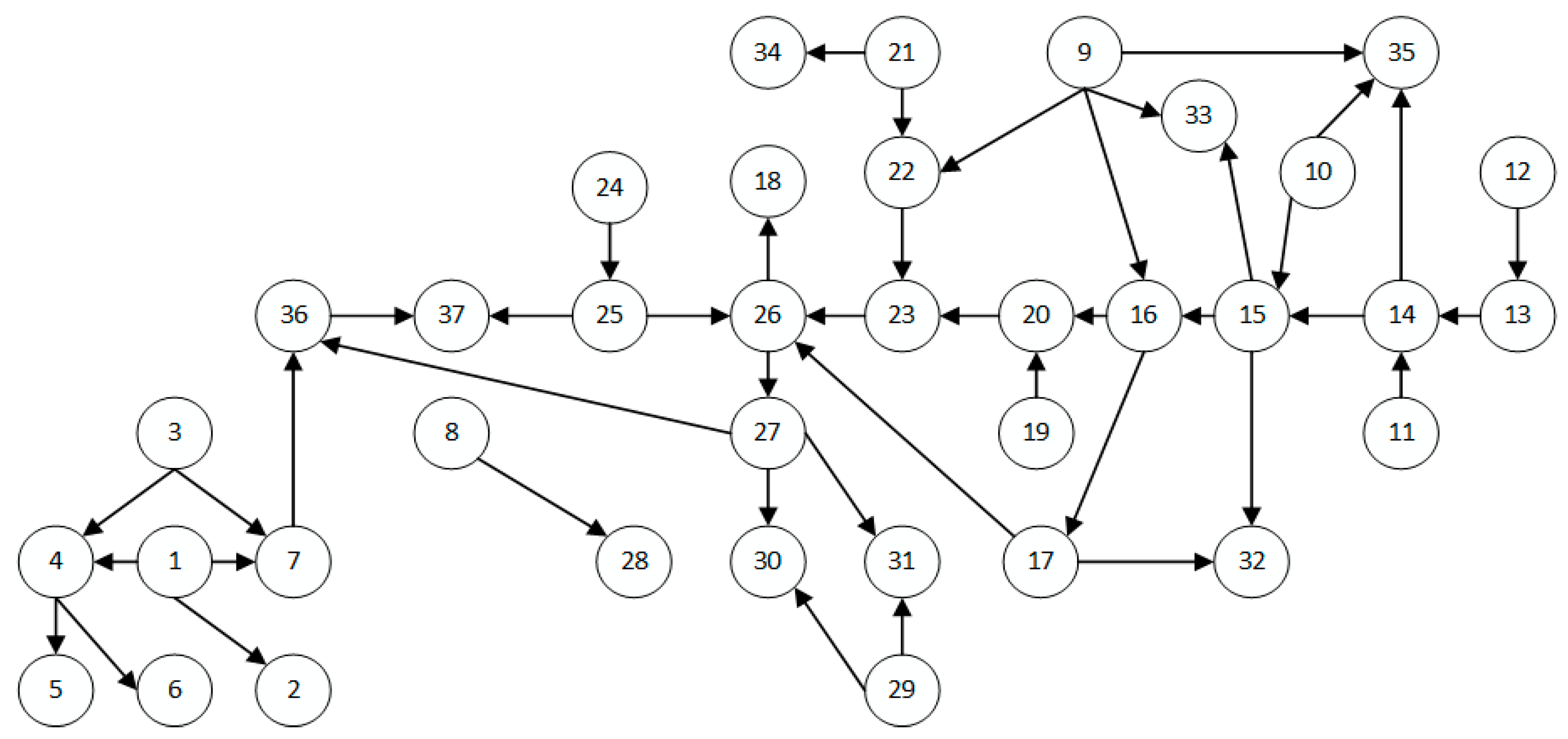
- Beinlich, I.A.; Suermondt, H.J.; Chavez, R.M.; Cooper, G.F. The ALARM Monitoring System: A Case Study with Two Probabilistic Inference Techniques for Belief Networks; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Zhang, P.; Liu, S.Y.; Zhu, M.M. Bayesian Network Structure Learning Based on Artificial Bee Colony Algorithm. J. Intell. Syst. 2014, 9, 325–329. [Google Scholar]
- Gheisari, S.; Meybodi, M.R. BNC-PSO: Structure learning of Bayesian networks by Particle Swarm Optimization. Inf. Sci. 2016, 348, 272–289. [Google Scholar] [CrossRef]
- Chickering, D.M. Learning equivalence classes of Bayesian network structures. In Proceedings of the Twelfth International Conference on Uncertainty in Artificial Intelligence, UAI’96, Portland, OR, USA, 1–4 August 1996; pp. 150–157. [Google Scholar]
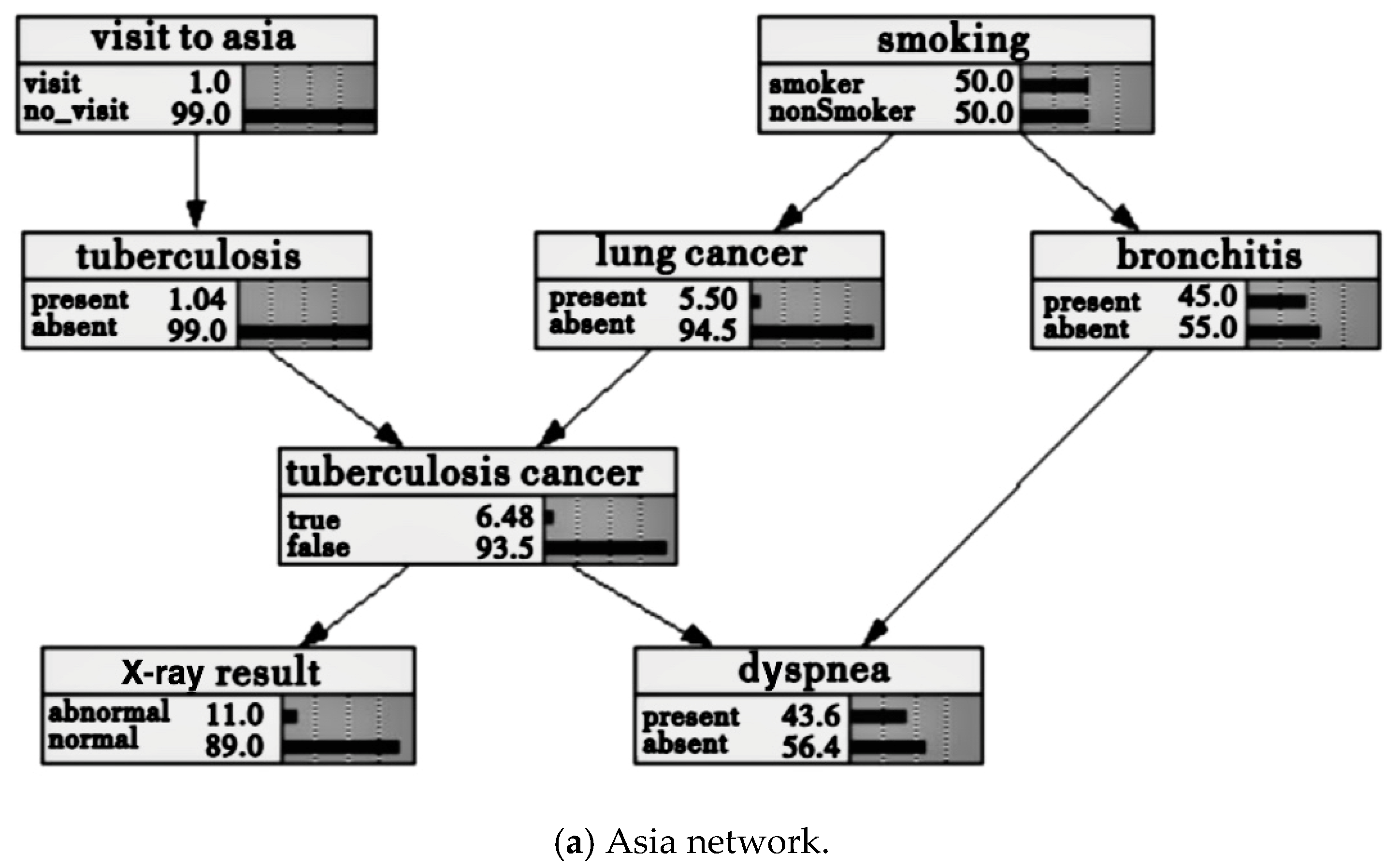
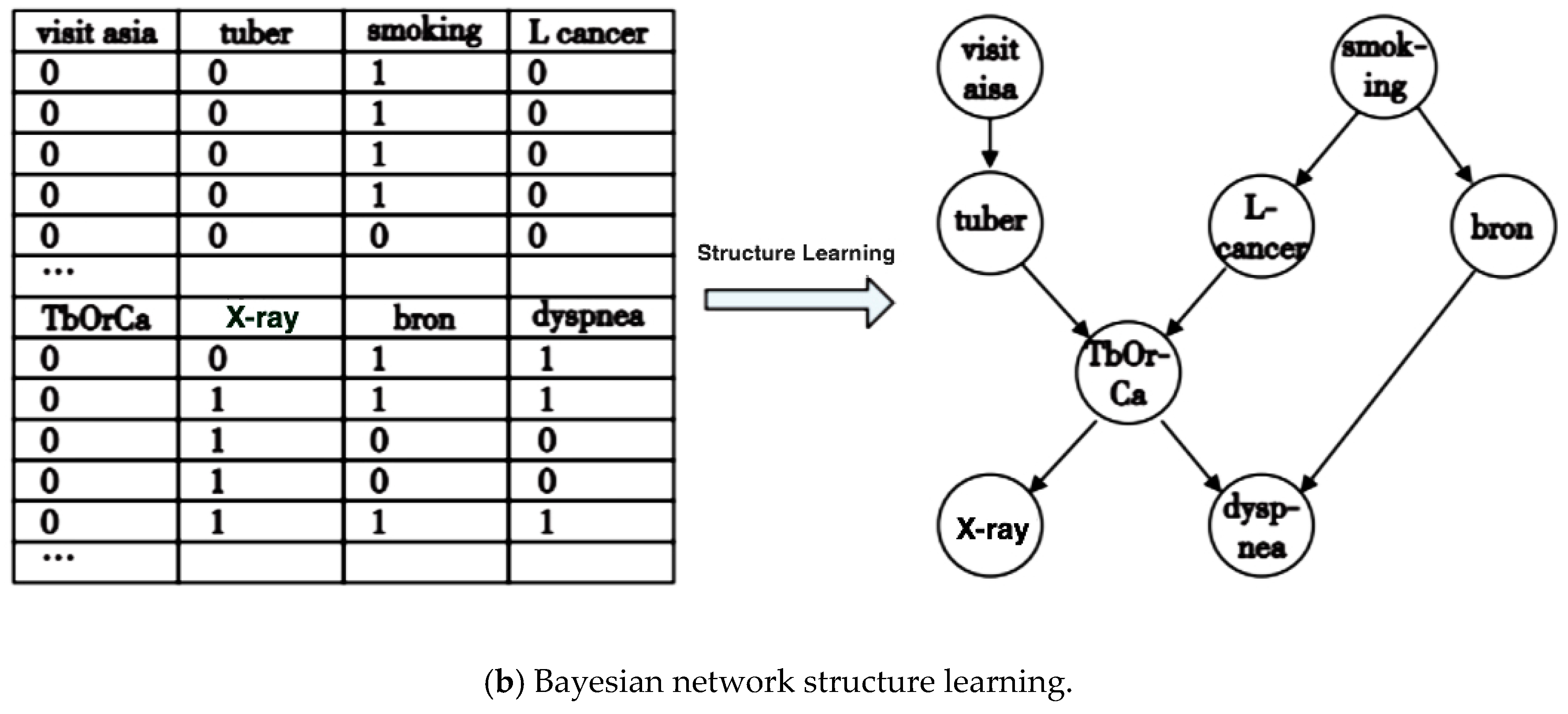
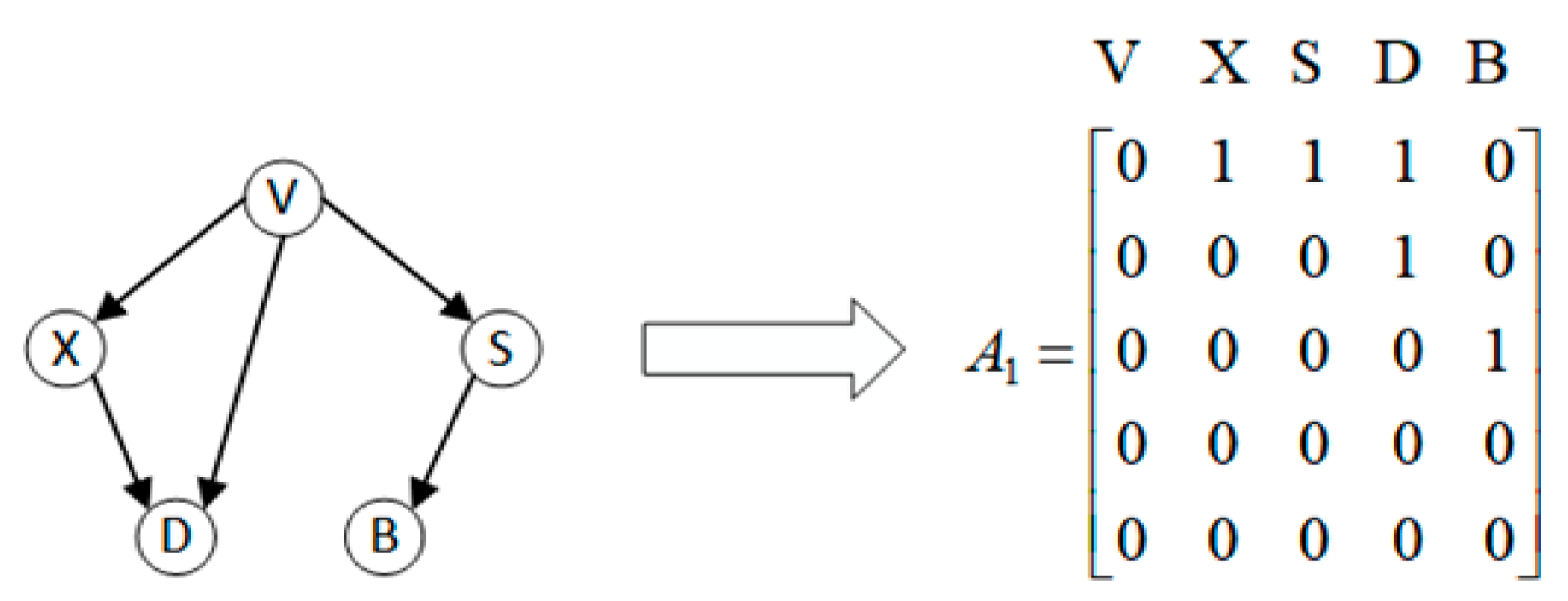
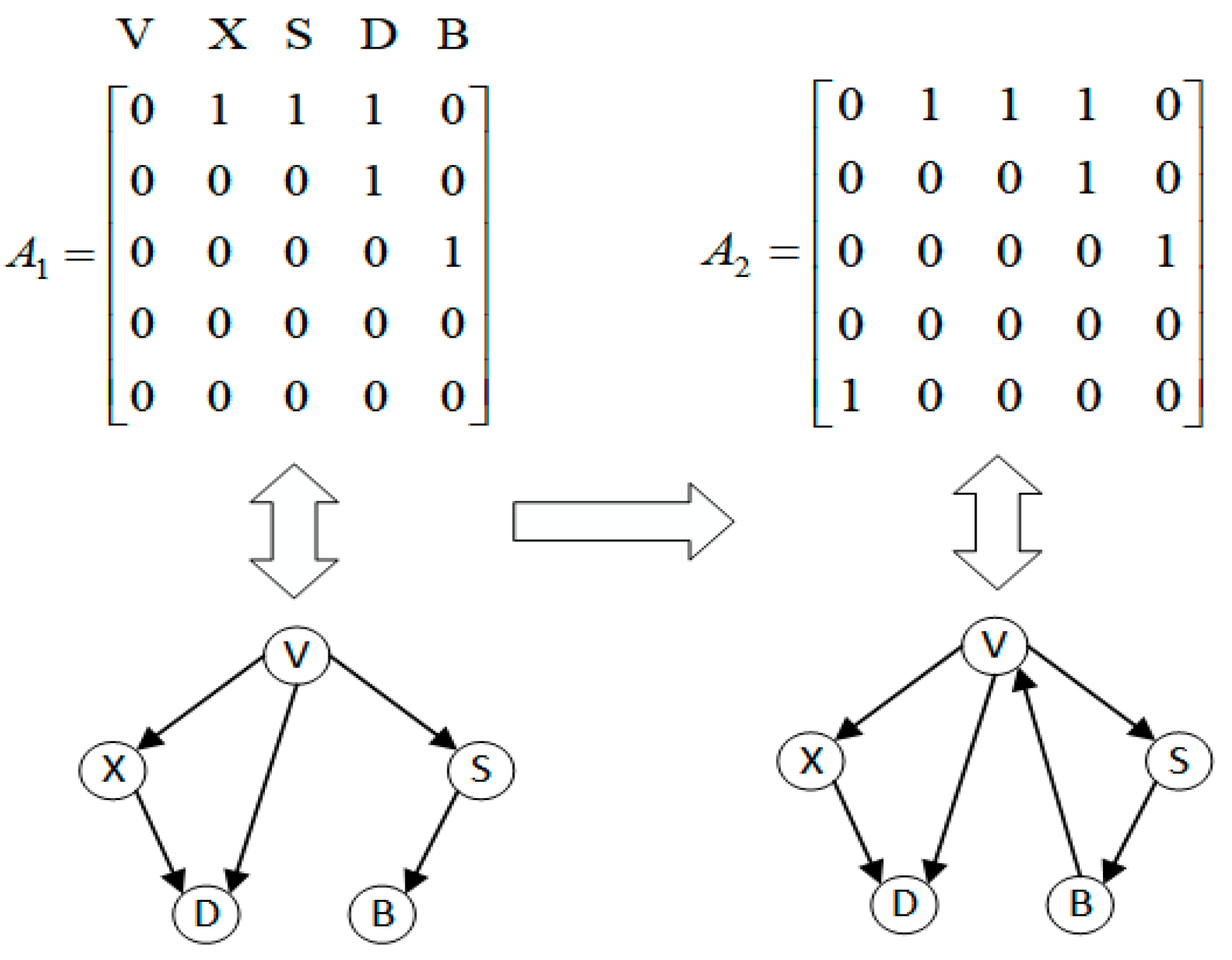
| Bee Colony Searching for Food Source | Bayesian Network Structure Learning |
|---|---|
| Food source | Bayesian network structure |
| Food source quality | Bayesian network structure score |
| Optimal food source | Optimal Bayesian network structure |
| Bayesian Network | Nodes | Directed Edges |
|---|---|---|
| ASIA | 8 | 8 |
| ALARM | 37 | 46 |
| INSURANCE | 27 | 52 |
| Bayesian Network | Samples | Objective Function Value | Hamming Distance (SHD) | Average Execution Time (Ext) (s) |
|---|---|---|---|---|
| ASIA | 500 | 8.36 × 10−4 | 0.9 | 2.96 |
| 1000 | 4.42 × 10−4 | 0.4 | 4.05 | |
| 2000 | 2.18 × 10−4 | 0.1 | 4.75 | |
| 5000 | 9.01 × 10−5 | 0 | 6.03 | |
| ALARM | 500 | 1.44 × 10−4 | 13.8 | 2.54 × 102 |
| 1000 | 8.07 × 10−5 | 7.5 | 3.85 × 102 | |
| 2000 | 4.27 × 10−5 | 5.6 | 4.61 × 102 | |
| 5000 | 1.75 × 10−5 | 3.4 | 7.12 × 102 | |
| INSURANCE | 500 | 1.55 × 10−4 | 13.2 | 76.7 |
| 1000 | 9.08 × 10−5 | 10.3 | 1.52 × 102 | |
| 2000 | 6.35 × 10−5 | 8.4 | 2.43 × 102 | |
| 5000 | 2.17 × 10−5 | 4.4 | 3.81 × 102 |
| Training Data | Algorithm | Value | SHD | Ext(s) | F1 Value |
|---|---|---|---|---|---|
| ASIA-1000 | CMABC-BNL | 4.24 × 10−4 | 0.4 | 5.05 | 0.635 |
| ABC-BN | 4.34 × 10−4 | 1.5 | 4.27 | 0.616 | |
| GA | 4.17 × 10−4 | 2.4 | 6.58 | 0.624 | |
| GES | 4.35 × 10−4 | 2.6 | 0.9 | 0.627 | |
| BNC-PSO | 4.26 × 10−4 | 1.1 | 3.6 | 0.638 | |
| ASIA-5000 | CMABC-BNL | 9.01 × 10−5 | 0 | 6.03 | 0.687 |
| ABC-BN | 9.01 × 10−5 | 0 | 4.34 | 0.646 | |
| GA | 9.01 × 10−5 | 0 | 8.9 | 0.655 | |
| GES | 9.01 × 10−5 | 0 | 1.3 | 0.663 | |
| BNC-PSO | 9.01 × 10−5 | 0 | 4.8 | 0.692 | |
| ALARM-1000 | CMABC-BNL | 8.07 × 10−5 | 7.5 | 3.85 × 102 | 0.645 |
| ABC-BN | 7.83 × 10−5 | 8.7 | 3.13 × 102 | 0.621 | |
| GA | 7.45 × 10−5 | 11.6 | 5.41 × 102 | 0.627 | |
| GES | 8.22 × 10−5 | 12.3 | 1.47 × 102 | 0.635 | |
| BNC-PSO | 8.14 × 10−5 | 7.9 | 4.06 × 102 | 0.640 | |
| ALARM-5000 | CMABC-BNL | 1.71 × 10−5 | 3.4 | 7.12 × 102 | 0.696 |
| ABC-BN | 1.69 × 10−5 | 4.8 | 6.04 × 102 | 0.658 | |
| GA | 1.63 × 10−5 | 6.1 | 1.20 × 103 | 0.669 | |
| GES | 1.83 × 10−5 | 6.9 | 2.24 × 102 | 0.675 | |
| BNC-PSO | 1.79 × 10−5 | 4 | 6.92 × 102 | 0.690 | |
| INSURANCE-1000 | CMABC-BNL | 8.73 × 10−5 | 8.1 | 2.08 × 102 | 0.633 |
| ABC-BN | 8.56 × 10−5 | 9.2 | 1.97 × 102 | 0.614 | |
| GA | 8.33 × 10−5 | 10.7 | 3.40 × 102 | 0.618 | |
| GES | 8.54 × 10−5 | 12.2 | 1.02 × 102 | 0.625 | |
| BNC-PSO | 8.62 × 10−5 | 8.6 | 1.67 × 102 | 0.632 | |
| INSURANCE-5000 | CMABC-BNL | 2.67 × 10−5 | 4.3 | 3.80 × 102 | 0.689 |
| ABC-BN | 2.62 × 10−5 | 5.7 | 3.77 × 102 | 0.647 | |
| GA | 2.50 × 10−5 | 7.2 | 6.48 × 102 | 0.654 | |
| GES | 2.47 × 10−5 | 8.9 | 1.31 × 102 | 0.675 | |
| BNC-PSO | 2.35 × 10−5 | 5 | 3.54 × 102 | 0.683 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Chen, C.; Wang, L.; Kang, H.; Shen, Y.; Chen, Q. Hybrid Optimization Algorithm for Bayesian Network Structure Learning. Information 2019, 10, 294. https://doi.org/10.3390/info10100294
Sun X, Chen C, Wang L, Kang H, Shen Y, Chen Q. Hybrid Optimization Algorithm for Bayesian Network Structure Learning. Information. 2019; 10(10):294. https://doi.org/10.3390/info10100294
Chicago/Turabian StyleSun, Xingping, Chang Chen, Lu Wang, Hongwei Kang, Yong Shen, and Qingyi Chen. 2019. "Hybrid Optimization Algorithm for Bayesian Network Structure Learning" Information 10, no. 10: 294. https://doi.org/10.3390/info10100294





