Linear Offset-Free Model Predictive Control in the Dynamic PLS Framework
Abstract
1. Introduction
2. DyPLS Framework and Control Scheme
2.1. DyPLS Modeling
2.2. Controller Design in the DyPLS Framework
3. Offset-Free Model Predictive Control in the DyPLS Framework
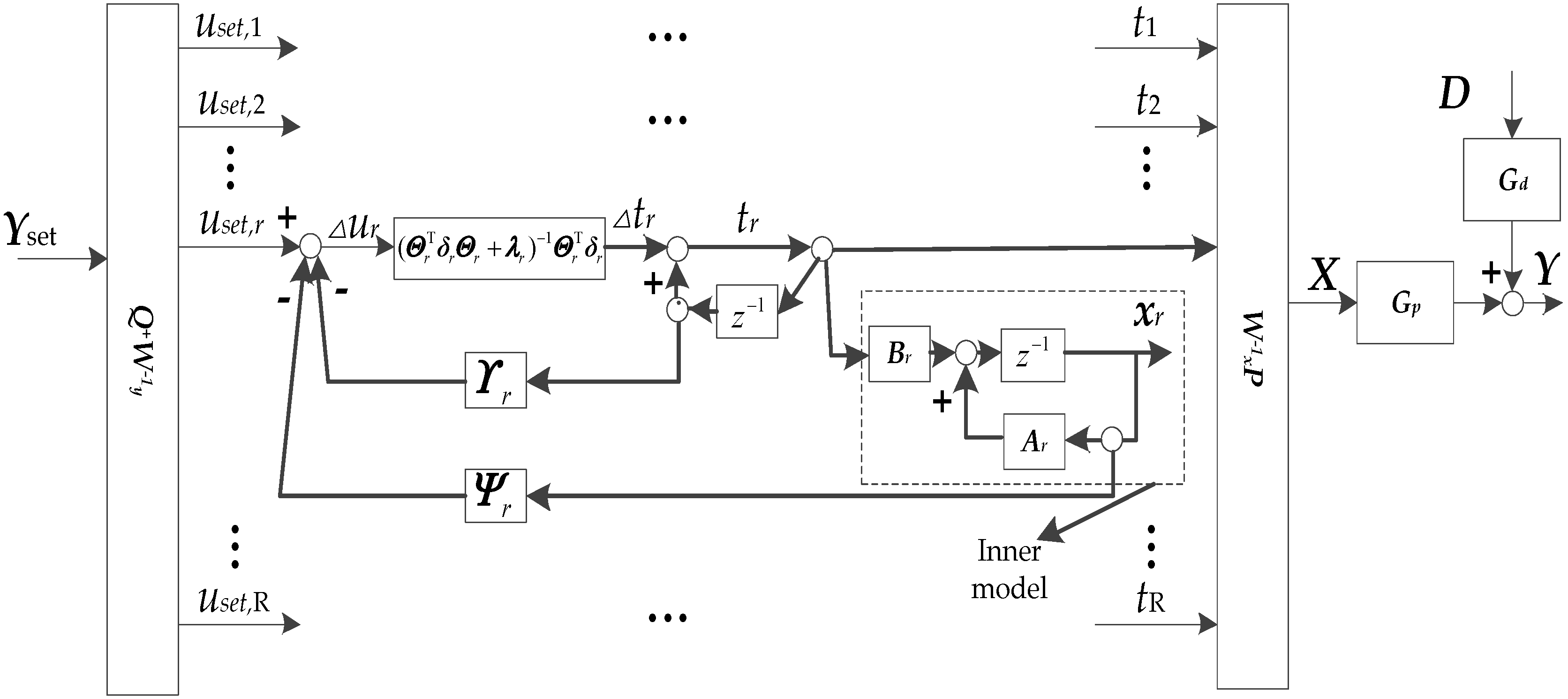
3.1. State Space-Based MPC in the DyPLS Framework
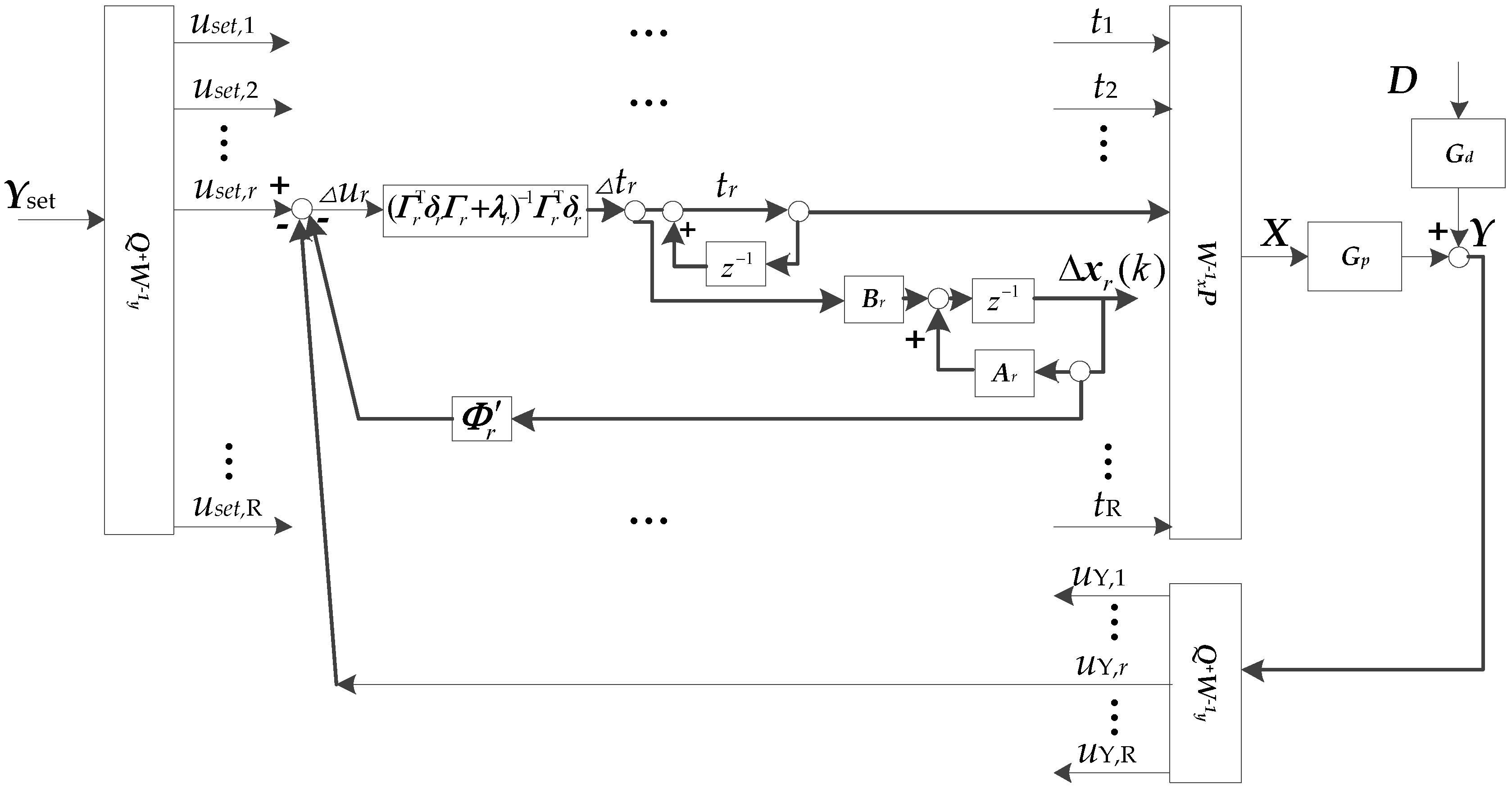
3.2. Offset-free MPC Method A
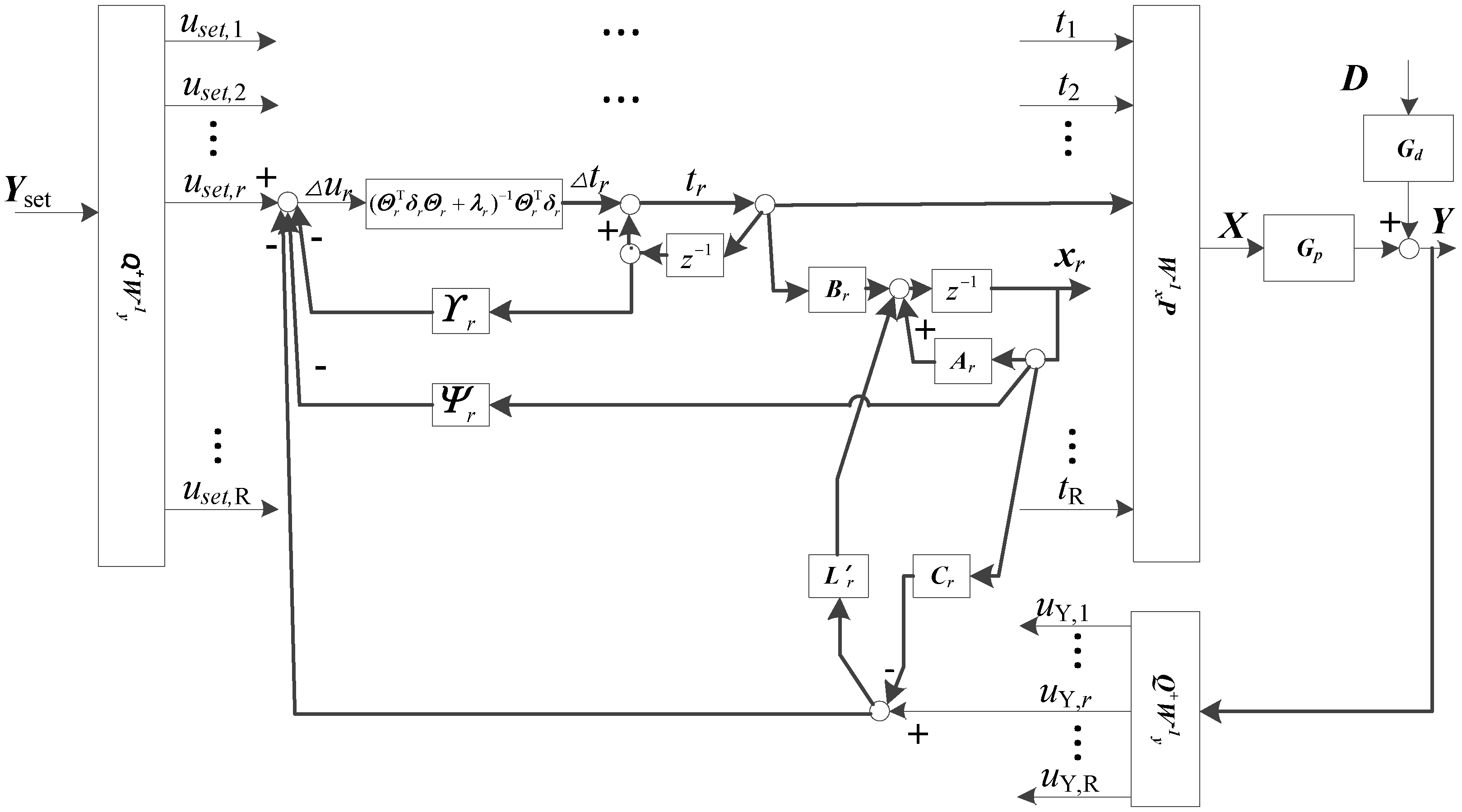
3.3. Offset-free MPC Method B
4. Case Study
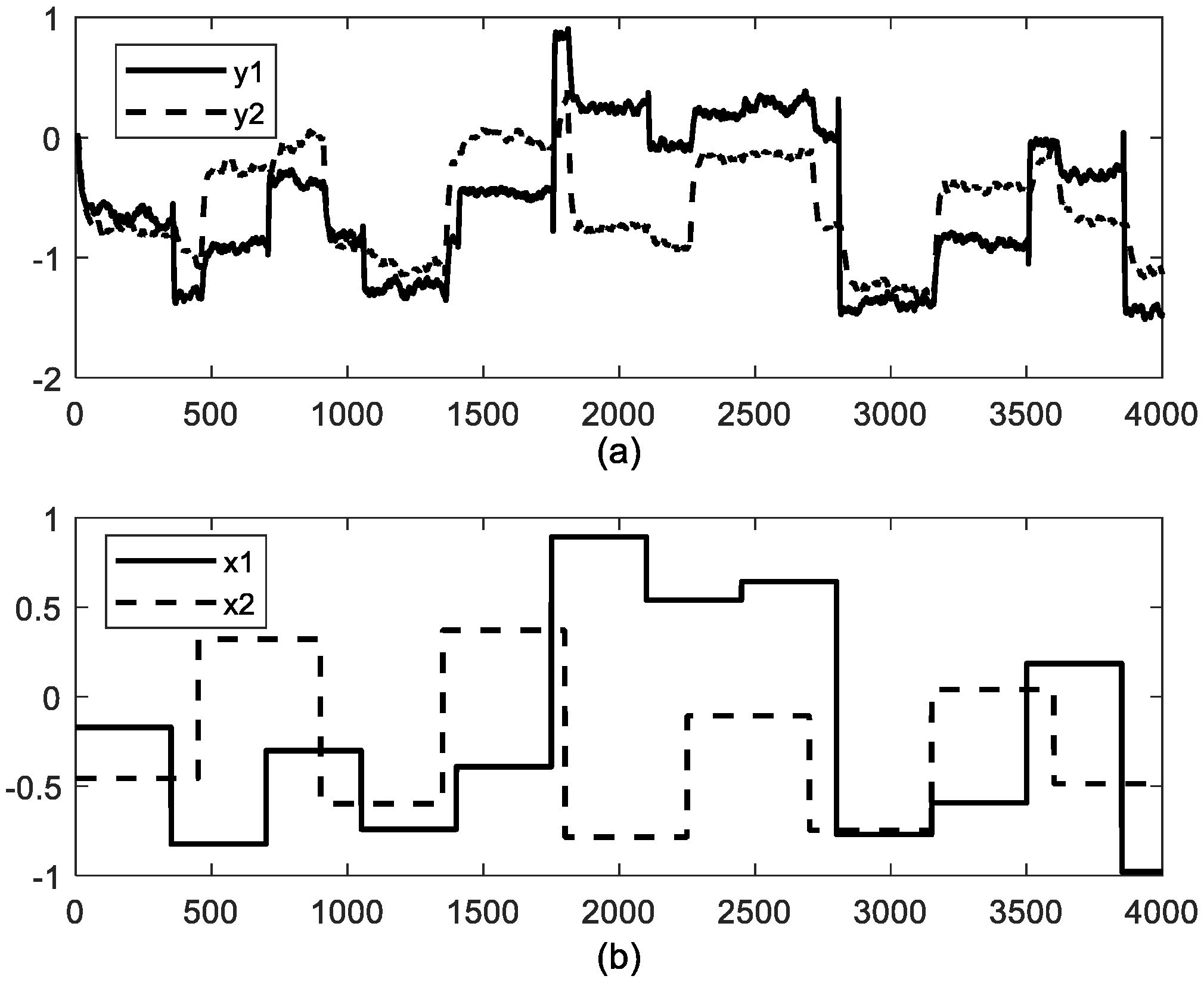
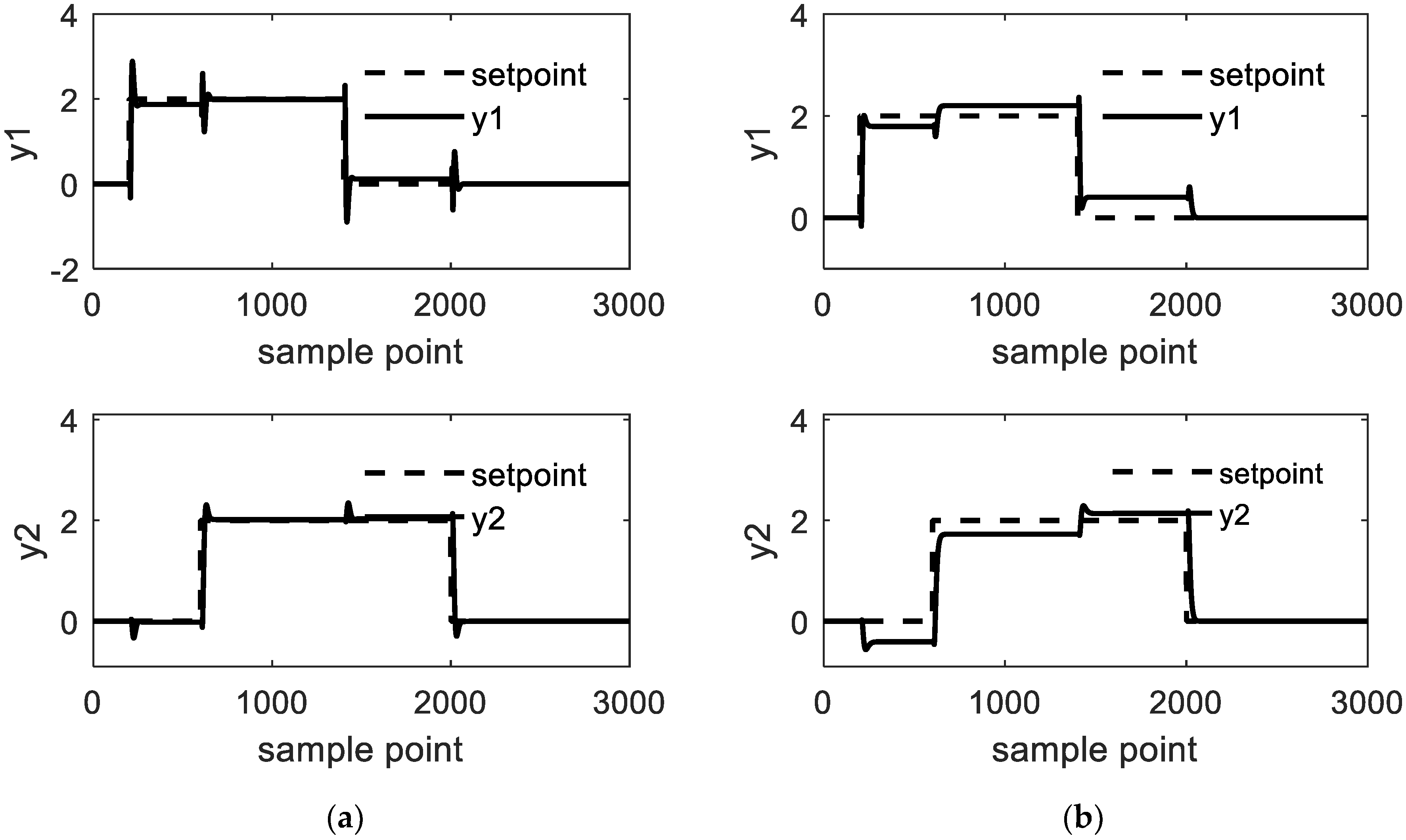
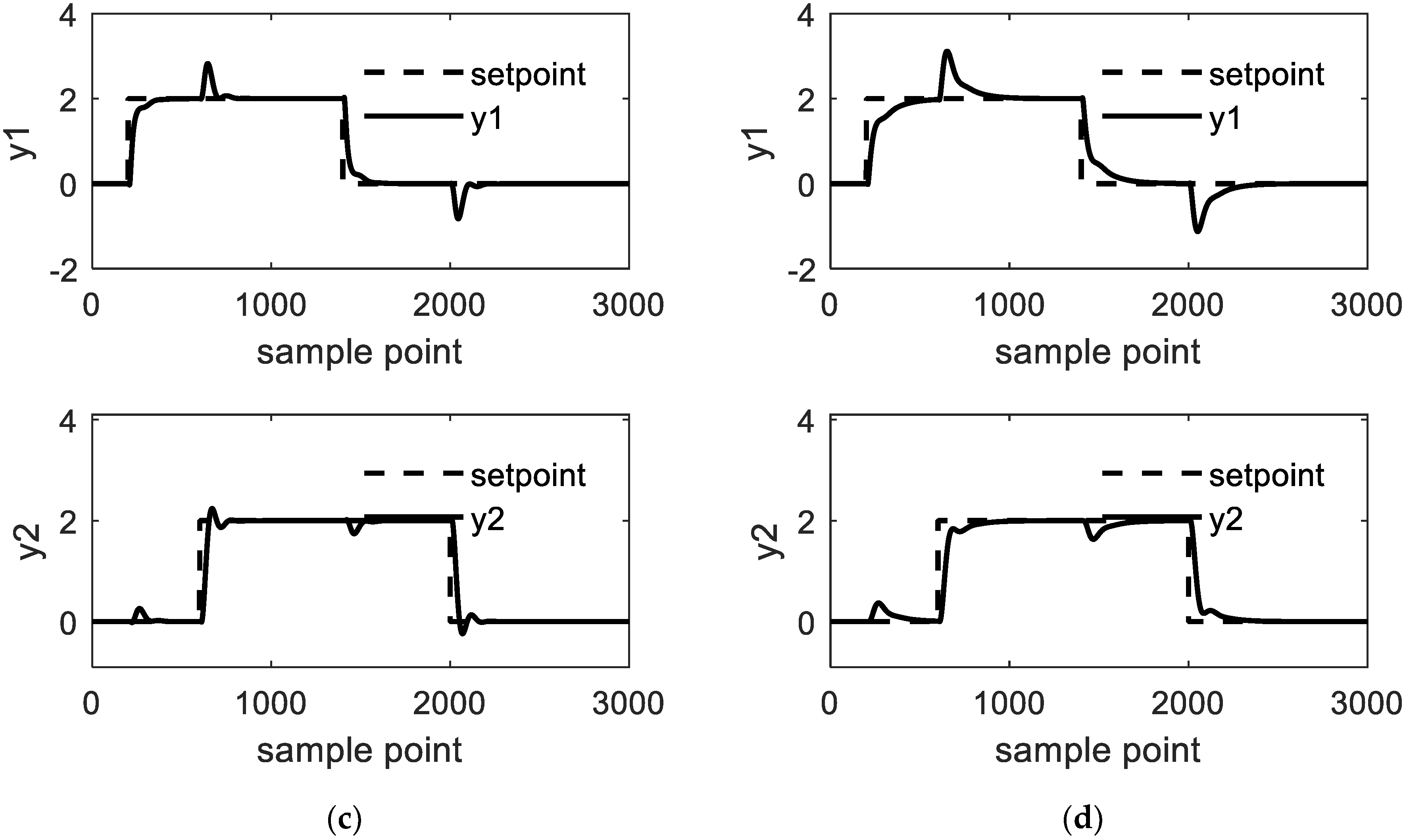
4.1. Study Case 1: Jerome-Ray Distillation Column
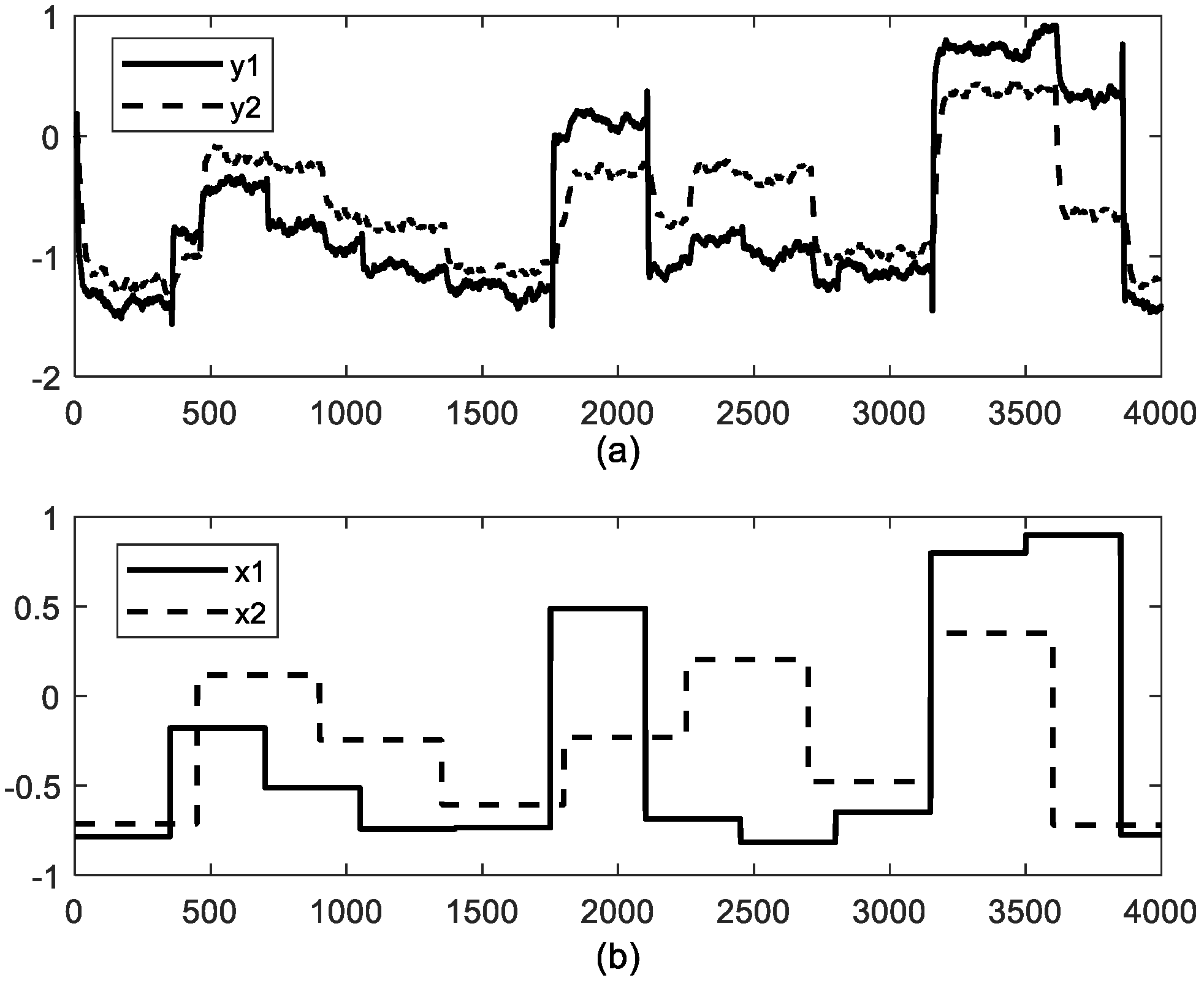
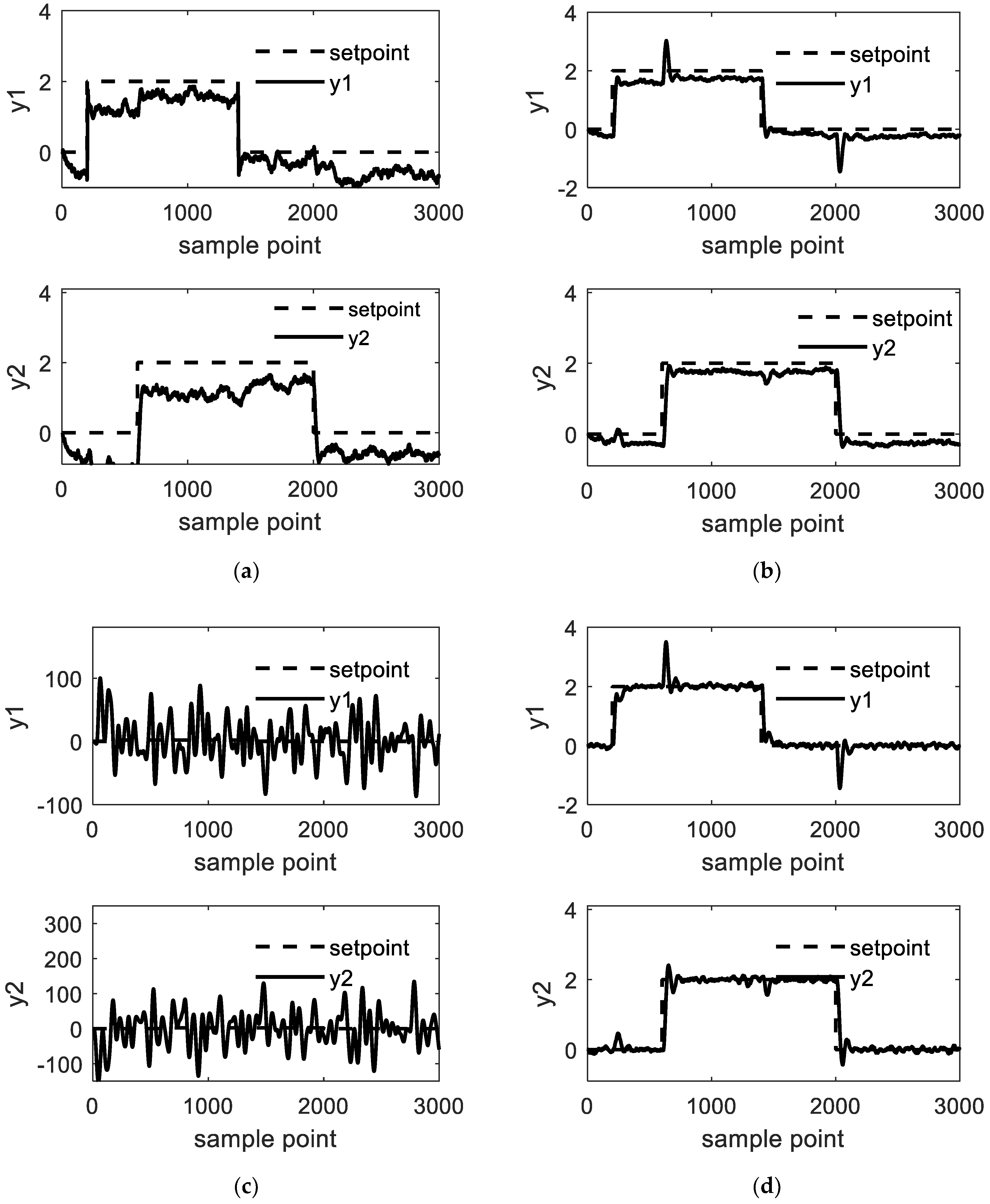
4.2. Study Case 2: Industrial Polyethylene Reaction
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Clarke, D.W.; Mohtadi, C.; Tuffs, P.S. Generalized perdictive control 1. The basic algorithm. Automatica 1987, 23, 137–148. [Google Scholar] [CrossRef]
- Muske, K.R.; Rawlings, J.B. Model predictive control with linear-models. AIChE J. 1993, 39, 262–287. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Ljung, L. System identification—Theory for the User. Prentice Hall Information and System Sciences Series, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Wang, X.; Ding, B.; Yang, X.; Ye, Z. Design and application of offset-free model predictive control disturbance observation method. J. Control Sci. Eng. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Askari, M.; Moghavvemi, M.; Almurib, H.A.F.; Muttaqi, K.M. Multivariable offset-free model predictive control for quadruple tanks system. IEEE Trans. Ind. Appl. 2016, 52, 1882–1890. [Google Scholar] [CrossRef]
- Paulson, J.A.; Xie, L.; Mesbah, A. Offset-free robust mpc of systems with mixed stochastic and deterministic uncertainty. IFAC-PapersOnLine 2017, 50, 3530–3535. [Google Scholar] [CrossRef]
- Betti, G.; Farina, M.; Scattolini, R. A robust mpc algorithm for offset-free tracking of constant reference signals. IEEE Trans. Autom. Control 2013, 58, 2394–2400. [Google Scholar] [CrossRef]
- Yao, Y.; Gao, F. A survey on multistage/multiphase statistical modeling methods for batch processes. Annu. Rev. Control 2009, 33, 172–183. [Google Scholar] [CrossRef]
- Dong, Y.; Qin, S.J. Dynamic-inner partial least squares for dynamic data modeling. IFAC-PapersOnLine 2015, 48, 117–122. [Google Scholar] [CrossRef]
- Kaspar, M.H.; Ray, W.H. Dynamic pls modelling for process control. Chem. Eng. Sci. 1993, 48, 3447–3461. [Google Scholar] [CrossRef]
- Chi, Q.; Fei, Z.; Liu, K.; Liang, J. Latent-variable nonlinear model predictive control strategy for a ph neutralization process. Asian J. Control 2015, 17, 2427–2434. [Google Scholar] [CrossRef]
- Chen, J.; Cheng, Y.-C.; Yea, Y. Multiloop pid controller design using partial least squares decoupling structure. Korean J. Chem. Eng. 2005, 22, 173–183. [Google Scholar] [CrossRef]
- LÜ, Y.; Liang, J. Multi-loop constrained iterative model predictive control using arx -pls decoupling structure. Chin. J. Chem. Eng. 2013, 21, 1129–1143. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, M.; Chen, J.; Xu, J.; Li, K. Pls-based multi-loop robust h 2 control for improvement of operating efficiency of waste heat energy conversion systems with organic rankine cycle. Energy 2017, 123, 460–472. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, M.; Chen, J.; Li, K.; Xu, J. Multiloop robust h ∞ control design based on the dynamic pls approach to chemical processes. Chem. Eng. Res. Des. 2015, 100, 518–529. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, H.; Pu, J.; Hou, G. Model predictive control based on the dynamic pls approach to waste heat recovery system. In Advanced Computational Methods in Energy, Power, Electric Vehicles, and Their Integration; Springer: Singapore, 2017; pp. 509–518. [Google Scholar]
- Xin, J.; Yue, W.; Lin, L. Offset free tracking predictive control based on dynamic pls framework. Information 2017, 8, 121. [Google Scholar] [CrossRef]
- Tatjewski, P. Disturbance modeling and state estimation for offset-free predictive control with state-space process models. Int. J. Appl. Math. Comput. Sci. 2014, 24, 313–323. [Google Scholar] [CrossRef]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Qin, S.J.; McAvoy, T.J. Nonlinear pls modeling using neural networks. Comput. Chem. Eng. 1992, 16, 379–391. [Google Scholar] [CrossRef]
- Lakshminaravanan, S.; Shah, S.L.; Nandakumar, K. Modeling and control of multivariable processes: Dynamic pls approach. AIChE J. 1997, 43, 2307–2322. [Google Scholar] [CrossRef]
- Huusom, J.K.; Poulsen, N.K.; Jorgensen, S.B.; Jorgensen, J.B. Tuning siso offset-free model predictive control based on arx models. J. Process Control 2012, 22, 1997–2007. [Google Scholar] [CrossRef]
- Laurí, D.; Salcedo, J.V.; Martínez, M.; García-Nieto, S. Model predictive control relevant identification: Multiple input multiple output against multiple input single output. IET Control Theory Appl. 2010, 4, 1756–1766. [Google Scholar] [CrossRef]
- Mori, J.; Yu, J. A quality relevant non-gaussian latent subspace projection method for chemical process monitoring and fault detection. AIChE J. 2014, 60, 485–499. [Google Scholar] [CrossRef]
- Chi, Q.; Fei, Z.; Zhao, Z.; Zhao, L.; Liang, J. A model predictive control approach with relevant identification in dynamic pls framework. Control Eng. Pract. 2014, 22, 181–193. [Google Scholar] [CrossRef]
- Wang, L. A tutorial on model predictive control: Using a linear velocity-form model. Dev. Chem. Eng. Miner. Process. 2004, 12, 573–614. [Google Scholar] [CrossRef]
- Betti, G.; Farina, M.; Scattolini, R.; IEEE. An mpc algorithm for offset-free tracking of constant reference signals. In Proceedings of the 2012 IEEE 51st Annual Conference on Decision and Control, Maui, HI, USA, 10–13 December 2012; pp. 5182–5187. [Google Scholar]
- Maciejowski, J.M. Predictive Control: With Constraints; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Maeder, U.; Borrelli, F.; Morari, M. Linear offset-free model predictive control. Automatica 2009, 45, 2214–2222. [Google Scholar] [CrossRef]
- Jerome, N.F.; Ray, W.H. High-performance multivariable control strategies for systems having time delays. AIChE J. 1986, 32, 914–931. [Google Scholar] [CrossRef]
- Zhao, Z.; Hu, B.; Liang, J. Multi-loop adaptive internal model control based on a dynamic partial least squares model. J. Zhejiang Univ.-Sci. A 2011, 12, 190–200. [Google Scholar] [CrossRef]
- Embirucu, M.; Fontes, C. Multirate multivariable generalized predictive control and its application to a slurry reactor for ethylene polymerization. Chem. Eng. Sci. 2006, 61, 5754–5767. [Google Scholar] [CrossRef]

| (na, nb) | (1,1) | (2,2) | (3,3) | (4,4) | (5,5) | (6,6) | (7,7) | (8,8) | (9,9) |
|---|---|---|---|---|---|---|---|---|---|
| φ(r = 1) | 802.35 | 805.49 | 806.92 | 806.27 | 805.32 | 804.62 | 805.53 | 804.63 | 803.88 |
| φ(r = 2) | 549.53 | 538.15 | 538.97 | 538.02 | 537.54 | 537.39 | 541.68 | 537.99 | 538.32 |
| SMPC | SMDP | OSMDP1 | OSMDP2 | |
|---|---|---|---|---|
| Np | 9 | 6 | 6 | 6 |
| Nu | 5 | 5 | 5 | 5 |
| Computing time (ms) | 406.01 | 386.36 | 283.45 | 385.52 |
| Number of Latent Variable | (na, nb) | |||
|---|---|---|---|---|
| (2,2) | (4,4) | (6,6) | (8,8) | |
| 2 | 8975.50 | 8976.50 | 8977.00 | 8961.8 |
| 3 | 1195.2 | 1193.5 | 1182.4 | 1187.6 |
| 4 | 126.88 | 114.67 | 128.3 | 130.08 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, L.; Wu, Z.; Jin, X.; Wang, Y. Linear Offset-Free Model Predictive Control in the Dynamic PLS Framework. Information 2019, 10, 5. https://doi.org/10.3390/info10010005
Hou L, Wu Z, Jin X, Wang Y. Linear Offset-Free Model Predictive Control in the Dynamic PLS Framework. Information. 2019; 10(1):5. https://doi.org/10.3390/info10010005
Chicago/Turabian StyleHou, Ligang, Ze Wu, Xin Jin, and Yue Wang. 2019. "Linear Offset-Free Model Predictive Control in the Dynamic PLS Framework" Information 10, no. 1: 5. https://doi.org/10.3390/info10010005
APA StyleHou, L., Wu, Z., Jin, X., & Wang, Y. (2019). Linear Offset-Free Model Predictive Control in the Dynamic PLS Framework. Information, 10(1), 5. https://doi.org/10.3390/info10010005






