Visual Object Tracking Robust to Illumination Variation Based on Hyperline Clustering
Abstract
1. Introduction
2. Related Work
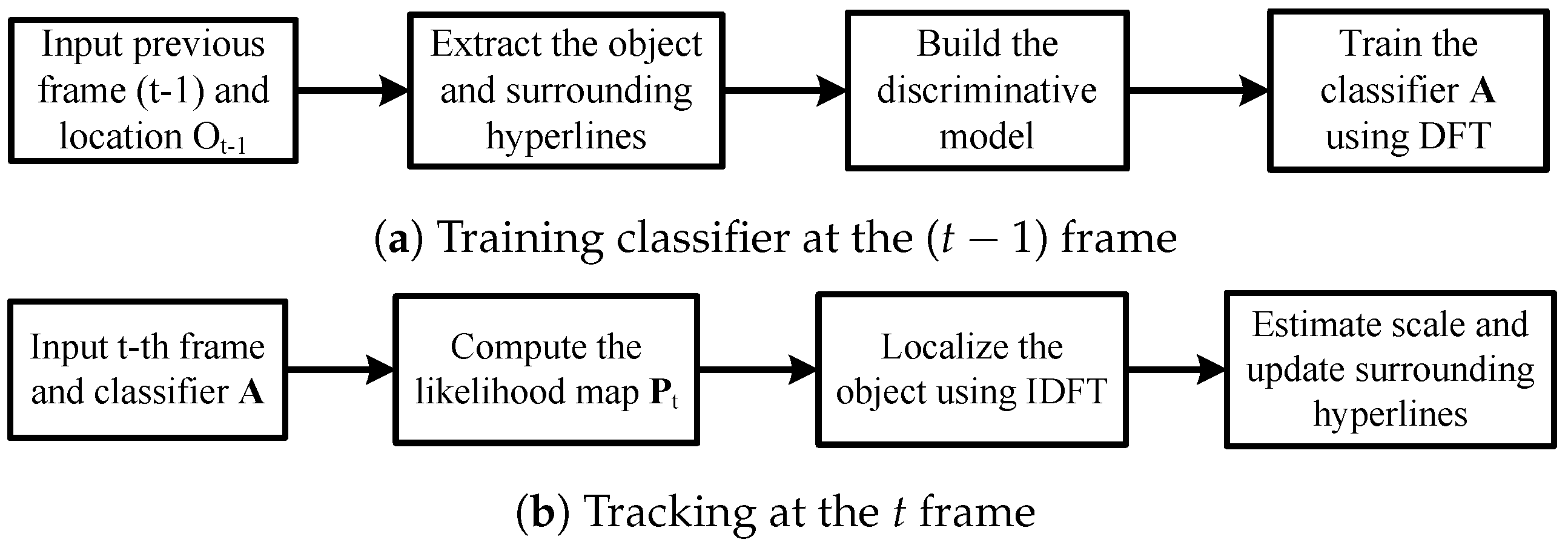
3. Hyperline Clustering-Based Tracking
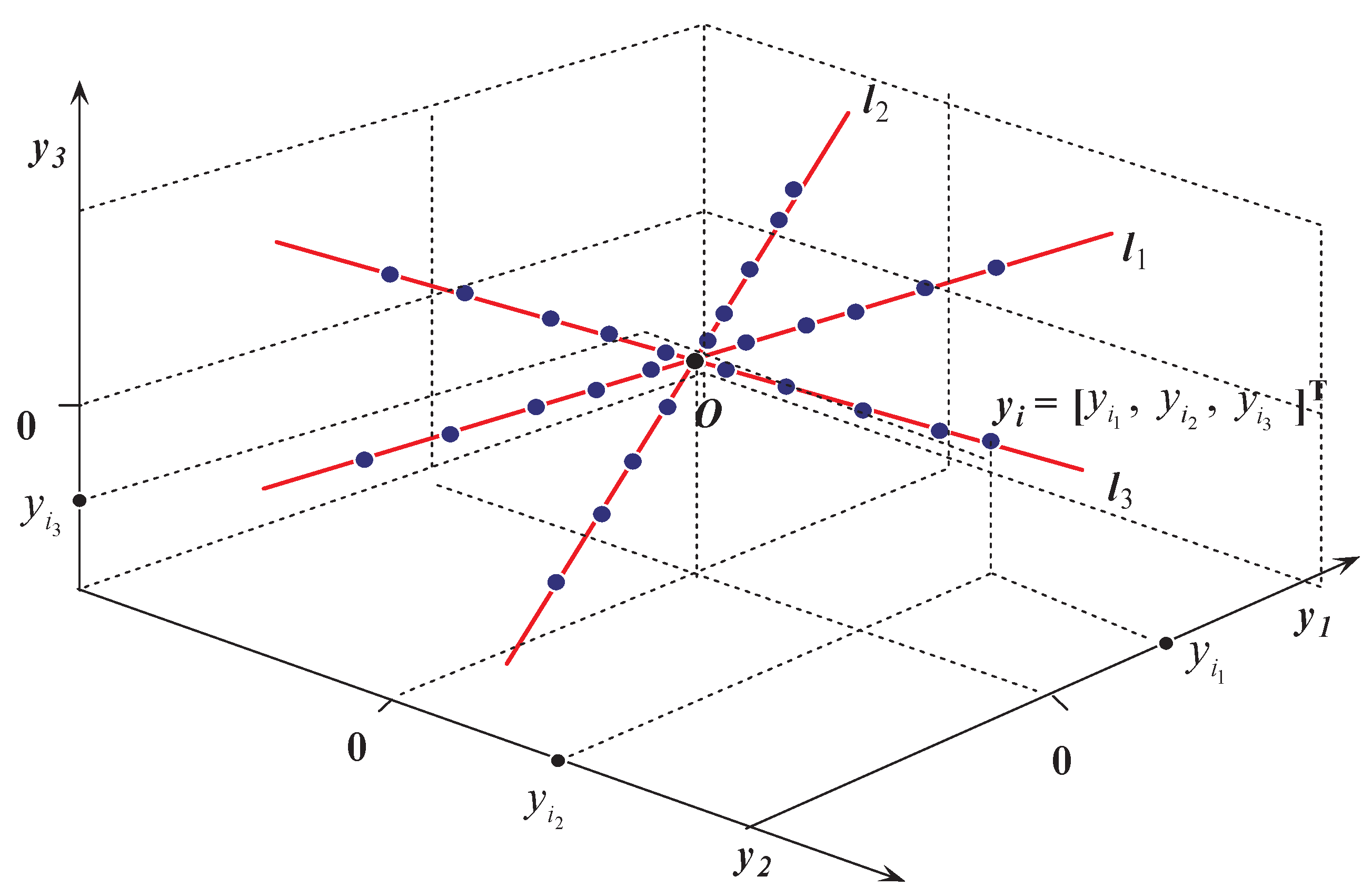
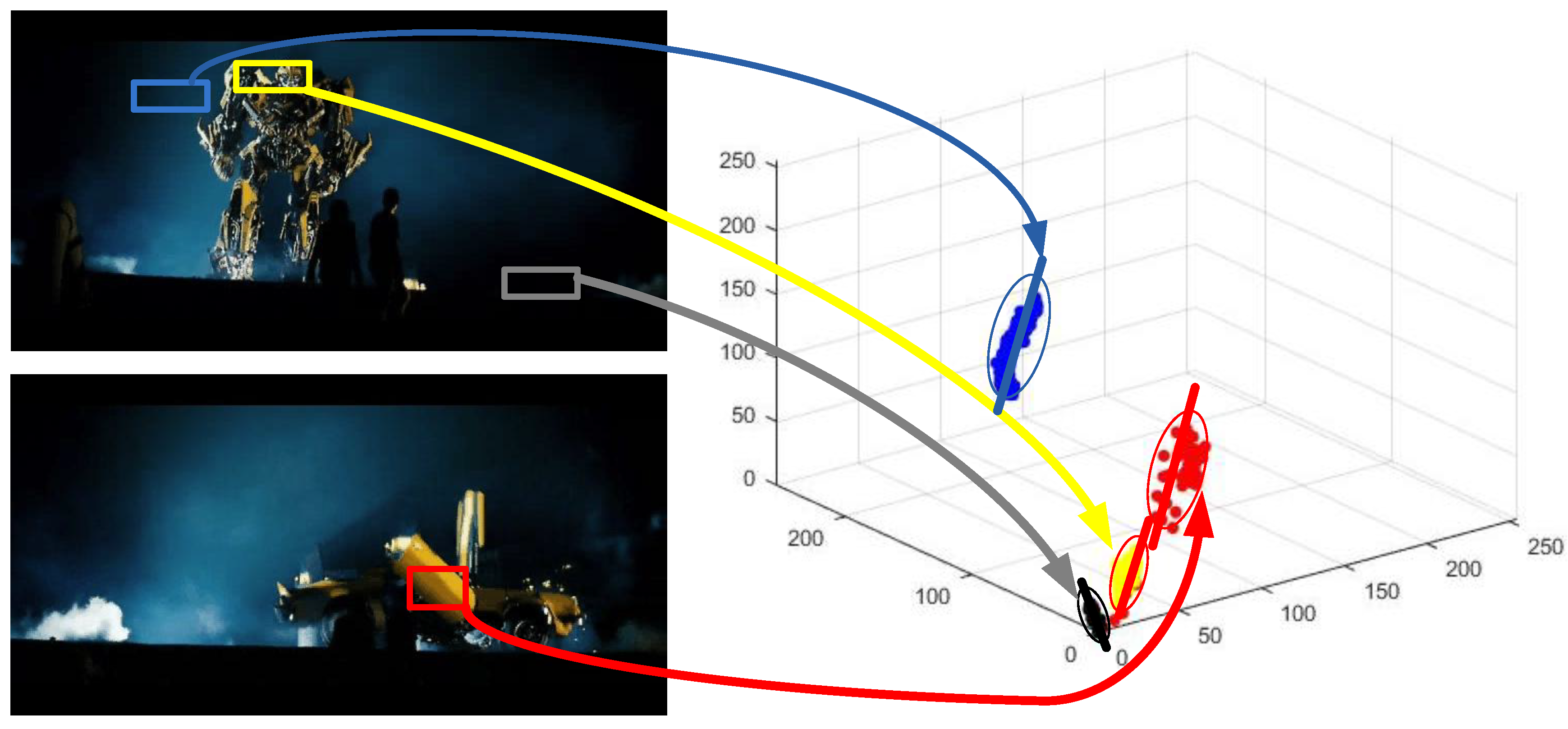
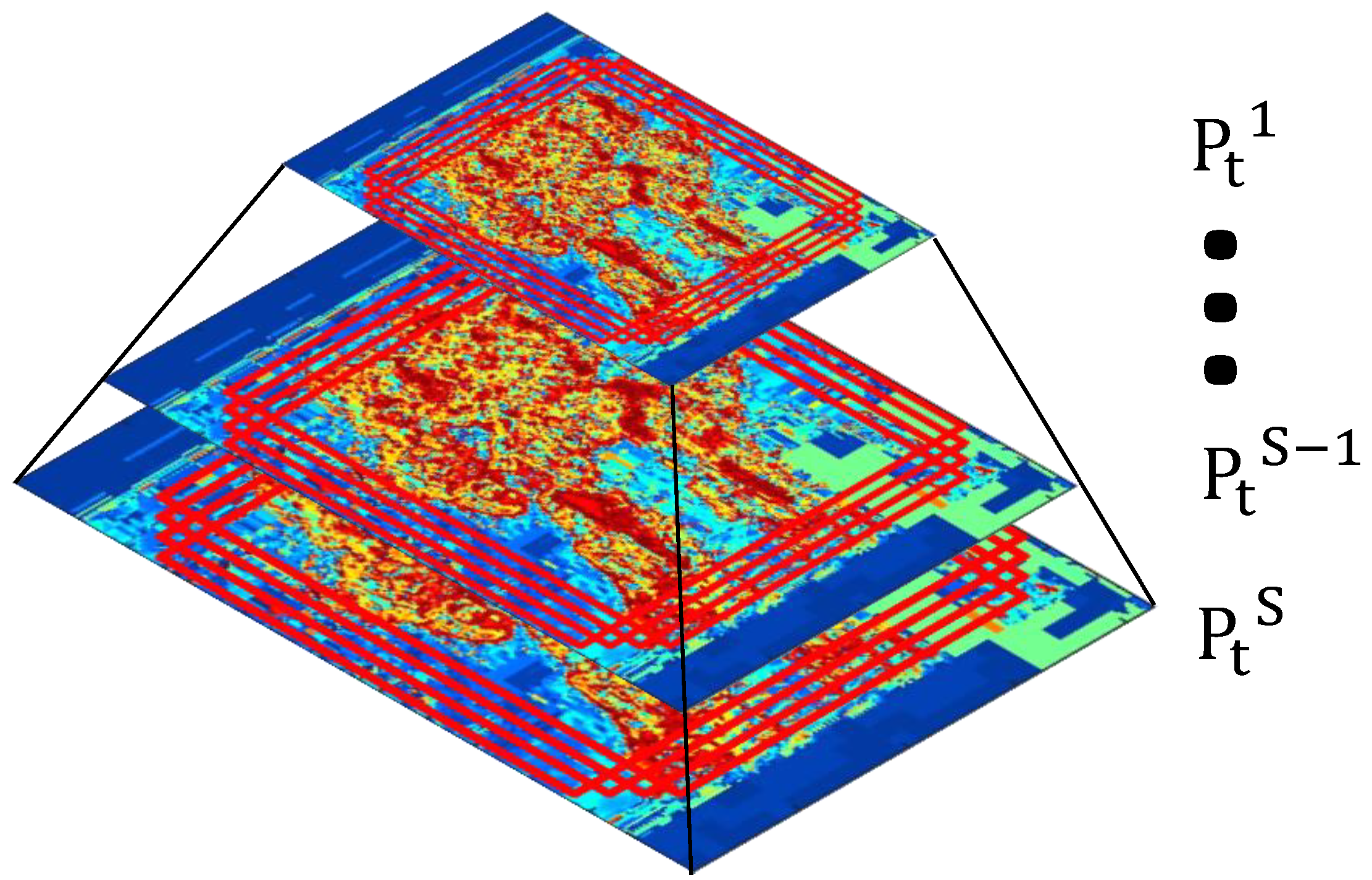
3.1. Hyperline Clustering Representation
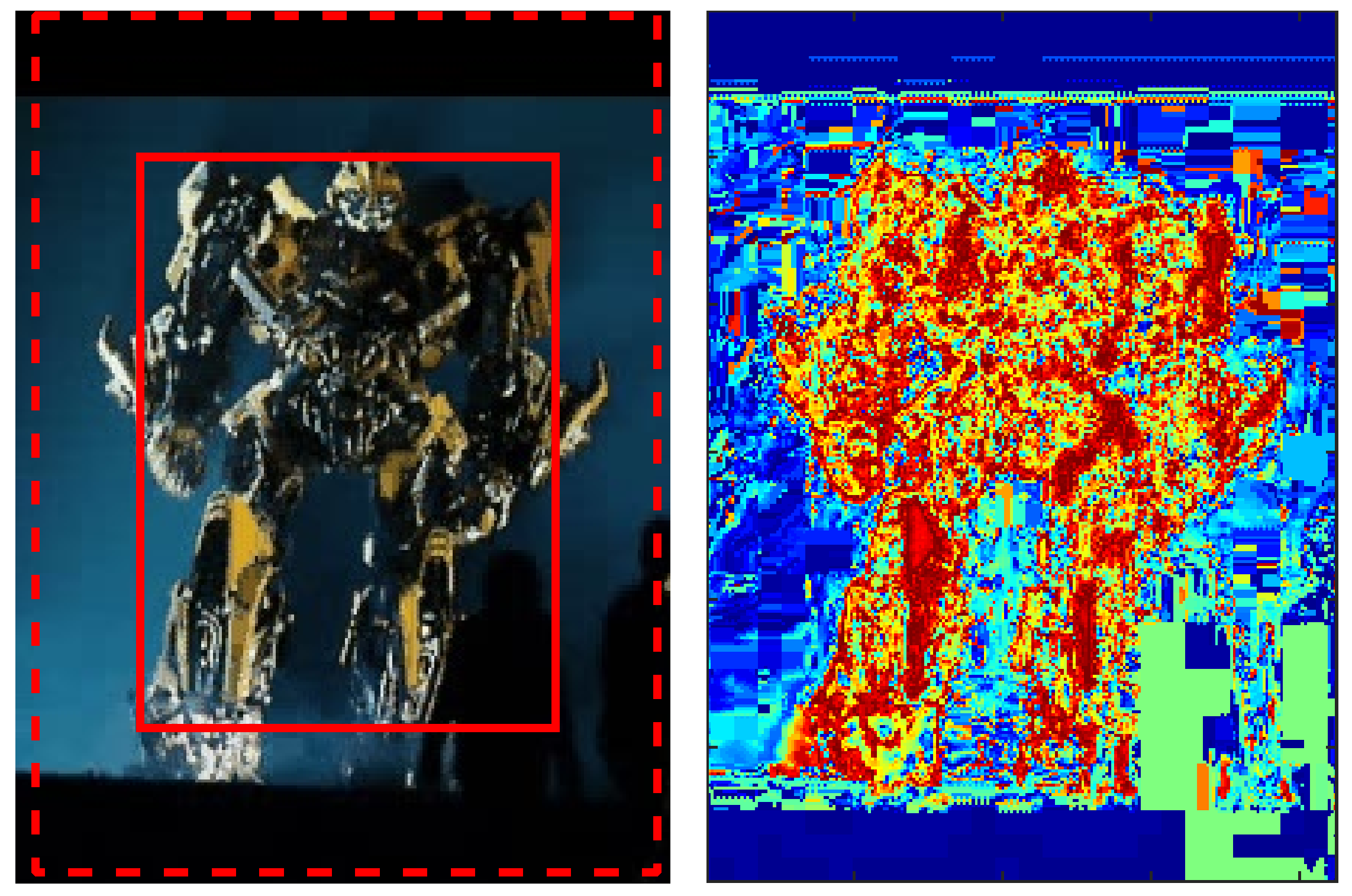
3.2. Discriminative Model
| Algorithm 1 The update scheme of surrounding hyperlines. |
|
3.3. Localization
3.4. Anchor Box Based Scale Estimation
4. Experiments
4.1. Implementation Details
4.2. Experiment Setup
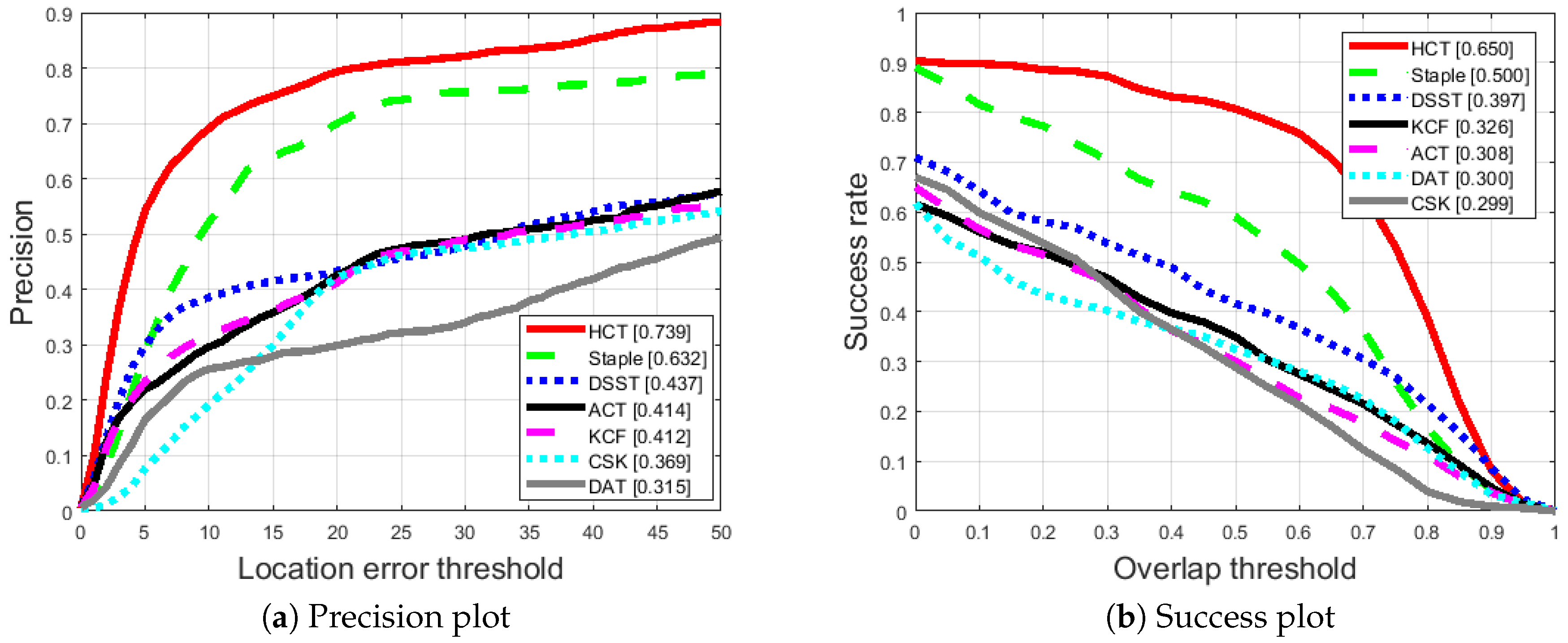
4.3. Comparison with State-of-the-Art
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Avidan, S. Ensemble tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 261–271. [Google Scholar] [CrossRef] [PubMed]
- Grabner, H.; Leistner, C.; Bischof, H. Semi-supervised On-Line Boosting for Robust Tracking. In Proceedings of the European Conference on Computer Vision (ECCV), Marseille, France, 12–18 October 2008; pp. 234–247. [Google Scholar]
- Babenko, B.; Yang, M.H.; Belongie, S. Robust object tracking with online multiple instance learning. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1619–1632. [Google Scholar] [CrossRef] [PubMed]
- Ciuonzo, D.; Buonanno, A.; D’Urso, M.; Palmieri, F.A.N. Distributed classification of multiple moving targets with binary wireless sensor networks. In Proceedings of the 14th International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 1–8. [Google Scholar]
- Buonanno, A.; D’Urso, M.; Prisco, G.; Felaco, M.; Meliadò, E.F.; Mattei, M.; Palmieri, F.; Ciuonzo, D. Mobile sensor networks based on autonomous platforms for homeland security. In Proceedings of the 2012 Tyrrhenian Workshop on Advances in Radar and Remote Sensing (TyWRRS), Naples, Italy, 12–14 September 2012; pp. 80–84. [Google Scholar] [CrossRef]
- Danelljan, M.; Khan, F.S.; Felsberg, M.; Weijer, J.V.D. Adaptive Color Attributes for Real-Time Visual Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1090–1097. [Google Scholar]
- Possegger, H.; Mauthner, T.; Bischof, H. In defense of color-based model-free tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2113–2120. [Google Scholar] [CrossRef]
- Ross, D.A.; Lim, J.; Lin, R.S.; Yang, M.H. Incremental Learning for Robust Visual Tracking. Int. J. Comput. Vis. 2008, 77, 125–141. [Google Scholar] [CrossRef]
- Zhong, W.; Lu, H.; Yang, M.H. Robust object tracking via sparse collaborative appearance model. IEEE Trans. Image Process. 2014, 23, 2356–2368. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhang, L.; Yang, M.H. Fast compressive tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 2002–2015. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Liu, P.; Du, Y.; Luo, Y.; Zhang, W. Correlation Tracking via Self-Adaptive Fusion of Multiple Features. Information 2018, 9, 241. [Google Scholar] [CrossRef]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-Speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Liu, F. Online Learning of Discriminative Correlation Filter Bank for Visual Tracking. Information 2018, 9, 61. [Google Scholar] [CrossRef]
- Bertinetto, L.; Valmadre, J.; Golodetz, S.; Miksik, O.; Torr, P.H.S. Staple: Complementary Learners for Real-Time Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1401–1409. [Google Scholar] [CrossRef]
- Wu, Y.; Lim, J.; Yang, M. Object Tracking Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Li, P.; Wen, H.; Xie, Y.; He, Z. K-Hyperline Clustering-Based Color Image Segmentation Robust to Illumination Changes. Symmetry 2018, 10, 610. [Google Scholar] [CrossRef]
- Comaniciu, D.; Ramesh, V.; Meer, P. Kernel-based object tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 564–577. [Google Scholar] [CrossRef]
- Sevilla-Lara, L.; Learned-Miller, E. Distribution fields for tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 1910–1917. [Google Scholar]
- Shen, C.; Kim, J.; Wang, H. Generalized kernel-based visual tracking. IEEE Trans. Circuits Syst. Video Technol. 2010, 20, 119–130. [Google Scholar] [CrossRef]
- Mei, X.; Ling, H.; Wu, Y.; Blasch, E.; Bai, L. Minimum error bounded efficient l1 tracker with occlusion detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 1257–1264. [Google Scholar]
- Liu, B.; Huang, J.; Kulikowski, C.; Yang, L. Robust visual tracking using local sparse appearance model and k-selection. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2968–2981. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Lu, H.; Yang, M.H. Robust superpixel tracking. IEEE Trans. Image Process. 2014, 23, 1639–1651. [Google Scholar] [CrossRef] [PubMed]
- Kristan, M.; Leonardis, A.; Matas, J.; Felsberg, M.; Pflugfelder, R.; Čehovin Zajc, L.; Vojir, T.; Häger, G.; Lukežič, A.; Fernandez, G. The Visual Object Tracking VOT2016 Challenge Results. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 191–217. [Google Scholar]
- Kristan, M.; Matas, J.; Leonardis, A.; Felsberg, M.; Cehovin, L.; Fernandez, G.; Vojir, T.; Hager, G.; Nebehay, G.; Pflugfelder, R. The Visual Object Tracking VOT2017 Challenge Results. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; pp. 1949–1972. [Google Scholar] [CrossRef]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Discriminative Scale Space Tracking. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1561–1575. [Google Scholar] [CrossRef] [PubMed]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. Exploiting the circulant structure of tracking-by-detection with kernels. In Proceedings of the European Conference on Computer Vision (ECCV), Florence, Italy, 7–13 October 2012; pp. 702–715. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 21–37. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1137–1149. [Google Scholar] [CrossRef] [PubMed]
- Xie, K.; He, Z.; Cichocki, A.; Fang, X. Rate of Convergence of the FOCUSS Algorithm. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 1276–1289. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Cichocki, A.; Li, Y.; Xie, S.; Sanei, S. K-hyperline clustering learning for sparse component analysis. Signal Process. 2009, 89, 1011–1022. [Google Scholar] [CrossRef]
- Swain, M.J.; Ballard, D.H. Color indexing. Int. J. Comput. Vis. 1991, 7, 11–32. [Google Scholar]
- Čehovin, L.; Leonardis, A.; Kristan, M. Robust visual tracking using template anchors. In Proceedings of the 2016 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Placid, NY, USA, 7–10 March 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Xu, Y.; Wang, J.; Miao, Z. Robust Scale Adaptive Kernel Correlation Filter Tracker with Hierarchical Convolutional Features. IEEE Signal Process. Lett. 2016, 23, 1136–1140. [Google Scholar] [CrossRef]
- Milan, A.; Leal-Taixé, L.; Reid, I.D.; Roth, S.; Schindler, K. MOT16: A Benchmark for Multi-Object Tracking. arXiv, 2016; arXiv:1603.00831. [Google Scholar]
- Ristani, E.; Solera, F.; Zou, R.; Cucchiara, R.; Tomasi, C. Performance Measures and a Data Set for Multi-target, Multi-camera Tracking. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 17–35. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Xie, Y.; Li, P.; Wen, H.; Luo, H.; He, Z. Visual Object Tracking Robust to Illumination Variation Based on Hyperline Clustering. Information 2019, 10, 26. https://doi.org/10.3390/info10010026
Yang S, Xie Y, Li P, Wen H, Luo H, He Z. Visual Object Tracking Robust to Illumination Variation Based on Hyperline Clustering. Information. 2019; 10(1):26. https://doi.org/10.3390/info10010026
Chicago/Turabian StyleYang, Senquan, Yuan Xie, Pu Li, Haoxiang Wen, Huan Luo, and Zhaoshui He. 2019. "Visual Object Tracking Robust to Illumination Variation Based on Hyperline Clustering" Information 10, no. 1: 26. https://doi.org/10.3390/info10010026
APA StyleYang, S., Xie, Y., Li, P., Wen, H., Luo, H., & He, Z. (2019). Visual Object Tracking Robust to Illumination Variation Based on Hyperline Clustering. Information, 10(1), 26. https://doi.org/10.3390/info10010026




