Quantum-Behaved Particle Swarm Optimization with Weighted Mean Personal Best Position and Adaptive Local Attractor
Abstract
:1. Introduction
2. Background
2.1. Paritcle Swarm Optimization
2.2. Quantum-Behaved Particle Swarm Optimization
2.3. Population Diversity
3. Quantum-Behaved Particle Swarm Optimization with Weighted Mean Personal Best Position and Adaptive Local Attractor (ALA-QPSO)
3.1. Weighted Mean Personal Best Position
3.2. Adaptive Local Attractor
3.3. Quantum-Behaved Particle Swarm Optimization with Adaptive Local Attractor (ALA-QPSO)
| Algorithm 1 ALA-QPSO |
|
4. Experiments and Discussion
4.1. Benchmark Functions
4.2. Experimental Settings
4.3. Results and Discussions
4.3.1. Comparison of the Solution Accuracy and Stability
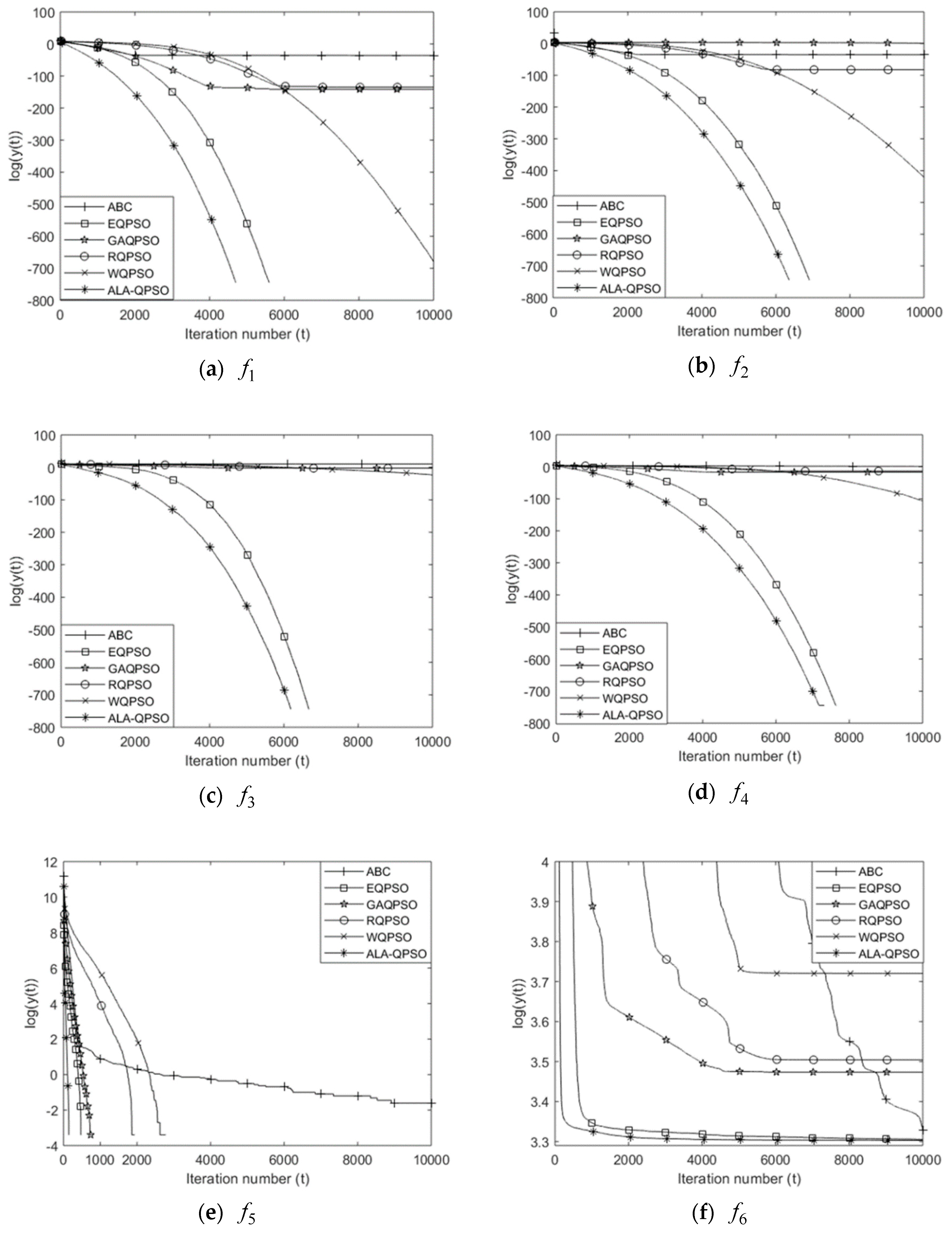
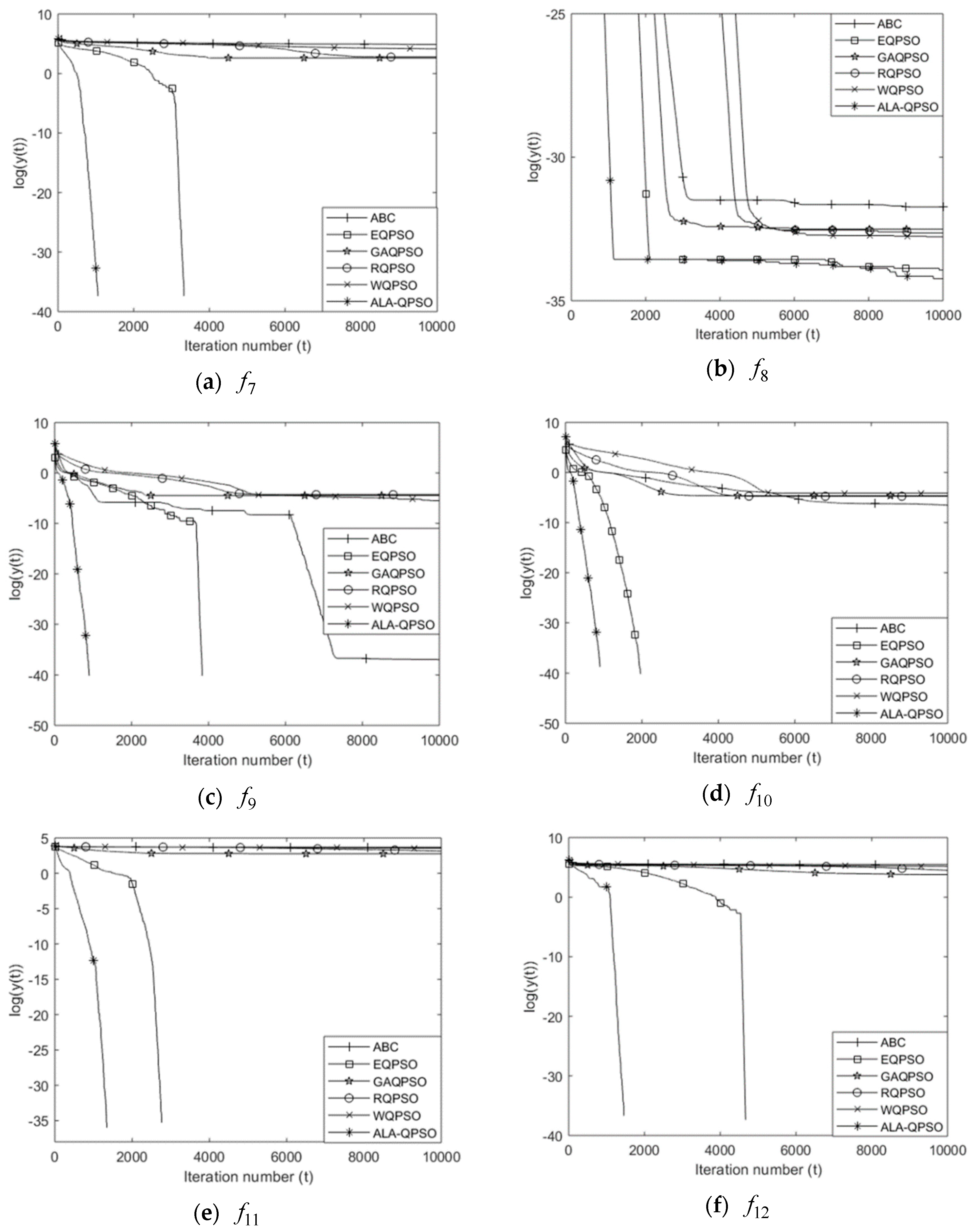
4.3.2. Comparison of the Convergence Speed and Reliability
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks, Nagoya, Japan, 4–6 October 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Ji, G.L. A comprehensive survey on particle swarm optimization algorithm and its applications. Math. Probl. Eng. 2015, 2015, 38. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Wang, S.H.; Sui, Y.X.; Yang, M.; Liu, B.; Cheng, H.; Sun, J.D.; Jia, W.J.; Phillips, P.; Gorriz, J. Multivariate approach for Alzheimer’s disease detection using stationary wavelet entropy and predator-prey particle swarm optimization. J. Alzheimers Dis. 2018, 65, 855–869. [Google Scholar] [CrossRef] [PubMed]
- Tian, D.P.; Shi, Z.Z. MPSO: Modified particle swarm optimization and its applications. Swarm Evol. Comput. 2018, 41, 49–68. [Google Scholar] [CrossRef]
- Nickabadi, A.; Ebadzadeh, M.M.; Safabakhsh, R. A novel particle swarm optimization algorithm with adaptive inertia weight. Appl. Soft Comput. 2011, 11, 3658–3670. [Google Scholar] [CrossRef]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evolut. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Sun, J.; Xu, W.B.; Feng, B. A global search strategy of quantum-behaved particle swarm optimization. In Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems, Singapore, 1–3 December 2004; pp. 111–116. [Google Scholar]
- Sun, J.; Feng, B.; Xu, W.B. Particle swam optimization with particles having quantum behavior. In Proceedings of the 2004 IEEE Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; pp. 326–331. [Google Scholar]
- Zhang, Y.D.; Ji, G.L.; Yang, J.Q.; Wang, S.H.; Dong, Z.C. Preliminary research on abnormal brain detection by wavelet-energy and quantum-behaved PSO. Biomed. Eng. 2016, 61, 431–441. [Google Scholar] [CrossRef]
- Li, L.L.; Jiao, L.C.; Zhao, J.Q.; Shang, R.H.; Gong, M.G. Quantum-behaved discrete multi-objective particle swarm optimization for complex network clustering. Pattern Recogn. 2017, 63, 1–14. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T. Multi-objective quantum-behaved particle swarm optimization for economic environmental hydrothermal energy system scheduling. Energy 2017, 131, 165–178. [Google Scholar] [CrossRef]
- Fang, W.; Sun, J.; Wu, X.; Palade, V. Adaptive web QoS controller based on online system identification using quantum-behaved particle swarm optimization. Soft Comput. 2015, 19, 1715–1725. [Google Scholar] [CrossRef]
- Sing, M.R.; Mahapatra, S.S. A quantum behaved particle swarm optimization for flexible job shop scheduling. Comput. Ind. Eng. 2016, 93, 36–44. [Google Scholar] [CrossRef]
- Tang, D.; Cai, Y.; Xue, Y. A quantum-behaved particle swarm optimization with memetic algorithm and memory for continuous non-linear large scale problems. Inf. Sci. 2014, 289, 162–189. [Google Scholar] [CrossRef]
- Yang, Z.L.; Wu, A.; Min, H.Q. An improved quantum-behaved particle swarm optimization algorithm with elitist breeding for unconstrained optimization. Comput. Intell. Neurosci. 2015, 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Fang, W.; Palade, V.; Wu, X.J.; Xu, W.B. Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point. Appl. Math. Comput. 2011, 218, 3763–3775. [Google Scholar] [CrossRef]
- Jia, P.; Duan, S.; Yan, J. An enhanced quantum-behaved particle swarm optimization based on a novel computing way of local attractor. Information 2015, 6, 633–649. [Google Scholar] [CrossRef]
- Han, F.; Liu, Q. A diversity-guided hybrid particle swarm optimization algorithm based on gradient search. Neurocomputing 2014, 137, 234–240. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Lu, Z.S.; Hou, Z.R.; Du, J. Particle swarm optimization with adaptive mutation. Front. Electr. Electron. Eng. China 2006, 1, 99–104. [Google Scholar] [CrossRef]
- Chen, K.; Zhou, F.Y.; Liu, A.L. Chaotic dynamic weight particle swarm optimization for numerical function optimization. Knowl-Based Syst. 2018, 139, 23–40. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A modified Artificial Bee Colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar]
- Xi, M.L.; Sun, J.; Xu, W.B. An improved quantum-behaved particle swarm optimization algorithm with weighted mean best position. Appl. Math. Comput. 2008, 205, 751–759. [Google Scholar] [CrossRef]
- Zhang, L.P.; Yu, H.J.; Hu, S.X. Optimal choice of parameters for particle swarm optimization. J. Zhejiang Univ. Sci. 2005, 6, 528–534. [Google Scholar]
- Ye, W.X.; Feng, W.Y.; Fan, S.H. A novel multi-swarm particle swarm optimization with dynamic learning strategy. Appl. Soft Comput. 2017, 61, 832–843. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 675–701. [Google Scholar] [CrossRef]
| Group | Name | Test Function 1 | Search Space | Global opt. | |
|---|---|---|---|---|---|
| Unimodal | Sphere | 0 | |||
| Schwefel’s 2.22 | 0 | ||||
| Schwefel’s 1.2 | 0 | ||||
| Schwefel’s 2.21 | 0 | ||||
| Step | 0 | ||||
| Multimodal | Rosenbrock | 0 | |||
| Rastrigin | 0 | ||||
| Ackley | 0 | ||||
| Griewank | 0 | ||||
| Rotated | Rotated Griewank | , is an orthogonal matrix. | 0 | ||
| Rotated Weierstrass | , is an orthogonal matrix. | 0 | |||
| Rotated Rastrigin | , is an orthogonal matrix. | 0 |
| Criteria | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO | |
|---|---|---|---|---|---|---|---|
| Mean | 3.2115 × 10−16 | 0 | 4.3697 × 10−62 | 3.0586 × 10−59 | 1.0489 × 10−295 | 0 | |
| SD | 6.4479 × 10−17 | 0 | 2.3700 × 10−61 | 9.3210 × 10−59 | 0 | 0 | |
| Mean | 6.5535 × 10−16 | 0 | 2.6295 | 1.8088 × 10−36 | 1.9995 × 10−183 | 0 | |
| SD | 7.4422 × 10−17 | 0 | 9.6839 × 10−1 | 9.8507 × 10−36 | 0 | 0 | |
| Mean | 2.5595 × 104 | 0 | 9.4301 × 10−2 | 6.8640 × 10−2 | 5.8909 × 10−11 | 0 | |
| SD | 3.4939 × 103 | 0 | 8.8509 × 10−2 | 7.5320 × 10−2 | 1.5317 × 10−10 | 0 | |
| Mean | 3.1831 | 0 | 4.8093 × 10−8 | 1.3798 × 10−6 | 6.8607 × 10−47 | 0 | |
| SD | 2.1421 | 0 | 6.9539 × 10−8 | 2.0440 × 10−6 | 3.0515 × 10−46 | 0 | |
| Mean | 2.0000 × 10−1 | 0 | 0 | 0 | 0 | 0 | |
| SD | 4.0684 × 10−1 | 0 | 0 | 0 | 0 | 0 | |
| Mean | 2.7875 × 101 | 2.7256 × 101 | 3.2247 × 101 | 3.3247 × 101 | 4.1283 × 101 | 2.7188 × 101 | |
| SD | 2.4684 × 101 | 3.4765 × 10−2 | 2.1339 × 101 | 2.2535 × 101 | 3.0141 × 101 | 2.0527 × 10−1 | |
| Mean | 1.3148 × 102 | 0 | 1.3565 × 101 | 1.5995 × 101 | 6.2577 × 101 | 0 | |
| SD | 3.9721 × 101 | 0 | 3.7272 | 4.1657 | 2.8038 × 101 | 0 | |
| Mean | 1.6520 × 10−14 | 1.8356 × 10−15 | 7.6383 × 10−15 | 6.6909 × 10−15 | 5.8620 × 10−15 | 1.3619 × 10−15 | |
| SD | 3.2788 × 10−15 | 1.5283 × 10−15 | 2.8908 × 10−15 | 1.8027 × 10−15 | 1.0840 × 10−15 | 1.7413 × 10−15 | |
| Mean | 8.5117 × 10−17 | 0 | 1.1383 × 10−2 | 1.3693 × 10−2 | 4.1262 × 10−3 | 0 | |
| SD | 8.5915 × 10−17 | 0 | 1.6879 × 10−2 | 1.4073 × 10−2 | 7.9803 × 10−3 | 0 | |
| Mean | 1.4624 × 10−3 | 0 | 9.8340 × 10−3 | 8.7590 × 10−3 | 1.6271 × 10−2 | 0 | |
| SD | 4.1486 × 10−3 | 0 | 1.5979 × 10−2 | 1.5123 × 10−2 | 2.3173 × 10−2 | 0 | |
| Mean | 3.9661 × 101 | 0 | 1.5813 × 101 | 2.2942 × 101 | 3.4979 × 101 | 0 | |
| SD | 1.0377 | 0 | 3.3834 | 7.3531 | 4.7694 | 0 | |
| Mean | 2.3683 × 102 | 0 | 4.3726 × 101 | 9.0690 × 101 | 1.7675 × 102 | 0 | |
| SD | 1.2881 × 101 | 0 | 2.3307 × 101 | 5.9659 × 101 | 1.6948 × 101 | 0 |
| Criteria | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO | |
|---|---|---|---|---|---|---|---|
| Mean | 3.6199 × 10−4 | 0 | 6.7392 × 10−29 | 6.0020 × 10−23 | 1.1225 × 10−187 | 0 | |
| SD | 1.3183 × 10−3 | 0 | 1.5822 × 10−28 | 1.6548 × 10−22 | 0 | 0 | |
| Mean | 2.0161 × 10−15 | 0 | 3.2628 × 101 | 1.8119 × 10−15 | 1.8498 × 10−122 | 0 | |
| SD | 3.4824 × 10−16 | 0 | 3.9216 | 6.1161 × 10−15 | 4.8665 × 10−122 | 0 | |
| Mean | 9.4472 × 104 | 0 | 2.1336 × 102 | 6.1731 × 102 | 1.0466 × 102 | 0 | |
| SD | 8.6811 × 103 | 0 | 6.1093 × 101 | 3.2722 × 102 | 2.0518 × 102 | 0 | |
| Mean | 6.0318 × 101 | 4.9407 × 10−324 | 2.1843 × 10−2 | 2.4619 × 10−1 | 2.7663 × 10−19 | 0 | |
| SD | 9.1391 | 0 | 9.5378 × 10−3 | 9.7297 × 10−2 | 9.2674 × 10−19 | 0 | |
| Mean | 2.2833 × 101 | 0 | 0 | 3.3333 × 10−2 | 0 | 0 | |
| SD | 4.5945 | 0 | 0 | 1.8257 × 10−1 | 0 | 0 | |
| Mean | 6.2760 × 106 | 4.7372 × 101 | 5.3485 × 101 | 5.8728 × 101 | 8.3258 × 101 | 4.7255 × 101 | |
| SD | 2.7022 × 106 | 2.5471 × 10−1 | 2.1756 × 101 | 2.7264 × 101 | 4.4773 × 101 | 2.1455 × 10−1 | |
| Mean | 3.9881 × 102 | 0 | 3.0224 × 101 | 3.9652 × 101 | 1.9921 × 102 | 0 | |
| SD | 3.3527 × 101 | 0 | 9.7823 | 1.1177 × 101 | 5.6608 × 101 | 0 | |
| Mean | 1.6808 × 10−6 | 2.6645 × 10−15 | 9.9654 × 10−14 | 6.0201 × 10−13 | 7.1646 × 10−15 | 2.6645 × 10−15 | |
| SD | 3.3123 × 10−6 | 0 | 1.2662 × 10−13 | 7.5045 × 10−13 | 2.4567 × 10−15 | 0 | |
| Mean | 4.1901 × 10−4 | 0 | 2.3000 × 10−3 | 4.6762 × 10−3 | 1.5135 × 10−3 | 0 | |
| SD | 2.2474 × 10−3 | 0 | 4.4326 × 10−3 | 9.5542 × 10−3 | 3.4264 × 10−3 | 0 | |
| Mean | 1.3995 | 0 | 1.9316 × 10−2 | 2.1549 × 10−2 | 1.4702 × 10−1 | 0 | |
| SD | 8.3632 × 10−1 | 0 | 9.5536 × 10−3 | 1.2197 × 10−2 | 1.0084 × 10−1 | 0 | |
| Mean | 7.4129 × 101 | 0 | 3.4137 × 101 | 5.9507 × 101 | 6.9111 × 101 | 0 | |
| SD | 1.2208 | 0 | 6.4357 | 1.1104 × 101 | 5.8322 | 0 | |
| Mean | 5.3144 × 102 | 0 | 1.3132 × 102 | 2.5030 × 102 | 3.7453 × 102 | 0 | |
| SD | 1.9377 × 101 | 0 | 5.3289 × 101 | 9.9465 × 101 | 3.1666 × 101 | 0 |
| Criteria | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO | |
|---|---|---|---|---|---|---|---|
| Mean | 5.6282 × 104 | 8.9938 × 10−270 | 1.2873 × 101 | 7.8668 × 101 | 6.8659 × 10−16 | 4.9774 × 10−283 | |
| SD | 9.1711 × 103 | 0 | 9.3089 | 4.2189 × 101 | 1.0448 × 10−15 | 0 | |
| Mean | 2.4596 × 1016 | 1.6177 × 10−150 | 3.6510 × 103 | 1.9578 | 5.3771 × 10−13 | 4.0840 × 10−155 | |
| SD | 8.1969 × 1016 | 8.7797 × 10−150 | 1.7832 × 104 | 5.7540 × 10−1 | 4.7000 × 10−13 | 7.1024 × 10−155 | |
| Mean | 4.4087 × 105 | 1.6281 × 10−171 | 2.5833 × 104 | 3.9155 × 104 | 7.3538 × 104 | 8.8599 × 10−172 | |
| SD | 4.5889 × 104 | 0 | 4.1772 × 103 | 6.8323 × 103 | 1.4797 × 104 | 0 | |
| Mean | 9.1993 × 101 | 3.6553 × 10−108 | 2.0536 × 101 | 2.9877 × 101 | 1.7931 × 101 | 1.9923 × 10−108 | |
| SD | 1.2479 | 8.9262 × 10−108 | 2.5961 | 3.4435 | 9.7999 | 3.7736 × 10−108 | |
| Mean | 5.2736 × 104 | 0 | 7.1800 × 101 | 1.7167 × 102 | 0 | 0 | |
| SD | 1.2741 × 104 | 0 | 7.1461 × 101 | 1.0108 × 102 | 0 | 0 | |
| Mean | 2.0590 × 108 | 9.8213 × 101 | 2.0340 × 103 | 2.2630 × 104 | 9.7107 × 101 | 9.8063 × 101 | |
| SD | 6.1190 × 107 | 2.4313 × 10−1 | 1.0493 × 103 | 2.1261 × 104 | 4.4917 × 10−1 | 3.7079 × 10−1 | |
| Mean | 1.1560 × 103 | 0 | 1.5749 × 102 | 2.4022 × 102 | 6.7970 × 102 | 0 | |
| SD | 6.9418 × 101 | 0 | 2.8214 × 101 | 4.8421 × 101 | 1.2108 × 102 | 0 | |
| Mean | 1.7282 × 101 | 2.6645 × 10−15 | 1.4915 | 2.7322 | 2.8350 × 10−9 | 2.6645 × 10−15 | |
| SD | 7.5513 × 10−1 | 0 | 5.3252 × 10−1 | 5.0710 × 10−1 | 1.8879 × 10−9 | 0 | |
| Mean | 4.6645 × 102 | 0 | 1.0690 | 1.6927 | 4.9550 × 10−3 | 0 | |
| SD | 9.1110 × 101 | 0 | 1.3023 × 10−1 | 3.6188 × 10−1 | 1.2937 × 10−2 | 0 | |
| Mean | 2.1488 × 103 | 0 | 7.0063 | 1.3661 × 101 | 5.0429 × 10−2 | 0 | |
| SD | 3.8195 × 102 | 0 | 2.6842 | 6.1557 | 1.3579 × 10−1 | 0 | |
| Mean | 1.6597 × 102 | 0 | 6.9628 × 101 | 8.3404 × 101 | 1.2400 × 102 | 0 | |
| SD | 1.8829 | 0 | 7.5849 | 6.3336 | 2.7652 × 101 | 0 | |
| Mean | 1.8132 × 103 | 0 | 5.7674 × 102 | 8.8909 × 102 | 9.7741 × 102 | 0 | |
| SD | 6.7997 × 101 | 0 | 1.2077 × 102 | 1.5362 × 102 | 5.4787 × 101 | 0 |
| T | Criteria | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO | p-Value | |
|---|---|---|---|---|---|---|---|---|---|
| 30 | 10,000 | Mean | 5.17 | 1.71 | 4.17 | 4.33 | 4.08 | 1.54 | 7.02 × 10−8 |
| SD | 4.83 | 1.71 | 4.42 | 4.50 | 3.67 | 1.88 | 1.18 × 10−6 | ||
| 50 | 10,000 | Mean | 5.67 | 1.63 | 3.71 | 4.58 | 3.88 | 1.54 | 3.16 × 10−9 |
| SD | 5.00 | 1.67 | 3.96 | 5.00 | 3.79 | 1.58 | 3.85 × 10−8 | ||
| 100 | 2000 | Mean | 6.00 | 1.83 | 3.75 | 4.58 | 3.42 | 1.42 | 7.45 × 10−10 |
| SD | 5.25 | 1.58 | 4.17 | 4.67 | 3.83 | 1.50 | 1.70 × 10−8 |
| SR (%) | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO |
|---|---|---|---|---|---|---|
| 0.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 100.0 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 13.3 | 100.0 | |
| 90.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | |
| 83.3 | 100.0 | 83.3 | 83.3 | 90.0 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 10.0 | 100.0 | |
| 26.7 | 100.0 | 50.0 | 46.7 | 66.7 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 3.3 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | |
| 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 |
| AIN | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO |
|---|---|---|---|---|---|---|
| 1.0000 × 104 | 2.6734 × 103 | 3.5675 × 103 | 5.4186 × 103 | 5.6027 × 103 | 1.6216 × 103 | |
| 1.0000 × 104 | 3.3180 × 103 | 1.0000 × 104 | 1.0000 × 104 | 6.4183 × 103 | 2.4406 × 103 | |
| 1.0000 × 104 | 3.9438 × 103 | 1.0000 × 104 | 1.0000 × 104 | 1.0000 × 104 | 2.7628 × 103 | |
| 1.0000 × 104 | 4.0493 × 103 | 1.0000 × 104 | 1.0000 × 104 | 9.9972 × 103 | 3.0298 × 103 | |
| 4.7939 × 103 | 4.0820 × 102 | 5.6233 × 102 | 1.7512 × 103 | 2.3136 × 103 | 1.1700 × 102 | |
| 3.9238 × 103 | 1.7044 × 103 | 2.5791 × 103 | 3.7521 × 103 | 4.1808 × 103 | 8.8953 × 102 | |
| 1.0000 × 104 | 2.5510 × 103 | 1.0000 × 104 | 1.0000 × 104 | 1.0000 × 104 | 8.5687 × 102 | |
| 1.0000 × 104 | 2.0492 × 103 | 1.0000 × 104 | 1.0000 × 104 | 9.9056 × 103 | 1.0859 × 103 | |
| 8.7063 × 103 | 2.3023 × 103 | 6.0576 × 103 | 7.3058 × 103 | 7.5273 × 103 | 8.3030 × 102 | |
| 1.0000 × 104 | 1.8583 × 103 | 1.0000 × 104 | 1.0000 × 104 | 9.9930 × 103 | 8.4923 × 102 | |
| 1.0000 × 104 | 2.3043 × 103 | 1.0000 × 104 | 1.0000 × 104 | 1.0000 × 104 | 1.1307 × 103 | |
| 1.0000 × 104 | 3.7039 × 103 | 1.0000 × 104 | 1.0000 × 104 | 1.0000 × 104 | 8.9340 × 102 |
| Time (S) | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO |
|---|---|---|---|---|---|---|
| 5.3178 | 1.4530 | 2.1226 | 2.6127 | 4.3395 | 0.8115 | |
| 5.0471 | 2.7620 | 8.4172 | 5.1515 | 4.0062 | 1.2683 | |
| 7.3963 | 4.3318 | 6.1789 | 6.2239 | 6.0860 | 1.8055 | |
| 6.3163 | 3.4015 | 4.8744 | 5.0325 | 4.8261 | 1.4174 | |
| 3.1655 | 0.3873 | 0.2949 | 0.7712 | 1.0777 | 0.0748 | |
| 2.7310 | 1.6312 | 1.3465 | 1.7113 | 2.1007 | 0.4562 | |
| 5.2583 | 2.1870 | 4.9350 | 4.5979 | 4.5153 | 0.4413 | |
| 5.0777 | 2.0003 | 4.3977 | 4.5203 | 4.8249 | 0.5535 | |
| 3.5959 | 2.2915 | 2.7715 | 3.4466 | 3.6319 | 0.4417 | |
| 6.1578 | 2.7307 | 7.6677 | 7.0954 | 7.8027 | 0.6347 | |
| 24.0117 | 8.4135 | 23.0703 | 18.4729 | 23.8336 | 2.4332 | |
| 7.7361 | 2.5692 | 6.4690 | 6.6778 | 6.9953 | 0.6512 |
| Criteria | ABC | EQPSO | GAQPSO | RQPSO | WQPSO | ALA-QPSO | p-Value |
|---|---|---|---|---|---|---|---|
| Time | 5.50 | 2.17 | 3.67 | 4.17 | 4.50 | 1.00 | 7.94 × 10−9 |
| AIN | 5.08 | 2.00 | 4.17 | 4.50 | 4.25 | 1.00 | 6.88 × 10−10 |
| SR | 5.08 | 1.79 | 4.42 | 4.50 | 3.42 | 1.79 | 3.90 × 10−9 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S. Quantum-Behaved Particle Swarm Optimization with Weighted Mean Personal Best Position and Adaptive Local Attractor. Information 2019, 10, 22. https://doi.org/10.3390/info10010022
Chen S. Quantum-Behaved Particle Swarm Optimization with Weighted Mean Personal Best Position and Adaptive Local Attractor. Information. 2019; 10(1):22. https://doi.org/10.3390/info10010022
Chicago/Turabian StyleChen, Shouwen. 2019. "Quantum-Behaved Particle Swarm Optimization with Weighted Mean Personal Best Position and Adaptive Local Attractor" Information 10, no. 1: 22. https://doi.org/10.3390/info10010022
APA StyleChen, S. (2019). Quantum-Behaved Particle Swarm Optimization with Weighted Mean Personal Best Position and Adaptive Local Attractor. Information, 10(1), 22. https://doi.org/10.3390/info10010022




