Generalized RDP Code Based Concurrent Repair Scheme in Cloud Storage Nodes
Abstract
:1. Introduction
2. Related Work and Research Status
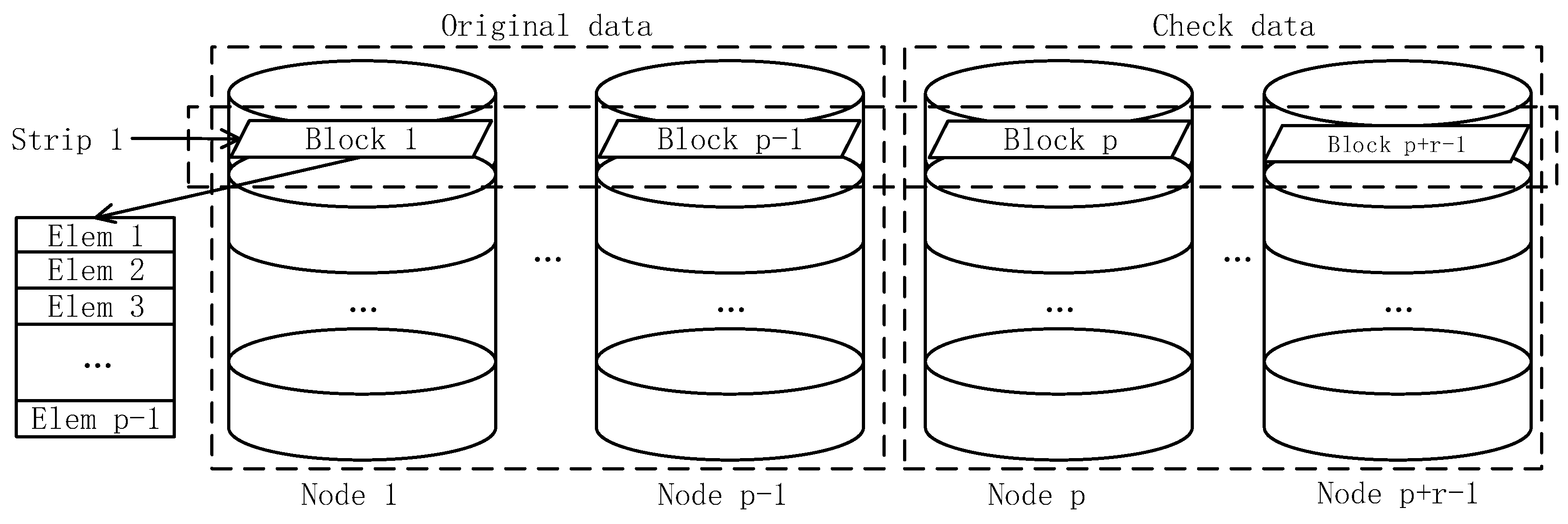
3. Concurrent Node Repair in Generalized RDP Codes
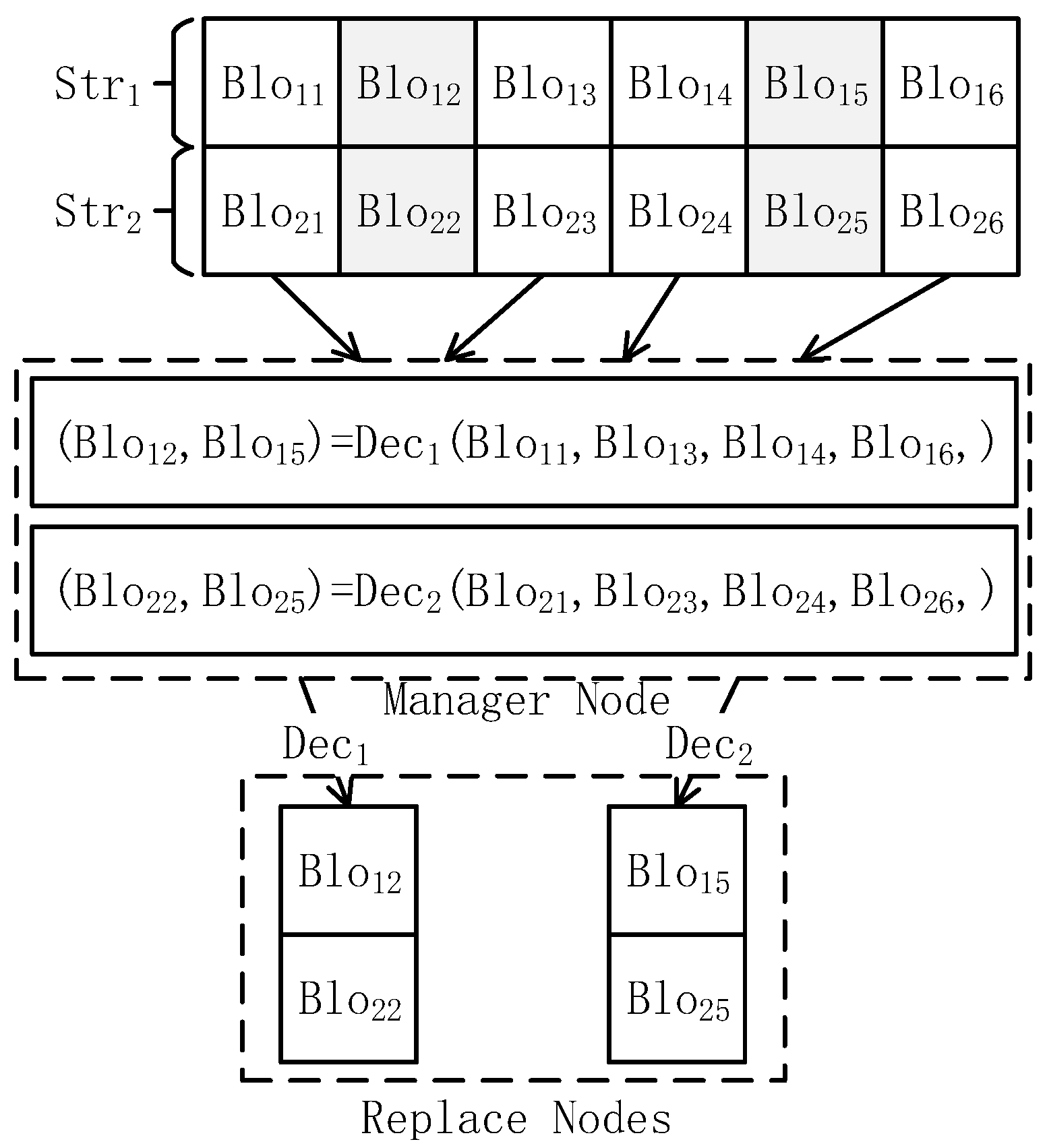
3.1. DCRS Repair Model
3.2. DCRS Repair Scheme
3.2.1. DCRS Repair Algorithm
| Algorithm 1. DCRS Repair Algorithm |
| Input: Damaged Node ID; Output: Replace node |
| Step 1: Initialize the data. Obtain the damaged nodes’ ID and the replaced nodes’ ID. Then, the number of damaged stripes N is obtained from the NameNode, and initialize the number of repaired stripes ; |
| Step 2: Get the repair nodes’ status. The status of each repair node is obtained from the NameNode. may have two states, working or free, represented by false and true respectively; |
| Step 3: Data is allocated to repair nodes. If the state of is true, data blocks of the are obtained from the surviving nodes, and transmitted to node, then change the state of to false; |
| Step 4: Data reorganization of repair nodes. When the damaged stripe is received by , the corrupted data blocks in the stripe are restored. Then, change the state of to true; |
| Step 5: Data distribution of repair nodes. If data blocks reparation in are completed, the repaired -th data block is distributed to Node , then ; |
| Step 6: Program judgment. If , the repair is complete; otherwise, return to Step 2. |
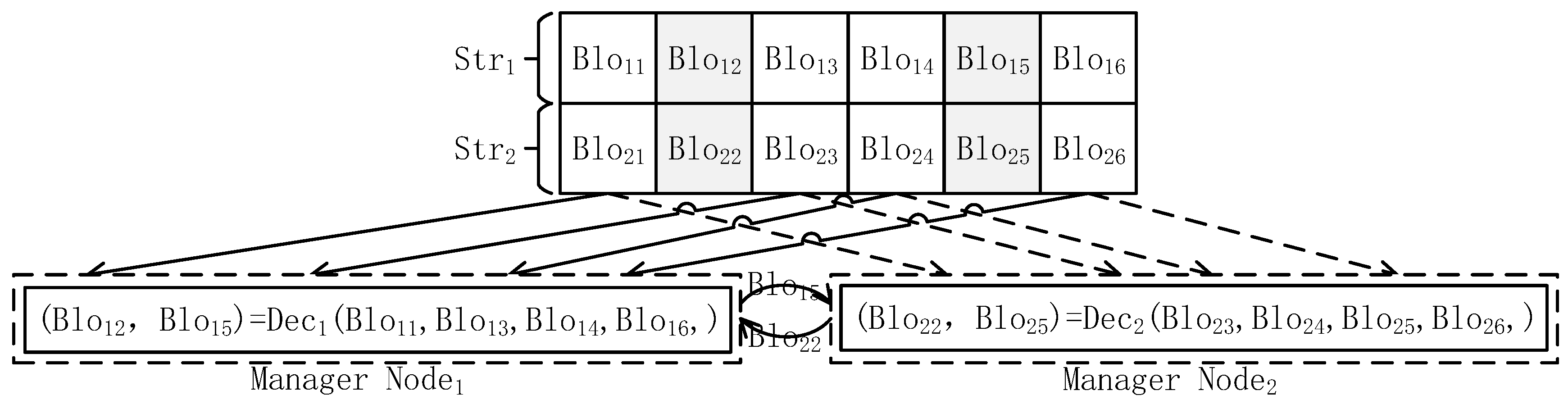
3.2.2. DCRS Repair Efficiency
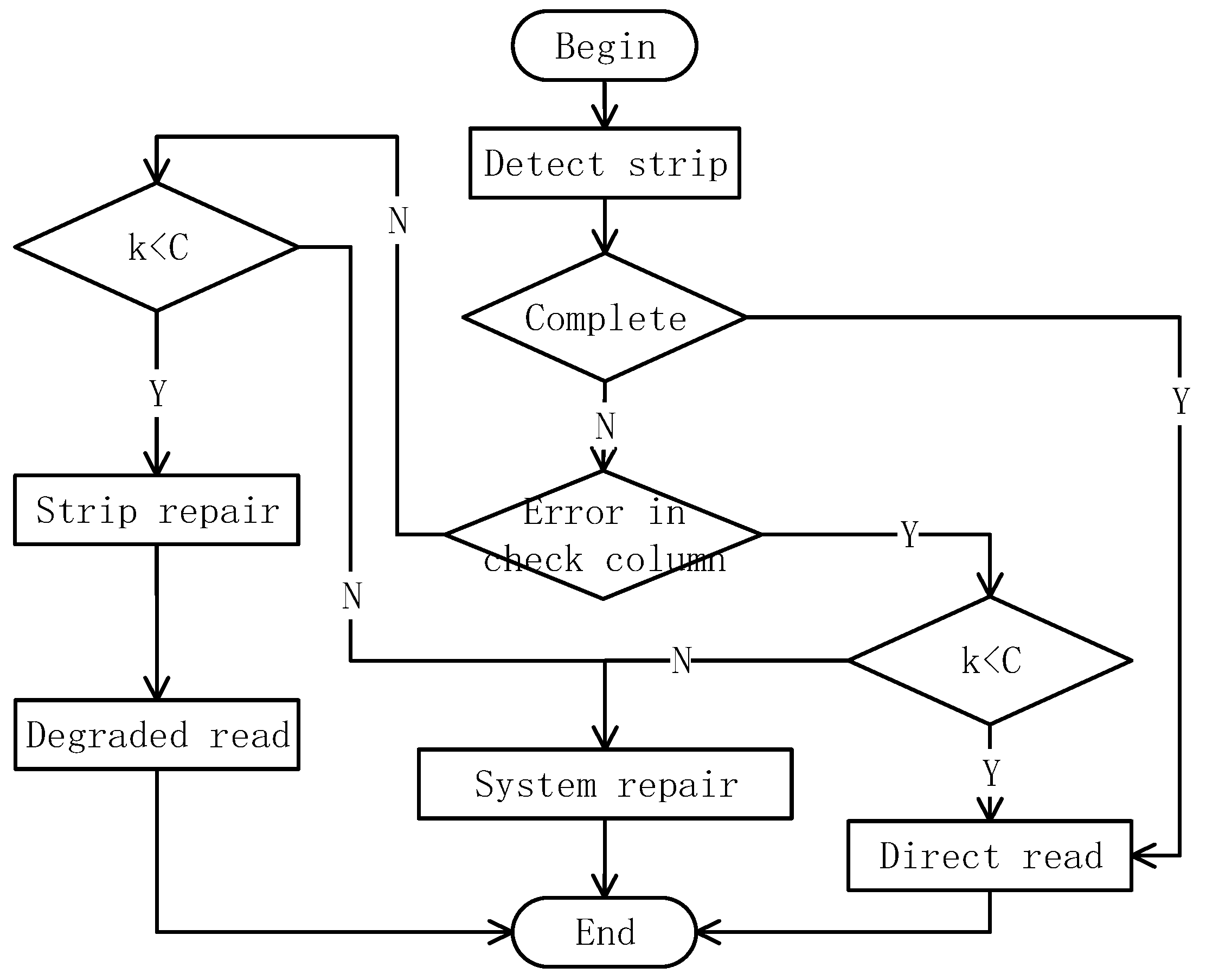
3.3. DCRS Repair Trigger Mechanism
4. Performance Evaluation
4.1. Simulation Platform and Parameters
4.2. Degraded Read Delay
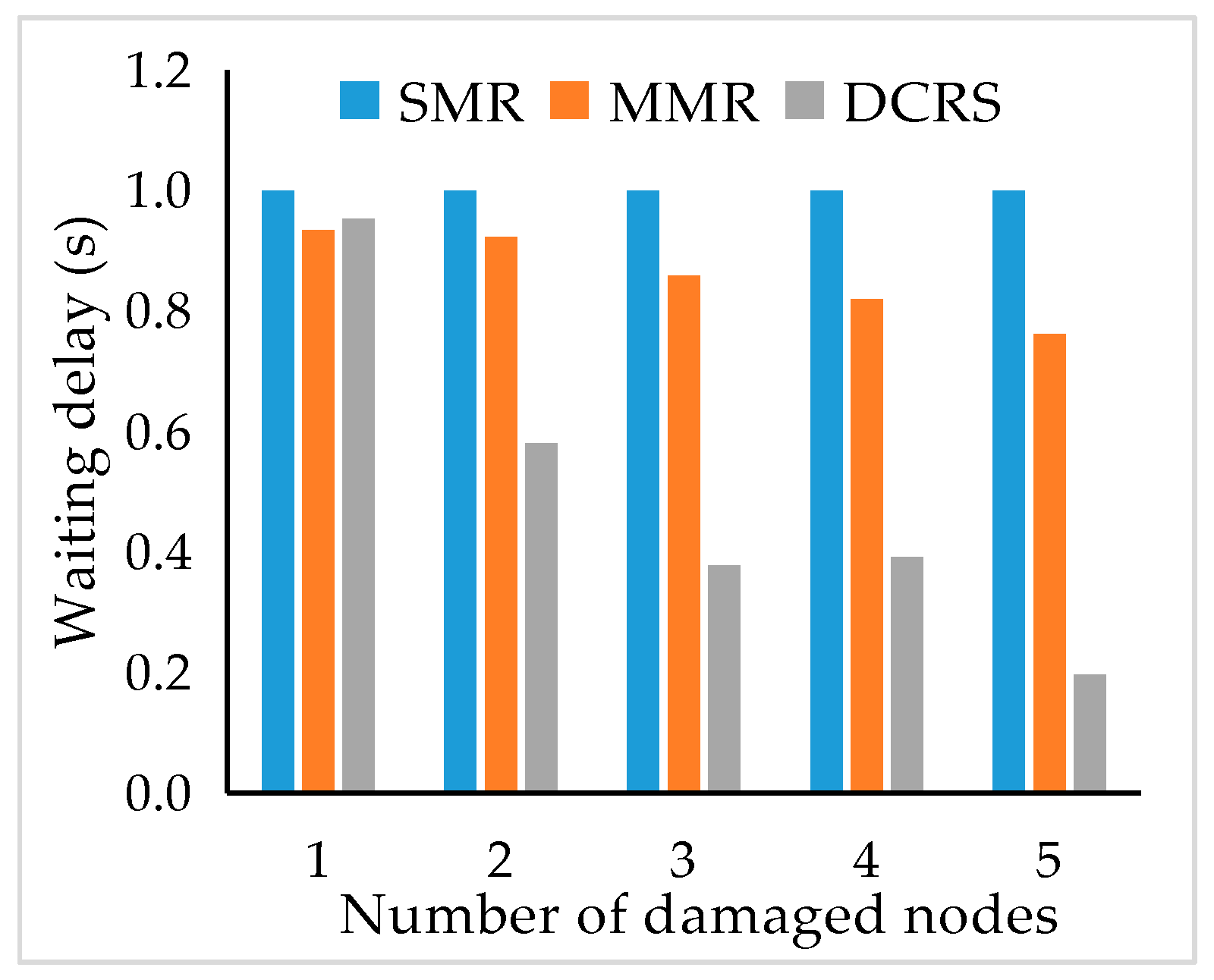
4.3. System Repair Delay
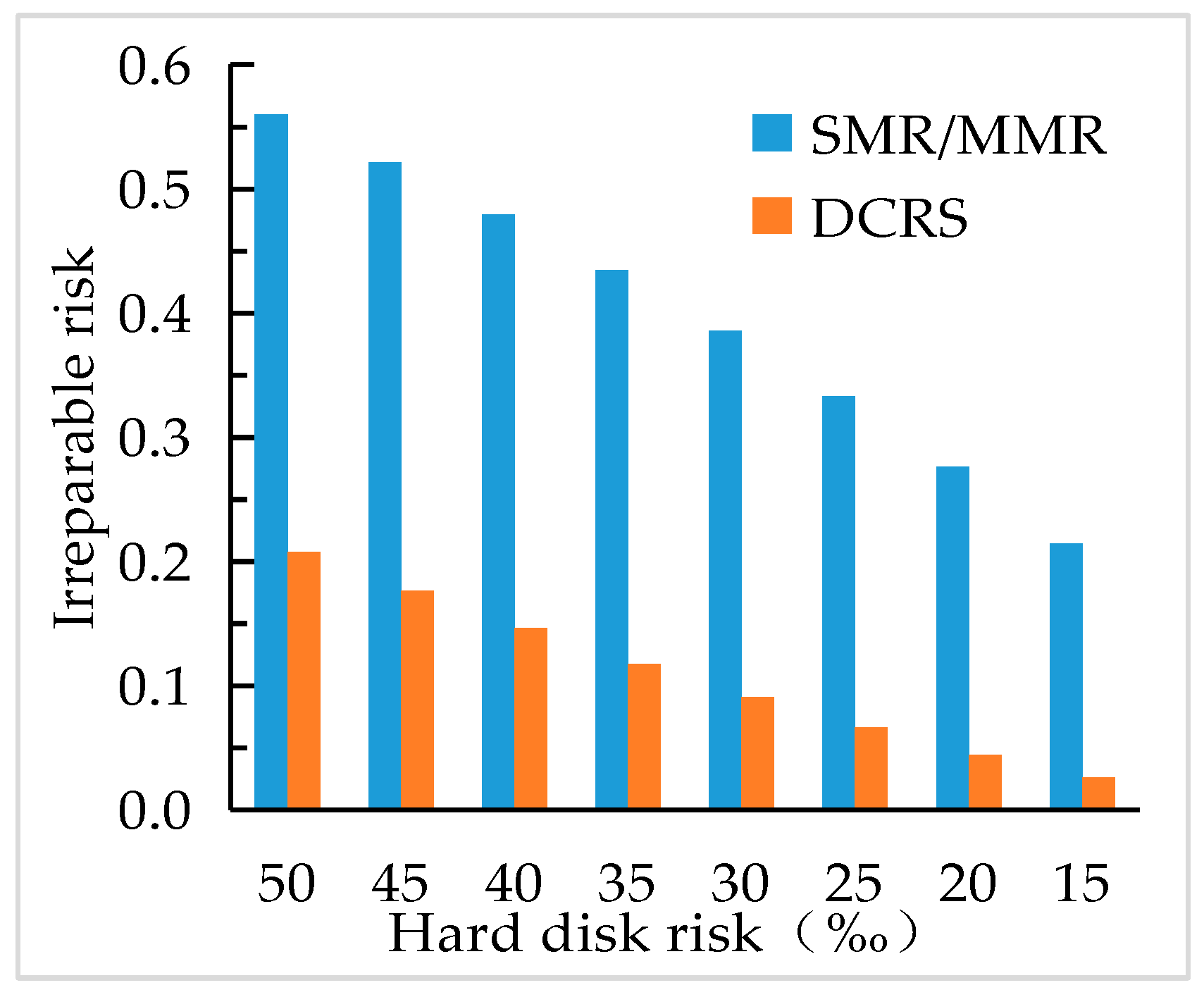
4.4. System Repair Risk
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic Flow Prediction with Big Data: A Deep Learning Approach. IEEE Trans. Intell. Transp. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, W.Y.; Yong, K.L.; Aung, K.M.M. Building a Robust and Efficient Middleware for Geo-replicated Storage Systems. In Proceedings of the 2015 International Conference on Cloud Computing Research and Innovation (ICCCRI), Singapore, 26–27 October 2015; pp. 148–155. [Google Scholar] [CrossRef]
- Du, M.; Wang, Q.; He, M.; Weng, J. Privacy-preserving Indexing and Query Processing for Secure Dynamic Cloud Storage. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2320–2332. [Google Scholar] [CrossRef]
- Yang, T.; Wang, M.; Zhang, Y.; Zhao, Y.; Pen, H. HDFS Differential Storage Energy-saving Optimal Algorithm in Cloud Data Center. Chin. J. Comput. 2018, 1–14. Available online: http://kns.cnki.net/kcms/detail/11.1826.TP.20180303. 1344.010.html (accessed on 8 January 2019). (In Chinese).
- Fu, Y.; Zhang, M.; Chen, K.; Feng, D. Proofs of Data Possession of Multiple Copies. J. Comput. Res. Dev. 2014, 51, 1410–1416. (In Chinese) [Google Scholar] [CrossRef]
- Moniz, H.; Leitão, J.; Dias, R.J.; Gehrke, J.; Preguiça, N.; Rodrigues, R. Blotter: Low latency transactions for geo-replicated storage. In Proceedings of the 26th International Conference on World Wide Web, Perth, Australia, 3–7 April 2017; pp. 263–272. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, D.; Zhang, B. Cloud Storage Fault-tolerant Research Based on Adaptive Switching Scheme Between Replication and Erasure Codes. J. Electr. Syst. Inf. Technol. 2016, 39, 1–6. (In Chinese) [Google Scholar] [CrossRef]
- Lin, X.; Wang, Y.; Pei, X.; Xu, F. GRC: A High Fault-Tolerance and Low Recovery-Overhead Erasure Code for Multiple Losses. J. Comput. Res. Dev. 2014, 51, 172–181. (In Chinese) [Google Scholar]
- Liu, C.; Wang, Q.; Chu, X.; Leung, Y.W. G-CRS: GPU Accelerated Cauchy Reed-Solomon Coding. IEEE Trans. Parallel Distrib. Syst. 2018, 7, 1484–1498. [Google Scholar] [CrossRef]
- Xu, Q.Q.; Xi, W.Y.; Yong, K.L.; Jin, C. CRL: Efficient Concurrent Regeneration Codes with Local Reconstruction in Geo-Distributed Storage Systems. J. Comput. Sci. Technol. 2018, 33, 1140–1151. [Google Scholar] [CrossRef]
- Wan, W.; Yang, W.; Chen, Y. Research on MDS Array Codes in Fault-Tolerant Storage Systems. J. B. Univ. Post. Telecommun. 2014, 37, 75–79. (In Chinese) [Google Scholar] [CrossRef]
- Bao, X.; Lu, P.; Yang, L. Recognition of RS Coding Based on Galois Field Fourier Transform. J. Univ. Electr. Sci. Technol. Chin. 2016, 45, 30–35. (In Chinese) [Google Scholar]
- Hou, H.; Lee, P.P.C. A New Construction of EVENODD Codes with Lower Computational Complexity. IEEE Commun. Lett. 2018, 22, 1120–1123. [Google Scholar] [CrossRef]
- Huang, Z. Research on MDS Array Codes in Fault-Tolerant Storage Systems. J. Huazhong Univ. Sci. Technol. 2016, 5. (In Chinese) [Google Scholar]
- Ding, S.; Tong, X.; Chen, Y.; Ye, B. Bandwidth-Aware Node Repair Optimization for Distributed Storage System Based on Simple Regenerating Code. J. Soft. 2017, 28, 1940–1951. (In Chinese) [Google Scholar] [CrossRef]
- Zhong, R.; Liu, C.; Wang, C.; Xiang, F. Cost-Aware Data Reliability Provision Algorithm for the Cloud Providers. J. Soft. 2014, 25, 1874–1886. (In Chinese) [Google Scholar] [CrossRef]
- Xu, Q.; Xi, W.; Yong, K.L.; Jin, C. Concurrent regeneration code with local reconstruction in distributed storage systems. In Advanced Multimedia and Ubiquitous Engineering; Springer: Berlin/Heidelberg, Germany, 2016; pp. 415–422. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S.; Liao, X. REDU: Reducing redundancy and duplication for multi-failure recovery in erasure-coded storages. J. Supercomput. 2016, 72, 3281–3296. [Google Scholar] [CrossRef]
- Pei, X.; Wang, Y.; Ma, X.; Xu, F. Efficient in-place update with grouped and pipelined data transmission in erasure-coded storage systems. Future Gener. Comput. Syst. 2017, 69, 24–40. [Google Scholar] [CrossRef]
- Prakash, N.; Abdrashitov, V.; Medard, M. The Storage vs Repair-Bandwidth Trade-off for Clustered Storage Systems. IEEE Trans. Inf. Theory 2018. [Google Scholar] [CrossRef]
- Su, Y.S. Pliable Fractional Repetition Codes for Distributed Storage Systems: Design and Analysis. IEEE Trans. Commun. 2018, 66, 2359–2375. [Google Scholar] [CrossRef]
- Li, P.; Jin, X.; Stones, R.J.; Wang, G.; Li, Z.; Liu, X.; Ren, M. Parallelizing degraded read for erasure coded cloud storage systems using collective communications. IEEE Trustcom/BigDataSE/ISPA 2016, 1272–1279. [Google Scholar] [CrossRef]

| Variables | Meanings |
|---|---|
| Total time to transfer and repair a data block | |
| Total time to transfer and repair a stripe | |
| Required transmission time, and , same as below | |
| Required repair time | |
| Required time for node[i] to repair a single data block | |
| Total time to system repair | |
| Number of check columns | |
| Number of stripes | |
| Number of data columns | |
| Number of failed columns (number of failed nodes) | |
| Repair node[i]’s computational performance parameters |
| Name | Parameter |
|---|---|
| Network bandwidth (Mbit/s) | 1000 |
| Number of nodes | 30 |
| Number of data nodes | 16 |
| Number of check nodes | 5 |
| Number of stripes (per node) | 20 |
| Data block size (MB) | 64 |
| Storage Size | SMR (s) | MMR (s) | DCRS (s) | MMR/SMR | DCRS/SMR |
|---|---|---|---|---|---|
| 10 | 119.92 | 91.77 | 23.16 | 0.7653 | 0.1931 |
| 20 | 239.47 | 182.48 | 45.65 | 0.7620 | 0.1906 |
| 30 | 358.83 | 274.06 | 69.28 | 0.7638 | 0.1931 |
| 40 | 478.72 | 365.51 | 91.54 | 0.7635 | 0.1912 |
| 50 | 598.20 | 456.48 | 114.67 | 0.7631 | 0.1917 |
| 60 | 719.80 | 547.46 | 138.36 | 0.7606 | 0.1922 |
| 70 | 836.05 | 638.03 | 160.27 | 0.7631 | 0.1917 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, G.; Shen, J.; Yang, H. Generalized RDP Code Based Concurrent Repair Scheme in Cloud Storage Nodes. Information 2019, 10, 20. https://doi.org/10.3390/info10010020
Xie G, Shen J, Yang H. Generalized RDP Code Based Concurrent Repair Scheme in Cloud Storage Nodes. Information. 2019; 10(1):20. https://doi.org/10.3390/info10010020
Chicago/Turabian StyleXie, Guojun, Jiquan Shen, and Huanhuan Yang. 2019. "Generalized RDP Code Based Concurrent Repair Scheme in Cloud Storage Nodes" Information 10, no. 1: 20. https://doi.org/10.3390/info10010020
APA StyleXie, G., Shen, J., & Yang, H. (2019). Generalized RDP Code Based Concurrent Repair Scheme in Cloud Storage Nodes. Information, 10(1), 20. https://doi.org/10.3390/info10010020





