A Recommendation Model Based on Multi-Emotion Similarity in the Social Networks
Abstract
:1. Introduction
- (1)
- To solve the “cold start” problem, the RM-MES scheme uses the historical purchase records of an existing store to guide a recently opened store, which aims to form a recommendation probability matrix of both the existing store and the new store for the target users;
- (2)
- To improve the accuracy of recommendation results, we propose a scheme based on multi-emotional analysis. The LDA topic model is used to subdivide user evaluation into six indexes. Considering user preferences for different levels of goods, the similarity of users is deeply analyzed, and the similarity results show its advantages;
- (3)
- With the considerations of the different performances of users, the behaviors of those users can be divided into three aspects, including browsing goods, buying goods only, and purchasing–evaluating goods. According to the three categories, the browsing similarity, purchasing similarity, and emotional similarity among users can be identified;
- (4)
- We adopt the metadata of Amazon goods to verify the effectiveness and performance of the RM-MES scheme through comprehensive experiments. In addition, we analyze the impact of transition probability influence factor through the experiments.
2. Related Works
- Most of the recommendation schemes only consider the “cold start” problem of new users, but do not consider the “cold start” problem for a recently opened store, so as to affect the recommend quality of recommendation system;
- Some recommendation schemes search for user preferences by extracting user Facebook and Twitter data. However, it is difficult to extract the user’s personal information due to issues such as permissions and technology. Additionally, because information that includes user emotions is often incomplete and fuzzy, it is not easy to directly analyze the emotions in the information from Facebook and Twitter;
- These recommendation systems based on emotion only consider positive and negative emotions but do not consider users’ preferences in other aspects;
- When calculating the similarities of users’ behaviors, most recommendation schemes do not take the correlation between projects into consideration;
- Most recommendation schemes fail to consider the trust factor of each piece of merchandise, which may cause the recommendation system to provide distrusted items to target users.
3. The RM-MES Algorithm
3.1. Search for Existing and Similar Reference Users in the Existing Shop for the Taget User
3.1.1. The Calculation Method for Similar Shops
3.1.2. Emotional Analysis of User Reviews
3.1.3. The Calculation Method for Similar Users
3.2. Establishment of the Recommendation Model
3.2.1. The Recommendation Probability for Each Good According to the Historical Purchase Records
3.2.2. The Calculation Method for the Correlation Relationships between Goods
3.2.3. The Mean Recommendation Probability Matrix of Goods
3.2.4. The Trust Factor of Goods in the RM-MES Scheme
3.2.5. The Latent Factors of Users in the RM-MES Scheme
3.2.6. The Establishment of Combination Calculation
| Algorithm 1. The main RM-MES Algorithm |
| Input: Output: |
| 1: for each 2: 3: end for 4: for each 5: for each 6: 7: end for 8: 9: Calculate according to Equations (4)–(8); 10: end for |
| 11: Reverse order by and obtain = 12: for each |
| 13: Calculate the transfer matrix according to Equations (10) and (11); |
| 14: Calculate the transfer matrix S based on the relationship: 15: 16: end for 17: Calculate the final transfer matrix based on and : 18: 19: Calculate the recommendation probability at the next time instance based on the historical purchase records of users: 20: 21: for each 22: Calculate the trust degree of each good: 23: 24: Calculate the latent factor if the target user is new; 25: Comprehensively compute the probability: 26: Combine the recommendation probabilities of the reference shop and new shop: 27: 28: end for |
| 29: Return |
4. Experimental Evaluations and Results
4.1. Experimental Settings
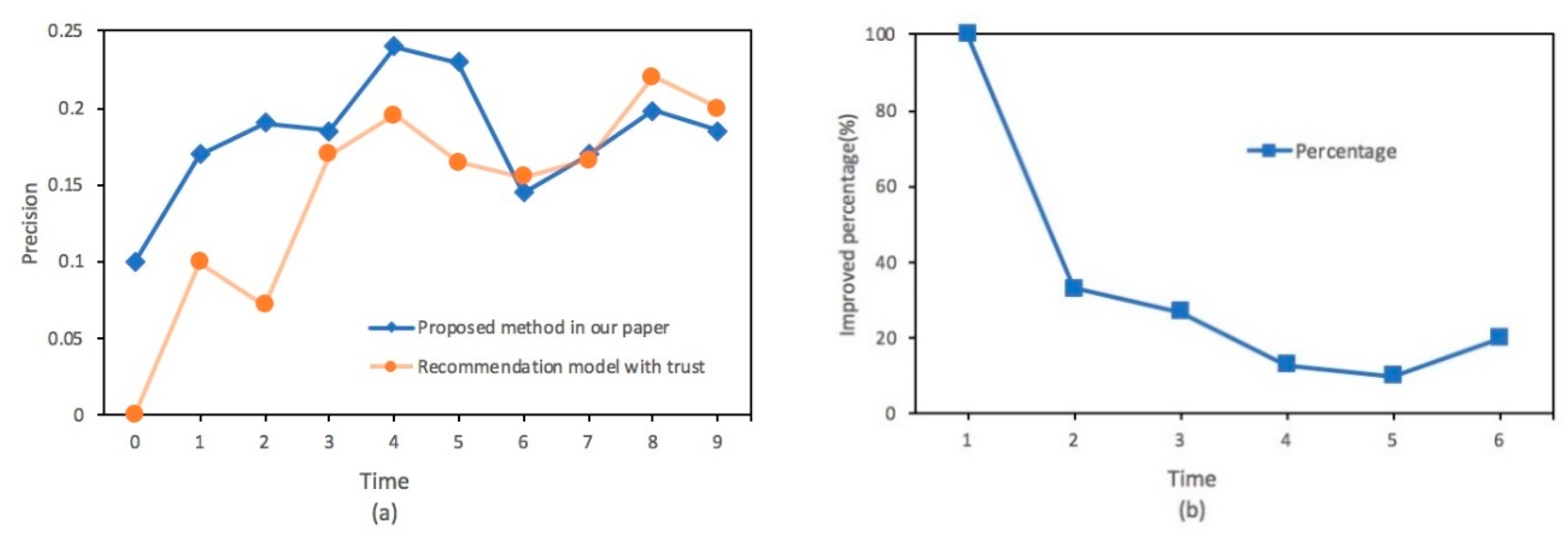
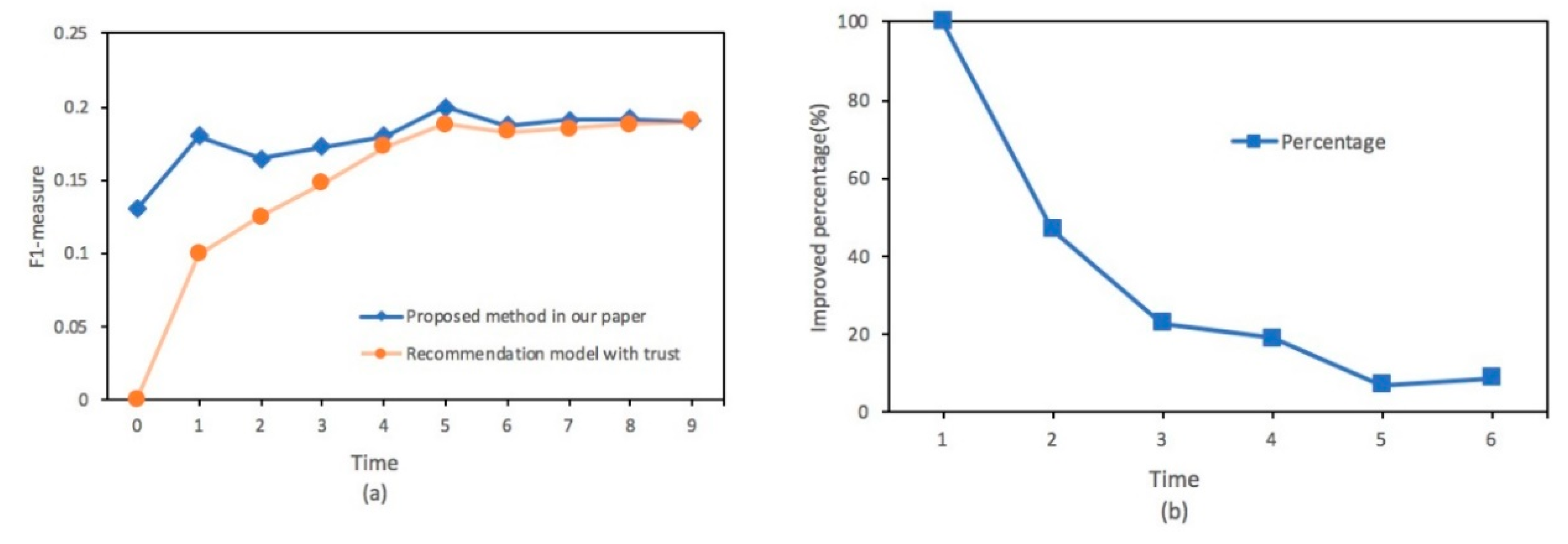
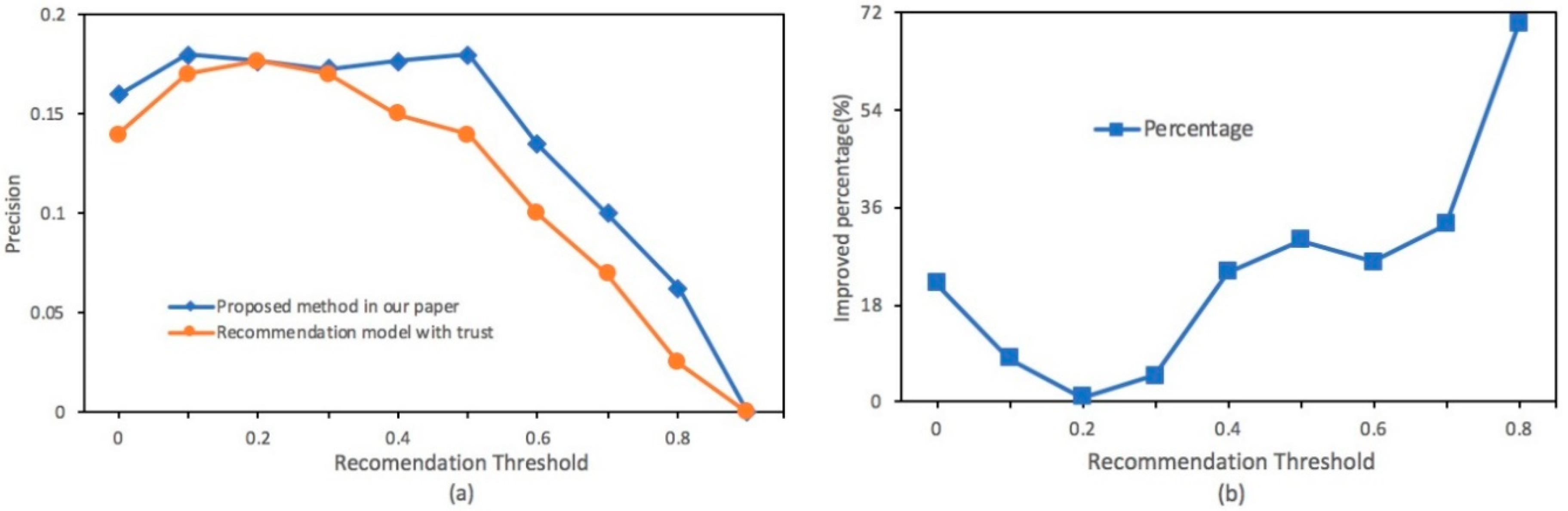
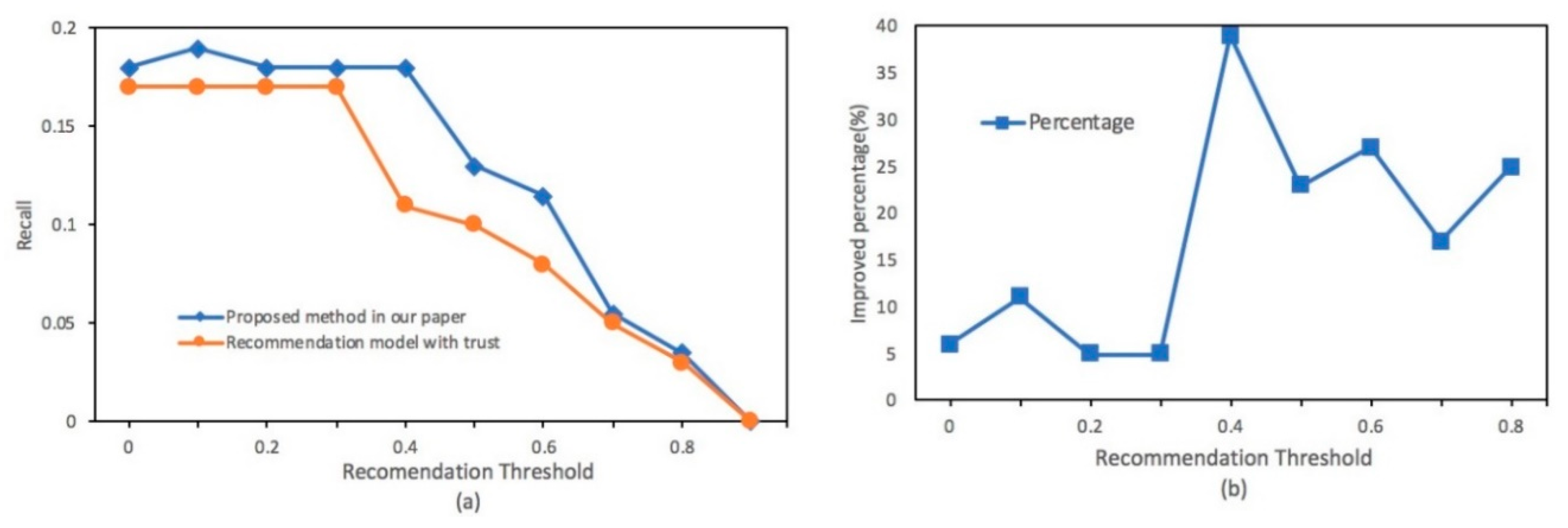
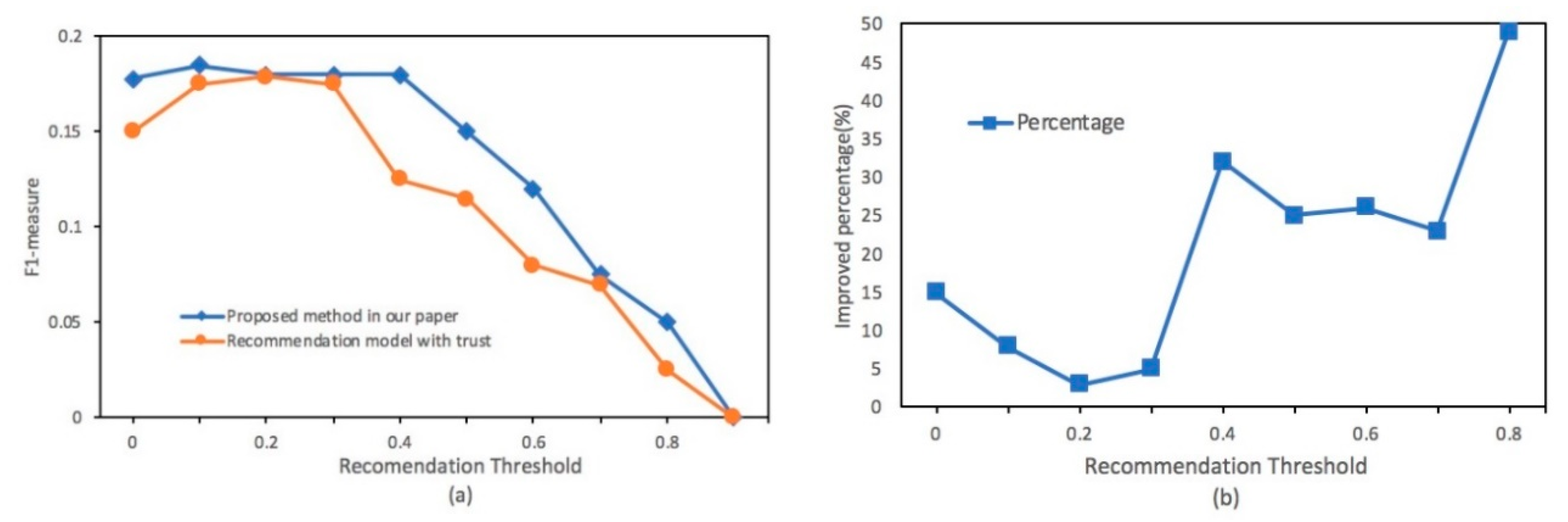
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Y.; Yin, G.; Cai, Z.; Dong, Y.; Dong, H. A trust-based probabilistic recommendation model for social networks. J. Netw. Comput. Appl. 2015, 55, 59–67. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, J. Improvement of matrix factorization-based recommender systems using similar user index. Int. J. Softw. Eng. Appl. 2015, 9, 189–200. [Google Scholar]
- Joshi, B.; Iutzeler, F.; Amini, M.R. ′16-Asynchronous Distributed Matrix Factorization with Similar User and Item Based Regularization. In Proceedings of the 10th ACM Conference on Recommender Systems-RecSys, Boston, MA, USA, 15–19 September 2016; pp. 75–78. [Google Scholar]
- Thorat, P.B.; Goudar, R.M.; Barve, S. Survey on Collaborative Filtering, Content-based Filtering and Hybrid Recommendation System. Int. J. Comput. Appl. 2015, 110, 31–36. [Google Scholar]
- Polatidis, N.; Kapetanakis, S.; Pimenidis, E.; Kosmidis, K. Reproducibility of experiments in recommender systems evaluation. In Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations, Rhodes, Greece, 22 May 2018; pp. 401–409. [Google Scholar]
- Zhu, J.; Zhang, J.; Zhang, C.; Wu, Q.; Jia, Y.; Zhou, B.; Yu, S. CHRS: Cold Start Recommendation across Multiple Heterogeneous Information Networks. IEEE Access 2017, 99, 1. [Google Scholar] [CrossRef]
- Alam, A.; Khusro, S.; Ullah, I.; Karim, M.S. Confluence of social network, social question and answering community, and user reputation model for information seeking and experts generation. J. Inf. Sci. 2017, 43, 260–274. [Google Scholar] [CrossRef]
- Mao, X.; Mitra, S.; Swaminathan, V. Feature Selection for FM-Based Context-Aware Recommendation Systems. IEEE Comput. Soc. 2017, 42, 252–255. [Google Scholar]
- Liu, X. An improved clustering-based collaborative filtering recommendation algorithm. Cluster Comput. 2017, 20, 1281–1288. [Google Scholar]
- Chen, T.; Hong, L.; Shi, Y.; Sun, Y. Joint Text Embedding for Personalized Content-based Recommendation. arXiv, 2017; arXiv:1706.01084. [Google Scholar]
- Mcauley, J.; Targett, C.; Shi, Q.; Hengel, A.V.D. Image-Based Recommendations on Styles and Substitutes. In Proceedings of the International Acm Sigir Conference on Research and Development in Information Retrieval, Santiago, Chile, 9–13 August 2015; pp. 43–52. [Google Scholar]
- Chen, M.; Wang, S.; Liang, P.P.; Baltrušaitis, T.; Zadeh, A.; Morency, L.P. Multimodal Sentiment Analysis with Word-Level Fusion and Reinforcement Learning; ACM: New York, NY, USA, 2017; pp. 163–171. [Google Scholar]
- Li, J.; Sun, C.; Lv, J. TCMF: Trust-Based Context-Aware Matrix Factorization for Collaborative Filtering. In Proceedings of the IEEE International Conference on TOOLS with Artificial Intelligence, Limassol, Cyprus, 10–12 November 2014; pp. 815–821. [Google Scholar]
- Wang, Y.; Zhu, L. Research on Collaborative Filtering Recommendation Algorithm Based on Mahout. In Proceedings of the 2016 4th International Conference on Applied Computing and Information Technology/3rd International Conference on Computational Science/Intelligence and Applied Informatics/1st International Conference Big Data, Cloud Computing, Data Science & Engineering (ACIT-CSII-BCD), Las Vegas, NV, USA, 12–14 December 2016; pp. 400–405. [Google Scholar]
- He, R.; Mcauley, J. Ups and Downs: Modeling the Visual Evolution of Fashion Trends with, One-Class Collaborative Filtering. In Proceedings of the 25th International Conference on World Wide Web International World Wide Web Conferences Steering Committee, Montreal, QC, Canada, 4 February 2016; pp. 507–517. [Google Scholar]
- Sun, L.; Michael, E.I.; Wang, S.; Li, Y. A Time-Sensitive Collaborative Filtering Model in Recommendation Systems. In Proceedings of the IEEE International Conference on Internet of Things, Chengdu, China, 15–18 December 2017; pp. 340–344. [Google Scholar]
- Song, H.; Pei, Q.Q.; Xiao, Y.; Li, Z.; Wang, Y. A Novel Recommendation Model Based on Trust Relations and Item Ratings in Social Networks. In Proceedings of the International Conference on Networking and Network Applications, Kathmandu, Nepal, 16–19 October 2018; pp. 17–23. [Google Scholar]
- Samundeeswary, K.; Krishnamurthy, V. Comparative study of recommender systems built using various methods of collaborative filtering algorithm. In Proceedings of the International Conference on Computational Intelligence in Data Science, Chennai, India, 2–3 July 2018; pp. 1–6. [Google Scholar]
- Guo, G.; Zhang, J.; Zhu, F.; Wang, X. Factored similarity models with social trust for top-N item recommendation. Knowl.-Based Syst. 2017, 122, 17–25. [Google Scholar] [CrossRef]
- Maha, A.; Gabriella, P.; Fabio, S.; Rim, F. An LDA-Based Approach to Scientific Paper Recommendation. In Proceedings of the 21st International Conference on Applications of Natural Language to Information Systems, Salford, UK, 17 June 2016; pp. 200–210. [Google Scholar]
- Yan, G.; Shi, H.; Chong, D.; He, W. Mining e-commerce satisfaction sentiment through a bilingual model. In Proceedings of the IEEE International Conference on Image, Vision and Computing (ICIVC), Chengdu, China, 2–4 July 2017; pp. 1029–1033. [Google Scholar]
- Guo, L.; Liang, J.; Zhu, Y.; Luo, Y.; Sun, L.; Zheng, X. Collaborative filtering recommendation based on trust and emotion. J. Intell. Inf. Syst. 2018, 1–23. [Google Scholar] [CrossRef]
- Guo-Qiang, Z.; Xu, L.; Xi-Hui, Y. User Collaborative Recommendation Model Based on Emotional Weight. J. Chin. Comput. Syst. 2016, 37, 4–5. [Google Scholar]
- Wijayanti, R.; Arisal, A. Ensemble approach for sentiment polarity analysis in user-generated Indonesian text. In Proceedings of the International Conference on Computer, Control, Informatics and ITS Applications, Jakarta, Indonesia, 23–26 October 2018; pp. 158–163. [Google Scholar]
- Vagliano, I.; Monti, D.; Morisio, M. Semrevrec: A recommender system based on user reviews and linked data. In Proceedings of the Poster Track of the 11th ACM Conference on Recommender Systems, Como, Italy, 28 August 2017; pp. 1–3. [Google Scholar]
- Musto, C.; Gemmis, M.; Semeraro, G.; Lops, P. A multi-criteria recommender system exploiting aspect-based sentiment analysis of users’ reviews. In Proceedings of the 11th ACM Conference on Recommender Systems, Como, Italy, 27–31 August 2017; pp. 321–325. [Google Scholar]
- Contratres, F.G.; Alves-Souza, S.N.; Filgueiras, L.V.L.; Liu, S.D.S. Sentiment Analysis of Social Network Data for Cold-Start Relief in Recommender Systems. Adv. Intell. Syst. Comput. 2018, 746, 122–132. [Google Scholar]
- Seo, Y.D.; Kim, Y.G.; Lee, E.; Baik, D. Personalized recommender system based on friendship strength in social network services. Expert Syst. Appl. 2017, 69, 135–148. [Google Scholar] [CrossRef]
- Meng, X.; Wang, S.; Liu, H.; Zhang, Y. Exploiting Emotion on Reviews for Recommender System. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]

| Symbol | Description |
|---|---|
| The set of similar users to the target user a | |
| The purchase matrixes of similar users | |
| The relationship among good i and good j | |
| The proportion of the mean recommendation probability | |
| The number of final purchases in the new shop | |
| The number of recommended goods in each round | |
| The length of the time window | |
| y | The proportion of the influence factor of trust |
| The proportion of the influence factor of the latent factor | |
| The recommendation matrix of the target user based on the similarity of users | |
| The recommendation matrix of the target user based on the correlation relationship among goods | |
| The recommendation probability matrix of the target user based on | |
| The value of trust for good i | |
| The reputation of good i | |
| The purchase frequency of good i | |
| The proportion of the recommendation probability for the new shop | |
| recall | The probability that users purchase what they like in the recommendation list |
| The standard measurement for the classification accuracy of a recommendation algorithm | |
| The number of goods that user i likes | |
| The number of goods that user i has purchased in the recommendation list |
| TB | X = 0.3 | X = 0.4 | X = 0.5 | X = 0.6 | |
|---|---|---|---|---|---|
| Precision | 0.115 | 0.140 | 0.130 | 0.131 | 0.105 |
| Recall | 0.106 | 0,137 | 0.133 | 0.131 | 0.1 |
| F1-measure | 0.110 | 0.139 | 0.138 | 0.133 | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, J.; Wang, Y.; Yuan, X.; Li, T.; Liu, Q. A Recommendation Model Based on Multi-Emotion Similarity in the Social Networks. Information 2019, 10, 18. https://doi.org/10.3390/info10010018
Long J, Wang Y, Yuan X, Li T, Liu Q. A Recommendation Model Based on Multi-Emotion Similarity in the Social Networks. Information. 2019; 10(1):18. https://doi.org/10.3390/info10010018
Chicago/Turabian StyleLong, Jun, Yulou Wang, Xinpan Yuan, Ting Li, and Qunfeng Liu. 2019. "A Recommendation Model Based on Multi-Emotion Similarity in the Social Networks" Information 10, no. 1: 18. https://doi.org/10.3390/info10010018
APA StyleLong, J., Wang, Y., Yuan, X., Li, T., & Liu, Q. (2019). A Recommendation Model Based on Multi-Emotion Similarity in the Social Networks. Information, 10(1), 18. https://doi.org/10.3390/info10010018





