An Improved Reversible Image Transformation Using K-Means Clustering and Block Patching

Abstract

Recently, reversible image transformation (RIT) technology has attracted considerable attention because it is able not only to generate stego-images that look similar to target images of the same size, but also to recover the secret image losslessly. Therefore, it is very useful in image privacy protection and reversible data hiding in encrypted images. However, the amount of accessorial information, for recording the transformation parameters, is very large in the traditional RIT method, which results in an abrupt degradation of the stego-image quality. In this paper, an improved RIT method for reducing the auxiliary information is proposed. Firstly, we divide secret and target images into non-overlapping blocks, and classify these blocks into K classes by using the K-means clustering method. Secondly, we match blocks in the last (K-T)-classes using the traditional RIT method for a threshold T, in which the secret and target blocks are paired with the same compound index. Thirdly, the accessorial information (AI) produced by the matching can be represented as a secret segment, and the secret segment can be hided by patching blocks in the first T-classes. Experimental results show that the proposed strategy can reduce the AI and improve the stego-image quality effectively.

1. Introduction

With the development of cloud computing, more and more images are outsourced to cloud servers for storage or processing. However, some important private information, such as design drawings and internet sales data, may be leaked, and eavesdroppers are easily able to steal these contents.

Nowadays, there are two common ways to protect from leakages: data hiding [1,2,3,4] and encryption [5]. Encryption technology is more easy to cause the eavesdropper’s suspicious because of the messy codes of cipher texts with the special form. Therefore, data hiding has been attracting more and more attention from researchers in recent years, and many related algorithms have been proposed. For example, Chan et al. [1] applied an optimal pixel adjustment process to the stego-image obtained by the simple LSB substitution method, and the stego-image quality can be greatly improved with low extra computational complexity. Wu et al. [4] designed a novel steganography approach using a reversible texture synthesis, which weaves in the texture synthesis process to conceal secret messages.

However, this is a problem for sensitive applications such as military images and medical images. Reversible data hiding (RDH) [6,7,8,9] is an effective method for these special scenarios, which aims to recover both embedded data and the original image. In the past two decades, many classic RDH algorithms have been proposed, such as lossless image compression methods [6], difference expansion based methods [7] and histogram shifting based methods [8]. Pakdaman et al. [9] proposed a new reversible watermarking scheme based on error prediction in Hadamard domain, in which an adaline neural network is used to determine the coefficients of the predictor function to reduce error values.

With the popularity of cloud storage services, the traditional RDH methods are not suitable in these scenarios, especially with regard to the requirement of high security. Therefore, the research of privacy protection in cloud computing has attracted considerable attention in recent years. Reversible data hiding in encrypted images (RDH-EI) provides the possibility that the image owner can encrypt the image before uploading it to the cloud, and then the cloud manager can embed some additional message into the comprehensible encrypted image for steganography or authentication. The receiver or authorized user can recover both the additional message and the original image.

For these reasons, Zhang [10] designed a framework for a vacating room after encryption (VRAE), in which some additional information will be embedded after encrypting the original image; then, the encrypted image blocks will be divided into two sets by the cloud manager, and the manager can embed additional information by flipping three LSBs of a set. However, this process is irreversible, and has a low embedded capacity. In order to reduce the extracted-bits error rate, Hong et al. [11] evaluated the complexity of image blocks. Zhou et al. [12] utilized a two-class support vector machine classifier to distinguish the encrypted and non-encrypted image patches to recover original images and secret data. Yin et al. [13] designed an RDH-EI method for AMBTC images in which the redundant space of the encrypted AMBTC-compressed image can be exploited utilizing the histogram of prediction error in the data embedding phase. Despite all of this, it is hard to use the traditional RDH method for the cloud manager in this framework since the correlation between neighbor pixels in the encrypted image is destroyed. To solve this problem, Ma et al. [14] proposed the framework of a reserving room before encryption (RRBE), in which the image owner can reverse the room of LSBs by using an RDH method, and encrypt the self-embedded image; then, the cloud manager embeds secret data into the reversed LSBs of the encrypted image. Cao et al. [15] compressed pixels in the local patch by sparse representation, and achieved a higher reversed room than other previous methods.

In conclusion, the framework of “VRAE” used by the cloud manager should be specified together with the receiver, and the framework of “RRBE” needs the sender to undertake the algorithm complexity since the original image in the sender should be compressed and reversed for data hiding. In other words, the RDH method used by the cloud manager in these two frameworks is receiver- or sender-related. However, the cloud manager may be semi-honest and should not know the encryption or decryption methods, which concern the sender and receiver in the public cloud environment. Therefore, data embedding in the cloud sever should not affect the encryption and decryption methods, and the cloud manager can utilize arbitrary classic RDH methods to embed secret information into encrypted image which is similar to the other image. The framework is independent of the receiver-related or sender-related frameworks. To achieve this framework, the original image should be encrypted into a meaningful image. Thus, how to transform reversibly the original image to the meaningful image, which is similar to the other image, is a more challenging problem, called “reversible image transform” (RIT).

In this paper, we propose an improved RIT method, in which the rest image blocks are patched to hide the AI generated by the last (K-T)-classes transformation. The main contribution of this paper is that the stego-image quality is improved by patching image blocks to embed the AI.

The rest of this paper is organized as follows. In Section 2, we introduce previous related works. Section 3 introduces our method, which can be divided into an image pairing phase and a proposed algorithm phase. In Section 4, we demonstrate the advantages of the proposed method by presenting our experimental results. Lastly, we give a conclusion in Section 5.

2. Related Work

The RIT method was designed for image privacy protection, in which secret information is the image itself. Although Yang et al. [16] can embed an image into several other images for “secret sharing”, the transmission and storage of multiple images cause practicability to be low. Therefore, it is very hard and important to hide one image inside other of the same size, which is called “image transformation”. Lai et al. [17] proposed the first image transformation method. They chose a target image similar to the secret image in an image database, and transformed each secret block to generate the transformed image by the map between secret blocks and target blocks; then, they embedded the map into the transformed image to obtain the final stego-image. However, the visual quality of stego-images in Lai et al.’s method was not good because the AI is very large, and it needs extra time to select a target image in a database. In order to improve Lai et al.’s method, Lee et al. [18] transformed a secret image to a freely-selected target image and reduced the auxiliary information. But this only recovers a good estimation of the secret image because traditional color transformation methods are not reversible.

Inspired by Lai et al.’s and Lee et al.’s methods, Hou et al. [19] designed a reversible image transformation (RIT) method, in which they transformed a secret image to a freely-selected target image and obtained a stego-image similar to the target image by designing a reversible shift transformation. Before shifting image blocks, an effective clustering algorithm is used to pair secret and target blocks, which are able to not only to improve the visual quality of the transformed image, but also to reduce the auxiliary information for recording block indexes. Based on Hou et al.’s method, Zhang et al. [20] transformed the original image into the encrypted image, which looks like the target image, and proposed the RDH-EI framework based on RIT. The RDH-EI method used by the cloud sever is not affected by the encryption and decryption algorithm, and thus, it is irrelevant to the sender or the receiver. Thus, it is a very meaningful task to improve the visual quality of stego-image by reducing the auxiliary information in the traditional RIT method.

The RIT method may be described with three steps: (1) feature extraction for image blocks matching; (2) reversible shift and rotate transformation; (3) secret image extraction. Details are introduced in Figure 1.

2.1. Feature Extraction for Image Blocks Matching

In this RIT method, image blocks are paired by similar means and standard deviations (SDs) between the original and target images. Firstly, we divide secret and target images into N non-overlapping blocks with the same size. Let secret block A be a set of pixels such that $A=\left\{p_1,p_2,\dots ,p_n\right\}$, and the corresponding target block $B=\left\{p_1\prime ,p_2\prime ,\dots ,p_n\prime \right\}$. Then calculate the mean value and standard deviation (SD) as follows:

$$u_A=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{p}_i,u_B=\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{p}_i\prime .$$

(1)

$${\sigma }_A=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{(p_i-u_A)}^2},{\sigma }_B=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_{i=1}^n{\left(p_i\prime -u_B\right)}^2}.$$

(2)

After matching the features of mean value and SD, the class index of blocks matching must be recorded in order to recover the secret and cover images, which will produce a lot of auxiliary information and will cause the degradation of transformation image. Thus, the proposed method focuses on reducing the distortion of the setgo-image by reducing the auxiliary information in traditional RIT method.

2.2. Reversible Shift and Rotate Transformation

After block matching, the transformed image blocks will be shifted to make it as similar as possible to the target image. Let the shifted block $C$ be a set of pixels $C=\left\{p_i″,p_2″,\dots ,p_n″\right\}$; the pixels can be calculated as:

$$\Delta u=round\left(u_B-u_A\right),p_i^{″}=p_i+\Delta u.$$

(3)

To solve the overflow/underflow problem, $\Delta u$ should be modified as follows. The maximum overflow and the minimum underflow pixel values are denoted as $O{V}_{max}$ and $U{N}_{min}$ for $\Delta u\ge 0$ and $\Delta u<0$, respectively.

When $\Delta u\ge 0$:

$$\Delta u=\{\begin{array}{ll}\Delta u+255-O{V}_{max},& if255-O{V}_{max}<0\\ \Delta u-U,& if255-O{V}_{max}\ge 0\end{array}.$$

(4)

or when $\Delta u<0$:

$$\Delta u=\{\begin{array}{ll}\Delta u-U{N}_{min},& ifU{N}_{min}<0\\ \Delta u+U,& ifU{N}_{min}\ge 0\end{array}.$$

(5)

where $U$ is an adjustable parameter for the balance between the number of overflow and underflow and the distance from the mean value of target image. To reduce the amount of auxiliary information, $\Delta u$ should be quantized to a little integer.

$$\Delta u=\{\begin{array}{ll}\lambda \times round\left(\frac{\Delta u}{\lambda }\right),& ifu\ge 0\\ \lambda \times floor\left(\frac{\Delta u}{\lambda }\right)+\frac{\lambda }{2},& ifu<0\end{array}.$$

(6)

where the quantization step $\lambda$ must be an even parameter, $round(·)$ and $floor(·)$ are integral functions. Then, $\Delta u^{\prime }=2\left|\Delta u\right|/\lambda$ should be recorded as the final auxiliary information, which is embedded into the transformed image, and $\lambda$ is a parameter to make a trade-off between the amount of auxiliary information and the distance from the mean value of target image.

Even when modifying the amplitude $u_B-u_C$ to the final $\Delta \mathrm{u}$, the overflow/underflow problem may still occur. To solve this problem, the overflow pixels will be truncated back to the range of [0, 255], then $LM=\left(l{m}_1,l{m}_2,\dots ,l{m}_n\right)$ can be generated to record the position of overflow/underflow pixels.

$$l{m}_i=\{\begin{array}{cc}-p_i^{″},& if{p}_i^{″}<0\hfill \\ p_i^{″}-255,& if{p}_i^{″}>255\hfill \end{array}.$$

(7)

Note that $LM$ is very small and can be compressed well.

To further maintain the similarity between the transformed and target images as much as possible, the shifted block $\mathrm{C}$ can be rotated into one of the four angles $0^{°}$, ${90}^{°}$, ${180}^{°}$ or ${270}^{°}$. The best angle $\vartheta \in \left\{0^{°},{90}^{°},{180}^{°},{270}^{°}\right\}$ is selected for minimizing the root of mean square error (RMSE) between the rotated block and the target block.

Thus, the transformed image is generated, and the auxiliary information containing the class index of secret image, quantified difference $\Delta u^{\prime }$, small overflow/underflow information $LM$ and rotation angle $\vartheta$, which can also be embedded into transformed image by the arbitrary traditional RDH methods. Before embedding, the auxiliary information should be compressed by a classic method, such as the Huffman code method, and should be encrypted by a traditional method, such as by AES encryption, for security.

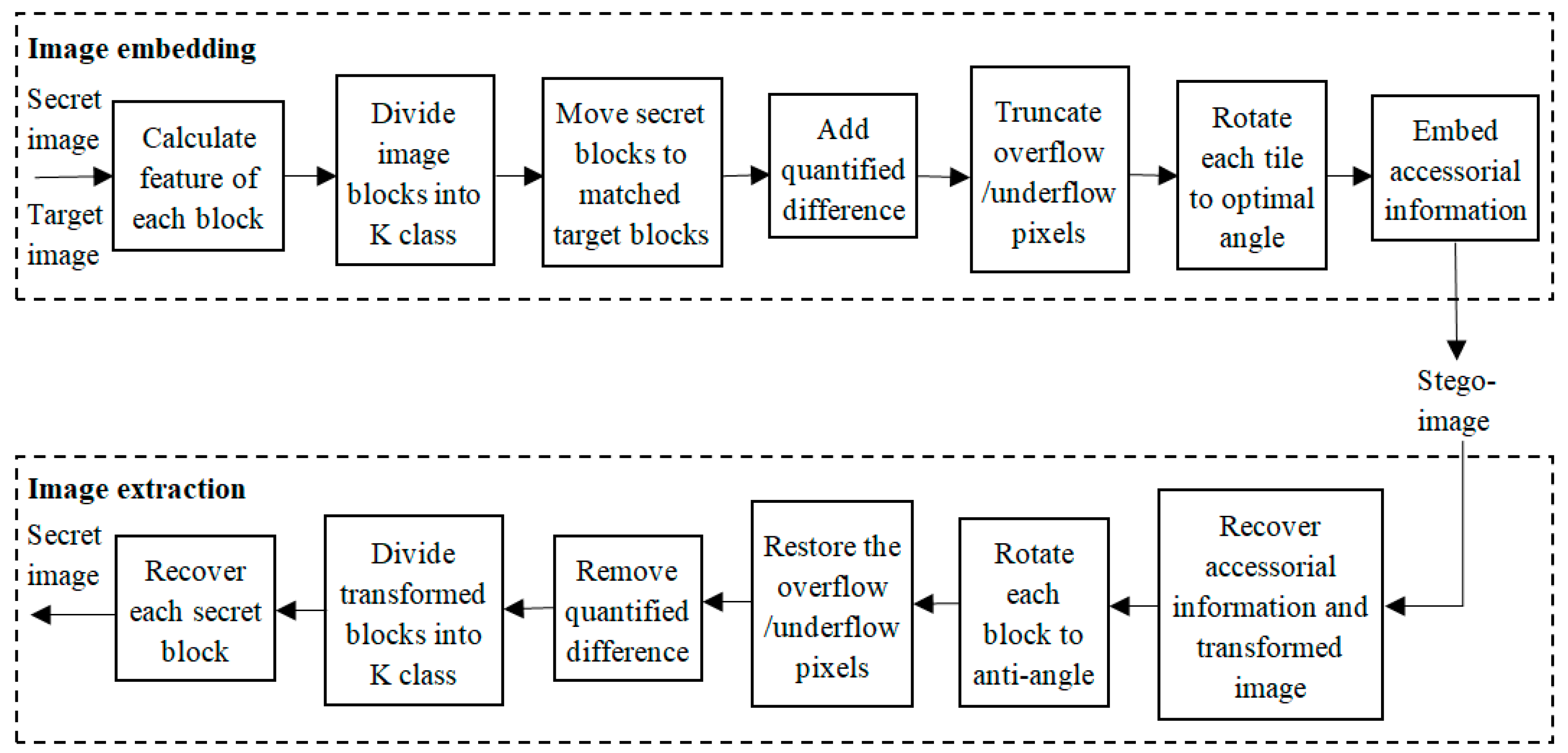
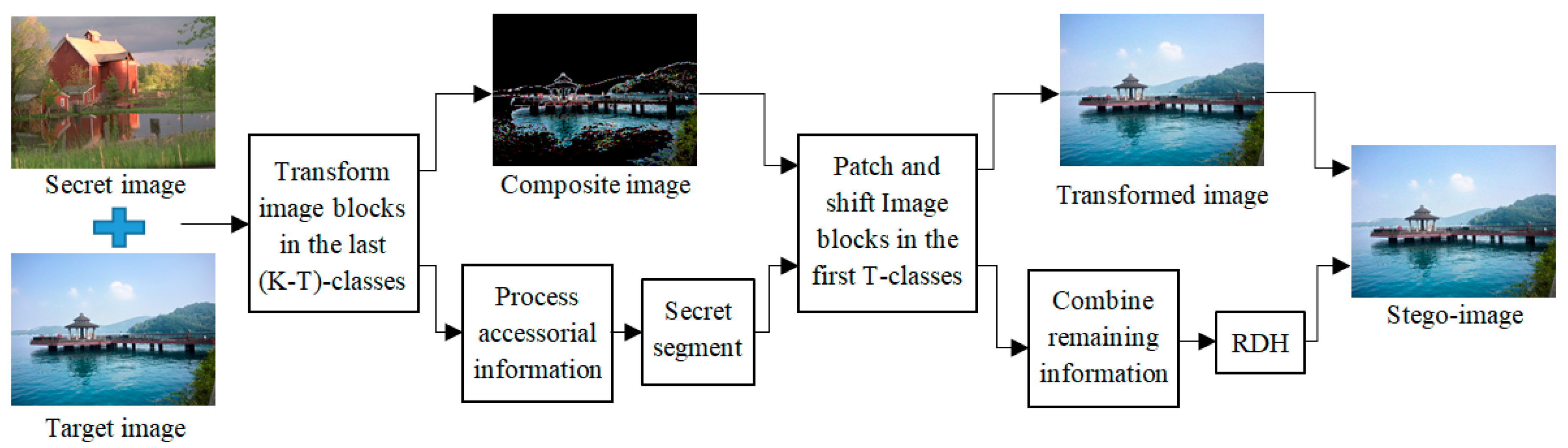
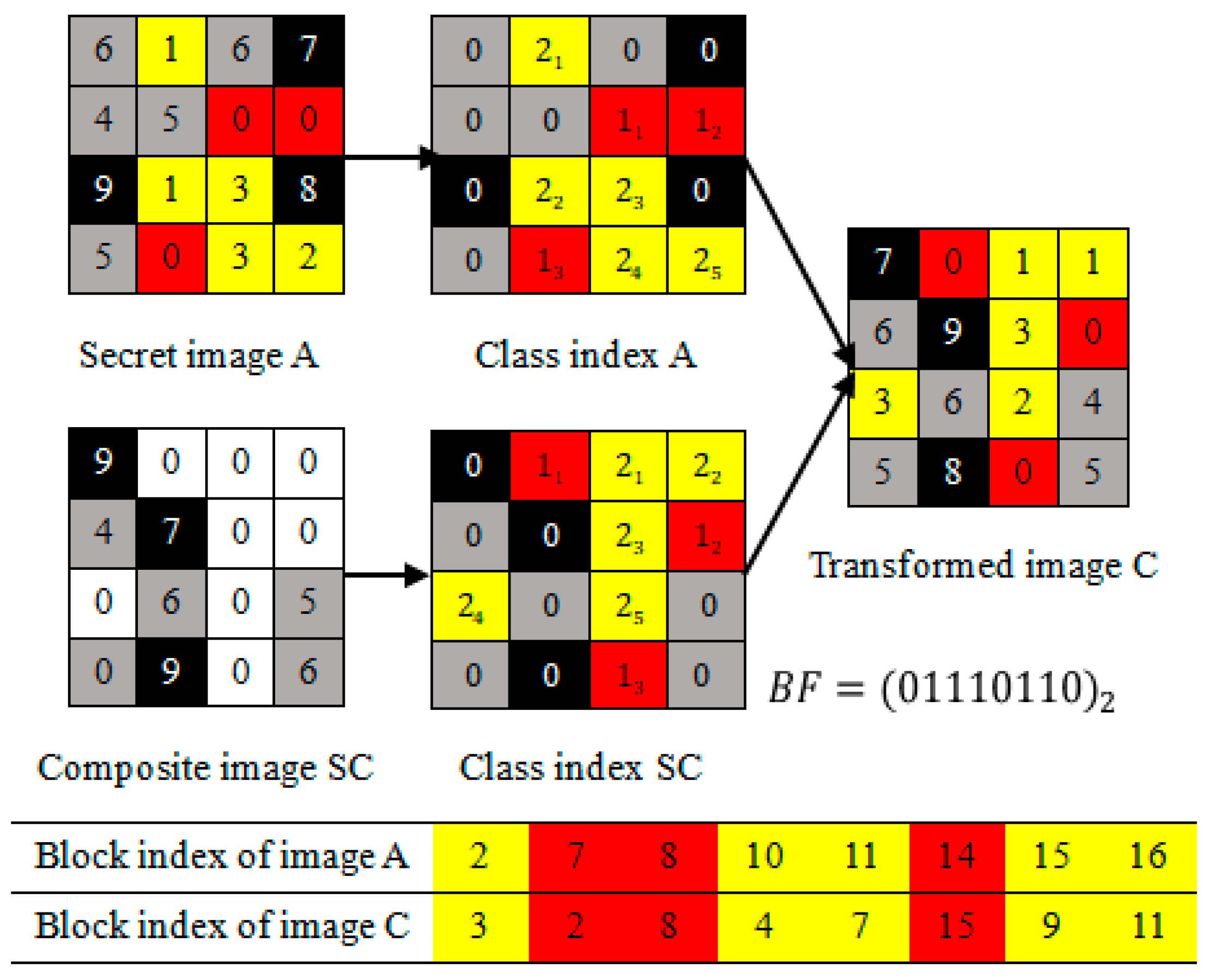
3. The Proposed Method

To reduce the AI, we designed an improved RIT method by patching image blocks according to the secret segment. The proposed framework of image embedding is shown in Figure 2. We transformed the image in the last (K-T)-classes using traditional RIT firstly. Secondly, the partial AI from the last (K-T)-classes is represented as the secret segment; it will be hidden in the composite image by patching the blocks in the first-T classes. Then, the pixel values of these image blocks will be shifted to generate the transformed image. Thirdly, the remaining AI is processed and embedded by an RDH method. Finally, the process of image embedding is completed, and the stego-image is generated. Note that the secret image extraction is the symmetrical process of image embedding, which is not described in detail here. Since the proposed method mainly improves image block matching, we will focus on this step.

Before image block matching, we firstly classify the blocks according to their SD values. In fact, Zhang et al. [20] counted the distribution of SDs of $4\times 4$ block for various sizes of 10,000 natural images from a BossBass image database, and found that the SD values of most blocks concentrate on a small range close to zero, and the frequency quickly drops down with the increase of the SD value. Thus, it will be more efficient for the blocking transformation using SD classification.

In addition, we divided these images into K classes using a K-means clustering method, and calculated the number of each class when $K=10$, as in Figure 3. Then, we can find that when $\mathrm{M}$ is larger, the number of image blocks will decrease and SDs are increased. Therefore, we divide the K classes’ blocks into two parts with unequal proportions: the first T-classes for blocks with smaller SDs, and the last (K-T)-classes for blocks with larger SDs. Thus, blocks in the last (K-T)-classes can be transformed by a traditional RIT method to maintain the transformed image quality, and blocks in the first T-classes can be patched according to the secret segment for reducing AI.

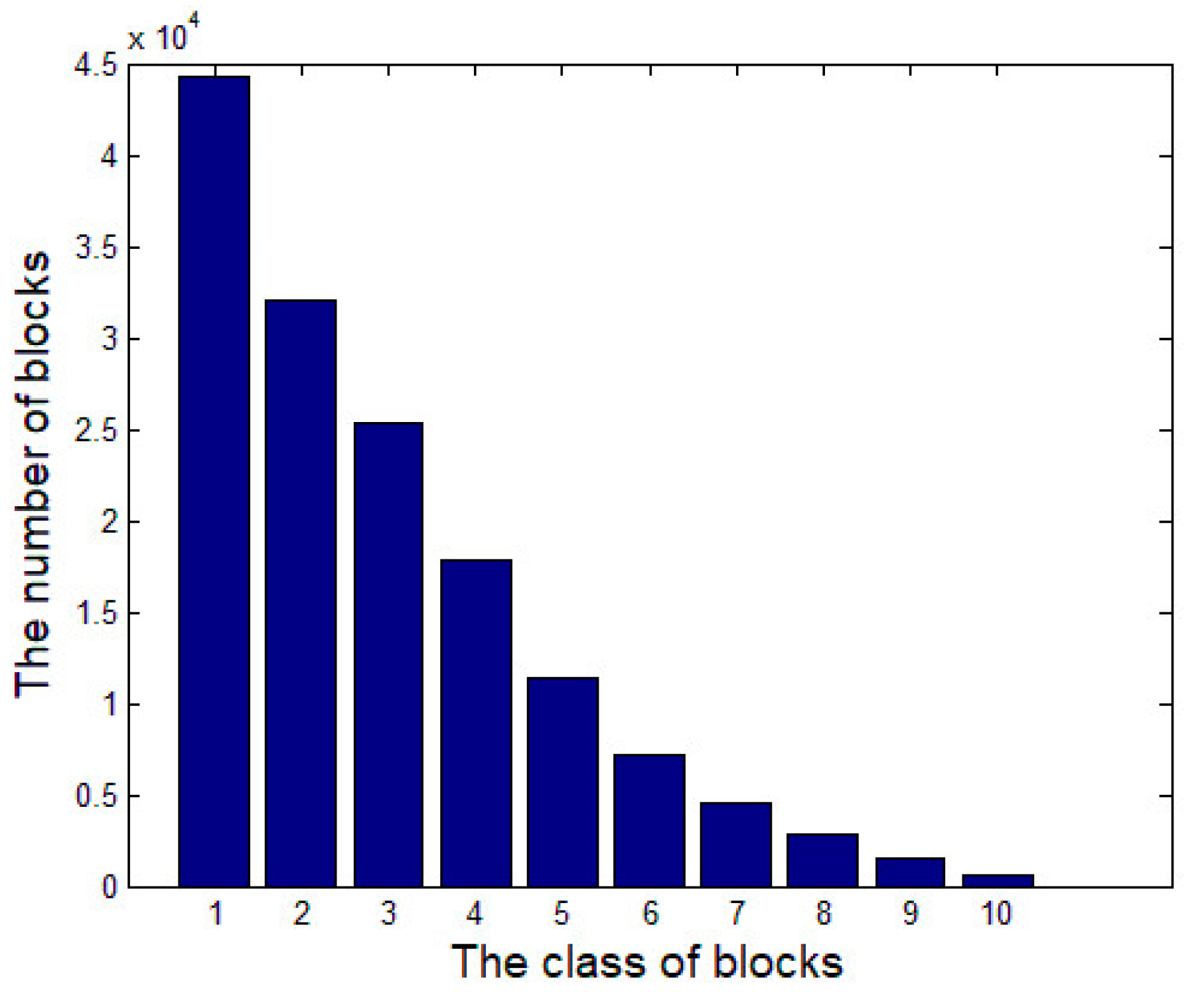
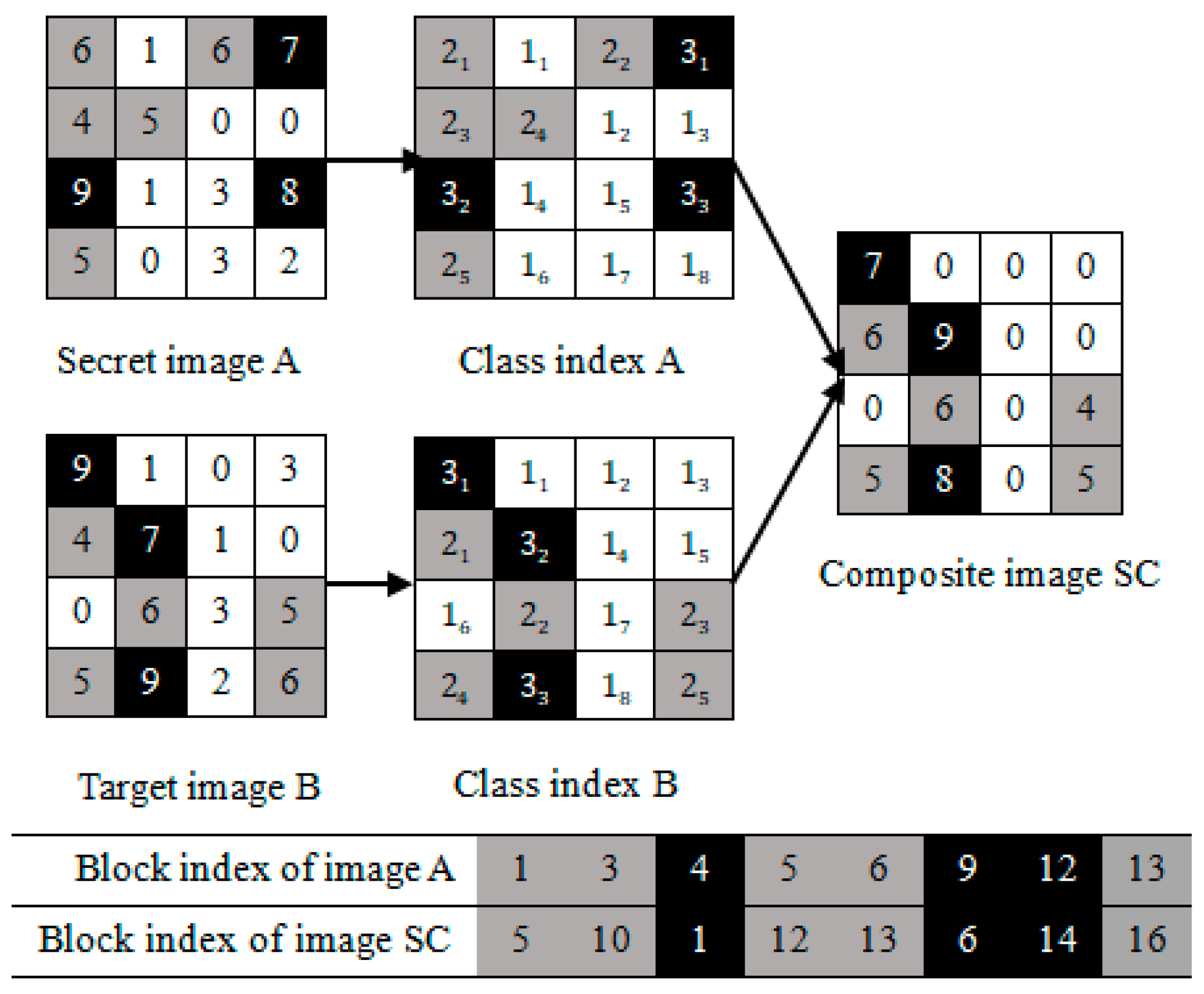
3.1. Image Blocks Matching of the Last (K-T)-Classes

The image blocks matching for the last (K-T)-classes is described as follows:

Firstly, cluster all $\mathrm{SDs}$ of secret blocks into K classes by a traditional clustering method such as K-means, and sort the last (K-T)-classes in ascending order for $K-T+1<i<j\le K$.

Secondly, classify the target blocks with the classes’ volumes of secret image, so that each target class has a same volume with the corresponding secret class. Suppose the $\mathsf{\alpha }\mathrm{th}$ secret class contains ${\mathrm{n}}_{\mathsf{\alpha }}$ image blocks, where $K-T+1\le \alpha \le K$. Then, the first $n_{K-T+1}$ target blocks are divided into the first class, the subsequent $n_{K-T+2}$ target blocks are divided into the second class, and so on, until the Kth class.

Finally, distribute a class index ${\alpha }_{\beta }$ to each block, where ${\alpha }_{\beta }$ is the $\beta th$ block of the $\alpha th$ class and $1\le \beta \le n_{\alpha }$. And the ${\alpha }_{\beta }th$ secret blocks should be replaced to ${\alpha }_{\beta }th$ target blocks, and the initial composite image is generated.

In order to explain the process of the last (K-T)-classes, suppose $K=3$ and $T=1$, a simple example of block matching in last 2-classes are shown in Figure 4.

The secret tiles are divided into three classes here:

(1) $SDs\left\{0,1,2,3\right\}$ belong to the class 1, they are labeled as “white”;

(2) $SDs\left\{4,5,6\right\}$ belong to the class 2, they are labeled as “gray”;

(3) $SDs\left\{7,8,9\right\}$ belong to class 3, they are labeled as “black”.

Next, cluster target blocks based on the classes’ volumes of secret images, then the class index of block can be obtained by scanning $\mathrm{SDs}$ classes in the raster order.

For example, in secret image A, the second secret block is the first of class 1 that is assigned as $1_1$, the seven block is the second of class 1 that is assigned as $1_2$,…, and so on, a one-to-one map between secret and target blocks will be created. The ${\mathsf{\alpha }}_{\mathsf{\beta }}\mathrm{th}$ secret blocks in last 2-classes can be transformed to ${\alpha }_{\beta }th$ target blocks and replace them, while the pixel values of the class 1 are changed to 0, and they will be patched in Section 3.2. Finally, the composite image SC is generated.

The SC has a similar texture pattern with the target image because it has pretty big SDs with the secret image, which results in the SC having a similar appearance to the target image while hiding the secret image. Moreover, the secret image can be recovered using the SC.

To recover the secret image from the composite image, the receiver only needs to know the class index A. According to the table in Figure 4, the receiver will know how to rearrange the composite blocks to restore the secret blocks. For example, the first block of the composite image should be put back to position 4, and the fifth block should be put back to position 1, as indicated in the table.

3.2. Image Blocks Patching of the First T-Classes

To embed the AI from the last (K-T)-classes transformation, the AI should be represented as a secret segment, and the image blocks in the first T-classes can be patched according to the secret segment. Before that, the AI can be compressed by the Huffman code method, and is denoted as $F_1$. However, the number of image blocks in the first T-classes is not sufficient to hide $F_1$ through patching image blocks because the length of $F_1$ is very large. Therefore, $F_1$ will be divided into two parts called $B{F}_1$ and $S{F}_1$, in which $B{F}_1$ can be hidden by patching blocks, and $S{F}_1$ can be embeded by final RDH. But determining the length of $B{F}_1$ remains a challenge.

Suppose the length of secret segment is $l$, and each block in the first T-classes can be divided into $M$ categories ($M=2^l$). We use each block to represent different secret segments. For example, if $M=4$, the block may be represented secret segments “00”, “01”, “10” or “11”.

The total number of image blocks in the first T-classes is $TN=n_1+\dots +n_T$, where $n_1,\dots ,n_T$ is the number of each classes’ blocks, respectively. Thus, the length of $B{F}_1$ is $l\ast TN$, and ${\mathrm{BF}}_1$ should be divided into $TN$ secret segments and each segment contains l bits. We calculate the decimal values $E_i$($1<i<TN$) for all segments, and count the frequency $n_1,\dots ,n_M$ of each $E_i$. Then, we divide the secret blocks in the first T-classes into new $M$ categories by the frequency $n_1,\dots ,n_M$, and the secret blocks in each class have the same volume as the corresponding frequency.

Suppose the $\alpha th$ image class contains $n_{\alpha }$ blocks, where $1\le \alpha \le M$. The first $n_1$ secret blocks with the smallest $\mathrm{SDs}$, the second $n_2$ secret blocks with second-smallest $\mathrm{SDs}$, and so on, until the unmatched secret blocks are divided. Next, distribute a compound index ${\alpha }_{\beta }$ to each secret block, where ${\alpha }_{\beta }$ is the $\beta th$ block of the $\alpha th$ class and $1\le \beta \le n_{\alpha }$. Then, the blank blocks of composite image can be divided into new $M$ categories by the scanning order of $B{F}_1$, in which the blocks will be distributed a class index ${\alpha }_{\beta }$ accordding to the decimal values $E_i$ of each secret segment. Finally, the unmatched secret blocks can be patched into composite image, in which the ${\alpha }_{\beta }th$ secret block should be replaced to the ${\alpha }_{\beta }th$ blank block, and the final transformed image is generated.

To explain the process of image blocks patching in the first T-classes, based on the example of Figure 4, block patching in the first class are shown in Figure 5. Assuming $M=2$ and $B{F}_1={\left(01110110\right)}_2$, the secret image blocks should be patched to composite image blocks in the first class, which are labeled as “white”. Firstly, $B{F}_1$ can be divided into the secret segment “0” and “1”, and we can count that the number of “0” is three, and the number of “1” is five. Then, according to the number of “0” and “1”, the secret blocks of the first T-classes can be sorted by SDs, and divided into two new categories:

(1)

The first-3 image blocks of the ascending sequence belong to class 1; they are labeled as “red”;

(2)

The last-5 image blocks of the ascending sequence belong to class 2; they are labeled as “yellow”.

Next, the blank blocks in the composite image can be divided by the scanning order of $B{F}_1$. For example, the first bit in the $BF$ is 0. Thus, the first position of unmatched blocks in the composite image belongs to class 1; they are labeled as “red”. The second bit is 1. Thus the second position of unmatched blocks belongs to class 2; they are labeled as “yellow”. Then, the new class index ${\alpha }_{\beta }$ for the unmatched block can be defined. Finally, the ${\alpha }_{\beta }th$ secret blocks should be replaced to the ${\alpha }_{\beta }th$ blank block, and the final transformed image is generated.

To recover $B{F}_1$ and the composite image, the receiver only needs to know the class index A. Note that the class index A is different from Section 3.1. We can combine these two class indexes to record the final class index to reduce the amount of additional information. Firstly, the total number $TN$ and different classes’ volume of transformed image in the first T-classes can be obtained by the class index A. In the example of Figure 5, $TN=8$, the volume of image block belonging to class 1 is 3, and the volume of image block belonging to class 2 is 5. Next, we select the transformed image blocks in the first $8$ by ascending SD, in which image blocks in the top 3 by ascending SD belong to class 1, and image blocks in the last 5 by ascending SD belong to class 2. Therefore, $B{F}_1$ and the class index SC can be restored. In fact, by the class index A and the class index SC, the receiver can reconstruct the table in Figure 5 completely, and according to the table, the secret blocks can be recovered by rearranging the transformed blocks. For example, the second block of the transformed image should be put back to position 7, and the third block should be put back to position 2, as indicated in the table.

3.3. Algorithm Explaining of the Proposed Method

According to Section 3.1 and Section 3.2, the framework of image embedding in the proposed method is shown in Figure 2, and the detailed algorithm about stego-image creation is described as follows (Algorithm 1).

Algorithm 1 Stego-image creation

Input: A secret image, target image and secret key sk.

Output: A stege-image.

1: for each color channel of secret and target images do

2:        Divide each color channel of two images into non-overlapping $4\times 4$ blocks.

3:        for each block in these images do

4:                Calculate the mean and SD of each block.

5:        Cluster secret blocks into K classes by K-means clustering according to their SDs, and classify target blocks into K classes according to their SDs, the scanning order and the classes volumes of secret image. Assign a class index for each color channel of two images.

6:        for each block in the last (K-T)-classes do

7:                Match image blocks having same class index.

8:                Shift pixel values with Equations (3)–(5) and (7), and rotate each block with the optimal angel.

9:        Record the $LM$, $\Delta u^{\prime }=2\left|\Delta u\right|/\lambda$ and $\vartheta$ as the parameters for restoring the image.

10:        Replace the target image blocks with the corresponding transformed blocks in the last (K-T)-classes, and generate the composite image.

11:      Compress the AI $F_1$, which brings from the last (K-T)-classes transformation, and divide them into $B{F}_1$ and $S{F}_1$.

12:        for each block in the first T-classes do

13:                Distribute a class index ${\alpha }_{\beta }$ to these blocks of secret and composite images by $B{F}_1$, then patch the ${\alpha }_{\beta }th$ secret image blocks into current position of composite image to hide $B{F}_1$.

14:                Shift pixel values with Equations (3)–(5) and (7), and rotate patched blocks with the optimal angel.

15:        Compress new parameters including $LM$, $\Delta u^{\prime }=2\left|\Delta u\right|/\lambda$ and $\vartheta$ as $F_2$.

16:        Replace the target image blocks with the corresponding transformed blocks.

17: Combine three color channels to generate the final transformed image.

18: Combine $S{F}_1$ and $F_2$ to obtain AI, and use secret key sk to encrypt the information, then embed the encrypted sequence into the transformed image by RDH method.

19: return The stego-image.

And then the processing of secret image recovery can be described as follows (Algorithm 2):

Algorithm 2 Secret image recovery

Input: A stege-image and secret key sk.

Output: A secret image.

1: Extract the encrypted sequence and recover the transformed image by RDH method.

2: Decrypt and decompress the sequence to obtain $S{F}_1$ and $F_2$.

3: for each color channel of transformed images do

4:        Divide each color channel of transformed image into non-overlapping $4\times 4$ blocks.

5:        for each block in the image do

6:              Calculate the mean and SD of each block.

7:        Obtain class index A according to $F_2$, and classify the transformed blocks into K classes by their SDs and class index A, then generate $B{F}_1$, class index SC and B.

8:        for each block in the first T-classes do

9:              Rotate the block in the reverse direction and shift pixel values according to $F_2$.

10:              Rearrange the transformed blocks in the first T-classes to generate the composite image by the mapping relation between class indexes A and SC.

11:        Combine $B{F}_1$ and $S{F}_1$ to obtain $F_1$.

12:        for each block in the last (K-T)-classes do

13:              Rotate the block in the reverse direction and shift pixel values according to $F_1$.

14:              Reassign the transformed blocks in the last (K-T)-classes by the mapping relation between class indexes A and B.

15: return The original secret image.

4. Experimental Results

In the RIT method, the AI can be embedded into the transformed image to obtain the stego-image using an RDH method. Since a stego-image with poor quality will arouse suspicion from attackers, we mainly focus on improving the stego-image quality. While the stego-image quality will decrease sharply with the increase of the amount of AI, several experiments have been designed to test the proposed method from the perspectives of AI and stego-image quality in this section.

In Section 4.1, we bring some performance indexes to measure AI and stego-image quality. In Section 4.2, we give an example that reflects the security of the proposed algorithm, and determine the optimal parameters for different test images by the relationship between AI and transformed image quality. In Section 4.3, we introduce the transformed results of secret image and compare our method with previous methods from performance and feature evaluation results. Moreover, we conduct a detailed analysis and discussion of the evaluation results.

4.1. Performance Indexes

The number of AIs is one of factors which leads to the degradation of transformed image quality. To measure AIs, assuming the size of secret image is $N_1\times N_2$, and the rate of AI in the color image can be calculated by:

$$bpp=\frac{AI}{3\times N_1\times N_2}.$$

(8)

The visual quality of stego-image is very important because the stego-image can be not detected by the attacker. The root mean square error (RMSE) and structural similarity index measurement (SSIM) are two objective evaluation indexes which are widely used in image quality evaluation. RMSE is represented by:

$$RMSE=\sqrt{{{\displaystyle \sum }}_{c=1}^3{{\displaystyle \sum }}_{i=1}^{N_1}{{\displaystyle \sum }}_{j=1}^{N_2}{\left(I\left(i,j\right)-I\prime \left(i,j\right)\right)}^2}.$$

(9)

where $I\left(i,j\right)$ and $I\prime \left(i,j\right)$ are pixels in the secret image and the stego-image, respectively. SSIM is calculated by the following formula:

$$SSIM\left(x,y\right)=l{\left(x,y\right)}^{\alpha }·c{\left(x,y\right)}^{\beta }·s{\left(x,y\right)}^{\gamma }.$$

(10)

and $l\left(x,y\right)=\frac{2u_x{u}_y+C_1}{u_x{}^2+u_y{}^2+C_1}$, $c\left(x,y\right)=\frac{2{\sigma }_x{\sigma }_y+C_2}{{\sigma }_x{}^2+{\sigma }_y{}^2+C_2}$, $s\left(i,j\right)=\frac{{\sigma }_{xy}+C_3}{{\sigma }_x{\sigma }_y+C_3}$, ${\sigma }_{xy}=\frac{1}{N-1}{{\displaystyle \sum }}_{i=1}^N\left(x-{\sigma }_x\right)\left(y-{\sigma }_y\right)$, where $x$ and $y$ are secret image and stego-image, respectively; $u_x$, $u_y$, ${\sigma }_x{}^2$, ${\sigma }_y{}^2$, ${\sigma }_{xy}$ are the mean values, variances and covariance, respectively; $C_1$, $C_2$ and $C_3$ are small constants for avoiding a zero denominator in Formula (11). $\alpha$, $\beta$ and $\gamma$ are more than 0, and they are used to adjust the proportion of components $l\left(x,y\right)$, $c\left(x,y\right)$ and $s\left(x,y\right)$. SSIM can evaluate quality of brightness, contrast and structure of nd the structure is the main influencing factor. When $\alpha =\beta =\gamma =1$ and $C_3=C_2/2$, SSIM is simimage, aplified as:

$$SSIM\left(x,y\right)=\frac{\left(2u_x{u}_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left(u_x{}^2+u_y{}^2+C_1\right)\left({\sigma }_x{}^2+{\sigma }_y{}^2+C_2\right)}.$$

(11)

4.2. Parameter Settings

In order to improve the safety, we firstly adopt the Huffman code to compress AI, and encrypt them using the secret key sk, then use the RDH method in [8] to embed the encrypted information.

Figure 6 gives an example that reflects security of the algorithm. Figure 6a is the secret image, Figure 6c is the stego-image, which is similar to the target image Figure 6b. If the attacker has a wrong key, he only can obtain the messy image such as Figure 6d. Thus, only the receiver with the correct key can recover the secret image.

We used MATLAB-R2014a to perform the experiments; our test machine was an Asus PC with 4200 CPU @2.80 GHz and 8.00 GB RAM. The test images shown in our experiments are listed in Figure 7, which are adopted by much computer or camera equipment in the PNG format. In this subsection, four typical combinations of secret and target images in Figure 7 are applied to discuss how to correctly set the parameters of the proposed method. Moreover, we can obtain different AI and transformed image qualities by setting different parameters for these test images. However, the ultimate stego-image quality can be improved when we have higher stego-image quality and lower AI. Therefore, the optimal parameters of the proposed method can be found by the relationship of AI and transformed image quality.

In the traditional RIT method [19], they divide secret and target images into non-overlapping $S\times S$ blocks, and classify these blocks into K classes for block matching. After block matching, the image blocks will be shifted by Equations (3)–(5) and (7) in order to be as similar as possible with the target image. In Equations (4) and (5), to solve the overflow/underflow problem, $U$ is set as a parameter to control the balance between the number of overflow and underflow and mean’s bias of target image. In Equation (6), to reduce the amount of AI, $\lambda$ also is set as a parameter to make a trade-off between the amount of AI and the mean’s bias of target image. Thus, $K$, $U$, $\lambda$ and $S$ are four parameters which can affect the AI and transformed image quality. However, the parameter $K$, $U$, $\lambda$ and $S$ are independent and are not affected by our improved algorithm. Therefore, we set $K=10$, $U=10$, $\lambda =4$ and $S=4$, which is same as the traditional RIT method, and adjust $T$ and $M$ to the optimal parameter.

To verify that the original optimal parameters are also applicable to the improved algorithm, we take the block size parameter $S$ as an example. As the block size $S$ increases, the quality of transformed image will decrease because the mean of the secret block deviates from the target block, while the AI will decrease because the number of image blocks decreases. Therefore, in

Table 1. The results with different block sizes.

Block Size	Transformed Image (RMSE)	Stego-Image (RMSE)	AI (bpp)
$3\times 3$	10.725	14.990	0.852
$4\times 4$	13.001	13.310	0.488
$6\times 6$	16.000	16.060	0.227
$8\times 8$	17.918	17.947	0.134

, we can see that when the block size is set to be $3\times 3$, the amount of the AI will reach 0.852 bpp, which is quite large for RDH method. By increasing the block size, the amount of the AI (AI) will reduce, but the quality of the transformed image and stego-image will decrease. When the block size is larger than 4, the RMSE of the transformed image and stego-image will increase rapidly but the amount of the AI decreases slowly. Therefore, we still set $S=4$.

Next, since different $T$ and $M$ have effect on AI and transformed image quality, we can determine the appropriate $T$ and $M$ by measuring the amount of AI and the root of mean square error (RMSE) of the transformed image. The AI and RMSE of the transformed image with different parameters $T$ and $M$ for four examples are shown in

Table 2. The results for setting parameters $\mathrm{T}$ and $\mathrm{M}.$

	Example 1		Example 2		Example 3		Example 4		Average
	AI	RMSE	AI	RMSE	AI	RMSE	AI	RMSE	AI	RMSE
$T=1$	0.852	18.868	0.738	12.841	1.070	16.631	0.973	11.139	0.908	14.870
$T=3$	0.541	19.131	0.494	13.023	0.584	16.756	0.495	11.242	0.529	15.038
$T=5$	0.564	19.959	0.495	13.756	0.573	17.251	0.489	11.762	0.530	15.621
$T=7$	0.552	21.050	0.475	14.777	0.561	18.426	0.471	12.442	0.515	15.682
$M=1$	0.555	19.143	0.484	12.982	0.599	16.927	0.499	11.249	0.652	15.075
$M=2$	0.540	19.111	0.490	12.971	0.586	17.369	0.493	11.250	0.627	15.175
$M=3$	0.542	19.068	0.490	12.994	0.573	17.704	0.496	11.237	0.620	15.175
$M=4$	0.540	20.138	0.510	13.023	0.578	17.900	0.496	11.248	0.618	15.251

.

In our method, the parameter $T$ is used to divide the original classes into two part. When the $T$ increases, the transformed image quality will decrease because the number of image blocks used to match by traditional RIT method is reduced, while the amount of AI will decrease because the number of image blocks used to hide partial AI is increased. To choose an appropriate $T$, we maintain the parameter $M$ such as $M=3$, and change $\mathrm{T}$. In the average values of the table, when $T$ is larger than 3, the average RMSE of the transformed image will increase rapidly but the average AI increases slowly. Thus, $T=3$ is an appropriate value.

As mentioned in Section 3.2, the parameter $M$ is used to express the number of secret segments represented by each image block. When $M$ increases, the AI will decrease because each image block can represent more secret bits to be patched into the composite image, while the transformed image quality is not changed too much. To choose an appropriate $M$, we maintain the parameter $T=3$, and change the value of $M$. In the average values of the table, when $M$ is larger than 3, the average AI is decreased very slowly because the amount for recording the class index is also increased, while the transformed image quality is increased. Thus, $M=3$ is an appropriate value.

4.3. Comparison the Proposed Method with Previous Methods

4.3.1. Performance Comparison

In order to represent the results of each transformed phase and prove the algorithm’s feasibility, the transformed results of secret image are shown in Figure 8. There is the secret image, composite image, transformed image and stego-image of four example. Take Figure 8(a1–d1) as an example, we firstly transform the secret image (a1) blocks in the last (K-T)-classes to generate the composite image (b1). Note that the pixel values of unmatched blocks in the first T-classes is set to 0. By the composite image, we only obtain the texture details of target image because these matched blocks have slightly big SDs. Then, we patch the secret blocks according to the AI from the last (K-T)-classes transformation to obtain the transformed image (c1). Finally, we embed the AI by the RDH method to achieve the stego-image (d1).

To make comparison with Hou et al.’s method, the proposed method uses the Huffman coding method to compress AI, and encrypts the compressed information by using secret key sk, then adopts RDH scheme in [8] to embed the encrypted information into the transformed image, which are same with Hou et al.’s method.

In Figure 9, we select another target image (Figure 9b) which is irrelevant with the secret image (Figure 9a). Although the transformed image (Figure 9c) in Hou et al.’s method has less visual distortion than the proposed method (Figure 9e), the ultimate stego-image created by the proposed method (Figure 9f) has better visual quality than Hou et al.’s method (Figure 9d). Note that stego-image quality is the key because it is the final image sent to the receiver. Therefore, we can develop the RIT by improving the stego-image quality.

To shows the performance intuitively, we test the secret and target images in Figure 7, and the average results are listed in

Table 3. The average result comparison with Hou et al.’s method.

Methods	Stego-Image (RMSE)	Stego-Image (SSIM)	AI
Hou et al.’s method	17.653	0.593	0.647
Proposed method	17.178	0.602	0.527

. From the table we can see, the proposed method outperforms Hou et al.’s method on both lower AI and higher stego-image quality. There are two reasons for this: firstly, we can patch the secret blocks in the first T-classes to hide the partial AI produced by transforming the last (K-T)-classes, which leads to the quite large reduction of AI. Secondly, we need to embed the AI into the transformed image to generate the stego-image. Thus, the visual quality of stego-image is determined by the amount of AI and the visual quality of the transformed image. In this experiment, the visual quality of transformed image is not changed too much, while the AI is decreased significantly. Therefore, the visual quality of stego-image can be improved.

4.3.2. Feature Comparison

In addition to performance comparison, a feature comparison in terms of reversibility, high capacity, image expansion and high security is shown in

Table 4. Feature comparison with previous methods.

Method	Reversibility	High Capacity	Image Expansion	High Security
Zhou et al.’s method	No	No	No	Yes
Wu et al.’s method	Yes	No	Yes	No
Yang et al.’s method	Yes	Yes	No	Yes
Lai et al.’s method	Yes	Yes	Yes	Yes
Lee et al.’s method	No	Yes	No	Yes
Proposed method	Yes	Yes	No	Yes

. The proposed method is reversible, whereas the recovered image is only similar to the secret image in Zhou et al.’s method and Lee et al.’s method. In other words, their methods are not reversible. Although Wu et al.’s method is reversible, it can not ensure a relatively large payload (more than 1 bit per pixel), while the proposed method can achieve high capacity. Compared with Lai et al.’s method, the stego-image in the proposed method is not expanded because it has the same size as the secret image. Moreover, the secret image of the proposed method has high security because it is hard to recover the secret image only by the stego-image which looks like the freely-selected target image.

5. Conclusions

In this paper, we propose a new RIT technique for color images by patching secret blocks in the first T-classes to hide the partial AI. Thus, AI for recovering each secret block is largely reduced, meaning that we improve the quality of stego-image significantly. In the scheme of RIT, the RDH scheme is required to embed the AI into the transformed image. As we can see from the given examples, sometimes the RDH scheme will destroy the quality of transformed image; thus, a good RDH method is desired. Moreover, more block features should be chosen to improve the visual quality of transformed image, and thus improve the visual quality of stego-image. Therefore, in the future, we will try to design new RDH technique and feature extraction algorithm for the RIT scheme, by which we will continue to improve the visual quality of the ultimate camouflage image.