1. Introduction
Information is generally available online through various mediums such as the world wide web (WWW). This information is primarily provided as unstructured data, such as text that lacks sufficient information for advanced applications to exploit the content effectively. The desire to address this problem has led to the development of new standards and formats that enable consumption and distribution of publicly structured data between different parties; this structured shareable data is known as Linked Open Data (LOD). There are four principles of Linked Open Data [
1]. Firstly, the Uniform Resource Identifier (URI) must be used to identify resources in any LOD dataset. Secondly, HTTP URIs must be used to look up resources. Thirdly, useful information must be provided on standard formats (e.g., RDF, SPARQL) at each URI. Lastly, resources are linked for further exploration. There are over one thousand linked data datasets in different fields [
2]; some specialize in a particular knowledge domain such as books or music while others are generic, covering many cross-domain concepts such as the popular LOD provider, DBpedia [
3]. Due to the extensive offering of structured data in different domains, LOD has been investigated in the field of recommender systems. In particular, LOD provides comprehensive open datasets with multi-domain concepts and relationships to each other, and these relationships enable recommender systems to identify relevant concepts across collections [
4]. Furthermore, the LOD standards and techniques facilitate the task of recommender systems by providing standard interfaces for retrieving the data (e.g., RDF, SPARQL), eliminating the need for additional raw data processing. LOD also provides ontological knowledge of data that allows recommender systems to identify the relationship between concepts [
5].
The usage of LOD has been explored in different ways in recommender systems, mainly by exploiting its graph nature representation or by various statistical measures [
6]. Content-based recommender systems recommend items based on their similarity to the preferences of the user. There are various approaches to estimate the similarity between entities: Distance-based, feature-based, statistical, and hybrid approaches [
7]. Distance-based methods estimate the similarity between entities through a distance function such as SimRank [
8], PageRank [
9], and HITS [
10]. Feature-based methods assume that entities can be represented as feature sets, and the similarity of entities is based on the common characteristics between their feature sets; e.g., the Jaccard index [
11], Dice’s coefficient [
12], and Tversky [
13]. Statistical-based similarity methods rely on statistical data generated from the entity underline information and the hybrid methods combines some of these approaches into one.
One approach that exploits the graph structure of LOD estimates resource relatedness as a function of their semantic distance in the graph. The intuition behind this approach is that the more resources linked to each other in the LOD graph, the more related they are. This intuition is the principal of LOD resource relatedness measures, the Linked Data Semantic Distance (LDSD) [
14], along with a more recent measure based on it, Resource Similarity (Resim) [
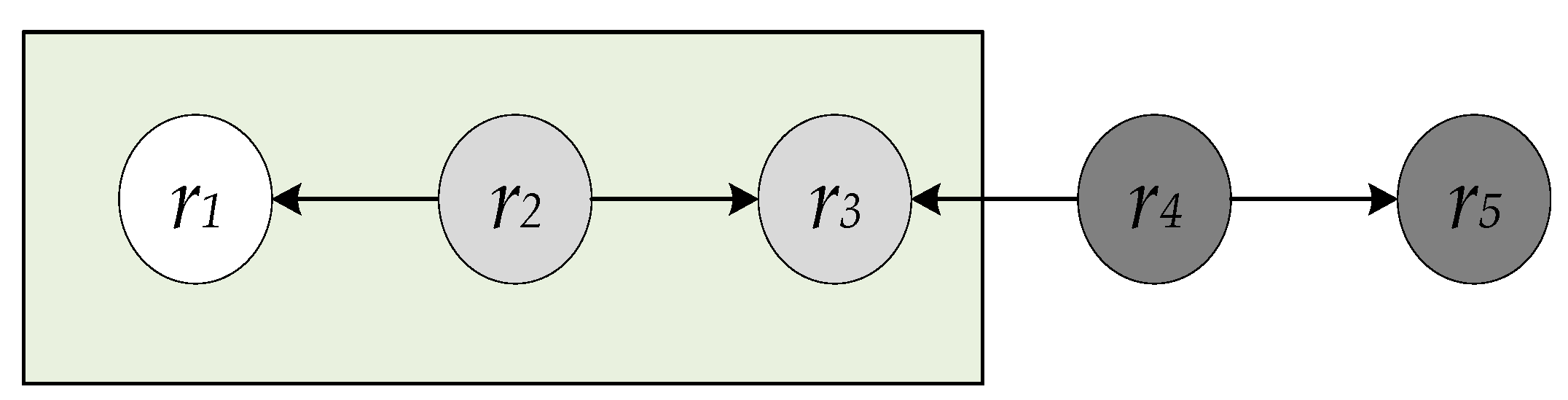
15]. One of the disadvantages of the LDSD approach is that it calculates only the semantic distance between directly connected resources or indirectly via an intermediate resource. As a result, resources located more than two links away are automatically considered unrelated to each other. For instance,
Figure 1 shows an example snapshot of a LOD dataset with five resources. In this example, resources r
2 and r
3 are reachable to the resource r
1 in LDSD; however, resources r
4 and r
5 are not reachable to resource r
1 and therefore are considered as unrelated to r
1. In contrast, Resim improves this limitation by including an additional measure of similarity exclusively to resources that are more than two links apart. However, this additional measure calculates the similarity between resources based on their properties only without considering the graph structure for these more distant resources.
In this paper, we first extend the indirect distance calculations in LDSD to include the effect of multiple links of differing properties within LOD while prioritizing link properties [
16]. This extension is incorporated within LDSD to measure the effect of including heterogeneous link types in the calculation of semantic distance, resulting in a new variation of the LDSD approach, called wtLDSD. Next, we introduce an approach that extends the coverage of LDSD-based semantic distance approaches to resources that are more than two links apart [
17]. This approach is beneficial in several ways; one of which is to enrich related resources for those isolated resources with sparse links to others. Notably, there is a strong correlation between LOD-based recommender systems performance and the number of resource links, as the accuracy of LOD-based recommender systems declines for sparse resources [
15]. Therefore, propagating semantic links further through the graph of LOD increases resource coverage and may lead to a larger recall. Furthermore, even for well-linked resources, propagating links more widely might be beneficial for recommending related resources from another domain, e.g., linking a movie to a related book.
To accomplish this propagation, we utilize an all-pairs shortest path algorithm, the famous Floyd–Warshall algorithm [
18], to propagate the semantic distances throughout the graph of linked resources. For the evaluation, we conducted an experiment to estimate the relatedness between musical artists in DBpedia, and it showed that our approach not only increases the span of the semantic distance calculations; it also improves the accuracy of the resulting recommendations over LDSD-based approaches.
This paper is organized as follows:
Section 2 presents the related work, followed by background information about Linked Data Semantic Distance (LDSD) in
Section 3. Next,
Section 4 extends the indirect distance calculations to include the effect of multiple links of differing properties within LOD.
Section 5 proposes a propagating approach that extends semantic distance calculations.
Section 6 then presents the evaluation of the approaches we propose. Lastly,
Section 7 summaries this document and discusses future work.
2. Related Work
There are several works that have focused on distance-based similarity approaches in LOD. Passant [
14] introduced an approach, named Linked Data Semantic Distance (LDSD), that enables recommender systems to utilize LOD by estimating the similarity between LOD resources. This similarity is estimated by calculating a semantic distance between LOD resources. This approach depends on only direct links between resources as well as indirect resources through an intermediate resource to compute a semantic distance. Exploiting this approach, Passant in [
19] has built a recommender system for music, called dbrec, that utilizes the popular LOD provider, DBpedia, to recommend musical artists and bands. The first step in this system is creating a reduced LOD dataset to enable efficient semantic distance computations. Next, semantic distances are calculated between each pair of resources that represent musical artists or bands using LDSD. Lastly, related musical artists or bands are predicted for the user. Piao et al. [
15] introduced another variation of the linked data semantic distance approach named Resource Similarity (Resim) that refined the original LDSD to overcome some of its weaknesses such as equal self-similarity, symmetry, and minimality. They also enhanced Resim in [
20] by applying some normalization methods that rely on path occurrences in the data set. They also expanded the number of resources that participate in the semantic distance by using a property-based similarity measure for resources more than two links away. Similarly, Leal et al. [
21] introduced another semantic relatedness approach, called Shakti, that estimated the relatedness between LOD resources. The relatedness in this approach is measured through resources proximity. Particularly, the proximity is measured based on the number of indirect links between resources penalized by their distance length. Though, LDSD and Resim accuracy outperform Shakti as confirmed by [
15]. Besides, Alfarhood et al. [
16] presented improved resource semantic relatedness approaches, wLDSD and wResim, which introduced weights for every link-based calculation in LDSD and Resim. These weights are predicted by estimating the correlation between link properties with their linked resource classes.
Different from distance-based similarity approaches, Likavec et al. [
22] proposed a feature-based similarity measure, called Sigmoid similarity, for domain specific ontologies. This method is based on the Dice measure and takes the underlying hierarchy into account. The main idea behind this approach is that similarity between entities increases when they share common features. Additionally, Meymandpour and Davis [
7] introduced a semantic similarity measure, called PICSS, based on common and characteristic features between resources. Thus, the similarity between two resources increases when they share more informative features such as features with a low number of occurrences. In addition, Traverso-Ribón and Vidal [
23] proposed a semantic similarity approach, called GARUM, based on machine learning. In this approach, a supervised regression algorithm receives several similarity measures of hierarchy, neighborhood, shared information, and attributes and then predicts a final similarity score. The intuition behind this approach is that knowledge represented in the entities accurately describes the entities and makes it possible to determine more precise similarity values. Nguyen et al. [
24] studied the usage of two structural context similarity approaches of graphs, SimRank and PageRank, in the domain of LOD recommender systems. They show that the two metrics are capable in this application, and they can generate some novel recommendations but with a high-performance cost.
Damljanovic et al. [
4] presented a LOD-based concept recommender system that helps users to improve their web search by using appropriate concept tags and topics. They used both a graph-based and a statistical-based method to estimate concept similarities. They found that the graph-based method outperforms their baseline in accuracy whereas the statistical technique produced better-unexpected results. Likewise, Fernández-Tobías et al. [
25] have developed a LOD-based cross-domain recommender system to link concepts from two different domains. They first extract information about the two domains from the LOD datasets, and they then connect concepts using a graph-based distance.
Di Noia et al. [
26] demonstrated that LOD could be effectively employed in content-based recommender systems to overcome issues such as the cold start problem. They introduced a content-based recommender system that uses LOD datasets, in particular, DBpedia, Freebase, and LinkedMDB to recommend movies. Their system gathers contextual information about movies such as actors, directors, and genres from LOD datasets, and it then applies a content-based recommendation algorithm to generate recommendation results. Additionally, Ostuni et al. [
27] presented a hybrid LOD-based recommender system that relies on users’ implicit feedback. Semantic information about items from the user profile and items in DBpedia are combined into one graph in which path-based features could be extracted from. Ostuni et al. [
28] also introduced a content-based recommender system based on semantic item similarities in DBpedia. The semantic similarity between resources is estimated using a neighborhood-based graph kernel that finds local neighborhoods of these items. Figueroa et al. [
29] presented a framework, called AlLied, to deploy and various recommendation algorithms in LOD. This framework allows algorithms to be tested with different domains and datasets.
Clearly, there is an active research community working on the concept of exploiting LOD in recommender systems. Our proposed work builds on these projects but differs in that it expands the coverage and accuracy of LDSD-based approaches.
3. Background
Linked Open Data (LOD) is a graph representation of interlinked data in which resources (nodes) are linked semantically to each other by links (edges) which define the relationship between these resources. In this paper, we use a similar definition for LOD datasets to the one stated in [
14]:
A Linked Open Data dataset is a graph G such as G = (R, L, I) in which:
R = {r1, r2, …, rx} is a set of resources identified by their URI (Unique universal identifier),
L = {l1, l2, …, ly} is a set of typed links identified by their URI,
I = {i1, i2, …, iz} is a set of instances of these links between resources, such as ii = <lj, ra, rb>.
In graphs, links could indicate relatedness between resources, so the more linked the resources the more related they are. In this context, a direct connection between two resources exists when there is a distinct direct link (directional edge) between them. Thus, we define a direct distance (
Cd) between two resources
ra and
rb through a link with a property
li is equal to one if there a link with a property
li exists that links the resource
ra to the resource
rb. The direct distance (
Cd) is defined as:
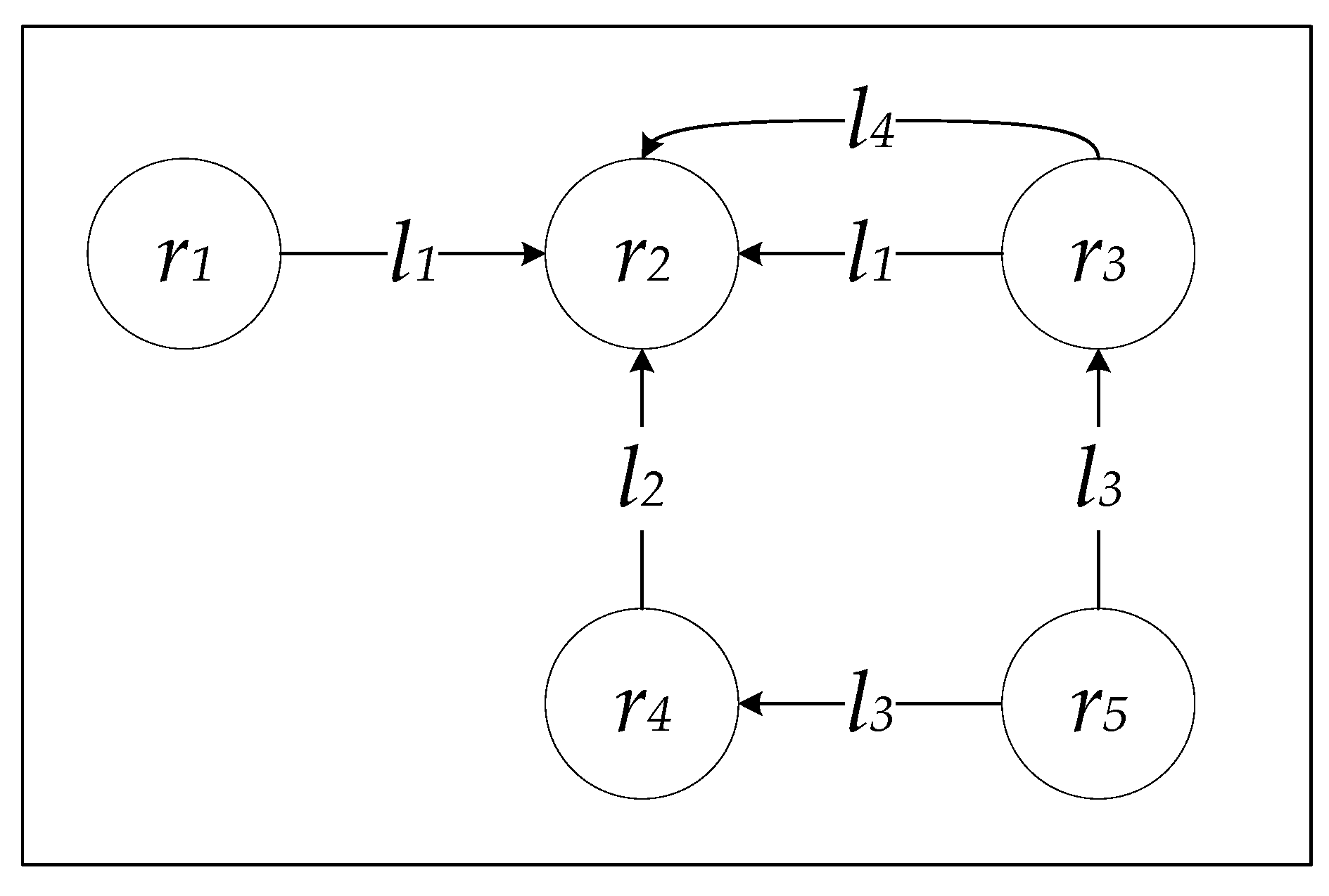
Following the example displayed in
Figure 2, the direct distance between
r3 and
r2 is two (
) because they are linked by links
l1 and
l4, and the direct distance between
r2 and
r3 is zero (
) as there are no direct links originating from
r2.
Resources are not always linked directly to each other; they can be indirectly linked through other resources. Thus, indirect connectivity between two resources happens when they are linked via another resource, and these connections can be either incoming or outgoing from the intermediate resource. Accordingly, there are two types of indirect connections: Incoming and outgoing. Formally, an incoming indirect distance (
Cii) between two resources
ra and
rb is equal to one if there exists a resource
rc such that
rc is directly linked to both
ra and
rb via links of property
li. The incoming indirect distance (
Cii) is defined as:
Similarly, an outgoing indirect distance (
Cio) between two resources
ra and
rb is equal to one if there exists a resource
rc such that both
ra and
rb are directly linked to
rc via links of property
li. The outgoing indirect distance (
Cio) is defined as:
The aforementioned indirect distance notation can be generalized for all intermediate resources as defined below (These versions of
Ci accept three inputs instead of four as in the regular
Ci):
According to the example in
Figure 2, the incoming indirect distance between
r3 and
r4 is one (
) through the resource
r5 linked by the link property
l3, however, the outgoing indirect distance between
r3 and
r4 is zero (
) since there is no resource such that both
r3 and
r4 are directly linked to through the same link property.
Linked Data Semantic Distance (LDSD)
Utilizing the direct and indirect distance concepts, [
14] outlines an approach that measures the relatedness between two resources in the LOD. This approach is called Linked Data Semantic Distance (LDSD) and defined as:
where
is the direct distance (
Cd) between the resources
ra and
rb normalized by the log of all outgoing links from
ra, and it can be calculated as:
is the direct distance (
Cd) between the resources
rb and
ra normalized by the log of all outgoing links from
rb, and it can be calculated as:
is the incoming indirect distance (
Cii) between the resources
ra and
rb normalized by the log of all incoming indirect links from
ra, and it can be calculated as:
is the outgoing indirect distance (
Cio) between the resources
ra and
rb normalized by the log of all outgoing indirect links from
ra, and it can be calculated as:
The LDSD approach produces semantic distances values that range from zero to one. When a semantic distance between two resources equals zero, it means that the two resources are 100% related to each other. On the other hand, if it equals one, it indicates that there is no relatedness whatsoever between these two resources. Nevertheless, LDSD employs only the direct distance (Cd) and the indirect distance (Cii and Cio) in calculating the semantic distance, and it does not include other resources that are located more than one resource away. Therefore, those other resources are automatically considered unrelated to each other.
4. Typeless Indirect Semantic Distance
One of the advantages of LOD is the massive amount of interconnected information, but the sheer volume of data causes several challenges. One of these challenges is that data accuracy in LOD can vary from one dataset to another and even within a given dataset. Several LOD datasets, including DBpedia, have their data composed and linked via human effort. For example, a link in DBpedia that represents the relationship between a song and its album can have different properties (labels) such as “fromAlbum” or “title” depending on the editor who updated the song or album page in Wikipedia. However, when applying LOD in recommender systems, the recommender system must be capable of recommending items even if the resources to be recommended are linked using different properties. Therefore, it may be necessary for a recommender system to consider the relationship between resources even when their links have different properties. This case is especially true when mining a relationship from multiple LOD datasets, each of which may have its own ontology or set of link properties. Despite this, the indirect distance (Ci) of LDSD does not consider these cases when calculating the indirect distance. In this section, we asses extending indirect distance calculations to include the effect of multiple links of differing properties within LOD. This extension is incorporated within LDSD to estimate the effect of including heterogeneous link properties in the semantic distance calculation.
Following the example in
Figure 2, the outgoing indirect distance between
r1 and
r4 is zero (
) since there is no resource such that both
r1 and
r4 are directly linked to through the same link property. However, both
r1 and
r4 are directly connected to
r2 but this is via different link properties (
l1 and
l2). In this section, we develop a typeless incoming and outgoing indirect distance between two resources
ra and
rb to broaden the indirect distance to include cases where the two resources can be linked by two different link properties (
lk and
lp) as displayed in
Figure 3.
Formally, the incoming typeless indirect distance,
TICi, between two resources
ra and
rb is the sum of the incoming typeless indirect link distance,
TILCi, of all links that connect them as follows:
The Incoming Typeless Indirect Link Distance (
TILCi) between two resources
ra and
rb is equal to one if there is a resource
rn such that
rn is directly connected to both
ra and
rb via links of properties
lk and
lp, and it is defined as:
Similarly, the outgoing typeless indirect distance,
TICo, between two resources
ra and
rb is the sum of the outgoing typeless indirect link distance,
TILCo, of all links that connect them as follows:
The Outgoing Typeless Indirect Link Distance (
TILCo) between two resources
ra and
rb is equal to one if there is a resource
rn such that both
ra and
rb are directly connected to
rn via links of properties
lk and
lp, and it is defined as:
Even though as previously stated, the outgoing typeless indirect distance between r1 and r4 is one () through the resource r2 with the links properties (l1, l2), which shows that r1 and r4 are indirectly connected to each other with the typeless variation.
The typeless indirect link distance (
TILC) notation can be generalized for all intermediate resources as:
Weighted Typeless Linked Data Semantic Distance (wtLDSD)
Based on the extended indirect distance calculations to include the effect of multiple links of differing properties within LOD, we introduce another variation of the LDSD approach that measures the effect of including heterogeneous link properties in the semantic distance calculation. This new variation, called wtLDSD, is based on the work we introduced in [
16]:
where
is the direct distance (
Cd) weighted by
for each link with a property
li as follows:
is the direct distance (
Cd) weighted by
for each link with a property
li as follows:
is the incoming typeless indirect distance (
TICi) between resources
ra and
rb normalized by the log of all incoming typeless indirect links to the resource
ra and weighted by
or
for each link of types
lj or
lk correspondingly as follows:
is the outgoing typeless indirect distance (
TICo) between resources
ra and
rb normalized by the log of all outgoing typeless indirect links from the resource
ra and weighted by
or
for each link of types
lj or
lk correspondingly as follows:
The value of every weight
or
is a positive rational number between zero and one (
) and (
). The weight of each link (
or
) can be calculated using several approaches, and we use the Resource-Specific Link Awareness Weights (RSLAW) as it was the best performing approach in [
16]. The weighting factors
and
are introduced in every link-based operation. Thus, higher direct and indirect distance values are produced for those links with high weights (
and
; on the contrary, less emphasis is resulted on these links when they have a low weight, while some link properties are cancelled if their corresponding weight is zero.