Application of Information—Theoretic Concepts in Chemoinformatics
Abstract
:1. Introduction
2. Chemical Descriptors and Shannon Entropy
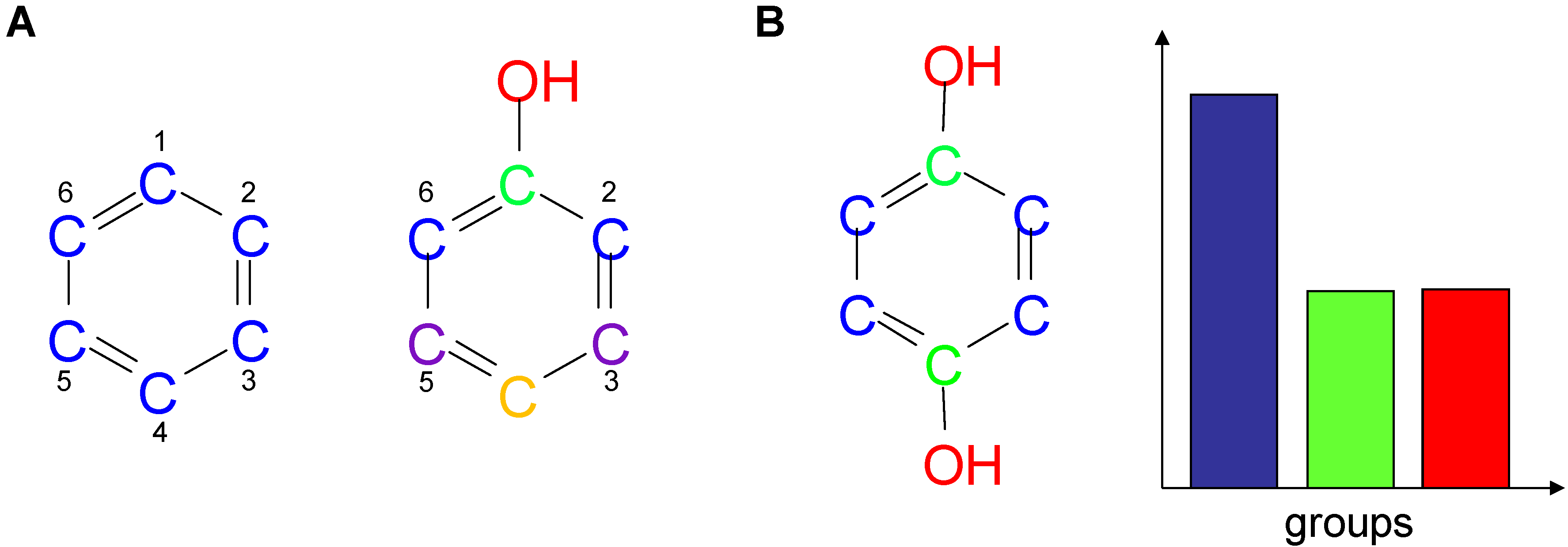
2.1. Information-Theoretic Concepts for Characterizing Topological Properties of Molecules
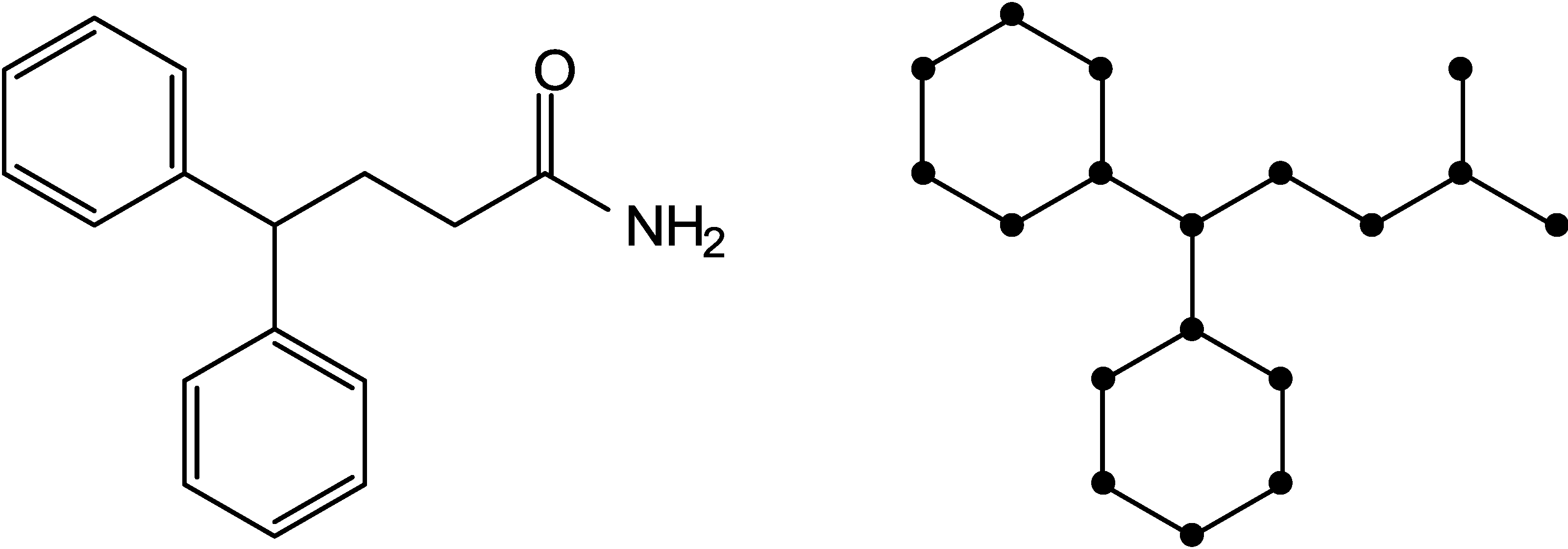
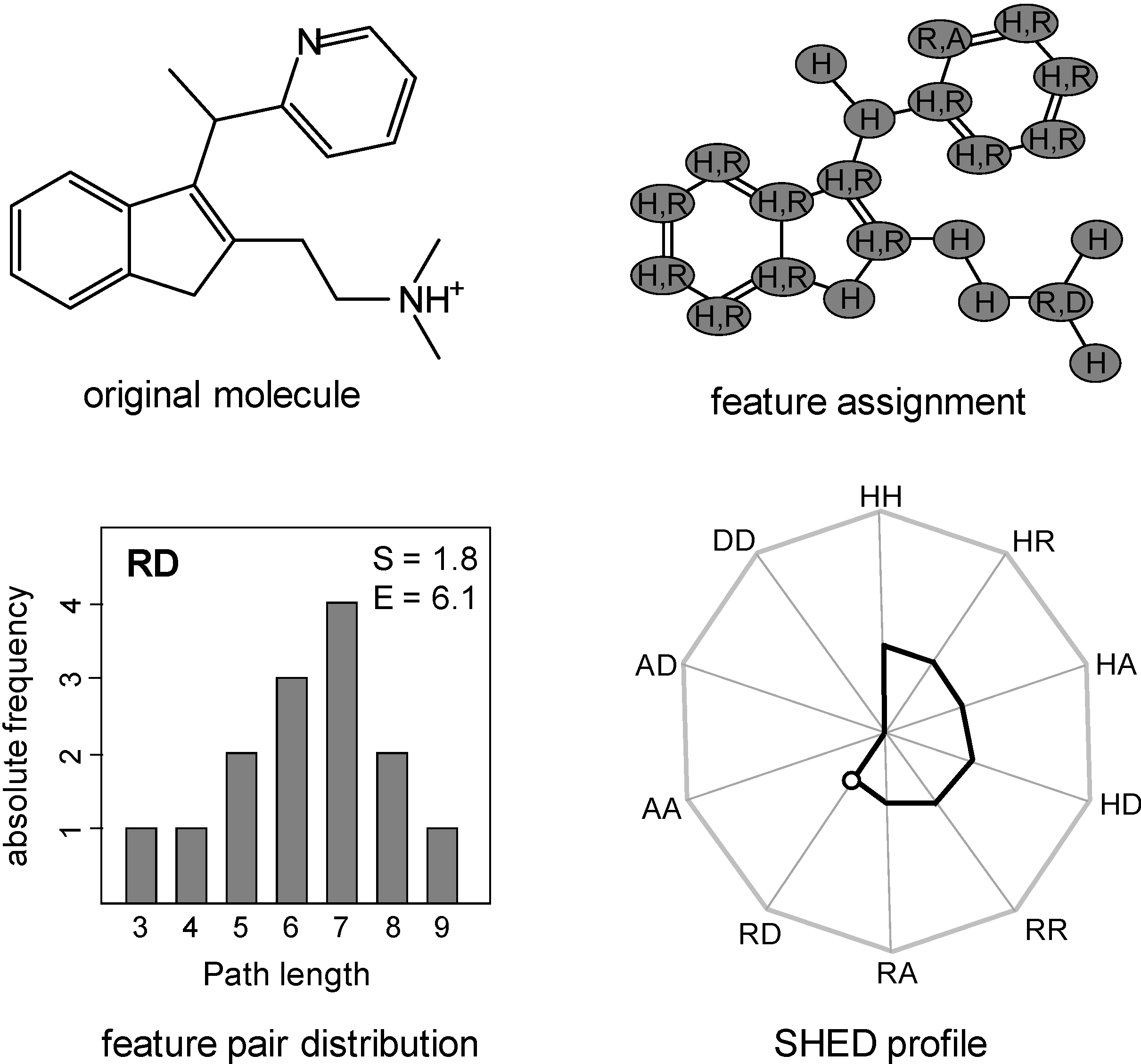
2.2. Shannon Entropy Descriptors (SHED)
3. Information Theory-Based Assessment of Feature Significance in Active Compounds
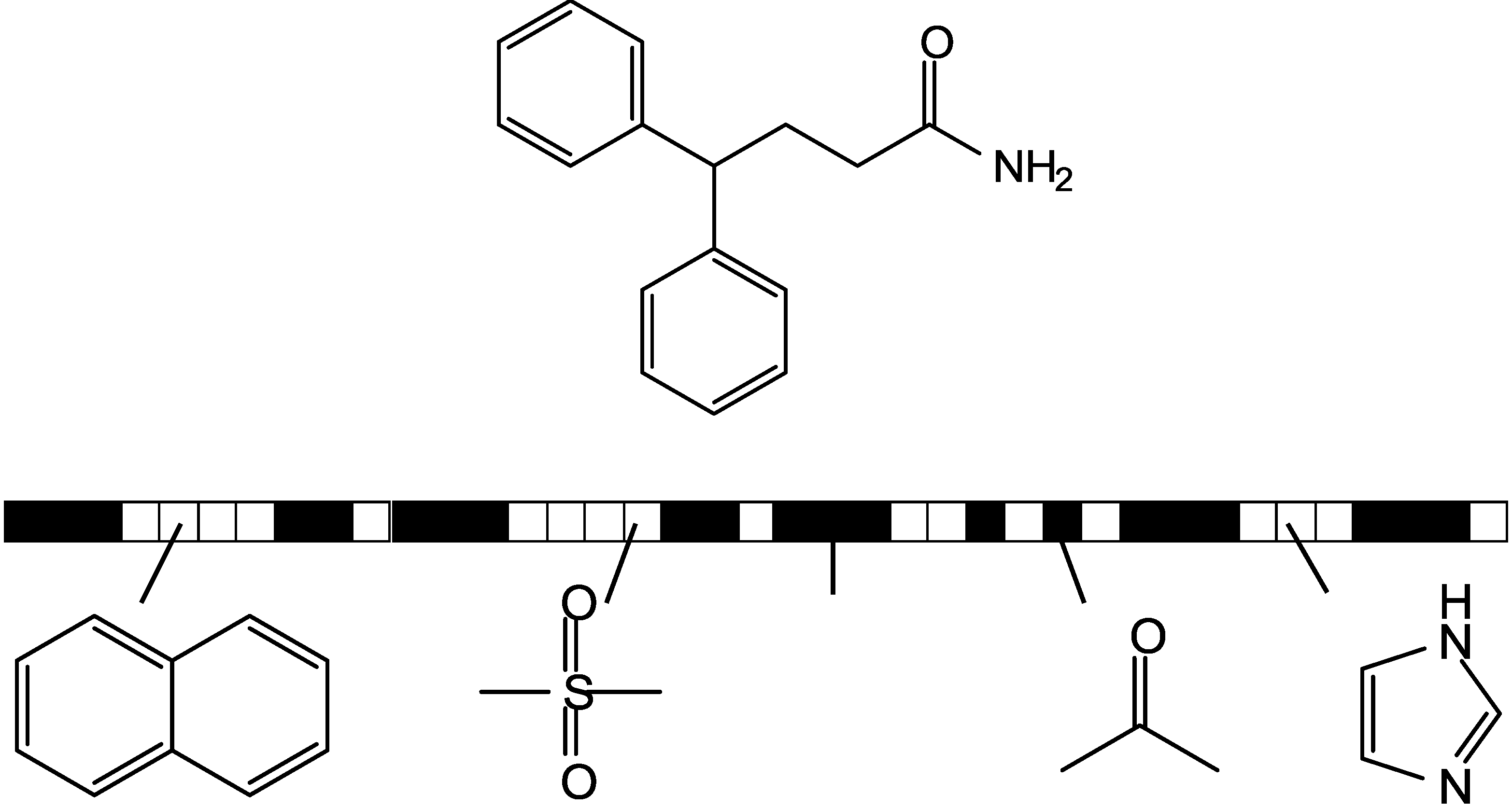
3.1. Kullback-Leibler (KL) Divergence
3.2. Mutual Information (MI)
3.3. Shannon Entropy-Based Fingerprint Similarity Search Strategy

4. Conclusions
References
- Engel, T. Basic overview of chemoinformatics. J. Chem. Inf. Model. 2006, 46, 2267–2277. [Google Scholar] [CrossRef] [PubMed]
- Brown, F.K. Chemoinformatics: What is it and how does it impact drug discovery. Annu. Rep. Med. Chem. 1998, 33, 375–384. [Google Scholar]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar]
- Bajorath, J. Integration of virtual and high-throughput screening. Nat. Rev. Drug. Discov. 2002, 1, 882–894. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1963. [Google Scholar]
- Rashevsky, N. Life, information theory, and topology. Bull. Math. Biophys. 1955, 17, 229–235. [Google Scholar] [CrossRef]
- Trucco, E. A note on the information content of graphs. Bull. Math. Biophys. 1956, 18, 129–135. [Google Scholar] [CrossRef]
- Trucco, E. On the information content of graphs: Compound symbols; Different states for each point. Bull. Math. Biophys. 1956, 8, 237–253. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of graphs: I. An index of the relative complexity of a graph. Bull. Math. Biophys. 1968, 30, 175–204. [Google Scholar] [CrossRef] [PubMed]
- Mowshowitz, A. Entropy and the complexity of graphs: II. The information content of digraphs and infinite graphs. Bull. Math. Biophys. 1968, 30, 225–240. [Google Scholar] [CrossRef] [PubMed]
- Mowshowitz, A. Entropy and the complexity of graphs: III. Graphs with prescribed information content. Bull. Math. Biophys. 1968, 30, 387–414. [Google Scholar] [CrossRef]
- Mowshowitz, A. Entropy and the complexity of graphs: IV. Entropy measures and graphical structure. Bull. Math. Biophys. 1968, 30, 533–546. [Google Scholar] [CrossRef]
- Bertz, S.H. The first general index of molecular complexity. J. Am. Chem. Soc. 1981, 103, 3599–3601. [Google Scholar] [CrossRef]
- Bertz, S.H. On the complexity of graphs and molecules. Bull. Math. Biol. 1983, 45, 849–855. [Google Scholar] [CrossRef]
- Bonchev, D.; Kamenski, D.; Kamenska, V. Symmetry and information content of chemical structures. Bull. Math. Biol. 1976, 38, 119–133. [Google Scholar] [CrossRef]
- Bonchev, D.; Trinajstić, N. Information theory, distance matrix, and molecular branching. J. Chem. Phys. 1977, 67, 4517–4533. [Google Scholar] [CrossRef]
- Gregori-Puigjané, E.; Mestres, J. SHED: Shannon entropy descriptors from topological feature distributions. J. Chem. Inf. Model. 2006, 46, 1615–1622. [Google Scholar] [CrossRef] [PubMed]
- Eckert, H.; Bajorath, J. Molecular similarity analysis in virtual screening: foundations, limitations and novel approaches. Drug Discov. Today 2007, 12, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.A.; Maggiora, G. (Eds.) Concepts and Applications of Molecular Similarity; John Wiley & Sons: New York, NY, USA, 1990.
- Willett, P.; Barnard, J.M.; Downs, G.M. Chemical similarity searching. J. Chem. Inf. Comput. Sci. 1998, 38, 983–996. [Google Scholar] [CrossRef]
- Wang, Y.; Bajorath, J. Bit silencing in fingerprints enables the derivation of compound class-directed similarity metrics. J. Chem. Inf. Model. 2008, 48, 1754–1759. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Lounkine, E.; Bajorath, J. Improving the performance of extended connectivity fingerprints through activity-oriented feature filtering and application of a bit density-dependent similarity function. ChemMedChem. 2009, 4, 540–548. [Google Scholar] [CrossRef] [PubMed]
- Kullback, S. Information Theory and Statistics; Dover Publications: Mineola, MN, USA, 1997. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar]
- Nisius, B.; Vogt, M.; Bajorath, J. Development of a fingerprint reduction approach for Bayesian similarity searching based on Kullback-Leibler divergence analysis. J. Chem. Inf. Model. 2009, 49, 1347–1358. [Google Scholar] [CrossRef] [PubMed]
- Vogt, M.; Godden, J.W.; Bajorath, J. Bayesian interpretation of a distance function for navigating high-dimensional descriptor spaces. J. Chem. Inf. Model. 2007, 47, 39–46. [Google Scholar] [CrossRef] [PubMed]
- Vogt, M; Bajorath, J. Bayesian similarity searching in high-dimensional descriptor spaces combined with Kullback-Leibler descriptor divergence analysis. J. Chem. Inf. Model. 2008, 48, 247–255. [Google Scholar] [CrossRef] [PubMed]
- Nisius, B.; Bajorath, J. Molecular fingerprint recombination: generating hybrid fingerprints for similarity searching from different fingerprint types. ChemMedChem 2009, 4, 1859–1863. [Google Scholar] [CrossRef] [PubMed]
- Nisius, B.; Bajorath, J. Reduction and recombination of fingerprints of different design increase compound recall and the structural diversity of hits. Chem. Biol. Drug Des. 2010, 75, 152–160. [Google Scholar] [CrossRef] [PubMed]
- Vogt, M.; Bajorath, J. Introduction of an information-theoretic method to predict recovery rates of active compounds for Bayesian in silico screening: Theory and screening trials. J. Chem. Inf. Model. 2007, 47, 337–341. [Google Scholar] [CrossRef]
- Vogt, M.; Bajorath, J. Introduction of a generally applicable method to estimate retrieval of active molecules for similarity searching using fingerprints. ChemMedChem 2007, 2, 1311–1320. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Liu, Y. A Comparative study on feature selection methods for drug discovery. J. Chem. Inf. Model. 2004, 44, 1823–1828. [Google Scholar]
- Venkatraman, V.; Dalby, A.R.; Yang, Z.R. Evaluation of mutual information and genetic programming for feature selection in QSAR. J. Chem. Inf. Comput. Sci. 2004, 44, 1686–1692. [Google Scholar] [CrossRef] [PubMed]
- Rogers, D.; Hahn, M. Extended-connectivity fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef] [PubMed]
- Bender, A; Mussa, H.Y.; Glen, R.C.; Reiling, S. Similarity searching of chemical databases using atom environment descriptors (MOLPRINT 2D): Evaluation of performance. J. Chem. Inf. Comput. Sci. 2004, 44, 1708–1718. [Google Scholar] [CrossRef] [PubMed]
- Lin, J. Divergence measures based on Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Godden, J.W.; Bajorath, J. Differential Shannon entropy as a sensitive measure of differences in database variability of molecular descriptors. J. Chem. Inf. Comput. Sci. 2001, 41, 1060–1066. [Google Scholar] [CrossRef] [PubMed]
- Stahura, F.L.; Godden, J.W.; Bajorath, J. Differential Shannon entropy analysis identifies molecular property descriptors that predict aqueous solubility of synthetic compounds with high accuracy in binary QSAR calculations. J. Chem. Inf. Comput. Sci. 2002, 42, 550–558. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Geppert, H.; Bajorath, J. Shannon entropy-based fingerprint similarity search strategy. J. Chem. Inf. Model. 2009, 49, 1687–1691. [Google Scholar] [CrossRef] [PubMed]
- Hert, J.; Willett, P.; Wilton, D.J.; Acklin, P.; Azzaoui, K.; Jacoby, E.; Schuffenhauer, A. Comparison of fingerprint-based methods for virtual screening using multiple bioactive reference structures. J. Chem. Inf. Comput. Sci. 2004, 44, 1177–1185. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vogt, M.; Wassermann, A.M.; Bajorath, J. Application of Information—Theoretic Concepts in Chemoinformatics. Information 2010, 1, 60-73. https://doi.org/10.3390/info1020060
Vogt M, Wassermann AM, Bajorath J. Application of Information—Theoretic Concepts in Chemoinformatics. Information. 2010; 1(2):60-73. https://doi.org/10.3390/info1020060
Chicago/Turabian StyleVogt, Martin, Anne Mai Wassermann, and Jürgen Bajorath. 2010. "Application of Information—Theoretic Concepts in Chemoinformatics" Information 1, no. 2: 60-73. https://doi.org/10.3390/info1020060
APA StyleVogt, M., Wassermann, A. M., & Bajorath, J. (2010). Application of Information—Theoretic Concepts in Chemoinformatics. Information, 1(2), 60-73. https://doi.org/10.3390/info1020060






