Ice XVII as a Novel Material for Hydrogen Storage

Abstract

Hydrogen storage is one of the most addressed issues in the green-economy field. The latest-discovered form of ice (XVII), obtained by application of an annealing treatment to a H${}_2$-filled ice sample in the C${}_0$-phase, could be inserted in the energy-storage context due to its surprising capacity of hydrogen physisorption, when exposed to even modest pressure (few mbars at temperature below 40 K), and desorption, when a thermal treatment is applied. In this work, we investigate quantitatively the adsorption properties of this simple material by means of spectroscopic and volumetric data, deriving its gravimetric and volumetric capacities as a function of the thermodynamic parameters, and calculating the usable capacity in isothermal conditions. The comparison of ice XVII with materials with a similar mechanism of hydrogen adsorption like metal-organic frameworks shows interesting performances of ice XVII in terms of hydrogen content, operating temperature and kinetics of adsorption-desorption. Any application of this material to realistic hydrogen tanks should take into account the thermodynamic limit of metastability of ice XVII, i.e., temperatures below about 130 K.

1. Introduction

The ever increasing requirement of clean energy in modern industrial societies has driven the researchers and engineers to consider hydrogen as one possible choice as an energy vector [1]. Indeed hydrogen is the most abundant element, it can be produced by various sources, and its usage is environmentally safe. Nowadays, one of the main hurdles preventing the transition to the so-called hydrogen economy is represented by the lack of a really efficient system for its storage, especially in mobile applications, e.g., automotive. A reason for this is the extreme low density of hydrogen gas (0.0899 kg/m${}^3$ at standard conditions) compared to other fuels, both liquids (e.g., petroleum) or gases (e.g., methane and propane). The hydrogen content, the thermodynamic conditions of synthesis and storage, the capacity of on-board release, the life cycle and the kinetic properties are the key issues in conceiving and realising a hydrogen storing system [1]. Nowadays, three different methods are mainly employed for this purpose. The most commonly used is the high pressure compressed hydrogen, which is characterised by a volumetric density of 15 g/L at a pressure of about 350 bar and standard temperature. However, the limits of this storage method are constituted by the strength and safety, including embrittlement problems, of the material of the tank, which results in being too heavy and voluminous for mobile applications. By storing hydrogen in the liquid state, one attains a high volumetric density (70 g/L), but the low liquid–vapour equilibrium temperature (20 K at standard pressure) is an important obstacle for its use because of the high energy requirements for liquefaction and the remarkable boil-off losses. Many of the practical issues of these two methods are solved by storing hydrogen in a solid framework, which is able to adsorb hydrogen [2,3,4]. In this case, there are two possible mechanisms of adsorption: chemisorption, according to which a reversible chemical reaction occurs between the solid substrate material and molecular hydrogen, causing the dissociation of the hydrogen molecule and the formation of a new compound, typically a metal or complex hydride; and physisorption, according to which the diatomic molecule does not dissociate and its bond with the solid framework is realized by means of van der Waals interaction. Porous materials able to adsorb hydrogen are, for example, high surface area carbon structures, carbon nanotubes, metal-organic frameworks (MOFs), zeolites and organic polymers of intrinsic porosity (PIM) [1].

Some molecular compounds as the hydrogen clathrate-hydrate can also be ascribed to the family of hydrogen storing materials [2,5]. The clathrate is one of several crystalline phases of the binary system H${}_2$-H${}_2$O, stable at high pressure (above 1 kbar) and around 0 ${}^{\circ }$C [6]. Its structure, consisting of water molecules tetrahedrally linked by hydrogen bonds, presents polyhedral cavities inside which the guest molecules (H${}_2$) are trapped and perform a quantum motion, thoroughly studied in the past, by means of neutron and Raman spectroscopy [7,8,9,10]. Hydrogen clathrates can contain up to 4% of H${}_2$ in weight, but their application for hydrogen storage is hindered by the slow diffusion rate of hydrogen inside the water skeleton. Other stable phases of the H${}_2$-H${}_2$O binary system are known. These are the so-called filled ices, found with different crystal symmetries, named C${}_1$- and C${}_2$-structure [11], which are stable at higher pressure, namely at values higher than 7 and 23 kbar, respectively. Only recently, two experimental studies [12,13] have discovered a new phase of the hydrogen-water system, named the C${}_0$-phase filled ice, which is stable in the intermediate thermodynamic region between the stability region of sII clathrate and C${}_1$-phase filled ice.

In addition to this, low density solid water structures, such as those formed by clathrate–hydrates, have sparked large interest since the discovery in 2014 of ice XVI, a new form of ice which is obtained by emptying an sII neon clathrate hydrate [14]. Furthermore, an empty clathrate structure, named sIII, has been theoretically proposed as a stable phase of water under negative pressure [15]. These works greatly contribute to the discussion about the role of the guest molecule in the stabilization of the hydrate structure. From this perspective, we have studied the stability of the hydrogen filled ice in the C${}_0$-phase, synthesized in our high-pressure laboratory (ISC-CNR, Sesto Fiorentino, Italy) and recovered at room pressure and liquid nitrogen temperature [16]. By the application of thermal annealing treatment, we have obtained the complete removal of the H${}_2$ guest molecules from the H${}_2$O host framework, and only slight structural modifications of the water lattice structure have occurred. The emptied C${}_0$-structure, which is metastable up to 130 K, is a new metastable form of water ice, namely ice XVII [17]. A really interesting and surprising property of this new form of ice is its porosity, i.e., its capacity of adsorbing gas, even at pressure well below the atmospheric one.

In light of what was mentioned above, the aim of this work is to characterize quantitatively the reversible adsorption properties of ice XVII in order to speculate about its applicability as an innovative material in the hydrogen storage field. Here, we present a complete set of measurements of the adsorption and desorption isotherms at several different temperatures in the range 15–80 K, obtained by the combined analysis of both Raman spectra and volumetric measurements. By means of experimental data between 50 and 80 K and the extrapolated ones between 80 and 110 K, obtained by the use of an adsorption equation of state fitted to the data [18], we have derived the gravimetric and volumetric capacity of this porous structure and the behaviour of the usable capacity, i.e., the amount of hydrogen released between two reference values of pressure (usually the maximum tank pressure and the back pressure of a fuel cell), as a function of temperature.

This material is able to safely store a good amount of hydrogen, especially from a volumetric point of view. The adsorption process results as completely reversible, with a kinetic that strongly depends on the temperature at which the adsorption has occurred. Anyway, the limit of thermodynamic metastability has to be taken into account for practical applications.

2. Results

2.1. Thermal Treatment to Obtain Ice XVII

The starting sample is constituted by an H${}_2$-filled ice in the C${}_0$-phase, that is, the stable phase at high pressure (about 4 kbar) and low temperature (about 255 K) of the binary system H${}_2$-H${}_2$O. The new form of solid water, namely ice XVII, has been realized by exposing the pristine sample to an annealing treatment, which is performed by keeping the sample under dynamic vacuum at a temperature in the range 110–120 K. The whole treatment is done in the Raman optical cell, thus measuring the Raman spectrum of the sample during the annealing process. We had previously verified that the C${}_0$-structure transforms into ice, probably Ih, at about 130 K with a fast kinetic, hence the annealing temperature is set prudentially at 120 K and the sample is kept under dynamic vacuum for about one hour.

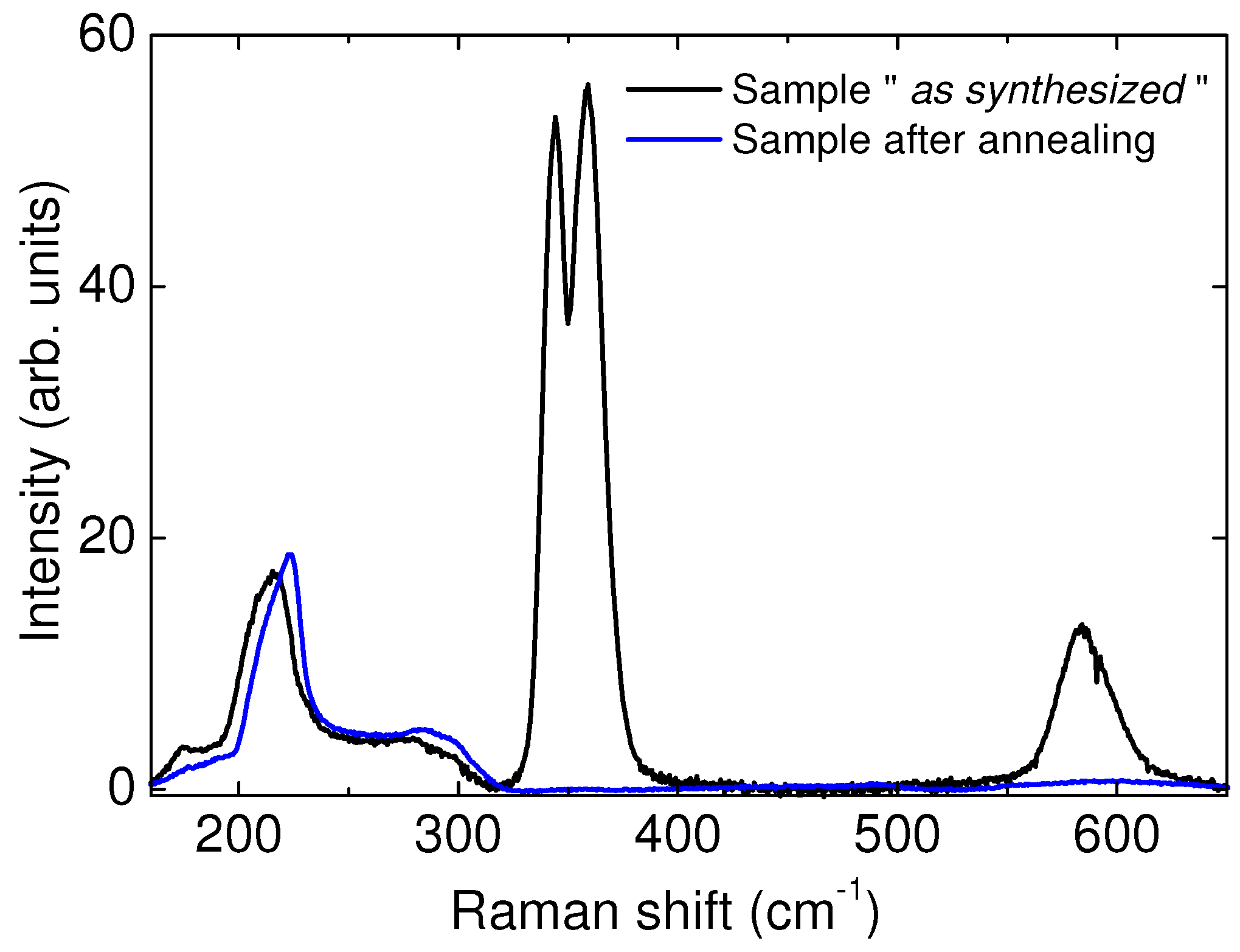
As is shown in Figure 1, the spectrum of the pristine sample in the region 150–650 cm${}^{-1}$ contains both the H${}_2$O lattice band (from ≃150 to ≃300 cm${}^{-1}$) and the two H${}_2$ rotational bands S${}_0$(0) and S${}_0$(1) (≃350 and ≃580 cm${}^{-1}$, respectively). The shape of the rotational bands is characteristic of the hydrogen molecule experiencing a relatively strong interaction with the host water framework [19], and is very different from the one observed in the gas. This demonstrates the presence of hydrogen molecules inside the host framework. During the annealing treatment, the lattice band remains similar to the one measured before the treatment, but a gradual decrease of the rotational band intensities is observed, up to their complete undetectability. From these data, it is possible to ascertain that there is a complete release of the hydrogen from the sample, while no evident structural phase transition occurs.

It has been demonstrated that nitrogen molecules can also be trapped in these filled ice samples, as spurious guests [20], and our Raman measurements have confirmed this. Probably, this is due to the use of liquid nitrogen during the transfer process of the samples from the autoclave (or Dewar container) to the sample cell and for the cryo-conservation of the sample. After the annealing process, the N${}_2$ Raman line disappears, demonstrating a complete evacuation of the sample also by the N${}_2$ guest impurity. The nature of the effect of the annealing on the structure of the samples in the C${}_0$-phase is due to the combined effect of the removal of both H${}_2$ and N${}_2$ from the sample and to the decrease of defects in the structure. The emptied C${}_0$-structure has been considered a new form of metastable ice called Ice XVII, according to the current nomenclature of ice polymorphisms [16,17]. 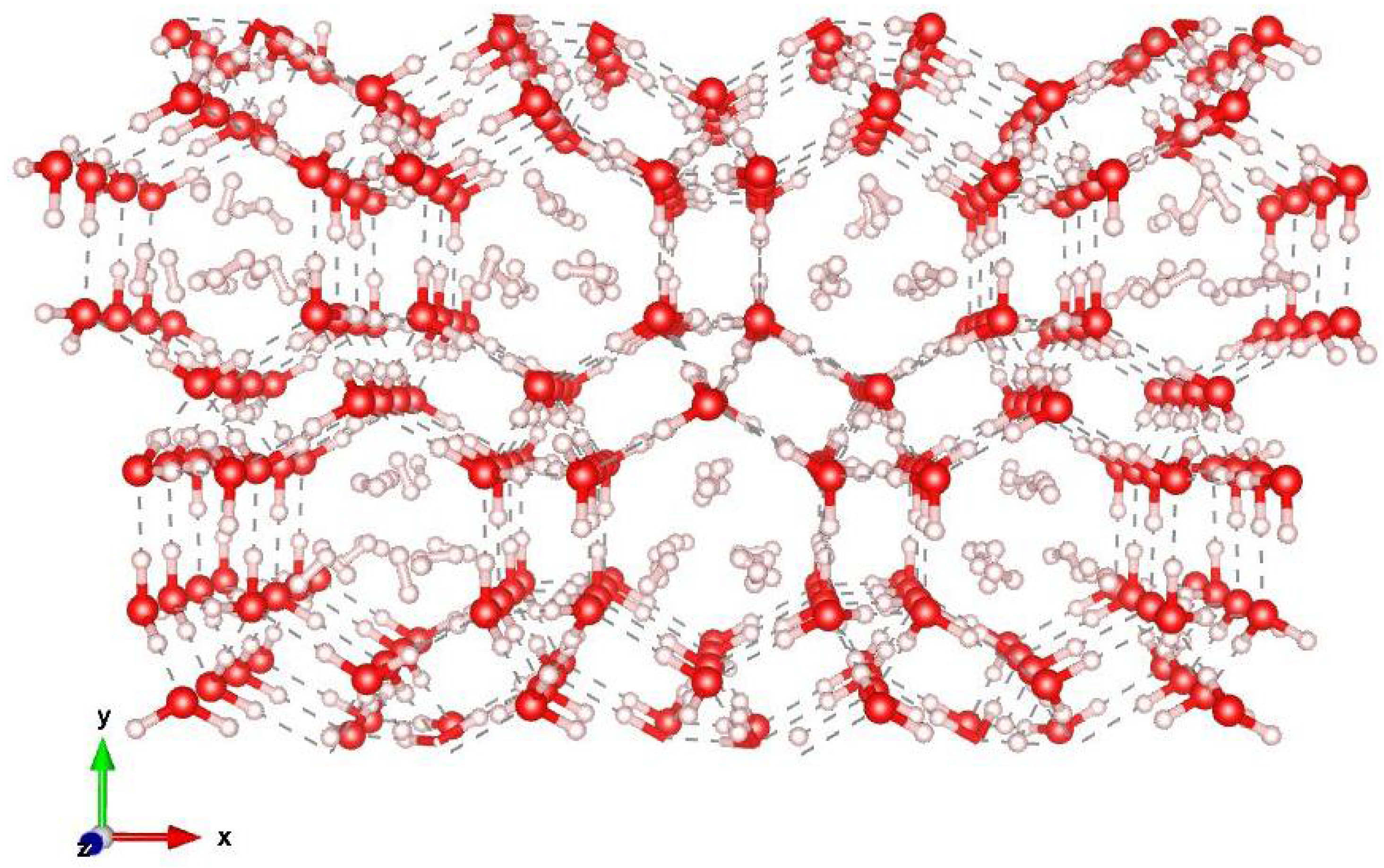The overall similarity of the host Raman band shape before and after the annealing treatment [16] and the structure refinement of ice XVII by means of neutron diffraction [17] led us to state that the lattice structures of the C${}_0$-phase and that of ice XVII are very similar. The water molecules are arranged forming pentagonal rings and giving rise to empty channels, having a diameter of about 6 Å, where the H${}_2$ molecules can be accommodated, probably in a spiralling configuration. A picture of the arrangements of the water molecules is shown in Figure 2, where one can observe the existence of channels along the z-axis, which can host the hydrogen molecules.

2.2. Porosity of Ice XVII

An interesting property of ice XVII is its capability of a very rapid adsorption of hydrogen molecules when exposed to this gas even at a very low pressure (lower than atmospheric one at a temperature below 40 K) [16]. The fast diffusion of hydrogen in and out of ice XVII makes this system more similar to MOFs than to hydrogen clathrate hydrates, which can efficiently release hydrogen only with a melting process. The amount of hydrogen that is trapped can be deduced measuring the intensity of the rotational Raman bands, which is proportional to the number of adsorbed molecules. The shape of the rotational lines does not change significantly during the hydrogen refilling, demonstrating that the H${}_2$ molecules penetrate again in the same positions inside the channels as those initially occupied at the time of the C${}_0$-phase synthesis.

From the intensity of the Raman bands, it is possible to obtain a quantitative measurement of the hydrogen content in the hydrate sample, which we express in terms of hydrogen molar fraction X, i.e., number of H${}_2$ moles per H${}_2$O mole. We can obtain X from the intensity ratio of the hydrogen rotational lines $I_{rot}$ and the lattice phonon band $I_{phon}$

$$X=f\frac{I_{rot}}{I_{phon}}=f\frac{\frac{I_0}{{\sigma }_0}+\frac{I_1}{{\sigma }_1}}{I_{phon}},$$

(1)

where f is a calibration factor, and ${\sigma }_0$ and ${\sigma }_1$ are the Raman cross sections for the $S_0\left(0\right)$ and $S_0\left(1\right)$ rotational lines having intensities $I_0$ and $I_1$, respectively. In this way, $I_{rot}$ is proportional to the number of H${}_2$ molecules in the lowest two J = 0 and J = 1 rotational states, that are, at low temperature, the sole rotational states with a non-negligible population. The quantity obtained by the ratio of $I_{rot}$ and $I_{phon}$ is independent of laser intensity and detector efficiency, and proportional to the H${}_2$/H${}_2$O molar ratio in the sample, under the hypothesis that the intensities of the bands are proportional to the number of molecules giving rise to them [22].

The calibration factor f, that allows for converting the weighted intensity ratio into a hydrogen molar fraction, is calculated by fitting data arising from two independent experimental methods based on our previous Raman results relative to hydrogen sII clathrate [22] and on volumetric measurements, performed with the apparatus connected to the Raman optical cell, of the gas adsorbed during refilling of the ice XVII sample at different temperatures. A detailed description of this Raman intensity calibration is reported in Ref. [16].

The C${}_0$-phase filled ice samples, examined just after the synthesis, are characterized by $X\simeq 25$%, while for the refilled ice XVII in some instances, the measured X value exceeds 40%, reaching higher values than the established theoretical maximum for sII clathrates $48/136\simeq 35$%. The lower hydrogen content in the pristine samples compared to the refilled ones can be ascribed to the initial presence of nitrogen molecules in the sample that partially fill the channel structure, as well as to unwanted warming of the sample, with consequent H${}_2$ release, during the loading of Raman optical cells.

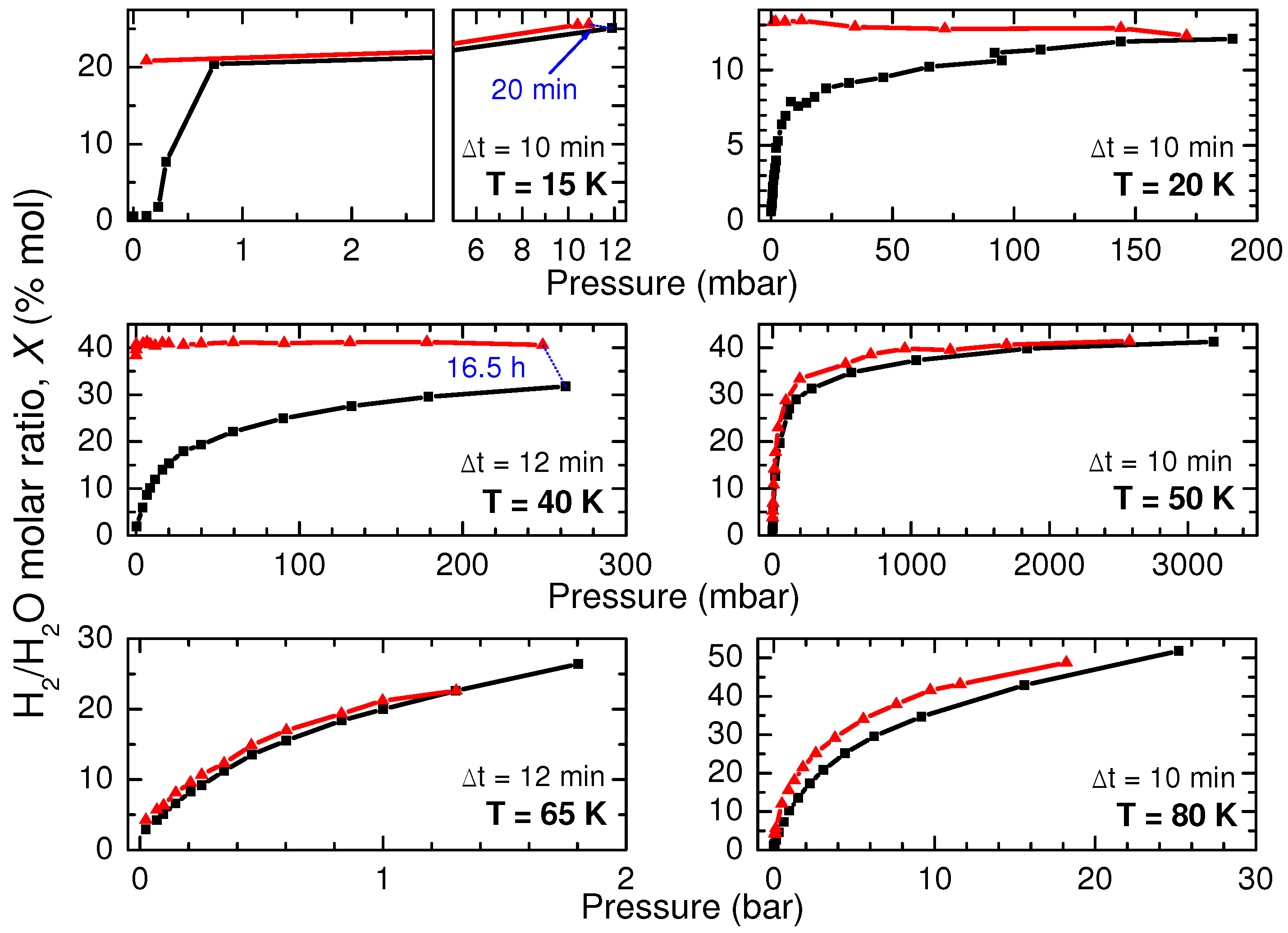
To derive the amount of adsorbed H${}_2$ as a function of pressure, we have measured several adsorption isotherms at six different temperatures between 15 to 80 K. The results are reported in Figure 3. Pressure is increased gradually and, when possible, each measurement is taken waiting the same time interval $\Delta t$ (indicated in each panel) after each pressure increase step. The pressure at which the saturation is reached is strongly dependent on temperature and ranges between a few millibar at 15 K to several bar at 80 K. In addition, the maximum value of the measured adsorption is strongly temperature-dependent because it depends on the kinetics of hydrogen diffusion.

By using the same method, we examined the gas desorption while releasing pressure (red triangles in Figure 3). A large hysteresis and other kinetic effects are evident at the lower temperatures. As it is shown in the case of 15 K, 20 K and 40 K, after decreasing pressure down to zero, the sample does not sensibly release hydrogen in $\Delta t$ = 10 min. The relevant increase of the adsorbed hydrogen observed after the long exposure to hydrogen performed after the completion of the 40 K adsorption isotherm testifies that the system is not at equilibrium conditions, and this is probably due to the slow molecular diffusion inside the host channels that hinders a further adsorption. At the highest temperatures, i.e., 50, 65 and 80 K, a very small hysteresis is observed. Hence, only these three experimental isotherms are taken as reference for the following characterization of the storage capacity of ice XVII.

In order to study the mechanism of adsorption in a porous material, it can be useful to estimate its enthalpy of adsorption. For a given hydrogen uptake X, the enthalpy of adsorption $\Delta H$ is obtained by means of the Van’t Hoff equation

$$\frac{\Delta H}{R}={\left[\frac{\partial ln\left(\frac{p}{p_0}\right)}{\partial \frac{1}{T}}\right]}_X,$$

(2)

where R is the gas constant. For the calculation of the temperature derivative, adsorption isotherms at different temperatures are necessary. We have used those measured at 50, 65 and 80 K, estimating the temperature derivative with a straight line fit.

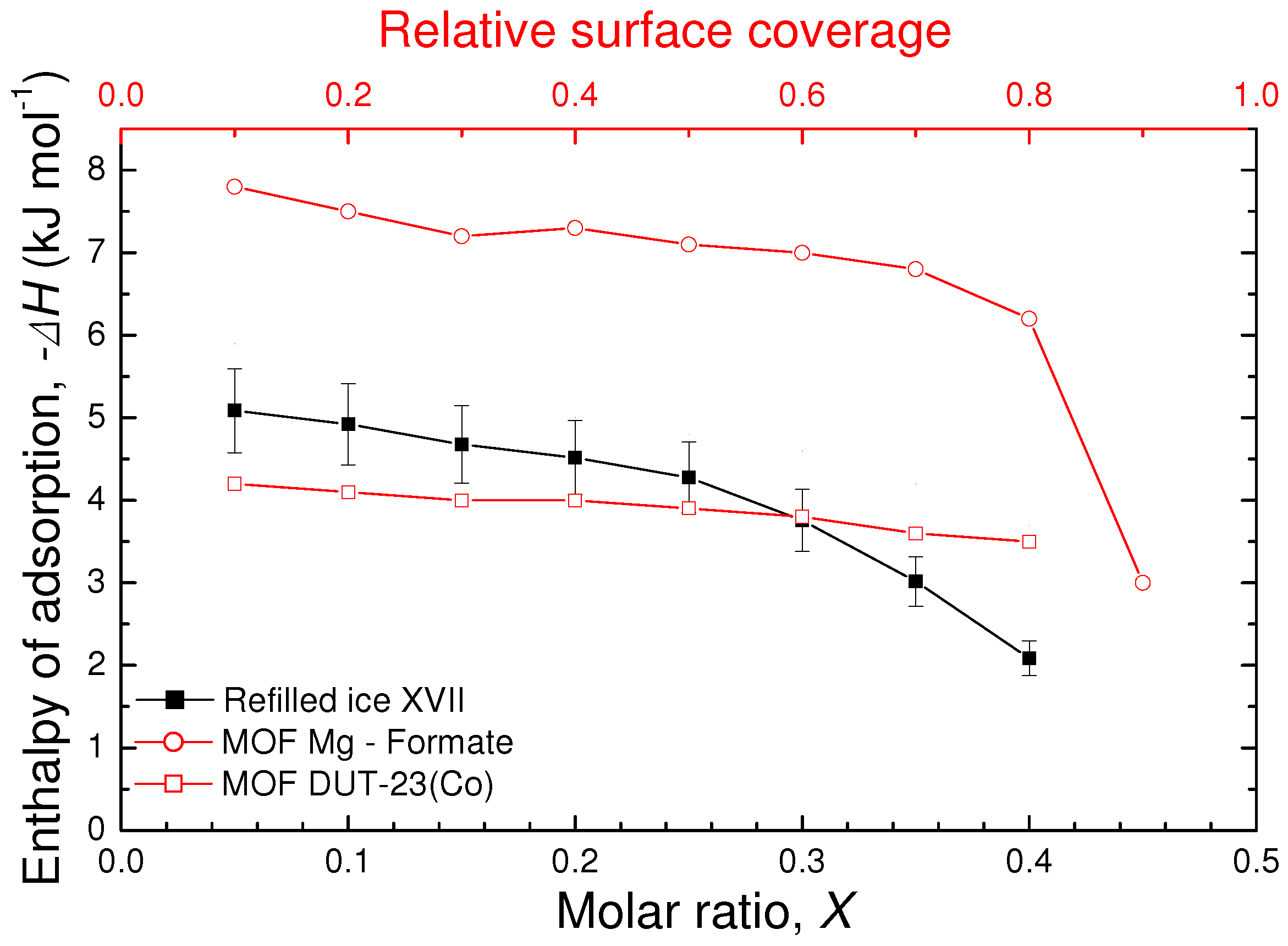
As shown in Figure 4, the resulting value of $-\Delta H$ decreases with increasing molar ratio X starting from about 5 kJ/mol at $X\simeq$ 10% down to about 2 kJ/mol at $X\simeq$ 40%. Values in these range are typical for molecular physisorption in porous material like MOFs [4], whose mechanism of hydrogen adsorption is similar to that in ice XVII and, being driven by van der Waals interactions, does not involve any chemical bond. At lower filling, the intermediate value of the enthalpy of ice XVII compared to those of the DUT-23(Co) and Mg-Formate compounds can be explained with the diameter of the channels in ice XVII (about 0.6 nm) with respect to the MOF compounds considered (about 2 nm [23] and 0.4 nm [24], respectively). The decrease of the enthalpy with increasing hydrogen content could suggest the presence of different adsorption sites, that is, different binding energy for molecules placed deep into the channels with respect to those at the entrance of the channels, or even a cooperative effect of the already adsorbed hydrogen molecules on extra adsorbed ones. Moreover, potential little structural changes during the entire filling process could induce the enthalpy behaviour observed above [17].

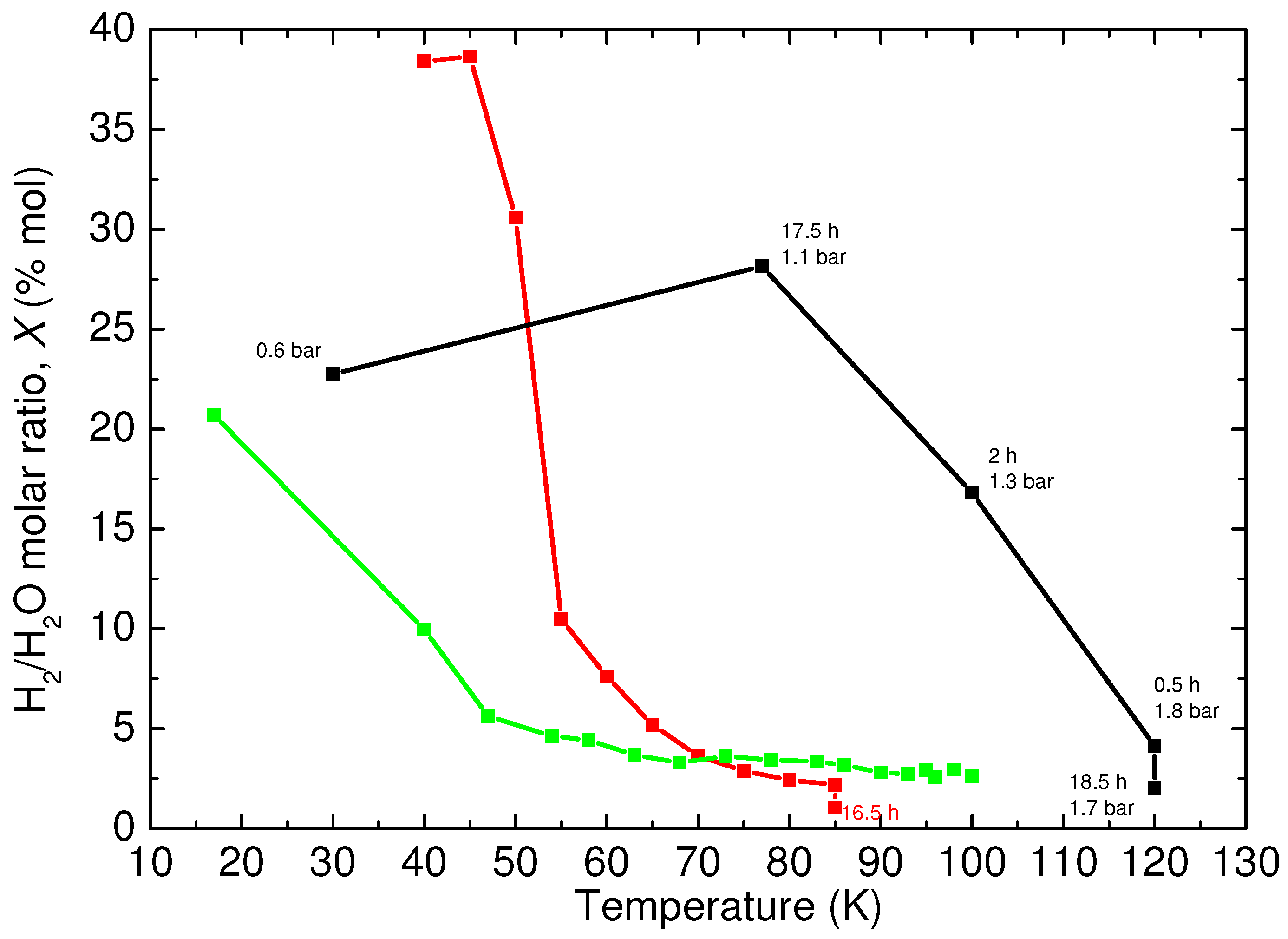
To describe the stability of the sample with respect to H${}_2$ release, for both the C${}_0$-structure filled ice and the H${}_2$-refilled ice XVII, it can be useful to measure the amount of hydrogen trapped in the samples as a function of increasing temperature. We have performed this analysis on one pristine sample and on two samples of the refilled ice XVII. As is shown in Figure 5, the C${}_0$-structure filled ice seems to have a wider region of thermal stability, considering that it starts to lose hydrogen at a temperature higher than 75 K and reaches an almost complete evacuation at 120 K.

The annealed samples, even with different initial filling, show faster kinetics of hydrogen release, which starts at about 40 K, and the complete emptying is reached at about 100 K. Even if these results are affected by the same uncertainty, it is clear that the filled ice directly quenched in liquid nitrogen after synthesis has a higher capacity of keeping the hydrogen guest trapped. This is probably due to the presence of nitrogen molecules in the pristine crystal, or to structural defects that hinder the diffusive motion of the hydrogen molecules along the channels of the ice structure.

A further increase of the temperature has led to the complete decomposition of ice XVII at 130 K with a relatively fast kinetic (about one hour). The resulting phase is probably ice Ih, according to the Raman H${}_2$O lattice and O–H stretching bands, even if only diffraction data on this resulting structure would allow a clear determination of its crystal symmetry.

2.3. Applicability in the Hydrogen Storage Field

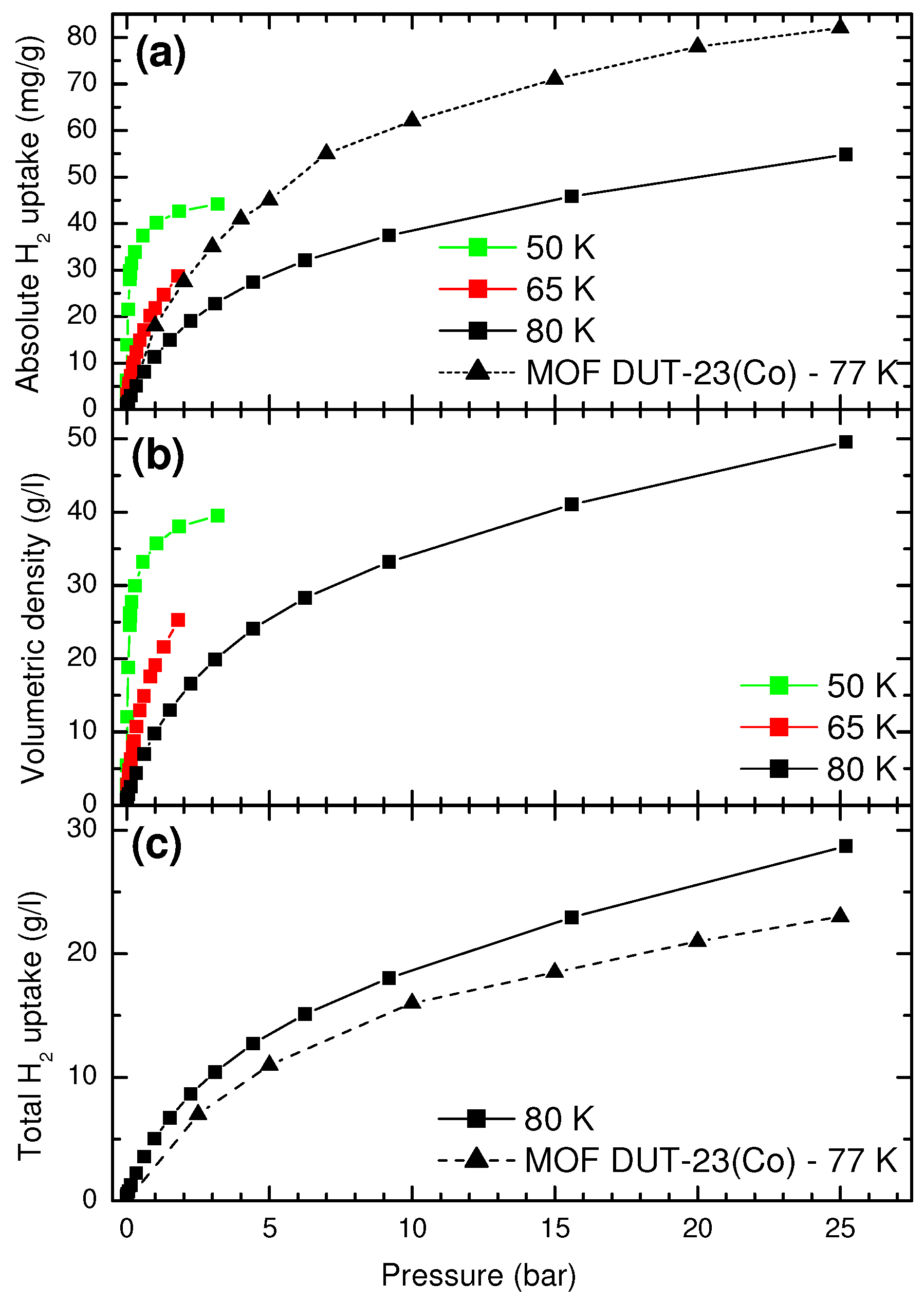
In order to characterize the adsorption capacity of this new material, we have calculated both gravimetric and volumetric capacities. The adsorption properties of ice XVII can be compared with those of materials with highly porous structure, able to realize hydrogen physisorption. Among them, the so-called metal-organic frameworks (MOFs) show the highest hydrogen uptakes and are taken as reference standard in this work.

From the previously measured hydrogen molar ratio X, we have derived, in isotherm conditions, the absolute hydrogen uptake $n_{abs}\left(P\right)$ (milligrams of H${}_2$ per grams of H${}_2$ + H${}_2$O) and the volumetric hydrogen density $n_{vol}\left(P\right)$ (grams of H${}_2$ per liter of H${}_2$ + H${}_2$O). These isotherms are reported in panels (a,b) of Figure 6, respectively. To calculate these quantities, we consider only the amount of H${}_2$ which is adsorbed in the pores, that is, the one that is revealed by Raman spectroscopy.

Since the ice XVII sample has the form of a fine powder, for real tank application, we have also to consider the free gas present between ice grains. Hence, we need to evaluate all hydrogen present in a given volume, independently from its state (gas or adsorbed), that is, the total hydrogen uptake $n_{total}\left(P\right)$ (grams of H${}_2$ per liter of H${}_2$ + H${}_2$O). We know from our measurements that, for a given volume of compacted ice powder, roughly one half is filled by ice crystallites. In this hypothesis, the total hydrogen uptake is given by

$$n_{total}\left(P\right)=\frac{1}{2}{n}_{vol}\left(P\right)+\frac{1}{2}{n}_{gas}\left(P\right),$$

(3)

where $n_{gas}\left(P\right)$ is the density of the free hydrogen gas at pressure P [25]. The total uptake is reported in panel (c) of Figure 6.

Always in the view of storage applications, e.g., portable tanks, we report the usable capacity $u_{p_{max},p_{back}}\left(T\right)$, which is given by

$$u_{p_{max},p_{back}}\left(T\right)=n_{abs}(p_{max},T)-n_{abs}(p_{back},T),$$

(4)

where $p_{max}$ is the maximum allowed tank pressure (some tens of bar for standard tanks) and $p_{back}$ is the minimum pressure required by a hydrogen consumer to operate (e.g., 2 bar for a fuel cell). Due to the experimental limit on the maximum pressure (about 25 bar) of the gas circuit connected to our Raman cell, we have measured the equilibrium isotherms only in a narrow temperature range (50–80 K). Thus, to gain information on the usable capacity and on the general thermodynamic behaviour of our system also outside this temperature range, we have fitted the experimental data and extrapolated them at higher temperatures (up to 110 K) with an equation of state, suitable for type I isotherms, which allow for obtaining the pressure P as a function of the amount of hydrogen adsorbed X and temperature T [18]

$$P(X,T)=\frac{X}{K}\left(\frac{m}{m-X}\right)\exp \left(C_{1}X+C_2{X}^2\right)\exp \left(\frac{\Delta H\left(X\right)}{R}\left(\frac{1}{T}-\frac{1}{T^{*}}\right)\right),$$

(5)

where K is the Henry’s constant, m is the saturation capacity, $C_{1,2}$ the arbitrary coefficients and $T^{*}$ the reference temperature. The values of the enthalpy of adsorption can be derived by fitting the experimental values (Figure 4) with an inverse polynomial. The parameters K, m and $C_{1,2}$ can be obtained by fitting all at once the three sets of experimental values (50, 65 and 80 K), once normalized to the temperature-dependent exponential factor in Equation (5), i.e.,

$$\frac{P^{exp}(X,T)}{\exp \left(\frac{\Delta H^{fit}\left(X\right)}{R}\left(\frac{1}{T}-\frac{1}{T^{*}}\right)\right)}=\frac{X}{K}\left(\frac{m}{m-X}\right)\exp \left(C_{1}X+C_2{X}^2\right).$$

(6)

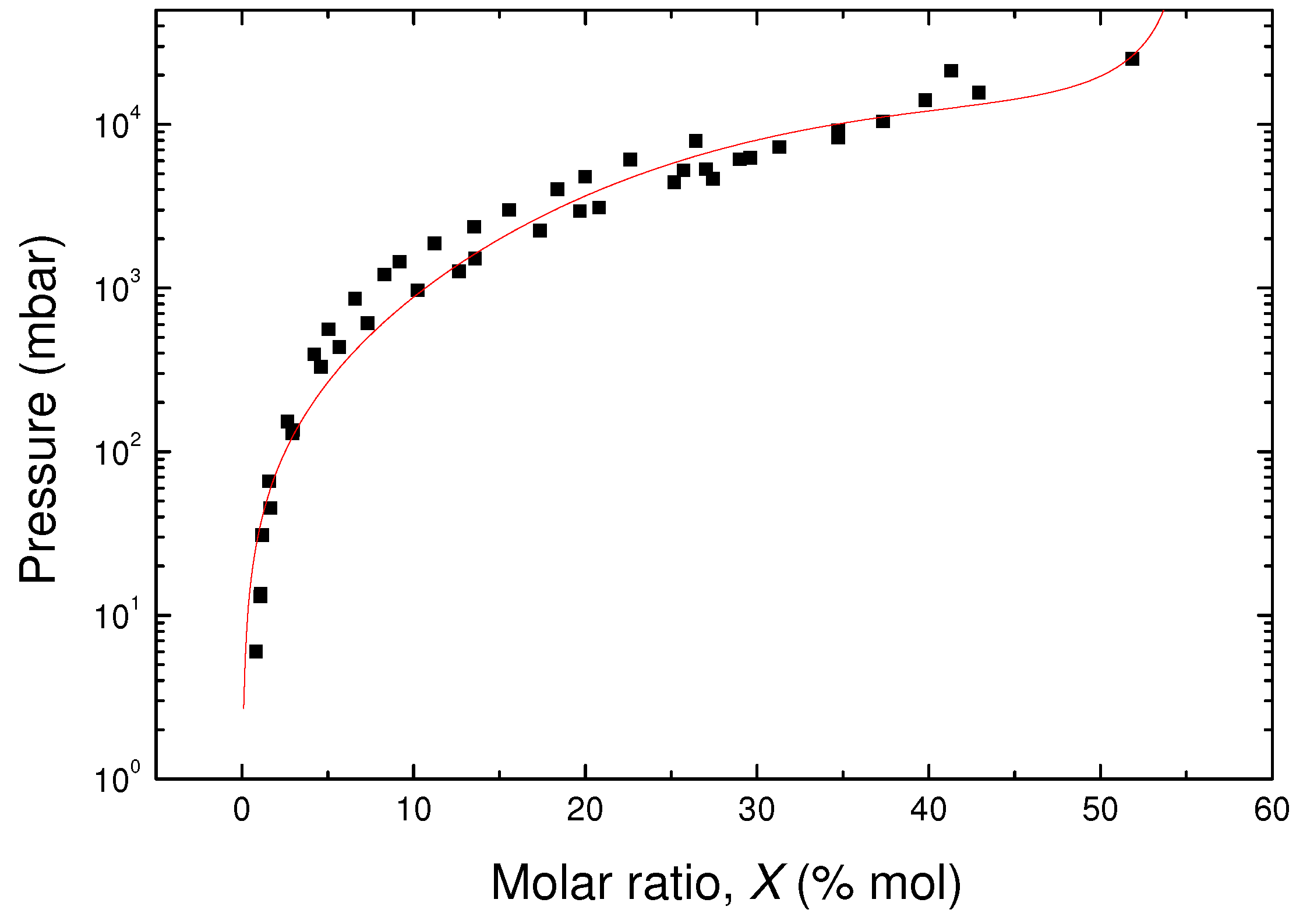
Since we are interested in the extrapolation at temperatures higher than 80 K, we have taken $T^{*}$ = 80 K. The resulting best fit is reported with a red line in Figure 7.

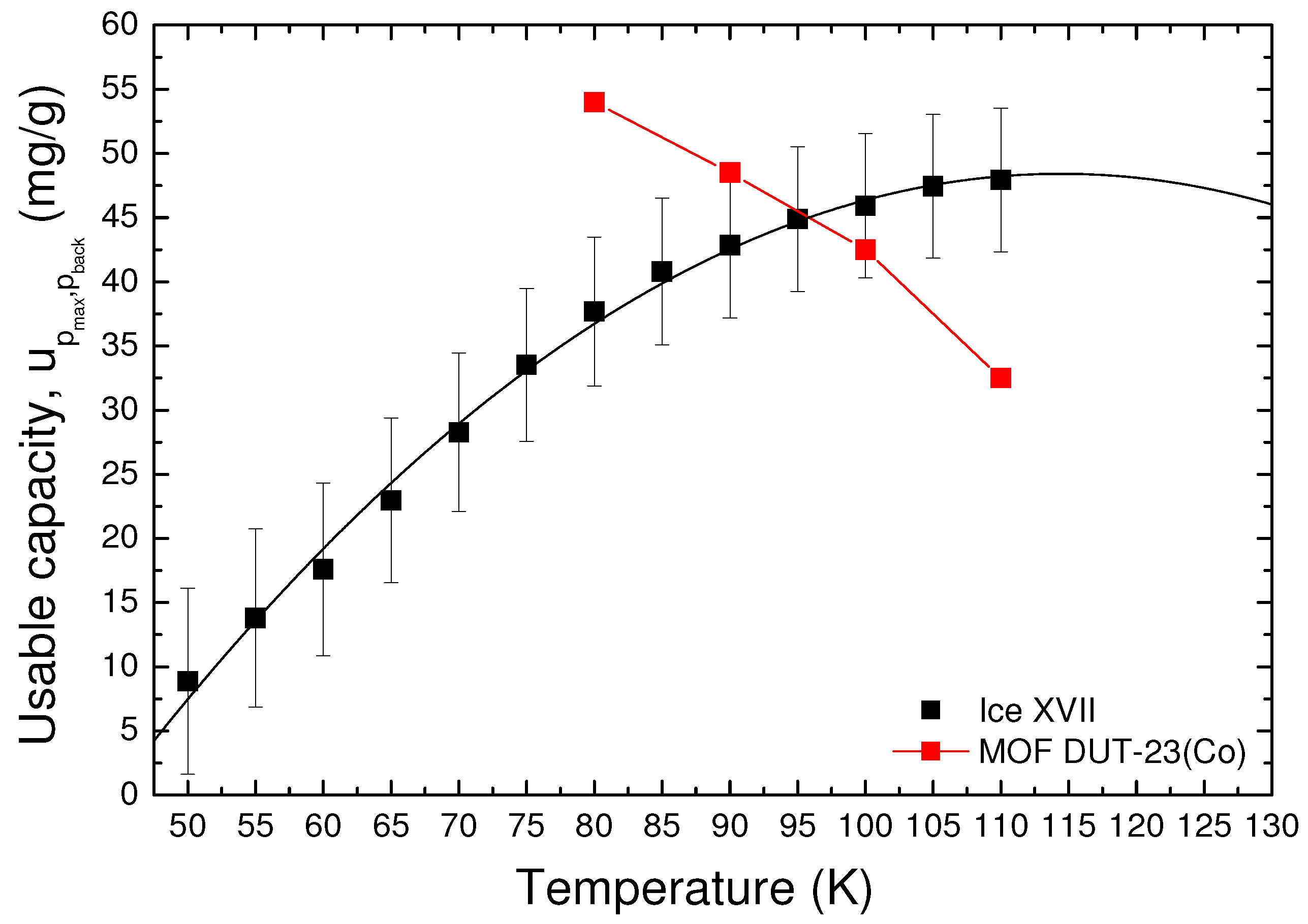
We have calculated the isotherms $P\left(X\right)$ for temperatures in the range 50–110 K, so as to be able to derive the usable capacity in this entire range of temperature. The results are reported in Figure 8. In order to have our system in saturation conditions at the maximum pressure in the entire range of temperature considered, in these calculations, we have considered the maximum tank pressure equal to 40 bar, while, for the reference sample, DUT-23(Co) is 25 bar because this is the maximum pressure at which the isotherms have been measured in this case [4].

By means of a parabolic fit of the extrapolated data, we have derived the temperature at which the usable capacity should assume the maximum value. This temperature, usually called optimum operating temperature $T_{opt}$, represents the working temperature at which the storage system has the best performances. For ice XVII, this value is about 114 K.

All the estimated quantities are summarized in

Table 1. Main results obtained by hydrogen uptake measurements for refilled ice XVII and some metal-organic framework (MOF) systems [4].

Material	P (bar)	T (K)	Absolute Uptake (mg/g)	Average Enthalpy of Adsorption (kJ/mol)	Optimum Operating Temperature ${\mathit{T}}_{\mathit{opt}}$ (K)	Usable Capacity at ${\mathit{T}}_{\mathit{opt}}$ (mg/g)
Ice XVII	25	80	55	4.0	114${}^a$	48${}^a$
DUT-23(Co) [23]	25	77	82.3	3.9	<77	55
Mg-Formate [24]	25	77	7.8	7.2	112	3.2
PAF-1 [26]	25	77	72.7	4.2	<77	46.5
MFU-4(Co) [27]	25	77	33.9	4.7	98	14.6

The usable capacity and the optimum operating temperature are calculated considering the range between 25 bar (maximum pressure) and 2 bar (back pressure) [4], except for the ice XVII (${}^a$), for which the maximum pressure is 40 bar.

, where the values belonging to some MOF systems are reported for comparison.

3. Discussion

The experimental results about physisorption properties of Ice XVII demonstrate that the adsorption and desorption processes are completely reversible, with a (theoretically) infinite number of cycles. In fact, despite its thermodynamic metastability, ice XVII has a substantial mechanical stability for temperatures below 130 K. This is testified by the absence of any phase transition towards the stable phase during both the cryo-storing in liquid nitrogen (several weeks long) and all the adsorption–desorption experiments performed in this work. Moreover, this material shows fast kinetics in the physisorption process. Indeed, after a variation of hydrogen pressure, the system reaches equilibrium in about 10 min for temperature over 50 K. The maximum hydrogen content, in terms of both gravimetric and volumetric density, is comparable to one of the best MOF materials in terms of hydrogen uptake (e.g., DUT-23(Co)). These results, together with a discrete level of usable capacity at temperatures higher than the liquid nitrogen one (77 K) and with the optimum operating temperature higher than any MOF materials, make ice XVII a viable candidate for hydrogen storage systems based on cryo-adsorption.

The mechanism of solid state gas adsorption seems to be applicable also to molecular nitrogen. Indeed, we have verified the presence, in the pristine sample, of N${}_2$ molecules, adsorbed during the handling of the sample under atmospheric conditions of dry N${}_2$ gas. More investigations about adsorption of other types of guests are necessary to address this additional aspect of ice XVII.

4. Materials and Methods

4.1. Sample Synthesis and Recovering

Several instances of solid H${}_2$-H${}_2$O compound are produced using a well established procedure. A few grams of ice powder are introduced in a copper–beryllium autoclave, designed and manufactured at the ISC-CNR mechanical laboratories (Sesto Fiorentino, Italy) previously cooled below 273 K. All of these operations are carried out in a dry nitrogen atmosphere. Once the autoclave is closed and connected to the high pressure circuit, it is placed into a thermostatic bath and kept cold (≃255 K) for a few hours in order to obtain a complete thermalization of the sample. After this procedure, the ice sample is exposed isothermally to 99.995% pure hydrogen gas at a pressure in the range or above 4.3 kbar for a few days. After the synthesis, in order to recover the sample at ambient pressure, the autoclave is quenched in a liquid nitrogen bath and, after the release of pressure, it is opened. Then, the sample is recovered in the form of a fine powder. The transfer process, either for ex situ measurements or for storing in a Dewar container, is a delicate process and has to be accomplished in a liquid nitrogen bath and dry-nitrogen atmosphere in order to avoid unintentional heating and humidity condensation, which would compromise the sample quality. In any case, to check the quality of each sample batch, a small amount of powder is submitted to a rapid offline check with Raman spectroscopy at liquid nitrogen temperature, thus verifying the absence of ice Ih or other spurious phases.

4.2. Spectroscopic and Volumetric Apparatus

The experimental technique used to study the vibrational dynamics of hydrates systems is Raman spectroscopy. A small amount of sample powder is safely transferred in a dry-nitrogen atmosphere from the vials stored in a Dewar container to the Raman optical cell, that is in thermal contact with the cold finger of a closed-cycle He cryostat. The aluminum optical cell, designed and manufactured at the ISC-CNR laboratories, is equipped with a 20 mm diameter optical window and a stainless steel capillary, connected to a low pressure circuit for gas insertion or evacuation. The gas circuit is designed for providing volumetric measurements of the gas inserted into the cell or released by sample during heating. The light source for the excitation of the Raman spectra is an Ar ion laser (Coherent Innova I 304-A), which emits a green line at 514.5 nm. The laser beam is focused on the sample cell, with a resulting power of about 30 mW. The scattered light is collected in quasi-backscattering geometry and re-focused on the entrance slit of a Czerny–Turner double monochromator (Horiba Spex 1401). A “Super Notch” spectral filter is inserted in the optical path before the monochromator to remove scattered radiation at the laser frequency, which would hide the Raman signal, especially in the spectral region close to the laser frequency. The original exit slit of the first stage of the spectrometer has been replaced by a flange holding a Charge Coupled Device (CCD) detector (Andor C DU401A-BV) on the exit focal plane of the spectrometer. The CCD is cooled with a Peltier cell down to 200 K. The spectral resolution of the spectroscopy apparatus is 0.4 cm${}^{-1}$.

5. Conclusions

Ice XVII shows interesting properties from the perspective of a possible use as a novel material for hydrogen storage, despite the temperature limits of metastability of the ice XVII, and the necessity of conceiving a cooling system to maintain the temperature below 130 K when a real hydrogen storage tank is designed. The relatively low storage pressure reduces the cost for the realization of tanks suitable for mobile applications, e.g., fuel cell vehicles, while the high volumetric capacity allows its use also for stationary devices, e.g., gas accumulator tanks. Moreover, a very interesting aspect is related to the simplicity and cost effectiveness of the chemicals involved for its production, which are only water and hydrogen.