A Review of System Strength and Inertia in Renewable-Energy-Dominated Grids: Challenges, Sustainability, and Solutions
Abstract
1. Introduction
- An analysis of recent events and SO market intervention in the deregulated and weakly interconnected electricity markets of Australia, Ireland, and Texas.
- A critical review of current mitigation techniques including synchronous condensers and ancillary services.
- An evaluation of research gaps in system strength and inertia estimation methods, high-IBR grid modelling, and non-linear GFMI output current control techniques.
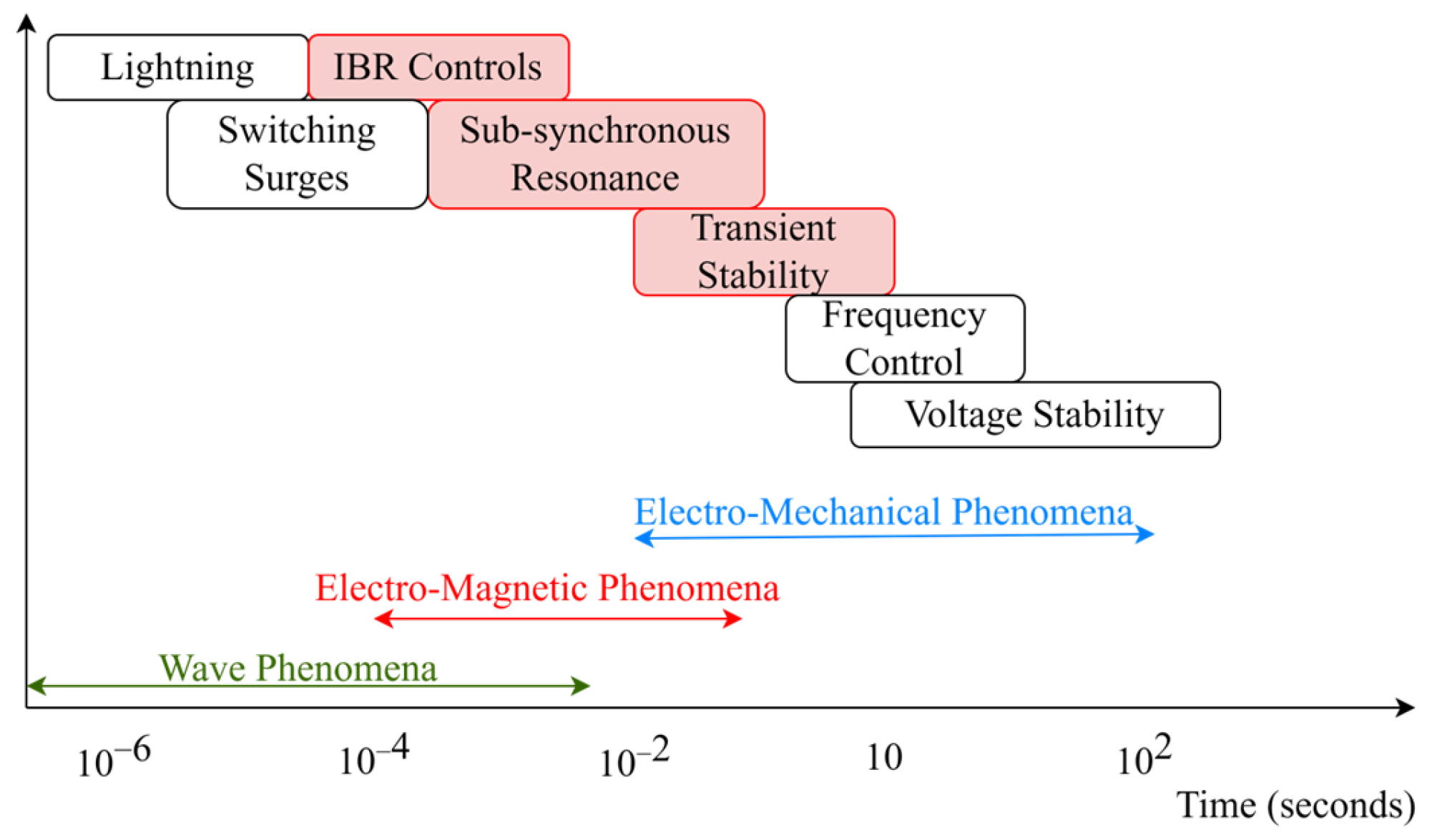
2. Understanding System Strength and Inertia
2.1. Definitions and Key Concepts
2.2. Impact of IBR Generation
3. System Strength and Inertia Challenges
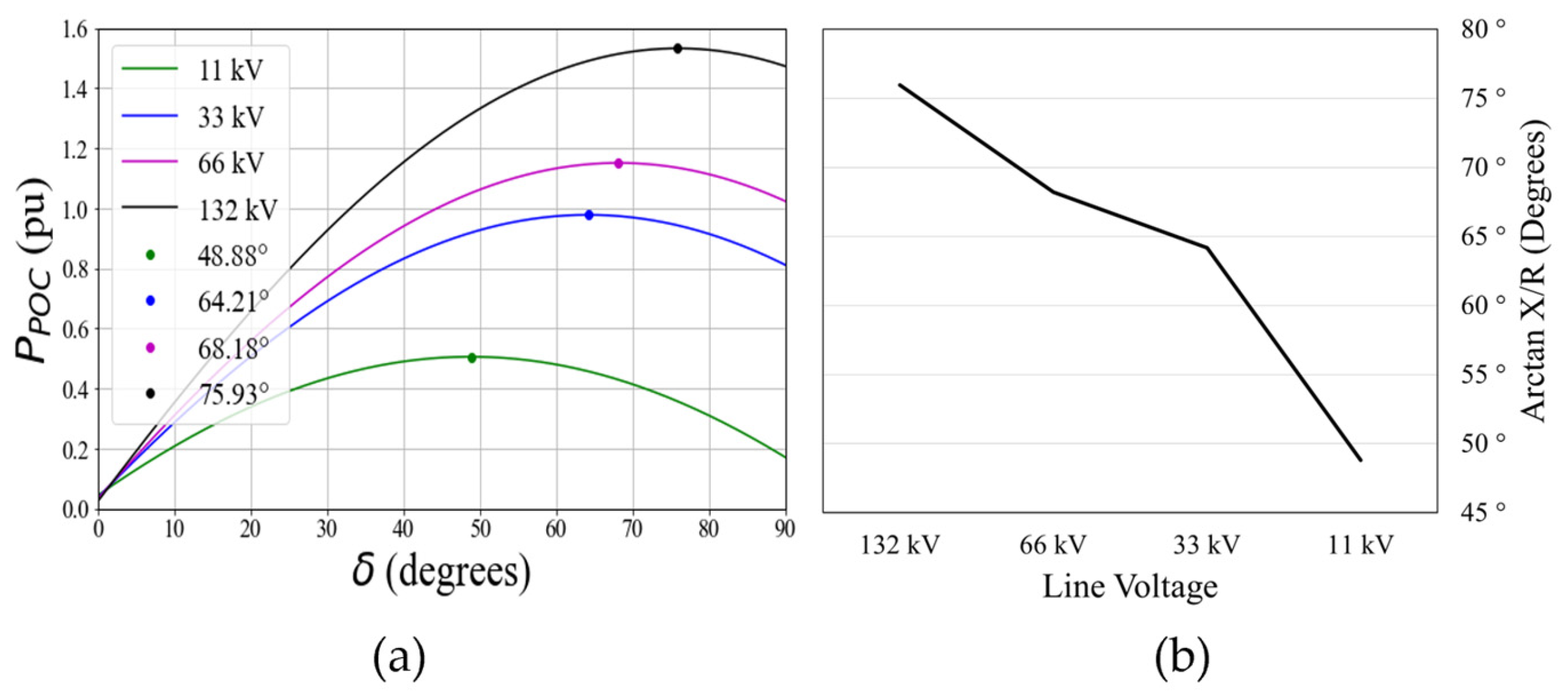
3.1. System Strength Issues
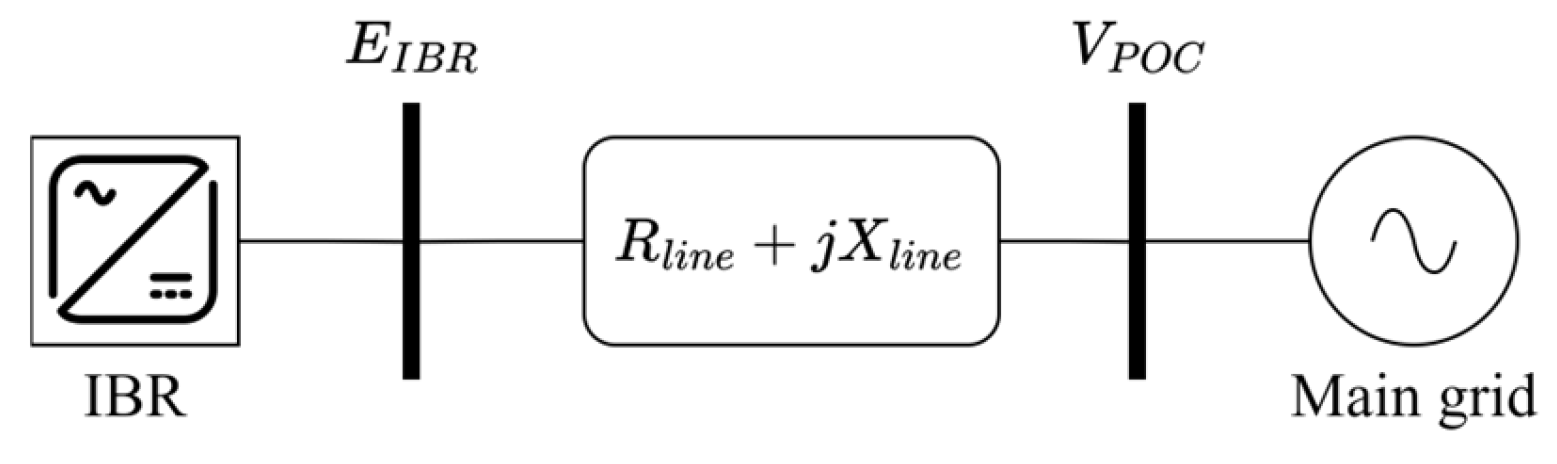
Voltage Stability
- IBRs cause a drop in SCR making the node voltage more susceptible to rapid current changes caused by transient conditions.
- GFLI algorithms demonstrate suboptimal performance under faulted conditions. IBR plant tripping during faulted conditions is a significant problem as shown by the examples provided in Section 4.3.
- The tripping in item 2 can lead to further voltage instability and entire plant tripping.
3.2. Inertia Issues
3.2.1. Frequency Stability
3.2.2. Angle Stability
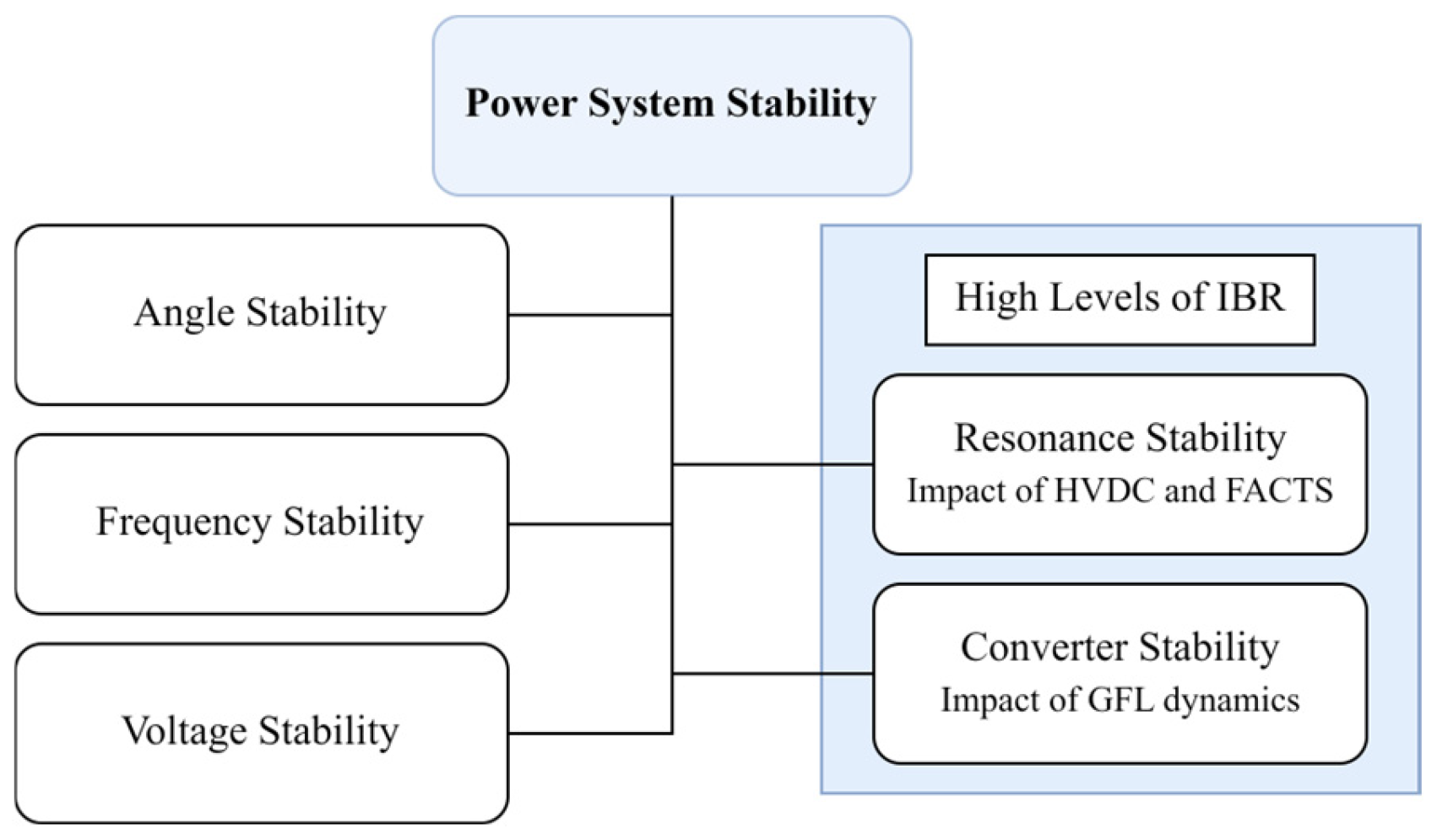
3.2.3. Emerging Stability Categories
- Resonance stability, related to the impact of HVDC and FACTS devices.
- Converter stability, relating to the impact of GFLI (both current and voltage source).
4. Case Studies from Regions with High Renewable Energy
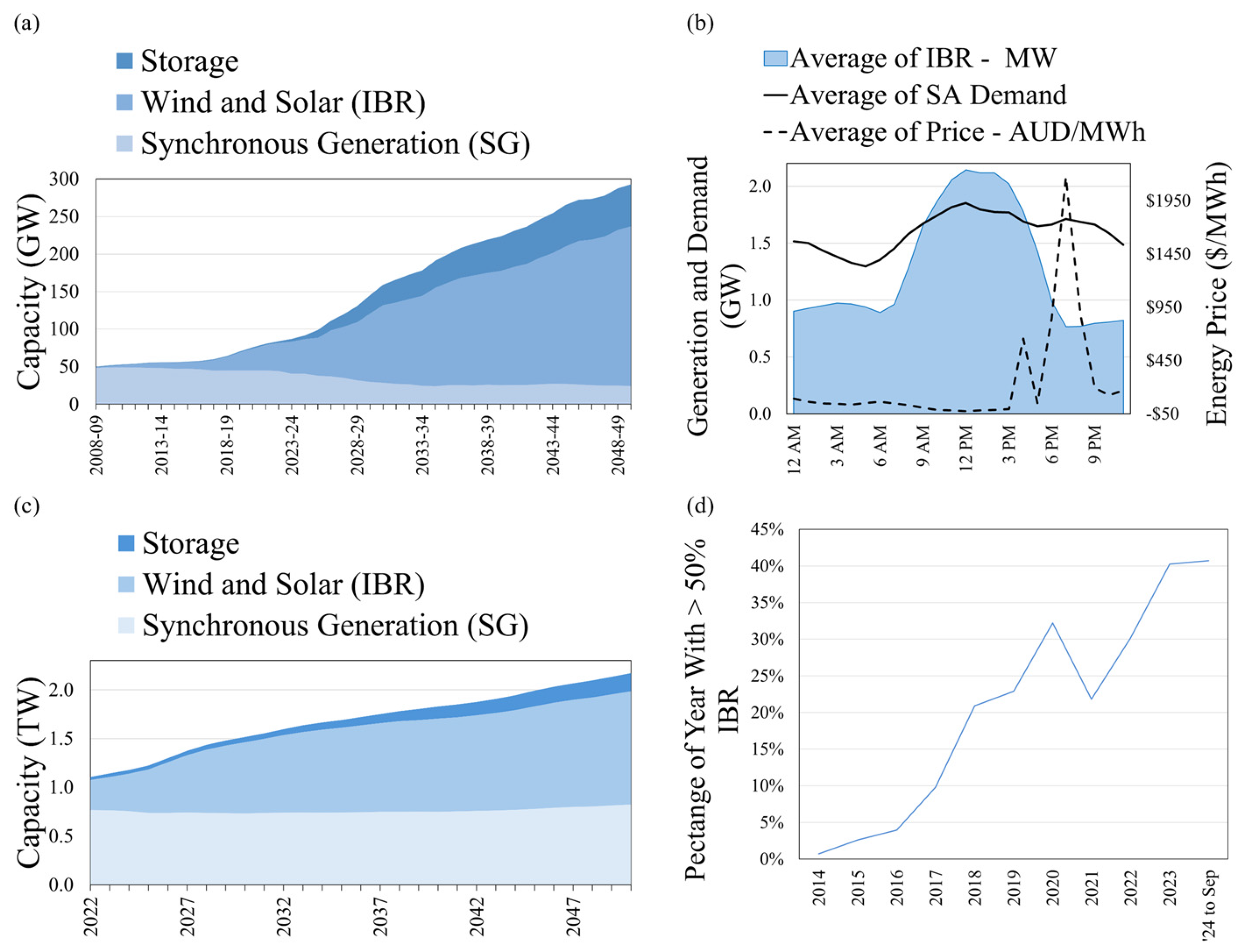
4.1. IBR Penetration Levels
4.2. System Operator Interventions
- Maximum system non-synchronous penetration (SNSP) limit of 75%.
- A minimum number of conventional units on (MUON) of seven units.
4.3. System Strength and Inertia Events
5. Mitigation Strategies
5.1. Synchronous Condensers
5.2. Flexible AC Transmission Systems
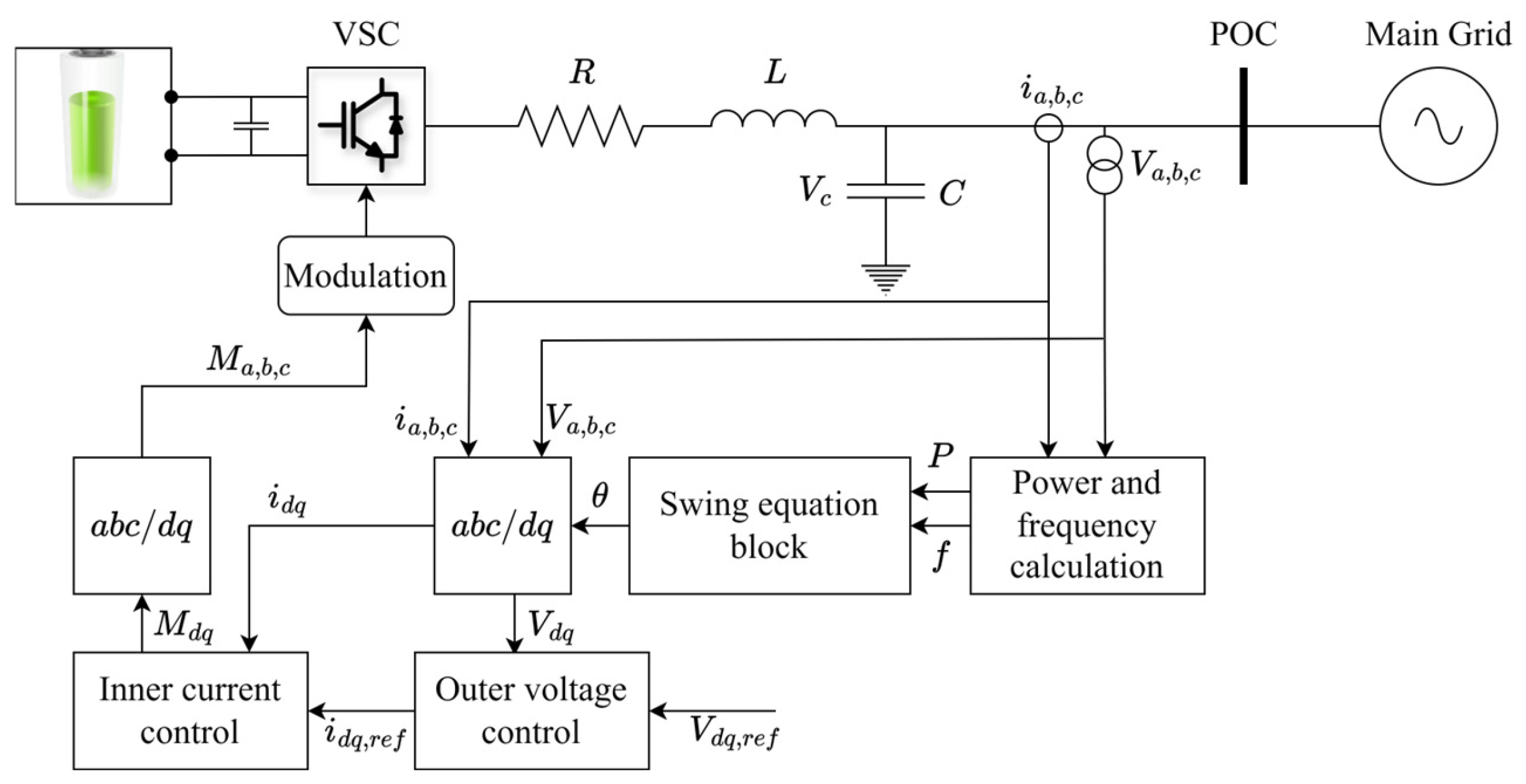
5.3. Grid-Forming Inverters
5.4. Ancillary Services
6. Future Research Direction
6.1. Improve System Strength and Inertia Evaluation Methodology
6.1.1. System Strength
| Method | Formula | Contribution | Ref |
|---|---|---|---|
| SCRPOC | Commonly used metric. Suitable for single inverter connection at POC. | [104,105] | |
| WSCR-MW | Considered N IBRs in the locality and provided a weighted value. | [104,105] | |
| WSCR-MVA | As per WSCR-MW but considered IBR reactive power capability. | [104] | |
| CSCR | Created composite bus and provides an average SCR. Assumes perfect bus coupling. | [104,107] | |
| ESCR | Enhanced SCR by including shunt reactive compensation. | [108] | |
| IILSCR | Used power tracing to reflect bus interactions | [106] |
6.1.2. Inertia
6.2. Improved Grid Modelling
6.3. Advanced GFLI/GFMI Control
6.3.1. Droop Control
6.3.2. Virtual Synchronous Machine
- The energy storage ramp rate impact on VSM stability requires further study. Research is required before the integration and impact of energy storage for VSM systems is clear.
- The transient stability issue remains for VSM. This is due to the use of linear control techniques, such as PI, in many current implementations. Issues such as energy storage ramping and filter parameter changes have also been shown to impact stability. Non-linear techniques, SMC and MPC, have demonstrated increased stability margin and robustness for VSM, but research and real-world implementation remain limited.
- Smart-grid technologies like VSM involve the use of communications and can be computationally expensive. As VSMs are a critical power grid infrastructure, further research is required in this area to ensure that new solutions are secure, cost-effective, and implementable on existing inverter technology.
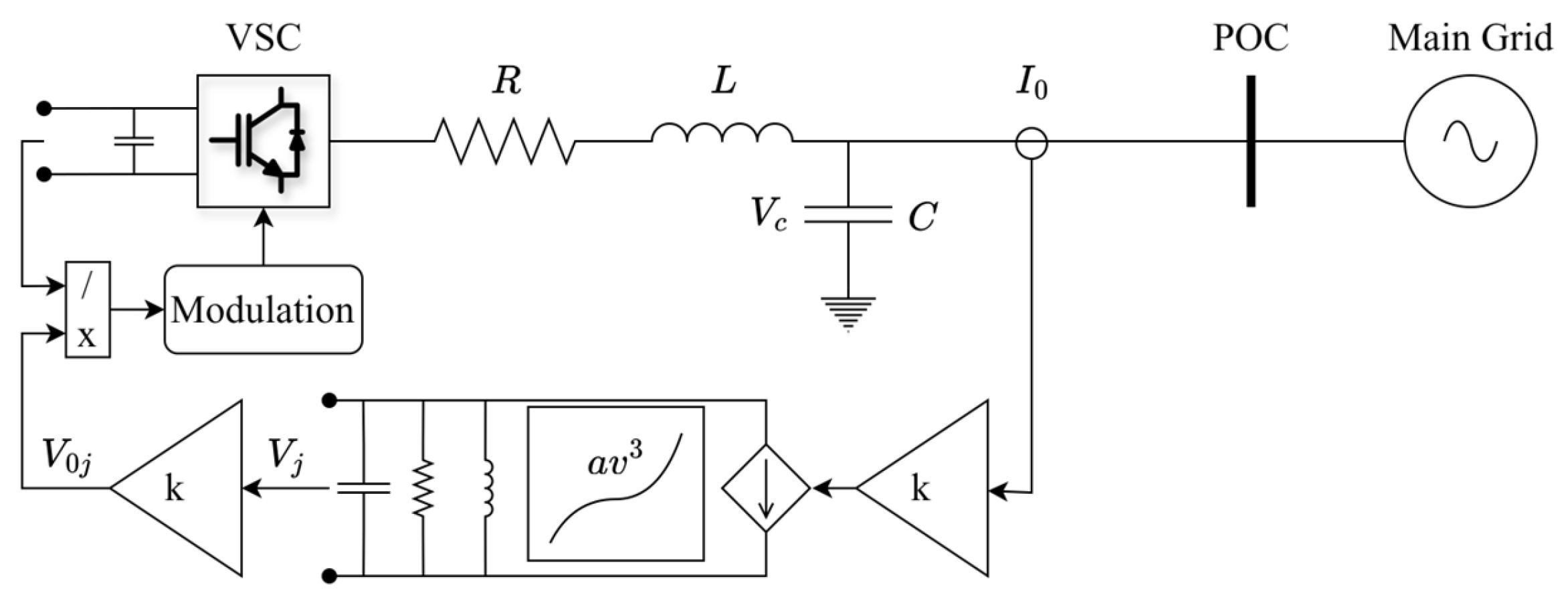
6.3.3. Dispatchable Virtual Oscillator Control
6.3.4. GFMI Fault Current
6.3.5. Swing Equation Derivation from Energy
7. Discussion
Benefit to Planetary Health
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United Nations Climate Change The Paris Agreement | UNFCCC. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement (accessed on 13 September 2024).
- Graham, P.; Hayward, J.; Foster, J. GenCost 2023-24: Final Report; CSIRO: Canberra, ACT, Australia, 2023. [Google Scholar]
- CEC Quarterly Carbon Market Report December Quarter 2023. Available online: https://cer.gov.au/markets/reports-and-data/quarterly-carbon-market-reports/quarterly-carbon-market-report-december-quarter-2023/state-of-total-renewables (accessed on 13 September 2024).
- Vorwerk, J.; Dozein, M.G.; Mancarella, P.; Hug, G. Analytical Discussion on Dynamics of Inverter-Based Resources under Small-Signal Conditions. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023; pp. 1–6. [Google Scholar]
- Gu, H.; Yan, R.; Saha, T.K.; Muljadi, E. System Strength and Inertia Constrained Optimal Generator Dispatch Under High Renewable Penetration. IEEE Trans. Sustain. Energy 2020, 11, 2392–2406. [Google Scholar] [CrossRef]
- Aljarrah, R.; Fawaz, B.B.; Salem, Q.; Karimi, M.; Marzooghi, H.; Azizipanah-Abarghooee, R. Issues and Challenges of Grid-Following Converters Interfacing Renewable Energy Sources in Low Inertia Systems: A Review. IEEE Access 2024, 12, 5534–5561. [Google Scholar] [CrossRef]
- Gu, H.; Yan, R.; Saha, T.K. Review of System Strength and Inertia Requirements for the National Electricity Market of Australia. CSEE J. Power Energy Syst. 2019, 5, 295–305. [Google Scholar] [CrossRef]
- Peng, Q.; Jiang, Q.; Yang, Y.; Liu, T.; Wang, H.; Blaabjerg, F. On the Stability of Power Electronics-Dominated Systems: Challenges and Potential Solutions. IEEE Trans. Ind. Appl. 2019, 55, 7657–7670. [Google Scholar] [CrossRef]
- Qays, M.O.; Ahmad, I.; Habibi, D.; Aziz, A.; Mahmoud, T. System Strength Shortfall Challenges for Renewable Energy-Based Power Systems: A Review. Renew. Sustain. Energy Rev. 2023, 183, 113447. [Google Scholar] [CrossRef]
- Boričić, A.; Torres, J.L.R.; Popov, M. System Strength: Classification, Evaluation Methods, and Emerging Challenges in IBR-Dominated Grids. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Singapore, 1–5 November 2022; pp. 185–189. [Google Scholar]
- Ghazavi, M.; Mancarella, P.; Saha, T.; Yan, R. System Strength and Weak Grids: Fundamentals, Challenges, and Mitigation Strategies. In Proceedings of the 2018 Australasian Universities Power Engineering Conference (AUPEC), Auckland, New Zealand, 27–30 November 2018; pp. 1–7. [Google Scholar]
- AEMO. System Strength in the NEM Explained; Australian Energy Market Operator: Melbourne, VIC, Australia, 2020. [Google Scholar]
- Hosseinzadeh, N.; Liyanarachchi, L.; Gargoom, A.; Alhelou, H.H.; Bahrani, B.; Fahiman, F.; Farahani, E. Power System Strength Assessment with High Penetration of Inverter-Based Resources—A Conceptual Approach. In Power System Strength Evaluation Methods, Best Practise, Case Studies, and Applications; Institution of Engineering and Technology: Stevenage, UK, 2023. [Google Scholar]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Alkhazim, H.A.; Bajunaid, S.I.; Alsulami, W.A.; Alghamdi, M.S. Impact of Inverter Based Resources on Power System Protective Relaying, Fault Calculation and Protection Setting: A Systematic Literature Review. In Proceedings of the 2022 Saudi Arabia Smart Grid (SASG), Riyadh, Saudi Arabia, 12–14 December 2022; pp. 1–11. [Google Scholar]
- Matevosyan, J.; MacDowell, J.; Miller, N.; Badrzadeh, B.; Ramasubramanian, D.; Isaacs, A.; Quint, R.; Quitmann, E.; Pfeiffer, R.; Urdal, H.; et al. A Future With Inverter-Based Resources: Finding Strength From Traditional Weakness. IEEE Power Energy Mag. 2021, 19, 18–28. [Google Scholar] [CrossRef]
- Ghosh, S.; Alhatlani, A.; Safayatullah, M.; Batarseh, I. Review of MPPT Methods for LLC Converters in Photovoltaic Applications. In Proceedings of the 2022 IEEE Energy Conversion Congress and Exposition (ECCE), Detroit, MI, USA, 9–13 October 2022; pp. 1–6. [Google Scholar]
- Alharbi, M. Control Approach of Grid-Connected PV Inverter under Unbalanced Grid Conditions. Processes 2024, 12, 212. [Google Scholar] [CrossRef]
- Yu, L.; Meng, K.; Zhang, W.; Zhang, Y. An Overview of System Strength Challenges in Australia’s National Electricity Market Grid. Electronics 2022, 11, 224. [Google Scholar] [CrossRef]
- Modi, N.; Farahani, E.M.; Jalali, A.; Ramamurthy, J.; Chin, C.; Soetantijo, B. Replication of Real-World Sub-Synchronous Oscillations in Inverter-Based Resources Dominated Grid. IEEE Trans. Power Deliv. 2024, 39, 1399–1406. [Google Scholar] [CrossRef]
- Alshareef, A.; Shah, R.; Mithulananthan, N.; Alzahrani, S. A New Global Index for Short Term Voltage Stability Assessment. IEEE Access 2021, 9, 36114–36124. [Google Scholar] [CrossRef]
- Feng, F.; Fang, J. Weak Grid-Induced Stability Problems and Solutions of Distributed Static Compensators with Voltage Droop Support. Electronics 2022, 11, 1385. [Google Scholar] [CrossRef]
- Zhang, Q.; Mao, M.; Ke, G.; Zhou, L.; Xie, B. Stability Problems of PV Inverter in Weak Grid: A Review. IET Power Electron. 2020, 13, 2165–2174. [Google Scholar] [CrossRef]
- Saleem, M.I.; Saha, S.; Ang, L.; Izhar, U.; Roy, T.K. Factors Affecting Voltage Stability While Integrating Inverter Based Renewable Energy Sources into Weak Power Grids. IET Gener. Transm. Distrib. 2023, 17, 1216–1231. [Google Scholar] [CrossRef]
- Yan, N.; Shi, L. Transient Voltage Stability Assessment Incorporating Uncertainties of Wind-PV Generation and Load. In Proceedings of the 12th International Conference on Renewable Power Generation (RPG 2023), Shanghai, China, 14–15 October 2023; The Institution of Engineering and Technology: Stevenage, UK, 2023; Volume 2023, pp. 773–778. [Google Scholar]
- Li, M.; Zhang, X.; Fu, X.; Geng, H.; Zhao, W. Stability Studies on PV Grid-Connected Inverters under Weak Grid: A Review. Chin. J. Electr. Eng. 2024, 10, 1–19. [Google Scholar] [CrossRef]
- Yallamilli, R.S.; Dwibhashyam, T.; Bavisetti, K. Weak Grid Integrated PV Plant Design Considerations for Improved Voltage Stability. In Proceedings of the 2022 22nd National Power Systems Conference (NPSC), New Delhi, India, 17–19 December 2022; pp. 59–64. [Google Scholar]
- Hu, B.; Cao, W.; Yang, M.; Lu, Y. The Optimal Ratio of GFM-Converters to GFL-Converters for Transient Voltage Regulation with Weak Grid Condition. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 1993–1998. [Google Scholar]
- Alanazi, M.; Salem, M.; Sabzalian, M.H.; Prabaharan, N.; Ueda, S.; Senjyu, T. Designing a New Controller in the Operation of the Hybrid PV-BESS System to Improve the Transient Stability. IEEE Access 2023, 11, 97625–97640. [Google Scholar] [CrossRef]
- Ravanji, M.H.; Zhou, W.; Mohammed, N.; Bahrani, B. Comparative Analysis of the Power Output Capabilities of Grid-Following and Grid-Forming Inverters Considering Static, Dynamic, and Thermal Limitations. IEEE Trans. Power Syst. 2024, 39, 2693–2705. [Google Scholar] [CrossRef]
- Cheng, X.K.; Liu, H.; Song, P.; Sun, D.W.; Zhang, R.F. Review on Transient Power Angle Stability of System with Doubly-Fed Induction Generator Based on Virtual Synchronous Generator. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 1614–1619. [Google Scholar]
- Yu, L.; Sun, H.; Xu, S.; Zhao, B.; Zhang, J. A Critical System Strength Evaluation of a Power System with High Penetration of Renewable Energy Generations. CSEE J. Power Energy Syst. 2022, 8, 710–720. [Google Scholar] [CrossRef]
- Dong, X.; Kang, C.; Ding, Y.; Wang, C. Estimating the Wind Power Integration Threshold Considering Electro-Thermal Coupling of Overhead Transmission Lines. IEEE Trans. Power Syst. 2019, 34, 3349–3358. [Google Scholar] [CrossRef]
- He, L.; Yu, S. Systematic Decoupling Grid-Forming Control for Utility-Scale Inverter-Based Distributed Energy Resources in Weak Distribution Grids. IEEE Open Access J. Power Energy 2024, 11, 27–39. [Google Scholar] [CrossRef]
- Mohammed, N.; Udawatte, H.; Zhou, W.; Hill, D.J.; Bahrani, B. Grid-Forming Inverters: A Comparative Study of Different Control Strategies in Frequency and Time Domains. IEEE Open J. Ind. Electron. Soc. 2024, 5, 185–214. [Google Scholar] [CrossRef]
- Kundur, P. Classification of Stability. In Power System Stability and Control; Power Engineering Series; McGraw Hill: New York, NY, USA, 1994. [Google Scholar]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Sainz, L.; Cheah-Mane, M.; Monjo, L.; Liang, J.; Gomis-Bellmunt, O. Positive-Net-Damping Stability Criterion in Grid-Connected VSC Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1499–1512. [Google Scholar] [CrossRef]
- Surinkaew, T.; Emami, K.; Shah, R.; Islam, S.; Mithulananthan, N. Forced Oscillation in Power Systems With Converter Controlled-Based Resources–A Survey With Case Studies. IEEE Access 2021, 9, 150911–150924. [Google Scholar] [CrossRef]
- Damas, R.N.; Son, Y.; Yoon, M.; Kim, S.-Y.; Choi, S. Subsynchronous Oscillation and Advanced Analysis: A Review. IEEE Access 2020, 8, 224020–224032. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, X.; Liu, F.; Xin, K.; Liu, Y. Sub-Synchronous Control Interaction in Grid-Forming VSCs with Droop Control. In Proceedings of the 2019 4th IEEE Workshop on the Electronic Grid (eGRID), Xiamen, China, 11–14 November 2019; pp. 1–6. [Google Scholar]
- Zhao, F.; Wang, X.; Zhou, Z.; Sun, Y.; Harnefors, L.; Zhu, T. Robust Grid-Forming Control With Active Susceptance. IEEE Trans. Power Electron. 2023, 38, 2872–2877. [Google Scholar] [CrossRef]
- AEMO. 2024 ISP Chart Data; Australian Energy Market Operator: Melbourne, VIC, Australia, 2024. [Google Scholar]
- OpenNEM. Open Electricity: South Australia; The SuperPower Institute: Fitzroy, VIC, Australia, 2024. [Google Scholar]
- Chaudhuri, B.; Ramasubramanian, D.; Matevosyan, J.; O’Malley, M.; Miller, N.; Green, T.; Zhou, X. Rebalancing Needs and Services for Future Grids: System Needs and Service Provisions With Increasing Shares of Inverter-Based Resources. IEEE Power Energy Mag. 2024, 22, 30–41. [Google Scholar] [CrossRef]
- U.S. Energy Information Administration. Table 9. Electricity Generating Capacity. 2024. Available online: https://www.eia.gov/outlooks/aeo/data/browser/#/?id=9-AEO2023&cases=ref2023&sourcekey=0 (accessed on 7 November 2024).
- EirGrid. System and Renewable Data Reports; EirGrid: Dublin, Ireland, 2024. [Google Scholar]
- AEMO. 2023 Inertia Report; Australian Energy Market Operator: Melbourne, VIC, Australia, 2023. [Google Scholar]
- Harper, K. FCAS Model in NEMDE; Australian Energy Market Operator: Melbourne, VIC, Australia, 2024. [Google Scholar]
- AEMO. Market Notices. Available online: https://aemo.com.au/market-notices (accessed on 4 November 2024).
- AEMO. 2023 System Strength Report; Australian Energy Market Operator: Melbourne, VIC, Australia, 2023. [Google Scholar]
- EirGrid; SONI System Strength Requirements Secure Operation of the All-Island Power System in the Presence of High Shares of Inverter Based Resources; EirGrid: Dublin, Ireland, 2024.
- EirGrid; SONI DS3 Rate of Change of Frequency Modification Recommendation to the CER; EirGrid: Dublin, Ireland, 2012.
- EirGrid; SONI Annual Renewable Energy Constraint and Curtailment Report 2023; EirGrid SONI: Dublin, Ireland, 2024.
- Matevosyan, J. Benefits of Grid-Forming Energy Storage Resources: A Unique Window of Opportunity in ERCOT. ESIG (Energy Systems Integration Group): Reston, VA, USA, 2022. [Google Scholar]
- Lee, D. Keeping Up with the Curtailment Part 2: The What and the Where; WattClarity: Brisbane, QLD, Australia, 2024. [Google Scholar]
- IMM. 2023 State of the Market Report for the ERCOT Electricity Markets; Independent Market Monitor (Potomac Economics): Fairfax, VA, USA, 2024. [Google Scholar]
- AEMO. West Murray Zone Intermittent Power System Oscillations—Sample 19 Hz Oscillations Data; Australian Energy Market Operator: Melbourne, VIC, Australia, 2021. [Google Scholar]
- Khan, M.; Wu, W.; Li, L. Grid-Forming Control for Inverter-Based Resources in Power Systems: A Review on Its Operation, System Stability, and Prospective. IET Renew. Power Gener. 2024, 18, 887–907. [Google Scholar] [CrossRef]
- Cheng, Y.; Fan, L.; Rose, J.; Huang, S.-H.; Schmall, J.; Wang, X.; Xie, X.; Shair, J.; Ramamurthy, J.R.; Modi, N.; et al. Real-World Subsynchronous Oscillation Events in Power Grids With High Penetrations of Inverter-Based Resources. IEEE Trans. Power Syst. 2023, 38, 316–330. [Google Scholar] [CrossRef]
- Modi, N.; Escudero, M.V.; Aramaki, K.; Zhou, X.; Partinen, P. High Inverter-Based Resource Integration: The Experience of Five System Operators. IEEE Power Energy Mag. 2024, 22, 78–88. [Google Scholar] [CrossRef]
- Parkinson, G. Flicker Fest: Production Halted at Australia’s Biggest Wind and Solar Farm After Voltage Issues. Available online: https://reneweconomy.com.au/flicker-fest-production-halted-at-australias-biggest-wind-and-solar-farm-after-voltage-issues/ (accessed on 31 December 2024).
- NERC. 2022 Odessa Disturbance; North American Electric Reliability Corporation: Atlanta, Georgia, 2022. [Google Scholar]
- NERC. Odessa Disturbance 2021; North American Electric Reliability Corporation: Atlanta, Georgia, 2021. [Google Scholar]
- Fan, L.; Wang, Z.; Miao, Z. Large Angle Deviation in Grid-Following IBRs Upon Grid Voltage Dip. IEEE Trans. Energy Convers. 2024, 39, 368–378. [Google Scholar] [CrossRef]
- Hadavi, S.; Mansour, M.Z.; Bahrani, B. Optimal Allocation and Sizing of Synchronous Condensers in Weak Grids With Increased Penetration of Wind and Solar Farms. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 199–209. [Google Scholar] [CrossRef]
- Hadavi, S.; Saunderson, J.; Mehrizi-Sani, A.; Bahrani, B. A Planning Method for Synchronous Condensers in Weak Grids Using Semi-Definite Optimization. IEEE Trans. Power Syst. 2023, 38, 1632–1641. [Google Scholar] [CrossRef]
- Zhang, Y.; Gole, A.M. Quantifying the Contribution of Dynamic Reactive Power Compensators on System Strength at LCC-HVdc Converter Terminals. IEEE Trans. Power Deliv. 2022, 37, 449–457. [Google Scholar] [CrossRef]
- Hadavi, S.; Rathnayake, D.B.; Jayasinghe, G.; Mehrizi-Sani, A.; Bahrani, B. A Robust Exciter Controller Design for Synchronous Condensers in Weak Grids. IEEE Trans. Power Syst. 2022, 37, 1857–1867. [Google Scholar] [CrossRef]
- Hadavi, S.; Mohammed, N.; Mehrizi-Sani, A.; Bahrani, B. Quantifying Stability in Inverter-Based Weak Grids in the Presence of Synchronous Condensers. IEEE Open Access J. Power Energy 2024, 11, 314–324. [Google Scholar] [CrossRef]
- Yamada, Y.; Tsusaka, A.; Nanahara, T.; Yukita, K. A Study on Short-Circuit-Ratio for an Inverter-Based Resource With Power-Voltage Curves. IEEE Trans. Power Syst. 2024, 39, 6076–6086. [Google Scholar] [CrossRef]
- Siemens. Supporting Grid Stability—Building a New Energy System with Synchronous Condenser Conversion; Siemens Energy Global GmbH: Erlangen, Germany, 2024; Available online: https://www.siemens-energy.com/global/en/home/publications/technical-paper/download-grid-stability-synchronous-condenser-conversion.html (accessed on 23 October 2024).
- ElectraNet Power System Strength (Synchronous Condensers). Available online: https://www.electranet.com.au/what-we-do/projects/power-system-strength/ (accessed on 16 March 2024).
- Conn, J.; Huang, S.H.; Schmall, J.; Atallah, A.; Kynev, S. Synchronous Condenser for Integration of Wind Generation in Texas Panhandle Area; CIGRE US National Committee 2019 Grid of the Future Symposium; CIGRE: Paris, France, 2019. [Google Scholar]
- Sharma, S.; Gupta, S.; Zuhaib, M.; Bhuria, V.; Malik, H.; Almutairi, A.; Afthanorhan, A.; Hossaini, M.A. A Comprehensive Review on STATCOM: Paradigm of Modeling, Control, Stability, Optimal Location, Integration, Application, and Installation. IEEE Access 2024, 12, 2701–2729. [Google Scholar] [CrossRef]
- Arabi, S.; Kundur, P. Stability Modelling of Storage Devices in FACTS Applications. In Proceedings of the 2001 Power Engineering Society Summer Meeting. Conference Proceedings (Cat. No.01CH37262), Vancouver, BC, Canada, 15–19 July 2001; Volume 2, pp. 767–771. [Google Scholar]
- Su, J.; Chen, C. Dynamic Modeling and Stability Analysis of the Composite Power System with Power Electronic Equipments. In Proceedings of the Proceedings. International Conference on Power System Technology, Kunming, China, 13–17 October 2002; Volume 3, pp. 1488–1492. [Google Scholar]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid Forming Inverter Modeling, Control, and Applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Badrzadeh, B.; Cardozo, C.; Hishida, M.; Shah, S.; Huq, I.; Modi, N.; Morton, A. Grid-Forming Inverters: Project Demonstrations and Pilots. IEEE Power Energy Mag. 2024, 22, 66–77. [Google Scholar] [CrossRef]
- AEMO. Voluntary Specification for Grid-Forming Inverters; Australian Energy Market Operator: Melbourne, VIC, Australia, 2023. [Google Scholar]
- Transgrid. Stable Voltage Waveform Support Specifications for Grid-Forming BESS; Meeting System Strength Requirements in NSW’ Project Assessment Draft Report (PADR); Tansgrid: Sydney, NSW, Australia, 2024. [Google Scholar]
- Hoke, A.; Boemer, J.C.; Badrzadeh, B.; MacDowell, J.; Kurthakoti, D.; Marszalkowski, B.; Meuser, M. Foundations for the Future Power System: Inverter-Based Resource Interconnection Standards. IEEE Power Energy Mag. 2024, 22, 42–54. [Google Scholar] [CrossRef]
- Liyanage, C.; Nutkani, I.; Meegahapola, L. A Comparative Analysis of Prominent Virtual Synchronous Generator Strategies Under Different Network Conditions. IEEE Open Access J. Power Energy 2024, 11, 178–195. [Google Scholar] [CrossRef]
- Jiang, S.; Zhu, Y.; Xu, T.; Konstantinou, G. Current-Synchronization Control of Grid-Forming Converters for Fault Current Limiting and Enhanced Synchronization Stability. IEEE Trans. Power Electron. 2024, 39, 5271–5285. [Google Scholar] [CrossRef]
- Ghosh, R.; Tummuru, N.R.; Rajpurohit, B.S. Dynamic Voltage Stiffness Control Technique for a Virtual Oscillator-Based Grid- Forming Controller. IEEE Trans. Ind. Electron. 2024, 71, 5725–5733. [Google Scholar] [CrossRef]
- Ducoin, E.A.S.; Gu, Y.; Chaudhuri, B.; Green, T.C. Analytical Design of Contributions of Grid-Forming and Grid-Following Inverters to Frequency Stability. IEEE Trans. Power Syst. 2024, 39, 6345–6358. [Google Scholar] [CrossRef]
- Bahrani, B.; Ravanji, M.H.; Kroposki, B.; Ramasubramanian, D.; Guillaud, X.; Prevost, T.; Cutululis, N.-A. Grid-Forming Inverter-Based Resource Research Landscape: Understanding the Key Assets for Renewable-Rich Power Systems. IEEE Power Energy Mag. 2024, 22, 18–29. [Google Scholar] [CrossRef]
- ElectraNet. ESCRI-SA Battery Energy Storage Final Knowledge Sharing Report; ElectraNet: Adelaide, SA, Australia, 2021. [Google Scholar]
- ARENA. Green Light for Australia’s Largest Grid-Forming Battery. Available online: https://arena.gov.au/news/green-light-for-australias-largest-grid-forming-battery/ (accessed on 5 January 2025).
- Phurailatpam, C.; Flynn, D. Requirements and Grid Standards for Grid-Forming Inverters. In Grid-Forming Power Inverters Control and Applications; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- AEMO. Hornsdale Wind Farm 2 FCAS Trial; Australian Energy Market Operator: Melbourne, VIC, Australia, 2018. [Google Scholar]
- Gilmore, J.; Nolan, T.; Simshauser, P. The Levelised Cost of Frequency Control Ancillary Services in Australia’s National Electricity Market. Energy J. 2022, 45, 201–229. [Google Scholar] [CrossRef]
- Corbet, L. Very Fast Raise and Lower FCAS Markets to Start on 9 October 2023; WattClarity: Brisbane, QLD, Australia, 2023. [Google Scholar]
- AEMO. Market Ancillary Service Specification 8.2; Australian Energy Market Operator: Melbourne, VIC, Australia, 2024. [Google Scholar]
- AEMO. Review of NEM Load Relief; Australian Energy Market Operator: Melbourne, VIC, Australia, 2023. [Google Scholar]
- NEMBESS. Available online: https://nembess.com (accessed on 2 January 2025).
- Corbet, L. Very Fast FCAS—A Week in Review; WattClarity: Brisbane, QLD, Australia, 2023. [Google Scholar]
- AEMO. NEM Registration and Exemption List; Australian Energy Market Operator: Melbourne, VIC, Australia, 2025. [Google Scholar]
- Boyle, J.; Littler, T. A Review of Frequency-Control Techniques for Wind Power Stations to Enable Higher Penetration of Renewables onto the Irish Power System. Energy Rep. 2024, 12, 5567–5581. [Google Scholar] [CrossRef]
- Al Kez, D.; Foley, A.M.; Ahmed, F.; Morrow, D.J. Overview of Frequency Control Techniques in Power Systems with High Inverter-Based Resources: Challenges and Mitigation Measures. IET Smart Grid 2023, 6, 447–469. [Google Scholar] [CrossRef]
- Hu, J.; Yan, Z.; Xu, X.; Chen, S. Inertia Market: Mechanism Design and Its Impact on Generation Mix. J. Mod. Power Syst. Clean Energy 2023, 11, 744–756. [Google Scholar] [CrossRef]
- Liang, Z.; Mieth, R.; Dvorkin, Y. Inertia Pricing in Stochastic Electricity Markets. IEEE Trans. Power Syst. 2023, 38, 2071–2084. [Google Scholar] [CrossRef]
- Zhu, Y.; Green, T.C.; Zhou, X.; Li, Y.; Kong, D.; Gu, Y. Impedance Margin Ratio: A New Metric for Small-Signal System Strength. IEEE Trans. Power Syst. 2024, 39, 7291–7303. [Google Scholar] [CrossRef]
- NERC. Integrating InverterBased Resources into Low Short Circuit Strength Systems; North American Electric Reliability Corporation: Atlanta, GA, USA, 2017; December. [Google Scholar]
- Liyanarachchi, L.; Hosseinzadeh, N.; Gargoom, A. Power System Strength Assessment with Inverter Based Resources: Case Studies. In Proceedings of the 2023 5th International Conference on Smart Power & Internet Energy Systems (SPIES), Shenyang, China, 1–4 December 2023; pp. 35–40. [Google Scholar]
- Kim, D.; Lee, B. Impact of Renewable Energy Sources on AC System Strength Using Inverter Interaction Level. In Proceedings of the 2019 IEEE Sustainable Power and Energy Conference (iSPEC), Beijing, China, 21–23 November 2019. [Google Scholar]
- Li, B.; Xu, S.; Sun, H.; Li, Z.; Yu, L. System Strength Assessment Based on Multi-Task Learning. CSEE J. Power Energy Syst. 2024, 10, 41–50. [Google Scholar] [CrossRef]
- Ni, X.; Gole, A.M.; Zhao, C.; Guo, C. An Improved Measure of AC System Strength for Performance Analysis of Multi-Infeed HVdc Systems Including VSC and LCC Converters. IEEE Trans. Power Deliv. 2018, 33, 169–178. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Lee, G.-S.; Yoon, J.-S.; Moon, S.-I. Evaluation for Maximum Allowable Capacity of Renewable Energy Source Considering AC System Strength Measures. IEEE Trans. Sustain. Energy 2022, 13, 1123–1134. [Google Scholar] [CrossRef]
- Kim, Y.-K.; Lee, G.-S.; Kim, C.-K.; Moon, S.-I. An Improved AC System Strength Measure for Evaluation of Power Stability and Temporary Overvoltage in Hybrid Multi-Infeed HVDC Systems. IEEE Trans. Power Deliv. 2022, 37, 638–649. [Google Scholar] [CrossRef]
- Henderson, C.; Egea-Alvarez, A.; Kneuppel, T.; Yang, G.; Xu, L. Grid Strength Impedance Metric: An Alternative to SCR for Evaluating System Strength in Converter Dominated Systems. IEEE Trans. Power Deliv. 2024, 39, 386–396. [Google Scholar] [CrossRef]
- Tan, B.; Zhao, J.; Netto, M.; Krishnan, V.; Terzija, V.; Zhang, Y. Power System Inertia Estimation: Review of Methods and the Impacts of Converter-Interfaced Generations. Int. J. Electr. Power Energy Syst. 2022, 134, 107362. [Google Scholar] [CrossRef]
- Bizzarri, F.; del Giudice, D.; Grillo, S.; Linaro, D.; Brambilla, A.; Milano, F. Inertia Estimation Through Covariance Matrix. IEEE Trans. Power Syst. 2024, 39, 947–956. [Google Scholar] [CrossRef]
- Dhara, P.K.; Rather, Z.H. Non-Synchronous Inertia Estimation in a Renewable Energy Integrated Power System With Reduced Number of Monitoring Nodes. IEEE Trans. Sustain. Energy 2023, 14, 864–875. [Google Scholar] [CrossRef]
- Liu, M.; Chen, J.; Milano, F. On-Line Inertia Estimation for Synchronous and Non-Synchronous Devices. IEEE Trans. Power Syst. 2021, 36, 2693–2701. [Google Scholar] [CrossRef]
- Gayathri, K.; Jena, M.K. A Practical Approach to Inertia Distribution Monitoring and Impact of Inertia Distribution on Oscillation Baselining Study for Renewable Penetrated Power Grid. IEEE Syst. J. 2023, 17, 3593–3601. [Google Scholar] [CrossRef]
- Best, R.J.; Brogan, P.V.; Morrow, D.J. Power System Inertia Estimation Using HVDC Power Perturbations. IEEE Trans. Power Syst. 2021, 36, 1890–1899. [Google Scholar] [CrossRef]
- Choi, W.Y.; Kook, K.S.; Lee, J.-O. Frequency Stability-Based Penetration Limit Evaluation of Variable Energy Resources in Power Systems for Online Application. IEEE Access 2024, 12, 56503–56516. [Google Scholar] [CrossRef]
- Madura, B.T.; Wolter, M.; Glende, E. Dynamic Grid Modeling for Estimation of Influence of Inertia on Frequency Behavior. In Proceedings of the PESS 2020; IEEE Power and Energy Student Summit, Online, 5–7 October 2020. [Google Scholar]
- Liu, X.; Fang, X.; Gao, N.; Yuan, H.; Hoke, A.; Wu, H.; Tan, J. Frequency Nadir Constrained Unit Commitment for High Renewable Penetration Island Power Systems. IEEE Open Access J. Power Energy 2024, 11, 141–153. [Google Scholar] [CrossRef]
- Monit, A.; Quint, R.; Ramasubramanian, D. Simulation Methods, Models, and Analysis Techniques to Represent the Behavior of Bulk Power System Connected Inverter-Based Resources; PES-TR113; IEEE Power & Energy Society: Piscataway, NJ, USA, 2023. [Google Scholar]
- Ghassemian, A. EMT Simulation. In Proceedings of the Oak Ridge National Laboratory EMT Workshop, Manufacturing Demonstration Facility, Knoxville, TN, USA, 12–13 August 2024. [Google Scholar]
- Chen, P.; Zhao, P.; Lu, L.; Ruan, X.; Luo, C. Dynamic Phasor-Based Stochastic Transient Simulation Method for MTDC Distribution System. IEEE Trans. Ind. Electron. 2023, 70, 11516–11526. [Google Scholar] [CrossRef]
- Gurumurthy, S.K.; Mirz, M.; Amevor, B.S.; Ponci, F.; Monti, A. Hybrid Dynamic Phasor Modeling Approaches for Accurate Closed-Loop Simulation of Power Converters. IEEE Access 2022, 10, 101643–101655. [Google Scholar] [CrossRef]
- Khodaparast, J. A Review of Dynamic Phasor Estimation by Non-Linear Kalman Filters. IEEE Access 2022, 10, 11090–11109. [Google Scholar] [CrossRef]
- Misyris, G.; Ramasubramanian, D.; Escudero, M.V.; Kërçi, T.; Murray, S. Weak Grid Analysis for Interconnecting Inverter-Based Generation—Ireland Case Study. CIGRE Sci. Eng. 2023, 29, 1–19. [Google Scholar]
- Katuri, K.; Nguyen, H.T.; Anagnostou, E. Advanced EMT Simulation Techniques for Large Scale Transmission & Distribution Networks. In Proceedings of the 2023 North American Power Symposium (NAPS), Asheville, NC, USA, 15–17 October 2023; pp. 1–6. [Google Scholar]
- Maramba Gamage, D.; Ranasinghe, M.; Dinavahi, V. Application of Artificial Intelligence Techniques on Computational Electromagnetics for Power System Apparatus: An Overview. IEEE Open Access J. Power Energy 2024, 11, 130–140. [Google Scholar] [CrossRef]
- Gomis-Bellmunt, O.; Fanals-Batllori, J.; Song, J. Short-Circuit Calculations and Grid Equivalents of Modern Power Systems with Power Electronics. In Proceedings of the Short-Circuit Calculations and Grid Equivalents of Modern Power Systems with Power Electronics, IEEE PES Conferences, Online, 18 October 2023. [Google Scholar]
- Busada, C.; Jorge, S.G.; Solsona, J.A. Current-Controlled Synchronverter: A Grid Fault Tolerant Grid Forming Inverter. IEEE Trans. Ind. Electron. 2024, 71, 3233–3241. [Google Scholar] [CrossRef]
- Liu, B.; Song, Z.; Yu, B.; Yang, G.; Liu, J. A Feedforward Control-Based Power Decoupling Strategy for Grid-Forming Grid-Connected Inverters. Energies 2024, 17, 424. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.A. Virtual Synchronous Machines—Classification of Implementations and Analysis of Equivalence to Droop Controllers for Microgrids. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–7. [Google Scholar]
- Zhang, Y.; Duan, J.; Tao, J.; Li, Z.; Li, L. Fuzzy Droop Control Strategy for Doubly-Fed Wind Turbines Considering Frequency Influencing Factors. In Proceedings of the 2024 6th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 28–31 March 2024; pp. 529–533. [Google Scholar]
- Chen, Y.; Li, Z.; Deng, C.; Zhang, W.; Zhang, S.; Gao, T. Improved Droop Control for Power Grid Considering State-of-Charge of Battery Energy Storage. In Proceedings of the 2023 3rd International Conference on Electrical Engineering and Control Science (IC2ECS), Hangzhou, China, 29–31 December 2023; pp. 224–228. [Google Scholar]
- Oraa, I.; Samanes, J.; Lopez, J.; Gubia, E. Single-Loop Droop Control Strategy for a Grid-Connected DFIG Wind Turbine. IEEE Trans. Ind. Electron. 2024, 71, 8819–8830. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, B.; Qiu, D.; Chen, Y.; Xie, F.; Sun, H. Switched Active Power Control of a Grid-Connected Inverter With Reduced RoCoF and Frequency Overshoot. IEEE Trans. Power Electron. 2024, 39, 4062–4077. [Google Scholar] [CrossRef]
- D’Arco, S.; Suul, J.; Fosso, O. A Virtual Synchronous Machine Implementation for Distributed Control of Power Converters in SmartGrids. Electr. Power Syst. Res. 2015, 122, 180–197. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Shi, Y.; Liu, J. A Full Comparison between Droop Control and Virtual Synchronous Generator Control Considering Reactive Power Dynamics in Grid-Forming Inverters. In Proceedings of the 2023 IEEE 14th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Shanghai, China, 9–12 June 2023; pp. 651–660. [Google Scholar]
- Li, K.; Cheng, P.; Wang, L.; Tian, X.; Ma, J.; Jia, L. Improved Active Power Control of Virtual Synchronous Generator for Enhancing Transient Stability. IET Power Electron. 2023, 16, 157–167. [Google Scholar] [CrossRef]
- Chen, L.; Tang, J.; Qiao, X.; Chen, H.; Zhu, J.; Jiang, Y.; Zhao, Z.; Hu, R.; Deng, X. Investigation on Transient Stability Enhancement of Multi-VSG System Incorporating Resistive SFCLs Based on Deep Reinforcement Learning. IEEE Trans. Ind. Appl. 2024, 60, 1780–1793. [Google Scholar] [CrossRef]
- Yang, W.; Tu, C.; Xiao, F.; Yu, J. A Method to Improve Both Frequency Stability and Transient Stability of Virtual Synchronous Generators during Grid Faults. Sustainability 2024, 16, 1769. [Google Scholar] [CrossRef]
- Markovic, U.; Chu, Z.; Aristidou, P.; Hug, G. LQR-Based Adaptive Virtual Synchronous Machine for Power Systems With High Inverter Penetration. IEEE Trans. Sustain. Energy 2019, 10, 1501–1512. [Google Scholar] [CrossRef]
- Li, T.; Wen, B.; Wang, H. A Self-Adaptive Damping Control Strategy of Virtual Synchronous Generator to Improve Frequency Stability. Processes 2020, 8, 291. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; Milano, F.; O’Donnell, T. Adaptive Virtual Synchronous Generator Considering Converter and Storage Capacity Limits. CSEE J. Power Energy Syst. 2022, 8, 580–590. [Google Scholar] [CrossRef]
- Deng, W.; Zhong, J.; Huang, M.; Zhang, J.; Zhang, Z. Adaptive Control Strategy with Threshold of Virtual Inertia and Virtual Damping for Virtual Synchronous Generator. J. Phys. Conf. Ser. 2022, 2203, 012039. [Google Scholar] [CrossRef]
- Liu, P.; Bi, Y.; Liu, C. Data-Based Intelligent Frequency Control of VSG via Adaptive Virtual Inertia Emulation. IEEE Syst. J. 2022, 16, 3917–3926. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, Y.; Gao, W.; Davari, M.; Deng, C. Adaptive, Optimal, Virtual Synchronous Generator Control of Three-Phase Grid-Connected Inverters Under Different Grid Conditions—An Adaptive Dynamic Programming Approach. IEEE Trans. Ind. Inform. 2022, 18, 7388–7399. [Google Scholar] [CrossRef]
- Yang, X.; Li, H.; Jia, W.; Liu, Z.; Pan, Y.; Qian, F. Adaptive Virtual Synchronous Generator Based on Model Predictive Control with Improved Frequency Stability. Energies 2022, 15, 8385. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, R.; Dan, Y.; Wang, Z. Adaptive Virtual Inertia Control Based on Nonlinear Model Predictive Control for Frequency Regulation. In Proceedings of the 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), Beijing, China, 9–12 December 2022; pp. 1036–1041. [Google Scholar]
- Jin, N.; Jia, K.; Guo, L.; Wu, Z. Virtual Synchronous Generator Parameter Adaptive Adjustment Model. In Proceedings of the 2023 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics (PRECEDE), Wuhan, China, 16–19 June 2023; pp. 1–6. [Google Scholar]
- Ling, Z.; Liu, Y.; Wang, Z.; Yin, J. Adaptive Inertia and Damping of Grid-Connected Inverter with Improved VSG Control. IET Power Electron. 2023, 16, 2769–2781. [Google Scholar] [CrossRef]
- Quedan, A.; Wang, W.; Ramasubramanian, D.; Farantatos, E.; Asgarpoor, S. An Adaptive Virtual Oscillator Control Structure for Grid-Forming Inverters. IEEE Syst. J. 2023, 17, 3447–3455. [Google Scholar] [CrossRef]
- Ren, B.; Li, Q.; Fan, Z.; Sun, Y. Adaptive Control of a Virtual Synchronous Generator with Multiparameter Coordination. Energies 2023, 16, 4789. [Google Scholar] [CrossRef]
- Shi, D.; Lv, L.; Wang, X.; Zhang, L. Proposed Adaptive Control Strategy of Modular Multilevel Converter Based on Virtual Synchronous Generator. Electronics 2023, 12, 4274. [Google Scholar] [CrossRef]
- Suvorov, A.; Askarov, A.; Ruban, N.; Rudnik, V.; Radko, P.; Achitaev, A.; Suslov, K. An Adaptive Inertia and Damping Control Strategy Based on Enhanced Virtual Synchronous Generator Model. Mathematics 2023, 11, 3938. [Google Scholar] [CrossRef]
- Utkarsha, P.; Naidu, N.K.S.; Sivaprasad, B.; Singh, K.A. A Flexible Virtual Inertia and Damping Control Strategy for Virtual Synchronous Generator for Effective Utilization of Energy Storage. IEEE Access 2023, 11, 124068–124080. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, H.; Hu, X.; Hou, X.; Su, C.; Sun, K. Adaptive Inertia and Damping Coordination (AIDC) Control for Grid-Forming VSG to Improve Transient Stability. Electronics 2023, 12, 2060. [Google Scholar] [CrossRef]
- Luo, R.; Gao, H.; Peng, F.; Guo, Y. An Adaptive Low-Voltage Ride-Through Method for Virtual Synchronous Generators During Asymmetrical Grid Faults. IEEE Trans. Sustain. Energy 2024, 158, 1589–1600. [Google Scholar] [CrossRef]
- Shi, T.; Sun, J.; Han, X.; Tang, C. Research on Adaptive Optimal Control Strategy of Virtual Synchronous Generator Inertia and Damping Parameters. IET Power Electron. 2024, 17, 121–133. [Google Scholar] [CrossRef]
- Yu, Y.; Chaudhary, S.K.; Tinajero, G.D.A.; Xu, L.; Vasquez, J.C.; Guerrero, J.M. Active Damping for Dynamic Improvement of Multiple Grid-Tied Virtual Synchronous Generators. IEEE Trans. Ind. Electron. 2024, 71, 3673–3683. [Google Scholar] [CrossRef]
- Areed, E.F.; Yan, R.; Saha, T.K. Impact of Battery Ramp Rate Limit on Virtual Synchronous Machine Stability During Frequency Events. IEEE Trans. Sustain. Energy 2024, 15, 567–580. [Google Scholar] [CrossRef]
- Akram, U.; Mithulananthan, N.; Shah, R.; Alzahrani, S. Design of Energy Storage for Frequency Stability in Low-Inertia Power Grid. IEEE Syst. J. 2023, 17, 4763–4774. [Google Scholar] [CrossRef]
- Reißner, F.; De Carne, G. Virtual Synchronous Machine Integration on a Commercial Flywheel for Frequency Grid Support. IEEE Trans. Power Electron. 2024, 39, 12086–12090. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Z.; Li, S.; Si, J.; Gao, J.; Dong, W.; Das, H.S. Virtual Synchronous Generator and SMC-Based Cascaded Control for Voltage-Source Grid-Supporting Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2722–2736. [Google Scholar] [CrossRef]
- Oshnoei, A.; Blaabjerg, F. Sliding Mode-Based Model Predictive Control of Grid-Forming Power Converters. In Proceedings of the 2023 European Control Conference (ECC), Bucharest, Romania, 13–16 June 2023; pp. 1–6. [Google Scholar]
- Jongudomkarn, J.; Liu, J.; Ise, T. Virtual Synchronous Generator Control With Reliable Fault Ride-Through Ability: A Solution Based on Finite-Set Model Predictive Control. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 3811–3824. [Google Scholar] [CrossRef]
- Ademola-Idowu, A.; Zhang, B. Frequency Stability Using MPC-Based Inverter Power Control in Low-Inertia Power Systems. IEEE Trans. Power Syst. 2021, 36, 1628–1637. [Google Scholar] [CrossRef]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. MPC-Controlled Virtual Synchronous Generator to Enhance Frequency and Voltage Dynamic Performance in Islanded Microgrids. IEEE Trans. Smart Grid 2021, 12, 953–964. [Google Scholar] [CrossRef]
- Guo, L.; Xu, Z.; Jin, N.; Li, Y.; Wang, W. A Weighted Voltage Model Predictive Control Method for a Virtual Synchronous Generator with Enhanced Parameter Robustness. Prot. Control Mod. Power Syst. 2021, 6, 38. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Guo, L.; Jin, N.; Lu, F. Current Sensor-Less Virtual Synchronous Generator Model Predictive Control Based on Sliding Mode Observer. IEEE Access 2021, 9, 17898–17908. [Google Scholar] [CrossRef]
- Long, B.; Liao, Y.; Chong, K.T.; Rodríguez, J.; Guerrero, J.M. Enhancement of Frequency Regulation in AC Microgrid: A Fuzzy-MPC Controlled Virtual Synchronous Generator. IEEE Trans. Smart Grid 2021, 12, 3138–3149. [Google Scholar] [CrossRef]
- Pouresmaeil, M.; Sangrody, R.; Taheri, S.; Montesinos-Miracle, D.; Pouresmaeil, E. Enhancing Fault Ride Through Capability of Grid-Forming Virtual Synchronous Generators Using Model Predictive Control. IEEE J. Emerg. Sel. Top. Ind. Electron. 2024, 5, 1192–1203. [Google Scholar] [CrossRef]
- Benhmidouch, Z.; Moufid, S.; Abbou, A.; Ait-Omar, A.; Laabassi, H.; Chatri, C.; Ali, I.H.O.; Bouzekri, H. A Fuzzy Logic Based Controller for Synchronization of VSG Controlled Grid-Forming Inverters. In Proceedings of the 2023 IEEE PES/IAS PowerAfrica, Marrakech, Morocco, 6–10 November 2023; pp. 1–5. [Google Scholar]
- Thiruveedula, M.; Asokan, K. Harmonics Reduction in Virtual Synchronous Generator Using Fuzzy Logic Controller. Int. J. Eng. Technol. Manag. Sci. 2024, 8, 159–167. [Google Scholar]
- Awal, M.A.; Yu, H.; Tu, H.; Lukic, S.M.; Husain, I. Hierarchical Control for Virtual Oscillator Based Grid-Connected and Islanded Microgrids. IEEE Trans. Power Electron. 2020, 35, 988–1001. [Google Scholar] [CrossRef]
- Moulichon, A.; Alamir, M.; Debusschere, V.; Garbuio, L.; Hadjsaid, N. Polymorphic Virtual Synchronous Generator: An Advanced Controller for Smart Inverters. Energies 2023, 16, 7075. [Google Scholar] [CrossRef]
- Awal, M.A.; Husain, I. Unified Virtual Oscillator Control for Grid-Forming and Grid-Following Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 4573–4586. [Google Scholar] [CrossRef]
- Luo, S.; Wu, W.; Koutroulis, E.; Chung, H.S.-H.; Blaabjerg, F. A New Virtual Oscillator Control Without Third-Harmonics Injection For DC/AC Inverter. IEEE Trans. Power Electron. 2021, 36, 10879–10888. [Google Scholar] [CrossRef]
- Awal, M.A.; Rachi, M.R.K.; Yu, H.; Husain, I.; Lukic, S. Double Synchronous Unified Virtual Oscillator Control for Asymmetrical Fault Ride-Through in Grid-Forming Voltage Source Converters. IEEE Trans. Power Electron. 2023, 38, 6759–6763. [Google Scholar] [CrossRef]
- Niu, S.; Wang, W.; Zhang, G.; Chen, A. A Sliding Mode Control-Based Pre-Synchronization Strategy for Virtual Oscillator Controlled Grid-Forming Inverters. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 1860–1864. [Google Scholar]
- Kong, L.; Xue, Y.; Qiao, L.; Wang, F. Enhanced Synchronization Stability of Grid-Forming Inverters With Passivity-Based Virtual Oscillator Control. IEEE Trans. Power Electron. 2022, 37, 14141–14156. [Google Scholar] [CrossRef]
- Cheng, H.; Li, C.; Ghias, A.M.Y.M.; Blaabjerg, F. Dynamic Coupling Mechanism Analysis Between Voltage and Frequency in Virtual Synchronous Generator System. IEEE Trans. Power Syst. 2024, 39, 2365–2368. [Google Scholar] [CrossRef]
- Elshenawy, M.A.; Radwan, A.; Mohamed, Y.A.-R.I. Unified Sequence Impedance Models of Synchronous Generator-and Virtual Oscillator-Based Grid-Forming Converters. IEEE Trans. Power Deliv. 2024, 39, 56–70. [Google Scholar] [CrossRef]
- Gu, Y.; Green, T. Power System Stability With a High Penetration of Inverter-Based Resources. Proc. IEEE 2022, 111, 832–853. [Google Scholar] [CrossRef]
- Mago, A.; Dhali, A.; Kumar, H.; Maity, R.; Kumar, B. Planetary Health and Its Relevance in the Modern Era: A Topical Review. SAGE Open Med. 2024, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Ani, E.C.; Olajiga, O.K.; Sikhakane, Z.Q.; Olatunde, T.M. Renewable Energy Integration for Water Supply: A Comparitive Review of African and U.S. Initiatives. Eng. Sci. Technol. J. 2024, 5, 1086–1096. [Google Scholar] [CrossRef]
- THE 17 GOALS | Sustainable Development. Available online: https://sdgs.un.org/goals (accessed on 5 February 2025).






| Grid System | System Operator | Platform | Action | Outcome |
|---|---|---|---|---|
| NEM | AEMO | NEM Dispatch Engine (NEMDE) | Network curtailment Economic constraint | 9.44% of solar in the NEM was curtailed during October 2023 [56]. |
| SEM | EirGrid/SONI | SEMOpx | SNSP limit of 75% MUON of 6 SGs Dispatch down instruction | 1795 GWh of RESs was curtailed in 2023 [54]. |
| ERCOT | ERCOT | Security-Constrained Economic Dispatch (SCED) | GTCs | Almost 6000 h of GTC-based curtailment in 2023 [57]. |
| Plant Category | Plant Loss (MW) |
|---|---|
| SG | 884 |
| IBR | 1771 |
| Service | GFLI | GFMI | Synchronous Machine |
|---|---|---|---|
| Inertia | - | Virtual | Physical |
| Damping | Limited | Virtual | Physical |
| Fault current | - | 1.2–1.5 p.u. | 6–8 p.u. |
| Voltage/reactive power support | Yes | Yes | Yes |
| System strength support | - | Yes | Yes |
| Phase jump support | - | Yes | Yes |
| Primary frequency response | Yes | Yes | Yes |
| Fast frequency response | Yes | Yes | - |
| Service Provider | Locations | Capacity |
|---|---|---|
| Enel-X | NSW, SA, QLD, VIC | 134 MW |
| Grid Beyond | SA, VIC, NSW | 145 MW |
| VIOTAS | SA, VIC, NSW, QLD, TAS | 53 MW |
| Simulation Category | Complexity | Computational Demand | Fidelity | Application | Assumptions | Domain |
|---|---|---|---|---|---|---|
| Phasor Based (RMS) | Low | Low | Low | Long-term dynamic analysis such as load flow and stability analysis. | Linearity, stable, and pure system frequency | Frequency |
| Positive Sequence | Low | Low | Medium | Stability analysis. | Balanced system | Steady state |
| Electromagnetic Transient (EMT) | High | High | High | Analysing EMT phenomena such as switching, IBR dynamics, and protection system operation. | None | Time |
| Ref. | Method | Research Contribution | Limitation |
|---|---|---|---|
| [103,105,107,109,110] | Improved system strength metrics | Research has developed new metrics that better reflect the reactive power control capabilities of IBRs. | Proposed methods such as QESCR are not yet sufficiently studied to gain widespread industry adoption by SOs. |
| [113,114,115,116,117,118] | Improved inertia estimation | Significant research has been conducted to obtain real-time online estimates of grid inertia. Notably, refs. [104,105] consider virtual inertia contribution. | SOs take a conservative approach in the absence of accurate real-time inertia estimates. More research is required to develop solutions that can be widely adopted. |
| [121,122,123,124,125,126,127,128] | EMT grid modelling | Advancements have been made, notably with hybrid modelling techniques. | Further research is required to develop modelling techniques with required EMT level fidelity to represent IBR dynamics while adhering to reasonable computational requirements. Modelling for grid connection approvals remains a bottle neck as noted in Section 5.3. |
| [131,133,134,135,136] | Droop control | Droop control aims to emulate governor control in a steam turbine. Improved concepts such as adaptive droop control and blending non-linear techniques, such as fuzzy logic, have been made. | Droop controllers generally rely on PLLs for synchronisation. Droop is a measured and control response and, therefore, limited to primary frequency control. This is a valuable service in declining inertia. |
| [130,131,136,138,139,140,141,144,145,146,147,148,149,150,151,153,154,155,156,157,158,159,160,161,163,164,165,167,168,169,170,171,172,173,176,182,183] | Virtual synchronous machine | VSM can replace declining inertia with a virtual form by emulating the swing equation for SGs. Non-linear control methods such as SMC and MPC are gaining traction with improved transient stability and recovery characteristics. | Energy storage requirements and integration techniques for inertia provision has limited research. VSM transient stability remains a problem in strong grids. Fault current provision remains a limitation as most proposed research solutions involve performance compromises. Communication and computational requirements need to be carefully managed. |
| [85,152,177,178,179,180,181,183] | Dispatchable Virtual Oscillator Control | Like non-linear VSM, dVOC is emerging as a solution in the literature for fast transient response for inverters and reliable recovery from faulted conditions. | dVOC techniques struggle to provide good system strength due to its time-domain-based control. dVOC experiences 3rd order harmonics that require new solutions to meet grid requirements. dVOC is not as active in the research as VSM; as a result, development appears slower. |
| Theme 1. Addressing system strength decline | ||
| Recommendation | Commentary | Paper section reference |
| Improved system strength metrics. | Seek new methods of system strength evaluation, beyond SCRPOC, that appropriately recognise the reactive power control capability of IBRs. This is important to avoid unnecessary curtailment of RESs and delay of RES projects. The QESCR method is of particular interest to achieve this goal. | Section 6.1.1 |
| Voltage and frequency support requirements. | Droop control algorithms can increase the primary control effectiveness of IBRs in providing both voltage and frequency support to the grid. Clearly quantified SO requirements for frequency and voltage support will greatly aid researchers in further developing solutions. | Section 6.3.1 |
| Theme 2. Compensation for falling inertia | ||
| Recommendation | Commentary | Section reference |
| Demand side solutions. | Demand response, often used for peak demand reduction, can also provide valuable primary frequency control services. These services support declining inertia. Demand response is low cost, quick to implement, and effective. SOs should consider demand response as a key component of their primary frequency control strategy. | Section 5.4 |
| Improved inertia estimation. | Accurate dispatch of inertia supporting services becomes critical in high-IBR grids. SOs require accurate real-time inertia data to determine ancillary service requirements. Joint research and development with academia is highly recommended. | Section 5.4 and Section 6.1.2 |
| Theme 3. Market incentives | ||
| Recommendation | Commentary | Section reference |
| Market-based incentives for advanced GFLI/GFMI asset investments. | Market incentives to compensate for both GFMI and RESs for providing voltage, frequency, and inertia support. Provision of these services will come at an opportunity cost for plant operators; compensation will be required. A market-based approach can provide a low-cost path but requires more development. Incentives should consider industry and academic partnership approaches. | Section 4.1, Section 5.3, Section 5.4, and Section 6.3.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moore, P.; Alimi, O.A.; Abu-Siada, A. A Review of System Strength and Inertia in Renewable-Energy-Dominated Grids: Challenges, Sustainability, and Solutions. Challenges 2025, 16, 12. https://doi.org/10.3390/challe16010012
Moore P, Alimi OA, Abu-Siada A. A Review of System Strength and Inertia in Renewable-Energy-Dominated Grids: Challenges, Sustainability, and Solutions. Challenges. 2025; 16(1):12. https://doi.org/10.3390/challe16010012
Chicago/Turabian StyleMoore, Paul, Oyeniyi Akeem Alimi, and Ahmed Abu-Siada. 2025. "A Review of System Strength and Inertia in Renewable-Energy-Dominated Grids: Challenges, Sustainability, and Solutions" Challenges 16, no. 1: 12. https://doi.org/10.3390/challe16010012
APA StyleMoore, P., Alimi, O. A., & Abu-Siada, A. (2025). A Review of System Strength and Inertia in Renewable-Energy-Dominated Grids: Challenges, Sustainability, and Solutions. Challenges, 16(1), 12. https://doi.org/10.3390/challe16010012






