Abstract
The linear no-threshold (LNT) theory describes the linear relationship between a radiation dose and its effects. However, whether the linear relationship is maintained at low radiation doses has yet to be determined. Many previous studies support the radiation hormesis theory, which states that radiation has beneficial effects on health. In this viewpoint, we propose a mathematical function fitted to a model consistent with both the LNT at ≥100 mSv and radiation hormesis theories at <100 mSv, and the model requires a factor whose amount or activity takes a mountain-like shape versus the radiation dose and have one maximum value at 40.9 mSv. We searched a wide range of factors with these features based on searches on PubMed, and then evaluated whether these factors were suitable candidates consistent with both the LNT and radiation hormesis theories. Our consideration indicated that these factors did not completely follow the equation suggested at this time. Of course, other theories do not deny that these factors are involved in hormesis. However, based on our theory, still unknown factors may be involved in radiation hormesis, and then such unknown factors which are activated at <100 mSv should be searched.
1. Introduction
Radiation can ionize substances. The linear no-threshold (LNT) hypothesis [1] has been proposed for the management of radiation risks. However, the LNT hypothesis for radiation doses <100 mSv has not been proven to be correct (Figure 1A). On the other hand, many studies have described radiation hormesis theory, whereby radiation is thought to have beneficial effects on health [2,3,4]. If the indeterminacy of the LNT theory under 100 mSv were combined with the assumption of radiation hormesis (Figure 1B), a theory satisfying both radiation hormesis at low doses and the LNT theory at high doses could be suggested [5]. Herein, based on a previous theory [5], we aimed to obtain an equation to give the maximum hormesis region while satisfying the LNT theory at ≥100 mSv and to calculate the dose that maximizes the inhibitor factors. Next, from existing reports, we aimed to search candidate inhibitor factors whose quantities depend on the radiation dose with fluctuations in a mountain-like shape. Lastly, based on our calculations, we judge whether the listed factors are suitable candidates leading to hormesis.
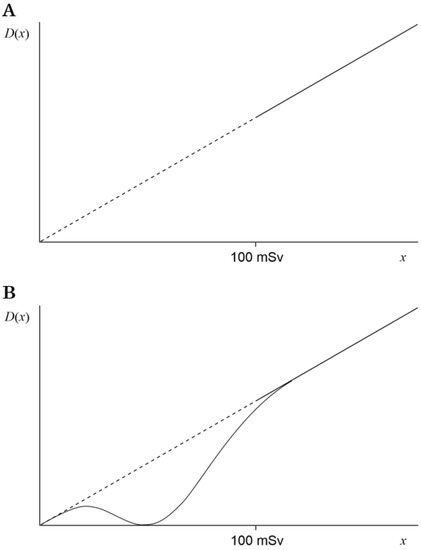
Figure 1.
Graph of the cancer death rate D(x). The radiation dose is defined as x. (A) The linear dashed line indicates the assumption of the LNT hypothesis under 100 mSv, and the linear solid line indicates the LNT hypothesis at 100 mSv or higher. (B) In addition to panel (A), the solid curve indicates D(x) with the maximum hormesis region and acceptance of ≤10% error at ≥100 mSv.
2. Methods
The equations for the graphs are described in Section 3.1. The graphs were constructed using Microsoft Excel for Mac 2011 (Microsoft Corporation, Washington, DC, USA). The data were calculated in increments of 1 mSv (Figure 2A,B) or 10 mSv (Figure 2C).
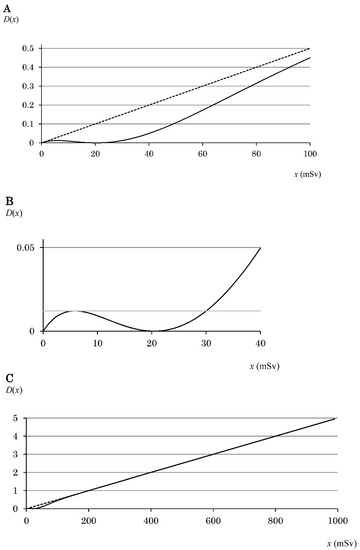
Figure 2.
Graph of D(x) following Equation (4). The radiation dose is defined as x. The graph is in the range of (A) 0–100 mSv, (B) 0–40 mSv, and (C) 0–1000 mSv. The solid curve indicates D(x) that obeys Equation (4). (A,C) The linear dashed line indicates the assumption of the LNT hypothesis. (B) The hormesis region (5.8–30.0 mSv) is obtained from two intersection points of Equation (4) and D(x3). The gray solid line indicates D(x3). The value of x for the local maximum of D(x) is defined as x3 [5].
From many previous reports, factors with an amount or activity that has only one maximum value versus radiation dose were initially selected. In Section 3.2, we consider whether such factors are appropriate candidates leading to hormesis using the equation obtained from Section 3.1.
3. Results and Discussion
3.1. Equations and Graphs
With reference to a previous report [5], we defined the radiation dose as x, the cancer death rate as D(x), and the inhibition effect as R(x). The radiation dose at which R(x) reaches a maximum is defined as x1, the value of x for the local minimum of D(x) as x2, the value of x for the local maximum of D(x) as x3, and the other value of x where D has the same value as D(x3) as x4. Therefore, such definitions lead the hormesis region to x3–x4 mSv [5].
Equation (1) was used because it gave the maximum hormesis region while satisfying the LNT at ≥100 mSv. Reconsidering the previous assumption [5], a ≤10% error was accepted at ≥100 mSv. Using Equation (1) and x5 corresponding to 100 mSv, it was necessary for Equation (3) to be satisfied.
Therefore, x5 corresponding to 100 mSv was determined to be ~4.890/a [5]. Exposure to 100 mSv is said to increase the cancer death rate by 0.5% [6]. Therefore, for kx5 to be 0.5, k must be 0.005. In addition, the value of a is 0.0489. Using Equation (1) and the values of k and a, Equation (4) was obtained, and then graphs such as those shown in Figure 2 were obtained.
Figure 2A shows D(x) in the range of 0–100 mSv. From x5, it was determined that x3 = ~0.285/a and x4 = ~1.469/a [5], which correspond to ~5.8 and ~30.0 mSv, respectively, and give a hormesis region of 5.8–30.0 mSv (Figure 2B). In Figure 2B, D(x) is in the range of 0–40 mSv, and the hormesis region is shown in an easy-to-understand manner. Furthermore, in Figure 2C, D(x) is in the range of 0–1000 mSv, and the LNT at ≥100 mSv is shown in an easy-to-understand manner.
R(x) reaches a maximum when the radiation dose is x1, and the value of x1 is 2/a [5], while R(2/a) is (2/ea)2. Setting the maximum value of R(x) to 100 yielded Equation (5), and a graph shown in Figure 3 was obtained. When the value of a was 0.0489, x1 was 40.9 mSv (Figure 3).
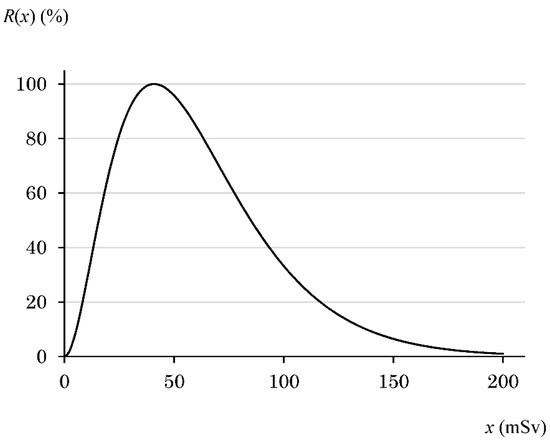
Figure 3.
Graph of R(x) following Equation (5). The radiation dose is defined as x. As the values used in the text, R(0) is 0%, R(25) is 81%, R(50) is 96%, R(63) is 81%, R(75) is 63%, R(100) is 33%, R(125) is 15%, R(150) is 6.5%, and R(x) at 250 mSv or higher is almost 0%.
3.2. Discussion of Whether the Listed Factors Are Appropriate Candidates Whose R(x) Follows Equation (5)
From many previous reports, the factors or mRNA expression levels whose fluctuations have one maximum value versus the radiation dose were selected. The unit for the radiation dose in all references described below was Gy. Therefore, considering the radiation weighting factor of X-rays and γ-rays, the unit “Sv” for the x value calculated in Section 3.1 was replaced with “Gy”. Furthermore, we narrowed down the factors that allowed R(x) to reach the maximum value at 40.9 mGy obtained in Section 3.1. As a result, we identified the following factors: superoxide dismutase (SOD), catalase, glutathione peroxidase, heat shock protein 70 (hsp70), tumor necrosis factor-α (TNF-α), interferon-γ (IFN-γ), interleukin-10 (IL-10), interleukin-12 (IL-12), c-Raf, ERK1/2, MEK, 3-phosphoinositide-dependent protein kinase (PDK), AKT, p38, JNK, caspase-3, caspase-7, caspase-9, cAMP response element-binding protein (CREB), c-fos, Bcl-2, and LY6G5C. The change with respect to the radiation dose is described below, and, considering the calculated data (Figure 3) using Equation (5), it is judged whether the factor was a candidate. In addition, according to Equation (5), R(x) is 2.3% for the worldwide average dose of natural background radiation, which is almost the same as 0% at 0 mGy. Therefore, for the sake of simplicity, the x values in all controls of the references were set to 0 mGy.
3.2.1. Factors That Remove Reactive Oxygen Species: SOD, Catalase, and Glutathione Peroxidase
Super oxide, hydrogen peroxide, and lipid hydroperoxide are reactive oxygen species. SOD is an enzyme that degrades super oxide, and catalase degrades hydrogen peroxide. Glutathione peroxidase reduces lipid hydroperoxides to their corresponding alcohols and can reduce hydrogen peroxide to water. Because these enzymes can eliminate reactive oxygen species that promote canceration, they can be expected to be factors involved in the hormesis effect. An exhaustive search on PubMed found that the activity of SOD, catalase, and glutathione peroxidase has a mountain-like shape with one maximum value for the radiation dose. Each factor is considered separately below.
The SOD activity at control was 1.8 U/mg, and the activity at 24 h after 100 mGy γ-irradiation was 2.3 U/mg. It was 2.1 U/mg at 250 mGy and 1.9 U/mg at 500 mGy [7]. Assuming that R(x) at 40.9 mGy is 100%, from Equation (5), R(x) is 0% at control, 33% at 100 mGy, and almost 0% at 250 and 500 mGy. When the activity increase rate of 0.5 U/mg at 100 mGy with respect to control is regarded as 33%, the activity increase rates of 0.3 and 0.1 U/mg at 250 and 500 mGy are converted to 20% and 6.6%, respectively. The values of 20% and 6.6% clearly do not match the calculation results of Equation (5), so SOD is not considered a candidate factor that complies with Equation (5) and Figure 3.
The activity of catalase at control was 11.0 μmol H2O2 consumed/mg protein/min, and the activity at 24 h after 100 mGy, 250 mGy, or 500 mGy irradiation was 12.5, 12.0, or 10.8 μmol H2O2 consumed/mg protein/min, respectively [7]. Thus, the increase was calculated to be 1.5 μmol at 100 mGy, 1.0 μmol at 250 mGy, or –0.2 μmol at 500 mGy. Assuming that the increase of 1.5 μmol at 100 mGy was 33%, 1.0 μmol and –0.2 μmol were converted to 22% and –4.4%, respectively. As a result, the values at 250 mGy and 500 mGy in Ref. [7] clearly did not match the results calculated by Equation (5). In addition, the catalase activity at 4 h after irradiation also took a mountain-like shape, but the measured and calculated values collided. Therefore, catalase was also not considered a candidate factor that follows Equation (5).
Glutathione peroxidase activity at 24 h after 100 mGy, 250 mGy, or 500 mGy irradiation was 0.18, 0.17, or 0.16 μmol reduced nicotinamide adenine dinucleotide phosphate (NADPH) consumed/mg protein/min, respectively. From the activity at the control dose (0.16 μmol NADPH consumed/mg protein/min) and the calculation results by Equation (5), the increase in activity at 100 mGy was too small, so glutathione peroxidase was not considered a candidate factor complying with Figure 3.
Based on the above considerations, these enzymes that degrade reactive oxygen species were not the candidate factors we sought.
3.2.2. Hsp70
Hsp70, which is involved in protein folding, is a highly conserved molecular chaperone across species from archaea to humans. Hsp70 is widely known to protect cells from various environmental stresses such as heat stress and heavy metals. Therefore, we considered hsp70 as a candidate factor.
The expression of hsp70 mRNA in the adrenal glands at 50 mGy increased compared with 0 mGy, and that at 500 mGy decreased compared with 50 mGy [8]. Because the expression level at 500 mGy was the same as that at 1 Gy, hsp70 may be a factor that satisfies Equation (5). However, in the stomach, the expression at 500 mGy increased compared with 50 mGy [8], which does not satisfy Equation (5). Therefore, we thought that hsp70 cannot induce the hormesis effect regardless of the organ.
3.2.3. Cytokines TNF-α, IFN-γ, IL-10, and IL-12
Cytokines are proteins that are mainly secreted by cells in the immune system. TNF-α, IFN-γ, IL-10, and IL-12 are known as cytokines whose expression levels increase at low and decrease at high radiation doses [9,10]. These cytokines are produced by a wide range of cells in addition to those of the immune system. There are two types of TNF-α: membrane-bound and soluble. Soluble TNF-α promotes inflammation and cell survival. IFN-γ enhances the production of active oxygen species and nitric oxide from macrophages and exhibits bactericidal and antitumor effects. IL-12 is a heterodimer of p40 and p35 subunits. IL-12 activates T cells and NK cells to promote cell proliferation and induce the production of IFN-γ. On the other hand, IL-10 suppresses the production of inflammatory cytokines in T cells and macrophages and suppresses the immune response.
The amounts of TNF-α and IFN-γ produced at 0, 25, 75, 150, and 500 mGy have been analyzed [9]. From Figure 3 in Ref. [9], the amount of soluble TNF-α was read in order as 15, 16, 30, 22, and 5 pg/mL, whereas IFN-γ was 9, 10, 15, 10, and 3 pg/mL. These values were compared with the calculated values obtained from Equation (5): 0%, 81%, 63%, 6.5%, and 0%. As a result, because the amounts of TNF-α and IFN-γ were higher at 75 mGy than at 25 mGy, they were clearly different from the calculated values. Therefore, TNF-α and IFN-γ were not the desired candidate factors that comply with Figure 3.
Shigematsu et al. [10] described the enhancement of immunity by low-dose irradiation: IL-10 and IL-12 at 50 mGy increased compared with 0 mGy, and both at 1 Gy decreased compared with 50 mGy. According to the results of an analysis of IL-10, the amount produced at 1 Gy was much smaller than that at 0 mGy, so IL-10 was not a factor, as described in Section 3.1. On the other hand, the amount of IL-12 at 1 Gy was almost the same as that at 0 mGy; thus, IL-12 may be a factor satisfying Equation (5). However, a further analysis did not give results that maximized IL-12 production at 40.9 mGy [11].
From the above, it was concluded that these cytokines are not factors that follow Equation (5).
3.2.4. ERK MAP Kinase Signals: c-Raf, ERK-1, ERK-2, MEK
Liang et al. [12] reported that the phosphorylation of c-Raf, ERK-1, ERK-2, and MEK in 2BS cells depends on the radiation dose; these factors are ERK MAP kinase signals. The MAPK/ERK pathway is activated by stimulation with growth factors such as EGF and FGF to control cell proliferation and differentiation. Extracellular signals are received primarily by transmembrane receptors with tyrosine kinase activity, causing continuous protein kinase activation via the Ras proteins. Raf (MAP kinase kinase kinase) is phosphorylated by activated Ras or PKC, and MEK1/2 (MAP kinase kinase) is phosphorylated by phospho-Raf. Moreover, ERK1/2 (MAP kinase) is phosphorylated by phospho-MEK1/2. The quantitative result of phosphorylation for each factor at 0, 25, 50, 75, or 100 mGy seems to follow Equation (5).
Calculating R(x) at 0, 25, 50, 75, or 100 mGy yielded 0%, 81%, 96%, 63%, or 33%, respectively. Because the phosphorylation of c-Raf was 1-, 3.8-, 5.3-, 3.0-, or 1.3-fold with respect to c-Raf, each increase in value was 0, 2.8, 4.3, 2.0, or 0.3, respectively. When the maximum increased value of 4.3 was considered to be equivalent to 96%, the values of 2.8, 2.0, and 0.3 were converted to 63%, 45%, and 6.7%, respectively. As a result, it was clearly different from the theoretical value obtained from Equation (5), so the phosphorylation of c-Raf was not the desired factor complying with Equation (5) and Figure 3.
According to Ref. [12], the phosphorylation of ERK-1 was 1-, 10.9-, 12.8-, 4.7-, or 2.5-fold compared with non-phosphorylated ERK-1. When the same calculation as c-Raf was performed, each value was 0%, 81%, 96%, 30%, or 12%, respectively. In addition, 0%, 81%, 96%, 26%, and 12% were converted from the phospho-ERK-2 results of 1-, 11.5-, 13.4-, 4.4-, and 2.5-fold, respectively, with respect to non-phosphorylated ERK-2. From the above, phosphorylation at 0, 25, and 50 mGy for both ERK-1 and ERK-2 were surprisingly consistent with the calculated values (0%, 81%, and 96%, respectively), but no agreement was found at 75 or 100 mGy. Therefore, these factors do not have an R(x) maximized at 40.9 mGy.
Hladik et al. [13] analyzed the expressions of ERK1/2 and phospho-ERK1/2 at 0, 63, 125, and 500 mGy. When R(x) was calculated at each radiation dose, R(x) was 0%, 81%, 15%, or 0%, respectively. From Figure 3 of Ref. [13], ERK1/2, which did not maximize at 63 mGy, could be excluded as a candidate factor. The amount of phospho-ERK1/2 was the maximum at 63 mGy, but the measured values at 0 and 500 mGy were clearly not consistent with the calculated values, so ERK1/2 was not a candidate factor we sought. Other results (Figure 1D in Ref. [14] and Figure 1a in Ref. [15]) also led to the same consideration.
Furthermore, Liang et al. [12] described the phosphorylation of MEK as 1-, 2.5-, 3.8-, 2.1-, or 1.0-fold compared with non-phosphorylated MEK. The value at 100 mGy was the same as that at 0 mGy, which was clearly different from the theoretical value obtained from Equation (5).
From the above considerations, these ERK MAP kinase signals were considered unlikely to be factors that obey Equation (5).
3.2.5. p38 and JNK
p38 and JNK belong to the MAPK signaling pathways present in mammals and are activated by inflammatory cytokines such as TNF-α and IL-1β. In addition, p38 and JNK are activated by various environmental stress stimuli, such as oxidative stress, heat shock, and ultraviolet irradiation. p38 and JNK are involved in the induction of apoptosis, the immune response, and the control of inflammation. Similar to other MAPK signal pathways, signals are transmitted by the activation of p38 and JNK via phosphorylation of MEKK and MKK by extracellular stimulation. As a result of a PubMed search, we found that the expression levels of p38 and JNK for the radiation dose had a mountain-like shape with one maximum value.
For p38 and phospho-p38, expressions at 0, 63, 125, and 500 mGy have been analyzed [13]. R(x) calculated at each dose was 0%, 81%, 15%, or 0%, respectively. From Figure 3 of Ref. [13], p38 and phospho-p38 reached the maximum at 63 mGy, but the measured value at 0 or 500 mGy clearly did not match the calculated value. Thus, with or without phosphorylation, p38 is not the desired factor. The discrepancies between other results (Figure 1D in Ref. [14] and Figure 6a in Ref. [15]) and the calculated values led us to conclude that p38 was not a candidate factor complying with Equation (5).
JNK increased significantly at 24 h after 50 mGy irradiation compared with control, and the expression decreased to the control level after 500 mGy irradiation [16]. This result follows Equation (5), whereas the expression level at 100 Gy in Ref. [14] was higher than the control and did not follow Equation (5). Therefore, JNK was not an objective factor that obeys our theory. The results of Narang et al. [15] led to the same consideration.
3.2.6. PI3K/Akt/mTOR Signals: PDK and AKT
Liang et al. [12] reported that the phosphorylation of PDK and AKT in 2BS cells depends on the radiation dose. The stimulation of hormones such as insulin and growth factors activates PI3K/PDK and AKT, which are cell survival signaling pathways. PDK and AKT also activate mTOR, a kinase that promotes nutrient intake. PDK is activated by PIP3, and activated PDK then activates AKT, which is also referred to as protein kinase B. Liang et al. [12] quantified the phosphorylation of each factor at 0, 25, 50, 75, or 100 mGy, so the same R(x) as in Section 3.2.4 can be used: 0%, 81%, 96%, 63%, and 33%, respectively. In Ref. [12], the phosphorylation of PDK was 1-, 3.3-, 6.2-, 1.5-, or 1.1-fold with respect to non-phosphorylated PDK, and phosphorylated AKT was 1-, 1.2-, 3.2-, 1.4-, or 1.3-fold with respect to non-phosphorylated AKT. The results of PDK and AKT were clearly different from the values derived from Equation (5) of 0%, 81%, 96%, 63%, and 33%, respectively. From the above, the phosphorylation of PDK and AKT was not a factor complying with Figure 3.
3.2.7. Caspase-3, -7, and -9
Caspase-9 is an initiator caspase involved in the early induction of apoptosis, and caspase-3 and -7 are effector caspases involved in the execution of apoptosis itself. Initiator caspase is activated by various factors, and caspase-9 is activated by the intrinsic pathway caused by stress and DNA damage. We searched previous reports in which the expression levels of these three caspases increased at low doses and decreased at high doses.
Caspase-9 increased significantly at 1 h after 50 mGy irradiation, and the expression decreased to the control level after 500 mGy irradiation [16]; these results follow Equation (5). However, in another report, the expression level at 2 Gy was increased compared with control [17]. Using Equation (5), the calculated expression level at 2 Gy must be the same as control, so caspase-9 is not a factor that universally follows Equation (5).
The expression of caspase-3 increased 8.5-fold at 24 h after 50 mGy irradiation and decreased 6.3-fold after 500 mGy irradiation [16]. The expression of caspase-7 increased 8.3-fold at 1 h after 50 mGy irradiation and decreased 3-fold at 1 h after 500 mGy irradiation [16]. Twenty-four hours after γ irradiation, the expression was 4.5-fold at 50 mGy and 3.5-fold at 500 mGy [16]. From Equation (5), the expression level at 500 mGy must be the same as that at control; thus, these data indicate that caspase-3 and -7 are not factors that follow Equation (5).
3.2.8. Bcl-2
Bcl-2 is a protein that suppresses apoptosis localized in the outer mitochondrial membrane. In stressed and DNA-damaged cells, mitochondria release cytochrome c, which results in the activation of initiator caspases such as caspase-9. Bcl-2 inhibits caspase activation and negatively controls apoptosis by suppressing the release of cytochrome c from mitochondria in this intrinsic pathway. A PubMed search found that, compared with control, transcription of Bcl-2 increased at 75 mGy and decreased at 2 Gy [18]. To follow Equation (5), the relative level at 2 Gy must be the same as that at control. However, in Figures 20 and 21 of Ref. [18], it is not 1-fold. Thus, Bcl-2 m-RNA was not a candidate factor we sought. This was also clear based on the data from Ref. [16].
3.2.9. CREB
CREB is involved in the regulation of cell proliferation and differentiation and plays an important role in the formation of long-term memory in various species. PKA is activated by cAMP phosphorylates CREB. For CREB, phospho-CREB, expressions at 0, 63, 125, and 500 mGy have been analyzed [13]. When R(x) was calculated in the same manner as in Section 3.2.5, it was 0%, 81%, 15%, and 0%, respectively. According to Figure 3 of Ref. [13], phospho-CREB, which does not maximize at 63 mGy, can be excluded as a candidate. On the other hand, CREB reached its maximum at 63 mGy, but the measured values at 0 and 500 mGy were clearly not the same as the calculated R(x) values. Therefore, with or without phosphorylation, CREB was not the desired factor obeying our theory.
3.2.10. c-Fos
c-Fos is one of the most well-analyzed transcription factors for oncogenes. It forms a heterodimer with c-Jun to form a transcription factor complex and is deeply involved in the control of cell proliferation and differentiation. The transcription of c-fos in the thymus increased at 75 mGy and decreased at 2 Gy at 0.5, 1, and 2 h after whole-body X-ray irradiation [18]. Using Equation (5), R(x) at control, 75 mGy, and 2 Gy was 0%, 63%, and almost 0%, respectively. At 0.5 h after X-ray irradiation, the relative level for control was 3.8-fold at 75 mGy and 1-fold at 2 Gy (Figure 10 of Ref. [18]). Because the amount of transcription at 2 Gy was equal to that at control, these data satisfied Equation (5). However, at 1 h after X-ray irradiation, it was 1.9-fold at 75 mGy or 0.9-fold at 2 Gy, and at 2 h after X-ray irradiation, it was 1.7-fold at 75 mGy or 0.7-fold at 2 Gy. Because the relative levels at 2 Gy were not 1-fold, these data do not follow Equation (5). The transcription of c-fos in the spleen was also analyzed in Figure 11 of Ref. [18], but these data did not satisfy Equation (5). Thus, c-fos m-RNA is not a factor that universally complies with Equation (5) and Figure 3.
3.2.11. LY6G5C Gene
LY6G5C belongs to leukocyte antigen-6 (LY6) genes in the major histocompatibility complex class III region on chromosome 6 [19]. At 24 h after γ-ray irradiation, the expression of LY6G5C increased at 20 mGy compared with control, but the expression at 100 mGy reached the same level as control [20]. Because R(x) at 100 mGy is 33%, it contradicts the experimental data of Ref. [20]. Therefore, LY6G5C was also not a target factor that obeys our theory.
4. Conclusions, Problems, and Implications
4.1. Conclusions
When the following two conditions, (i) hormesis at ≤100 mSv and (ii) LNT with a ≤10% error at ≥100 mSv, were fulfilled at the same time, the maximum hormesis region became 5.8–30.0 mSv. Unknown hormesis factors that reduce the cancer death rate should have the maximum value when the radiation dose is 40.9 mSv, and its function for Equation (5) should take a mountain-like shape. From PubMed searches and reviews, the following factors had such a fluctuation and were identified first: SOD, catalase, glutathione peroxidase, hsp70, TNF-α, IFN-γ, IL-10, IL-12, c-Raf, ERK1/2, MEK, PDK, AKT, p38, JNK, caspase-3, caspase-7, caspase-9, CREB, c-fos, Bcl-2, and LY6G5C. However, after consideration, none of these factors obeyed Equation (5) universally and completely.
4.2. Problems
Currently, we could not find much data that seemed to follow our theory, so we included non-human data in our study. However, response to radiation per a given dose varies with species (mouse versus human) and cell types (normal tissue versus tumor). Mice exhibit higher radioresistance than humans, and there are differences in the use of DNA repair pathways among others. There is a difference in the radiation response between normal and tumor cells [12]. In addition, the rate of DNA damage caused by ionizing radiation is lower in lymphocytes than in fibroblasts, which will affect further signal transduction and cellular radiation response. Therefore, this viewpoint needs to be reconsidered in the future when human data are accumulated.
We considered only upregulation of radiation-associated factors. Likewise, in future works, the downregulation of certain factors that can play a significant role in the effect of radiation hormesis will have to be considered.
4.3. Implications
The existence of the hormesis effect in the low-dose range cannot be directly proven due to statistical problems. However, if unknown factors that completely follow Figure 3 can be found in the future, and the cancer death rate can be reduced to a statistically significant level by forcibly increasing these factors, it must be clarified indirectly whether hormesis occurs at 100 mSv or less. In addition, methodologies that forcibly increase these unknown factors may lead to improved cancer treatment and prevention.
Author Contributions
Conceptualization, investigation, data analysis, writing—original draft preparation, writing—review and editing, visualization, supervision, project administration, funding acquisition, K.K.; Writing—original draft preparation of Section 3.2, writing—review and editing, T.O., H.T., T.K. (Takanobu Kobayashi), T.K. (Taishu Kawada) and M.M.; Writing—review and editing, supervision, H.M. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by Tokushima Bunri University. In addition, the concepts in this manuscript were developed from other studies by the author, supported by research grants from Radiation Effects Association, the Nakatomi Foundation, KAKENHI (23510069 and 17K00558), and the Japan Prize Foundation, for which the author is grateful.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Acknowledgments
We thank the anonymous reviewers for their insights and critical review of the manuscript.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationship that could have appeared to influence the work reported in this paper.
References
- ICRP. Low-Dose Extrapolation of Radiation-Related Cancer Risk; ICRP Publication 99; International Commission on Radiological Protection; Elsevier: Oxford, UK, 2006. [Google Scholar]
- Luckey, T.D. Radiation Hormesis; CRC Press Inc.: Boca Raton, FL, USA, 1991. [Google Scholar]
- Kiefer, J. Biological Radiation Effect; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Sanders, C.L. Radiation Hormesis and the Linear-No-Threshold Assumption; Springer: Berlin, Germany, 2010. [Google Scholar]
- Kino, K. The prospective mathematical idea satisfying both radiation hormesis under low radiation doses and linear non-threshold theory under high radiation doses. Genes Environ. 2020, 42, 1–5. [Google Scholar] [CrossRef] [PubMed]
- ICRP. The 2007 Recommendations of the International Commission on Radiological Protection; ICRP Publication 103; International Commission on Radiological Protection; Elsevier: Oxford, UK, 2007. [Google Scholar]
- Pathak, C.M.; Avti, P.; Kumar, S.; Khanduja, K.L.; Sharma, S.C. Whole Body Exposure to Low-dose Gamma Radiation Promotes Kidney Antioxidant Status in Balb/c Mice. J. Radiat. Res. 2007, 48, 113–120. [Google Scholar] [CrossRef] [PubMed]
- Sato, E.F.; Yamaoka, K.; Yu, H.; Morishita, S.; Inoue, M. Low dose X-ray irradiation induces stress proteins but does not prevent gastric mucosal lesion. Physiol. Chem. Phys. Med. NMR 1996, 28, 103–109. [Google Scholar] [PubMed]
- Yang, G.; Kong, Q.; Wang, G.; Jin, H.; Zhou, L.; Yu, D.; Niu, C.; Han, W.; Li, W.; Cui, J. Low-Dose Ionizing Radiation Induces Direct Activation of Natural Killer Cells and Provides a Novel Approach for Adoptive Cellular Immunotherapy. Cancer Biother. Radiopharm. 2014, 29, 428–434. [Google Scholar] [CrossRef] [PubMed]
- Shigematsu, A.; Adachi, Y.; Koike-Kiriyama, N.; Suzuki, Y.; Iwasaki, M.; Koike, Y.; Nakano, K.; Mukaide, H.; Imamura, M.; Ikehara, S. Effects of Low-dose Irradiation on Enhancement of Immunity by Dendritic Cells. J. Radiat. Res. 2007, 48, 51–55. [Google Scholar] [CrossRef] [PubMed]
- Shan, Y.-X.; Jin, S.-Z.; Liu, X.-D.; Liu, Y.; Liu, S.-Z. Ionizing radiation stimulates secretion of pro-inflammatory cytokines: Dose–response relationship, mechanisms and implications. Radiat. Environ. Biophys. 2007, 46, 21–29. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Gu, J.; Yu, D.; Wang, G.; Zhou, L.; Zhang, X.; Zhao, Y.; Chen, X.; Zheng, S.; Liu, Q.; et al. Low-dose radiation induces cell proliferation in human embryonic lung fibroblasts but not in lung cancer cells: Importance of ERK1/2 and AKT signaling pathways. Dose Response 2016, 14, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Hladik, D.; Dalke, C.; Von Toerne, C.; Hauck, S.M.; Azimzadeh, O.; Philipp, J.; Ung, M.-C.; Schlattl, H.; Rößler, U.; Graw, J.; et al. CREB Signaling Mediates Dose-Dependent Radiation Response in the Murine Hippocampus Two Years after Total Body Exposure. J. Proteome Res. 2019, 19, 337–345. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.R.; Wang, X.; Templeton, D.; Davis, R.J.; Tan, T.H. The role of c-Jun N-terminal kinase (JNK) in apoptosis induced by ultraviolet C and gamma radiation. Duration of JNK activation may determine cell death and proliferation. J. Biol. Chem. 1996, 271, 31929–31936. [Google Scholar] [CrossRef] [PubMed]
- Narang, H.; Krishna, M. Mitogen-Activated Protein Kinases: Specificity of Response to Dose of Ionizing Radiation in Liver. J. Radiat. Res. 2004, 45, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Furlong, H.; Mothersill, C.; Lyng, F.; Howe, O. Apoptosis is signalled early by low doses of ionising radiation in a radiation-induced bystander effect. Mutat. Res. Mol. Mech. Mutagen. 2013, 741–742, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Qiao, L.; Yacoub, A.; McKinstry, R.; Park, J.S.; Caron, R.; Fisher, P.B.; Hagan, M.P.; Grant, S.; Dent, P. Pharmocologic Inhibitors of the Mitogen Activated Protein Kinase Cascade Have the Potential to Interact with Ionizing Radiation Exposure to Induce Cell Death in Carcinoma Cells by Multiple Mechanisms. Cancer Biol. Ther. 2002, 1, 168–176. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, S.-Z. Biological Defense and Adaptation Induced by Low Dose Radiation. Hum. Ecol. Risk Assess. Int. J. 1998, 4, 1217–1254. [Google Scholar] [CrossRef]
- Mallya, M.; Campbell, R.D.; Aguado, B. Transcriptional Analysis of a Novel Cluster of LY-6 Family Members in the Human and Mouse Major Histocompatibility Complex: Five Genes with Many Splice Forms. Genomics 2002, 80, 113–123. [Google Scholar] [CrossRef]
- Knops, K.; Boldt, S.; Wolkenhauer, O.; Kriehuber, R. Gene Expression in Low- and High-Dose-Irradiated Human Peripheral Blood Lymphocytes: Possible Applications for Biodosimetry. Radiat. Res. 2012, 178, 304–312. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).