How Accurately Could Early (622-900 C.E.) Muslims Determine the Direction of Prayers (Qibla)?
Abstract
1. Background
2. Objectives
3. Methods and Procedures
3.1. Approach
3.2. Sample
3.3. Analysis
4. Hypotheses
- The average direction of prayer. The null hypothesis is that the average direction of prayer will be centered on zero, as assessed by a one sample t-test and a chi-square test with one degree of freedom. If the null hypothesis is rejected, that might suggest a greater inaccuracy in qibla determination, with some type of systematic, rather than merely random, bias.
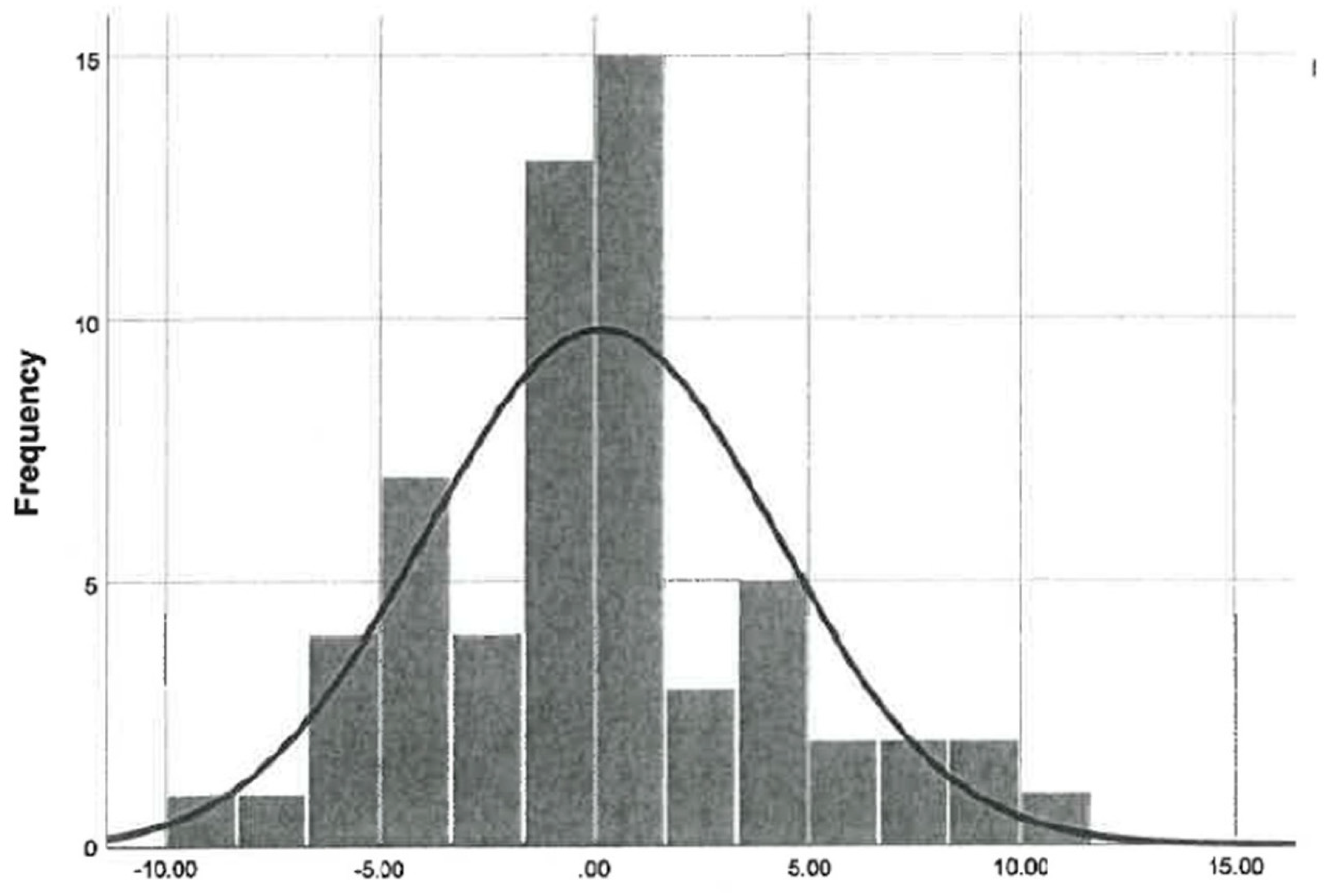
- The distribution of qiblas around their mean will be normally distributed by inspection and/or a test for non-normality, specifically a Kolmogorov-Smirnov one sample test of normality.
- The limits of 2, 3, and 5 degrees, plus or minus, were considered. My thinking was that if qiblas could be determined at those levels of accuracy, then ancient architects could probably distinguish between adjacent cities as long as those cities were several degrees apart in terms of their azimuths; otherwise, azimuths might not be distinguishable.
- Qibla accuracy and distance from holy city. The null hypothesis was that there would be no association between the qibla accuracy and distance from the holy city, tested with a Pearson zero-order correlation coefficient and a nonparametric Spearman rho correlation coefficient. I did not have a prediction here of the outcome.
- Qibla accuracy and approximate date of construction. The null hypothesis was that there would be no association between the qibla accuracy and the approximate time of construction of the buildings, tested with a Pearson zero-order correlation coefficient and a Spearman rho correlation coefficient. I was not sure if the qibla accuracy would improve or decline over time. I also planned to correlate the date of construction with the distance from the target city, which was expected to be positive on average.
5. Results
5.1. Under Gibson’s Assumptions
5.2. Under King’s Assumptions
6. Attempting a Synthesis with Independent Data
7. Further Critical Testing
8. Discussion
9. Limitations
10. Implications
11. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Anderson, Mark. 2018. Is Mecca or Petra Islam’s True Birthplace? Available online: https://understanding Islamtoday/is-mecca-or-petra-islams-true-birthplace (accessed on 26 November 2019).
- Avni, Gideon. 1994. Early mosques in the Negev highlands: New archaeological evidence on Islamicpenetration of southern Palestine. Bulletin of the American School of Oriental Research 294: 83–100. [Google Scholar] [CrossRef]
- Bazian, Hatem. 2018. Islamophobia, “Clash of civilizations”, and forging a post-cold war order! Religions 9: 282. [Google Scholar] [CrossRef]
- Brubaker, Danial Alan. 2019. Corrections in Early Qur’an Manuscripts: Twenty Examples. Lovettsville: Think and Tell Press. [Google Scholar]
- Cohen, Jacob. 1992. A power primer. Psychological Bulletin 112: 155–59. [Google Scholar] [CrossRef]
- De Wildt, Kim, Martin Radermacher, Volkhard Krech, Beate Loffler, and Wolfgang Sonne. 2019. Transformations of ‘sacredness in stone’: Religious architecture in urban space in 21st century Germany—New perspectives in the study of religious architecture. Religions 10: 602. [Google Scholar] [CrossRef]
- Firestone, Reuven. 2019. Muhammad, the Jews, and the composition of the Qur’an: Sacred history and counter-history. Religions 10: 63. [Google Scholar] [CrossRef]
- Gibson, Daniel. 2011. Qur’anic Geography. Vancouver: Independent Scholars Press. [Google Scholar]
- Gibson, Daniel. 2017. Early Islamic Qiblas: A Survey of Mosques Built Between 1AH/622 CE and 263 AH/ 876 CE. Vancouver: Independent Scholars Press. [Google Scholar]
- Haddad, Yvonne Yazbeck, and Nazir Nader Harb. 2014. Post-9/11: Making Islam an American Religion. Religions 5: 477–501. [Google Scholar] [CrossRef]
- Ilci, Veli, Ibrahim Murat Ozulu, Ersoy Arslan, and Reha Metin Alkan. 2018. Investigation on the accuracy of existing qibla directions of the mosques from different periods: A case study in Corum City, Turkey. Technical Gazette 25: 1642–49. [Google Scholar]
- Ismail, Siti Zubaidah, and Muhamad Zahiri Awang Mat. 2016. Faith and freedom: The Qur’anic notion of freedom of religion vs. the act of changing religion and thoughts on the implications for Malaysia. Religions 7: 88. [Google Scholar] [CrossRef]
- Khan, Mohsin Hassan, Hamedi Mohd Adnan, Surinderpal Kaur, Rashid Ali Khuhro, Rohail Asghar, and Sahira Jabeen. 2019. Muslims’ representation in Donald Trumps’ anti-Muslim-Islam statement: A critical discourse analysis. Religions 10: 115. [Google Scholar] [CrossRef]
- King, David A. 1986. Kibla. In Encyclopedia of Islam. Leiden: E. J. Brill, vol. 5, pp. 82–88. [Google Scholar]
- King, David A. 1990. Science in the service of religion: The case of Islam. Impact of Science on Society 40: 245–62. [Google Scholar]
- King, David A. 1993. Folk astronomy in the service of religion: The case of Islam. In Astronomies and Cultures: Papers Derived from the Third "Oxford" International Symposium on Archaeoastronomy, St. Andrews, UK, September 1990. Edited by C. L. N. Ruggles and Nicholas J. Saunders. Niwot: University of Colorado Press, pp. 124–38. [Google Scholar]
- King, David. A. 2018. The Petra Fallacy: Early Mosques Do Face the Sacred Kaaba in Mecca but Dan Gibson Doesn’t Know How. Available online: www.davidaking.academia.edu (accessed on 26 November 2019).
- King, David A. 2018–2019. Review of “Early Islamic Qiblas”. Suhayl: International Journal for the History of the Exact and Natural Sciences in Islamic Civilization 16–17: 347–66. [Google Scholar]
- Larsson, Goran. 2012. History strikes back! Scientific and pedagogical implications of the critical study of early Islam. Islam and Christian-Muslim Relations 23: 531–37. [Google Scholar] [CrossRef]
- Lecker, Michael. 2014. Review of “Qur’anic Geography”. Journal of Semitic Studies 59: 465–67. [Google Scholar] [CrossRef]
- Mohammed, Khaleel. 2018. Islam and Genesis 17: A study in scriptural intertextuality. Religions 9: 293. [Google Scholar] [CrossRef]
- Oakes, W. Richard. 2015. Review of “Qur’anic Geography”. The Muslim World 105: 423–26. [Google Scholar] [CrossRef]
- Petersen, Andrew. 1996. Qibla. In Dictionary of Islamic Architecture. Edited by Andrew Petersen. New York: Routledge, p. 240. [Google Scholar]
- Saifullah, M. S. M., M. Ghoniem, ‘Abd al-Rahman, Robert Squires, and M. Ahmed. 2001. The Qibla of Early Mosques: Jerusalem or Makkah? Available online: www.islamic-awareness.org/History/Islam/Dome_of_the_Rock/qibla.html (accessed on 23 February 2020).
- Schumm, Walter R. 2015. Navigating treacherous waters–One researcher’s 40 years of experience with controversial scientific research. Comprehensive Psychology 4: 1–40. [Google Scholar] [CrossRef]
- Schumm, Walter R., and Duane W. Crawford. 2020. Is research on transgender children what it seems? Comments on recent research on transgender children with high levels of parental support. Linacre Quarterly 87: 9–24. [Google Scholar] [CrossRef]
- Schumm, Walter R., Duane W. Crawford, and Lorenza Lockett. 2019a. Using statistics from binary variables to detect data anomalies, even possibly fraudulent research. Psychology Research and Applications 1: 112–18. [Google Scholar] [CrossRef]
- Schumm, Walter R., Duane W. Crawford, and Lorenza Lockett. 2019b. Patterns of means and standard deviations with binary variables: A key to detecting fraudulent research. Biomedical Journal of Scientific and Technical Research 23: 17151–53. [Google Scholar] [CrossRef]
- Sharify-Funk, Meena. 2013. Pervasive anxiety about Islam: A critical reading of contemporary ‘clash’ literature. Religions 4: 443–68. [Google Scholar] [CrossRef]
- Waugh, Daniel C. 2012. Review of “Qur’anic Geography”. The Silk Road 10: 201. [Google Scholar]
| Name of Mosque/Site | Date (C.E.) | Location | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|---|---|
| Quba Mosque | 622 | Medina, Saudi Arabia | X | ||||||
| Prophet’s Mosque | 623 | Medina, Saudi Arabia | X | ||||||
| Mosque of the Two Qiblas | 626 | Medina, Saudi Arabia | X | ||||||
| Janad Mosque | 627 | Janad, Yemen | X | ||||||
| Jowatha Mosque | 629 | Al-Kilabiyah, Saudi Arabia | X | ||||||
| Umar ibn al-Khattab Mosque | 634 | Dawmat al Jandal, Saudi Arabia | X | ||||||
| Mosque of the Prophet Jonah | 637 | Mosul, Iraq | X | ||||||
| Kufa Grand Mosque | 638 | Kufa, Iraq | X | ||||||
| Ugba Ibn Nafi Mosque | 640 | Kairoun, Tunisia | X | ||||||
| Hala Sultan Tekke | 649 | Larnaca, Cyprus | X | ||||||
| Iman Shafi’l Mosque | 649 | Jeddah, Saudi Arabia | X | ||||||
| Mosque of Sidi ‘Ukba | 686 | Biskra, Algeria | X | ||||||
| Dome of the Rock | 690 | Jerusalem | X | ||||||
| Qasr Burqu’ | 700 | Jordan desert | X | ||||||
| Masjid al Khamis | 717 | Manama, Bahrein | X | ||||||
| Mosque of Rusafa | 724 | Baghdad, Iraq | X | ||||||
| Grand Hussein Mosque | 725 | Amman, Jordan | X | ||||||
| Huajuexiang Mosque | 742 | Xian, China | X | ||||||
| Amra Bathhouse | 743 | Jordan desert | X | ||||||
| Shibam Palace | 753 | Shibam, Yemen | X | ||||||
| Masjid al Jami Grand Mosque | 772 | Ishfan, Iran | X | ||||||
| Qasr Uweinid | 8th C. | Jordan desert | X | ||||||
| Erbil Grand Mosque | 8th C. | Erbil, Iraq | X | ||||||
| Be’er Ora Qiblatain Mosque | 8th C. | Be’er Ora, Israel | X | ||||||
| Fenghuang Mosque | 8th C. | Hangzhou, China | X | ||||||
| Job’s Tomb Shrine | 8th C. | Salalah, Oman | X | ||||||
| Al-Asha’ir Mosque | 820 | Zabid, Yemen | X | ||||||
| Grand Mosque of Shibam | 871 | Shibam, Yemen | X | ||||||
| Sidi Ghanem Mosque | 678 | Mila, Algeria | X | ||||||
| Graveyard of Sidi Ukba | 686 | Biskra, Algeria | X | ||||||
| Jami’ al-Zaytuna | 732 | Tunis, Tunisia | X | ||||||
| Ribat Fortress | 770 | Ribat, Tunisia | X | ||||||
| Tauste Graveyard | 772 | Zaragoza, Spain | X | ||||||
| Cordoba Mosque | 784 | Cordoba, Spain | X | ||||||
| Shrine of Kazmiyya | 799 | Baghdad, Iraq | X | ||||||
| Dougga Mosque | 800 | Dougga, Tunisia | X | ||||||
| Rand Mosque of Kairoun | 817 | Kairoun, Tunisia | X | ||||||
| Moulay Idriss, II Tomb and Mosque | 828 | Fex, Morocco | X | ||||||
| Jami Uqba ibn Nafi | 836 | Kairoun, Tunisia | X | ||||||
| Great Mosque of Susa | c. 850 | Susa, Tunisia | X | ||||||
| Small mosque with graveyard | c. 850 | Houmt Souk, Tunisia | X | ||||||
| Great Mosque of Sfax | 850 | Sfax, Morocco | X | ||||||
| University of al-Qarawiyyin | 859 | Fez, Morocco | X | ||||||
| Mosque with Three Doors | 866 | Kairoun, Tunisia | X | ||||||
| Grand Mosque of Mahdia | 916 | Mahdia, Tunisia | X | X | |||||
| Medjez el-Bab | 944 | Beja, Tunisia | X | X | |||||
| Grand Mosque of Sale | 1028 | Sale, Morocco | X | X | |||||
| Grand Mosque of Tangier | 1196 | Tangier, Morocco | X | X | |||||
| Al-Muwaqqar graveyard | 723 | Muwaqqar, Jordan | X | ||||||
| Qasr el-Bai’j | 410 | Jordan desert | X | ||||||
| Harat Great Mosque | 1200 | Harat, Afghanistan | X | ||||||
| Abdul Qader Yagouri Mosque | c. 750 | Bini Abbas, Algeria | X | X | |||||
| Qasr Hallabat | 827 | Jordan desert | X | ||||||
| Masjid I Jami, Mosque of Fahraj | c. 850 | Fahraj, Iran | X |
| NAME of MOSQUE | DATE (CE) | Location | Original Azimuth | Error Petra | Error Mecca | Error Jerusalem | Error Between |
|---|---|---|---|---|---|---|---|
| Cheraman Juma | 629 | Methala, Kerala State, India | 304.3 Petra (J) | 0.26 | 75.01 | 1.65 | 37.64 |
| Hama Great Mosque | 637 | Hama, Syria | 193.87 Petra | 0.61 | 25.81 | −7.17 | 13.21 12.3 |
| Amr ibn Al-as | 642 | Fustat, Egypt | 90.00 Petra | 6.10 | −46.00 | 28.30 | 19.95 −29.4 |
| Aqaba Umayyad Mosque | ~650 | Aqaba, Jordan | 36.24 Petra | 10.80 | −114.40 | 31.20 | 51.80 −113.0 |
| Kathisma Church | ~650 | Bethlehem, Israel | 174.00 Petra | 1.90 | 16.90 | 147.70 | 9.30 8.5 |
| Seven Sleepers Mosque | ~650 | Amman, Jordan | 196.03 Petra | −0.30 | 35.10 | −63.30 | 17.40 21.9 |
| Jerash Umayyad Mosque | ~650 | Jerash, Jordan Also Abu Dulaf mosque | 196.32 Petra | 5.02 | 35.20 | −31.80 | 20.10 22.6 |
| Qasr Mushash Mosque | ~650 | Desert Castle, Jordan | 202.95 Petra | −4.10 | 40.60 | −65.10 | 18.25 25.1 |
| Zeila Qiblatain (Left) | ~650 | Zeila, Somalia | 339.10 Petra (J) | −0.60 | −2.20 | −1.80 | 0.80 0.50 |
| Dome of the Chain | 690 | Jerusalem | 172.03 Petra | −1.00 | 14.70 | −94.50 | 6.85 6.2 |
| Qasr Humeima | 699 | Humeima, Jordan | 20.64 Petra | 8.50 | −133.02 | 23.58 | −82.9 −138.2 |
| San’a Grand Mosque | 705 | San’a, Yemen | 333.60 Petra | 0.36 | 7.40 | −1.47 | 3.52 3.3 |
| Khirbat al Minya | 706 | Khirbat al Minya, Israel | 182.67 Petra | 0.80 | 22.14 | −10.58 | 11.47 11.5 |
| Hajjaj Mosque | 706 | Wasit, Iraq | 234.98 P/M | −26.5 | 25.3 | −35.4 | 0.60 −7.4 |
| Masjid al-Tarik Khana | 708 | Damghan, Iran | 244.82 249.56 P/M (P) | 10.30 −5.6 | 20.20 25.0 | 15.20 −10.5 | 4.95/10.9 5.0 |
| Al-Aqsa Mosque | 709 | Jerusalem | 169.61 Petra | −3.43 | 12.31 | −179.8 | 4.44 3.70 |
| Al-Umawi al-Kabir, Damascus Umayyad Mosque | 709 | Damascus, Syria | 177.21 P/M | −20.25 −16.0 | 8.33 12.5 | −30.53 | 1.75 −1.1 |
| Amman Umayyad Mosque | 710 | Amman, Jordan | 181.50 P/M | −13.2 | 20.7 | −72.1 | 7.7 |
| Qasr al-Kharana | 710 | Desert Castle, Jordan | 175.01 P/M | 32.30 −37.30 | 12.10 | −98.00 | 12.60 −4.4 or 3.01? |
| Khann al-Zabib | 712 | Qatrana, Jordan | 171.93 P/M | −33.80 | 11.10 | −118.10 | −11.35 −3.2 |
| Um Walid Mosque | 712 | Al Zafaran, Jordan | 197.41 Petra | 1.20 | 37.50 | −89.50 | 19.35 24.9 |
| Khirbat al-Mafjar | 714 | Jericho, Israel | 180.03 Petra | −0.59 | 21.51 | −61.34 | 10.46 11.5 |
| Anjar Palace Mosque | 714 | Anjar, Lebanon | 190.76 Petra | 3.61 | 27.36 | −6.17 | 15.49 15.3 |
| Aleppo Umayyad Mosque | 715 | Aleppo, Syria | 178.70 P/M | −15.50 | 8.40 | −21.70 | 3.55 −5.00 |
| Qasr Qastal | 720 | Qastal, Jordan | 191.74 Petra | −5.20 | 31.20 | −81.50 | 13.00 18.2 |
| Mosque of ‘Umar | 721 | Bosra, Syria | 183.63 P/M | −18.74 | 19.45 | −51.60 | 0.36 3.9 |
| Qasr Muwaqqar | 723 | Muwaqqar, Jordan | 182.98 P/M | −18.20 | 21.60 | −84.60 | 1.70 7.5 |
| Qasr al-Hayr al Gharbi | 726 | Hayr al Gharbi, Syria | 191.01 P/M | −13.86 | 20.27 | −27.10 | 3.21 3.3 |
| Banbhore Mosque | 727 | Banbhore, Pakistan | 265.78 Mecca | −22.61 | −2.44 | −25.55 | 12.53 −16.2 |
| Qasr Hayr al Sharqi | 728 | Hayr al Sharqi, Syria | 192.61 P/M | −21.2 | 15.6 | −32.6 | 2.80 −3.7 |
| Umayyad Palace | 730 | Amman Citadel, Jordan | 159.46 Mecca | −35.25 | −1.36 | −94.10 | 18.30 −14.3 |
| Ba’albeck Mosque | 740 | Ba’albeck, Lebanon | 176.86 P/M | −13.36 | 12.02 | −23.48 | 0.67 −0.80 |
| Qasr Bayir | 743 | Desert Castle, Jordan | 166.67 Mecca | −81.60 | 4.20 | −143.20 | 38.70 −15.8 |
| Mushatta Palace | 743 | Desert Castle, Jordan | 195.13 Petra | −4.10 | 34.32 | −78.52 | 15.10 20.8 |
| Qasr Tubah | 743 | Desert Castle, Jordan | 292.02 Jerusalem | 67.40 | 129.20 | 0.00 | 98.30 111.3 |
| Harran Mosque and University | 744 | Harran, Turkey | 191.74 P/M | −13.87 | 14.52 | −20.97 | 0.33 −1.5 |
| Um Jimal Umayyad Mosque | 749 | Um el-Jimal, Jordan | 180.00 P/M | −21.90 | 16.60 | −60.50 | 2.65 1.4 |
| Um Jimal Later Castellum Mosque | 749 | Um Jimal, Jordan | 203.03 Petra | 1.10 | 39.60 | −37.60 | 24.5 |
| Kufa Grand Mosque (rebuilt) | 749 | Kufa, Iraq | 195 Mecca | −65.0 | −6.0 | −75.0 | −29 |
| Qasr Aseikhin | ~750 | Desert Castle, Jordan | 163.89 Mecca | −55.20 | −1.70 | −100.00 | −28.45 −20.9 |
| Qasr Al-Fudayn | ~750 | Mufraq, Jordan | 178.19 P/M | −19.90 | 15.50 | −57.30 | 2.20 1.3 |
| Qasr ain as-Sil | ~750 | Azrak, Jordan | 180.30 P/M | −37.60 | 15.30 | −85.30 | 11.15 −3.4 |
| Azraq Fort Mosque | ~750 | Azraq, Jordan | 184.81 P/M | −33.00 | 19.90 | −81.30 | 6.55 1.3 |
| Um Jimal Later Castellum Umayyad Mosque | ~749 | Um Jimal, Jordan | 203.03 Petra | 1.10 | 39.60 | −37.60 | 20.21 24.5 |
| Bazaar Qaisaqiya | ~750 | Erbil, Iraq | 218.53 P/M | −14.60 | 23.50 | −22.80 | 4.45 0.9 |
| Al-Sawaf Mosque Grounds | ~750 | Erbil, Iraq | 234.35 Petra | 1.20 | 39.40 | −7.00 | 20.30 16.8 |
| Yamama Great Mosque | ~750 | Yamama, Saudi Arabia | 280.45 P/M | −22.30 | 30.70 | −27.60 | 4.20 −9.3 |
| Qiblatain Mosque of Oman | ~750 | Ibra, Oman | 294.00 Petra | −1.20 | 24.60 | −4.80 | 11.70 6.6 |
| Huaisheng Mosque | ~750 | Guangzhou, China | 291.66 P/M | −3.30 | 7.10 | −4.90 | 1.90 0.1 |
| Bibi Samarkan | ~750 | Samarkan, Uzbekistan | 261.64 Petra (J) | 1.78 | 21.86 | −1.23 | 11.82 8.5 |
| Sahi Ramdah Mosque | ~750 | Bowshar, Oman | 292.79 Petra | −0.58 | 26.19 | −4.24 | 12.81 7.5 |
| Mosque of Mansur | 762 | Baghdad, Iraq | 200.03 Mecca | −51.10 | 0.00 | −61.30 | 25.94 −30.5 |
| Qasr Ukhaydir | 764 | Kufa, Iraq | 198.24 Mecca | −61.61 −57.1 | 3.90 0.4 | 72.35 −68.7 | 32.75 −33.5 |
| Raqqa Mosque | 772 | Raqqa, Syria | 193.90 P/M | −15.17 | 16.89 | −24.12 | 0.86 −0.6 |
| Qasr al-Hallabat Mosque | 827 | Desert Castle, Jordan | 163.55 Mecca | −40.00 | 0.70 | −88.00 | 19.65 −14.5 |
| Great Mosque of Samarra | 847 | Samarra, Iraq | 197.79 Mecca | −46.01 | 1.13 | −56.10 | 22.44 −26.5 |
| Nine Domed Mosque | ~850 | Balkh Province, Afghanistan | 241.23 Mecca | −24.20 | −3.20 | −27.40 | −13.70 −17.3 |
| Ansaq Friday Mosque | ~850 | Ansaq, Iraq | 207.11 Mecca | −27.82 | 4.15 | −33.77 | −11.83 −15.7 |
| Al Balid Mosque | ~850 | Salalah, Oman (old Zafar) | 285.05 Mecca | −26.34 | −5.33 | −29.2 | −15.83 −20.2 |
| Abu Dalaf Mosque | 859 | Samarra, Iraq | 191.57 Mecca | −51.02 | −4.60 | −61.02 | −27.81 −31.8 |
| Ibn Tulun Mosque | 876 | Cairo, Egypt | 145.40 Mecca | 61.21 | 9.27 9.3 | 83.51 | 35.24 25.8 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schumm, W.R. How Accurately Could Early (622-900 C.E.) Muslims Determine the Direction of Prayers (Qibla)? Religions 2020, 11, 102. https://doi.org/10.3390/rel11030102
Schumm WR. How Accurately Could Early (622-900 C.E.) Muslims Determine the Direction of Prayers (Qibla)? Religions. 2020; 11(3):102. https://doi.org/10.3390/rel11030102
Chicago/Turabian StyleSchumm, Walter R. 2020. "How Accurately Could Early (622-900 C.E.) Muslims Determine the Direction of Prayers (Qibla)?" Religions 11, no. 3: 102. https://doi.org/10.3390/rel11030102
APA StyleSchumm, W. R. (2020). How Accurately Could Early (622-900 C.E.) Muslims Determine the Direction of Prayers (Qibla)? Religions, 11(3), 102. https://doi.org/10.3390/rel11030102





