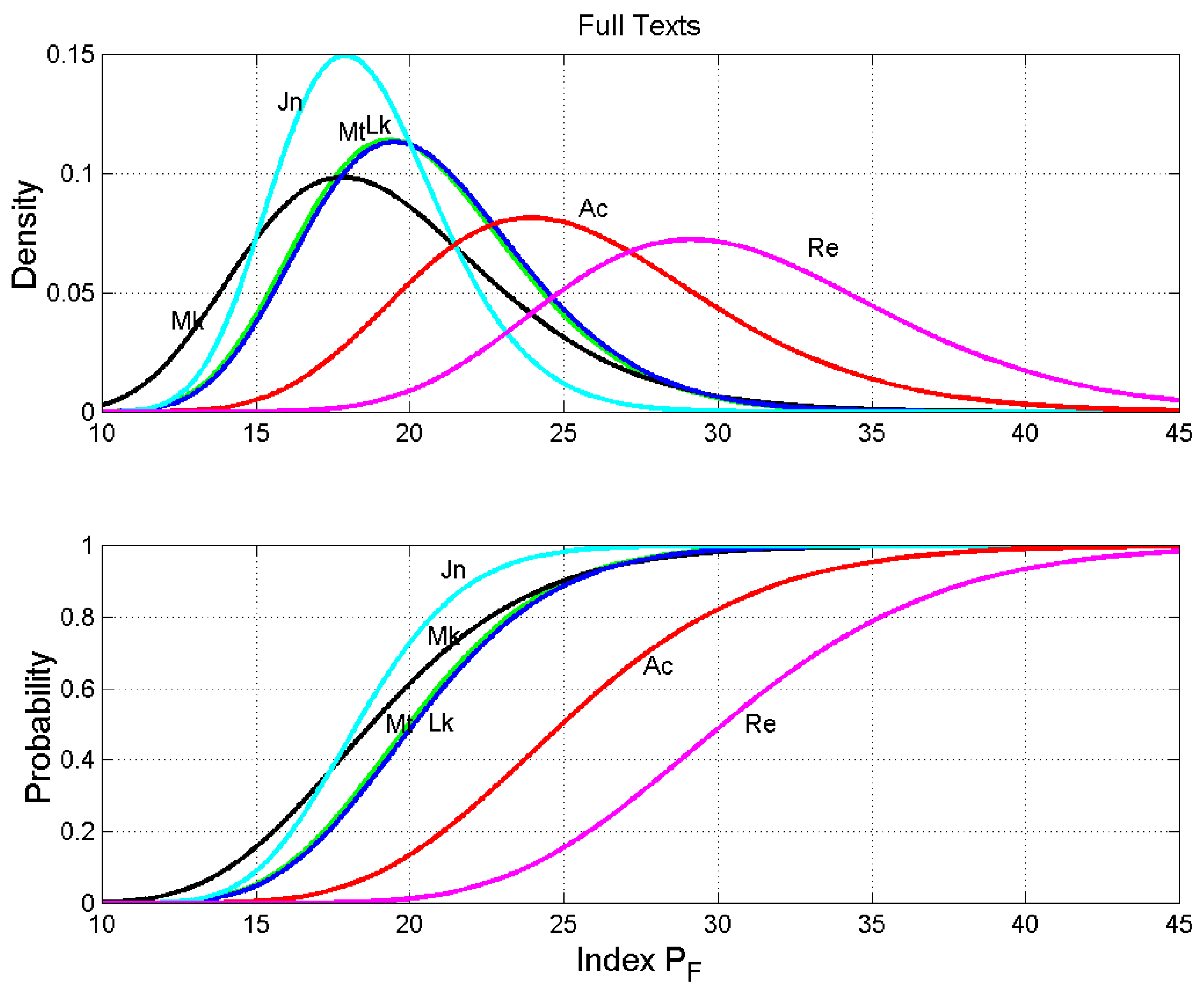
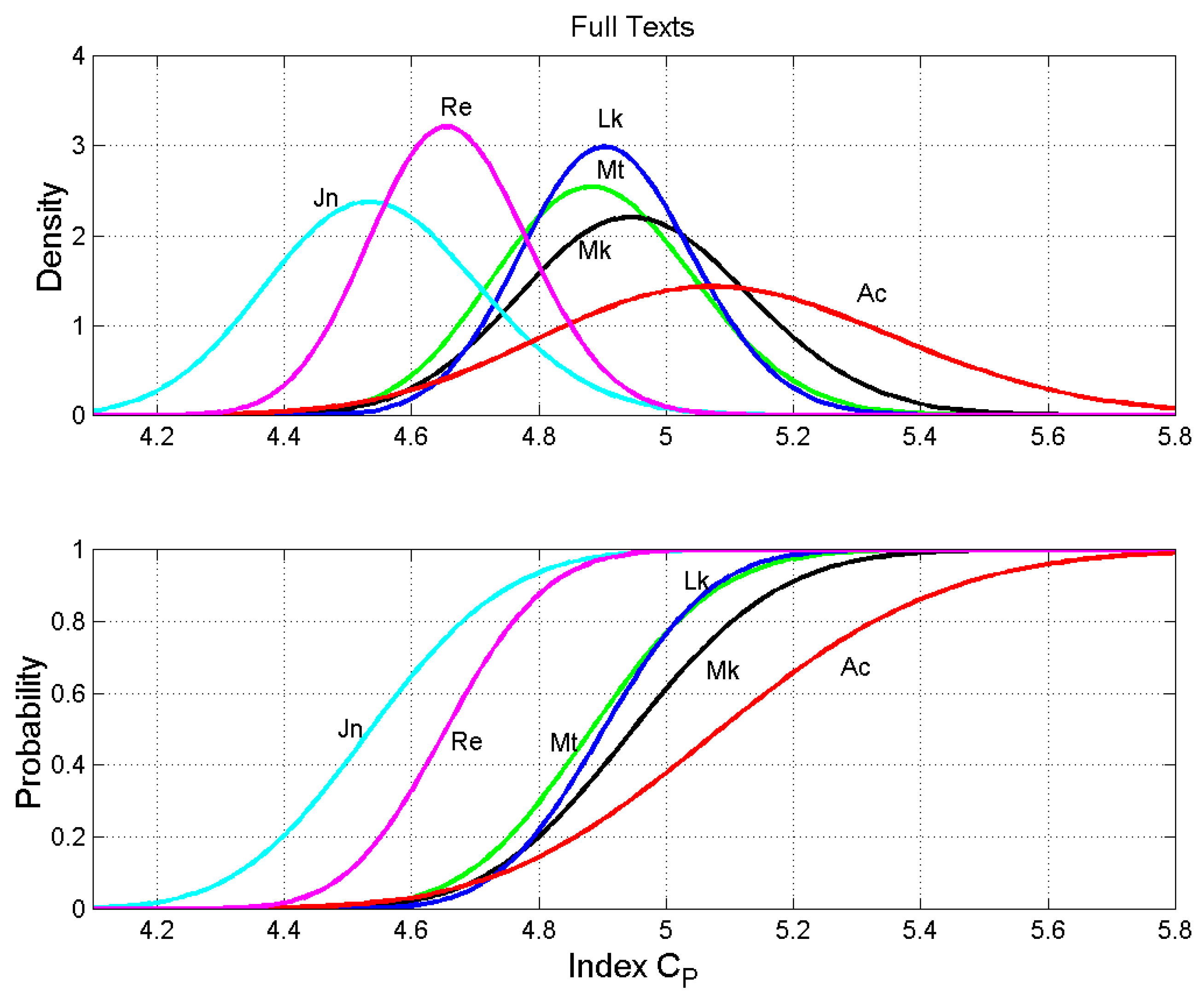
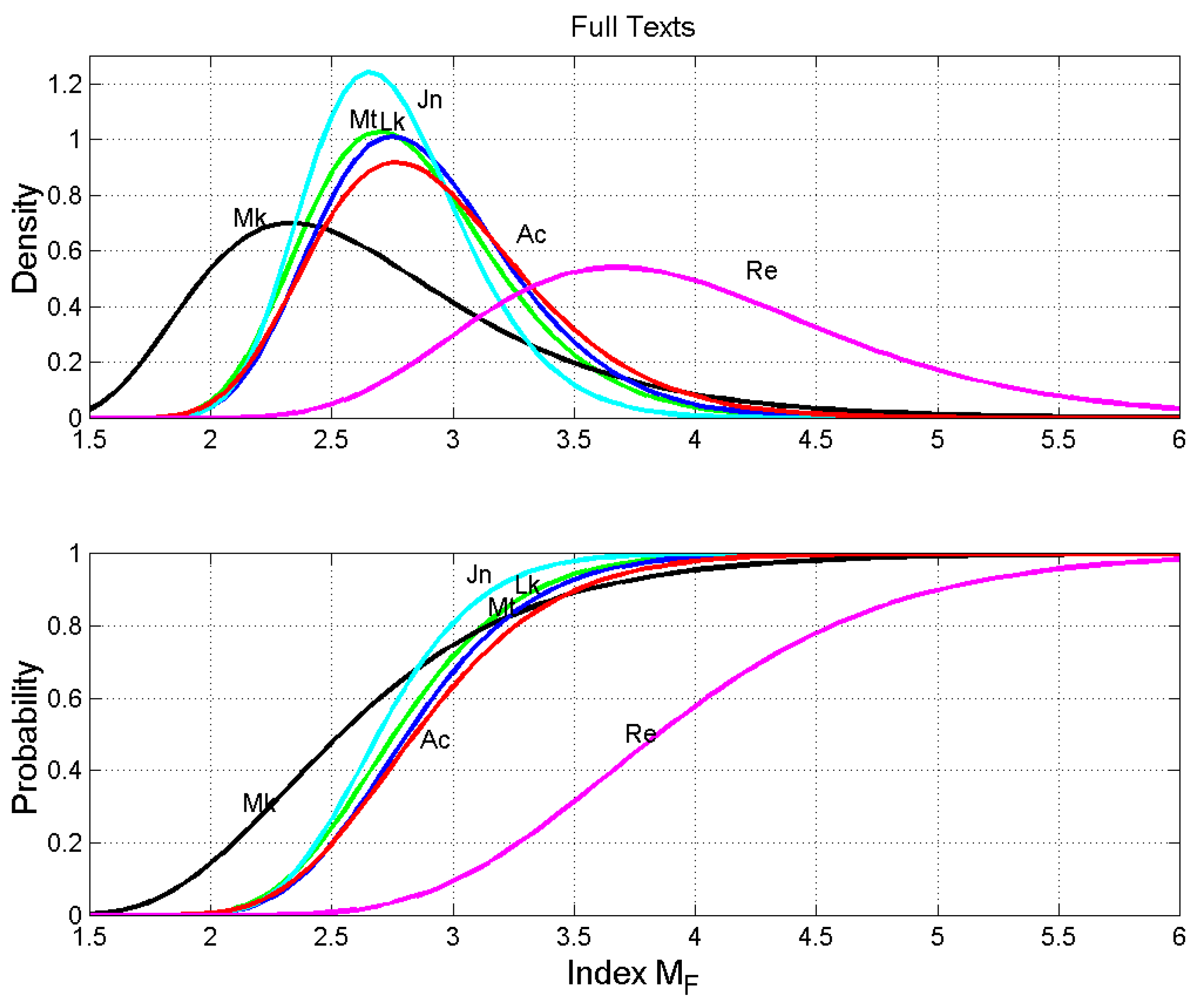
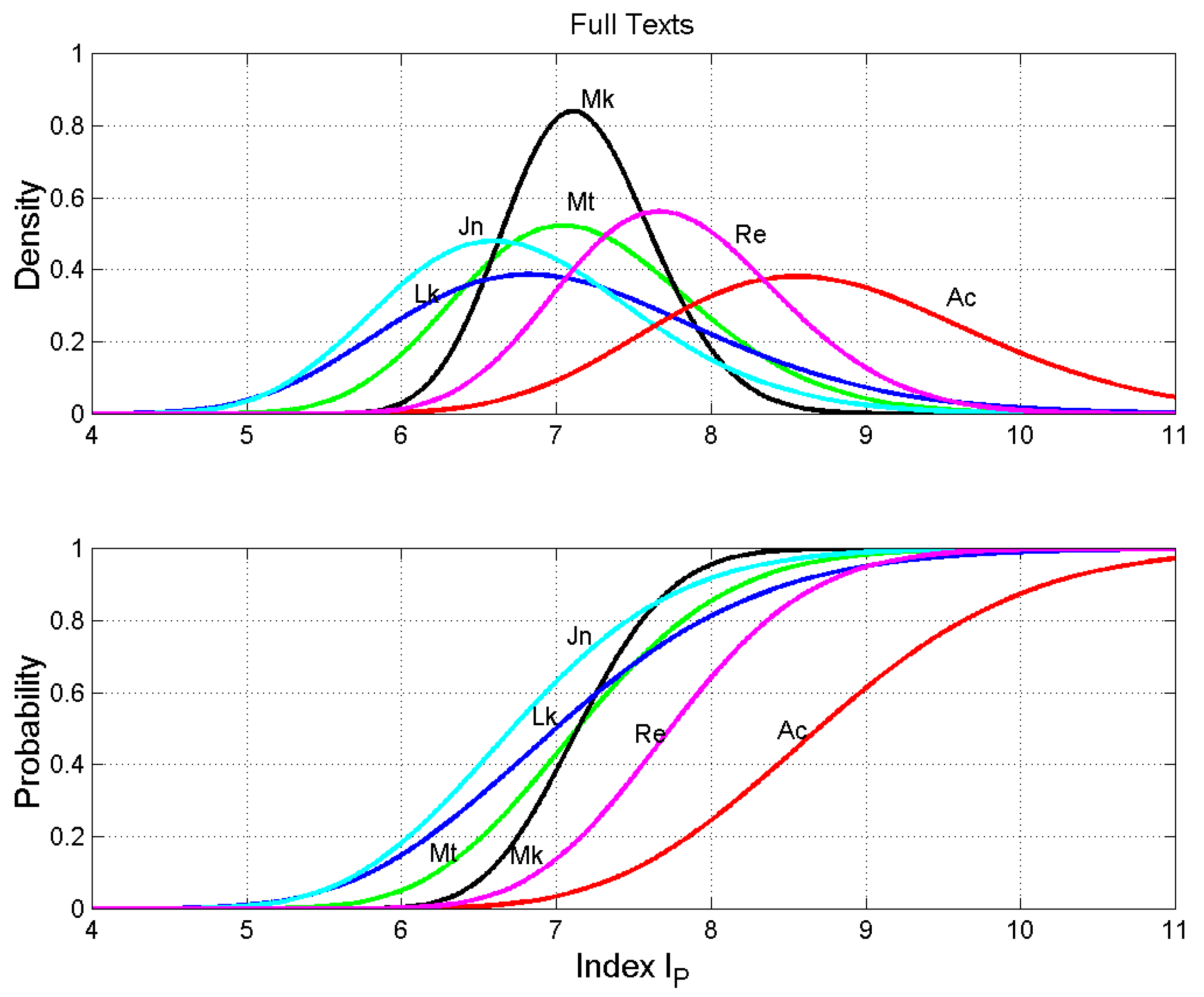
Figure 1.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 1.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 2.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 2.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 3.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of interpunctions per sentence . Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 3.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of interpunctions per sentence . Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 4.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 4.
Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; John: cyan line; Acts: red line; Revelation: magenta line.
Figure 5.
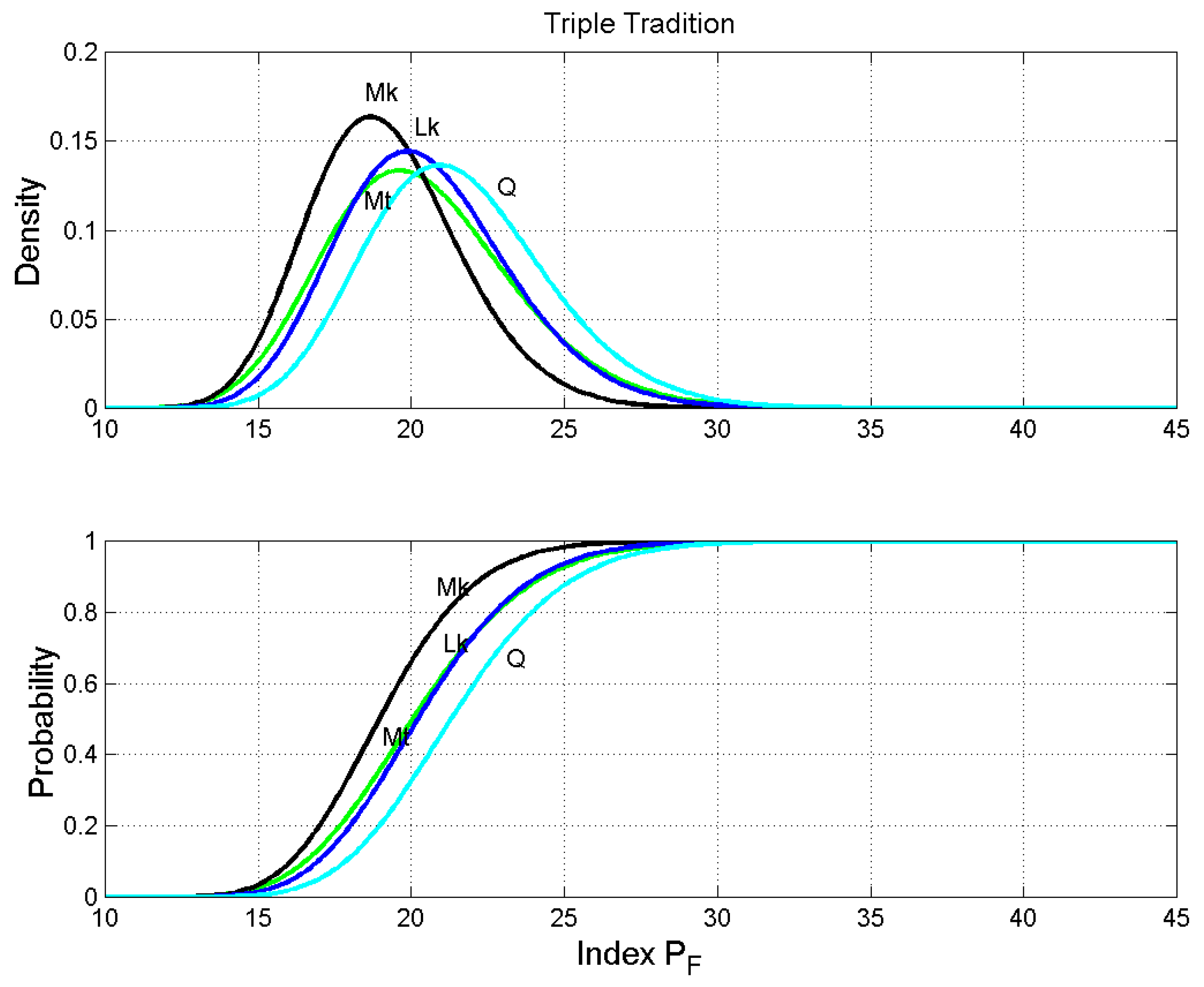
Triple Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
Figure 5.
Triple Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
Figure 6.
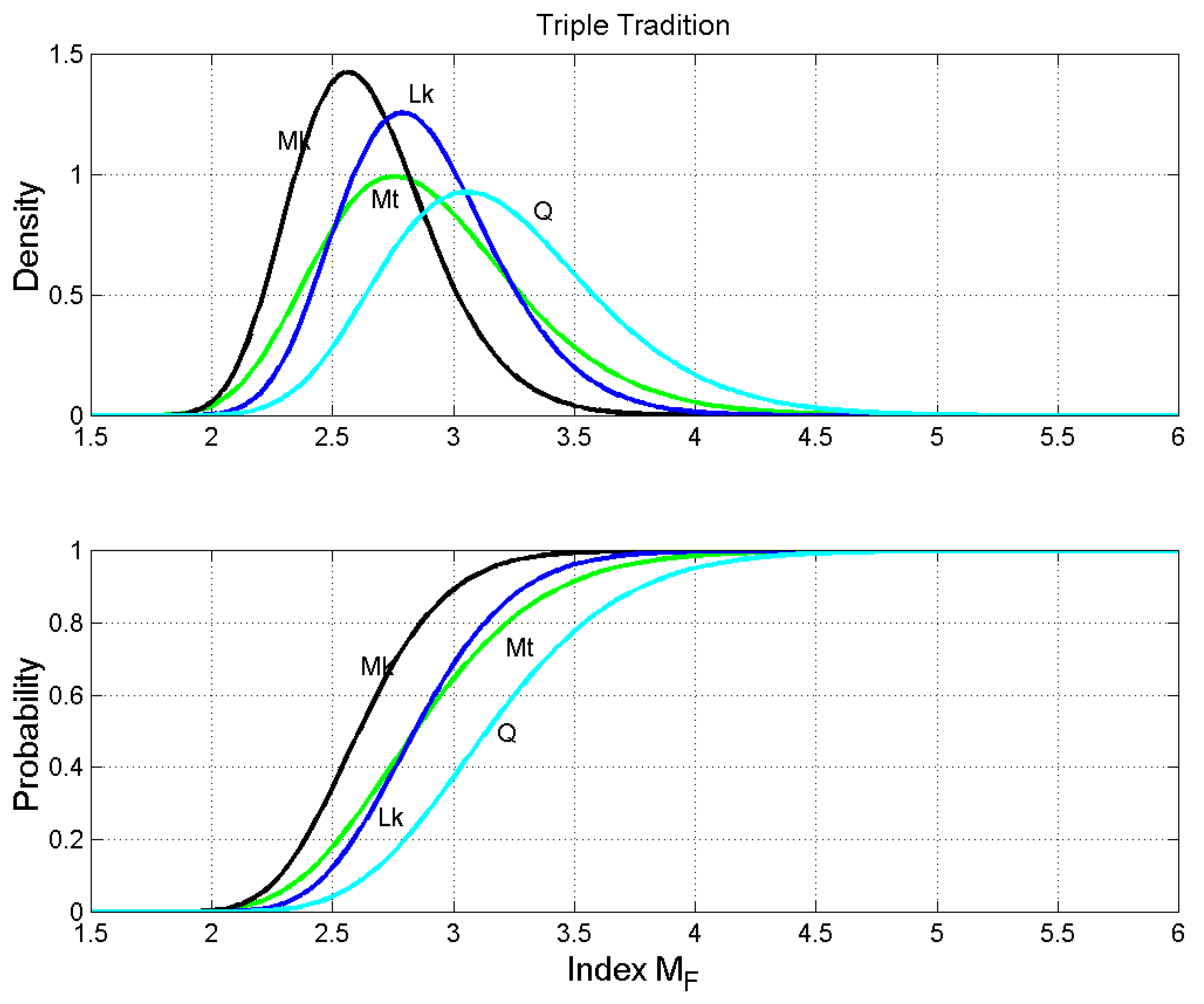
Triple Tradition and Q. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
Figure 6.
Triple Tradition and Q. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
Figure 7.
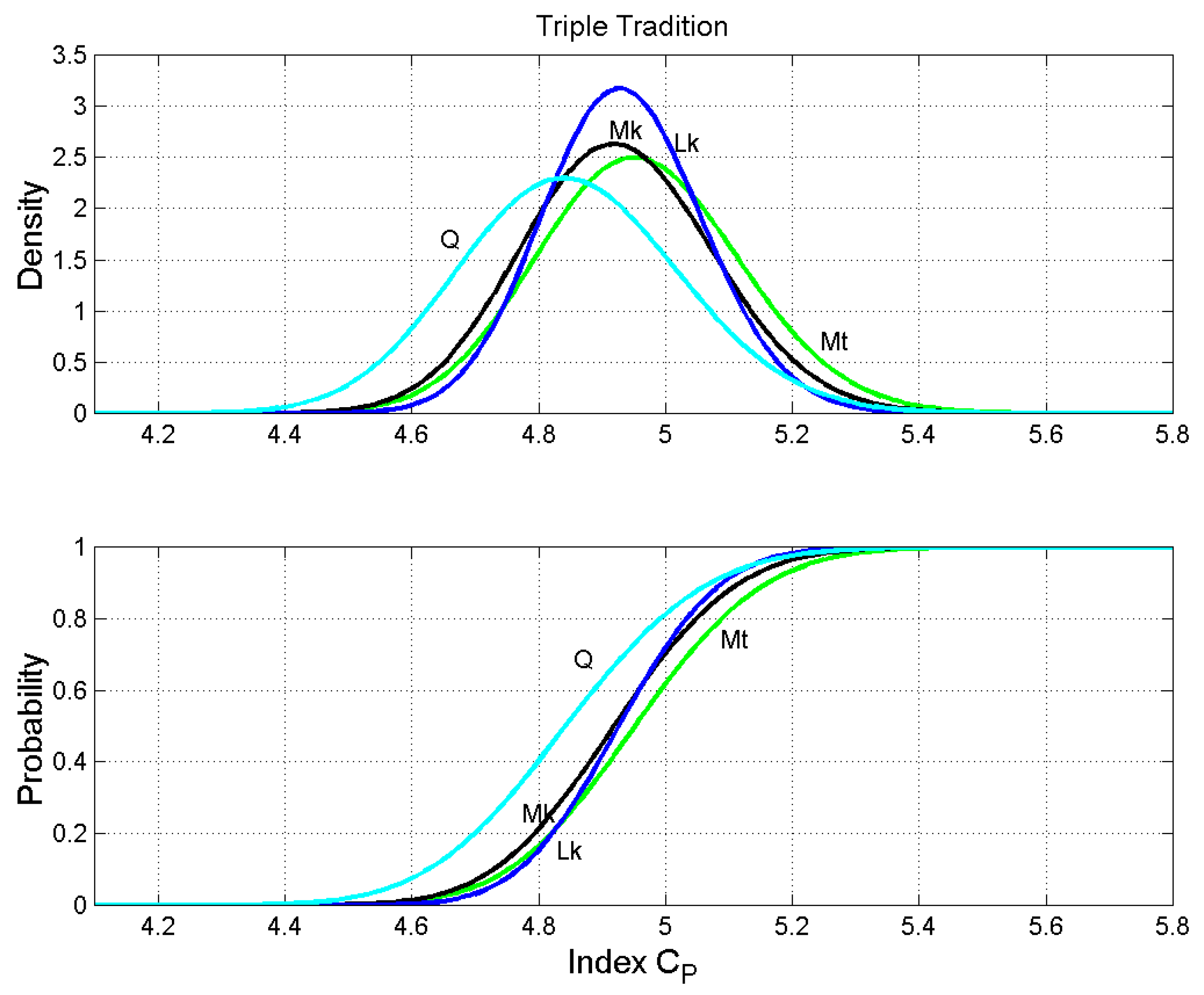
Triple Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence . Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
Figure 7.
Triple Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence . Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
Figure 8.
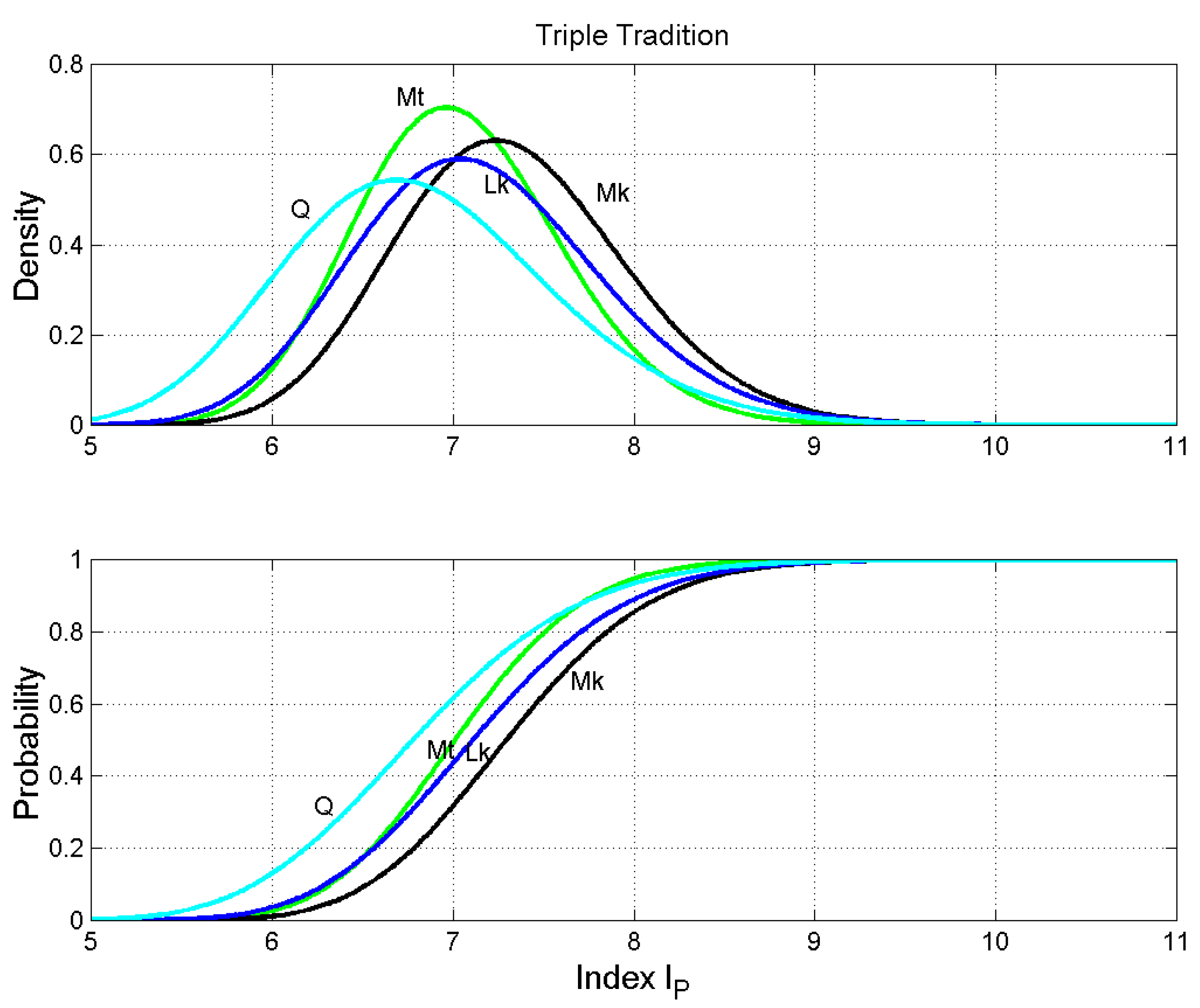
Triple Tradition and Q. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per interpunctions (word interval) . Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
Figure 8.
Triple Tradition and Q. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per interpunctions (word interval) . Matthew: green line; Mark: black line; Luke: blue line; Q: cyan line.
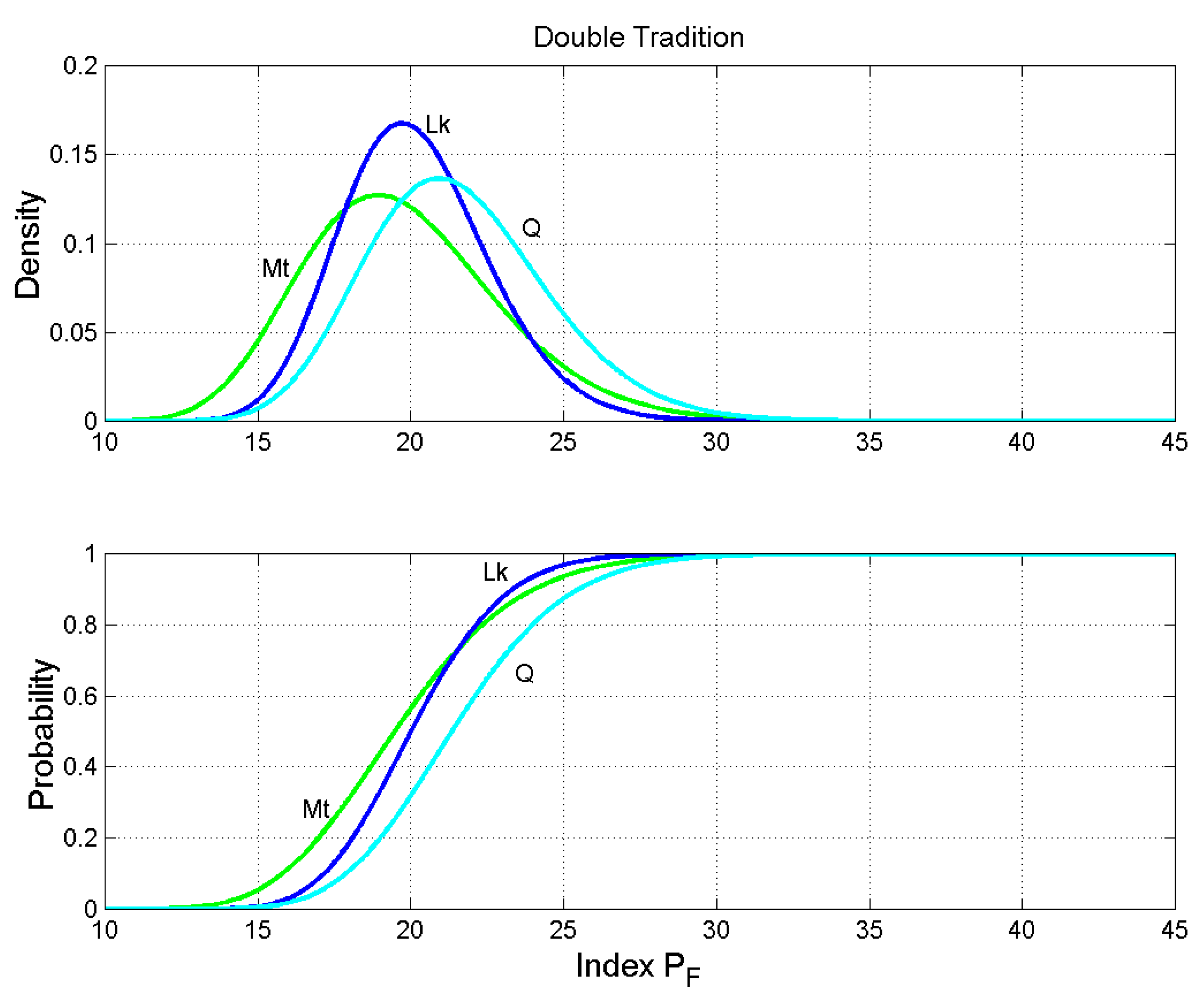
Figure 9.
Double Tradition and Q. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Luke: blue line; Q: cyan line.
Figure 9.
Double Tradition and Q. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Luke: blue line; Q: cyan line.
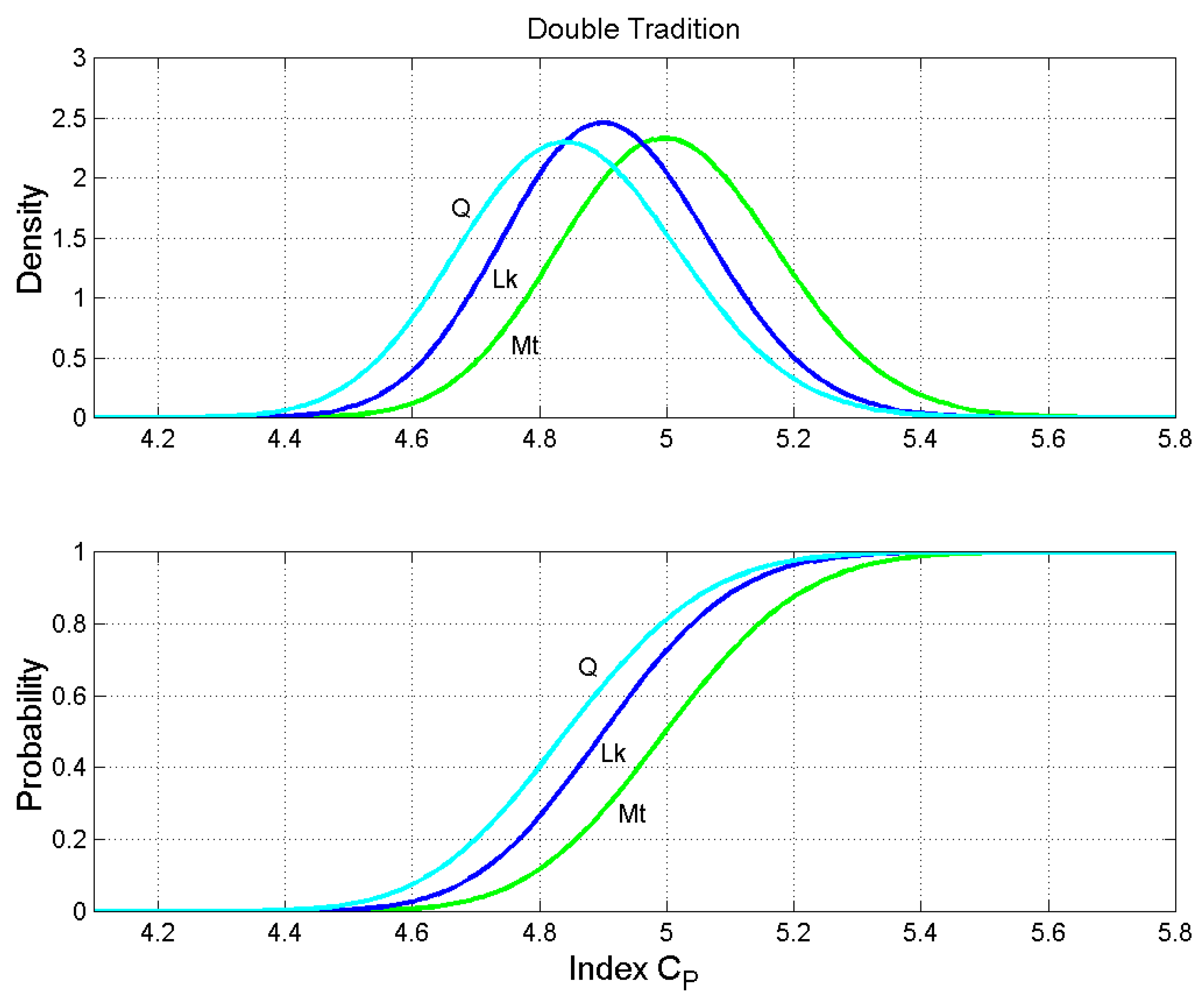
Figure 10.
Double Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of characters per word. Matthew: green line; Luke: blue line; Q: cyan line.
Figure 10.
Double Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of characters per word. Matthew: green line; Luke: blue line; Q: cyan line.
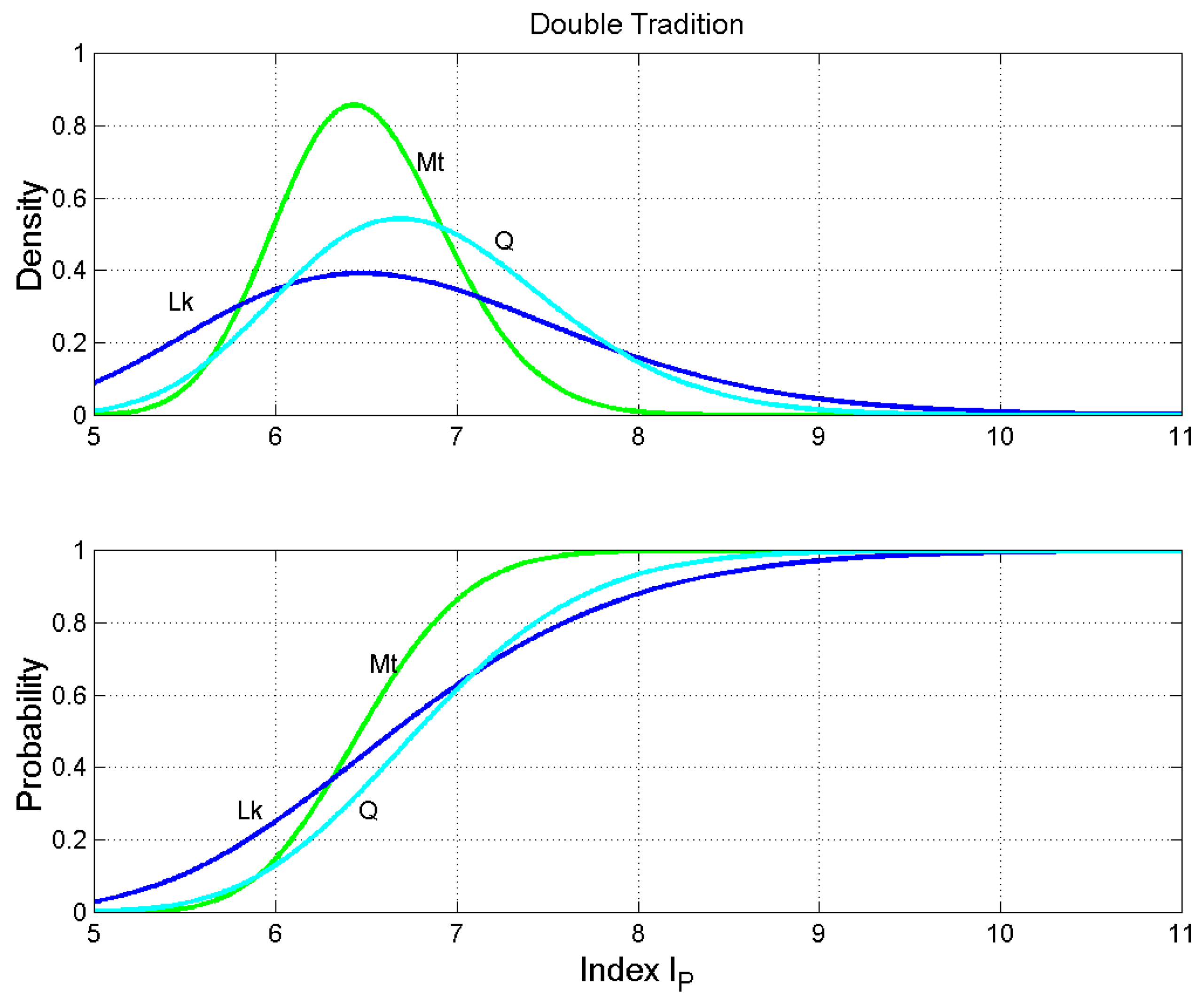
Figure 11.
Double Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of interpunctions per sentence. Matthew: green line; Luke: blue line; Proto–Luke: blue dashed line; Q: cyan line.
Figure 11.
Double Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of interpunctions per sentence. Matthew: green line; Luke: blue line; Proto–Luke: blue dashed line; Q: cyan line.
Figure 12.
Double Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per interpunctions (word interval). Matthew: green line; Luke: blue line; Q: cyan line.
Figure 12.
Double Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per interpunctions (word interval). Matthew: green line; Luke: blue line; Q: cyan line.
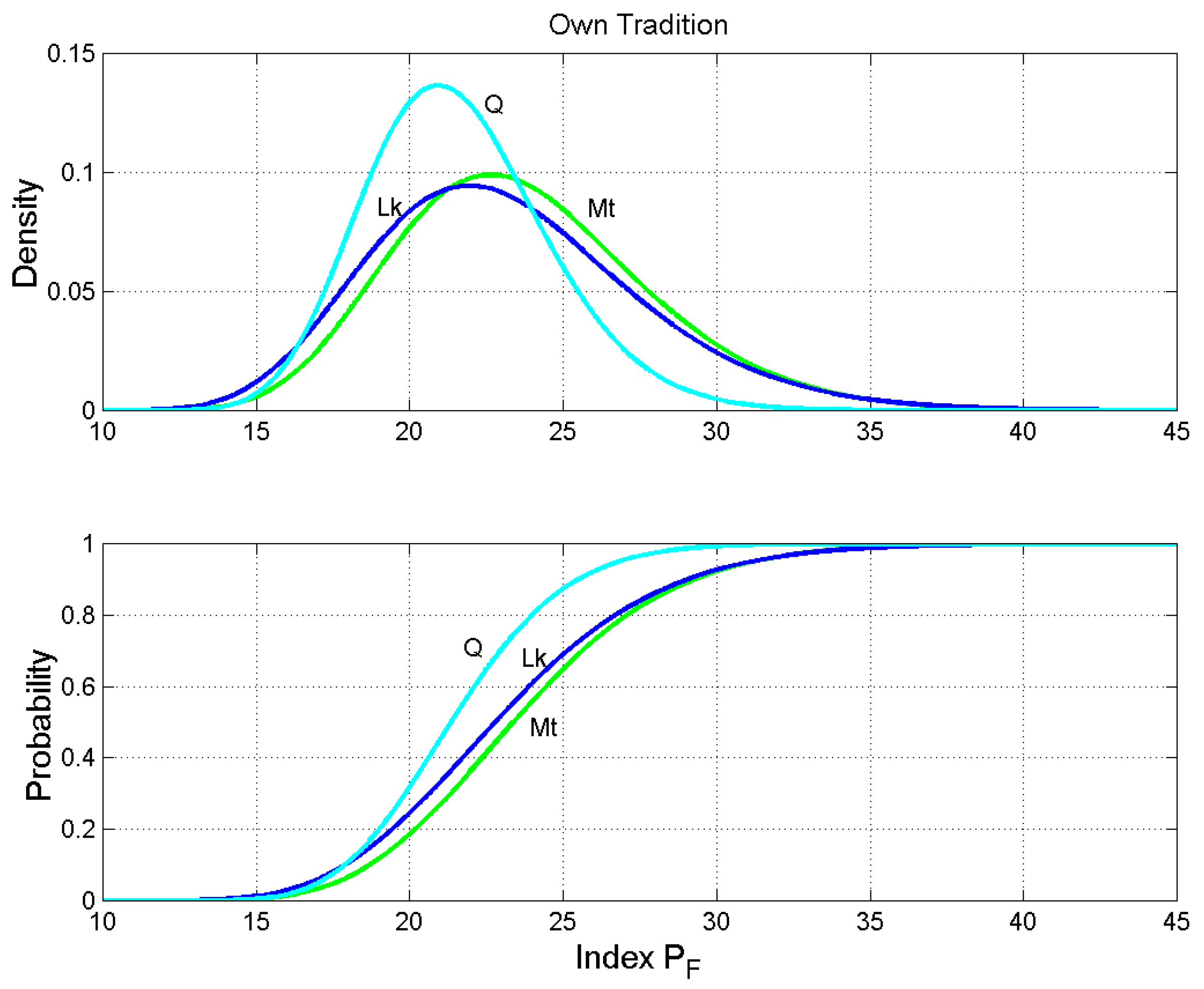
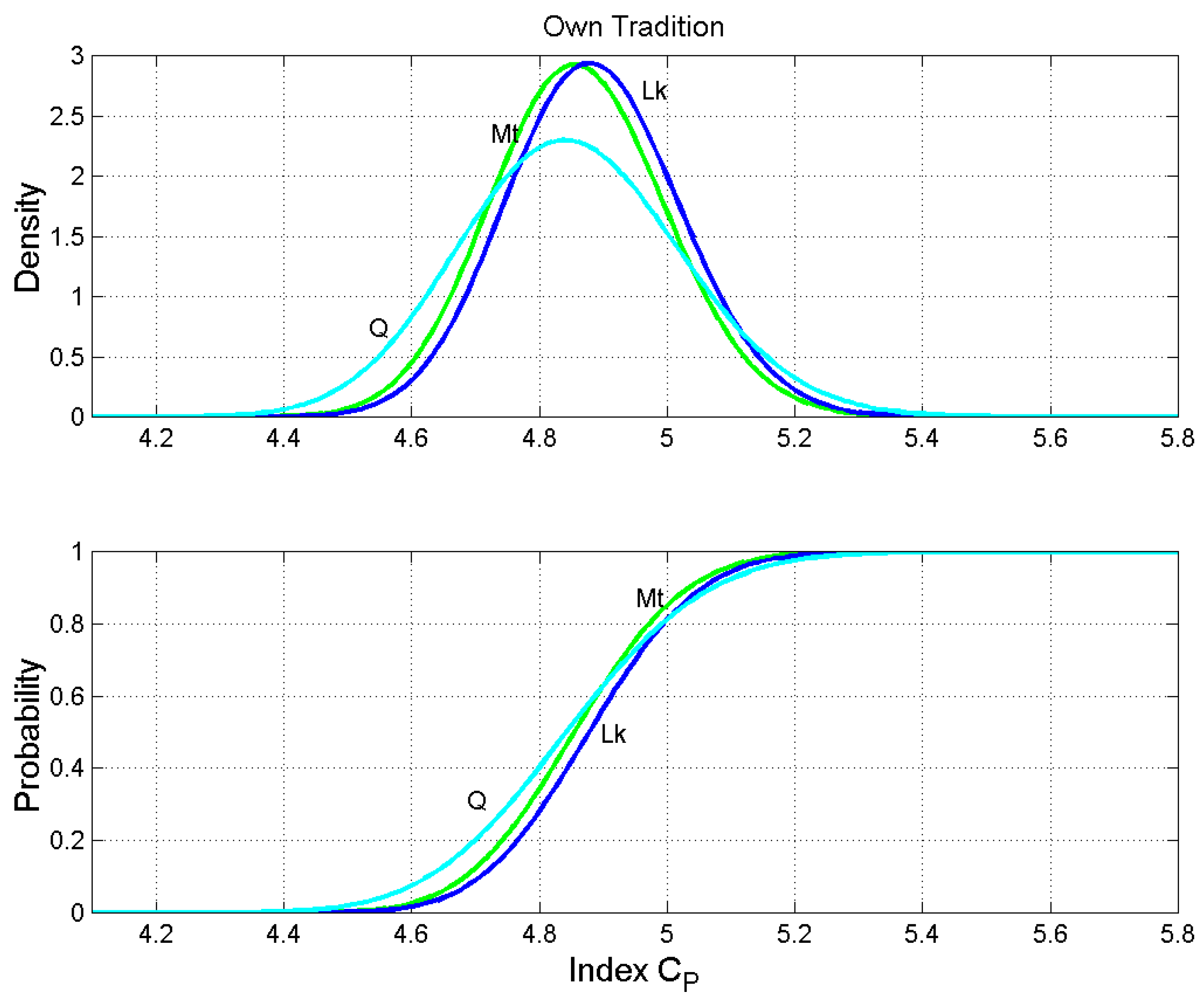
Figure 13.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Luke: blue line; Q: cyan line.
Figure 13.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per sentence. Matthew: green line; Luke: blue line; Q: cyan line.
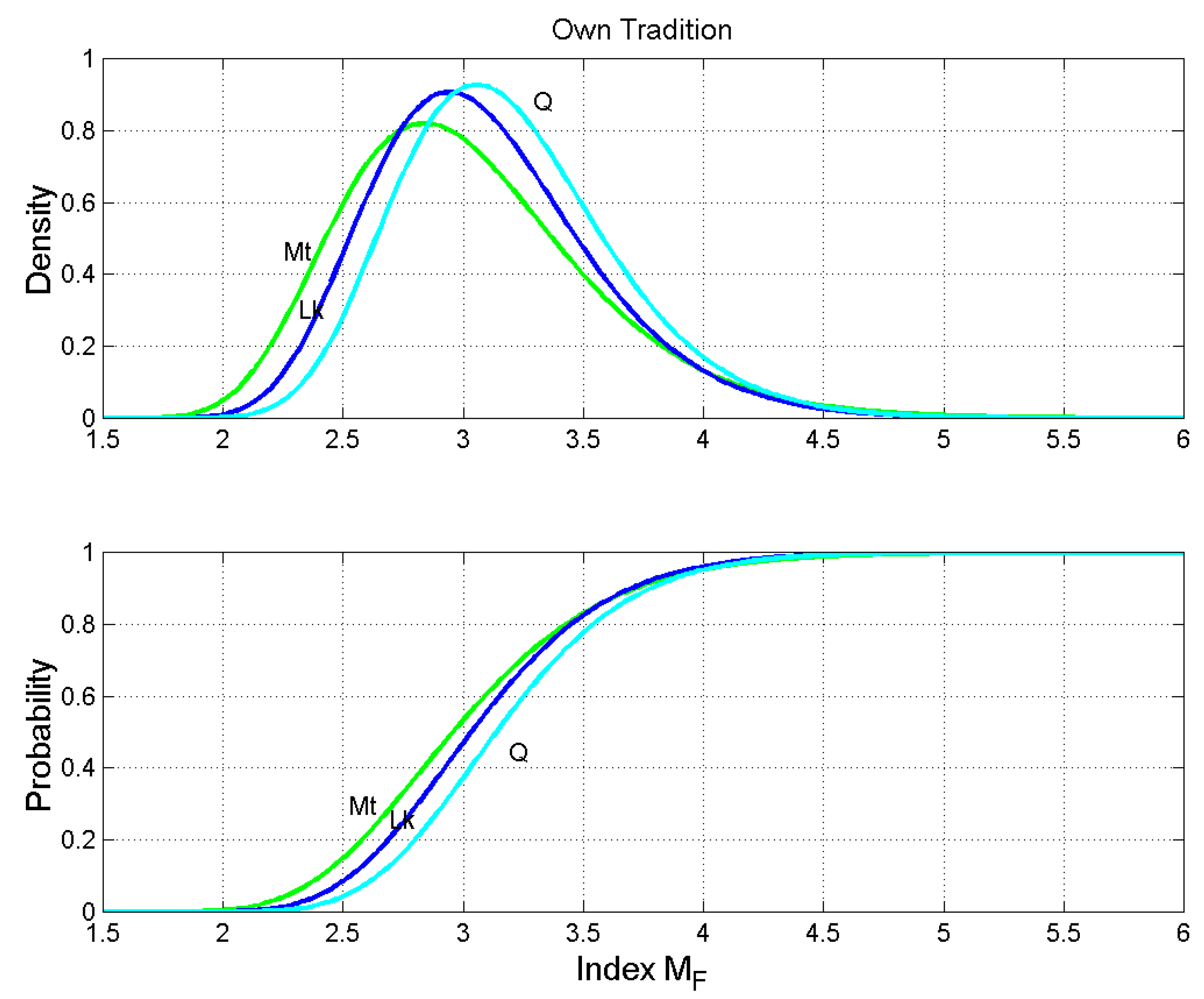
Figure 14.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of characters per word. Matthew: green line; Luke: blue line; Q: cyan line.
Figure 14.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of characters per word. Matthew: green line; Luke: blue line; Q: cyan line.
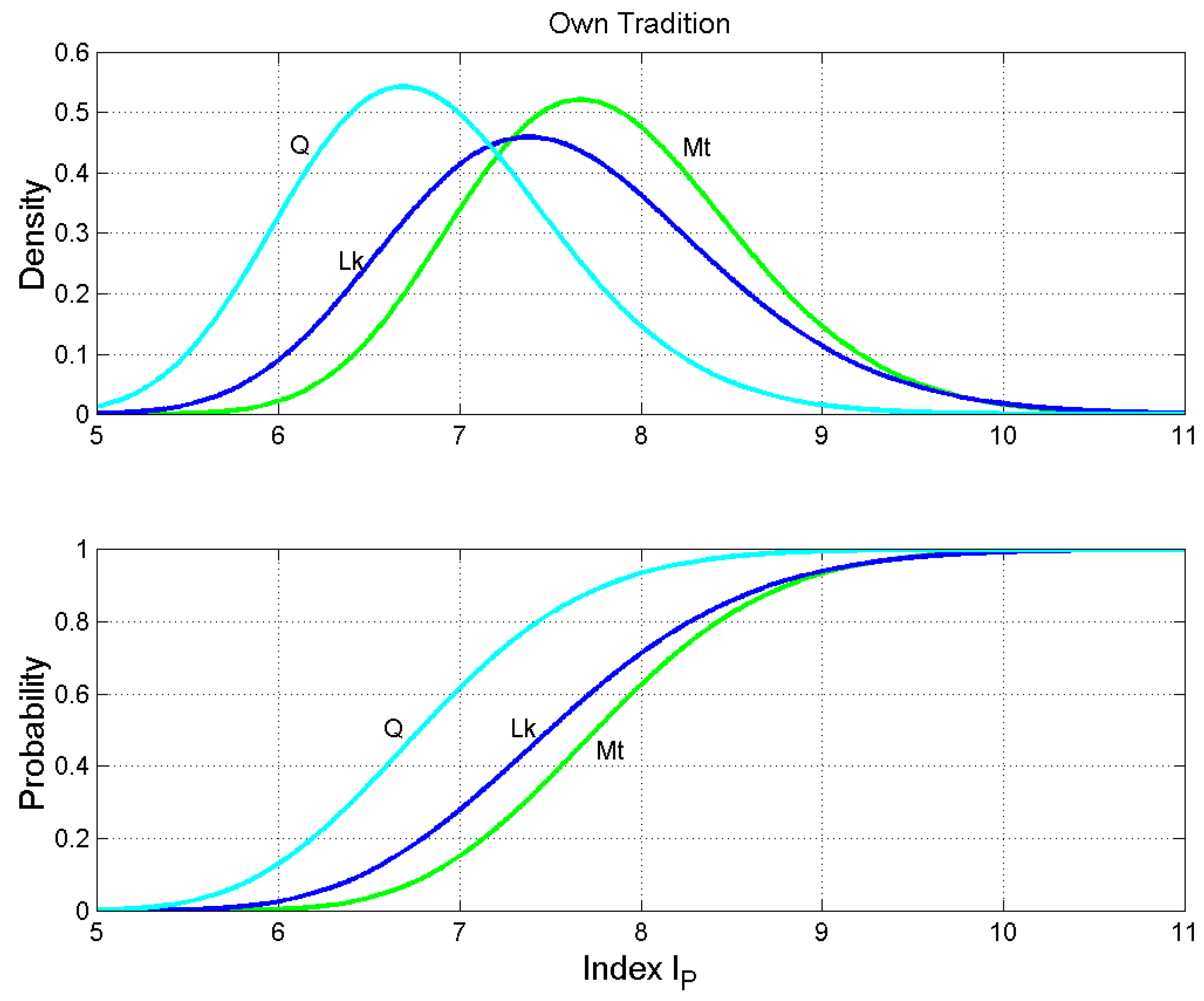
Figure 15.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of interpunctions per sentence. Matthew: green line; Luke: blue line; Q: cyan line.
Figure 15.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of interpunctions per sentence. Matthew: green line; Luke: blue line; Q: cyan line.
Figure 16.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per interpunctions (word interval) . Matthew: green line; Luke: blue line; Q: cyan line.
Figure 16.
Own Tradition. Probability density functions (upper panel) and probability distribution functions (lower panel) of the number of words per interpunctions (word interval) . Matthew: green line; Luke: blue line; Q: cyan line.
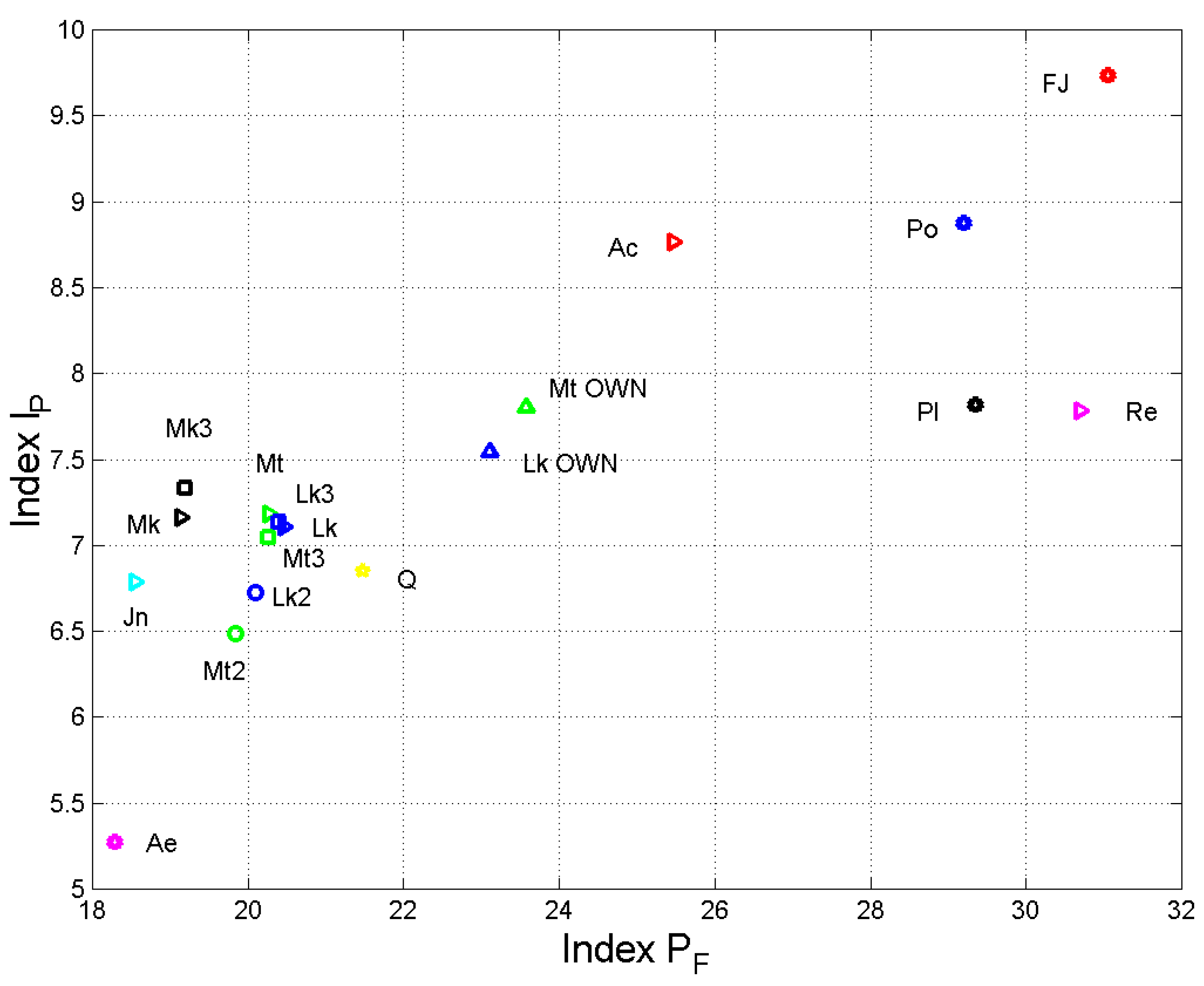
Figure 17.
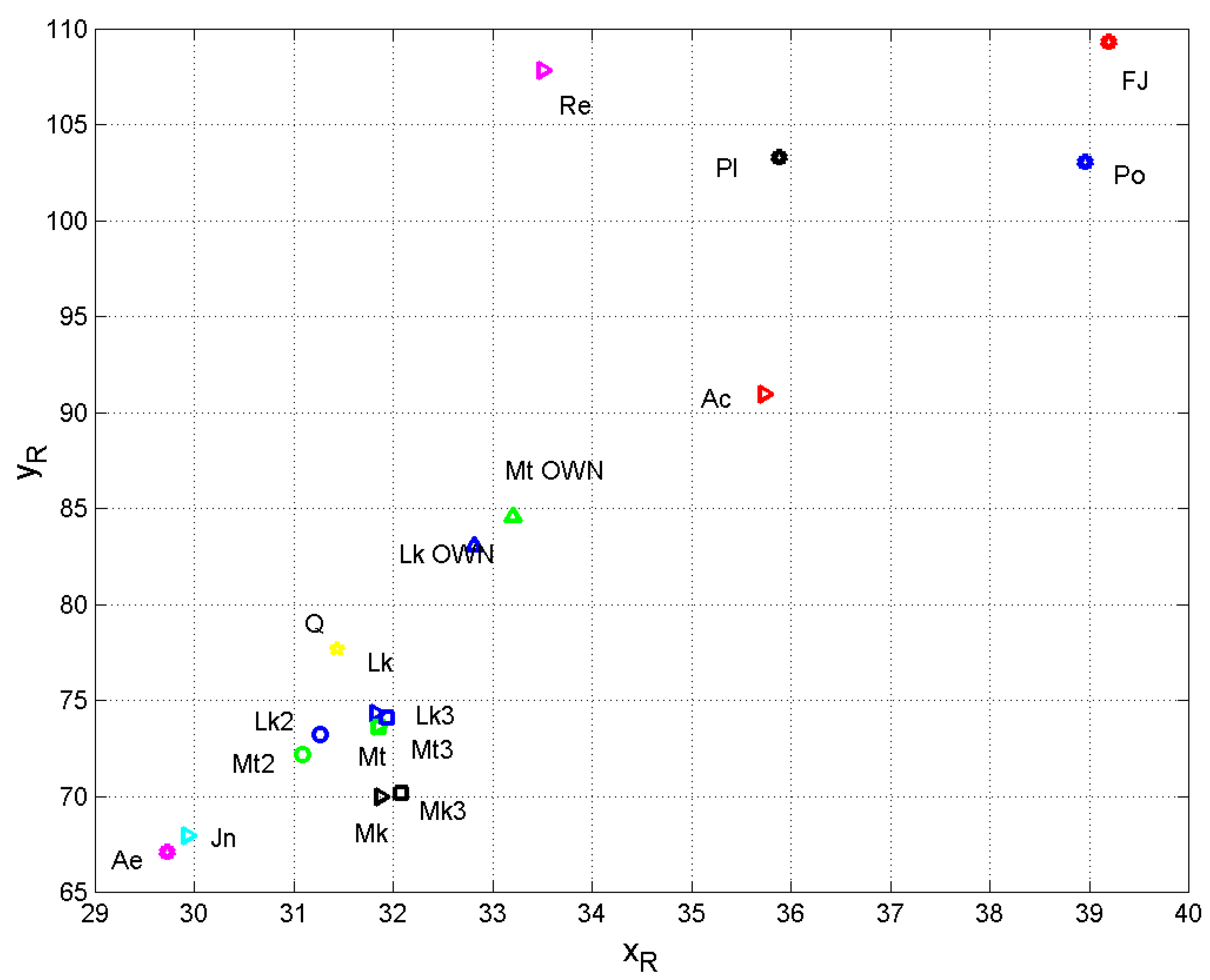
Average number of words per interpunctions, , versus the average number of words per sentence, . Triangles with vertex to the right refer to Full Texts. Squares refer to the Triple Tradition (e.g., Mt3). Circles refer to the Double Tradition (e.g., Mt2). Triangles with vertex up refer to the Own Tradition. Matthew: green; Mark: black; Luke: blue; John: cyan; Acts: red; Revelation: magenta; Q: yellow. Aesop (Ae): magenta star; Polybius (Po): blue star; Plutarch (Pl): black star; Flavius Josephus (FJ): red star.
Figure 17.
Average number of words per interpunctions, , versus the average number of words per sentence, . Triangles with vertex to the right refer to Full Texts. Squares refer to the Triple Tradition (e.g., Mt3). Circles refer to the Double Tradition (e.g., Mt2). Triangles with vertex up refer to the Own Tradition. Matthew: green; Mark: black; Luke: blue; John: cyan; Acts: red; Revelation: magenta; Q: yellow. Aesop (Ae): magenta star; Polybius (Po): blue star; Plutarch (Pl): black star; Flavius Josephus (FJ): red star.
Figure 18.
Coordinates and of the resulting vector (1) of the texts considered. Triangles with vertices to the right refer to Full Texts. Squares refer to the Triple Tradition (e.g., Mt3). Circles refer to the Double Tradition (e.g., Mt2). Triangles with vertices pointing up refer to the Own Tradition. Matthew: green; Mark: black; Luke: blue; John: cyan; Acts: red; Revelation: magenta; Q: yellow. Aesop (Ae): magenta star; Polybius (Po): blue star; Plutarch (Pl): black star; Flavius Josephus (FJ): red star.
Figure 18.
Coordinates and of the resulting vector (1) of the texts considered. Triangles with vertices to the right refer to Full Texts. Squares refer to the Triple Tradition (e.g., Mt3). Circles refer to the Double Tradition (e.g., Mt2). Triangles with vertices pointing up refer to the Own Tradition. Matthew: green; Mark: black; Luke: blue; John: cyan; Acts: red; Revelation: magenta; Q: yellow. Aesop (Ae): magenta star; Polybius (Po): blue star; Plutarch (Pl): black star; Flavius Josephus (FJ): red star.
Figure 19.
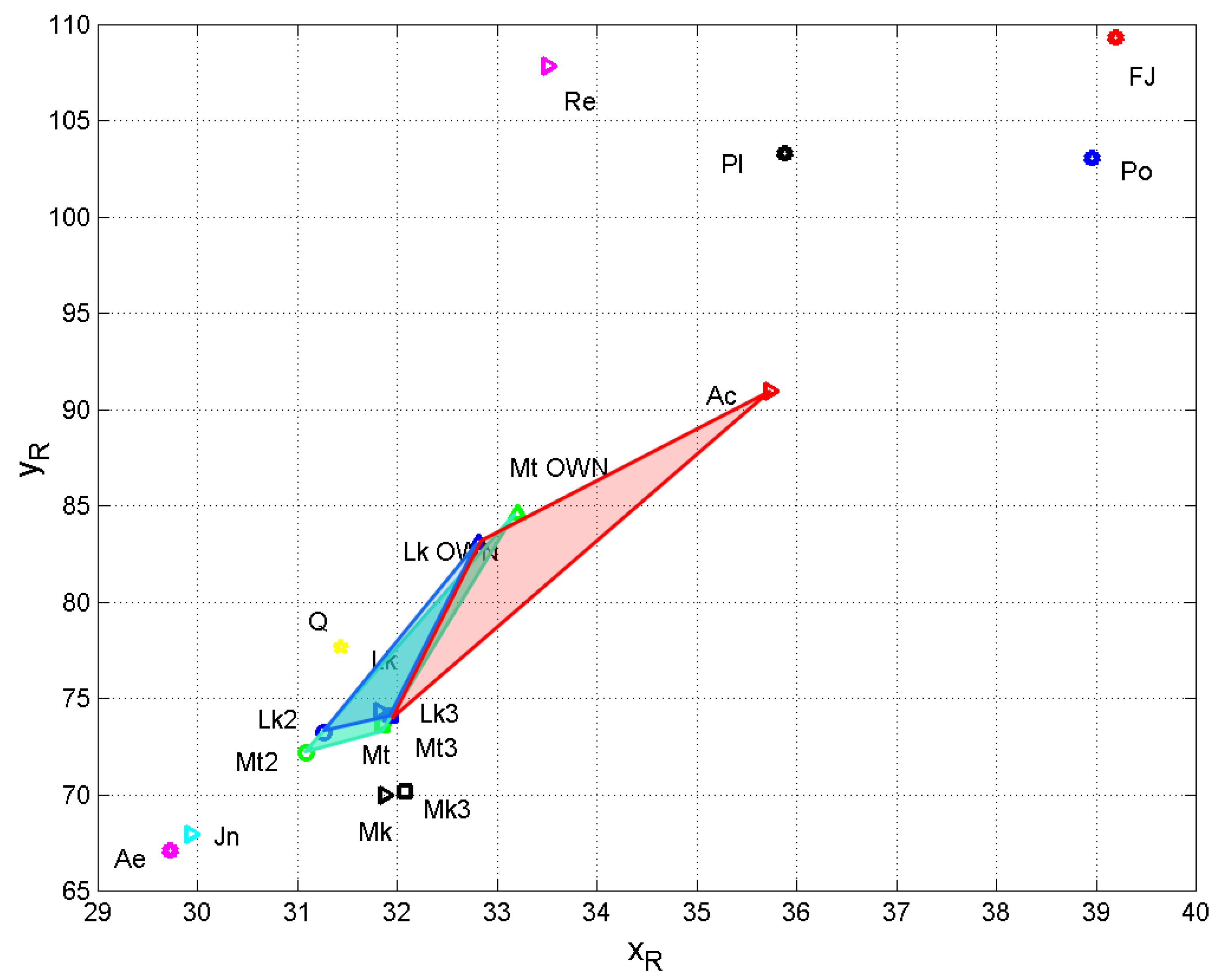
Coordinates
and
of the resulting vector (1) of the texts considered. Same symbols as
Figure 18. The green triangle refers to Matthew; the blue triangle refers to Luke. The red triangle extends Luke’s literary area (blue + red) to the Acts.
Figure 19.
Coordinates
and
of the resulting vector (1) of the texts considered. Same symbols as
Figure 18. The green triangle refers to Matthew; the blue triangle refers to Luke. The red triangle extends Luke’s literary area (blue + red) to the Acts.
Table 1.
List of the verses considered in Luke, in the indicated texts. The list of names (genealogy) in Verses 3.23–3.38 has not been considered in the statistical analyses.
Table 1.
List of the verses considered in Luke, in the indicated texts. The list of names (genealogy) in Verses 3.23–3.38 has not been considered in the statistical analyses.
| Luke Full Text | All Verses Except 3.23–3.38 (Genealogy) |
|---|
| Only in Luke (“Own”) | 1.1 et seq.; 2.1 et seq.; 7.11–17; 7.36–50; 8.1–3; 9.51–55; 10.1–12; 10.16–20; 10.29–42; 11.27–28; 12.13–20; 13.1–17; 14.1–14; 15.8–32; 16.1–15; 16.19–31; 17.11–19; 18.1–14; 19.1–10; 19.41–44; 24.13–53 |
| Matthew, Mark and Luke (“Triple Tradition”) | 3.1 et seq.; 4.1–30; 4.38–44; 5.1 et seq.; 6.1–19; 8.4–56; 9.1–48; 10.25–28;11.14–24; 11.29–33; 11.37–54; 12.33–48; 13.18–20; 14.34–35;16.18; 17.1–10; 17.20–37; 18.15–43; 19.28–40; 19.45–48; 20.1 et seq.; 21.5–37; 22.1 et seq.; 23.1 et seq.; 24.1–12 |
| Matthew and Luke (“Double tradition”) | 6.20–49; 7.1–10; 7.18–35; 9.57–62; 10.13–15; 10.21–24; 11.1–13; 11.34–35; 12.1–12; 12.22–32; 12.49–59; 13.22–35; 14.15–33; 15.1–7; 16.16–17; 19.11–27 |
| Q (Theory of the two sources) | 3.1–9; 3.15–17; 4.1–13; 6.20–23; 6.27–49; 7.1–10; 7.18–28; 7.31–35; 9.57–62; 10.1–16; 10.21–24; 11.1–4; 11.9–35; 11.39–52; 12.2–40; 11.42–46; 11.49–59; 13.18–21; 11.24–30; 11.34–35; 14.11–13; 14.16–35; 15.3–10; 16.13; 16.16–18; 17.1–4; 17.6; 17.23–37; 19.11–27; 22.28–30 |
Table 2.
List of the verses considered in Mark, in the indicated texts.
Table 2.
List of the verses considered in Mark, in the indicated texts.
| Only in Mark (“Own”) | 4.26–28; 7.31–37; 8.22–26;16.9–11 |
|---|
| Matthew, Mark and Luke (“Triple Tradition”) | Full text except the verses indicated in “Own” and “Dual Tradition” and Verses 1.1–1.17 (Genealogy) |
| Matthew and Mark (“Double Tradition”) | 4.33–34; 6.45–56; 7.1–30; 8.1–19; 11.12–14; 11.20–25; 14.3–9; 15.16–20 |
Table 3.
List of the verses considered in Matthew, in the indicated texts. The list of names (Genealogy) in Verses 1.1–1.17 17 has not been considered in the statistical analysis.
Table 3.
List of the verses considered in Matthew, in the indicated texts. The list of names (Genealogy) in Verses 1.1–1.17 17 has not been considered in the statistical analysis.
| Matthew Full Text | Except 1.1–1.17 |
|---|
| Only in Matthew (“Own”) | 1.1 et seq. (all chapter 1); 2.1 et seq.; 4.23–25 (from Verse 4.23 to Verse 4.25); 5.17–20; 5.27.37; 6.1–18; 9.35–38; 10.34–42; 12.15–21; 13.36–52; 17.24–27; 18.19–35; 20.1–16; 21.28–32; 25.31–46; 27.1–10;28.11–15 |
| Matthew, Mark and Luke (“Triple Tradition”) | 3.1 et seq.; 4.1–17; 5.13–16; 8.1–4;8.14–17; 8.23–34; 9.1–23; 10.1–33;12.1–14; 12.22–50; 13.1–35; 13.53–58; 14.1–21; 16.1 et seq.; 17.1–23; 18.1–10; 19.13–30; 20.17–34; 21.1–17; 21.23–27; 21.33–46; 22.15–46; 23.1–36; 24.1 et seq.; 26.1–5; 26.14–75; 27.11–26; 27.32–66; 28.1–10 |
| Matthew and Luke (“Double Tradition”) | 5.1–11; 5.21–26; 5.38–48; 6.19–34; 7.1 et seq.; 8.5–13; 8.18–22; 9.27–34; 11.1 et seq.; 18.12–18; 22.1–14; 23.37–38; 25.1–30 |
Table 4.
Full Texts. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The number between parentheses gives the standard deviation for text blocks of 500 words.
Table 4.
Full Texts. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The number between parentheses gives the standard deviation for text blocks of 500 words.
| Text | | | | |
|---|
| Matthew | 4.906 (0.157) | 20.27 (3.66) | 2.825 (0.413) | 7.182 (0.778) |
| Mark | 4.955 (0.182) | 19.14 (4.35) | 2.683 (0.693) | 7.165 (0.479) |
| Luke | 4.910 (0.134) | 20.47 (3.68) | 2.892 (0.419) | 7.105 (1.075) |
| John | 4.542 (0.169) | 18.56 (2.75) | 2.743 (0.336) | 6.785 (0.855) |
| Acts | 5.099 (0.280) | 25.47 (5.17) | 2.905 (0.467) | 8.766 (1.070) |
| Revelation | 4.658 (0.125) | 30.70 (5.78) | 3.970 (0.805) | 7.785 (0.721) |
Table 5.
Triple Tradition. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The numbers between parentheses give the standard deviations for text blocks of 500 words.
Table 5.
Triple Tradition. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The numbers between parentheses give the standard deviations for text blocks of 500 words.
| Text | | | | |
|---|
| Matthew | 4.958 (0.160) | 20.26 (3.08) | 2.888 (0.428) | 7.046 (0.573) |
| Mark | 4.929 (0.152) | 19.20 (2.50) | 2.628 (0.291) | 7.331 (0.640) |
| Luke | 4.931 (0.126) | 20.40 (2.84) | 2.871 (0.330) | 7.136 (0.687) |
Table 6.
Double Tradition. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The numbers between parentheses give the standard deviations for text blocks of 500 words.
Table 6.
Double Tradition. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The numbers between parentheses give the standard deviations for text blocks of 500 words.
| Text | | | | |
|---|
| Matthew | 5.009 (0.171) | 19.83 (3.26) | 3.085 (0.538) | 6.489 (0.470) |
| Luke | 4.906 (0.163) | 20.10 (2.43) | 3.095 (0.587) | 6.727 (1.060) |
Table 7.
Own Tradition. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The numbers between parentheses give the standard deviations for text blocks of 500 words.
Table 7.
Own Tradition. Average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals) , words per interpunctions (word interval) . The numbers between parentheses give the standard deviations for text blocks of 500 words.
| Text | | | | |
|---|
| Matthew | 4.855 (0.137) | 23.57 (4.20) | 3.043 (0.529) | 7.800 (0.777) |
| Luke | 4.884 (0.136) | 23.12 (4.44) | 3.074 (0.468) | 7.545 (0.888) |
Table 8.
Full Texts. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical. For example, the confidence level that the number of words per sentence, , in Mark and Luke are not identical is 1.25%, therefore the two probability distributions are, in effect, indistinguishable. The confidence level that the number of characters per word, , in Mark and Luke are not identical is 29.25%, therefore the two probability distributions are not very different, thus indicating that the words contained in their dictionary are of about the same length. The root mean square (RMS) value is calculated as follows. Example, Luke’s .
Table 8.
Full Texts. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical. For example, the confidence level that the number of words per sentence, , in Mark and Luke are not identical is 1.25%, therefore the two probability distributions are, in effect, indistinguishable. The confidence level that the number of characters per word, , in Mark and Luke are not identical is 29.25%, therefore the two probability distributions are not very different, thus indicating that the words contained in their dictionary are of about the same length. The root mean square (RMS) value is calculated as follows. Example, Luke’s .
| Text | Matthew | Mark | Luke | John | Acts | Revelation | RMS |
|---|
| Matthew | 0 | 29.65 | 9.92 | 99.98 | 94.41 | 98.68 | 76.97 |
| Mark | 45.49 | 0 | 28.41 | 99.95 | 65.70 | 99.18 | 71.87 |
| Luke | 1.25 | 52.70 | 0 | >99.99 | 95.61 | 99.63 | 77.42 |
| John | 80.25 | 36.83 | 85.81 | 0 | >99.99 | 74.21 | 95.39 |
| Acts | 99.91 | 99.92 | 99.89 | 99.99 | 0 | 99.92 | 92.04 |
| Revelation | >99.99 | >99.99 | >99.99 | 99.99 | 97.57 | 0 | 94.86 |
| RMS | 75.49 | 72.37 | 77.61 | 83.85 | 99.46 | 99.52 | |
Table 9.
Full Texts. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
Table 9.
Full Texts. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
| Text | Matthew | Mark | Luke | John | Acts | Revelation | RMS |
|---|
| Matthew | 0 | 82.94 | 9.63 | 24.32 | 22.74 | >99.99 | 60.13 |
| Mark | 30.51 | 0 | 89.89 | 81.70 | 89.72 | 99.99 | 89.09 |
| Luke | 39.61 | 77.86 | 0 | 48.89 | 6.13 | >99.99 | 64.19 |
| John | 78.00 | 94.17 | 45.87 | 0 | 65.71 | >99.99 | 69.25 |
| Acts | >99.99 | >99.99 | >99.99 | >99.99 | 0 | >99.99 | 67.71 |
| Revelation | 92.22 | 96.74 | 96.61 | 99.74 | 99.07 | 0 | >99.99 |
| RMS | 73.60 | 83.93 | 76.25 | 86.03 | 99.81 | 96.91 | |
Table 10.
Triple Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
Table 10.
Triple Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
| Text | Matthew | Mark | Luke | Q | RMS |
|---|
| Matthew | 0 | 15.03 | 22.10 | 63.87 | 39.97 |
| Mark | 46.21 | 0 | 6.61 | 40.26 | 25.10 |
| Luke | 3.03 | 50.66 | 0 | 58.28 | 36.19 |
| Q | 34.83 | 78.80 | 26.27 | 0 | 55.07 |
| RMS | 33.45 | 60.31 | 32.99 | 52.00 | |
Table 11.
Triple Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
Table 11.
Triple Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
| Text | Matthew | Mark | Luke | Q | RMS |
|---|
| Matthew | 0 | 81.58 | 7.70 | 67.98 | 61.47 |
| Mark | 54.01 | 0 | 81.40 | 74.24 | 79.15 |
| Luke | 14.65 | 23.57 | 0 | 11.31 | 47.66 |
| Q | 37.56 | 72.01 | 39.76 | 0 | 58.50 |
| RMS | 38.91 | 53.72 | 27.99 | 52.21 | |
Table 12.
Double Tradition. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
Table 12.
Double Tradition. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
| Text | Matthew | Luke | Q | RMS |
|---|
| Matthew | 0 | 27.74 | 60.03 | 46.76 |
| Luke | 9.43 | 0 | 15.05 | 22.32 |
| Q | 36.82 | 28.66 | 0 | 43.76 |
| RMS | 26.88 | 21.33 | 32.99 | |
Table 13.
Double Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
Table 13.
Double Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
| Text | Matthew | Luke | Q | RMS |
|---|
| Matthew | 0 | 0.50 | 11.73 | 8.30 |
| Luke | 29.70 | 0 | 11.71 | 8.29 |
| Q | 37.38 | 11.31 | 0 | 11.72 |
| RMS | 33.76 | 22.47 | 27.62 | |
Table 14.
Own Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
Table 14.
Own Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
| | Matthew | Luke | Q | RMS |
|---|
| Matthew | 0 | 3.77 | 4.87 | 4.35 |
| Luke | 3.34 | 0 | 16.77 | 12.15 |
| Q | 37.50 | 34.26 | 0 | 12.35 |
| RMS | 26.62 | 24.34 | 35.92 | |
Table 15.
Own Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
Table 15.
Own Tradition and Q. Kolmogorov–Smirnov test results for (below the diagonal of zeros) and (above the diagonal). The values reported are the confidence level (%) that the indicated couple of probability distributions are not identical.
| Text | Matthew | Luke | Q | RMS |
|---|
| Matthew | 0 | 5.47 | 20.89 | 15.27 |
| Luke | 14.73 | 0 | 10.30 | 8.25 |
| Q | 83.91 | 73.90 | 0 | 16.47 |
| RMS | 60.24 | 53.28 | 79.06 | |
Table 16.
Confidence levels (%) for the indicated Traditions (only Matthew and Luke).
Table 16.
Confidence levels (%) for the indicated Traditions (only Matthew and Luke).
| Tradition | | | | | RMS |
|---|
| Triple Tradition | 3.03 | 22.10 | 7.70 | 14.65 | 13.89 |
| Double Tradition | 9.43 | 27.74 | 0.50 | 29.70 | 20.86 |
| Own Tradition | 3.34 | 3.77 | 5.47 | 14.73 | 8.25 |
| RMS | 6.03 | 20.59 | 5.46 | 20.93 | |
Table 17.
Examples of classical Greek literature. Totals of characters, words, sentences; average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals, words per interpunctions (word interval) . The number between parentheses gives the standard deviation for text blocks of 500 words.
Table 17.
Examples of classical Greek literature. Totals of characters, words, sentences; average number of characters per word , words per sentence , interpunctions per sentence (also, number of word intervals, words per interpunctions (word interval) . The number between parentheses gives the standard deviation for text blocks of 500 words.
| Author | Characters | Words | Sentences | | | | |
|---|
| Polybius | 1,530,968 | 256,495 | 8830 | 5.969 (0.438) | 29.19 (7.45) | 3.302 (1.200) | 8.877 (1.975) |
| Plutarch | 2,750,711 | 499,683 | 17,905 | 5.505 (0.362) | 29.35 (22.81) | 3.730 (2.288) | 7.815 (2.428) |
| Flavius Josephus | 670,313 | 121,717 | 4004 | 5.507 (0.218) | 31.05 (7.61) | 3.199 (0.657) | 9.737 (1.523) |
| Aesop | 204,913 | 39,122 | 2172 | 5.238 (0.167) | 18.29 (3.34) | 3.463 (0.511) | 5.275 (0.382) |