1. Introduction
Following the introduction of Buddhism to the Korean Peninsula in 372 CE,
1 the pagodas of the Koguryŏ, Paekche, and Silla Kingdoms followed a unique formative system such as square and octagonal shapes. The Korean stone pagodas were transformed in several evolutionary phases starting with an imitation of the wooden pagodas in the Three Kingdoms period. The Koguryŏ pagodas were built as octagonal wooden constructions. Paekche-style and Silla-style pagodas are intimately associated with the territories of the Paekche and the Silla Kingdoms, respectively (
Chang 1996, p. 66).
After unification in the seventh century, newly constructed pagodas in the old Paekche territories were transformed into the wider expansion of Silla-style pagodas. The stone-brick pagoda at the temple of Punhwangsa (芬皇寺) is among the earliest pagodas in existence (
Chang 1990, p. 75). The stone pagodas at the Mirŭksa (彌勒寺) and Chŏngnimsa (定林寺) Temples are considered to be the earliest Paekche-style pagodas, but experts still have not agreed on their construction dates (
Kim 1984, pp. 2–6)
2. As the early stone pagodas are considered to have been transformed from wooden pagodas, details that originated with the timber-framed architecture appear in the expression of the stone members, and the construction methods are the same as those used for wood (
Kim 2011, pp. 198–99;
Kim and Park 2017, pp. 32–33).
In the case of the typical Paekche-style stone pagoda at the Mirŭksa Buddhist Monastery, pillars, transverse beams, and bracket sets are elaborately expressed with the abstract conversion of wooden members in stone, preserving the construction methods of wooden buildings into the transformation process from wood to stone materials (
Kim 2011, pp. 198–99). The stonework imitates a wooden structure, and stone cantilevers of the pagoda are slightly curved upwards. In contrast, the Punhwangsa Buddhist Monastery has a Silla-style stone pagoda that was built by cutting and trimming each stone into a brick shape; this does not imitate a wooden construction method but uses a typical way to set up a stone pagoda.
There is a wealth of research about the mathematical analysis of formative systems and design principles in stone pagodas. However, we have only design theories about how stone pagodas are shaped; nobody has yet proved these theories clearly. This study attempts to do so with an approach distinct from previous research. Rather than relying on the analysis of measurements, this study pays interpretative attention to the proportional composition regarding the vertical heights and horizontal widths of the stone members of three parts: kidan (foundation), t’apsin (pagoda body), and sangnyun (finial). Based on analysis through geometric and mathematical interpretation of the scale, height, and width of the layers that gradually diminish, this research shows that the two stone pagodas examined were built based on the proportional system and design principles drawing on the square root of 2 (√2).
1.1. Existing Studies on the Proportional System of Stone Pagodas on the Korean Peninsula
Studies on the stone pagodas of Korea began with surveys of ancient art and historic sites by Japanese scholars at the turn of the twentieth century. In an article in 1912, architectural historian Tadashi Sekino, quoting the
Samguk Sagi (三國史記) [Chronicles of the Three Kingdoms] and the
Tonggug Yŏji Sŭngnam (東國輿地勝覽) [Augmented Survey of the Geography of Korea], wrote that the Buddhist pagoda at the Mirŭksa Temple was the oldest pagoda in Korea (
Sekino 1941, pp. 512–74).
3 Gaijiro Fujishima, citing the
Samguk Yusa (三國遺事) [Memorabilia of the Three Kingdoms] and the
Tonggug Yŏji Sŭngnam, estimated the total height of the nine-story Mirŭksa pagoda as eighty
ch’ŏk (
chi, Ch.), the Tang cubit measured using a Tang ruler, the reference scale of the Tang Dynasty (
Fujishima 1930, pp. 530–36). Karube Jion (1897–1970), investigating the Mirŭksa Pagoda, found that the height and length of the stones filling the frame decreases from the bottom to the top by comparing it with a stable structure, the five-story pagoda at Chŏngnimsa Temple, and then estimated the Mirŭksa Pagoda as a seven-story pagoda (
Karube 1946). Sugiyama Nobuzo saw the Mirŭksa Pagoda as an intermediate stage between wood and stone pagodas (
Sugiyama 1944).
Since 1945, there have been significant studies by Korean scholars as well. In the
Chosŏn t’app’a Yŏn’gu [Research on Chosŏn Pagodas], Ko Yusŏp (1905–1944) also asserted that the Mirŭksa Pagoda was originally built with seven stories, as Karube had stated. Based on a proportional system, Im Yŏngbae’s study on “the design principles of pagoda architecture between Korea and Japan” also postulated the seven-story Mirŭksa Pagoda; he pointed out that the width of the body stone of each side steadily decreases, corresponding to one-tenth of the main central bay as a standard unit for stonemasonry, comparable to the wooden pagoda at Horyuji Temple in Japan (
I 1982, pp. 17–26). The overall width of each roof stone was gradually reduced by 2.5
ch’ŏk(
≒87.5 cm), according to the Koryŏ cubit from the first floor (30
ch’ŏk≒1050 cm). The Koryŏ cubit is based on the Koguryŏ ruler, the reference scale of the Koguryŏ Kingdom; the seventh floor was calculated to be 15
ch’ŏk (Koryŏ cubits,
≒525 cm). Its height was restored to 40.25
ch’ŏk (Koryŏ cubit, ≒1408.75 cm), decreasing every 0.2
ch’ŏk (Koryŏ cubit) up to the seventh floor. Yoneda Miyoji (d. 1942)’s measurement survey found that the
ch’ŏk unit employed to erect the pagoda at the Chŏngnimsa Temple was the Koryŏ cubit, which is about 35 cm long. He concluded that the width of the square platform of the pagoda was 14
ch’ŏk (
≒490 cm), and that 7
ch’ŏk (
≒245 cm), half width of the platform were used as the basic measure for the construction of this pagoda. Through the measurement survey of each member, these evidences reveal that the total height of the body and roof stones at the first floor is 7
ch’ŏk, and that the width of the body stone at the first floor is 7
ch’ŏk, in addition to that the height and the width of the foundation stone is each 3.5
ch’ŏk (
≒122.5 cm) and 10.5
ch’ŏk (
≒367.5 cm), which adds 7
ch’ŏk to 3.5
ch’ŏk. That is to say, Yoneda proved that the pagoda was constructed according to the principle of equivalent division with 7
ch’ŏk (
Yoneda 1976, pp. 107–22).
1.2. Research Methods and Scope
This research does not treat the Mirŭksa Pagoda as the earliest of the Paekche-style pagodas and the Punhwangsa Pagoda as the earliest of the Silla-style pagodas. The Mirŭksa Pagoda is still embroiled in controversy regarding its original construction and size because half the pagoda was destroyed by the 1910s. Japanese artisans repaired the Punhwangsa Pagoda, restoring three stories in 1915. There are still debates on whether the original height was seven or nine stories. The priority of research objects takes note of stone pagodas with a relatively complete appearance because they are useful for identifying the proportional systems and mathematical formulas of early stone pagodas and for drawing precisely measured data. Since the Koguryŏ stone and wood pagodas have no precisely measured drawings, they were excluded from this study. Instead, this research focuses on the five-story stone pagoda at the Chŏngnimsa Temple and the three-story stone pagoda at the Kamŭnsa Temple, both of which have been conserved in complete and authentic condition in their entire form (
Figure 1 and
Figure 2).
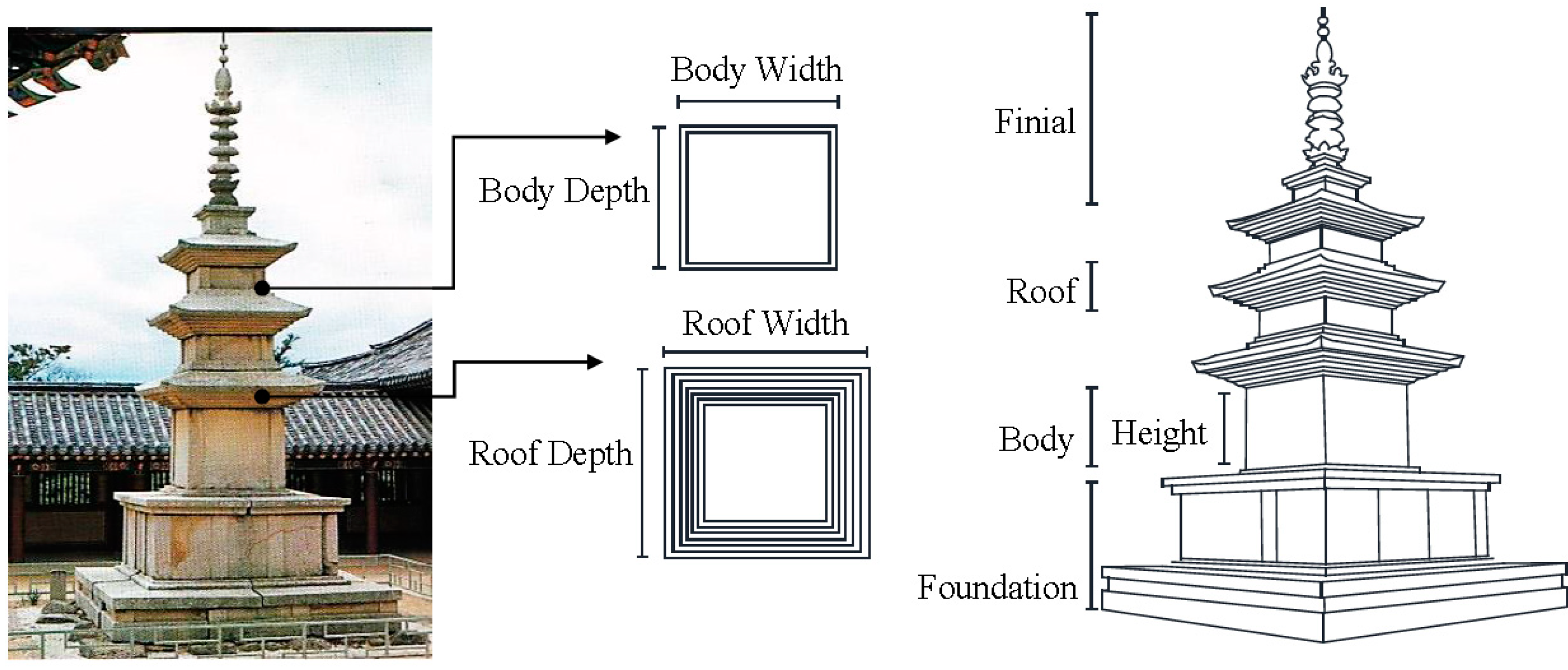
These two pagodas are composed of three parts;
kidan (foundation),
t’apsin (pagoda body), and
sangnyun (finial). The
kidan foundation contains dual bases that consist of an upper and a lower platform; the
t’apsin pagoda body is composed of multiple layers with roof and body stones; and the
sangnyun finial consists of a dew plate (
noban), an overturned bowl (
pokbal), and a central pillar adorning the top (
ch’alchu). In the pagoda body, particularly, the width and depth of the body and roof stones are interchangeable since they effectively have the same length in the square plane (
Figure 1,
Figure 2 and
Figure 3).
To find the mathematical grounds based upon the records of the
Samguk Sagi, this study reviewed the contents of the
Jiuzhang Suanshu (九章算術) [The Nine Chapters on the Mathematical Art] to recognize mathematical thoughts and design principles.
4 It then examined how arithmetic and geometric concepts in ancient mathematics and astronomy were applied to the construction of the stone pagodas by referring to the contents of the
Zhoubi Suanshu (周髀算經) [The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven], one of the oldest mathematics books in East Asia.
2. Discussing the Points at Issue in Jiuzhang Suanshu and Zhoubi Suanjing
The
Zhoubi Suanjing is generally considered the oldest of the mathematical classics in ancient China since the
Jiuzhang Suanshu is much fuller and represents a much more advanced state of mathematical knowledge than the
Zhoubi.
5 As the safest assumption on the publication date, if the
Zhoubi is considered as a Zhou nucleus with Former Han accretions, then the
Jiuzhang is a Chin and Former Han book with Later Han accretions (
Needham 1959, pp. 19–24). The
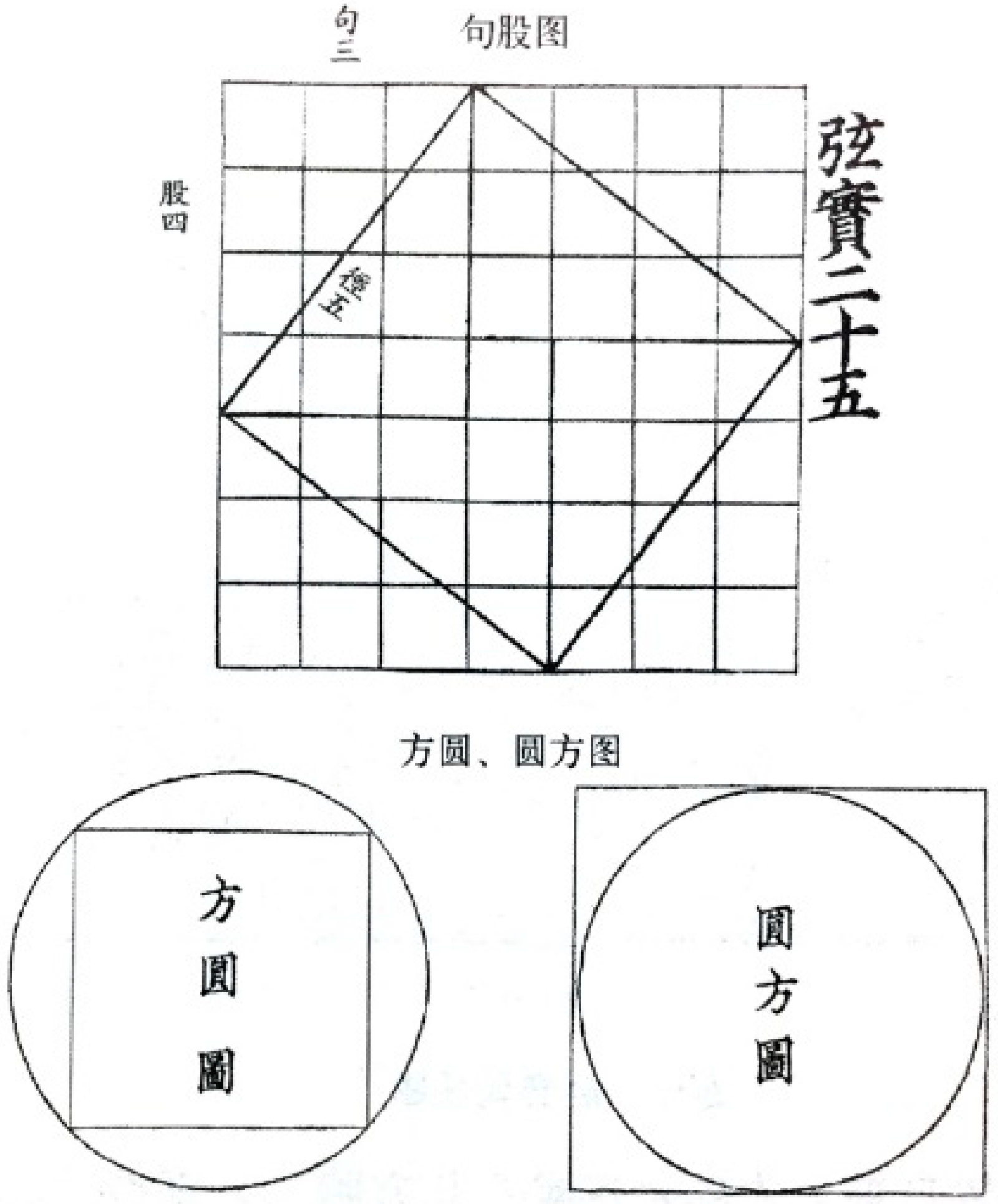
Jiuzhang Suanshu provides problems on length, proportion, geometric and arithmetic progression, and algebraic equations in its nine chapters. Among them, Chapter 1 contains the problem for finding lengths and widths related to various shapes of farm fields with “
Fangtian (方田) [Square Fields]” and combines stereographic and planar geometry such as square, rectangle, isosceles, trapezoids, and circles. Chapter 3, “
Shuaifen (衰分) [Distributions by Proportions],” covers problems in each quota associated with geometric and arithmetical progressions, all solved by proportion, as well as the distribution of property and money according to prescribed rules. Chapter 9 discusses “
Gougu (句股) [Base and Altitude],” or the Pythagorean Theorem, in reference to a right-angled triangle, where the
gou is the base, the
gu is the height, and the
xian is the hypotenuse that joins the
gou and
gu. The first passage of the introduction says this:
“In old days, Fuxi painted a
bagua (eight trigrams) in remote antiquity to acquire honorable virtues of the gods and resemble the state of all things. He joined changes about a number of strokes of a divinatory sign by making up a multiplication table” (昔在庖犧氏始畫八卦,以通神明之德,以類萬物之情,作九九之術,以合六爻之變) (
Guo 2009, p. 2).
This indicates that the changes of the bagua explain the circumstance of all things, and that those that “communicate the virtues of the gods” prove mathematics as a symbolic number, and those that “parallel the condition of all things” represent an important function of Chinese traditional mathematics.
“Nevertheless, the methods have been handed down from generation to generation, and we draw the figures with the carpenter’s compass, L-shaped try square and gnomon in measurement” (至于以法相传,亦犹规矩度量可得而共) (
Guo 2009, p. 7).
The book’s next passage talks about the method of mathematics, where the “law (
fa)” shows the mathematical method. The “regulation (
gui)” indicates devices for drawing a circle with a compass, and “try square (
ju)” points out tools used to make a square with an L-shaped try square. These represent the tools for drawing circles and squares, respectively. The “measurement (
duliang)” represents weights and measures and uses the method to calculate length, volume, and weight of all things in the world, reflecting the numerical relation of countless things. In other words, specifications and measurements indicate the relationship between spatial format and quantity. In ancient China, the geometrical methods related to numbers and amounts solve problems through arithmetic and algebras (
Figure 4).
Meanwhile, the
Zhoubi Suanjing is the first of ten classical works of ancient Chinese mathematics named the
Suanjing Shishu that were collected for use in the State Academy of the Tang Dynasty in 656 CE. As mentioned above, it is a safe assumption that the
Zhoubi Suanjing was published in the Western Han Dynasty in the first century BCE (
Ch’a 2006, p. 475). Zhao Shuang rewrote the text in the third century CE in the southern state of Wu, one of the Three Kingdoms into which China was divided at the end of the Han Dynasty. In the sixth century, Zhen Luan supplemented the text by finding every instance in the main text or in Zhao’s commentary where calculations took place and adding detailed workings; he held office under the Northern Zhou Dynasty (557–581 CE). Li Shunfu commented and corrected Zhao Shuang’s first commentary and Zhen Luan’s illustrative calculations during the Tang era. The book includes the Section of Shang Gao on classical mathematics, the Section of Chen Zi on mathematics and astronomy, and the Section of
Zhoubi astronomy on
Zhoubi’s theorem. One of the most remarkable assertions in the Shang Gao Section is that the circle and square are the rudimentary shapes of heaven and earth, as told through a dialogue between the Duke of Zhou (周公) and his minister Shang Gao(商高). Here is what Shang Gao said:
The laws for these numbers come from the circle and the square. The circle comes from the square, the square comes from the carpenter’s try square, and the try square comes from [the fact that] nine nines are eighty-one (商高曰,數之法出於圓方. 圓出於方,方出於矩,矩出於九九八十一) (
Chen 2012, p. 3).
In that the patterns of these numbers come from circles and squares, Shang Gao indicates that they represent mathematical methods through the arithmetical properties of circles and squares. The Duke of Zhou replies that they came out of mathematical thought during the Xia and Shang times. Since what the Duke of Zhou asked about was heaven and earth, Shang Gao set out the shapes of circles and squares to represent their counterparts, in line with ancient Chinese thought on production and life, together with religion, scientific activity, and philosophical thought. The circles and the squares are elements of basic geometry and are in opposition to each other, but it is possible to switch them by contraries. Likewise, the section of the Sang Gao mentions similar contents relevant to circles and squares repeatedly, expounding that the square belongs to the earth, and the circle belongs to the heavens because the heavens are round and the earth is square. The number of squares is considered as an underlying form, and the circles come from the squares (方屬地, 圓屬天, 天圓地方. 方數為典, 以方出圓).
In addition, Shang Gao talked with the Duke of Zhou about the methods used by the Great Yu, who was the patron saint of hydraulic engineers and all those concerned with water-control, irrigation, and conservancy, in governing the world derived from the numbers. When the Duke of Zhou asked the method for the use of the right-angled triangle, Shang Gao told him that the plane right-angled triangle (laid on the ground) serves to lay out (works) straight and square (by the aid of) cords. The revolution of a right-angled triangle (compass) may make a circle, while the synthesis of the right-angled triangle and the reversed form squares (oblongs) as a result. This reference of the Great Yu indicates the ancient demand for mensuration and applied mathematics (
Figure 5).
The last part of Shang Gao’s Section says the following:
Whoever knows the earth is a wise man, and whoever knows heaven is a sage. Knowledge is derived from the straight line, and the straight line comes from the right angle try square. The amalgamation of the right-angle try square with numbers is what guides and rules ten thousand things (是故, 知出者智, 知天者聖. 智出於勾, 勾出於矩. 夫矩之於數, 其載制萬物, 惟所為耳).
This passage shows in concrete terms that the straight line indicates the shadow reflected from the declination of the sun at the different times of the year, showing the paths and roads of the heavens, while the right-angle try square designates the gnomon with markings. It is intimately related to the original meanings of the words of
zhou (周) and
bi (髀). The word
zhou refers to the circular paths of the heavens, while the word
bi means counting-rods made of bone, indicating that a gnomon was used for the measurement by proportions of height and distances, both terrestrial and celestial (
Li 1978, p. 55). Likewise, in terms of
Fangshu Weidian (方數為典), the square is regarded as an arithmetic standard because it controls all things and can be transformed into a variety of shapes (
Chen 2012, p. 12).
Similar information follows in the Gougu Yuanfangtu (句股圓方圖) [Drawing for Bases, Altitudes, Circles, and Squares], Zhao Shuang’s commentaries on the Zhoubi, known as an illustrated commentary on the right-angled triangle.
There is a method to make circles and squares, all the things and their surroundings use circles and squares. Artisans use their compass and L-shaped try square when making them (此方圓之法, 萬物周事而圓方用焉, 大匠造制而規矩設焉) (
Chen 2012, p. 15).
This shows that myriad things are composed of circles and squares, and artisans use their compasses and L-shaped try squares for building construction. Both the
Zhoubi Suanjing [The Arithmetical Classic of the Gnomon and the Circular Paths of Heaven] and the
Jiuzhang Suanshu, on mathematical reasoning from various angles, say that all things are composed of circles and squares, along with the contents of
Tianyuan Difang (天圓地方) [Round Sky and Square Earth]. It is, therefore, possible to control all things by circles and squares. Furthermore, these works describe that the square converted into the circle, and vice versa, in interconnection with mathematical reasoning, and that the L-shaped try square and the compass appears to have no limits in the applicability to multiple things corresponding to the mathematical functions of circles and squares (
Chen 2012, p. 30;
Cullen 2007, pp. 181–82). Such recognition plays a very important role in helping us understand the design view of ancient oriental artisans. It stands to reason that the ancients implemented these concepts to build monuments such as pagodas, halls, and pavilions (
Figure 5).
3. The Design Systems of Paekche-Style and Silla-Style Pagodas
According to the
Samguk sagi [Chronicles of the Three Kingdoms], it is obvious that the old school books named the
Jiuzhang Suanshu already entered Silla in the seventh century CE. The idea of “
Gougu [Pythagoras Theorem]” in the
Jiuzhang Suanshu comes from the
Zhoubi Suanjing. The opening chapter of the
Zhoubi Suanjing deals with “a discourse on the properties of right-angled triangles as used for the measurement by proportions of heights and distances, both terrestrial and celestial.” (
Needham 1959, p. 19). Both academic fields include common elements. The
Fang Yuan Fang (方圓方) and the
Yuan Fang Yuan (圓方圓) from the
Zhoubi Suanjing can be interpreted as a concept of inscribed and circumscribed circles comparable to modern mathematics.
Fang Yuan Fang means that a square comes from a circle produced from a square, while
Yuan Fang Yuan means that a circle comes from a square created from a circle. One of the representative buildings that embodies the intentions of the construction is the Buddhist pagoda. The currently remaining pagodas in Korea, except for the Koguryŏ wooden pagodas with an octagonal plan, do not have any polygonal plans; most of them have square plans. Not only the ground plans but the elevations are constructed within a square outline and in accordance with a consistent law. If the carpenter’s L-try square and compass in the contents of the
Zhoubi Suanjing and the
Jiuzhang Suanshu represent a circle and a square respectively, it is possible to apply circular and square shapes as a regular principle for the construction of a pagoda.
3.1. Five-Story Stone Pagoda at Chŏngnimsa Temple
The original name of the five-story pagoda in the temple Chŏngnimsa cannot be found in such literature as the
Samguk Sagi or the
Samguk Yusa. In 1942, during the Japanese forced occupation, Fujisawa Kazuo unearthed a roof tile on the site. An inscription on the roof tile writes of the existence of the Chŏngnimsa Temple in the eighth
year of T’aep’yŏng, the Mujin year (太平八年戊辰定林寺大藏當草). The T’aep’yŏng is the era date (1021–1031) of the Liao Dynasty dominated by Emperor Shengzong (聖宗, r. 982–1031), and the eighth year of T’aep’yŏng (1028) corresponds to the ninth regime of Emperor Hyŏnjŏng (顯宗, r. 1009–1031) in the Koryŏ Dynasty. Thus, the Chŏngnimsa Temple was located at that site during the Koryŏ era. Several scholars referred to it as the Toyangsa Temple (道議寺) or the Paeksŏksa Temple (白石寺), related to Paekche’s collapse due to its important situation in the Paekche capital, Sabiseong (泗沘城). To mark the Tang-Silla allied forces’ triumph, General Su Dingfang (591–667) inscribed an official seal on the body wall of the first floor of the stone pagoda. The stele, called the “Stele of the Great Tang Empire’s conquest of the Paekche Kingdom (大唐平百濟國碑銘),” bears a carving with this inscription: “built on the fifteenth day of the eighth month in the fifth year of Xiangqing reign (660).” This inscription once led experts to believe that the Tang army constructed the stone pagoda. However, the same stele inscription is carved on a stone trough used in the Paekche period, currently displayed in the lobby of the Buyeo National Museum. These pagoda and trough inscriptions prove that the pagoda was made prior to the Tang army’s reuse of the pagoda to commemorate its military campaign (
Cultural Heritage Administration of Korea 2016, p. 46). Increasingly in recent years, research results have suggested that there was a wooden pagoda in place before the construction of the stone pagoda (
Kim 1984;
Kim 2012, pp. 38–53).
The current five-story pagoda of the Chŏngnimsa Temple consists of three divisions (foundation, pagoda body, and finial), as seen in the common configuration system of Buddhist pagodas, but the finial part remains only as a single member with a center-pole hole on a dew plate (noban) that supports an overturned bowl (pokpal). To investigate the gradual diminution in length to plan the pagoda, along with the entire proportional relationship between the body stone and the roof stone respectively, the authors of this article assumed that the horizontal width of the body stone at the first floor was X and the vertical height of the body stone at the first floor was Y. The interpretations are as follows:
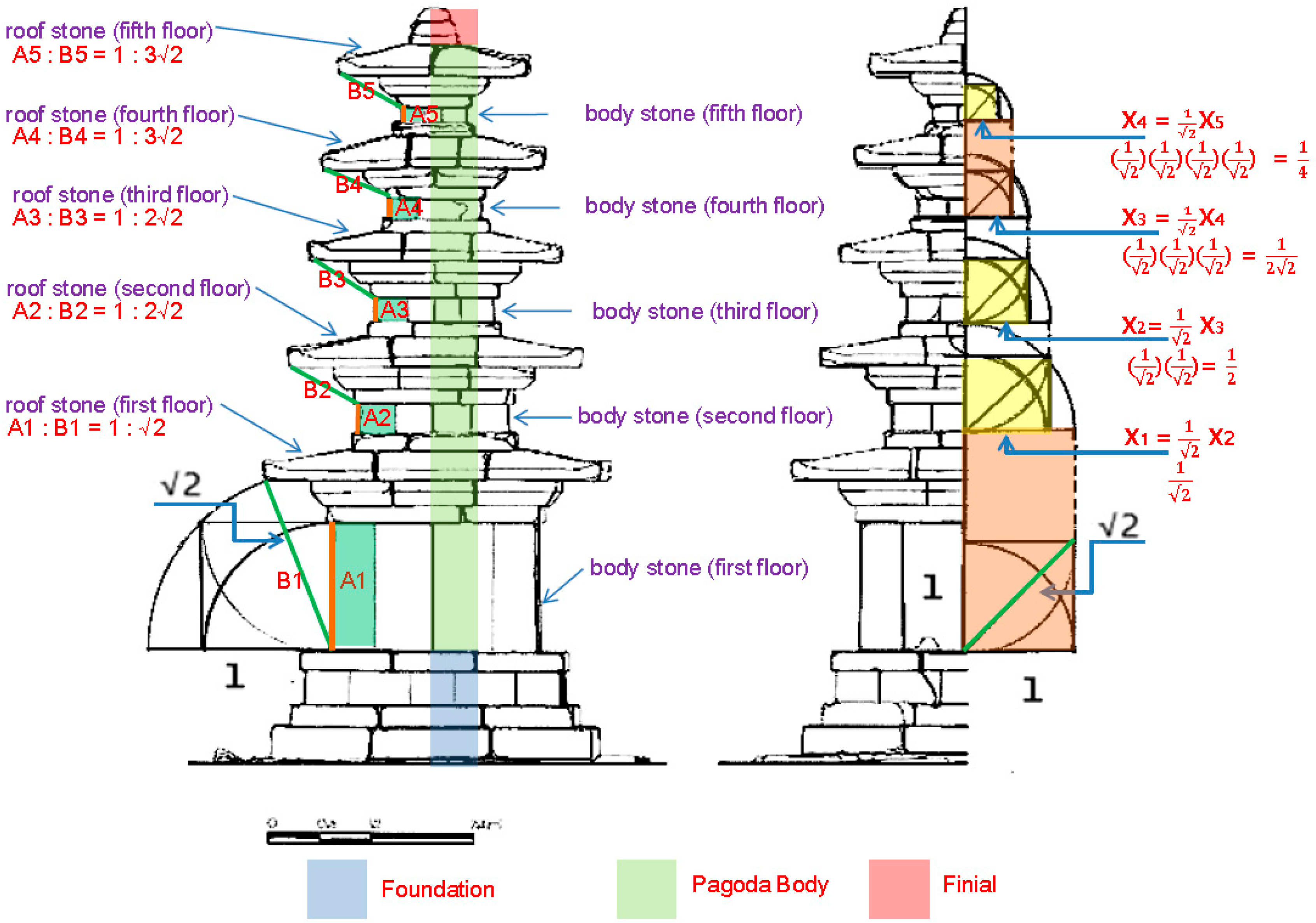
We confirmed a proportion of 1: √2 between the vertical height of the first floor’s body stone and the length from the ends of the eaves on the roof stone at the first floor to the bottom side of the body stone at the first floor. For the second and third floors, we calculated a ratio of 1:2√2 between the vertical height of the body stones and the length from the ends of the eaves on the roof stones to the upper side on the body stones. For the fourth and the fifth floors, we calculated a ratio of 1:3√2 under the identical conditions (
Figure 6, left image). The ratio of the vertical height of the body stones to the ends of the eaves on the roof stones from the upper or bottom side of the body stones shows an arithmetic proportion according to each story. Namely, there is a regular proportion between the height of each body stone and the length of the ends of the eaves on each roof stone from the upper or bottom side of the body stones (
Figure 6, left image). The difference of the criteria points such as the upper or bottom sides in line with each story, as mentioned above, appears because the vertical height of the body stone at the first floor is longer and the height of the body stone from the second floor to the fifth floor is relatively smaller.
The steady decline in the length of the pagoda follows the same pattern. If we multiply √2 times on the one-half (½) horizontal distance of the body stone at the second floor, we get the one-half (½) horizontal distance of the body stone on the first floor. This proportional system appears in the same manner on the third, fourth, and fifth floors. We derived the following formula to describe the size decrease, in which the horizontal width of the body stone at each floor is X
n and can be expressed as X
n = √2X
(n+1). The size reduction formula, therefore, would be X
n = 2(
)
n−1 as a geometric progression, multiplying two times by the one-half (½) horizontal width of the body stone at each floor. If the first floor is marked as X
1, the result will be 2 (
)
0 (=2) times; the second floor as X
2 will be 2 (
)
1; the third floor as X
3 will be 2 (
)
2 (=1); the fourth floor as X
4 will be 2 (
)
3 (=2
=
) times; and the fifth floor as X
5 will be 2(
)
4 (=½) times (
Figure 6, right image;
Figure 7, right image). One of the notable points is that the gradual diminution in length rests on the geometric progression dividing the one-half (½) width of the body stone by √2 times. The horizontal width that divides the one-half horizontal width of the lower floor by √2 times corresponds to the width of the body stone on the upper floor (
Figure 6, right image). This verifies that the horizontal width of the body stones is a main criterion.
When the horizontal half-width of the body stone at the first floor is multiplied by √2, applying twice times simultaneously, the measure has an equal vertical distance with that from the base of the body stone at the first floor to the top of the roof stone at the same floor. In addition, the horizontal half-width of the body stone has the same vertical height with that from the base side of the body stone at the second and third floors to the base side of the roof stone at the same floors respectively (
Figure 6, right image). The vertical height of the body stone at the first floor is relatively long, multiplying by √2 times, compared with those of the other floors, while those of the second and third floors have the same height and width. In the case of the fourth and fifth floors, the horizontal width of the body stone is relatively small compared with that at the first floor. Multiplying 2 by
times the one-half width of the body stone at the fourth floor is equal to the vertical height from the baseline of the body stone to the top of the roof stone at the same floor. In like manner, the fifth floor shows the same proportion as the second and third floor (
Figure 6, right image). The proportional numerical value is established by adjusting the vertical and horizontal lengths of the body stones.
In the Chŏngnimsa Temple, the gradual shrinkage in the horizontal and vertical lengths of the body stones works by multiplying by √2 times as a proportional value to grasp its overall numerical system. According to the steady decline in length, assuming that the one-half horizontal width of the body stone at each floor becomes a standard, the width of the body stone at each floor decreases by
times. The proportional system that multiplies by
times is appropriated to complete the stone pagoda. This explains why the distance between the body stone and the roof stone at each floor follows a regular pattern with a multiple of the square root of 2 (
Figure 6 and
Figure 7).
3.2. Three-Story Pagoda at Kamŭnsa Temple
The twin three-story stone pagodas at Kamŭnsa Temple represent a typical form in the whole synthesis of the Paekche-style construction methods with the existing Silla techniques in the Unified Silla era (
Chang 1996, p. 191;
National Research Institute of Cultural Heritage 2005). The construction date of the Kamŭnsa Pagodas is seen as the same as for the Kamŭnsa Temple, completed in 682 during the regime of King Sinmun (神文王, r. 681–692), the eldest son of Silla’s unifier-king, Munmu (
Chŏng 1985). Although the body stones and the foundation stones maintain the original shape, currently there is only an iron center pole on the top roof left as a finial part while other stone members surrounding the pole are missing. To analyze the proportional system of the stone pagoda, we assumed that the horizontal width of the first floor of the stone pagoda was X and the vertical height of the first floor of the pagoda was Y, like the five-story stone pagoda at the temple of Chŏngnimsa. The interpretation is as follows.
1. As with the five-story stone pagoda at Chŏngnimsa Temple, the Kamŭnsa Pagodas relies on the similar proportional coordination, with a ratio of 1:√2, between the vertical height of the body stone and the slant length from the ends of the eaves on the roof stone to the bottom side of the body stone at the same floor (
Figure 8, green lines). For the second and third floors, assuming that the height of the body stone is 1, the 2√2 times the distance from the bottom side of the body stone to the ends of the eaves on the roof stone has a definite proportional structure, unlike the five-story pagoda at the Chŏngnimsa Temple (
Figure 8, dotted green lines). Moreover, the horizontal width from the upper side of the body stone to that of the roof stone at the second and third floor respectively, assuming that the height of the body stone is 1, shows √2 times the distance, which plays an important role in molding an overall proportional system. This proves that the three-story stone pagodas at the Kamŭnsa Temple and the five-story pagoda at the Chŏngnimsa Temple shared common design principles (
Figure 8).
2. There is an unvarying proportion of the entire vertical distance between the body stones, the roof stones, and the bases on each floor. In the same manner as described above, assuming that the vertical height of the body stone on the first floor is 1, the vertical height of the foundation (from the bottom side of the stone foundation to the bottom side of the body stone at the first floor) is √2 times, and √2 times the height of the body stone at the second floor is the same as that of the roof stone at the first floor. In like manner, √2 times the vertical height of the body stone at the third floor correspond to that of the roof stone at the same floor (
Figure 8, dotted green lines). However, the vertical height of the roof stone at the second floor does not have any special proportion in the comparison with the second and third floors. The basic proportional system is closely related to the vertical height of the roof stone at each floor. In the case of the second floor, it shows an intermediate value in comparison with the first and third floors. In other words, the vertical height of the roof stone at the second floor is constructed with the arithmetic concept in line with the first and third floors. There is no evidence that the vertical height has any proportional relationship with the entire height.
3. The gradual reduction in the length of the Kamŭnsa Pagodas is confirmed through the horizontal width of each floor. Unlike the fifth floor of the pagoda at Chŏngnimsa Temple, a relatively clear numerical system can be identified at the Kamŭnsa Pagodas. The value calculated by multiplying √2 times the horizontal width of the body stone at the third floor is equal to the horizontal width of the body stone at the second floor. The value calculated by multiplying √2 times the horizontal width of the body stone at the second floor is equal to the horizontal width of the body stone at the first floor. This indicates that the Kamŭnsa Pagoda employs the manner of the geometric sequence of √2 times the height of each floor, analogous to the proportional concept applied at the pagoda of Chŏngnimsa Temple. The formula would be as follows. If the horizontal width of the body stone at the first floor is X
1, those at the second and third floors are X
2 and X
3 respectively. Assuming that dividing X
1 by √2 and the result is the horizontal width of the body stone at the second floor, a formula is established as follows, X
n = √2 X
n+1. Multiplying √2 times the horizontal width of the body stone at each floor causes a proportional system with a geometric concept (
Figure 8, right image).
The stone foundation was also constructed based on these same mathematical and geometric concepts. Multiplying √2 times the horizontal width of the body stone at the first floor is equivalent to the horizontal width on both sides of the corner-pillar stones (
ujusŏk) at the foundation part. The width is equal to the length of the horizontal width of the body stone at the first floor plus 0.414 (
Figure 8, foundation part). The width of a dew plate (
noban) also depends on this proportional system. The value calculated by multiplying √2 times the horizontal width of the bottom side at the
noban plate on the finial part, multiplied once more by √2, is equal to the horizontal width of the body stone at the third floor. In other words, grounded on the gradual decrease in the size of stone members from the
kidan foundation to the
noban plate on the finial part, the numerical value of √2 times puts a principal framework into shape that supports a basic proportional system. The use of arithmetic and geometric methods enhance the overall appearance of the pagoda.
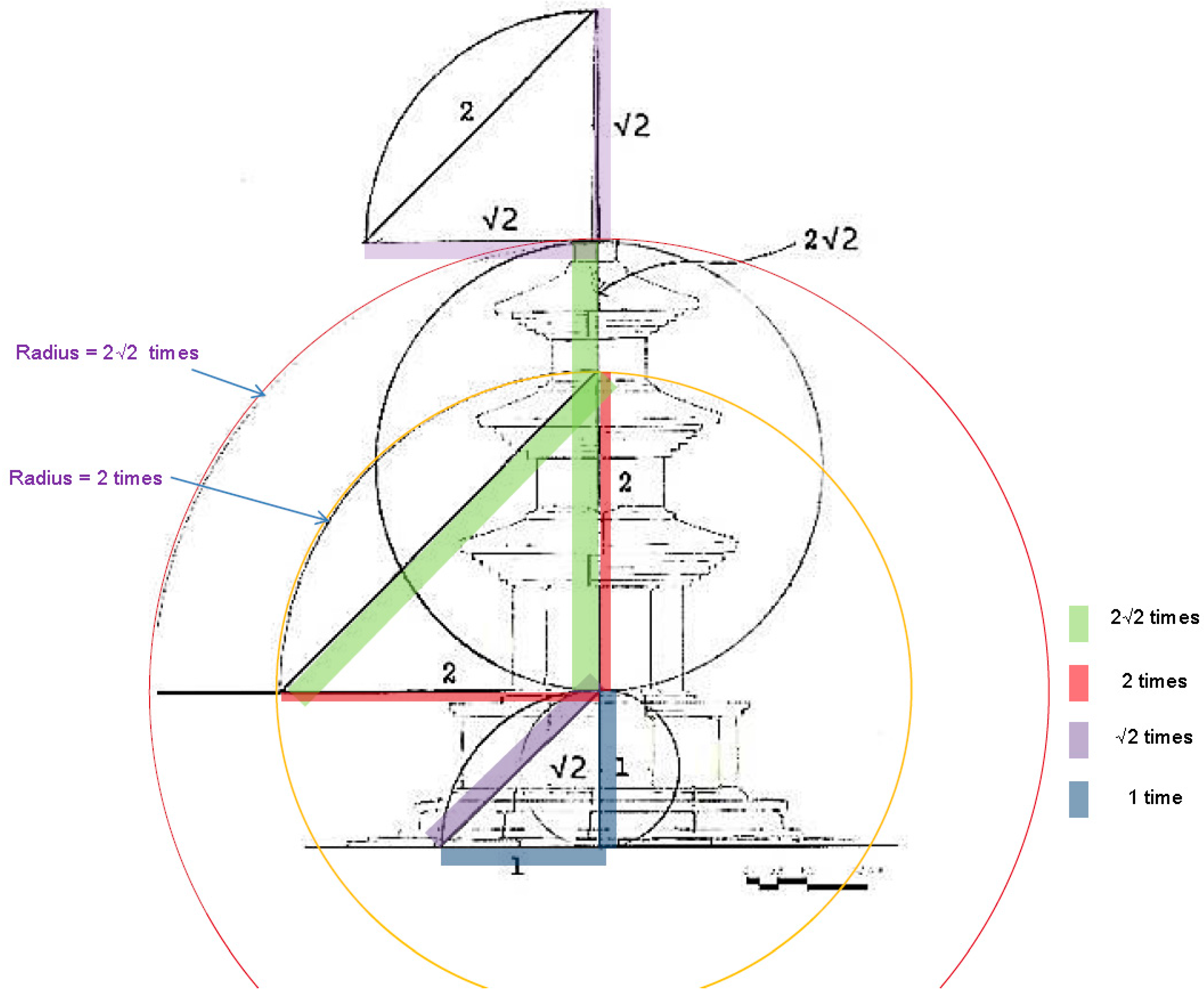
4. There are three divisions of the stone pagoda: the finial, the body, and the foundation part. The Kamŭnsa Pagoda’s finial part is incomplete; except for the
noban plate, the stone members from an overturned bowl (
pokpal) to a precious pearl (
poju) above the dew plate are currently missing. Assuming that the vertical height from the lower to the upper stone of the foundation is the numerical value 1, the proportional length from the top of the
noban plate to the end of the iron center pole (
ch’alchu) would be √2 times. Likewise, assuming that the height of the finial part is the numerical value √2, the finial’s height multiplied √2 times would be equal to the vertical height from the lower side of the body stone at the first floor to the upper side of the
noban plate at the finial part. In other words, the division concept between the finial, the body, and the foundation part follows a geometric progression with the multiple lengths of 1, √2, 2, and 2√2 times in regular sequence (
Figure 9).
Considering an overall proportional composition to construct a stone pagoda, the geometrical uses of the square root of 2 are deeply involved in the design principles that relate the three elements—the foundation, the pagoda body, and the finial—within a large framework and determine the design for the stone members to pile up each layer. However, lack of uniformity in numerical measures (e.g., reference scales such as the Zhou, the Koryŏ, and the Tang cubits) make it difficult to build based on measurements alone; to build a stone pagoda in the manner of those at the Chŏngnimsa and Kamŭnsa Buddhist Temples, decisions on the height and width are more dependent on proportional aspects based on arithmetical and geometrical progressions than on cubit measures or numerical values. That is, anyone with a calculator could begin with any desired foundation size and create a stone pagoda aesthetically and dimensionally identical to those built by the ancients.
This study showed that the standard measuring units vary according to the gradual decrease or the reference scale for a measurement unit of length in a proportional system. Future studies should continue to search for a reference scale to specify numerical values of the heights and widths of the stone monuments based on the regularity of advanced mathematical proportion in construction system.
4. Reviewing Measurement Criteria and Mathematical Relationships
In ancient East Asia, there were measurement criteria to construct monuments through the uses of rulers, which were typically marked at regular intervals to measure distances. They corresponded to the reference scales that conform to the arm, foot, and palm of the human body, although the measuring methods used on the Korean Peninsula varied from generation to generation. Among them, the Zhou cubit (
chi, Kr.
ch’ŏk, which is based on the forearm length)
6 is 19.91 cm
7 and is expounded upon in the
Zhouli Kaogongji (周禮 考工記) [Bound Volume of
The Rites of the Zhou Dynasty and
Notes on Examining the Artisans]. The
Kaogongji indicates the employment of the Zhou cubit for civil engineering and territorial arrangement works rather than building works. The Zhou cubit was also used in the Korean Peninsula up to pre-modern times, including the whole area setting of the Hwasŏng Fortress, constructed between 1794 and 1796 during the reign of King Chŏngjo (1752–1800). In contrast, the Tang cubit, introduced during the Unified Silla period as a reference scale, measured 29.694 cm. The Koryŏ cubit, the reference scale of the Koguryŏ Kingdom, measures 35.6328 cm and is one of the longest cubit systems among wooden rulers; it was used in the Liaodong and Shandong provinces in China and the Asuka and Heian territories in Japan in contemporary times.
8The construction of the five-story pagoda at the Chŏngnimsa Temple and the three-story pagoda at the Kamŭnsa Temple was based on the application of the Koryŏ and Tang cubits, respectively. The Koryŏ cubit system was used in the construction of capital cities, the Hwangnyongsa Temple, and the Pusosansŏng Mountain Fortress during the Three Kingdoms period. Meanwhile, the Tang cubit was used for most buildings constructed during the Unification Silla, including the Sach’ŏnwangsa Temple, the Mangdŏksa Temple, the anonymous Buddhist site in Ch’ŏn’gulli District, and the main hall of the Pusŏksa Temple. The Chŏngnimsa pagoda, based on research on the Koryŏ cubit’s use (
Chang 1990, p. 359), has a width for the surface stone (
myŏnsŏk) of the body stone at the first floor of 5.5
ch’ŏk within 7
ch’ŏk, which is the whole width of the body stone at the same floor. From the second floor to the fifth floor of the stone pagoda, five
ch’ŏk, four
ch’ŏk, three
ch’ŏk, and two
ch’ŏk each are reduced by one
ch’ŏk each floor for the gradual reduction in width. As one
ch’ŏk in the Koryŏ cubit is applied to 35.6328 cm, 5.5
ch’ŏk is applied to 195.9804 cm. 138.6 cm, which divides 195.9804 cm by √2, roughly amounts to ten times √2. Considering the assumption of 35.6328 cm (=1 Koryŏ cubit). When √2 (=1.414) is multiplied by 25 times, the result is 35.35 cm, which is less than 1% error of the Koryŏ reference scale (35.6328 cm).
In the case of the three-story stone pagoda of the Kamŭnsa Temple, the total sum of the width of surface stones (myŏnsŏk) (1820 mm) and that of corner pillar stones (ujusŏk) on both sides (500 mm × 2 = 1000 mm) is 2820 mm. Since there has been no research on the reference ch’ŏk used in designing the Kamŭnsa Temple, it is unclear whether the Kamŭnsa Pagoda was built with the Tang cubit or the Koryŏ cubit. However, it is reasonable to associate the Tang cubit with the ground plans of temples and the ground plans and façades of stone pagodas constructed during the Unified Silla since the cosmopolitan Unified Silla court pursued extensive contacts with the Tang Dynasty (618–907 CE) in China. Considering all these facts, the Kamŭnsa Pagoda might employ the Tang cubit for its construction with a precise mathematical proportion. When we divide 29.694 cm (1 Tang cubit) by √2 (=1.414), we get the natural number 21; this shows that the reference scale of the ruler and try squares used by the Tang’s artisans is closely related to √2. The square root of 2 (√2) is a figure embodied through inscribed and circumscribed circles in the amalgamation of circles with squares. The number √2 accurately corresponds to the Tang cubit. In consideration of an intimate link between the reference scale and the square root of 2, the exact application of 21 times √2 conforms to 29.694 cm of the Tang cubit, while the Koryŏ cubit (35.6328 cm) shows an error of less than 1% occurs in comparison with 35.35 cm, multiplying √2 by 25, as aforementioned.
5. Conclusions
Through two ancient Chinese mathematical books, Zhoubi Suanjing and Jiuzhang Suanshu, we understand the proportional systems and the design principles of ancient Korean pagodas that retain a wide range of cultural traditions and the arithmetical thought and interpretation of the ancients.
First, in both ancient oriental mathematics books, all things are composed of circles and squares, expressing innumerable things applicable by using the carpenter’s try square and compass, even showing that both circles and squares are replicable with each other. Their combination shows mathematical thought expressing inscribed and circumscribed circles, embedded in the ancient idea called Tianyuan Difang.
Second, these oriental documents, handed down through the Korean Peninsula since before the seventh century, included the myriad ideas of mathematical proportions. As a result of the design ideas applied in the early stone pagodas, we found that the employment of √2 times extracted from inscribed and circumscribed circles with squares was much involved in designing the ground plans and façades of stone pagodas. The preference of the design principle is seen inexisting wooden buildings constructed in pre-Liao and Liao China and in pre-Heian and Heian Japan. They have a ratio of 1:√2 between the height of the exterior columns or perimeter columns and the distance from the exterior column bases to the eaves’ purlins.
9 These grounds demonstrate that the Chŏngnimsa and Kamŭnsa stone pagodas are constructed based on multiplication by √2 times. Regarding the design principles described above, the structural frames of the stone pagodas resemble those of wooden buildings; the exterior columns in timber-framed buildings equate to the corner pillars, while the ends of the eaves on roof stones replicate the endpoints of the eaves with a slight curve upward supported by bracket complexes above pillars. This shows that their structural forms preserve the designs of timber-framed buildings consistently through the use of proportional systems and the imitation of wooden architectural elements in stone (
Kim 2011, pp. 198–99). Both stone pagodas represent sophisticated interpretations of wooden structures built on a high foundation in four directions.
Third, the Chŏngnimsa and the Kamŭnsa Pagodas are representative stone pagodas of the Paekche and Silla eras, respectively. The proportional framework to embody the separations between the foundation, the pagoda body, and the finial is closely relevant to the adoption of the square root of 2 (√2) in deciding the height of the body stone and the width of the roof stone with the gradual decrease to embrace the entire design of the pagodas. Consistent with such systematic principles, the mathematical concepts dwelling on the arithmetic and geometric progressions determine the overall proportion to construct the pagoda. Future studies should proceed with respect to the organization of the stone elements in the pagodas that become the significant criteria in accordance with the arithmetic and geometric declining methods in length.
Fourth, this study proved proportional systems dependent on the reference scale. For the Kamŭnsa Pagoda, the Tang cubit used in the Korean Peninsula (29.694 cm) was divided by √2 (=1.414); the result was 21, a natural number, suggesting that √2 times has a very close bond with the Tang cubit. Meanwhile, as seen in the Chŏngnimsa Pagoda, the Koryŏ cubit (35.6328 cm) has an error of less than 1% in comparison with 35.35 cm, multiplying √2 by 25. Accordingly, the establishment of √2 times in the combination of geometric and arithmetic serials acts as a fundamental instrument in designing the ground plans and elevations of the stone pagodas in an intended proportional composition. In fact, Yoneda Miyoji recognized that most of the ancient buildings were designed in the Unified Silla era, according to a multiple of the square root of 2. Investigating stone members in the historic sites of Buddhist temples, Yoneda found that the figures measured by a carpenter’s try square were a multiple of the square root of 2 and argued that there was another measurement unit, which he called the Tang cubit, on the basis of the figures (
Yoneda 1944,
1976; pp. 140–41). There should be future studies on the association between the Koryŏ and the Tang cubits through the in-depth understanding as to the acceptance of the square root of 2 (√2).