Precise Underwater Gliders Pitch Control with the Presence of the Pycnocline
Abstract
:1. Introduction
2. Dynamic Model Derivation
2.1. Model Derivations
2.2. Longitudinal Model Considering Varying Seawater Density
2.3. Parameters Determination
3. The Actuator Constrained Active Disturbance Rejection Control
3.1. The Actuator Constrains
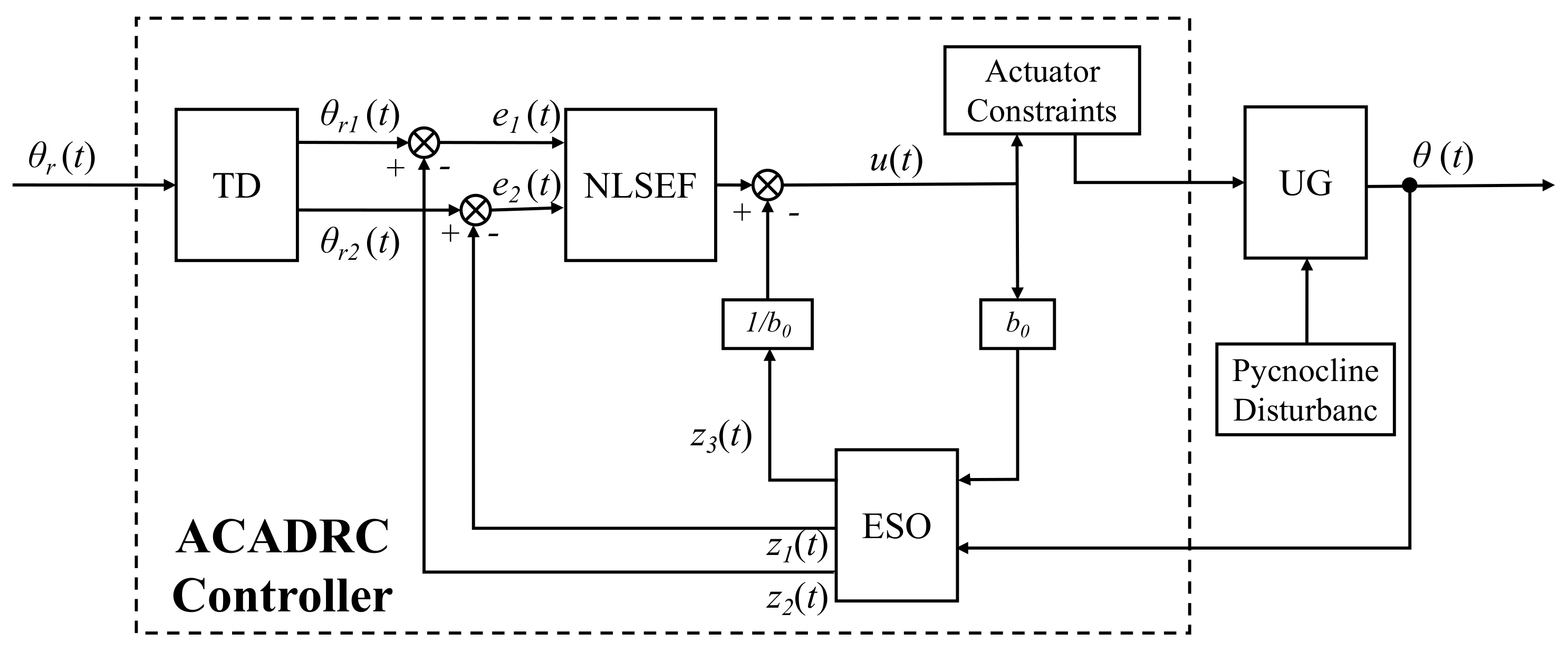
3.2. The ACADRC
3.3. The Comparison Methods
4. Discussion on Pycnocline and Control Metrics
4.1. Three Typical Types of Pycnocline
4.2. The Control Metrics of Pitch Control
5. Numerical Simulation Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| mass of the bladder | |
| mass of the glider static components | |
| mass of the movable block | |
| mass of the vehicle | |
| equivalent mass of net buoyancy | |
| inertia of glider: | |
| inertia of the glider’s static components | |
| added mass matrix: | |
| added inertia matrix: | |
| added coupling matrix: | |
| position vector of the vehicle in the body coordinate system | |
| position vector of static mass in the body coordinate system | |
| position vector of the movable mass in the body coordinate system | |
| position vector of the bladder in the body coordinate system | |
| position vector of the vehicle in the inertia coordinate system | |
| position vector of static mass in the inertia coordinate system | |
| position vector of the movable mass in the inertia coordinate system | |
| position vector of the bladder in the inertia coordinate system | |
| translational velocity in the body coordinate system, | |
| angular velocity in the body coordinate system, | |
| glider position in the inertia coordinate system, | |
| position vector of glider’s center of buoyancy in the inertia coordinate system | |
| glider attitude in the inertia coordinate system | |
| linear momentum of glider in the body coordinate system | |
| linear momentum of glider in the inertia coordinate system | |
| angular momentum of glider in the body coordinate system | |
| angular momentum of the glider in the inertia coordinate system | |
| the ith external force expressed in the inertia coordinate system | |
| the ith external moment expressed in the inertia coordinate system | |
| gravitational forces in the body coordinate system |
| gravitational moments in the body coordinate system | |
| the angle of attack | |
| the side slip angle | |
| hydrodynamic moments in the currents coordinate system | |
| hydrodynamic forces in the currents coordinate system | |
| lift force in the currents coordinate system, | |
| drag force in the currents coordinate system, | |
| lateral force in the currents coordinate system, | |
| moments around three axes in the currents coordinate system | |
| moments around three axes in the currents coordinate system | |
| Q | generalized force |
| generalized quantity | |
| T | the kinetic energy of the glider system |
| added kinetic energy in the body frame | |
| kinetic energy of the vehicle | |
| t | time |
| translational position of in body frame | |
| h | the metacentric height |
| the extreme of the pitch angle | |
| d | the diameter of the screw rod |
| the lead angle of screw | |
| the transmission efficiency | |
| the constrained velocity of the movable mass (the actuator constraints) | |
| the equivalent coefficient of friction | |
| i | the reduction gear ratio of planetary gear |
| L | the length of the screw rot |
| n | the rated speed of the DC motor |
References
- Petritoli, E.; Leccese, F.; Cagnetti, M. High accuracy buoyancy for underwater gliders: The uncertainty in the depth control. Sensors 2019, 19, 1831. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, H.; Niu, W.; Wang, S.; Yan, S. An optimization method for control parameters of underwater gliders considering energy consumption and motion accuracy. Appl. Math. Model. 2021, 90, 1099–1119. [Google Scholar] [CrossRef]
- Sun, W.; Zang, W.; Liu, C.; Guo, T.; Nie, Y.; Song, D. Motion pattern optimization and energy analysis for underwater glider based on the multi-objective artificial bee colony method. J. Mar. Eng. 2021, 9, 327. [Google Scholar] [CrossRef]
- Claus, B.; Bachmayer, R.; Cooney, L. Analysis and development of a buoyancy-pitch based depth control algorithm for a hybrid underwater glider. In Proceedings of the 2012 IEEE/OES Autonomous Underwater Vehicles (AUV), Southampton, UK, 24–27 September 2012; pp. 1–6. [Google Scholar]
- Tatone, F.; Vaccarini, M.; Longhi, S. Modeling and attitude control of an autonomous underwater glider. IFAC Proc. Vol. 2009, 42, 217–222. [Google Scholar] [CrossRef]
- De Fommervault, O.; Besson, F.; Beguery, L.; Page, Y.L.; Lattes, P. Seaexplorer underwater glider: A new tool to measure depth-resolved water currents profiles. In Proceedings of the OCEANS 2019-Marseille, Marseille, France, 17–20 June 2019; pp. 1–6. [Google Scholar]
- Ma, W.; Wang, Y.; Wang, S.; Zhang, H.; Zhang, H.; Gong, Q. Absolute current estimation and sea-trial application of glider-mounted ad2cp. J. Coast. Res. 2019, 35, 1343–1350. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Wang, S.; Zhang, L.; Wang, Y.; Zhang, H. Evaluation models and criteria of motion performance for underwater gliders. Appl. Ocean. Res. 2019, 102, 102286. [Google Scholar] [CrossRef]
- Song, D.; Chen, Z.; Fu, J.; Wang, X.; Jiang, W.; Wu, J. Novel underwater glider-based absolute oceanic current observation solutions. IEEE Sens. J. 2020, 21, 8045–8054. [Google Scholar] [CrossRef]
- Rusello, P.J.; Yahnker, C.; Morris, M. Improving depth averaged velocity measurements from seaglider with an advanced acoustic current profiler, the nortek ad2cp-glider. In Proceedings of the 2012 Oceans, Hampton Roads, VA, USA, 14–19 October 2012; pp. 1–8. [Google Scholar]
- Cassar, C. An Introduction to Underwater Gliders. Available online: http://ioi.research.um.edu.mt/GliderSouth/index.php/welcome/gliders_info (accessed on 15 September 2021).
- Zhang, Y.; Wu, D.-X.; Lin, X.-P. A study of thermocline and pycnocline calculations in the east china sea in summer. J. Ocean. China 2006, 36, 1–7. [Google Scholar]
- Ayyemperumal, S.; Jeyaseelan, T.; Minamino, T.; Arima, M. Development of an underwater glider with density-difference-engine. In Proceedings of the 2018 World Automation Congress (WAC), Stevenson, WA, USA, 3–6 June 2018; pp. 1–5. [Google Scholar]
- Zhou, H.; Fu, J.; Liu, C.; Zeng, Z.; Yu, C.; Yao, B.; Lian, L. Dynamic modeling and endurance enhancement analysis of deep-sea gliders with a hybrid buoyancy regulating system. Ocean. Eng. 2020, 217, 108146. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, J.; Ma, N.; Zhang, G. Path planning for underwater glider under control constraint. Adv. Mech. Eng. 2017, 9, 1687814017717187. [Google Scholar] [CrossRef]
- Kahveci, N.E.; Ioannou, P.A.; Mirmirani, M.D. A robust adaptive control design for gliders subject to actuator saturation nonlinearities. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007; pp. 492–497. [Google Scholar]
- Zhang, S.; Yu, J.; Zhang, A.; Zhang, F. Spiraling motion of underwater gliders: Modeling, analysis, and experimental results. Ocean Eng. 2013, 60, 1–13. [Google Scholar] [CrossRef]
- Petritoli, E.; Leccese, F.; Cagnetti, M. A high accuracy buoyancy system control for an underwater glider. In Proceedings of the 2018 IEEE International Workshop on Metrology for the Sea; Learning to Measure Sea Health Parameters (MetroSea), Bari, Italy, 8–10 October 2018; pp. 257–261. [Google Scholar]
- Petritoli, E.; Leccese, F. A high accuracy navigation system for a tailless underwater glider. In Proceedings of the IMEKO TC19 Workshop on Metrology for the Sea, MetroSea, Naples, Italy, 11–13 October 2017. [Google Scholar]
- Petritoli, E.; Leccese, F.; Cagnetti, M. Underwater Gliders: Mission Profiles and Utilisation Strategies in the Mediterranean Sea. In Proceedings of the 2019 IMEKO TC19 International Workshop on Metrology for the Sea: Learning to Measure Sea Health Parameters, Genova, Italy, 3–5 October 2019; pp. 254–258. [Google Scholar]
- Wu, H.; Niu, W.; Wang, S.; Yan, S. Sensitivity analysis of control parameters errors and current parameters to motion accuracy of underwater glider using sobol’ method. Appl. Ocean. Res. 2021, 110, 102625. [Google Scholar] [CrossRef]
- Guo, T.; Song, D.; Li, K.; Li, C.; Yang, H. Pitch angle control with model compensation based on active disturbance rejection controller for underwater gliders. J. Coast. Res. 2020, 36, 424–433. [Google Scholar] [CrossRef]
- Tchilian, R.d.; Rafikova, E.; Gafurov, S.A.; Rafikov, M. Optimal control of an underwater glider vehicle. Procedia Eng. 2017, 176, 732–740. [Google Scholar] [CrossRef]
- Noh, M.M.; Arshad, M.R.; Mokhtar, R.M. Depth and Pitch Control of Usm Underwater Glider: Performance Comparison pid vs. lqr. Indian J.-Geo-Mar. Sci. 2011, 40, 200–206. [Google Scholar]
- Cao, J.; Cao, J.; Yao, B.; Lian, L. Dynamics and adaptive fuzzy turning control of an underwater glider. In Proceedings of the OCEANS 2015-Genova, Genova, Italy, 18–21 May 2015; pp. 1–7. [Google Scholar]
- Mitchell, B.; Wilkening, E.; Mahmoudian, N. Developing an underwater glider for educational purposes. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 3423–3428. [Google Scholar]
- Ullah, B.; Ovinis, M.; Baharom, M.B.; Javaid, M.; Izhar, S. Underwater gliders control strategies: A review. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; pp. 1–6. [Google Scholar]
- Singh, Y.; Bhattacharyya, S.K.; Idichandy, V.G. CFD approach to steady state analysis of an underwater glider. In Proceedings of the 2014 Oceans-St. John’s, St. John’s, NL, Canada, 14–19 September 2014; pp. 1–5. [Google Scholar]
- Sahin, I.; Crane, J.W.; Watson, K.P. Application of a panel method to hydrodynamics of underwater vehicles. Ocean Eng. 1997, 24, 501–512. [Google Scholar] [CrossRef]
- Cheng, M.-H.; Hsu, J.R.-C. Effects of varying pycnocline thickness on interfacial wave generation and propagation. Ocean Eng. 2014, 88, 34–45. [Google Scholar] [CrossRef]
- Church, T.M.; Mooers, C.N.; Voorhis, A.D. Exchange processes over a middle atlantic bight shelfbreak canyon. Estuar. Coast. Shelf Sci. 1984, 19, 393–411. [Google Scholar] [CrossRef]
- Shaw, J.; Stastna, M. Feature identification in time-indexed model output. PLoS ONE 2019, 14, e0225439. [Google Scholar] [CrossRef] [PubMed]






| Parameters | Values |
|---|---|
| 8.669 | |
| 612.712 | |
| −67.415 | |
| −2.223 | |
| 572.727 | |
| −38.955 | |
| −23.694 | |
| 0.858 | |
| −53.524 | |
| −155.809 | |
| 77.862 | |
| −280.766 |
| Parameters | Values |
|---|---|
| Properties | Pycnocline 1 | Pycnocline 2 | Pycnocline 3 |
|---|---|---|---|
| 30 m | 50 m | 40 m, 80 m | |
| 70 m | 70 m | 55 m, 100 m | |
| 0.15 | −0.13 | 0.15, 0.11 | |
| 0.02 | −0.001 | 0.015, 0.01 | |
| 0.01 | 0.006 | 0.01, 0.006 |
| Pycnocline 1 | |||
|---|---|---|---|
| Metrics | Bangbang | PID | ACADRC |
| 54 | 54 | 44 | |
| 889 | 920 | 883 | |
| 835 | 866 | 839 | |
| −19.526 | −18.912 | −19.319 | |
| 3.683 | 3.255 | 1.437 | |
| 1078 | 1101 | 1071 | |
| 1897 | 1933 | 1826 | |
| 819 | 832 | 755 | |
| 20.016 | 18.534 | 19.336 | |
| 2.554 | 3.076 | 1.210 | |
| Pycnocline 2 | |||
| Metrics | Bangbang | PID | ACADRC |
| 91 | 91 | 44 | |
| 946 | 959 | 927 | |
| 855 | 868 | 883 | |
| −19.365 | −19.326 | −19.421 | |
| 3.401 | 0.975 | 1.315 | |
| 1097 | 1116 | 1091 | |
| 1988 | 1981 | 1906 | |
| 891 | 865 | 815 | |
| 19.280 | 18.977 | 19.119 | |
| 4.056 | 12.477 | 0.737 | |
| Pycnocline 3 | |||
| Metrics | Bangbang | PID | ACADRC |
| 54 | 54 | 44 | |
| 898 | 924 | 892 | |
| 844 | 870 | 848 | |
| −19.415 | −18.932 | −19.226 | |
| 3.667 | 2.934 | 1.303 | |
| 1056 | 1109 | 1071 | |
| 1882 | 1927 | 1840 | |
| 826 | 818 | 769 | |
| 19.910 | 18.889 | 19.217 | |
| 2.295 | 2.207 | 0.915 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, W.; Chen, M.; Guo, T.; Luan, X.; Song, D. Precise Underwater Gliders Pitch Control with the Presence of the Pycnocline. J. Mar. Sci. Eng. 2021, 9, 1013. https://doi.org/10.3390/jmse9091013
Zang W, Chen M, Guo T, Luan X, Song D. Precise Underwater Gliders Pitch Control with the Presence of the Pycnocline. Journal of Marine Science and Engineering. 2021; 9(9):1013. https://doi.org/10.3390/jmse9091013
Chicago/Turabian StyleZang, Wenchuan, Ming Chen, Tingting Guo, Xin Luan, and Dalei Song. 2021. "Precise Underwater Gliders Pitch Control with the Presence of the Pycnocline" Journal of Marine Science and Engineering 9, no. 9: 1013. https://doi.org/10.3390/jmse9091013
APA StyleZang, W., Chen, M., Guo, T., Luan, X., & Song, D. (2021). Precise Underwater Gliders Pitch Control with the Presence of the Pycnocline. Journal of Marine Science and Engineering, 9(9), 1013. https://doi.org/10.3390/jmse9091013





