Abstract
Barred macrotidal beaches are affected by continuous horizontal displacements of different hydrodynamic zones associated with wave transformation (shoaling, breaker and surf zones) due to significant tide-induced water level changes. A series of wave and current meters, complemented by a video imagery system, were deployed on a barred beach of northern France during a 6-day experiment in order to characterize the spatial and temporal variability of wave-induced processes across the beach. Wave and current spectral analyses and analyses of cross-shore current direction and asymmetry resulted in the identification of distinct hydrodynamic processes, including the development of infragravity waves and offshore-directed flows in the breaker and surf zones. Our results revealed a high spatial variability in the hydrodynamic processes across the beach, related to the bar-trough topography, as well as significant variations in the directions and intensity of cross-shore currents at fixed locations due to the horizontal translation of the different hydrodynamic zones resulting from continuous changes in water level due to tides.
1. Introduction
In recent years, an increasing number of papers were published on the morphodynamics of barred macrotidal beaches, which gave some insight into the morphological behavior of intertidal bar-trough systems (e.g., [1,2,3,4,5,6]). However, although hydrodynamics were generally investigated in these studies, most of them were primarily focused on either the morphodynamics of intertidal bars [3,4,7,8,9,10,11] or on sediment transport processes [12,13,14,15,16,17,18,19]. Comparatively, fewer papers were specifically concerned with the hydrodynamics of barred macrotidal beaches (e.g., [1,20,21]).
The hydrodynamics of barred macrotidal beaches are complex and highly variable both spatially and temporarily due to cross-shore morphological variations (bar-trough topography) and to large vertical tidal fluctuations that induce significant horizontal translations of the different hydrodynamic zones associated with wave transformations (shoaling, breaker and surf zones). The characterization of the hydrodynamic processes affecting macrotidal beaches is, therefore, further complicated by the perpetual shore-normal migration of the breaker and surf zones, which results in continual changes in wave breaking conditions across the intertidal bar topography [1,9,17]. The continuous changes in water level, due to vertical tidal variations, are not only responsible for changes in wave height and associated energy dissipation across the beach, but also affect the spatial distribution and vertical structure of wave-induced cross-shore currents, such as swash bore or undertow, across the spatially variable topography of barred beaches [9,22,23,24,25]. On the other hand, the changes in wave height and in current velocities and directions that take place over macrotidal beaches during a single tidal cycle have major impacts on the dynamics of intertidal bars that almost continuously experience changes in on-offshore shear stress at the bed which strongly control net sediment transport and, consequently, bar evolution [4,8,9,17]. Due to the complex interrelations between water level, wave heights and wave- and current-induced bed stress, which considerably vary over time at any given location, but also from place to place across the beach, the modeling of intertidal bar formation and evolution is still a challenging issue [26].
A better knowledge and understanding of barred beach hydrodynamics are not only useful for fundamental research, but also for a wide range of coastal engineering applications for which precise values of wave and current variables are needed. Breaking wave height, for example, is often a required parameter for computing longshore sediment transport on beaches [27,28] or for modelling coastal dune erosion [29,30,31] whereas breaker heights in many morphodynamic models are frequently indirectly derived from a semi-empirical breaking index (e.g., [32,33]. Values of wave height at breaking can be obtained through numerical modelling (e.g., [34,35]) or from in situ measurements of water surface elevation changes using a variety of acoustic or pressure sensors [36,37] or of flow data that can be transformed to surface elevation spectra [38,39]. However, the actual wave height at the breakpoint is often difficult to determine from direct measurements of flow or surface elevation data, since it can hardly be ascertained whether wave heights were obtained during breaking or non-breaking conditions.
In this paper, we report the results of a 6-day experiment carried out on a barred macrotidal beach during which an array of wave and current meters was deployed across the intertidal and nearshore zones down to 5 m water depth (below maximum low-tide level). These hydrodynamic measurements were complemented by the simultaneous acquisition of video camera images of the beach. These images enabled the determination of the location of the wave breaking zone (and hence of the other hydrodynamic zones) during distinct periods of the hydrodynamic field experiment. The aim of this study was to define the signatures of wave-induced hydrodynamics, characterizing the different zones of wave transformation across a macrotidal beach, based on wave spectral analysis and wave-induced cross-shore current analyses. This work resulted in the identification of a series of discrete hydrodynamic variables that can be easily extracted from standard wave and current data for discriminating the main hydrodynamic zones associated with wave transformation on barred macrotidal beaches.
2. Study Area
This study was conducted on a sandy macrotidal barred beach of northern France, near the Belgian border (Figure 1C). The study site consists of a 350 to 400 m wide, low sloping (1.4%), dissipative beach (Figure 2), facing the North Sea. The beach is characterized by a series of shore-parallel bars with a crest height that commonly exceeds 1 m above the surrounding seabed (Figure 2D). A number of studies conducted on the beaches of northern France showed that this bar-trough morphology is quasi-permanent, even under storm wave conditions [4,5,6]. The beach is composed of well-sorted fine sand (mean grain size = 0.20 mm). Some variation is observed in the grain-size of surface sediments, sand being finer on the lower beach compared to the middle and the upper beach, which is commonly observed on the barred beaches of the region [40].
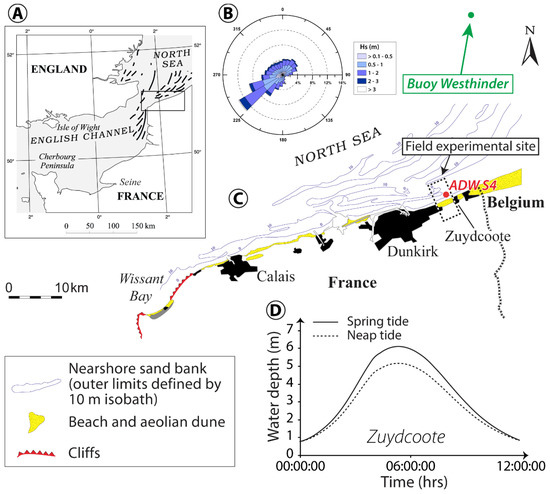
Figure 1.
(A) Location of the study area showing the location of offshore sand banks. (B) Deep-water wave rose diagram based on hourly wave measurements from 1997 to 2016 at the Westhinder wave buoy; the green arrow indicates the location of the nearshore current meter. (C) Map of the study area and field experiment site. (D) Typical tidal curves for spring and neap tides at the study site.
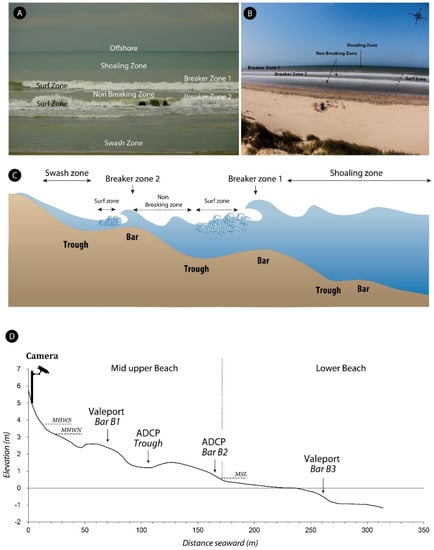
Figure 2.
(A) Photograph of multiple breaker and surf zones due to wave reformation on the studied beach; (B) example of an averaged image of 60 consecutive photographs showing the location of breaker zones and non-breaking zones; (C) schematic representation of the different hydrodynamic zones distinguished during the field experiment; (D) cross-shore profile showing the location of the video camera and hydrodynamic instruments deployed in the intertidal zone (elevations are relative to the French topographic chart datum). Altitudes of mean sea level (MSL) and of mean high-water neap (MHWN) and mean high water spring (MHWS) are indicated on the lower diagram.
The study site is affected by semi-diurnal tides with a mean tidal range of approximately 3.5 m to 5.5 m during neap and spring tides, respectively (Figure 1D) [41]. This relatively high tidal range is responsible for strong tidal currents that flow almost parallel to the shoreline on the shoreface and in the nearshore zone, the ebb currents being directed westward and the flood currents flowing eastward [42]. The reversing of tidal currents does not occur at high or low tide, but typically after a delay of two to three hours, which is consistent with the propagation of a dominantly progressive tidal wave in the Eastern Channel [4]. Current measurements conducted in previous studies show that the speeds of flood currents exceed those of the ebb, resulting in a net flood-dominated asymmetry in the coastal zone [19,43].
The prevailing winds in the region are from west to southwest, with a secondary wind direction from north to northeast [44]. As a result, the dominant wave directions are from southwest to west, originating from the English Channel, followed by waves from the northeast to north, generated in the North Sea (Figure 1B). In this relatively short-fetch environment, the modal offshore significant wave height is less than 1 m with wave periods typically ranging from 4 to 8 s, although maximum wave height may episodically exceed 5 m with periods of 9 to 10 s during major storms [45]. However, waves undergo significant shoaling and energy dissipation over the massive inner shelf sand banks (Figure 1A) and the gentle beach and nearshore slopes that characterize the coast of Northern France, resulting in significantly lower wave heights at the coast [37].
3. Materials and Methods
3.1. Hydrodynamics
A series of hydrographic instruments were deployed along a cross-shore transect from the upper beach (Figure 2D) down to a water depth of −5 m below Hydrographic Datum (Figure 1; Table 1), which corresponds to approximately the lower astronomical tide level, to measure wave and current parameters at different locations of the intertidal and subtidal zones. On the beach, instruments were deployed on the seaward side of intertidal bars and within the troughs. Waves and currents were measured using two Teledyne (San Diego, CA, USA) WorkHorse Sentinel (1200 kHz) Acoustic Doppler Current Profilers (ADCP) located on the upper and the lower beach, and three electromagnetic wave and current meters: two Midas (Totnes, UK) Valeport© meters deployed in the intertidal zone (Figure 2D) and an InterOcean (San Diego, CA, USA) directional wave and current meter ADW S4 moored in 5 m water depth (Figure 1). The morphology of the beach was surveyed at the beginning and at the end of the experiment, using a high resolution Differential Global Positioning System DGPS, for monitoring any change in bar-trough morphology and in the position relative to the instruments. Our measurements show that the intertidal bars stayed remarkably constant during the six-day long experiment.

Table 1.
Distance from shoreline and depth/elevation of hydrographic instruments relative to Hydrographic Datum (HD) and Chart Datum (CD). Distance was measured from the toe of foredune in the backshore, considered as the position of shoreline.
All instruments operated during 9 min intervals every 15 min at a frequency of 2 Hz. The duration of each burst of hydrodynamic measurements was chosen as a compromise between two opposite constraints. It had to be long enough to allow wave spectral analysis, but it also had to be short enough to respect stationary conditions as water depth is continuously changing over a tidal cycle on macrotidal beaches.
Wave parameters were obtained by spectral analysis, providing almost continuous records of significant wave height (Hs), wave period (T) and direction. The wave spectral analysis of each burst has been realized using the Matlab Toolbox “OceanlYZ” developed by Karimpour and Chen [46] using a fast Fourier transform (FFT) algorithm, the measured data being transformed from the time domain to the frequency domain. In addition, wave power spectral density was computed for each individual burst record through power spectral analysis of the time-series of surface elevation.
All instruments recorded mean current velocity (Vm) with an accuracy of 0.02 m·s−1, but at different elevations above the bed depending on each instrument. The ADW S4 and Valeport current meters recorded current velocity at 0.4 m and 0.2 m above the seabed, respectively, while the ADCP measured current velocity at intervals of 0.2 m through the water column from 0.4 m above the bed to the surface. Current velocity at 0.2 m above the bed was estimated using the ADCP data by applying a logarithmic regression curve to the measured velocities obtained at different elevations in the water column, the vertical structure of wave-driven longshore currents on beaches being well described by a logarithmic profile [47]. The mean currents were decomposed into cross-shore (Vt) and longshore (Vl) currents, normalized relative to shoreline orientation in order to evaluate the current patterns relative to the beach orientation.
Following the method used by Guza and Thornton [48] and by Greenwood and Osborne [49], the first three normalized moments of the cross-shore velocity field were computed for each burst of each instrument for calculating the horizontal asymmetry of the cross-shore flow (which is also known as velocity skewness):
where Vt is the shore normal velocity at location x and n is the sample size (1024 for the Midas Valeport records and 1200 for the ADCP records). The overbar indicates time-averaged values and the subscripts s and sk refer to the standard deviation and skewness, respectively. This method provides a simple way to define cross-shore velocity skewness considered here as the normalized time-averaged third moment about the mean, which is different from the time-averaged third moment of the total oscillatory velocity vector (<Vt3>) computed by Bowen [50] or Bailard [51]. It also differs from wave skewness (e.g., [52]) that is related to the wave shape and not to orbital velocities. The time-series of cross-shore current velocity (Vt) of individual burst records were also subject to power spectral analysis which provided the power spectral density of cross-shore currents.
3.2. Video Imagery
A video camera was installed in the backshore at an elevation of 10 m above the mean tide level and was programmed for recording a photograph of the beach and nearshore zone every 10 s. Series of 60 consecutive photographs were used for producing average images of the coastal zone that were used for distinguishing the shoaling, breaking and surf zones during each burst of hydrodynamic measurements realized during the day (Figure 2A,B). Because the camera system had to be installed and removed every day, photographs were not continuously obtained during the field experiment, but during discrete periods of several hours. A total of 4380 photographs were used to make 73 average pictures, which enabled the determination of the wave processes (shoaling, breaking or surf) that were occurring at and near the hydrographic instruments during the daytime, the location of each instrument being signaled by a red buoy at the surface. Several breaker zones may be observed on such beaches with multiple bars where waves commonly break on an outer (seaward) bar and reform for breaking once more on a shallower (landward) bar (Figure 2A). In these cases, a distinction was made between the shoaling zone seaward of the outer bar and a non-breaking zone with reformed waves landward (Figure 2A,C).
These observations allowed the calculation of a breaker index (Hb/hb) when waves were observed to break over an instrument, using the breaking wave height (Hb) and water depth (hb) measured by that particular instrument. Although, wave breaking could take place over any bar across the beach during the rising or falling tide, most of the observations of wave breaking were obtained over the bar B3 on the lower beach, because it was submerged and affected by waves longer than any other bars located landward (Figure 2D).
4. Results
4.1. Hydro-Meteorological Conditions during the Field Experiment
The field experiment was conducted under different hydro-meteorological forcing conditions associated with light to moderate winds (about 3 to 12 m s−1) blowing almost continuously obliquely onshore from NNE to NE (Figure 3A). The tidal range varied from 3.7 m to 4.6 m (Figure 3B), whereas offshore significant wave height ranged from approximately 0.8 to 2.0 m (Figure 3C) with periods of about 4 to 5 s. Wave heights tended to increase during the field experiment, with maximum wave heights recorded on 8 June in response to NE winds with speeds of 10 to 11 m s−1 (Figure 3A). Waves were much lower in the shallow nearshore and intertidal zones, where they barely reached 1.0 m on 8 June (Figure 3C) due to wave energy dissipation over the gently sloping shoreface and the inner shelf sand banks. Strong wave energy dissipation was observed across the beach at high tide, as shown by the substantial decrease in wave height from the bar on the lower beach (bar B3) to the upper bar (bar B1) (Figure 4). Continuous records of waves also showed that wave heights were strongly modulated by changes in water level due to tides, this being especially obvious in the shallow nearshore and intertidal zones (Figure 3C). These tidally induced changes in wave height have been well documented in previous studies of beach morphodynamics in the region [4,6].
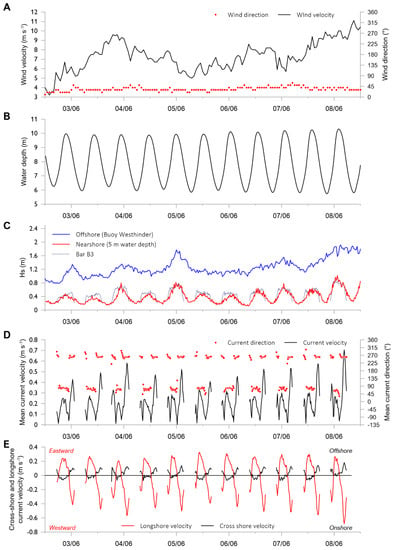
Figure 3.
Time series of wind data and hydrodynamic parameters recorded from 2 to 8 June 2013 on bar B3 on the lower beach (see Figure 2D for location) and offshore of the studied beach. (A) Wind velocity and direction recorded at the Dunkirk weather station; (B) water level changes recorded in 5 m water depth (relative to Hydrographic Datum); (C) significant wave height (Hs); (D) mean current velocity and (E) longshore and cross-shore current velocity recorded on bar B3.
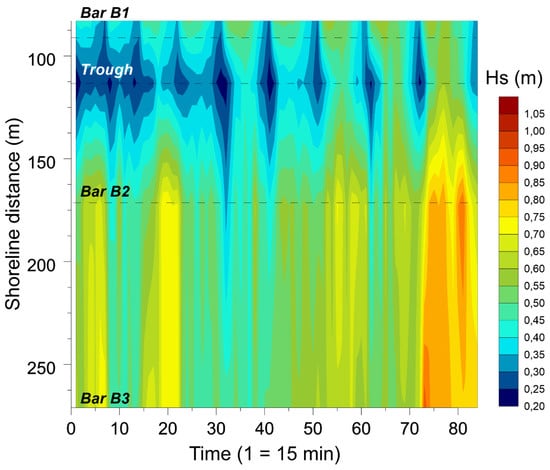
Figure 4.
Stacked burst records of significant wave height recorded at high tide showing changes in wave height across the intertidal zone. Wave height was measured on each intertidal bar and in the trough on the upper beach (locations are indicated by dashed lines). The horizontal axis does not correspond to a continuous time-series, but to the numbers of successive 15 min burst records obtained at high tide from 2 to 8 June 2013.
Current measurements on the lower beach (bar B3) show that the mean currents were essentially flowing alongshore, towards the east–northeast during flooding and towards the west–southwest during ebb, reaching 0.7 m s−1 on 8 June (Figure 3D). Peaks in current velocity, mostly ranging from approximately 0.4 to 0.6 m s−1, correspond to westward-directed ebb currents reinforced by northeasterly winds and waves. Analyses of cross-shore and longshore current velocities also show the dominance of westward-flowing currents compared to eastward-directed currents during the experiment, but furthermore show that longshore currents are significantly stronger than cross-shore currents over this sand bar located on the lower beach (Figure 3E). Our measurements also highlight that offshore-directed cross-shore flows reach higher velocities than onshore-directed flows. It is also clear from our observations that offshore-directed flows occur during both rising and falling tides, whereas (weak) onshore currents principally take place at high tide (Figure 3E).
4.2. Discrimination of Hydrodynamic Zones
The video camera system installed in the backshore was used from 3 to 7 June for determining the position of the different hydrodynamic zones in the intertidal zone during distinct current meter record bursts, based on 10 min time-averaged images obtained simultaneously during each burst. The determination of the position of the breaker zone during a current meter burst enabled to define the location of the shoaling, surf and swash zones during the same burst (Figure 2A,B), and hence to determine in which hydrodynamic zone each hydrographic instrument was located during that particular burst. These observations also allowed us to evaluate breaking wave height and water depth when breaking was occurring near an instrument.
Measurements obtained on the lower bar (Figure 2D, bar B3), which was submerged for longer periods of time and where the wave-current meter collected more data than the other instruments located landward, revealed that during breaking conditions the ratio of wave height to water depth (Hs/h) ranged from approximately 0.2 to 0.45 on the lower beach (Figure 5). During shoaling wave conditions, the Hs/h ratio was typically lower than 0.2, which is somewhat lower than the 0.3 to 0.35 relative wave height (Hs/h) value commonly given for discriminating between shoaling and breaking conditions on barred macrotidal beaches [9,16]. A comparison between relative wave height at breaking and wave steepness (Hn/Ln) measured seaward in 5 m water depth (relative to hydrographic datum) showed that low ratios of relative wave height to water depth during breaking conditions tend to correspond to higher wave steepness in the nearshore zone (Figure 5). This suggests that steeper waves break more rapidly and, therefore, in deeper water depths, which corresponds to lower relative wave height ratios (Hs/h). Conversely, breaker index values exceeding 0.3 are mostly associated with waves of low steepness <0.009. Surf zone processes were observed with relative wave height values of more than about 0.4, associated with low nearshore wave steepness (Hn/Ln) conditions (Figure 5). However, because both breaking and broken wave conditions were generally observed during these individual 10 min video records, these conditions were considered to be representative of a transition between breaking and surf zone processes.
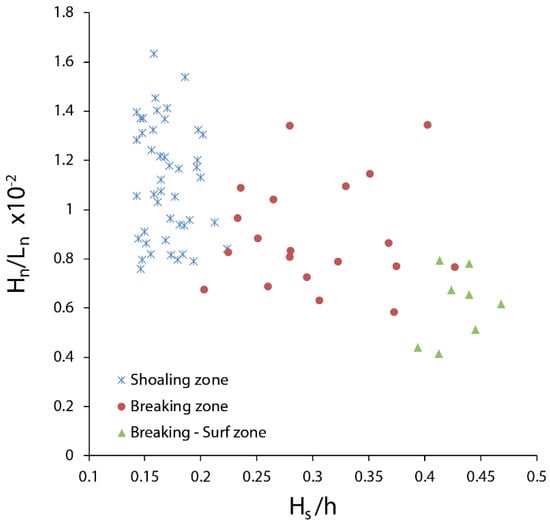
Figure 5.
Relationship between nearshore wave steepness (Hn/Ln) measured in 5 m water depth and wave height to depth ratio (Hs/h) measured on bar B3 on the lower beach (see Figure 2D for location). Wave length (Ln) was calculated according to linear wave theory. The distinction between shoaling, breaking and surf zones is based on visual determination from video images.
4.3. Characterization of Wave Spectra
Figure 6 shows power spectral density at different locations across the intertidal zone during two 10 min bursts during which waves were breaking over bar B2 near high tide (Figure 2D). During each burst measurement, a typical wave power spectrum is observed in each hydrodynamic zone. As waves were breaking over bar B2, bar B3 was affected by shoaling processes which were associated with frequencies that mostly ranged from 0.1 to 0.3 Hz (Figure 6).
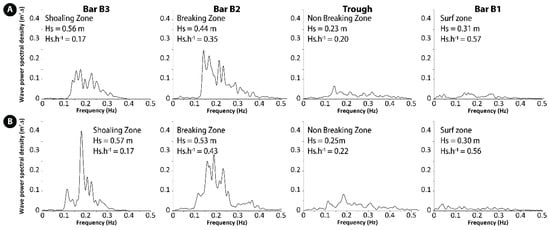
Figure 6.
Examples of wave power density spectra computed from wave data obtained at several locations across the intertidal zone on (A) 5 June 2013 (12:45 to 12:54 PM, 1 h before high tide) and (B) 6 June 2013 (01:45 to 01:54 PM, 1 h 30 min before high tide).
The wave power spectral densities can be either relatively evenly distributed over a wide range frequency, such as on 5 June when power spectral densities of approximately 0.1 to 0.15 m2 s were associated with wave frequencies of about 0.15 to 0.25 Hz (Figure 6A, Bar B3), corresponding to wave periods of 4 to 7 s, or can show a distinct peak like on 6 June when the power spectral density reached 0.4 m2 s, corresponding to surface gravity waves with a period of about 6 s (0.17 Hz) (Figure 6B, Bar B3). Over the landward bar B2 that was characterized by breaking wave conditions during these measurements, a widening of wave frequencies is observable with the presence of higher frequency waves (>0.4 Hz) as well as lower frequencies (<0.05 Hz) that may correspond to infragravity waves. Although a shoreward decrease in wave height, and hence in power spectral density, was generally observed from one bar to another, it was also observed that power spectral density could increase shoreward from bar B3 to bar B2. On 5 June, for example (Figure 6A), a maximum power spectral density of 0.15 m2 s was measured on bar B3, reaching 0.25 m2 s on bar B2, which may be due to an increase in wave height just before or during breaking on bar B2.
The significant dissipation of wave energy during breaking results in considerable flattening of the power spectrum in the landward trough (Figure 2D), with a peak in power spectral density that decreased from 0.25 m2 s to 0.07 m2 s from bar B2 to the landward trough on 5 June (Figure 6A), and from nearly 0.3 m2 s to approximately 0.1 m2 s on 6 June (Figure 6B), whereas the peak in wave frequency remained centered on the same value from the bar to the trough. When reaching bar B1 on the upper beach (Figure 2D), reformed waves have lost most of their energy as shown by the wave power spectral density values that are minimal and distributed over a wide range of frequencies (Figure 6A,B, Bar B1).
Such changes in the wave power spectrum are not only observable across the intertidal zone at a particular moment in time, but also at the same location as different hydrodynamic zones, and hence hydrodynamic processes, progressively take place with tide-induced changes in water level. These changes are clearly observable over bar B3 where most of these variations can be recorded due to its most seaward position. As water depth decreased from 3.1 m to 0.62 m over bar B3 during falling tide on 4 June, shoaling wave conditions were followed by breaking waves and eventually surf zone conditions (Figure 7A) as the wave breaking zone shifted seaward.
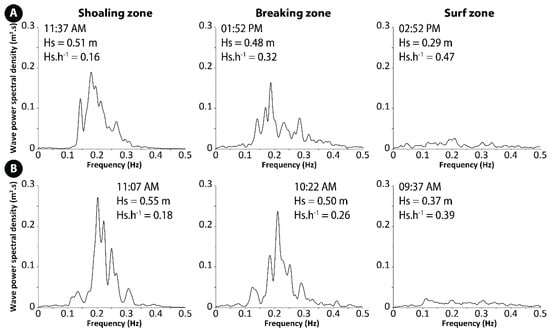
Figure 7.
Examples of wave power density spectra computed from wave data recorded on bar B3 (see Figure 2D for location) under different wave processes (shoaling, breaking and surf) as water depth decreased during falling tide on (A) 4 June 2013 (high tide at 10:30 AM and low tide at 05:30 PM) and during rising tide on (B) 6 June 2013 (low tide at 07:00 AM and high tide at 12:15 PM).
The opposite occurred during rising tide on 6 June, when bar B3 was the site of surf zone conditions, followed by breaking and then shoaling waves (Figure 7B). Similar ranges of wave frequency (0.1 to 0.3 Hz) were recorded under wave shoaling conditions during both rising and falling tides, and similarly to what was observed across the intertidal zone, a widening of wave frequencies is noticeable from shoaling to breaking conditions, accompanied by a decrease in wave power spectral density (Figure 7A,B). Alike, wave energy loss is maximum after breaking with extremely low power spectral density values when the bar is in the surf zone (Figure 7).
This progressive decrease in wave energy is also clearly visible on Figure 8 showing the temporal variations in power spectral density recorded on bar B3 during several falling tides. In all cases, peaks in power spectral density are observed during shoaling wave conditions, although some peaks were also recorded in the breaking zone on some occasions (e.g., on 5 and 6 June; Figure 8B,C). These peaks in wave energy can correspond to different wave frequencies, such as on 5 June (Figure 8B), or can be more restricted to the same wave frequency, as was the case on 6 June when higher energy waves with a period of about 5 to 6 s (≈0.17 to 0.2 Hz) were responsible for most of the wave energy expenditure over the bar (Figure 8C), similarly to what was shown for bar B3 in Figure 6A,B, respectively. Figure 8 also shows the obvious widening of the wave frequency spectra in the breaking and surf zones, with notably the development of low-frequency infragravity waves (<0.05 Hz).
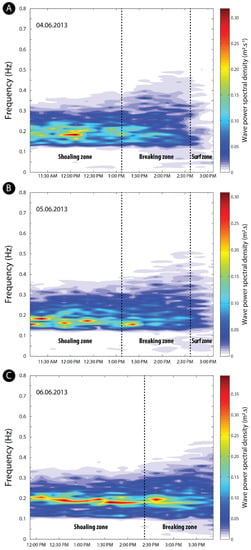
Figure 8.
Temporal variations in wave frequency and wave power spectral density over bar B3 (see Figure 2D for location) under non-breaking and breaking wave processes as water depth decreased during falling tide during moderate energy conditions (offshore Hs ≈ 1.2 m) on (A) 4 June (high tide at 10:30 AM and low tide at 05:30 PM) and (B) 5 June 2013 (high tide at 11:30 AM and low tide at 06:30 PM), and during higher energy conditions (offshore Hs ≈ 1.4–1.5 m) on (C) 6 June 2013 (high tide at 12:15 AM and low tide at 19:15 PM).
This decrease in wave power spectral density from shoaling to surf zone conditions over bar B3 is also clear when analyzing the peak wave power spectral density (PWPSD) during each burst as a function of Hs/h (Figure 9B). Some peak values of wave power spectral density under shoaling conditions are lower than others recorded during breaking conditions, which can be explained by different offshore wave energy levels at the moment of measurement, but also by the exact location of the breaking waves relative to the recording instrument. However, higher variability is observed when all data from all instruments across the intertidal zone are considered (Figure 9A). A large range of PWPSD is observed for shoaling and breaking conditions, depending on offshore wave energy conditions, but the highest values, exceeding 0.4 m2 s, essentially correspond to data obtained on bar B2. As shown on Figure 3A,B, wave heights are strongly modulated by water depth, notably in the nearshore zone where much lower wave heights are observed at low tide due to wave energy dissipation over the low-gradient shoreface. Consequently, for similar offshore wave energy levels, wave height and wave energy are higher when waves break on bar B2 on the middle beach than when they break over bar B3 located on the lower beach. Very low PWPSD values associated with high Hs/h ratio (>0.5) were also measured during breaking conditions, but these were essentially recorded on bar B1, due to wave energy dissipation over the lower intertidal bars, which resulted in very low amplitude waves breaking over the very shallow bar B1 on the upper beach.
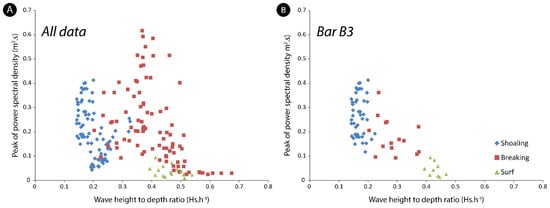
Figure 9.
Peak of wave power spectral density during individual burst records plotted as a function of wave height to depth ratio (Hs/h) for (A) data recorded by all instruments across the intertidal zone and (B) data recorded on bar B3.
4.4. Characterization of Cross-Shore Currents
Similar to what is observed with wave power spectral density, distinct signatures in cross-shore velocity spectral density can be recognized in each hydrodynamic zone from the current records. As for the waves, the frequency spectra of cross-shore currents are narrower in the shoaling and breaking zones compared to the surf zone where a much wider spectrum is observed (Figure 10). This can be seen on the current spectra recorded on bar B3 that experienced shoaling, breaking and eventually surf processes as the tide was falling on 4 June, with distinct frequency peaks under shoaling and breaking conditions and much subdued peaks when the bar was in the surf zone (Figure 10A). It is noteworthy that the peak frequencies in the shoaling and breaking zones in these records are mostly ranging from 0.15 to 0.2 Hz although a wider distribution is generally observed in the breaking zone, which is very similar to what was observed for the wave spectra (Figure 6 and Figure 7), suggesting that the cross-shore currents are mostly wave-generated currents. These (on)offshore-directed oscillatory currents mainly occur in the shoaling and breaking zone, whereas they tend to be much weaker in the surf zone after wave breaking. The analysis of the frequency distribution of cross-shore currents shows the existence of lower frequency flows (<0.1 Hz) in the surf zone (Figure 10), which were virtually absent in the shoaling zone and breaking zones, suggesting the development of near-steady cross-shore flows near the bed in this hydrodynamic zone. A similar cross-shore currents spectral characterization was observed over bar B3 during rising tide as well with peak frequencies mostly ranging from 0.18 to 0.25 Hz in the shoaling and breaking zones (Figure 10B), showing that these currents were associated with waves with periods of 4 to 5.5 s. Again, the values of power spectral density were significantly lower in the surf zone and distributed over a much wider frequency range.
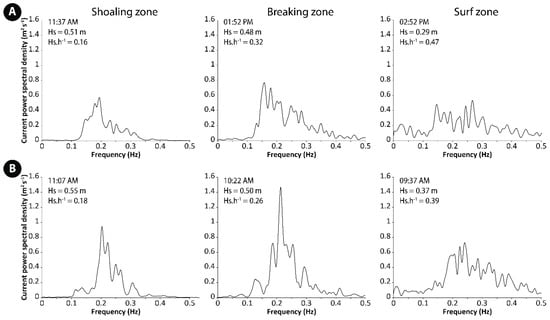
Figure 10.
Examples of cross-shore current power density spectra obtained from current data recorded on bar B3 (see Figure 2D for location) under different wave processes (shoaling, breaking and surf) during (A) falling tide on 4 June 2013 (high tide at 10:30 AM and low tide at 05:30 PM) and (B) rising tide on 6 June 2013 (low tide at 07:00 AM and high tide at 12:15 PM).
Figure 11 shows the temporal variations in cross-shore currents power spectral density recorded on bar B3 under breaking and non-breaking conditions during several falling tides. The figure highlights that the peak spectral densities of the cross-shore currents are observed in the breaker zone, and to a lesser extent in the shoaling zone, whereas the power spectral densities are much lower in the surf zone. Our results also show that the frequencies associated with the peaks in spectral density essentially range from 0.15 to 0.2 Hz, which correspond to wave periods of about 5 to 7 s, similar to what was observed for wave power spectral densities (Figure 7 and Figure 8).
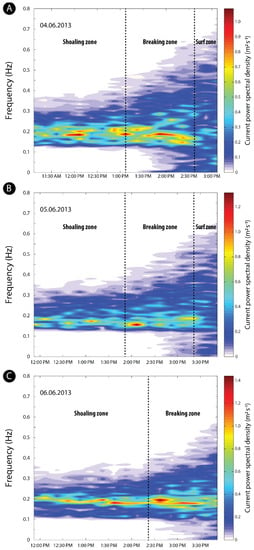
Figure 11.
Temporal variations in frequency and power spectral density of cross-shore currents over bar B3 (see Figure 2D for location) under non-breaking and breaking wave processes as water depth decreased during falling tide during moderate energy conditions (offshore Hs ≈ 1.2 m) on (A) 4 June (high tide at 10:30 AM and low tide at 05:30 PM) and (B) 5 June 2013 (high tide at 11:30 AM and low tide at 06:30 PM), and during higher energy conditions (offshore Hs ≈ 1.4–1.5 m) on (C) 6 June 2013 (high tide at 12:15 AM and low tide at 19:15 PM).
In addition to the analysis of the power spectral density of cross-shore currents, the frequency distribution of onshore- and offshore-directed currents was also examined. As shown in a series of cross-shore current records obtained over bar B3, the frequency distribution of onshore and offshore velocities is nearly symmetrical and characterized by low skewness values under shoaling processes (Figure 12). In the breaking zone, however, the frequency distribution of onshore- and offshore-directed flows is generally asymmetric with higher frequencies of offshore currents compared to onshore currents (Figure 12A). This asymmetry in cross-shore current distributions is even more pronounced in the surf zone where the proportion of offshore-directed currents is significantly higher than onshore currents of the same velocity, this being highlighted by the high values in cross-shore currents skewness (Figure 12A,B).
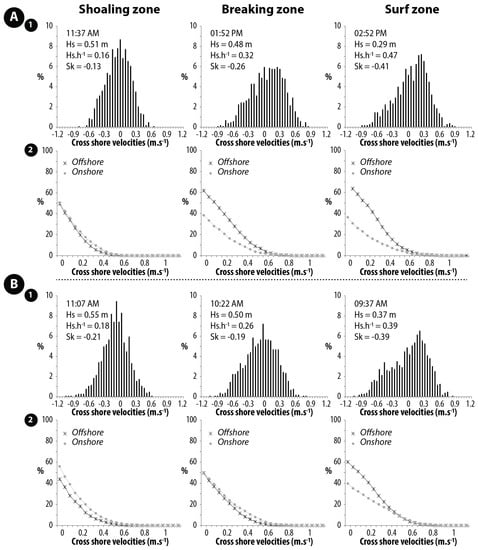
Figure 12.
Examples of (A1,B1) frequency distributions of cross-shore velocities, and (A2,B2) cumulative frequency distributions of onshore and offshore velocities from current measurements recorded on bar B3 and under different wave processes (shoaling, breaking and surf). Data recorded (A) during falling tide on 4 June and (B) during rising tide on 6 June 2013. The positive and negative values of cross-shore velocities in A1 and B1 correspond, respectively, to offshore- and onshore-directed flows.
These variations in cross-shore current distributions are especially obvious when looking at the changes in frequency of cross-shore current velocities over bar B3 that successively experienced shoaling, breaking and surf processes as water depth decreased during falling tides (Figure 13). In the three examples shown in Figure 13, the distribution of onshore- and offshore-directed currents in the shoaling zone is centered on low-velocity values that are mostly ranging from approximately −0.15 m s−1 to 0.1 m s−1, respectively. A slightly higher proportion of onshore flows can be observed for higher velocity cross-shore currents, which can probably be explained by the onshore asymmetry of shoaling waves. A lower proportion of low-velocity cross-shore currents were recorded on 6 June (Figure 13C), which can be explained by slightly higher offshore significant wave heights in the beginning of the afternoon compared to the two preceding days (Figure 3C), but the same distribution pattern of onshore- and offshore-directed flows remained.
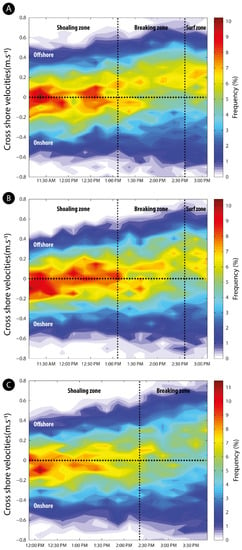
Figure 13.
Temporal variations in frequency of onshore- and offshore-directed cross-shore current velocities over bar B3 (see Figure 2D for location) under non-breaking and breaking wave processes as water depth decreased during falling tide during moderate energy conditions (offshore Hs ≈ 1.2 m) on (A) 4 June and (B) 5 June 2013, and higher energy conditions (offshore Hs ≈ 1.4–1.5 m) on (C) 6 June 2013.
The action of breaking waves over the bar resulted in an increase in cross-shore current velocities in both directions, which reached or exceeded 0.8 m s−1 in both directions on several occasions while maximum cross-shore currents hardly reached 0.6 m s−1 in the shoaling zone on the same days, especially for offshore flows (Figure 13). In addition, a clear shift towards offshore-directed flows is visible in the distribution of cross-shore currents, characterized by an increase in the frequency of offshore currents of any given velocity (Figure 13). This tendency proceeds further when the bar is in the surf zone and is affected by broken waves and dominated by offshore-directed flows, as observed on 4 June (Figure 13A) and 5 June (Figure 13B).
The variation in cross-shore current patterns across the beach could only be observed during limited time periods at, or near, high tide when all instruments were submerged. During these periods, the lower beach mostly experienced onshore-directed near bottom currents associated with shoaling waves as Figure 14 shows. Depending on wave conditions, bar B2 could be affected by shoaling processes and onshore-directed currents or by off-shore-directed flows when the bar was in the breaking or surf zone. It is quite clear from these measurements that offshore-directed currents tend to develop on the mid to the upper beach as water depth decreases and waves transform from shoaling to breaking.
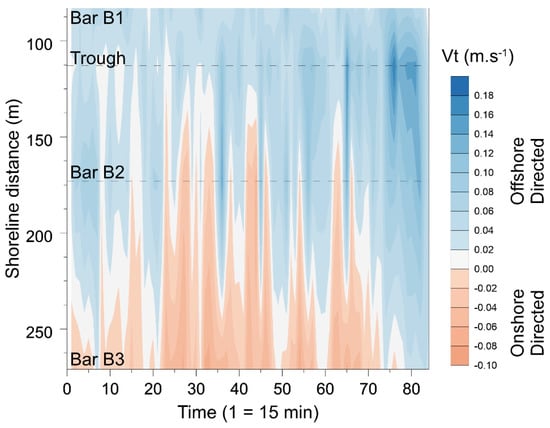
Figure 14.
Stacked burst records of mean cross-shore current velocities at high tide showing variations in current direction and velocity across the intertidal zone. Near-bottom currents were measured on each intertidal bar and in the trough on the upper beach (locations are indicated by dashed lines). The horizontal axis does not correspond to a continuous time-series, but to the numbers of successive 15 min burst records obtained at high tide from 2 to 8 June 2013.
5. Discussion
Our measurements of wave and current parameters across the surveyed beach showed distinct hydrodynamic signatures characterizing each zone dominated by either shoaling, breaking and surf processes, the limits of which having been determined visually by the position of breaking waves during discrete time periods. Our direct measurements of wave height and water depth during breaking conditions also allowed us to compute accurate wave height to depth ratios at breaking (Hb/hb), such data being rather limited in macrotidal beach environments. It is well known that wave height to depth ratios on natural beaches can considerably differ from the theoretically derived value of 0.78 (McCowan’s criterion), which is still a widely used breaker index in coastal hydrodynamics and/or sediment transport applications, even if a large numbers of experimental studies showed that the ratio of wave height to depth at breaking can considerably differ from this theoretical value, depending on several parameters, notably beach slope and wave steepness [39,53,54]. Wave height to depth ratios of 0.3 to 0.5 are commonly proposed for discriminating breaking wave conditions on barred macrotidal beaches [3,8,16], but very few field measurements have been carried out so far for verifying the validity of these values for random waves breaking on macrotidal beaches, since these values are mostly derived from measurements on mesotidal rather than macrotidal beaches. Masselink [8], for example, uses a breaker index of 0.4 in his morphodynamic model of intertidal bar formation on macrotidal beaches in which he places the start of the outer and inner surf zone at depths corresponding to H/h ratios of 0.3 and 0.5, respectively, based on hydrodynamic measurements conducted on a micro- to mesotidal shoreface [55] and on a mesotidal beach [38]. From video images and acoustic sensor data, Grasso and Ruessink [54] report Hb/hb values of approximately 0.3 as a boundary between non-breaking and breaking conditions on a meso- to macrotidal beach.
Although our results mostly agree with the breaking index values > 0.3 previously reported for macrotidal beaches, our measurements also show that waves can begin to break in deeper water than what could be predicted using these values, since breaking waves associated with Hb/hb ratios of 0.2 to 0.3 were observed on several occasions across the intertidal zone (Figure 9), especially on the lower beach (Figure 15). The discrepancies between our results and previously published breaker index values for macrotidal beaches may be due to the fact that some of the previous studies from which these values were derived were carried out in micro- to mesotidal coastal environments, as mentioned before, but could also be explained by different methods for determining the wave height at breaking or the breaker position (and thus the wave breaking depth). It is also possible that the very low gradients that characterize the investigated beach (tanβ = 1.4%) and nearshore zone (tanβ ≈ 1%) favor the initiation of wave breaking. The observed differences with the results obtained in previous studied may also be related to differences in ranges of wave height, since moderate energy conditions prevailed during our field experiment compared to the aforementioned experimental studies that were mostly carried out on more energetic beaches.
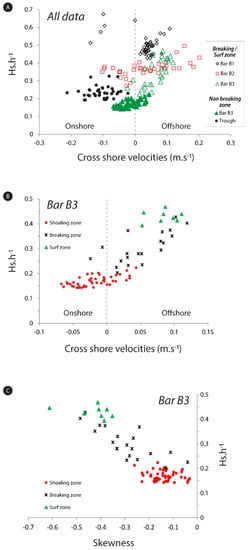
Figure 15.
Relationship between wave height to depth ratio (Hs/h) and (A,B) mean-cross-shore current velocity recorded across the intertidal zone by (A) all instruments and (B) on bar B3, and (C) cross-shore velocity skewness recorded on bar B3.
Interestingly, in their study of the hydrodynamics of four macrotidal beaches in Brittany, Dehouck et al. [20] proposed an empirical breaking index of 0.2–0.25 for separating the shoaling and the surf zones based on the occurrence of offshore-directed flows when the wave height to water depth ratio exceeded this value, arguing that these seaward currents corresponded to surf zone undertow. Although their criteria for discriminating between shoaling and surf processes is based on a different approach, these authors obtained similar values to what we observed in our study using video imagery. In accordance with their findings, offshore-directed currents were also recorded in the present study over intertidal bars for similar H/h values under breaking and surf processes (Figure 12 and Figure 15A). Velocities of offshore-directed cross-shore currents were relatively low during our experiment, rarely exceeding 0.2 m s−1 (Figure 15A), compared to undertow velocities that commonly reach values up to 0.4 m s−1 in the surf zone of other barred beaches [4,20,56,57]. This is probably due to the moderate wave energy regime that characterized our field experiment during which offshore Hs were constantly lower than 2 m (Figure 3C) while wave heights offshore of the Brittany coast during the experiment of Dehouck et al. [20], for example, ranged between 3 and 7 m during storms that took place during their experiment.
Onshore-directed flows were also observed in the surf and breaking zones during our field experiment, but they were essentially measured on the middle and the upper beach over bars B2 and B1 and especially in the trough between these bars (Figure 15A). Because the trough is the site of wave transformation after breaking, the onshore-directed currents measured in the trough are probably due to surf zone bores associated with asymmetric saw-tooth shape waves [9]. The occurrence of onshore flows over the inner bars (bars B2 and B1) may be due to reformed waves after breaking on the bar located immediately seaward, resulting in an onshore asymmetry of wave oscillatory currents.
In addition of the differences in the direction of cross-shore flows across the intertidal zone, other distinct hydrodynamic characteristics were observed within each hydrodynamic zone (Figure 16). The analysis of wave spectral density showed the development of both low-frequency and high-frequency waves in the breaking and surf zones (Figure 7 and Figure 8). The observed high frequencies presumably correspond to turbulent motions related to breaking waves. As waves break and transform in the surf zone, wave energy is transferred into turbulent motions through highly energetic processes associated with breaking waves time scales, and turbulence is then dissipated at smaller scales (i.e., smaller than the incident wave periods) [58,59]. Strong wave energy dissipation associated with high-frequency motions can be observed across the beach from the shoaling zone to the surf zone (Figure 6), but also over a particular bar through time due the horizontal tidal translation of the hydrodynamic zones (Figure 8).
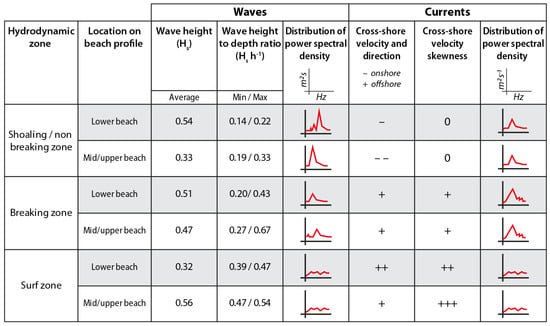
Figure 16.
Summary diagram of the main hydrodynamic characteristics observed in each hydrodynamic zone of the investigated beach. The numbers of + and − signs represent the relative intensity of cross-shore currents and.
Low-frequency waves (<0.05 Hz) were also measured in the breaking and surf zones (Figure 8) which probably result from infragravity-wave growth. Several mechanisms have been proposed for explaining the generation of infragravity waves in coastal regions including non-linear interactions between freely propagating short waves [60,61], bound long waves generated through wave–wave interaction within wave groups [62,63], and merging of bores in the surf zone [64]. Our records show the existence of wave groups with distinct peaks in frequencies in the short gravity range over intertidal bars (e.g., bars B2 and B3, Figure 5), which may be responsible for energy transfer to lower frequencies in the breaking and surf zones through wave–wave interaction. However, our measurements did not allow to discern trapped infragravity waves at the location of bars as described by Rijnsdorp et al. [61] in their study of infragravity wave dynamics over a barred beach.
Overall, our results are in general agreement with the conceptual model of Masselink et al. [9], describing changes in cross-shore sediment transport over intertidal bars based on the relative contribution of offshore- or onshore-directed flows that vary in direction and intensity in response to the shifting of wave processes across the beach profile, resulting from tide-induced water-level changes. However, more variability in cross-shore current directions was observed in the breaker and surf zones of the investigated beach, compared to what is theoretically predicted by this idealized model. This may possibly be explained by the fact that, for a given water depth in the intertidal zone, there will be distributions of both breaking and non-breaking waves at a particular moment in time due to the random character of natural wind-generated waves [34], resulting in a mixture of breaking and surf processes.
6. Conclusions
The results of this study show that the different zones of wave transformation, which almost continuously shift in position across a barred macrotidal beach, are characterized by distinct wave-induced processes. The analyses of wave power spectral density clearly show a widening of the frequencies of the incident gravity waves from the shoaling to the surf zone, with the development of both infragravity and turbulent frequencies associated with a major decrease in wave energy. Analyses of cross-shore flow asymmetry also showed significant differences between the shoaling zone, which is characterized by virtually symmetrical cross-shore current velocities, whereas offshore-directed cross-shore flow asymmetry is generally observed in the wave breaking and surf zones. These results suggest that these processes represent hydrodynamic signatures that can be used for discriminating the different hydrodynamic zones of barred macrotidal beaches from wave and current data (Figure 16).
However, the determination of a hydrodynamic zone can hardly be based on a single parameter because some overlap was observed in the hydrodynamic variables associated with the different wave transformation zones from the lower to the upper beach (Figure 16), requiring the use of several parameters for determining hydrodynamic zones from wave and current measurements.
Author Contributions
Conceptualization, A.H. and A.C.; field measurements—data acquisition, A.H. and A.C.; data processing, A.C. and F.G.S.; formal analysis and interpretation, A.H. and F.G.S.; writing—original draft preparation, A.H.; writing—review and editing, A.C. and F.G.S.; project supervision, A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available because they are not archived in a publicly accessible repository.
Acknowledgments
This work is part of the investigations carried out on the coast of northern France within the framework of the French Service National d’Observation DYNALIT. The authors thank Vincent Sipka for his assistance during the field experiment. Thanks are also due to Denis Marin for his help in the preparation of the figures.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Levoy, F.; Monfort, O.; Larsonneur, C. Hydrodynamic variability on megatidal beaches, Normandy, France. Cont. Shelf Res. 2001, 21, 563–586. [Google Scholar] [CrossRef]
- Masselink, G.; Anthony, E.J. Location and height of inter-tidal bars on macrotidal ridge and runnel beaches. Earth Surf. Process. Landf. 2001, 26, 759–774. [Google Scholar] [CrossRef]
- Kroon, A.; Masselink, G. Morphodynamics of intertidal bar morphology on a macrotidal beach under low-energy wave conditions, North Lincolnshire, England. Mar. Geol. 2002, 190, 591–608. [Google Scholar] [CrossRef]
- Anthony, E.J.; Levoy, F.; Montfort, O. Morphodynamics of intertidal bars on a megatidal beach, Merlimont, Northern France. Mar. Geol. 2004, 208, 73–100. [Google Scholar] [CrossRef]
- Reichmüth, B.; Anthony, E.J. Tidal influence on the intertidal bar morphology of two contrasting macrotidal beaches. Geomorphology 2007, 90, 101–114. [Google Scholar] [CrossRef]
- Cartier, A.; Héquette, A. The influence of intertidal bar-trough morphology on sediment transport on macrotidal beaches, northern France. Zeits. Geomorph. 2013, 57, 325–347. [Google Scholar] [CrossRef]
- Anthony, E.J.; Levoy, F.; Montfort, O.; Degryse-Kulkarni, C. Patterns of short-term intertidal bar mobility on a ridge and runnel beach, Merlimont, Northern of France. Earth Surf. Process. Landf. 2005, 30, 81–93. [Google Scholar] [CrossRef]
- Masselink, G. Formation and evolution of multiple intertidal bars on macrotidal beaches application of a morphodynamic model. Coast. Eng. 2004, 51, 713–730. [Google Scholar] [CrossRef]
- Masselink, G.; Kroon, A.; Davidson-Arnott, R. Morphodynamics of intertidal bars in wave-dominated coastal settings—A review. Geomorphology 2006, 73, 33–49. [Google Scholar] [CrossRef]
- Reichmüth, B.; Anthony, E.J. Dynamics of intertidal drainage channels on a multi barred macrotidal beach. Earth Surf. Process. Landf. 2008, 33, 142–151. [Google Scholar] [CrossRef]
- Poate, T.; Masselink, G.; Russell, P.; Austin, M. Morphodynamic variability of high-energy macrotidal beaches, Cornwall, UK. Mar. Geol. 2014, 350, 97–111. [Google Scholar] [CrossRef]
- Davidson, M.A.; Russell, P.; Huntley, D.; Hardisty, J. Tidal asymmetry in suspended sand transport on a macrotidal intermediate beach. Mar. Geol. 1993, 110, 333–353. [Google Scholar] [CrossRef]
- Voulgaris, G.; Simmonds, D.; Michel, D.; Howa, H.; Collins, M.B.; Huntley, D. Measuring and modelling sediment transport on a macrotidal ridge and runnel beach: An intercomparison. J. Coast. Res. 1998, 14, 315–330. [Google Scholar]
- Masselink, G.; Pattiaratchi, C. Tidal asymmetry in sediment resuspension on a macrotidal beach in northwestern Australia. Mar. Geol. 2000, 163, 257–274. [Google Scholar] [CrossRef]
- Corbau, C.; Ciavola, P.; Gonzalez, R.; Ferreira, O. Measurements of cross-shore sand fluxes on a macrotidal pocket beach (Saint-Georges Beach, Atlantic Coast, SW France). J. Coast. Res. 2002, 36, 182–189. [Google Scholar] [CrossRef][Green Version]
- Sedrati, M.; Anthony, E.J. Storm-generated morphological change and longshore sand transport in the intertidal zone of a multi-barred macrotidal beach. Mar. Geol. 2007, 244, 209–229. [Google Scholar] [CrossRef]
- Austin, M.; Masselink, G.; O’Harea, T.; Russell, P. Onshore sediment transport on a sandy beach under varied wave conditions: Flow velocity skewness, wave asymmetry or bed ventilation? Mar. Geol. 2009, 259, 86–101. [Google Scholar] [CrossRef]
- Cartier, A.; Héquette, A. Variation in longshore sediment transport under low to moderate conditions on barred macrotidal beaches. J. Coast. Res. 2011, 64, 45–49. [Google Scholar]
- Cartier, A.; Héquette, A. Vertical distribution of longshore sediment transport on barred macrotidal beaches, Northern France. Cont. Shelf Res. 2015, 93, 1–16. [Google Scholar] [CrossRef]
- Dehouck, A.; Dupuis, H.; Sénéchal, N. Pocket beach hydrodynamics: The example of four macrotidal beaches, Brittany, France. Mar. Geol. 2009, 266, 1–17. [Google Scholar] [CrossRef]
- Austin, M.; Scott, T.; Brown, J.; Brown, J.; MacMahan, J.; Masselink, G.; Russell, P. Temporal observations of rip current circulation on a macro-tidal beach. Cont. Shelf Res. 2010, 30, 1149–1165. [Google Scholar] [CrossRef]
- Haines, J.W.; Sallenger, A.H., Jr. Vertical structure of mean cross-shore currents across a barred surf zone. J. Geophys. Res. 1994, 99, 14223–14242. [Google Scholar] [CrossRef]
- Kuriyama, Y.; Nakatsukasa, T. A one-dimensional model for undertow and longshore current on a barred beach. Coast. Eng. 2000, 40, 39–58. [Google Scholar] [CrossRef]
- Rattanapitikon, W.; Shibayama, T. Simple model for undertow profile. Coast. Eng. Jour. 2000, 42, 1–30. [Google Scholar] [CrossRef]
- Cambazoglu, M.K.; Haas, K.A. Numerical modeling of breaking waves and cross-shore currents on barred beaches. J. Water. Port Coast. Ocean Eng. 2011, 137, 310–323. [Google Scholar] [CrossRef]
- Biausque, M.; Grottolia, E.; Jackson, D.W.T.; Cooper, J.A.G. Multiple intertidal bars on beaches: A review. Earth-Sci. Rev. 2020, 210, 103358. [Google Scholar] [CrossRef]
- Kamphuis, J.W. Alongshore sediment transport rate. J. Water. Port Coast. Ocean Eng. 1991, 117, 624–640. [Google Scholar] [CrossRef]
- Smith, E.R.; Wang, P.; Ebersole, B.A.; Zhang, J. Dependence of total longshore sediment transport rates on incident wave parameters and breaker type. J. Coast. Res. 2009, 25, 675–683. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Prediction of dune erosion due to storms. Coast. Eng. 2009, 56, 441–457. [Google Scholar] [CrossRef]
- Corbella, S.; Stretch, D.D. Predicting coastal erosion trends using non-stationary statistics and process-based models. Coast. Eng. 2012, 70, 40–49. [Google Scholar] [CrossRef]
- D’Alessandro, F.; Tomasicchio, G.R. Wave-dune interaction and beach resilience in large-scale physical model tests. Coast. Eng. 2016, 116, 15–25. [Google Scholar] [CrossRef]
- Giardino, A.; van der Werf, J.; van Ormondt, M. Simulating Coastal Morphodynamics with Delft3D: Case Study Egmond aan Zee. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2010; 78p. [Google Scholar]
- Simmons, J.A.; Harley, M.D.; Marshall, L.A.; Turner, I.L.; Splinter, K.D.; Cox, R.J. Calibrating and assessing uncertainty in coastal numerical models. Coast. Eng. 2017, 125, 28–41. [Google Scholar] [CrossRef]
- Hieu, P.D.; Katsutoshi, T.; Ca, V.T. Numerical simulation of breaking waves using a two-phase flow model. Appl. Math. Model. 2004, 28, 983–1005. [Google Scholar] [CrossRef]
- Cienfuegos, R.; Barthélemy, E.; Bonneton, P. Wave-breaking model for Boussinesq-type equations including roller effects in the mass conservation equation. J. Water. Port Coast. Ocean Eng. 2010, 136, 10–26. [Google Scholar] [CrossRef]
- Kasinatha Pandian, P.; Emmanuel, O.; Ruscoe, J.P.; Side, J.C.; Harris, R.E.; Kerr, S.A.; Bullen, C.R. An overview of recent technologies on wave and current measurement in coastal and marine applications. J. Ocean. Mar. Sci. 2010, 1, 1–10. [Google Scholar]
- Héquette, A.; Cartier, A. Theoretical and observed breaking wave height on a barred macrotidal beach: Implications for the estimation of breaker index on beaches with large tidal range. J. Coast. Res. 2016, 75, 861–866. [Google Scholar] [CrossRef]
- Thornton, E.B.; Guza, R.T. Energy saturation and phase speeds measured on a natural beach. J. Geophys. Res. 1982, 87, 9499–9508. [Google Scholar] [CrossRef]
- Sallenger, A.H., Jr.; Hollman, R.A. Wave energy saturation on a natural beach of variable slope. J. Geophys. Res. 1985, 90, 11939–11944. [Google Scholar] [CrossRef]
- Anthony, E.J.; Héquette, A. The grain-size characterisation of coastal sand from the Somme estuary to Belgium: Sediment segregation processes and sources consideration. Sed. Geol. 2007, 202, 369–382. [Google Scholar] [CrossRef]
- SHOM. Références Altimétriques Maritimes—Ports de France Métropolitaine et D’outre-Mer. In Cotes du Zéro Hydrographique et Niveaux Caractéristiques de la Marée; Service Hydrographique et Océanographique de la Marine: Brest, France, 2013; 116p. [Google Scholar]
- Héquette, A.; Hemdane, Y.; Anthony, E.J. Sediment transport under wave and current combined flows on a tide-dominated shoreface, northern coast of France. Mar. Geol. 2008, 249, 226–242. [Google Scholar] [CrossRef]
- Héquette, A.; Hemdane, Y.; Anthony, E.J. Determination of sediment transport paths in macrotidal shoreface environments: A comparison of grain-size trend analysis with near-bed current measurements. J. Coast. Res. 2008, 24, 695–707. [Google Scholar] [CrossRef]
- Ruz, M.H.; Héquette, A.; Maspataud, A. Identifying forcing conditions responsible for foredune erosion on the northern coast of France. J. Coast. Res. 2009, 56, 356–360. [Google Scholar]
- CEREMA. Dynamiques et Évolution du Littoral—Fascicule 1: De la Frontière Belge à la Pointe du Hourdel; Ministère de la Transition Écologique et Solidaire: Bron, France, 2018; 499p. [Google Scholar]
- Karimpour, A.; Chen, Q. Wind wave analysis in depth limited water using OCEANLYZ, A MATLAB toolbox. Comput. Geosc. 2013, 106, 181–189. [Google Scholar] [CrossRef]
- Garcez Faria, A.F.; Thornton, E.B.; Stanton, T.P.; Soares, C.V.; Lippmann, T.C. Vertical profiles of longshore currents and related bed shear stress and bottom roughness. J. Geophys. Res. 1998, 103, 3217–3232. [Google Scholar] [CrossRef]
- Guza, R.T.; Thornton, E.B. Velocity moments in nearshore. J. Water. Ports Coast. Ocean Eng. 1985, 111, 235–256. [Google Scholar] [CrossRef]
- Greenwood, B.; Osborne, P.D. Equilibrium slopes and cross-shore velocity asymmetries in a storm-dominated, barred nearshore system. Mar. Geol. 1991, 96, 211–235. [Google Scholar] [CrossRef][Green Version]
- Bowen, A.J. Nearshore Velocity Measurements and Beach Equilibrium. In Proceedings of the Canadian Coastal Conference, Burlington, ON, Canada, 22–24 April 1980; National Research Council Canada: Ottawa, ON, Canada, 1980; pp. 21–30. [Google Scholar]
- Bailard, J.A. An energetics model for a plane sloping beach. J. Geophys. Res. 1981, 86, 10938–10954. [Google Scholar] [CrossRef]
- Grasso, F.; Michallet, H.; Barthélemy, E. Sediment transport associated with morphological beach changes forced by irregular asymmetric, skewed waves. J. Geophys. Res. 2011, 116, C03020. [Google Scholar] [CrossRef]
- Galvin, C.J.; Eagleson, P.E. Experimental Study of Longshore Currents on a Plane Beach; Technical Memo No. 10; US Army Coastal Engineering Research Center: Washington, DC, USA, 1965; 80p. [Google Scholar]
- Grasso, F.; Ruessink, B.G. Vertical structure of the turbulent dissipation rate in the surf zone. J. Coast. Res. 2011, 64, 90–94. [Google Scholar]
- Ruessink, B.G.; Houwman, K.T.; Koestra, P. The systematic contribution of transporting mechanisms to the cross-shore sediment transport in water depths of 3 to 9 m. Mar. Geol. 1998, 152, 295–324. [Google Scholar] [CrossRef]
- Masselink, G.; Black, K.P. Magnitude and cross-shore distribution of bed return flow measured on natural beaches. Coast. Eng. 1995, 25, 165–190. [Google Scholar] [CrossRef]
- Garcez Faria, A.F.; Thornton, E.B.; Lippmann, T.C.; Stanton, T.P. Undertow over a barred beach. J. Geophys. Res. 2000, 105, 16999–17010. [Google Scholar] [CrossRef]
- Svendsen, I.A. Analysis of surf zone turbulence. J. Geophys. Res. 1987, 92, 5115–5124. [Google Scholar] [CrossRef]
- Schmitt, F.G.; Huang, Y.; Lu, Z.; Liu, Y.; Fernandez, N. Analysis of velocity fluctuations and their intermittency properties in the surf zone using empirical mode decomposition. J. Mar. Syst. 2009, 77, 473–481. [Google Scholar] [CrossRef]
- Elgar, S.; Guza, R.T. Observations of bispectra of shoaling surface gravity waves. J. Fluid Mech. 1985, 161, 425–448. [Google Scholar] [CrossRef]
- Rijnsdorp, D.P.; Ruessink, G.; Zijlema, M. Infragravity-wave dynamics in a barred coastal region, a numerical study. J. Geophys. Res. Oceans. 2015, 120, 4068–4089. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stress and mass transport in surface gravity waves with application to ‘surf beats’. J. Fluid Mech. 1962, 13, 481–504. [Google Scholar] [CrossRef]
- Battjes, J.A.; Bakkenes, H.J.; Janssen, T.T.; Van Dongeren, A.R. Shoaling of subharmonic gravity waves. J. Geophys. Res. 2004, 109, C02009. [Google Scholar] [CrossRef]
- Sénéchal, N.; Dupuis, H.; Bonneton, P.; Howa, H.; Pedreros, R. Observations of irregular wave transformation in the surf zone over a gently sloping sandy beach on the French Atlantic coastline. Ocean. Acta 2001, 24, 545–556. [Google Scholar] [CrossRef][Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).