1. Introduction
Ocean dynamic phenomena have been distributed in the global ocean. Among them, eddies are characterised by unstable, time-dependent water masses, which separate from their respective currents and enter water bodies with different physical, chemical and biological characteristics [
1]. More than half of the kinetic energy of the ocean circulation is stored in the mesoscale eddies, with the remainder contained in the large-scale circulation, swirling motions of eddies mixed between layers and consequent mixing of nutrients, heat and salinity. Sound propagation through eddies has a crucial impact on humans, marine animals and invertebrates [
2]. Under the influence of oceanic eddies, human underwater acoustic communication networks are impacted. The existence of eddies affects the detection and communication of marine creatures [
3]. Some whales, seals and fishes use low-frequency sound to communicate, perceive the environment and respond to those sounds [
4]. At present, there are some experiments to prove that the sound of deep-sea creatures is detected at a location of 15 km away. Fishes feed along with the density structure of the eddies, which indicates that eddies accelerate the transfer of energy and nutrients in the ocean. Anticyclonic eddies carry higher surface chlorophyll than cyclonic eddies. Because the mixed layer of cyclonic eddies is often shallower than that of anticyclonic eddies, the pycnocline depth of the anticyclonic eddies is deeper. More plankton in the deeper mixed layer therefore provides more nutrients for zooplankton [
5]. The study of sound propagation through the eddies clearly plays a significant role in the life of human and marine organisms. Regarding the deep-sea sound propagation issue, we always focus on the convergent position of sound energy and the acoustic intensity distribution. Aiming at the phenomenon of how the oceanic eddy affects the position of the convergence zone, this paper uses the parabolic equation method to solve sound field and combines it with the normal mode theory to analyse the difference of energy distribution of the acoustic wave at different positions.
It is of great significance for weather and marine scientific research to grasp the real-time movement of eddies. The nonlinear interaction of barotropic and baroclinic Rossby waves could lead to strong instability, which is a major source of the kinetic energy of eddies [
6]. These eddies are affected by Coriolis, which lifts high-temperature cyclones from subsurface water to the surface of the sea [
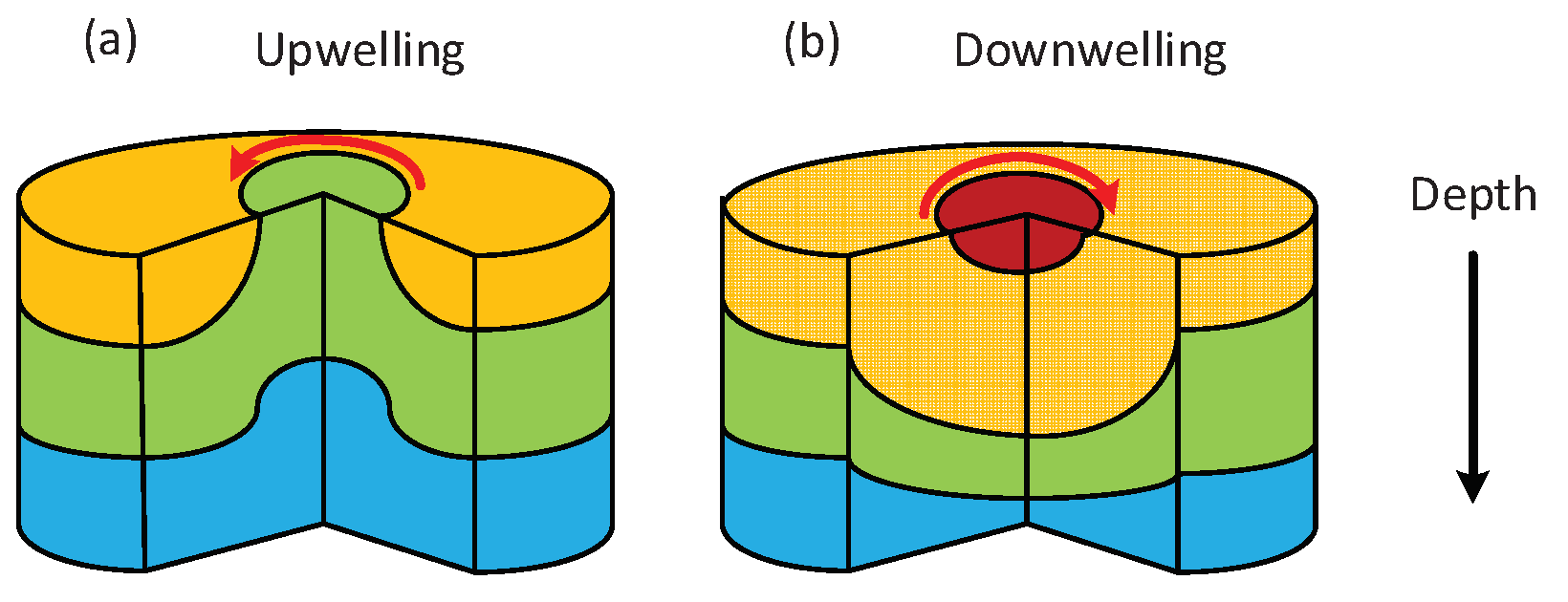
7]. Some smaller-scale eddies (tens of kilometres in diameter) are formed due to the instability of baroclinic at the horizontal density, while larger-scale eddies located near the warm current of Gulf Stream and the Kuroshio Current are generally due to strong horizontal shear motion, which intensely affects the temperature and salinity distribution in the depth direction. The dynamic model of the eddies was proposed as early as the 19th century. Taking the change of sea surface height and the temperature in the depth direction caused by the eddies into account, the sound speed shapes in space can be divided into the following types: bowl shape, lens-shaped, cone-shaped, moreover, the generation mechanism of eddies are divided into three types, sea surface wind, the interaction between ocean currents and bottom topography, and Kuroshio intrusion [
8]. In the northern hemisphere, these cyclonic eddies rotate clockwise, whereas, in the southern hemisphere, they rotate counterclockwise. The low-temperature anticyclonic eddies cause the downwelling of the surface layer and dent formed in opposite directions of rotation. Eddies could be distinguished through the combination of sea surface height and sea surface temperature anomalies. Some scholars used buoys to capture the formation, the movement and the extinction of eddies. Mesoscale eddies in the Pacific generally last several weeks. Their motion trajectories are approximately circular with a diameter of 100–200 km. The effect of the mesoscale eddies gradually concerns many scholars and has great investigation result. The oceanic eddies not only affect the circulation structure of the ocean but also ocean temperature, salinity, sound speed profile. Mesoscale eddies keep rotating and moving every moment, and momentum and energy are transported, interacting strongly with oceanic circulations, affecting the vertical profile structure of the marine environment. In 1977, based on practical experience, Henrick proposed a quasi-elliptical eddy model. To detect and track mesoscale eddies [
9], Dong used sea surface height fluctuations to study the distribution laws and characteristics of eddies from the perspective of oceanography [
10]. We study from the perspective of ocean acoustics the influence of spatial and temporal distribution characteristics of eddies.
Since the 1970s, hydro-acoustics scientists have been concerned about the influence of ocean eddies on sound propagation. The ray method is used for analysing the receiver’s time of arrival which is affected by the size, intensity and position of the eddy. By using the ray-tracing model, people could understand how rays refract and bend. Additionally, what people tracing is the ray stimulated from a particular source then propagating in free space [
11]. In the classical ray theory, the sound energy in the waveguide is shown in the form of acoustic rays. With regards to sound rays from the point source traveling along certain paths to the receiving point, the acoustic field at the receiver is the consequence of the superposition of all types of sound rays. Furthermore, the receivers’ signal phase shift is also calculated by Jian [
12] combining the current model with the acoustic field model when an eddy is present. In addition to the frequency domain, scholars have also done some research on sound propagation through the eddies. Nysen [
13,
14] studied how the acoustic energy leaked into the deep sound channel from the subsurface sound channel with the dependence of frequency off the east coast of Australia. The strong coupling between the two ducts leads to the near-surface acoustic energy being trapped in the duct area affected by water mass. Lawrence [
15] modelled a warm-core eddy propagation problem and expounded the widening of the acoustic convergence zone. Baer [
16] bonded split-step parabolic-equation and used Henrick eddy model to calculate a non-typical three-dimensional structure of eddy and examined the signal amplitude of vertical line array. Specifically, the gain of the hydrophone array increased, and the energy flows horizontal angle changed by over 0.5 degrees. As underwater acoustic horizontal refraction has attracted attention because of the eddy, Weinberg [
17] simulated acoustic propagation through ocean fronts and single mesoscale eddy. The received voltage amplitude was significantly dependent upon the position of the Gulf Stream ring by a fixed system experiment. Afterwards, the three-dimensional fully coupled parabolic equation method was applied to investigate the effect of the horizontal refraction of the sound field caused by mesoscale ocean dynamics on the impact of acoustic source localisation [
18].
Even though the parabolic equation and the ray method could solve the sound field problem of horizontal ocean environment fluctuations, the normal mode theory still plays an irreplaceable role of analysing the effect of deep-sea eddies on the sound field. Dozier and Tapert [
19] deduced the normal mode amplitude distribution in a random ocean, Colosi [
20] used the coupling coefficient of acoustic normal mode to analyse the average energy and sound pressure correlation characteristics of sound propagation under the influence of internal waves. Similarly, we use the coupling coefficient derived by Tapert to apply it to the ocean environment with an eddy to analyse the coupling relationship of the normal mode of various orders in the deep ocean environment. As the sea depth increases, the total of normal mode order increases. The theory of deep-sea normal modes is more complicated than that of shallow-sea. High-order normal mode of the energy coupling is more intense, according to the simulation results. Consistent with the coupling and transmission characteristics of shallow sea normal mode, however, as the sound source is located far away from the channel axis and closer to the sea surface, the low-order normal mode no longer maintains a stable propagation path over a long distance. As a consequence, we focus on the energy distribution of higher-order normal modes in the deep sea. Incidentally, due to the surface and seabed boundary limitation of the impedance character, the confined depth direction is expressed as a specific form of a standing wave, whereas the unconfined direction is known as a form of a travelling wave, which is called normal mode in a given waveguide. The modal expansion is a sum of resonances or eigenfunctions for the waveguide. The eigenfunction mentioned here is limited to the formal solution of the Helmholtz equation under the conditions of a given waveguide section and a fixed edge condition, and eigenfunction, namely, mode shape function expansion is often done in the numerical models based on the normal mode approach [
11]. Local eigenfunctions of different positions are used to analyse the redistribution of energy of the normal mode of each order in the eddy affecting the sound field and explain the root cause of the change of the convergence zone position. As follows in
Section 2, an eddy environment was tracked and used to resolve the sound propagation and the forecasting process of the sound transmission based on the parabolic equation method, and then, the sound propagation experiments in the Kuroshio are introduced, and the comparison between the measured results and numerical results is carried out in
Section 3. In
Section 4, the numerical results of the modelled cyclonic and anticyclonic eddies acoustic propagation and coupling characteristics are described, the character of sound propagation of different normal modes is analysed. Summary of the discussions is drawn in
Section 5.
3. Eddy Tracking Experiments and Underwater Acoustic Propagation Experiment
From May to July 2019, a joint acoustic propagation/mesoscale eddy physics experiment was carried out near the Kuroshio. The purposes of the experiment were to explore eddy hydrology structure and the influence of eddy on sound propagation. The expendable conductivity temperature depth (XCTD), conductivity temperature depth (CTD) and moving vessel profiler (MVP) were used to measure temperature and salinity in the ocean. Observational networks were extended to cover practically the entire mesoscale eddy area, a longitude from 148.5° E to 150.5° E and latitude from 33.65° N to 34.15° N. Receiver hydrophone line array coordinate is located at 150°30
E, 33°42
N. Moreover, the survey depth fluctuates obviously from 5900 to 6040 m. The surface sound speed approximately is 1520 m/s; the sound speed at the lowest channel axis position is 1484 m/s and increases to around 1547 m/s near the seabed. The equipment used for the experiment is shown in
Figure 2 to track and measure the distribution of sound speed which lasted four days since 16 June 2019. Two types of explosives were selected whose explosion depth is 100 m and 200 m, respectively. The deep-sea sound propagation experiment was conducted by 1 kg explosions, dropped evenly spaced at the constant latitude and along the direction of longitude. The broadband explosive was occurring every 3 km, and the ship sailing within 3 h at a speed of 5 knots on the survey line. Inasmuch as the impact of ocean currents, two depth meters are hung on the vertical hydrophone line array to determine the position of each hydrophone in actual time.
With the influence of sea conditions, the depth of the receiving hydrophones fluctuates up and down. After the depth of hydrophones is determined through depthometers, the signal of sound pressure at the same depths is corrected. The sampling frequency is 10 kHz. To guarantee the integrity of the received signal, the time window for intercepting the signal is selected according to the actual signal amplitude. What is more, the signal spectrum is distributed at 5–500 Hz. In a practical process of data processing, 320 Hz with the strongest received signal spectrum is truncated for one-third octave band filtering to process the voltage signal. The parabolic equation method is used for calculating the sound intensity at the receiving position, and the broadband average sound intensity is achieved by averaging the frequency points within the bandwidth to ensure the consistency of the processing result of the experiment and the propagation loss curve.
3.1. Hydrographic Data
The observation data and satellite remote sensing data are used for studying the evolution process of the vertical structure, such as the growth and extinction of this cyclonic eddy. The
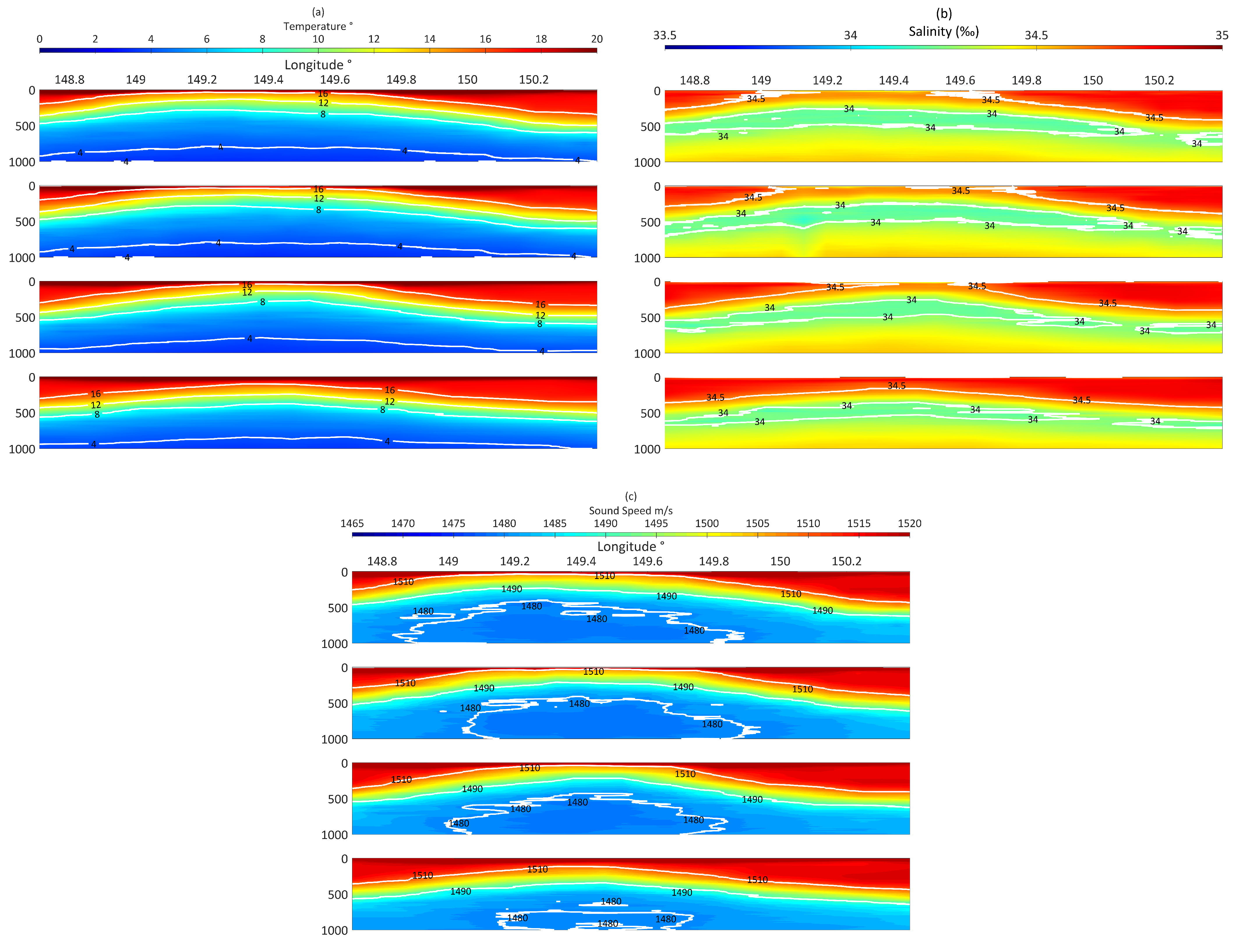
Figure 3 shows the temperature and salinity and the speed of sound profiles collected by MVP 33.7° N, 33.78° N, 33.95° N and 34.10° N, respectively. The sound propagation experiment is located at the latitude of 33.7° N section; the thermocline, halocline, sonic cline and sonic cline at each site are shown in the
Figure 4.
It is known from
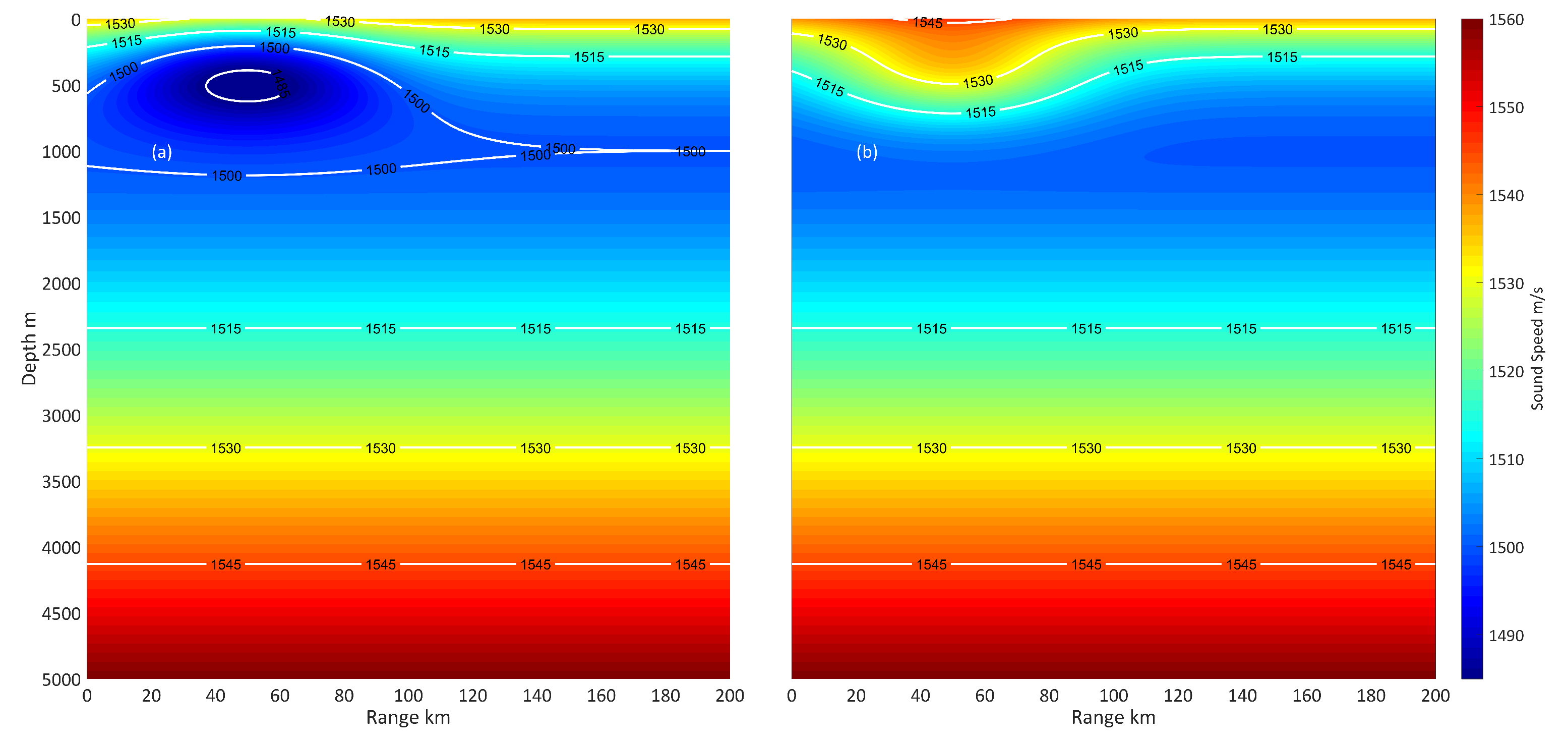
Figure 4 that the depths of the thermocline, halocline and pycnocline came close. The position of saltation is important for human submersible vehicle and marine animal in underwater navigation and action. Above those depths, oceans mix whereby winds, turbulence and currents, the temperature, salinity, density and sound speed differ greatly. Mesoscale eddy redistributes heat and brings carbon and other elements from one part of a body of water to another. Below those depths, the temperature and sound speed gradually decreased. Taking an eddy in the North Pacific as an example, in the section of 33.7° in latitude, the depth of the maximum salinity layer (34.68 psu) is located at about 70 m, and the depth of the minimum salinity layer (33.9 psu) is about 500 m. Sound speed approximate minimum at 1480 m/s, and the depth of the sound channel is nearly 800–1000 m. Judging from
Figure 3, from the surface to 300 m depth, along the latitude of the section, temperature, salinity, density and speed of sound have a peak and two valleys. The peak value position is near 149.3° E that also represents the centre of the cyclonic eddy, while the valley value locations are near 148.7° E and 150.5° E. Moreover, the difference in temperature and sound speed between the cyclonic centre and the surroundings is much weightier than that of the salinity and density. The temperature and sound speed at the eddy centre (0–1000 m vertical integral) is greater than the surrounding values by about 0.97
C and 3.5 ms
. While the salinity and density differences are about 0.05 psu and 0.14 kgm
, respectively.
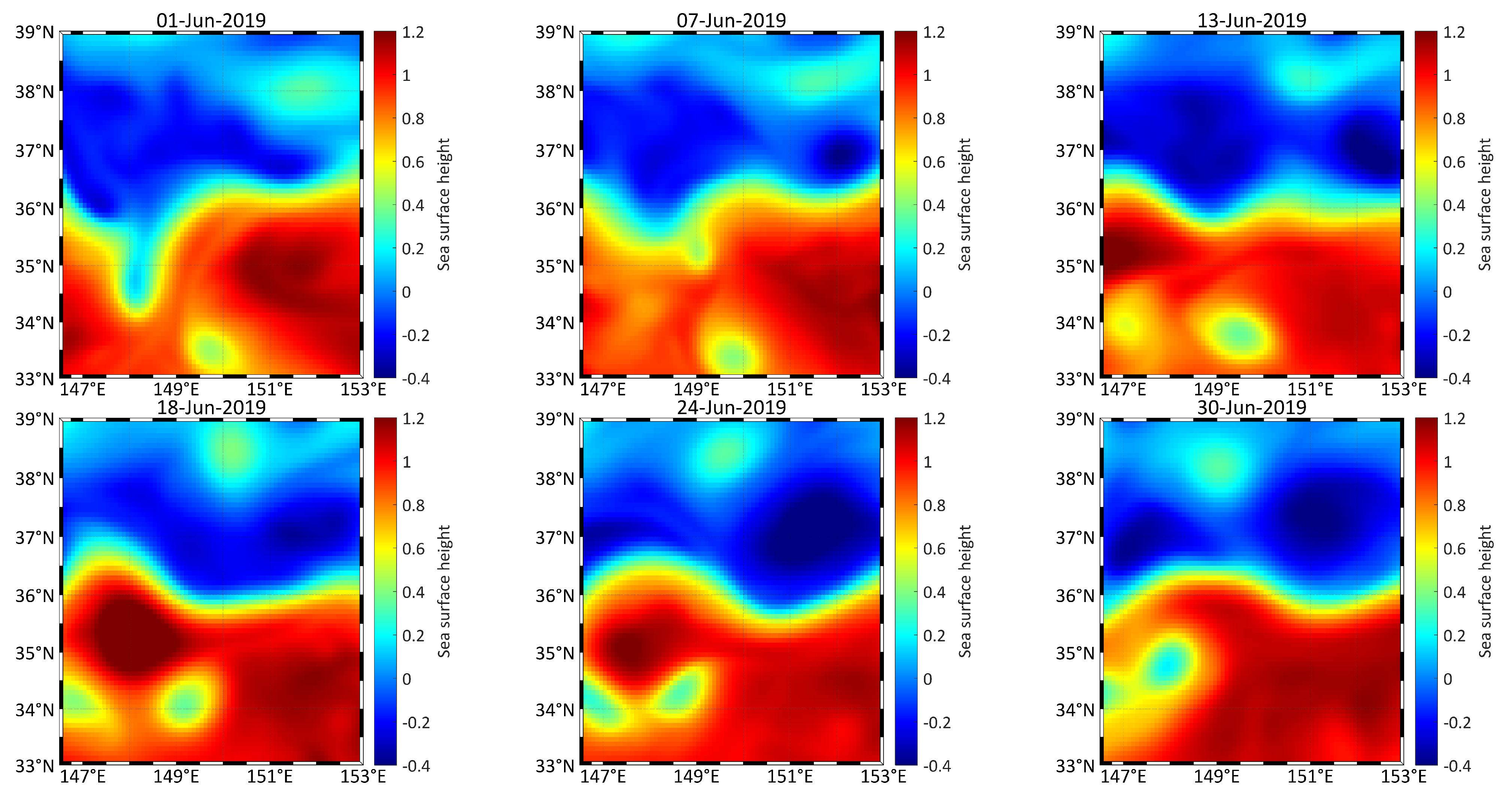
Satellite remote sensing data were obtained on the CMEMS website, and we tracked the position of the cyclonic eddy. The centre of the eddy moved westward by 18 min on the day of finishing the sound propagation experiment. The process of movement of the cyclonic was observed through sea surface height. The size, intensity and kinetic energy of the eddy increased at the early youth of the eddy’s life cycle; these characteristics remain stable in the later 3/5 of its adult period, and then rapidly decrease in the final old age of eddy’s life. As shown in
Figure 5, the research area was from 148.5
to 151
east longitudes and from 33.5
to 34.5
north latitudes. The North Pacific cyclonic eddy moved westward over time and merged into Kuroshio after about three weeks. In
Figure 6, the colour represents the satellite altimeters data and geostrophic velocity as the black arrow shows. Getting the information of marine and according to the sea surface temperature to determine the position of the eddy centre, we replan the acoustic propagation experiment, particularly the location of explosions. The scale of the tracked eddy is about 50 km. Combined with the distribution of hydrographic data, the eddy centre is predicted to be at 149.25° E and 34° N.
Figure 7 shows the topography of the experimental area in the western North Pacific, the path of MVP300 (red dots) and the position of the vertical line array (green circle) on 18 June 2019.
3.2. Acoustical Data
Considering multiple sources and a fixed receiver array, the acoustic reciprocity theorem was generalised. Moving explosions can be regarded as a receiver moving away from the sound source. Unfortunately, the measurement error was much higher because vertical spacing between the adjacent hydrophones is around 50 m. Only data whose standard deviation of receiver depth and hydrophones real depth are sufficiently small are selected when compared with the simulation of sound pressure transmission loss. Therefore, fewer receivers acoustic data are picked, calculated and analysed.
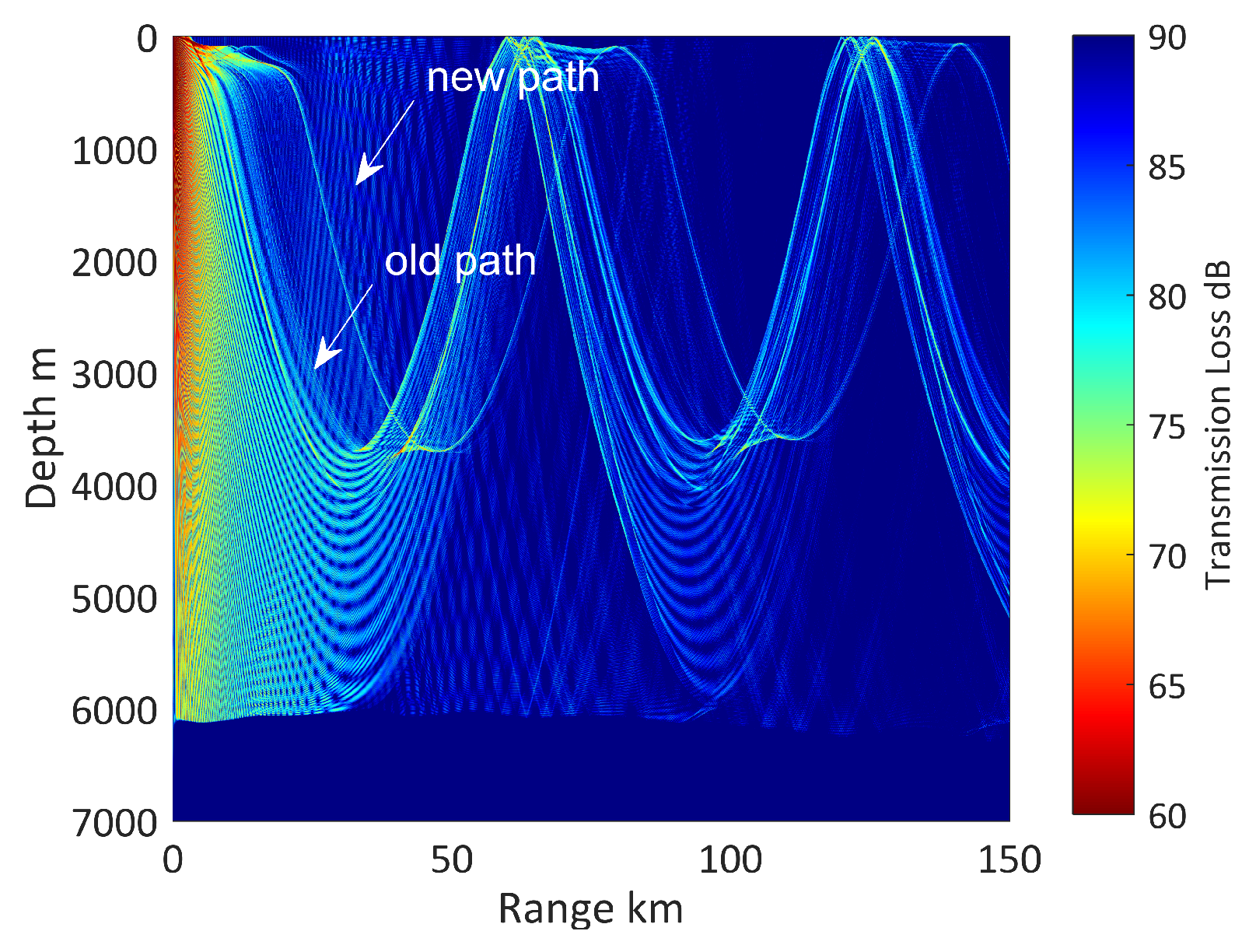
The whole depth of sound pressure transmission loss diagram is illustrated in
Figure 8, and the simulated acoustic source was located in depths of 200 m. The sediment parameter is as follows: sound speed is 1650 m/s, density is 1.5 g cm
, and the bottom attenuation coefficient is 0.5 dB/
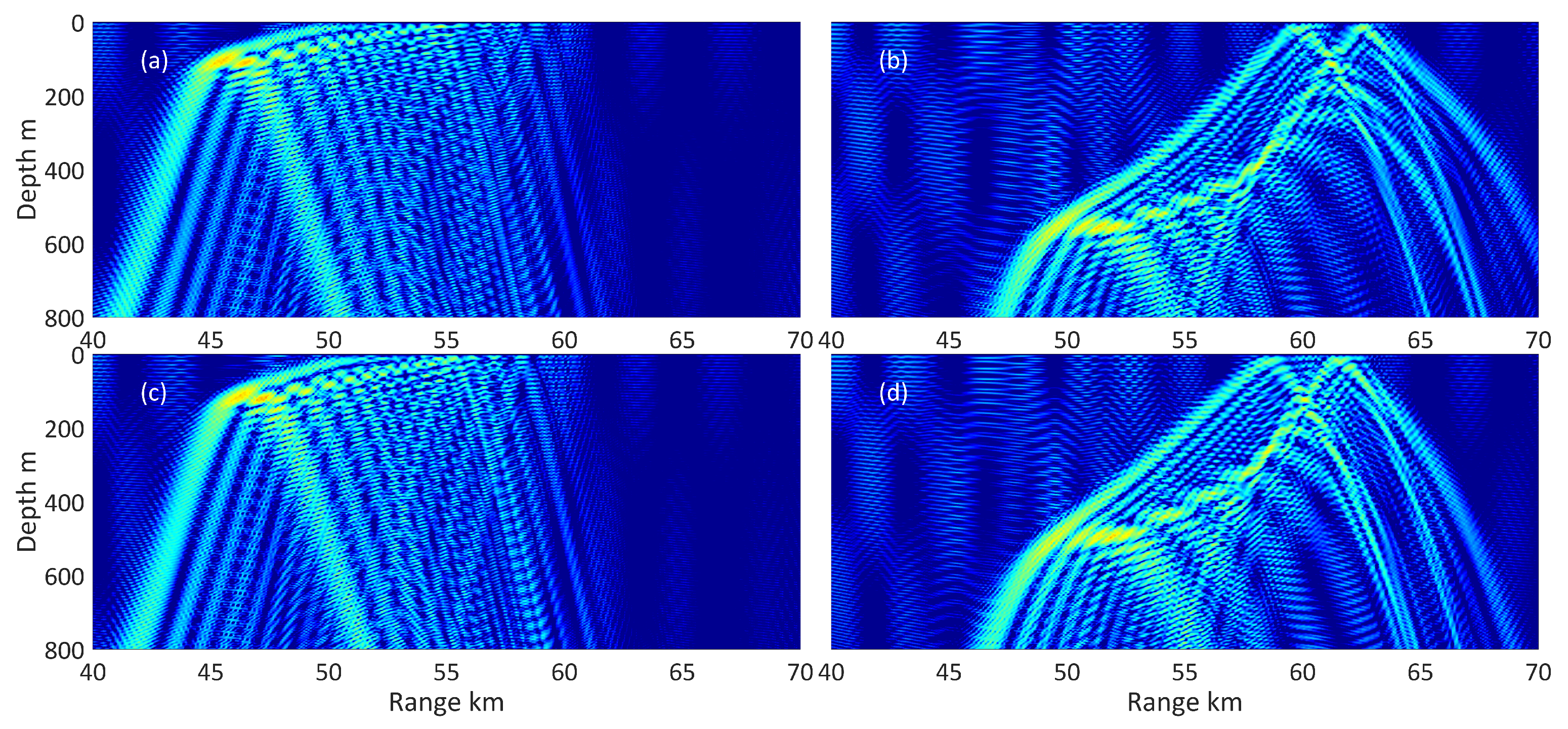
. The average depth of the ocean is 6137 m, which is approximately horizontal. Owing to the change of thermocline arising from cold-core eddy downwelling, surface sound channel (ranging from 0 m to 400 m in depth) is formed. New sound path markedly appears, as can be seen in
Figure 8, marked as “new path”.
According to the eddy structure discussed in the previous section, we select the position of placing the receiver hydrophones array and the place of dropping the explosions. Through the prior simulation results of sound propagation, we know that the convergence zone was expected to be the most affected on both the energy distribution and arrival time structure. Ultimately, we dropped explosions within the scope of the first and second convergence zones, removed the locations where the ocean current has a great impact on the depth of the hydrophones, and calculated the propagation loss distribution using the remaining locations. Compared with sound pressure transmission loss impact by oceanic eddy, topography could be ignored.
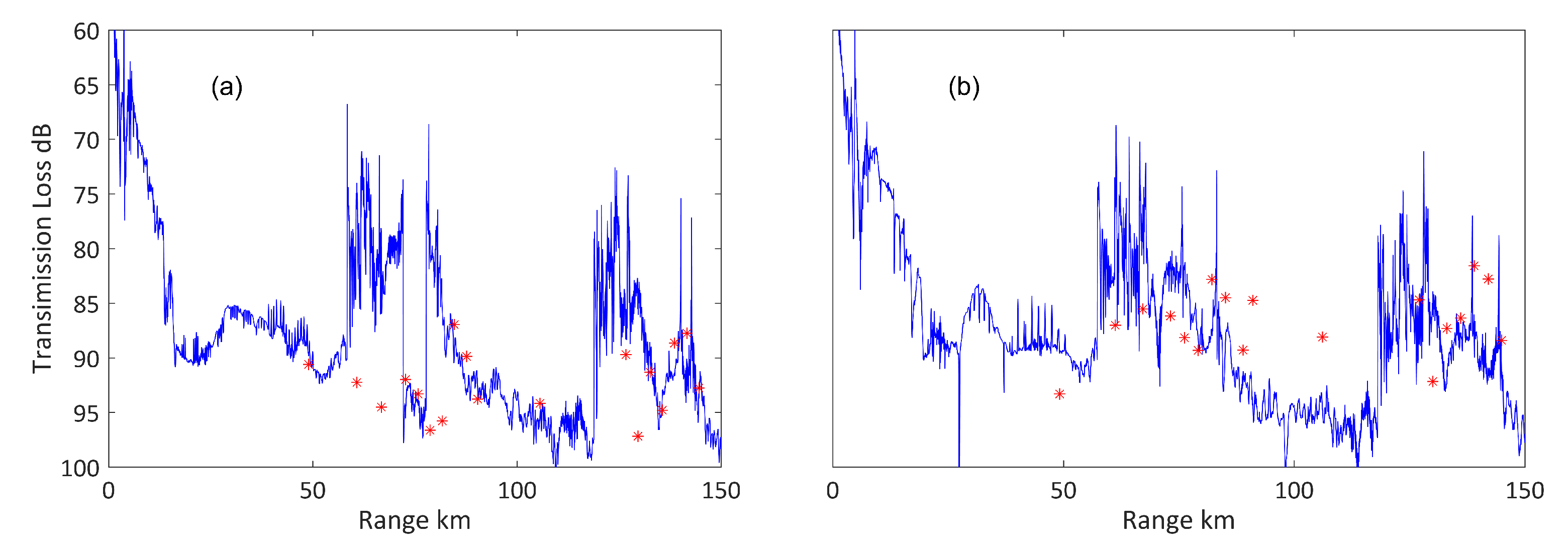
Figure 9 shows the comparison of the the numerical results with experimental data when the sound source was located in the mixed layer (200 m). The agreement of experiment and modelling can get a satisfactory result.
The curve of diagrams
Figure 9 best illustrates the existence of a “new path”, which can be seen in the splitting of convergent zone approximately at 70 and 140 km. It is a pity that we have not been able to measure the sound propagation at the same location in the absence of the eddy situation. Eventually, the comparison of the two simulations of travel times results is given in
Figure 10, which respectively are travel through the eddy and without the eddy.
For receiver at the depth of 200 m and at the range of 150 km, arrivals structure contain the number of echoes or arrivals. The direct path is missing under the circumstance of sound traversing the cyclonic eddy. An acoustic signal arrives earlier in range independent horizontal sound speed stratification environment than that of in cold-core eddy environment.