On the Slope Stability of the Submerged Trench of the Immersed Tunnel Subjected to Solitary Wave
Abstract
1. Introduction
2. Theoretical Formulations
2.1. Wave–Current Sub-Model
2.1.1. Continuity Equations and Momentum Equations
2.1.2. Turbulence Models
2.1.3. Boundary Conditions for Solitary Wave Generation
2.2. Seabed Sub-Model
2.2.1. Seepage Pressure
2.2.2. Strength Reduction Method for the Seabed
2.3. Boundary Conditions
2.4. Integration of Sub-Models
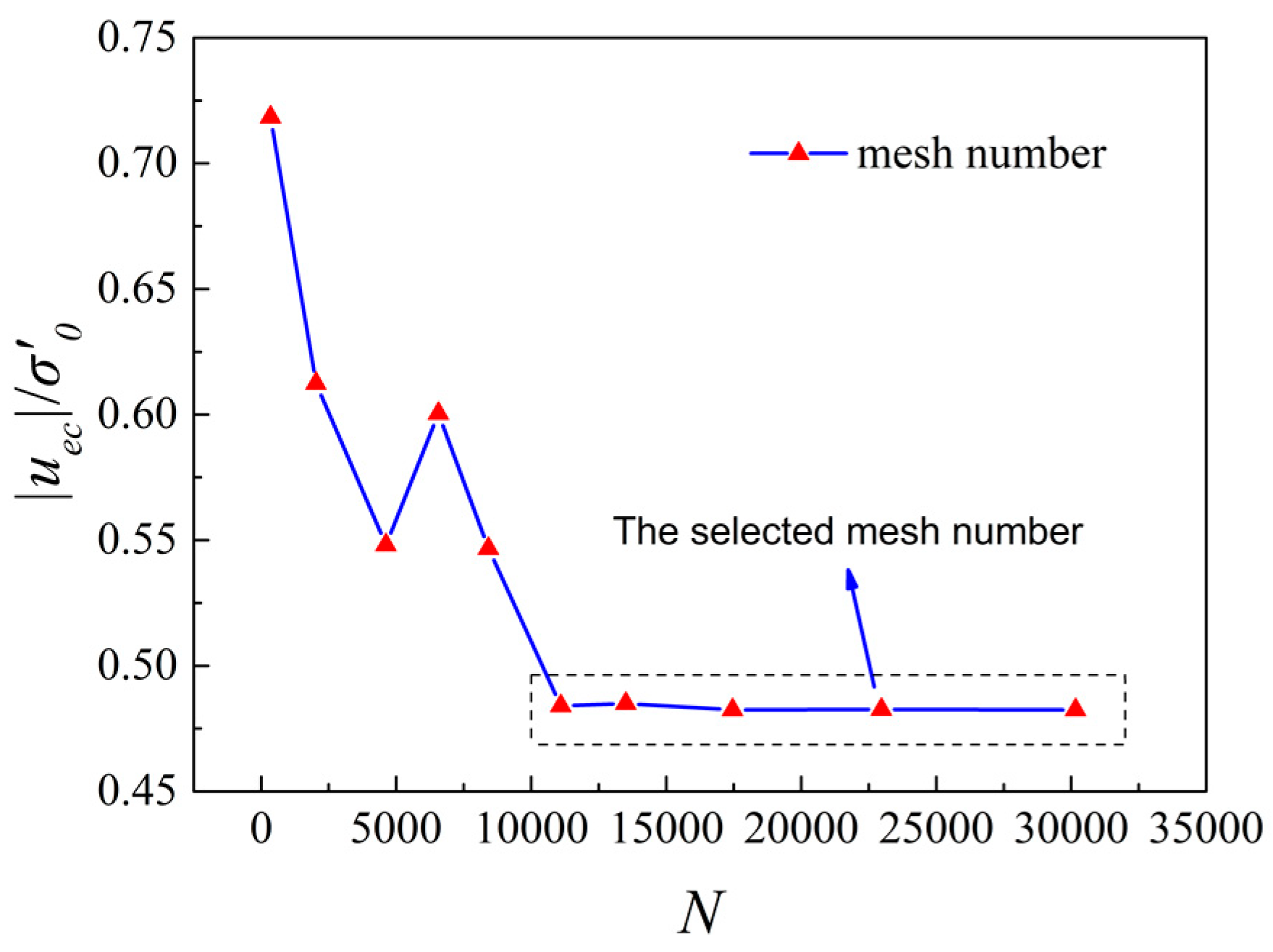
2.5. Convergence of the FEM Meshes
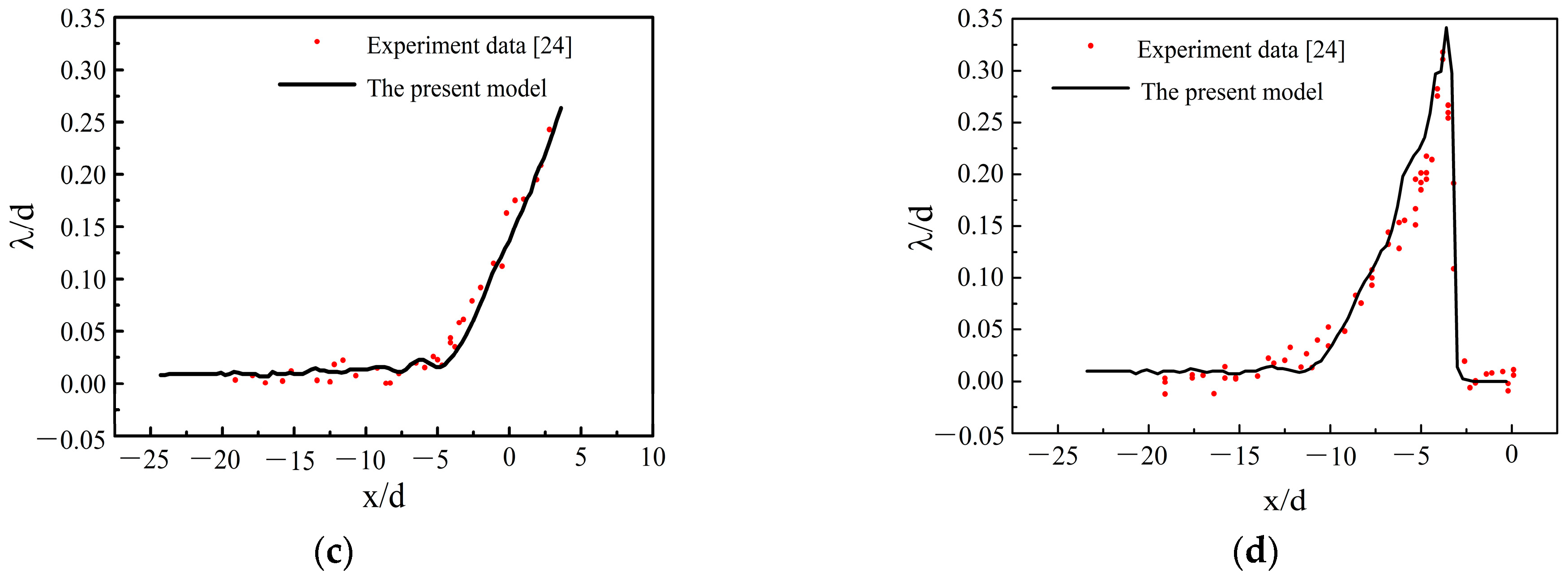
3. Model Validation
4. Results and Discussion
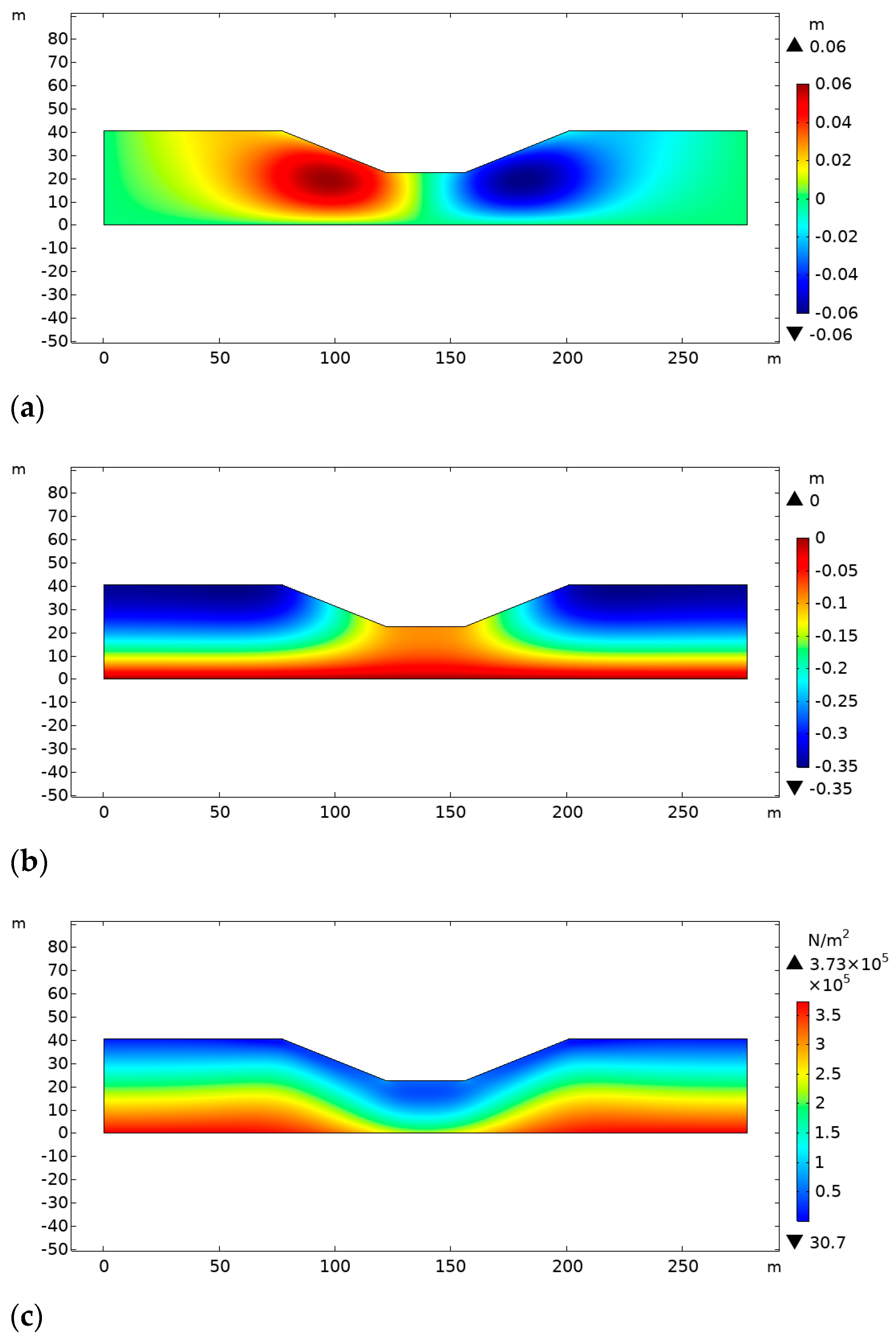
4.1. Consolidation of the Seabed
4.2. Stability Index for the One-Stage Slope under Solitary Wave Loading
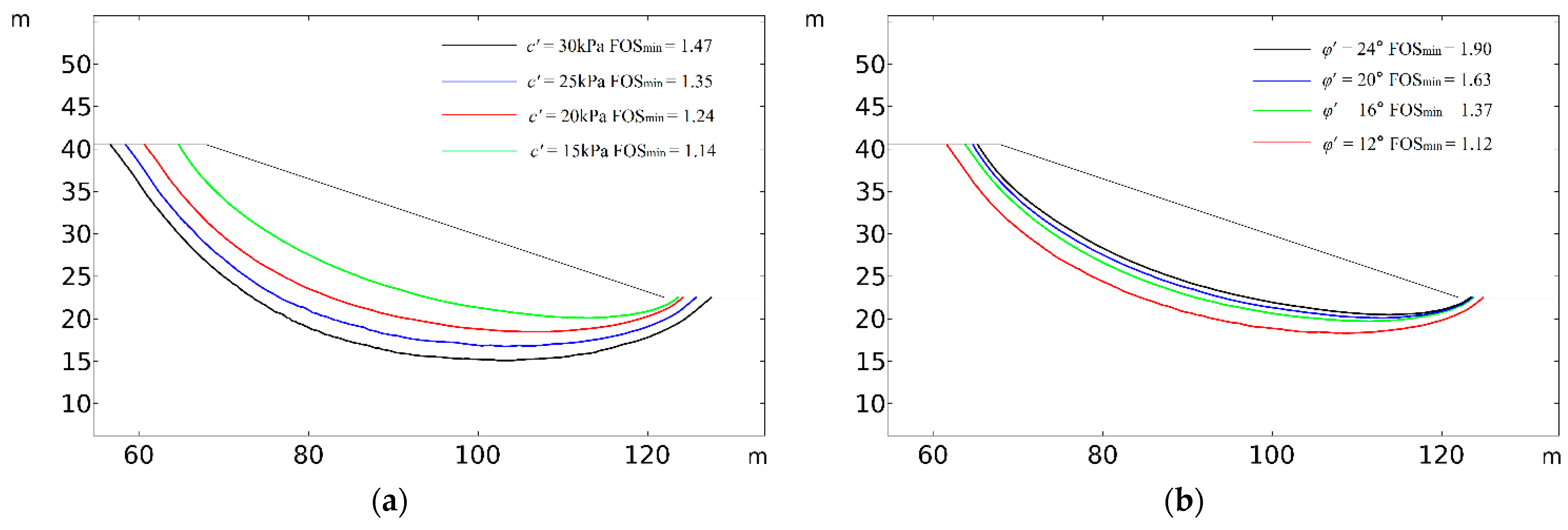
4.3. Influence of Soil Strength Parameters on the Slope Stability
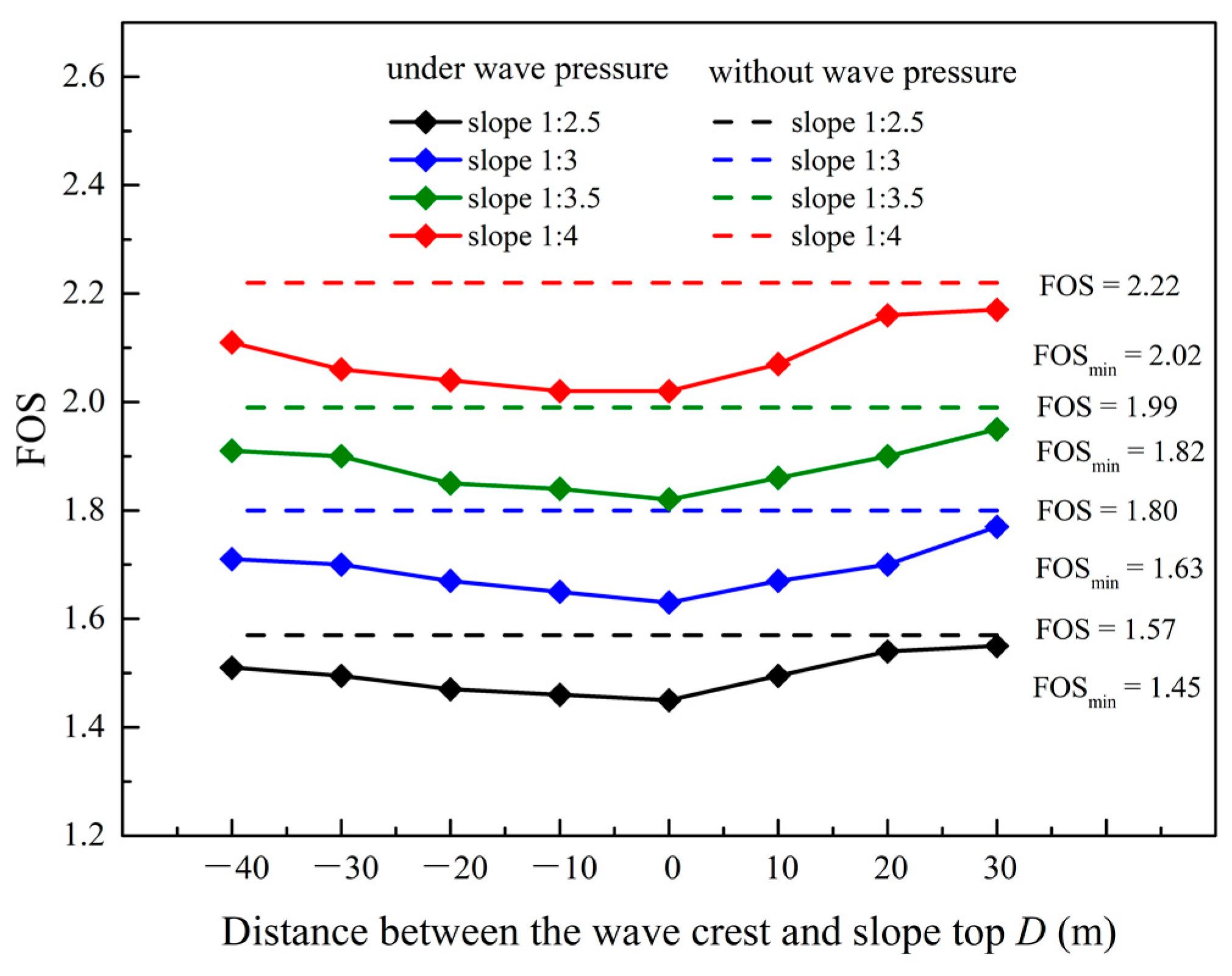
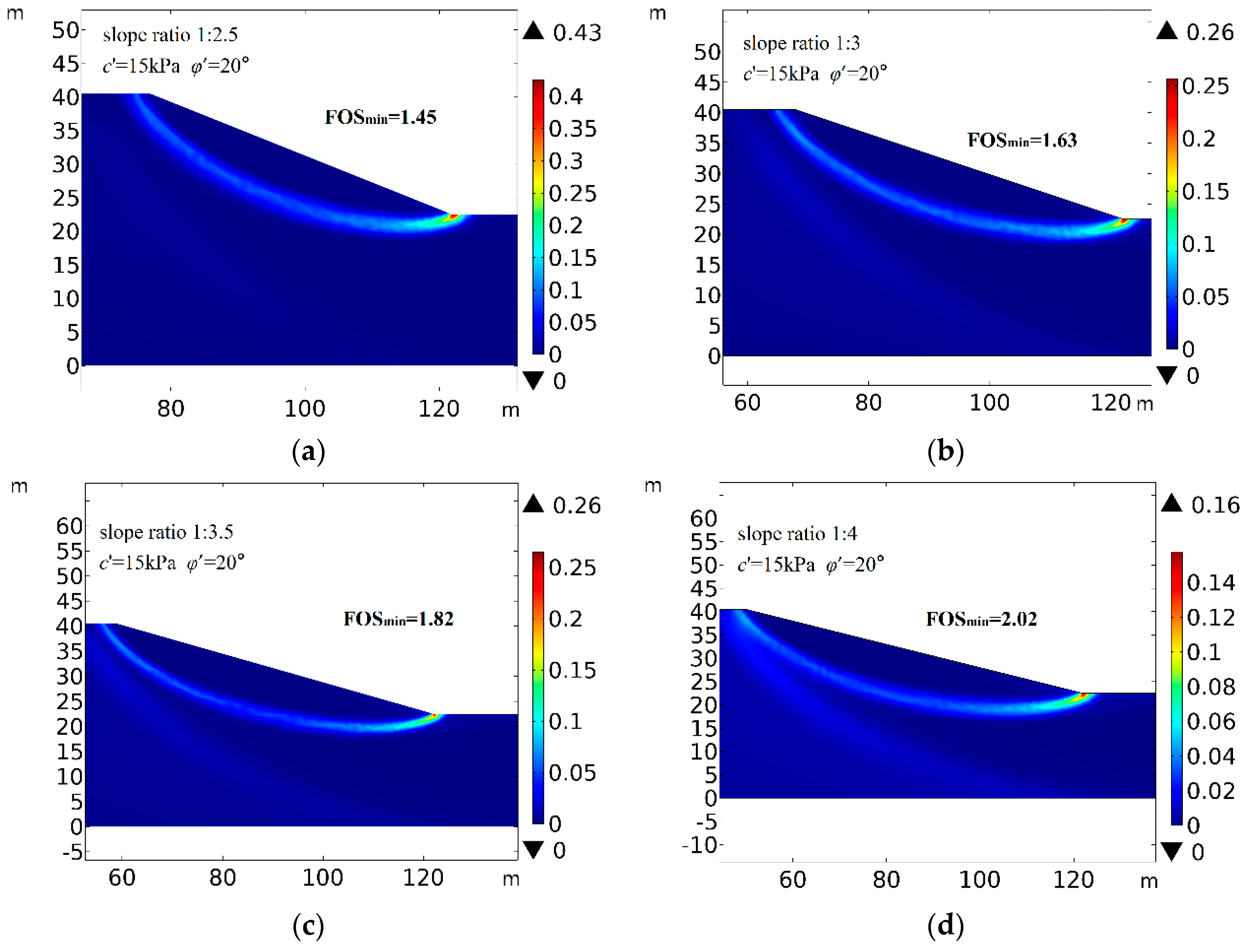
4.4. Influence of the Slope Ratio on Slope Stability
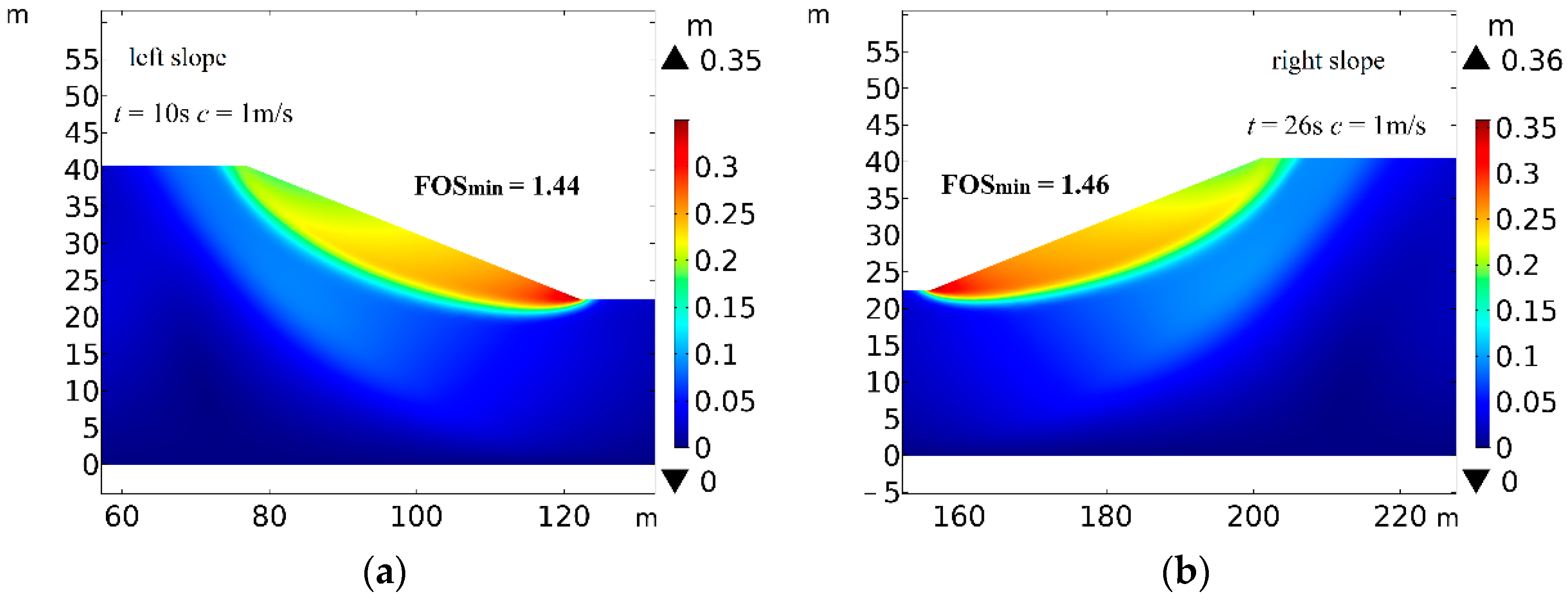
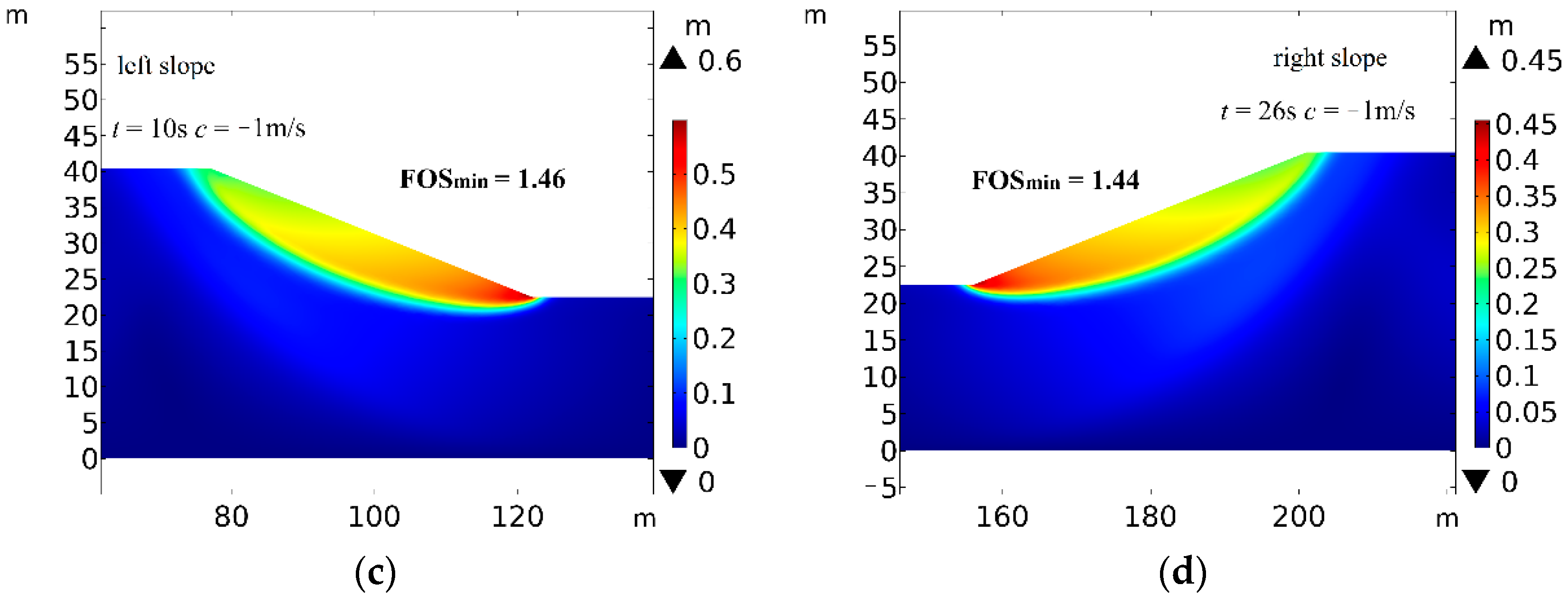
4.5. Influence of Current Direction on Slope Stability
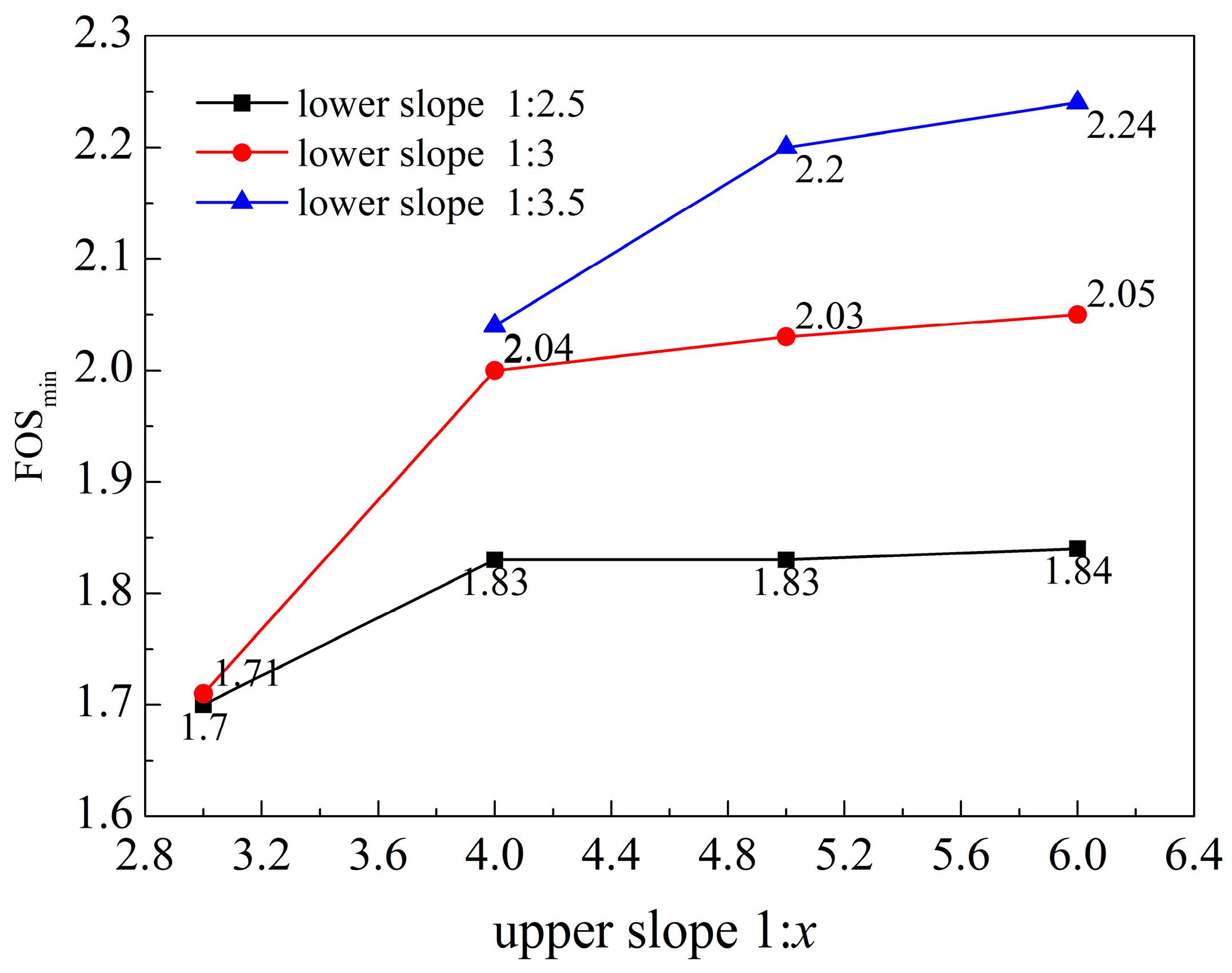
4.6. Influence of Slope Ratio on Two-Stage Slope
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Cui, J.; Zhang, Z.; Liu, H.; Huang, X.; Zhang, C. The role of TBM asymmetric tail-grouting on surface settlement in coarse-grained soils of urban area: Field tests and FEA modelling. Tunn. Undergr. Space Technol. 2021, 111, 103857. [Google Scholar] [CrossRef]
- Chen, W.Y.; Wang, Z.H.; Chen, G.X.; Jeng, D.S.; Wu, M.; Zhao, H.Y. Effect of vertical seismic motion on the dynamic response and instantaneous liquefaction in a two-layer porous seabed. Comput. Geotech. 2018, 99, 165–176. [Google Scholar] [CrossRef]
- Chen, W.Y.; Huang, Y.; Wang, Z.H.; He, R.; Chen, G.X.; Li, X.J. Horizontal and vertical motion at surface of a gassy ocean sediment layer induced by obliquely incident SV waves. Eng. Geol. 2017, 227, 43–53. [Google Scholar] [CrossRef]
- Chen, G.X.; Ruan, B.; Zhao, K.; Chen, W.Y.; Zhuang, H.Y.; Du, X.L.; Khoshnevisan, S.; Juang, C.H. Nonlinear Response Characteristics of Undersea Shield Tunnel Subjected to Strong Earthquake Motions. J. Earthq. Eng. 2020, 24, 351–380. [Google Scholar] [CrossRef]
- Xu, L.Y.; Song, C.X.; Chen, W.Y.; Cai, F.; Li, Y.Y.; Chen, G.X. Liquefaction-induced settlement of the pile group under vertical and horizontal ground motions. Soil Dyn. Earthq. Eng. 2021, 144, 106709. [Google Scholar] [CrossRef]
- Henkel, D. The Role of Waves in Causing Submarine Landslides. Geotechnique 1970, 20, 75–80. [Google Scholar] [CrossRef]
- Bubel, J.; Grabe, J. Stability of Submarine Foundation Pits Under Wave Loads. In Proceedings of the Asme International Conference on Ocean, Rio de Janeiro, Brazil, 1–6 July 2012; p. 11. [Google Scholar]
- Jeng, D.S. Wave-induced liquefaction potential at the tip of a breakwater: An analytical solution. Appl. Ocean Res. 1996, 18, 229–241. [Google Scholar] [CrossRef]
- Madsen, O.S. Wave-induced pore pressures and effective stresses in a porous bed. Géotechnique 1978, 28, 377–393. [Google Scholar] [CrossRef]
- Yamamoto, T. Wave-induced pore pressures and effective stresses in inhomogeneous seabed foundations. Ocean Eng. 1981, 8, 1–16. [Google Scholar] [CrossRef]
- Mei, C.C.; Foda, M.A. Wave-induced responses in a fluid-filled poro-elastic solid with a free surface—a boundary layer theory. Geophys. J. Int. 1981, 66, 597–631. [Google Scholar] [CrossRef]
- Liu, B.; Jeng, D.S.; Ye, G.L.; Yang, B. Laboratory study for pore pressures in sandy deposit under wave loading. Ocean Eng. 2015, 106, 207–219. [Google Scholar] [CrossRef]
- Zhang, C.; Titi, S.; Zheng, J.H.; Xie, M.X.; Nguyen, V.T. Modelling wave-induced 3D non-homogeneous seabed response. Appl. Ocean Res. 2016, 61, 101–114. [Google Scholar] [CrossRef]
- Lin, Z.B.; Guo, Y.K.; Jeng, D.S.; Liao, C.C.; Rey, N. An integrated numerical model for wave–soil–pipeline interactions. Coast. Eng. 2016, 108, 25–35. [Google Scholar] [CrossRef]
- Lin, Z.B.; Pokrajac, D.; Guo, Y.K.; Jeng, D.S.; Tang, T.; Rey, N.; Zheng, J.H.; Zhang, J.S. Investigation of nonlinear wave-induced seabed response around mono-pile foundation. Coast. Eng. 2017, 121, 197–211. [Google Scholar] [CrossRef]
- Duan, L.L.; Liao, C.C.; Jeng, D.S.; Chen, L.Y. 2D numerical study of wave and current-induced oscillatory non-cohesive soil liquefaction around a partially buried pipeline in a trench. Ocean Eng. 2017, 135, 39–51. [Google Scholar] [CrossRef]
- Zhai, Y.Y.; He, R.; Zhao, J.L.; Zhang, J.S.; Jeng, D.S.; Li, L. Physical Model of wave-induced seabed response around trenched pipeline in sandy seabed. Appl. Ocean Res. 2018, 75, 37–52. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, X.L.; Wang, J.H.; Guo, J.J. Wave-induced seabed response around an offshore pile foundation platform. Ocean Eng. 2017, 130, 567–582. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Zhu, J.F.; Zheng, J.H.; Zhang, J.S. Numerical modelling of the fluid–seabed-structure interactions considering the impact of principal stress axes rotations. Soil Dyn. Earthq. Eng. 2020, 136, 106242. [Google Scholar] [CrossRef]
- Hu, Z.N.; Xie, Y.L.; Wang, J. Challenges and strategies involved in designing and constructing a 6 km immersed tunnel: A case study of the Hong Kong–Zhuhai–Macao Bridge. Tunn. Undergr. Space Technol. 2015, 50, 171–177. [Google Scholar] [CrossRef]
- Lara, J.L.; Losada, I.J.; Maza, M.; Guanche, R. Breaking solitary wave evolution over a porous underwater step. Coast. Eng. 2011, 58, 837–850. [Google Scholar] [CrossRef]
- Synolakis, C.E.; Bernard, E.N. Tsunami science before and beyond Boxing Day 2004. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 2231–2265. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, S.C.; Lin, T.C. Tsunami-like solitary waves impinging and overtopping an impermeable seawall: Experiment and RANS modeling. Coast. Eng. 2010, 57, 1–18. [Google Scholar] [CrossRef]
- Synolakis, C.E. The Runup of Long Waves. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 1986. [Google Scholar]
- Sumer, B.M.; Sen, M.B.; Karagali, I.; Ceren, B.; Fredsøe, J.; Sottile, M.; Zilioli, L.; Fuhrman, D.R. Flow and sediment transport induced by a plunging solitary wave. J. Geophys. Res. 2011, 116, C1008. [Google Scholar] [CrossRef]
- Young, Y.L.; White, J.A.; Xiao, H.; Borja, R.I. Liquefaction potential of coastal slopes induced by solitary waves. Acta Geotech. 2009, 4, 17–34. [Google Scholar] [CrossRef]
- Xiao, H.; Young, Y.L.; Prévost, J.H. Parametric study of breaking solitary wave induced liquefaction of coastal sandyslopes. Ocean Eng. 2010, 37, 1546–1553. [Google Scholar] [CrossRef]
- Nichols, B.D.; Hirt, C.W.; Hotchkiss, R.S. SOLA-VOF: A Solution Algorithm for Transient Fluid Flow with Multiple Free Boundaries; Technology Report LA-8355; Los Alamos Scientific Lab.: Los Alamos, NM, USA, 1980; Volume 12, p. 39.
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Hirt, C.; Sicilian, J. A Porosity Technique for the Definition of Obstacles in Rectangular Cell Meshes. In Proceedings of the 4th International Conference on Numerical Ship Hydrodynamics, Washington, DC, USA, 1 January 1985; p. 19. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Method Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Harlow, F.H.; Nakayama, P.I. Turbulence Transport Equations. Phys. Fluids 1967, 10, 2323–2332. [Google Scholar] [CrossRef]
- Franke, R.; Rodi, W. Calculation of Vortex Shedding Past a Square Cylinder with Various Turbulence Models, Berlin, Heidelberg, 1 January 1993; Durst, F., Friedrich, R., Launder, B.E., Schmidt, F.W., Schumann, U., Whitelaw, J.H., Eds.; Springer: Berlin/Heidelberg, Germany, 1993; pp. 189–204. [Google Scholar]
- McCowan, J. VII. On the solitary wave. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1891, 32, 45–58. [Google Scholar] [CrossRef]
- Boussinesq, J.V. Théorie de l’intumescence liquide appelée onde solitaire ou de translation se propageant dans un canal rectangulaire. C. R. Hebd. Séances Acad. Sci. 1871, 72, 755–759. [Google Scholar]
- Munk, W.H. The solitary wave theory and its application to surf problems. Ann. N. Y. Acad. Sci. 1949, 51, 376–424. [Google Scholar] [CrossRef]
- Matsui, T.; San, K. Finite Element Slope Stability Analysis by Shear Strength Reduction Technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Chen, W.Y.; Liu, C.L.; Li, Y.; Chen, G.X.; Yu, J. An integrated numerical model for the stability of artificial submarine slope under wave load. Coast. Eng. 2020, 158, 103698. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Länsivaara, T.; Wei, W.B. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods. Comput. Geotech. 2007, 34, 137–150. [Google Scholar] [CrossRef]




| Parameters | Characteristics | Value | Unit |
|---|---|---|---|
| Wave Parameters | Wave height (H) | 3 | m |
| Water depth (d) | 10 | m | |
| Soil Parameters | Seabed thickness (h) | 40.5 | m |
| Shear modulus (G) | 6.56 × 106 | Pa | |
| Soil porosity (n) | 0.41 | - | |
| Poison’s Ratio (μ) | 0.35 | - | |
| Elastic modulus (E) | 1.77 × 107 | Pa | |
| Soil permeability (k) | 8 × 10−6 | m/s | |
| Density of soil grain (ρs) | 2.71 × 103 | kg/m3 | |
| Effective cohesion (c′) | 15 | kPa | |
| Effective internal friction angle (φ′) | 20 | ° | |
| Trench width (W) | 34 | m | |
| Trench height (B) | 18 | m | |
| Water parameters | Bulk modulus (Kw) | 2 × 109 | Pa |
| Density of water (ρw) | 1000 | kg/m3 |
| Parameters | Characteristics | Value | Unit |
|---|---|---|---|
| Soil Parameters in Upper Slope | Seabed thickness (h1) | 8 | m |
| Shear modulus (G1) | 4.33 × 106 | Pa | |
| Soil porosity (n1) | 0.56 | - | |
| Poison’s ratio (μ1) | 0.35 | - | |
| Elastic modulus (E1) | 1.17 × 107 | Pa | |
| Soil permeability (k1) | 1 × 10−9 | m/s | |
| Density of soil grain (ρs1) | 2.75 × 103 | kg/m3 | |
| Effective cohesion (c1′) | 12 | kPa | |
| Effective internal friction angle (φ1′) | 13 | ||
| Soil Parameters in Lower Slope | Seabed thickness (h2) | 32.5 | m |
| Shear modulus (G2) | 6.56 × 106 | Pa | |
| Soil porosity (n2) | 0.41 | - | |
| Poison’s ratio (μ2) | 0.35 | - | |
| Elastic modulus (E2) | 1.77 × 107 | Pa | |
| Soil permeability (k2) | 8 × 10−6 | m/s | |
| Density of soil grain (ρs2) | 2.71 × 103 | kg/m3 | |
| Effective cohesion(c2′) | 15 | kPa | |
| Effective internal friction angle (φ2′) | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Wang, D.; Xu, L.; Lv, Z.; Wang, Z.; Gao, H. On the Slope Stability of the Submerged Trench of the Immersed Tunnel Subjected to Solitary Wave. J. Mar. Sci. Eng. 2021, 9, 526. https://doi.org/10.3390/jmse9050526
Chen W, Wang D, Xu L, Lv Z, Wang Z, Gao H. On the Slope Stability of the Submerged Trench of the Immersed Tunnel Subjected to Solitary Wave. Journal of Marine Science and Engineering. 2021; 9(5):526. https://doi.org/10.3390/jmse9050526
Chicago/Turabian StyleChen, Weiyun, Dan Wang, Lingyu Xu, Zhenyu Lv, Zhihua Wang, and Hongmei Gao. 2021. "On the Slope Stability of the Submerged Trench of the Immersed Tunnel Subjected to Solitary Wave" Journal of Marine Science and Engineering 9, no. 5: 526. https://doi.org/10.3390/jmse9050526
APA StyleChen, W., Wang, D., Xu, L., Lv, Z., Wang, Z., & Gao, H. (2021). On the Slope Stability of the Submerged Trench of the Immersed Tunnel Subjected to Solitary Wave. Journal of Marine Science and Engineering, 9(5), 526. https://doi.org/10.3390/jmse9050526





