Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory
Abstract
1. Introduction
2. Numerical Long Short-Term Memory (N-LSTM) Network
2.1. Overall N-LSTM Model
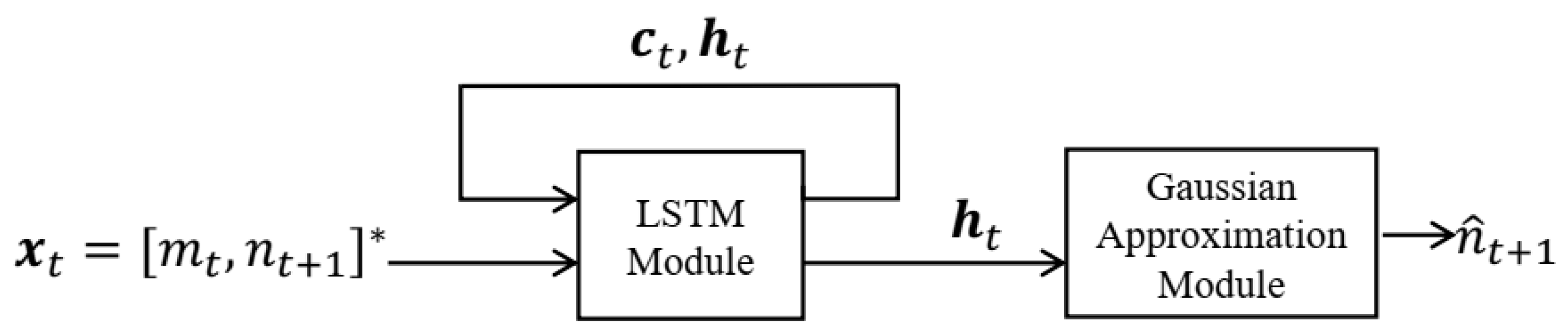
2.2. LSTM Module
2.3. Gaussian Approximation Module
2.4. Sampling for Correcting Numerical Predictions
2.5. N-LSTM Training
| Algorithm 1 The training procedure of the N-LSTM |
| 1: Input: The significant wave height numerical predictions and the real observations . 2: Output: The parameters of the autoregressive recurrent network. 3: for do 4: for do 5: Compute according to (2)–(7). 6: Compute and according to (9) and (10). 7: Construct the conditional probabilistic distribution according to (12). 8: end for 9: Maximize the log-likelihood according to (18). 10: Train the log-likelihood by stochastic gradient descent algorithm. 11: end for |
3. Numerical Wave Height Series Correction Based on N-LSTM
4. Results
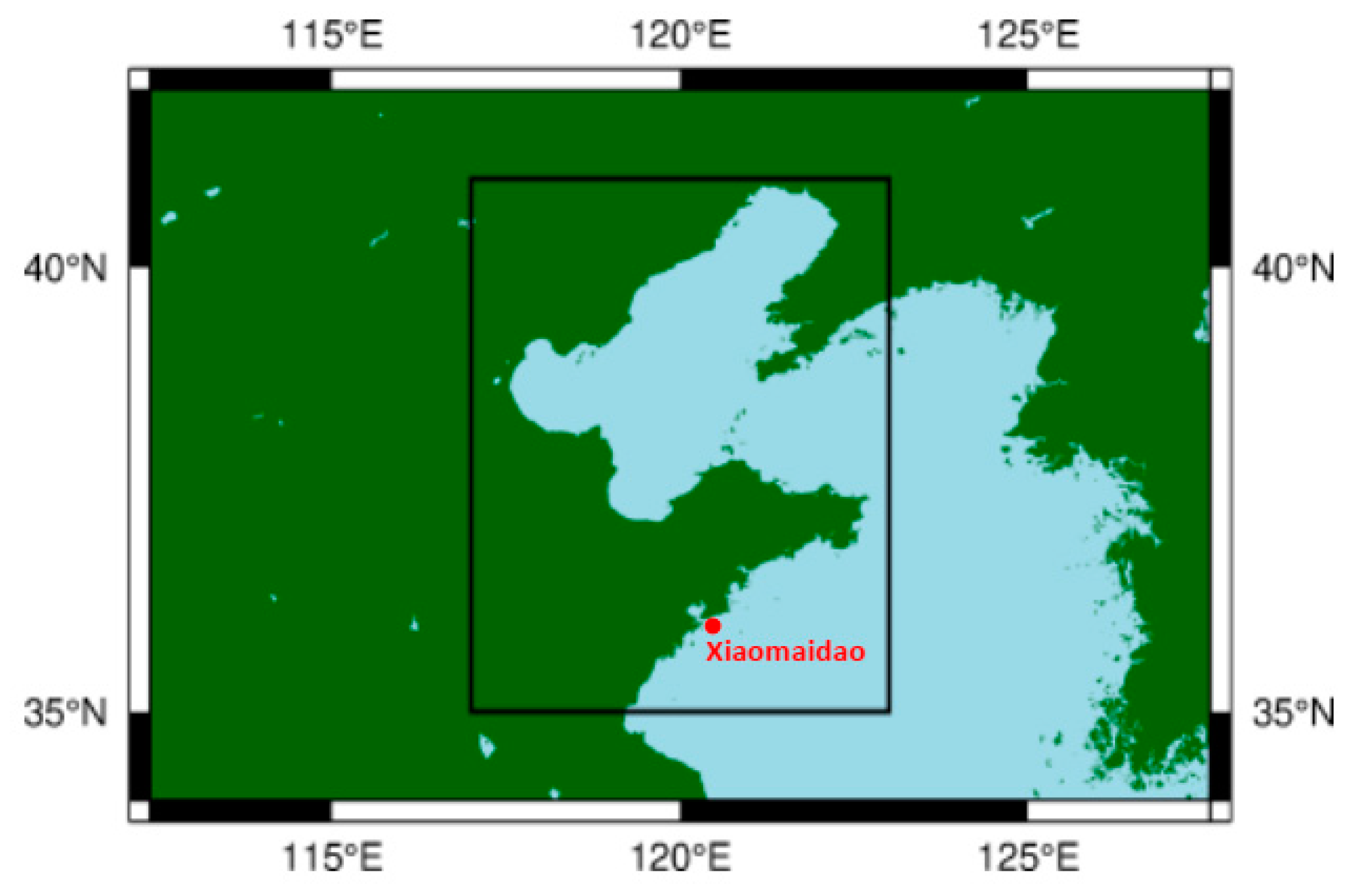
4.1. Data Collection and Evaluation Criterions
4.2. Empirical Evaluations
5. Discussion
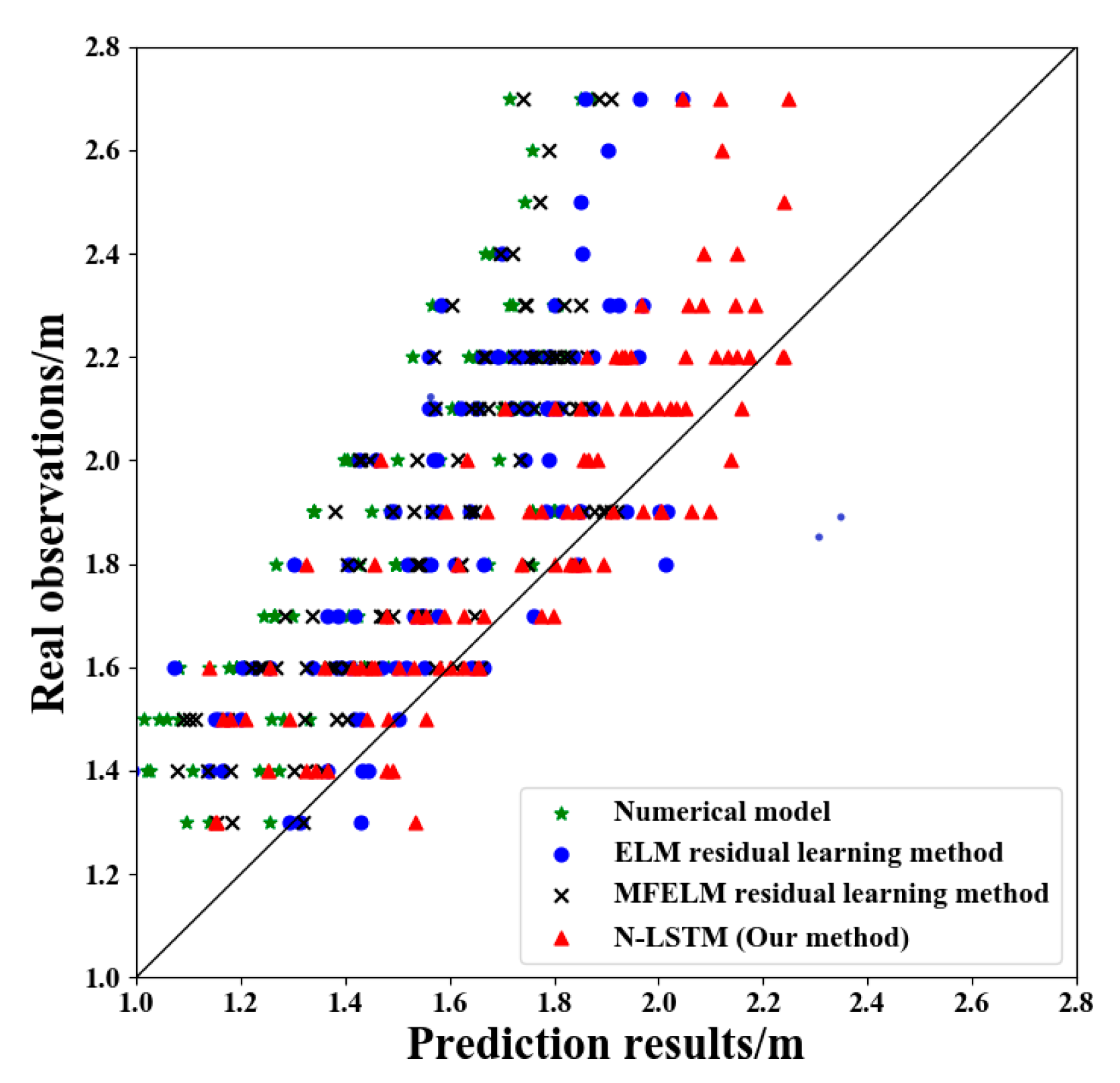
5.1. Analysis of Significant Wave Height Predictions between 1.25 m and 4 m
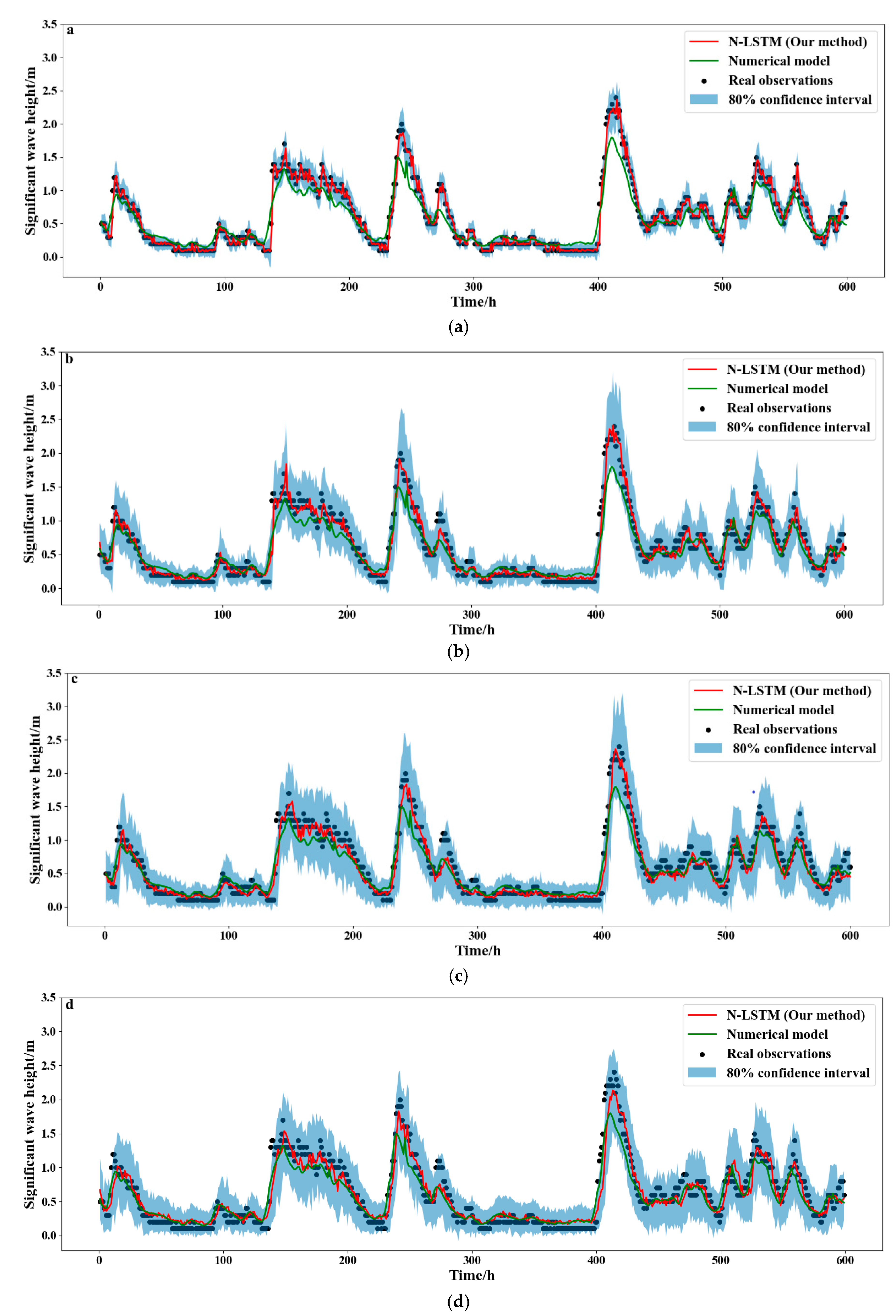
5.2. Analysis of Probabilistic Wave Height Predictions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, Z.; Shao, W.; Ding, Y.; Shi, J.; Ji, Q. Wave Simulation by the SWAN Model and FVCOM Considering the Sea-Water Level around the Zhoushan Islands. J. Mar. Sci. Eng. 2020, 8, 783. [Google Scholar] [CrossRef]
- Young, I.R.; Ribal, A. Multiplatform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef]
- Carter, D. Prediction of wave height and period for a constant wind velocity using the JONSWAP results. Ocean Eng. 1982, 9, 17–33. [Google Scholar] [CrossRef]
- Muzathik, A.M.; Nik, W.B.W.; Samo, K.B.; Ibrahim, M.Z. Ocean wave measurement and wave climate prediction of Penin-sular Malaysia. J. Phys. Sci. 2011, 22, 77–92. [Google Scholar]
- Simmons, H.L.; Jayne, S.R.; Laurent, L.C.; Weaver, A.J. Tidally driven mixing in a numerical model of the ocean general circulation. Ocean Model. 2004, 6, 245–263. [Google Scholar] [CrossRef]
- Mandal, S.; Prabaharan, N. Ocean Wave Prediction Using Numerical and Neural Network Models. Open Ocean Eng. J. 2010, 3, 12–17. [Google Scholar] [CrossRef]
- Dentale, F.; Furcolo, P.; Carratelli, E.P.; Reale, F.; Contestabile, P.; Tomasicchio, G.R. Extremewave analysis by integrating model and wave buoy data. Water 2018, 10, 373. [Google Scholar] [CrossRef]
- Group, T.W. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Bottcher, A.B.; Whiteley, B.J.; James, A.I.; Hiscock, J.G. Watershed Assessment Model (WAM): Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1367–1383. [Google Scholar] [CrossRef]
- Tolman, H.L. User manual and system documentation of WAVEWATCH III TM version 3.14. Technical note. MMAB Contrib. 2009, 276, 220. [Google Scholar]
- Mentaschi, L.; Besio, G.; Cassola, F.; Mazzino, A. Performance evaluation of Wavewatch III in the Mediterranean Sea. Ocean Model. 2015, 90, 82–94. [Google Scholar] [CrossRef]
- Booij, N.; Holthuijsen, L.; Ris, R. The “Swan” Wave Model for Shallow Water. Coast. Eng. 1996, 1997, 668–676. [Google Scholar] [CrossRef]
- Rogers, W.E.; Hwang, P.A.; Wang, D.W. Investigation of Wave Growth and Decay in the SWAN Model: Three Regional-Scale Applications. J. Phys. Oceanogr. 2003, 33, 366–389. [Google Scholar] [CrossRef]
- Swain, J.; Umesh, P.; Balchand, A. WAM and WAVEWATCH-III intercomparison studies in the North Indian Ocean using Oceansat-2 Scatterometer winds. J. Ocean. Clim. Sci. Technol. Impacts 2019, 9, 1–24. [Google Scholar] [CrossRef]
- Liu, Q.; Rogers, W.E.; Babanin, A.V.; Young, I.R.; Romero, L.; Zieger, S.; Qiao, F.; Guan, C. Observation-Based Source Terms in the Third-Generation Wave Model WAVEWATCH III: Updates and Verification. J. Phys. Oceanogr. 2019, 49, 489–517. [Google Scholar] [CrossRef]
- Akpınar, A.; van Vledder, G.P.; Kömürcü, M.İ.; Özger, M. Evaluation of the numerical wave model (SWAN) for wave sim-ulation in the Black Sea. Cont. Shelf Res. 2012, 50, 80–99. [Google Scholar] [CrossRef]
- Liang, B.; Gao, H.; Shao, Z. Characteristics of global waves based on the third-generation wave model SWAN. Mar. Struct. 2019, 64, 35–53. [Google Scholar] [CrossRef]
- Asma, S.; Sezer, A.; Ozdemir, O. MLR and ANN models of significant wave height on the west coast of India. Comput. Geosci. 2012, 49, 231–237. [Google Scholar] [CrossRef]
- Kumar, N.K.; Savitha, R.; Al Mamun, A. Ocean wave height prediction using ensemble of Extreme Learning Machine. Neurocomputing 2018, 277, 12–20. [Google Scholar] [CrossRef]
- Yu, T.; Wang, J. A Spatiotemporal Convolutional Gated Recurrent Unit Network for Mean Wave Period Field Forecasting. J. Mar. Sci. Eng. 2021, 9, 383. [Google Scholar] [CrossRef]
- Bidlot, J.-R.; Holmes, D.J.; Wittmann, P.A.; Lalbeharry, R.; Chen, H.S. Intercomparison of the Performance of Operational Ocean Wave Forecasting Systems with Buoy Data. Weather Forecast. 2002, 17, 287–310. [Google Scholar] [CrossRef]
- Fan, C.; Wang, X.; Zhang, X.; Gao, D. A newly developed ocean significant wave height retrieval method from Envisat AS-AR wave mode imagery. Acta Oceanol. Sin. 2019, 38, 120–127. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, J.; Yang, J.; Bao, W.; Wu, G.; Ren, Q. An evaluation of input/dissipation terms in WAVEWATCH III using in situ and satellite significant wave height data in the South China Sea. Acta Oceanol. Sin. 2017, 36, 20–25. [Google Scholar] [CrossRef]
- Deo, M.; Naidu, C.S. Real time wave forecasting using neural networks. Ocean Eng. 1998, 26, 191–203. [Google Scholar] [CrossRef]
- Tsai, C.-P.; Lin, C.; Shen, J.-N. Neural network for wave forecasting among multi-stations. Ocean Eng. 2002, 29, 1683–1695. [Google Scholar] [CrossRef]
- Deo, M.; Jha, A.; Chaphekar, A.; Ravikant, K. Neural networks for wave forecasting. Ocean Eng. 2001, 28, 889–898. [Google Scholar] [CrossRef]
- Berbić, J.; Ocvirk, E.; Carević, D.; Lončar, G. Application of neural networks and support vector machine for significant wave height prediction. Oceanologia 2017, 59, 331–349. [Google Scholar] [CrossRef]
- Dixit, P.; Londhe, S. Prediction of extreme wave heights using neuro wavelet technique. Appl. Ocean. Res. 2016, 58, 241–252. [Google Scholar] [CrossRef]
- Mikolov, T.; Kombrink, S.; Burget, L.; Cernocky, J.; Khudanpur, S. Extensions of recurrent neural network language model. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 5528–5531. [Google Scholar]
- Gers, F.A.; Schraudolph, N.N.; Schmidhuber, J. Learning precise timing with LSTM recurrent networks. J. Mach. Learn. Res. 2002, 3, 115–143. [Google Scholar]
- Zhang, C.; Zeng, J.; Wang, H.; Ma, L.; Chu, H. Correction model for rainfall forecasts using the LSTM with multiple meteorological factors. Meteorol. Appl. 2020, 27, 1852. [Google Scholar] [CrossRef]
- Mandal, S.; Prabaharan, N. Ocean wave forecasting using recurrent neural networks. Ocean Eng. 2006, 33, 1401–1410. [Google Scholar] [CrossRef]
- Pushpam P., M.M.; Enigo V.S., F. Forecasting Significant Wave Height using RNN-LSTM Models. In Proceedings of the 2020 4th International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 13–15 May 2020; pp. 1141–1146. [Google Scholar]
- Kaloop, M.R.; Kumar, D.; Zarzoura, F.; Roy, B.; Hu, J.W. A wavelet—Particle swarm optimization—Extreme learning machine hybrid modeling for significant wave height prediction. Ocean Eng. 2020, 213, 107777. [Google Scholar] [CrossRef]
- Deshmukh, A.N.; Deo, M.C.; Bhaskaran, P.K.; Nair, T.B.; Sandhya, K.G. Neural-network-based data assimilation to im-prove numerical ocean wave forecast. IEEE J. Ocean. Eng. 2016, 41, 944–953. [Google Scholar] [CrossRef]
- Wang, T.; Gao, S.; Xu, J.; Li, Y.; Li, P.; Ren, P. Correcting Predictions from Oceanic Maritime Numerical Models via Residual Learning. In Proceedings of the 2018 OCEANS—MTS/IEEE Kobe Techno-Oceans (OTO), Kobe, Japan, 28–31 May 2018; pp. 1–4. [Google Scholar]
- Campos, R.M.; Krasnopolsky, V.; Alves, J.-H.G.M.; Penny, S.G. Nonlinear Wave Ensemble Averaging in the Gulf of Mexico Using Neural Networks. J. Atmos. Ocean. Technol. 2019, 36, 113–127. [Google Scholar] [CrossRef]
- Campos, R.M.; Krasnopolsky, V.; Alves, J.-H.; Penny, S.G. Improving NCEP’s global-scale wave ensemble averages using neural networks. Ocean Model. 2020, 149, 101617. [Google Scholar] [CrossRef]
- Salinas, D.; Flunkert, V.; Gasthaus, J.; Januschowski, T. DeepAR: Probabilistic forecasting with autoregressive recurrent net-works. Int. J. Forecast. 2020, 36, 1181–1191. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference Learning Representations (ICLR), San Diego, CA, USA, 5–8 May 2015. [Google Scholar]
- Lv, X.; Yuan, D.; Ma, X.; Tao, J. Wave characteristics analysis in Bohai Sea based on ECMWF wind field. Ocean Eng. 2014, 91, 159–171. [Google Scholar] [CrossRef]
- Wu, W.; Li, P.; Zhai, F.; Gu, Y.; Liu, Z. Evaluation of different wind resources in simulating wave height for the Bohai, Yellow, and East China Seas (BYES) with SWAN model. Cont. Shelf Res. 2020, 207, 104217. [Google Scholar] [CrossRef]
- Wang, T.; Gao, S.; Bi, F.; Li, Y.; Guo, D.; Ren, P. Residual Learning with Multifactor Extreme Learning Machines for Wave height Prediction. IEEE J. Ocean. Eng. 2020, 46, 611–623. [Google Scholar] [CrossRef]
- Taboada, J.V.; Hirpa, G.L. Analysis of Wave Energy Sources in the North Atlantic Waters in View of Design Challenges. In Proceedings of the 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; pp. 1–9. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Bruno, M.F.; Molfetta, M.G.; Totaro, V.; Mossa, M. Performance Assessment of ERA5 Wave Data in a Swell Dominated Region. J. Mar. Sci. Eng. 2020, 8, 214. [Google Scholar] [CrossRef]




| Validation Method | Method | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h |
|---|---|---|---|---|---|---|---|
| RMSE | Numerical model | 0.4730 | 0.4325 | 0.3716 | 0.2728 | 0.2811 | 0.2807 |
| LSTM | 0.1372 | 0.1835 | 0.2163 | 0.1554 | 0.1706 | 0.2051 | |
| ELM residual learning | 0.2160 | 0.2525 | 0.2796 | 0.2409 | 0.2340 | 0.2427 | |
| MFELM residual learning | 0.1888 | 0.2133 | 0.2194 | 0.2126 | 0.2104 | 0.2103 | |
| N-LSTM (Our method) | 0.0581 | 0.1248 | 0.1479 | 0.1237 | 0.1500 | 0.1869 | |
| MAPE | Numerical model | 0.2688 | 0.2466 | 0.2267 | 0.2717 | 0.1544 | 0.1420 |
| LSTM | 0.0728 | 0.1025 | 0.1281 | 0.1522 | 0.0917 | 0.1092 | |
| ELM residual learning | 0.1172 | 0.1393 | 0.1569 | 0.2789 | 0.1219 | 0.1209 | |
| MFELM residual learning | 0.1039 | 0.1167 | 0.1192 | 0.2611 | 0.1026 | 0.1039 | |
| N-LSTM (Our method) | 0.0319 | 0.0691 | 0.0830 | 0.1233 | 0.0833 | 0.0946 | |
| SS | LSTM | 0.7412 | 0.5854 | 0.4343 | 0.5142 | 0.4360 | 0.2848 |
| ELM residual learning | 0.5598 | 0.4383 | 0.3128 | 0.1135 | 0.2189 | 0.1497 | |
| MFELM residual learning | 0.6362 | 0.5280 | 0.4626 | 0.2215 | 0.3267 | 0.2776 | |
| N-LSTM (Our method) | 0.8890 | 0.7221 | 0.6530 | 0.5670 | 0.5266 | 0.3655 |
| Validation Method | Method | 3 h | 6 h | 12 h | 24 h | 48 h | 72 h |
|---|---|---|---|---|---|---|---|
| RMSE | Numerical model | 0.1529 | 0.1181 | 0.1248 | 0.1547 | 0.1777 | 0.3243 |
| LSTM | 0.0610 | 0.0927 | 0.0838 | 0.1353 | 0.1593 | 0.2326 | |
| ELM residual learning | 0.0839 | 0.0402 | 0.0915 | 0.1119 | 0.1546 | 0.2713 | |
| MFELM residual learning | 0.0766 | 0.0440 | 0.0775 | 0.0849 | 0.1176 | 0.2944 | |
| N-LSTM (Our method) | 0.0174 | 0.0574 | 0.0765 | 0.0831 | 0.1166 | 0.1858 | |
| MAPE | Numerical model | 0.7639 | 0.4938 | 0.6443 | 0.7174 | 0.9697 | 1.2006 |
| LSTM | 0.2955 | 0.3278 | 0.4170 | 0.6332 | 0.8954 | 0.8170 | |
| ELM residual learning | 0.4171 | 0.1446 | 0.4574 | 0.4220 | 0.5910 | 0.8979 | |
| MFELM residual learning | 0.3815 | 0.1808 | 0.2968 | 0.3629 | 0.6095 | 1.1040 | |
| N-LSTM (Our method) | 0.0774 | 0.2191 | 0.3765 | 0.3516 | 0.6260 | 0.6229 | |
| SS | LSTM | 0.6131 | 0.2213 | 0.4069 | 0.1398 | 0.1206 | 0.3317 |
| ELM residual learning | 0.4540 | 0.7309 | 0.2968 | 0.3527 | 0.2518 | 0.1946 | |
| MFELM residual learning | 0.5005 | 0.6012 | 0.4339 | 0.5247 | 0.4092 | 0.0908 | |
| N-LSTM (Our method) | 0.8987 | 0.5825 | 0.4453 | 0.5321 | 0.4218 | 0.4891 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, Y.; Gao, S.; Ren, P. Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory. J. Mar. Sci. Eng. 2021, 9, 514. https://doi.org/10.3390/jmse9050514
Zhang X, Li Y, Gao S, Ren P. Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory. Journal of Marine Science and Engineering. 2021; 9(5):514. https://doi.org/10.3390/jmse9050514
Chicago/Turabian StyleZhang, Xiaoyu, Yongqing Li, Song Gao, and Peng Ren. 2021. "Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory" Journal of Marine Science and Engineering 9, no. 5: 514. https://doi.org/10.3390/jmse9050514
APA StyleZhang, X., Li, Y., Gao, S., & Ren, P. (2021). Ocean Wave Height Series Prediction with Numerical Long Short-Term Memory. Journal of Marine Science and Engineering, 9(5), 514. https://doi.org/10.3390/jmse9050514







