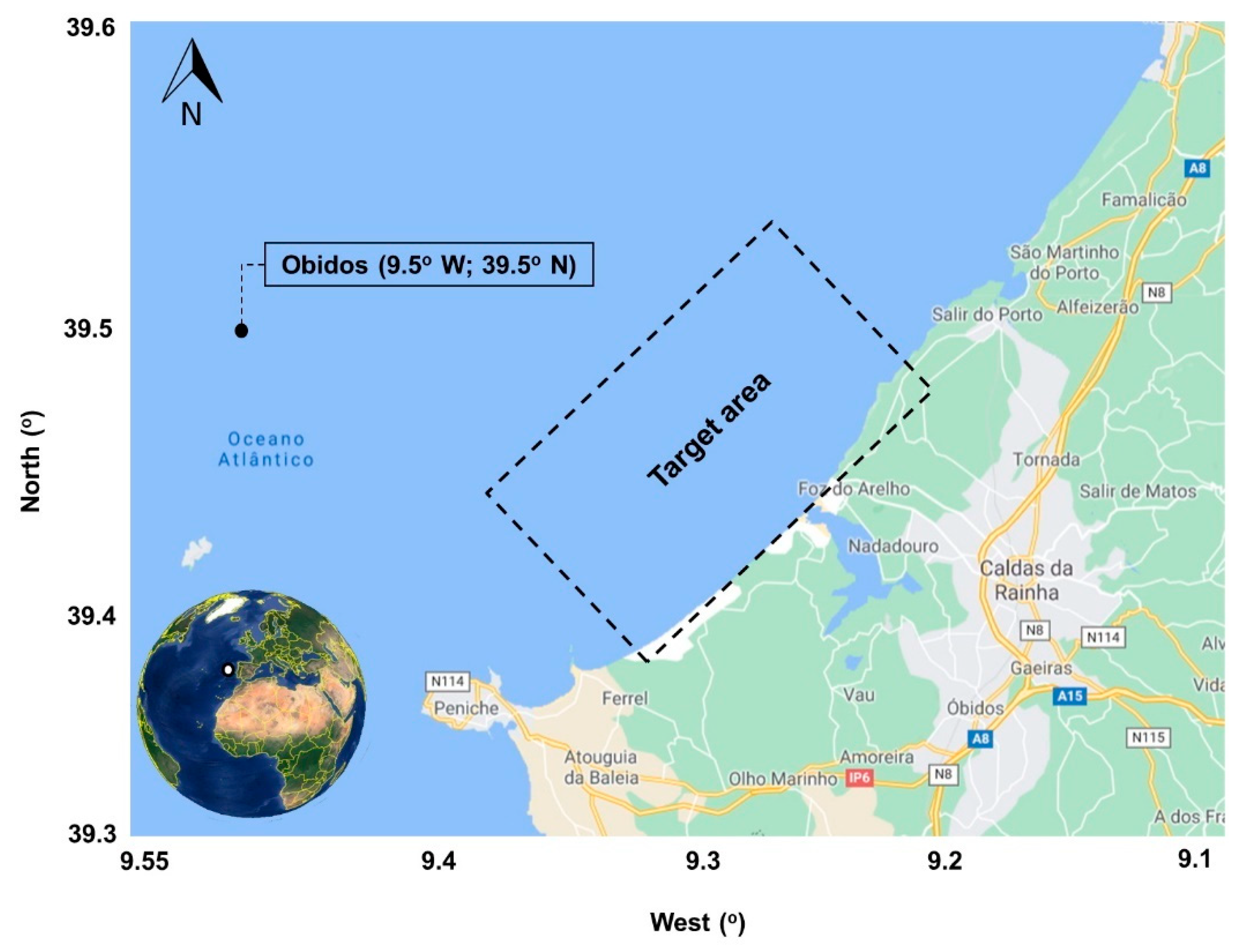
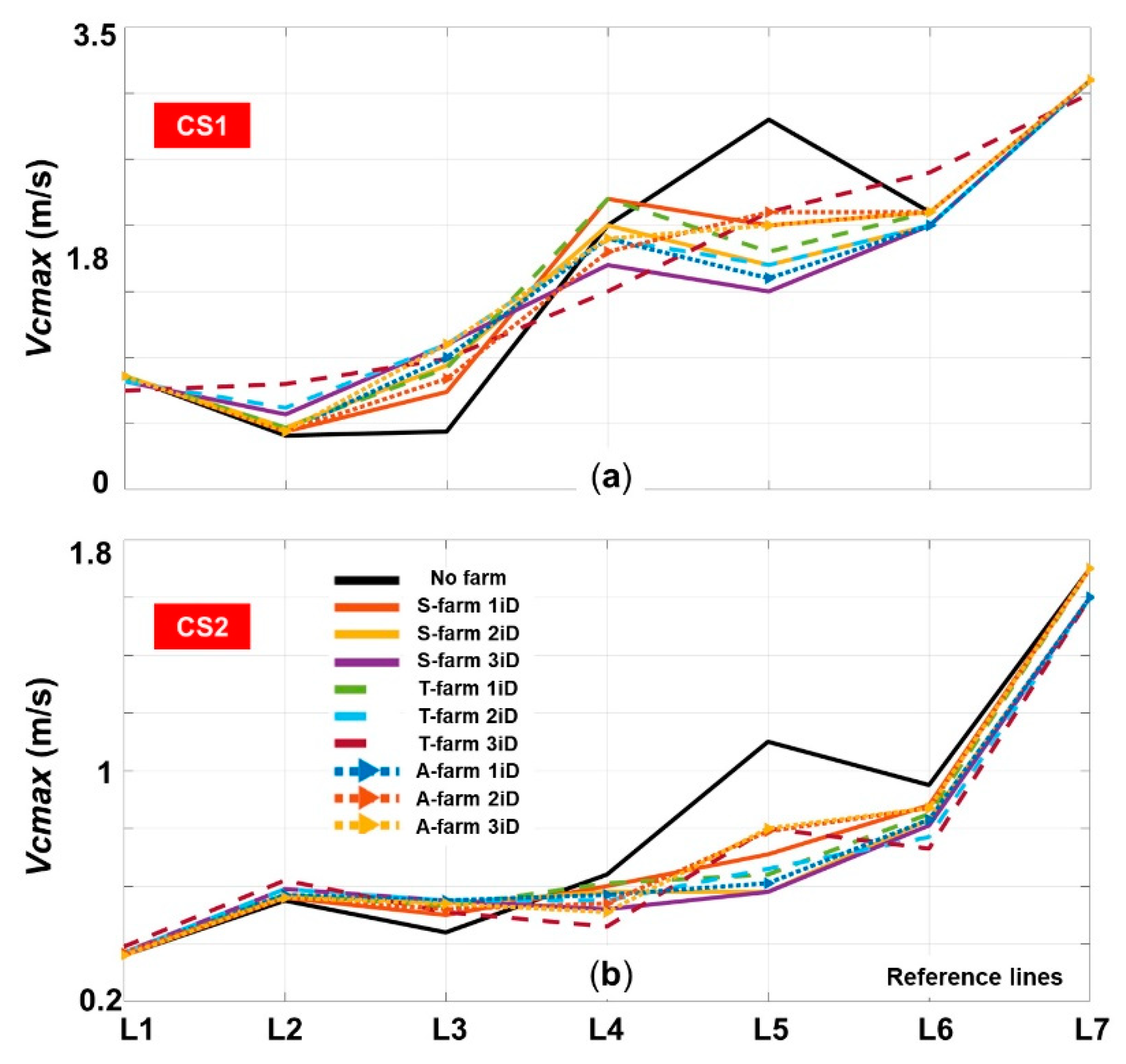
3.1. Evaluation of the Wave Characteristics
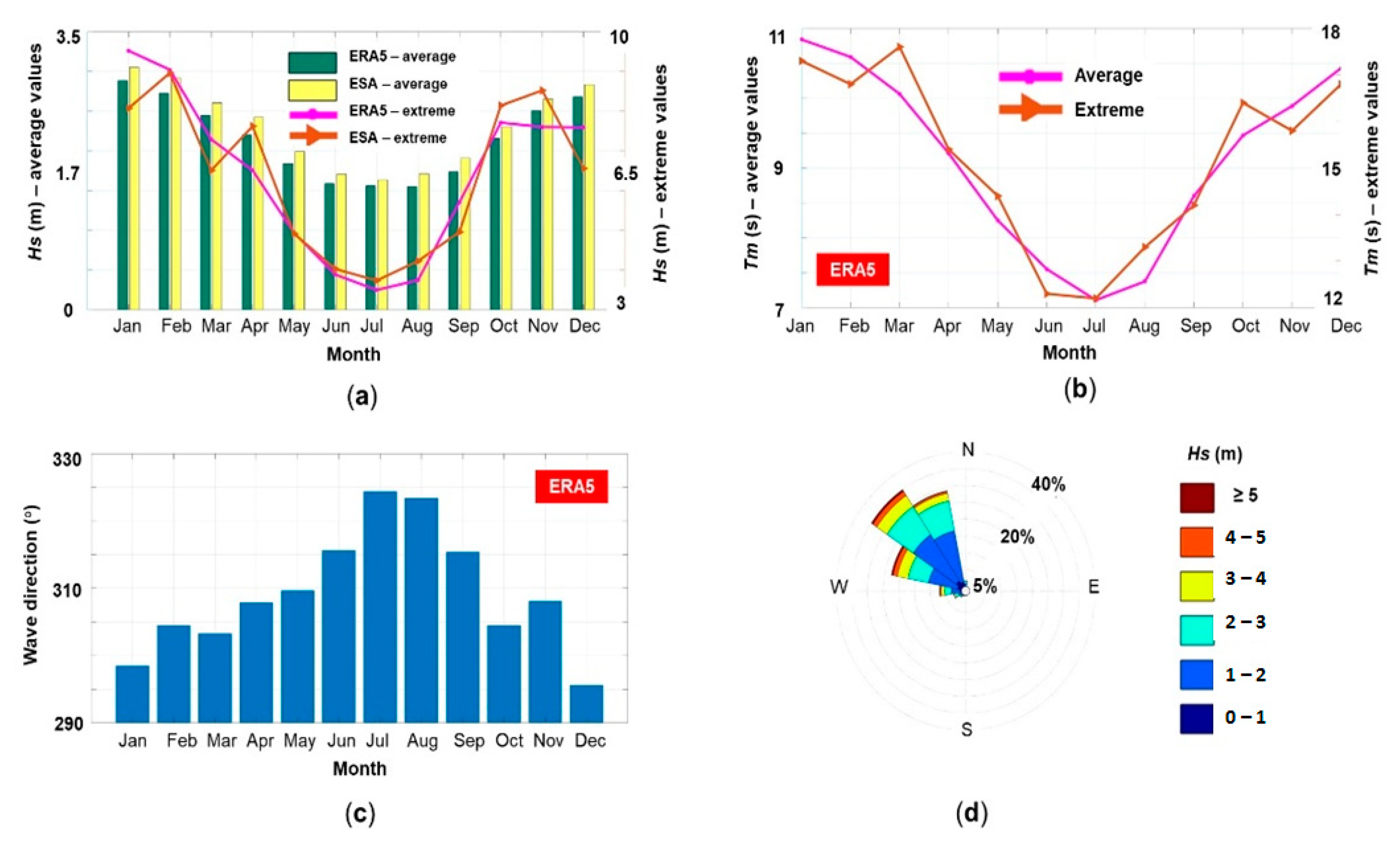
Figure 3 provides a general picture of the wave conditions from the Obidos area, by considering 27–years of combined satellite measurements and ERA5 data. In general, for the assessment of the wind and wave conditions, it is recommended to use at least 10–years of data [
53], with a large number of satellite data indicating the progress in this field. By looking at these results, we noticed that definitely, the wave conditions indicated a seasonal fluctuation, where for the
Hs and
Tm parameters, much higher values were noticed during the wintertime (October–March), while for the wave direction, the values increased during the summertime (above 310°). From the analysis of the
Hs data (
Figure 3a), the ESA results were higher than those from ERA5, especially in the case of the average values reported in the range of 1.64–3.05 m (July and January). As for ERA5, a similar pattern occurred, with values of 1.55 and 2.9 m (August and January). For the extreme values, there was a good agreement between the two datasets for February (9.04 m), May (4.94 m) and June (3.89 m), respectively. Higher values were provided by the ESA project during April (7.62 m), October (8.14 m) and November (8.52 m), while for January (8.07 m) and December (6.56 m), the values dropped below the ERA5 data.
Figure 3b presents the evolution of the
Tm parameter (only ERA5), which on average can go from 7.1 to 10.84 s (summer to winter), while the extreme values indicated a maximum of 17.6 s (in March) with a minimum of 12.2 s noticed between June and August, respectively.
The dominant wave direction (
Figure 3c) was in the range of 295.6–324.4°, with lower values occurring in January and December, compared to July and August when the values significantly increased. From the analysis of the wave roses (
Figure 3d), we could see that the waves were coming from the north-west sector, being oblique to the Obidos coastal sector, confirming the formation of the local sand spit.
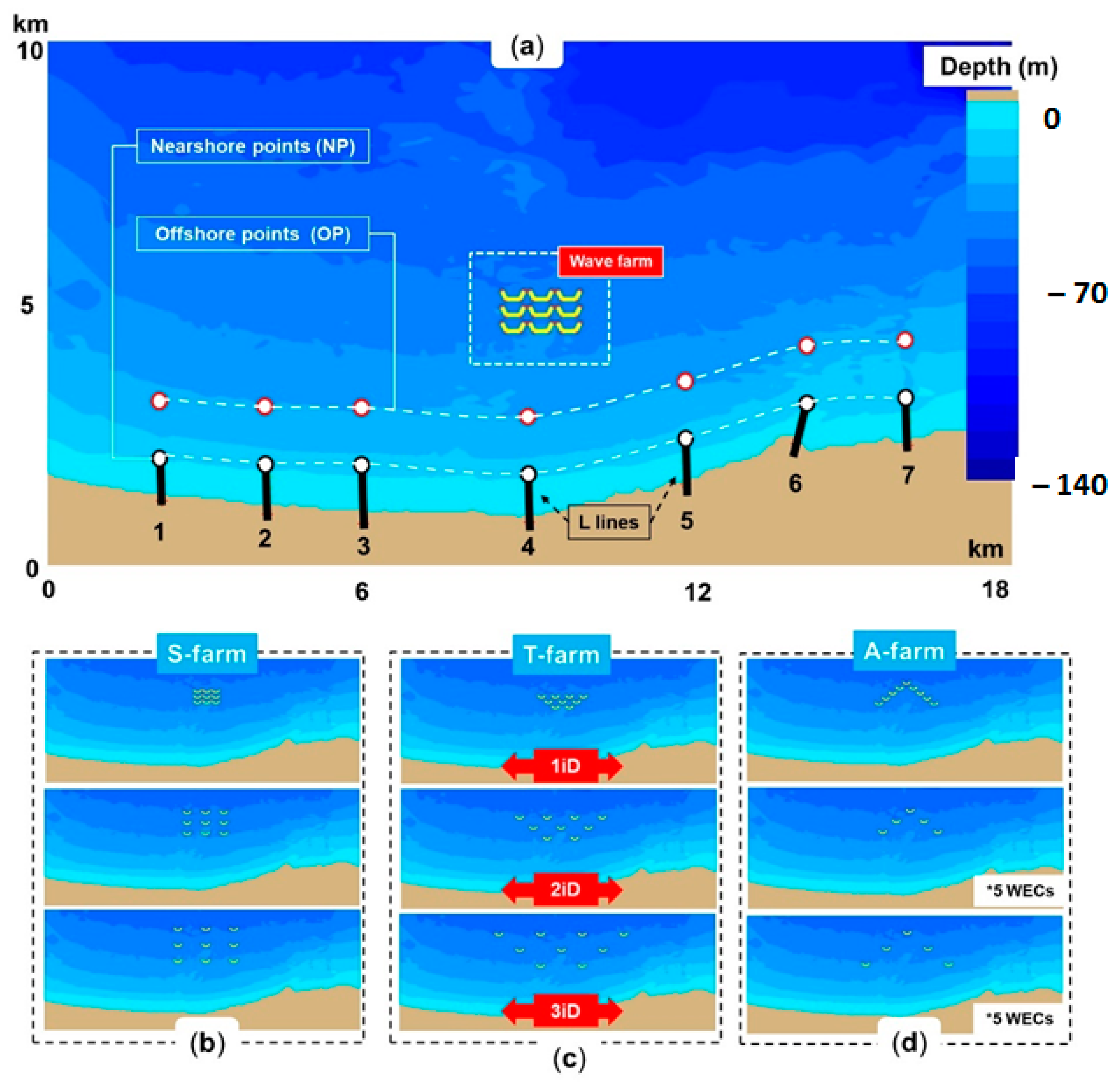
To run the numerical simulations in a stationary mode, some case studies (CS) needed to be defined and in
Table 3, such CS were selected that combined the ESA (
Hs values) and the ERA5 (
Tm and
Dir values) data. Relevant extreme conditions were selected from winter and summer (February and July), also including a January sea state that was considered representative for winter (average conditions).
At this point, it has to be highlighted that
Figure 3 presents the wave statistics based on information coming from the two databases considered (ERA5 and ESA). The reason for considering two different sources is that in this way, a more realistic picture of the wave conditions was provided. The satellite measurements presented more accurate results than the ERA5 model, with these also using data assimilation techniques to improve their hindcast. From this figure, we can define the average and extreme values corresponding to the seasons and to each individual month. In a first approach, in the present work, the winter extreme and average conditions were selected and they corresponded to the CS1 and CS2 case studies. The reason was that the extreme (CS1) corresponded to the most energetic situation that could be encountered while the winter average corresponded to the most representative conditions for the wintertime, which was also very representative for spring and autumn. Additionally, the extreme summer conditions were also considered (CS3), because these were high wave conditions that may have a significant impact on the nearshore. A fourth situation was also considered corresponding to the summer average wave conditions, but since the wave energy was quite low in this situation, this case was not considered relevant in relation to the objectives of the present work.
In
Table 4 the
Hs values are presented. These are illustrated by the nearshore/offshore points for all the case studies, in the absence of the wave farm. As expected, the CS1 scenario indicated the highest values that go from 8.01–8.42 m (offshore) to a minimum of 6.7 m near the coastline. The attenuation was more severe near the point NP7, compared to the central part (ex: NP5) where the waves could reduce by 0.3–0.6 m. Compared to CS1, in the case of the CS2 and CS3 scenarios, some nearshore points indicated slightly higher values than the offshore ones, this being the case of NP1–3.3 to 3.38 m (CS3) or NP6–2.87 to 2.97 m (CS2), respectively.
The wave direction indicated how the wave energy was distributed in the geographical space, being also directly related to the generation of the longshore currents.
Table 5 presents this distribution (no wave farm), for which we can notice that regardless of the case study, the direction was in the range 293–322°. For CS1 and CS2, the wave direction increased from offshore to nearshore in the case of the group points 1–2–3–4, while a reverse pattern was noticed for the remaining points. The CS3 scenario indicated no significant variation in the case of the group points NP1–NP3, while the differences started to increase from NP4 (−2°) to NP7 (−14°), respectively.
The wave-induced forces (N/m
2) provided important information concerning the wave intensity acting on a particular WEC system (ex: mooring lines) or how a coastal structure would be affected.
Table 6 presents the distribution of this characteristic (no wave farm), from which we could notice that higher values corresponded to the nearshore points. The values of the wave forces strongly depended on the severity of the wave conditions, this being the case of CS1 when the offshore points indicated wave forces with values in the range of 5.45 (OP2) and 46.2 N/m
2 (OP6).
Going further to the nearshore points, the value of the wave forces could easily jump to 70.9 N/m2 (NP1) or 91.5 N/m2 (NP6), while a minimum value of 7.86 N/m2 wads expected near NP5. The CS2 and CS3 conditions indicated relatively similar values for the offshore area, where much higher values were expected close to OP6–OP7 (ex: 4.98 N/m2), while close to the nearshore a maximum value of 16.8 N/m2 corresponded to NP6.
The wave action was in charge of the suspended sediments and through the orbital velocity near the bottom (
Ubot) these particles were carried to the shoreline. In
Table 7, a general picture of this parameter is provided (no farm), and from the information provided by CS1, we could notice that the sediment transport was initiated in the offshore area (
Ubot > 2 m/s) while close to the shore, this process was accelerated with reported values in the range of 2.74–3.17 m/s. In the case of CS2–CS3, the offshore conditions seemed to have a limited impact on the sediment circulation, with much higher values being encountered by the nearshore points (ex: 1.46 m/s). The Hjulström curve [
54] is designed to establish the sediment pattern corresponding to different sediment types, with a mention that for this work, the sand appears to be the dominant one, taking into account the presence of the Obidos sand spit [
35]. For velocities exceeding 0.1 m/s, the erosion processes were dominant, regardless of the sand sediment size (fine–medium–coarse), this being reflected by all the points considered in
Table 7. More than this, the higher
Ubot values could easily contribute to the erosion and transport of coarse material, such as cobbles (64–256 mm).
3.2. Coastal Impact of the Wave Farms
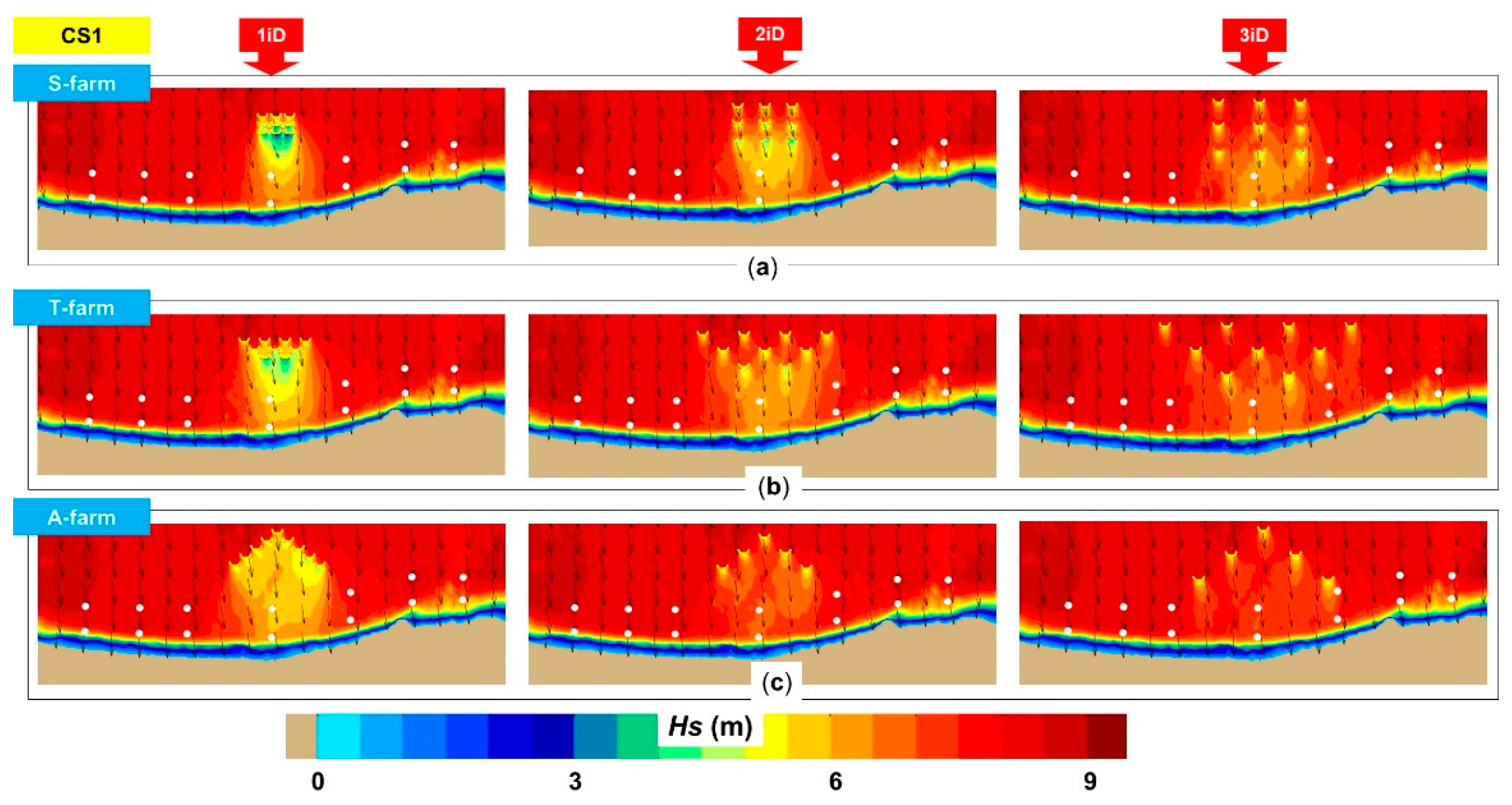
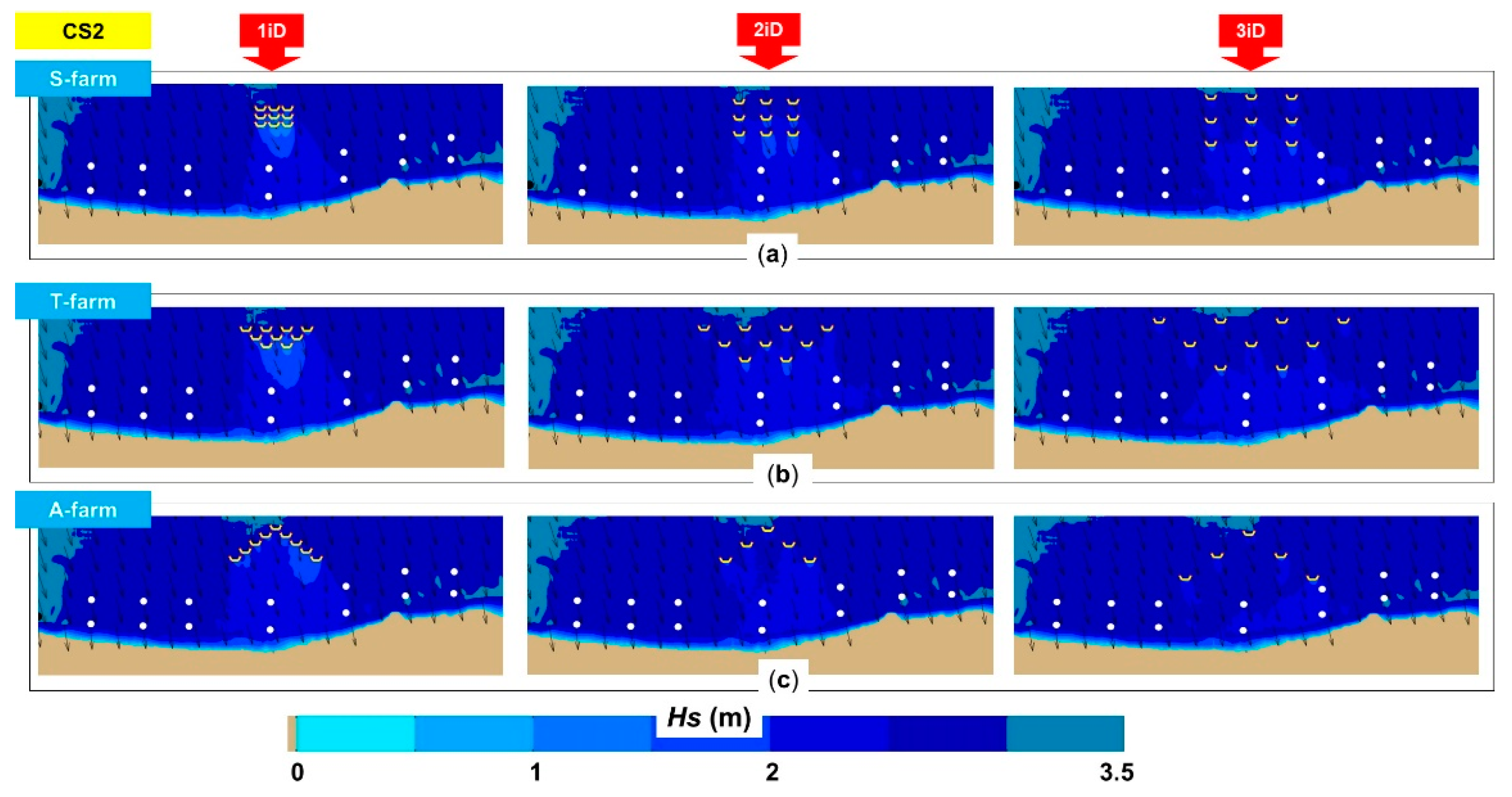
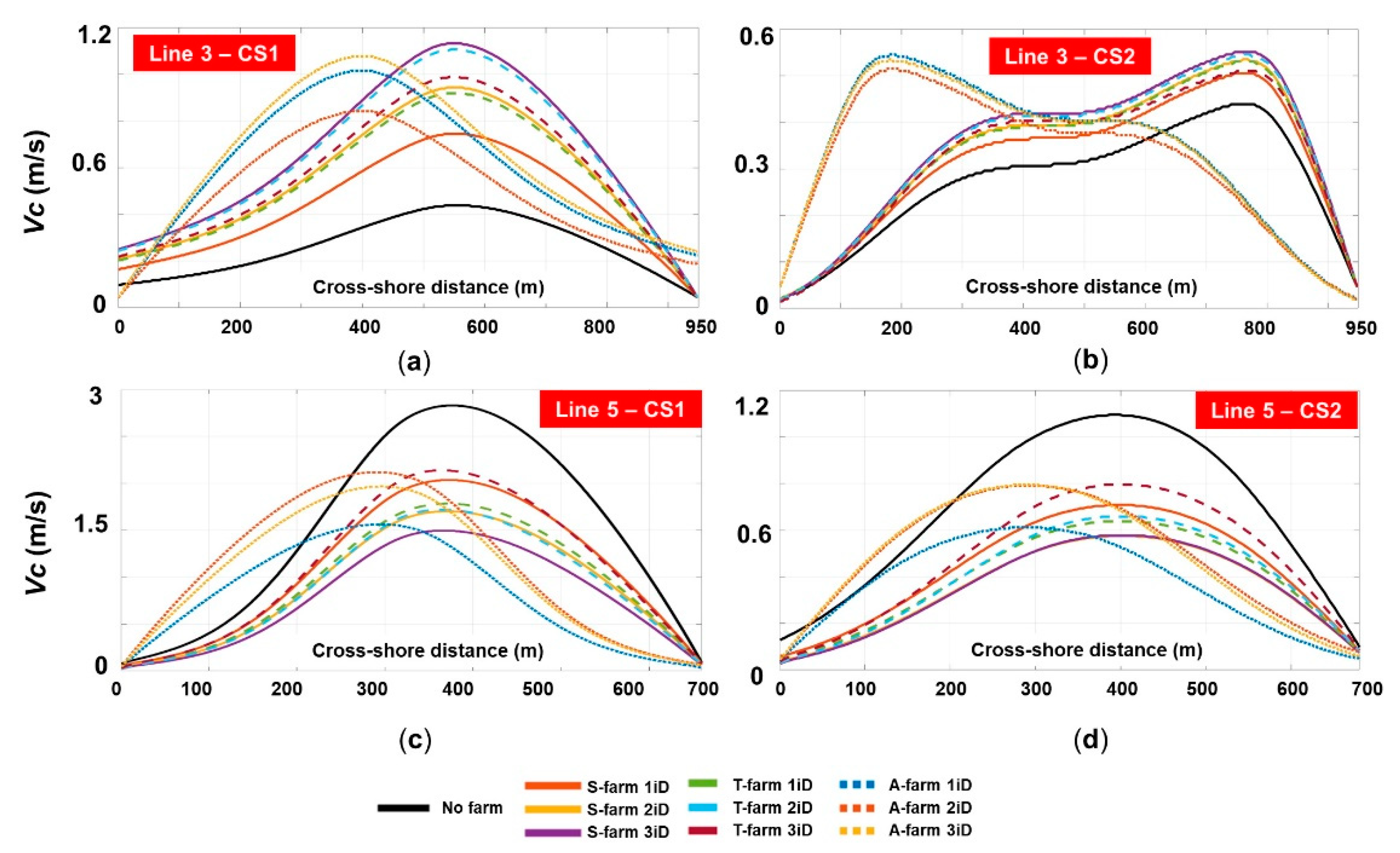
Figure 4 illustrates the spatial distribution of the significant wave height for the CS1 scenario. The shielding effect generated by the wave farms was visible in all cases, being more obvious for the 1iD scenario. By combining this information with the ones corresponding to the OP and NP points, we could obtain a more comprehensive picture of the expected impact. For example, in the case of the S-farm, the offshore points OP1 and OP7 indicated no variations, which was expected by looking at their position, the size of the farms and the wave direction. For the reference points NP2, NP3 and NP4, the
Hs values constantly decreased as we went from the 1iD to the 3iD scenario, but for the NP4, a 3iD configuration (6.35 m) was less efficient than a 1iD (6.08 m) or 2iD (5.99 m) layout. Since a T-farm is wider than an S-farm, this provided better protection for the point NP2 (from 8.36 to 8.09 m–3iD), and for the points NP3 and NP5. Nevertheless, for the point NP4 (located in the center of the target area), an S-farm performed much better.
Going to the nearshore points, the presence of these wave farms would significantly attenuate the wave heights in the central part (NP3, NP4 and NP5), with a mention that for the point NP4, some particular configurations were used, namely: 2iD for the S-farm; 1iD and 2iD for the T-farm; 1iD for the A-farm. For the point NP5, the Hs parameter could decrease from 8.15 m to a minimum of 7.55 m (S-farm/3iD), 7.43 m (T-farm/3iD) or 7.45 m (A-farm/3iD), with a mention that for the A-farm only, 5 WECs were included.
For the CS2 scenario (
Figure 5), the impact of the wave farms was more visible behind the last WEC line which gradually extended to the shoreline. In this case, the results showed that the T-farm/3iD provided some protection for the point NP7 (indicating a
Hs decrease from 2.84 to 2.78 m), in the condition when this was located at approximately 8.5 km from the centre of the farm. The point NP5 indicated, in this case, better protection than NP3, which was mainly related to the direction of the waves. The
Hs values could decrease from 2.76 m to: S-farm (2.54–2.45–2.39 m /1iD to 3iD), T-farm (2.48–2.39–2.4 m) or A-farm (2.44–2.55–2.43 m).
Figure 6 presents the impact of the wave farms for the CS3 scenario, where a
Hs value of 3.7 m and a wave direction of 324° were considered for the SWAN simulations. Close to the shoreline, the influence of the farm was minimal for the points NP1 and NP7, while in the case of NP2 and NP6, a T-farm configuration (3iD) reduced the waves from 3.31 to 3.01 m, and from 3.65 m to 3.57 m, respectively. The farm protected the central part of the target area (point NP4), with noticed attenuations of 0.62 m–S-farm/2iD, 0.68 m–T-farm/1iD or 0.7 m–A-farm/1iD, respectively. For the 3iD configuration, the differences observed between different farm configurations were very small, except for point NP4, where the A-farm was less efficient (ex: 2.9 m compared to 2.62 m–S-farm).
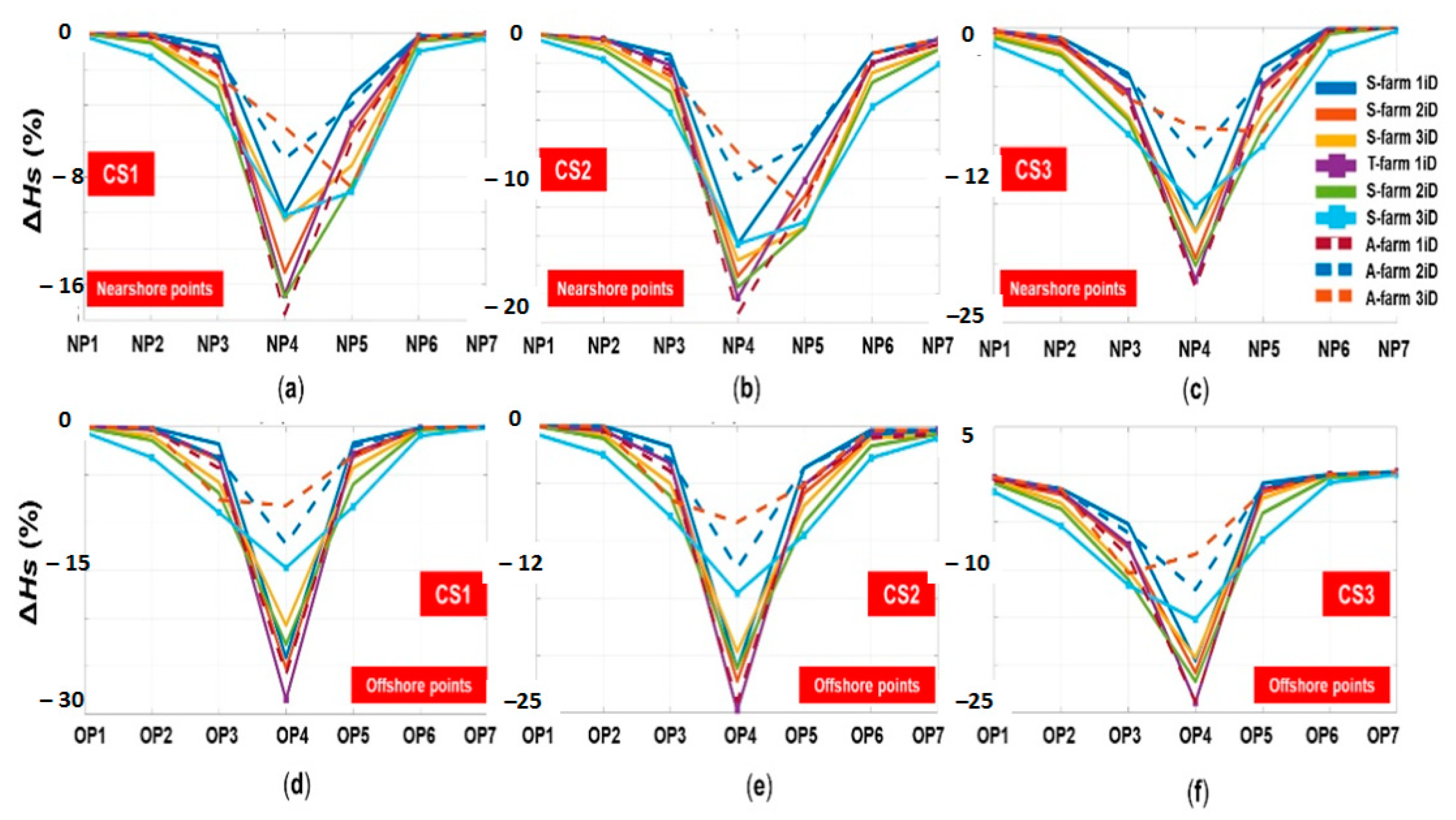
The
Hs differences (in %) reported between the no farm and the wave farm scenarios are presented in
Figure 7. From this, we can notice that most of the values were negative, which meant that the wave farm would reduce the wave heights in some way, with some positive values noticed for CS3-offshore points (
Figure 7f), which were, in fact, insignificant. Regardless of the scenarios, point 4 indicated the maximum
Hs attenuations that could go up to 30% (offshore) or 20% (nearshore), respectively. For the CS1 scenario (nearshore points), an A-farm/1iD configuration was more efficient indicating a maximum attenuation of 16% compared to 10% for the S-farm. For the 2iD and 3iD configurations, the maximum attenuation was similar for the T-farm and A-farm, with a mention that the T-farm had a slightly higher impact on the points NP3 and NP5. A similar pattern was noticed for the scenarios CS2 and CS3, with a mention that for CS2, the impact of the farms was also visible for NP6 (ex. 5.1%–T-farm/3iD).
The presence of the farm clearly influenced the direction of the waves, as we could notice from
Figure 8. For the offshore area, the points OP2 and OP3 indicated negative values, while an opposite pattern was noticed for the points OP4, OP5 and OP6. For CS2, the points OP3 and OP5 indicated the highest peaks of 1.7%, while for CS3, the peaks corresponded to OP3 (1.9%) and OP4 (2.2%), respectively. As for the nearshore points, the differences did not exceed 0.64% for NP3, these differences being mainly generated by the 3iD configurations. On the other hand, for the point NP4, a 1iD configuration had a higher impact, with an expected variation of 1.3% for the T-farm. For scenarios CS2 and CS3, the point NP5 indicated a positive peak (2%) while the negative peak changed between NP4 (2%) and NP3 (1.2%).
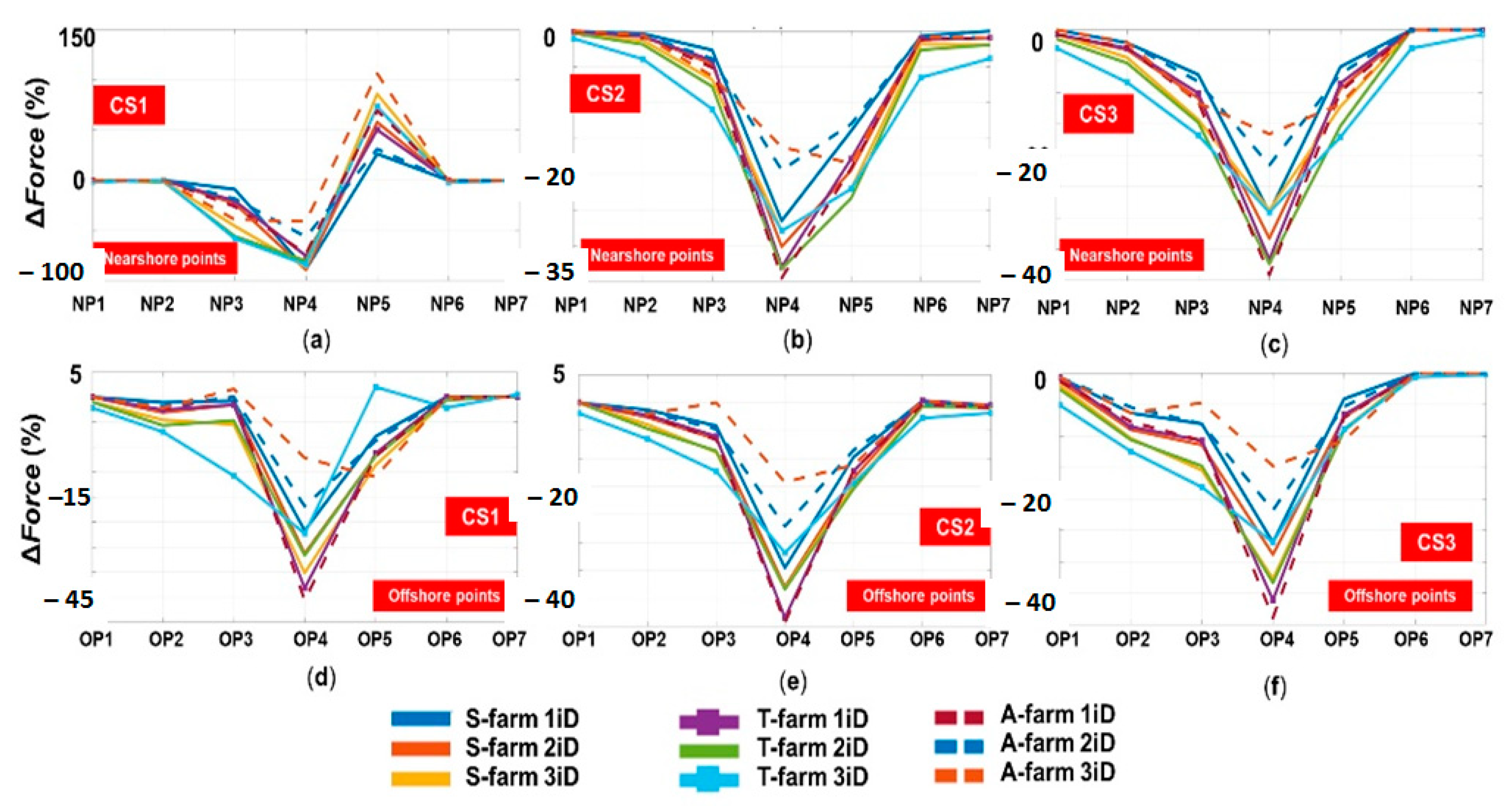
Figure 9 presents the variation of the wave forces by considering the presence of the wave farms. There was a big difference between the CS1–nearshore points where peaks of 90 or 110% (negative and positive, respectively) were noticed, while for the other scenarios and points, the peaks were negative and did not exceed 45%. For the nearshore points, a 1iD farm significantly reduced the forces for the point NP4 but increased the forces at NP5, especially if when considering a 3iD farm (+86% S-farm; +73%T-farm; +110% A-farm). On the extremity of the target area, the influence of the farms was negligible.
For scenario CS2, a 1iD farm provided a maximum force attenuation of 35% for the A-farm compared to 27% for the S-farm. Nevertheless, as we went from 1iD to 3iD, the A-farm was less efficient indicating for point NP4, a minimum value of 16% compared to 28% (S-farm and T-farm). From this perspective, the T-farm seemed to be the best solution, since the induced shielding effect covered a larger area including the points NP2 (3.9%) or NP6 (6.5%), respectively. As for scenario CS3, the distribution was almost symmetrical around the point NP4 with better performances observed: 37/39% –T-farm/A-farm (1iD); 37%–T-farm (2iD); 29%–S-farm/T-farm (3iD).
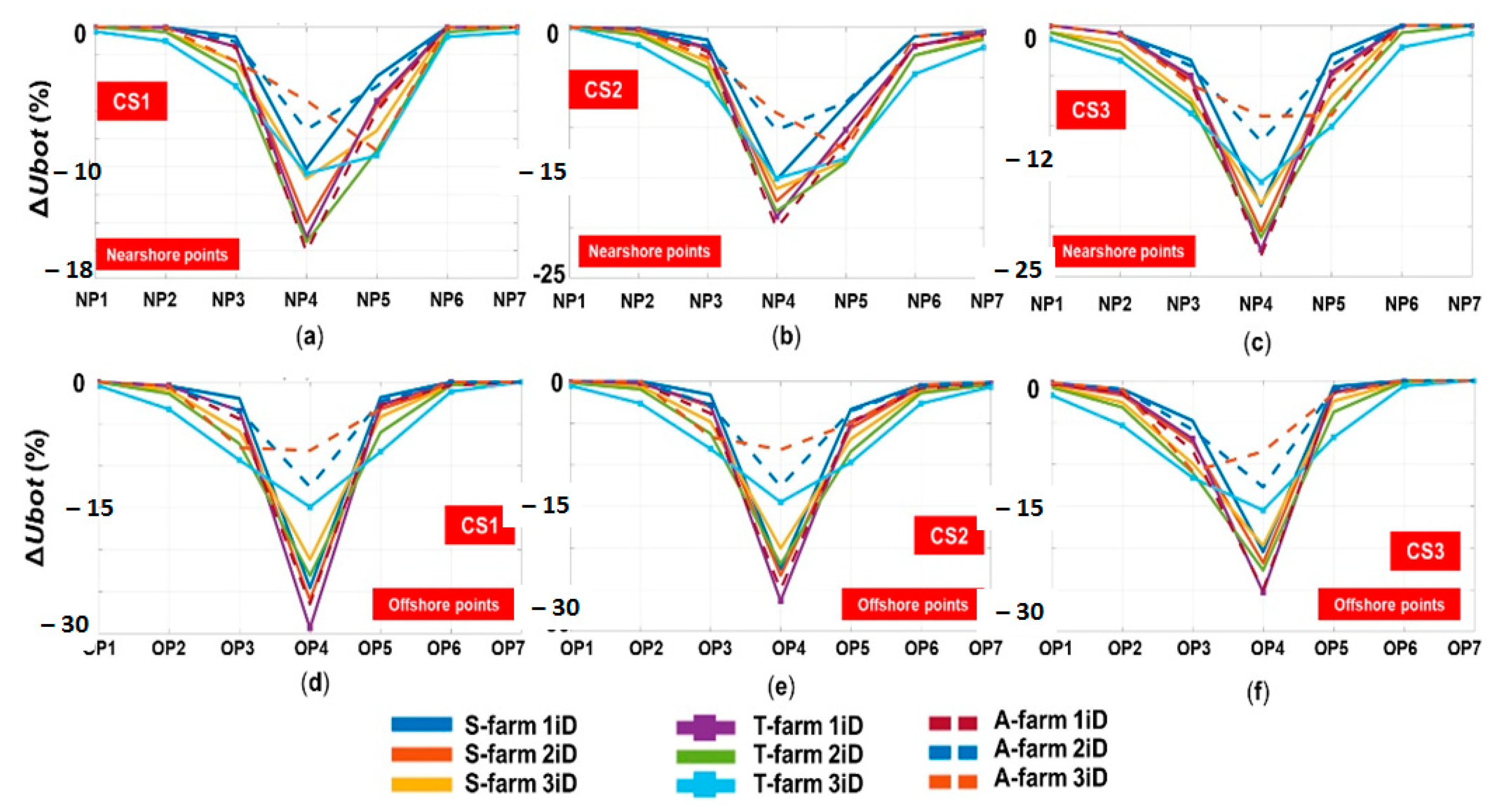
Figure 10 presents the variation of the parameter
Ubot, the differences noticed being very similar to the ones corresponding to the
Hs parameter (
Figure 7).
The main reason for this situation was related to the fact that the variation of the orbital bottom velocity [
55] is in the present work only related to the reduction in energy, which could be considered a limitation because the considered approach was not based on the frequency transmission coefficient. On the other hand, since the main objective of the present work was to provide a global picture of the down wave and shoreline impact of the marine energy farms, the approach considered could provide such a perspective. Furthermore, although the orbital velocity indicated, in general, a similar variation as the
Hs parameter, by using the Hjulström curve [
54] it was possible to establish some connections for the sediment circulation. Thus, the most important attenuations of the values were noticed in the central area, which meant that the wave balance could shift from erosion to sediment transport. By looking at the offshore points, in the case CS1, the erosion processes were dominant (
Ubot in the range 1.47–2.75 m/s). For CS2 (offshore points), in the case of the large sediments (ex: cobbles and pebbles), the transport was bedload and deposition was representative (ex: minimum
Ubot = 0.48 m/s). In this case, the presence of the wave farm increased the deposition processes. As for the nearshore points, the wave farm had little impact for the CS1 scenario, with more important changes noted for CS2 and CS3, where the suspension transport (ex: clay and silt) was accentuated.