Simulations of the Concentration Fields of Rosette-Type Multiport Buoyant Discharges Using Combined CFD and Multigene Genetic Programming Techniques
Abstract
:1. Introduction
2. Materials and Methods
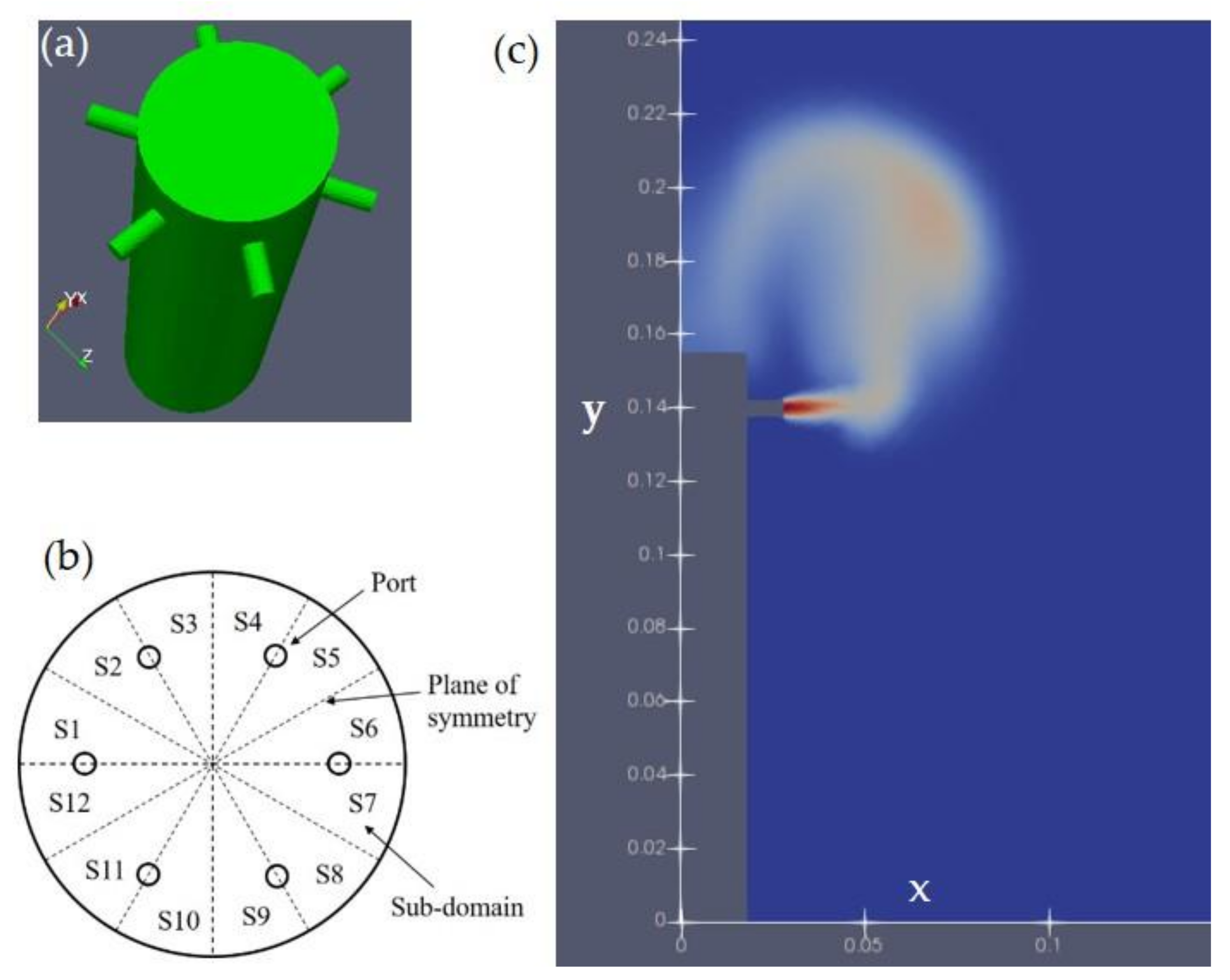
2.1. The 3D CFD Model
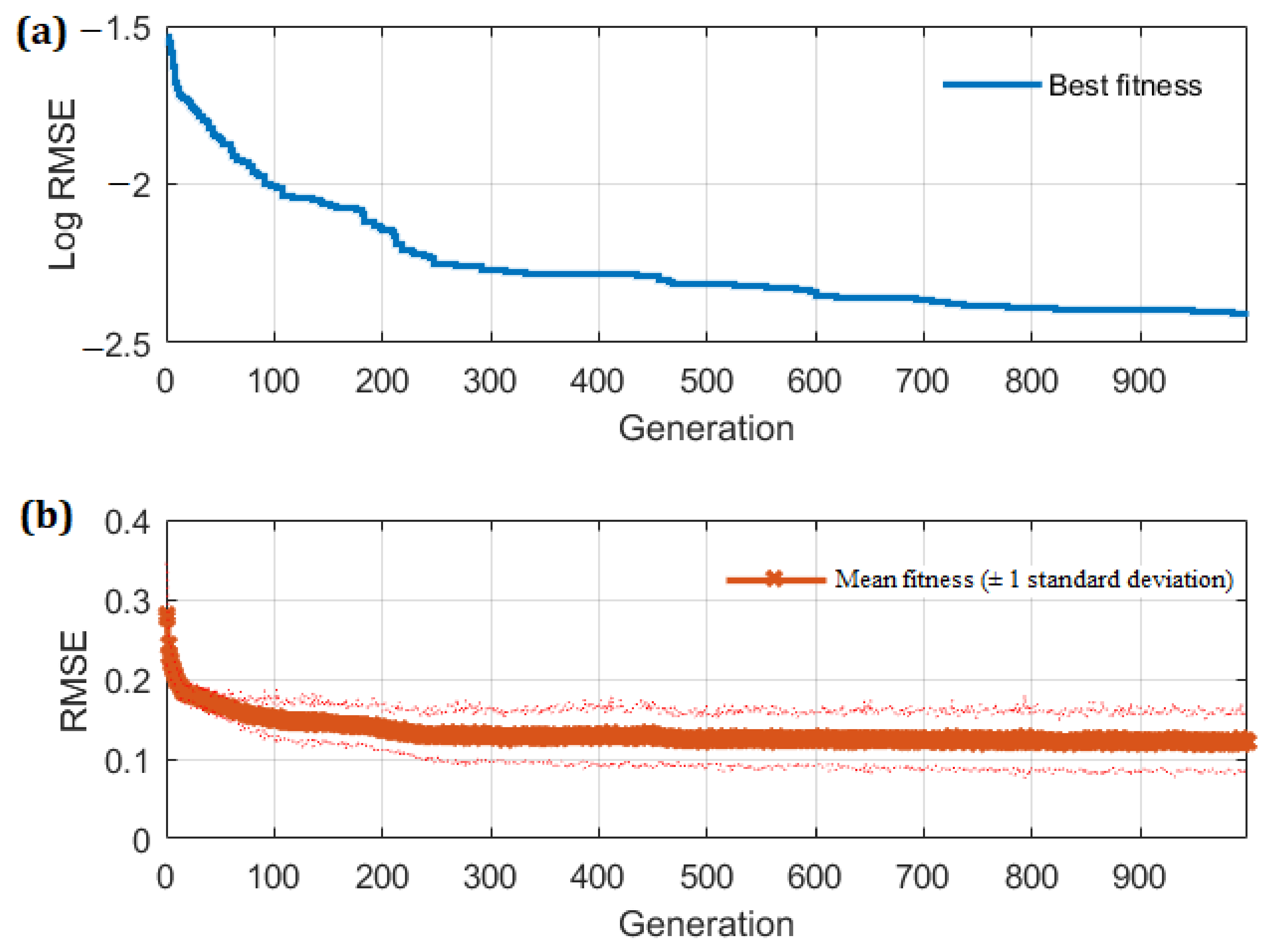
2.2. The MGGP Technique
2.3. The Combined CFD–MGGP Method
3. Results
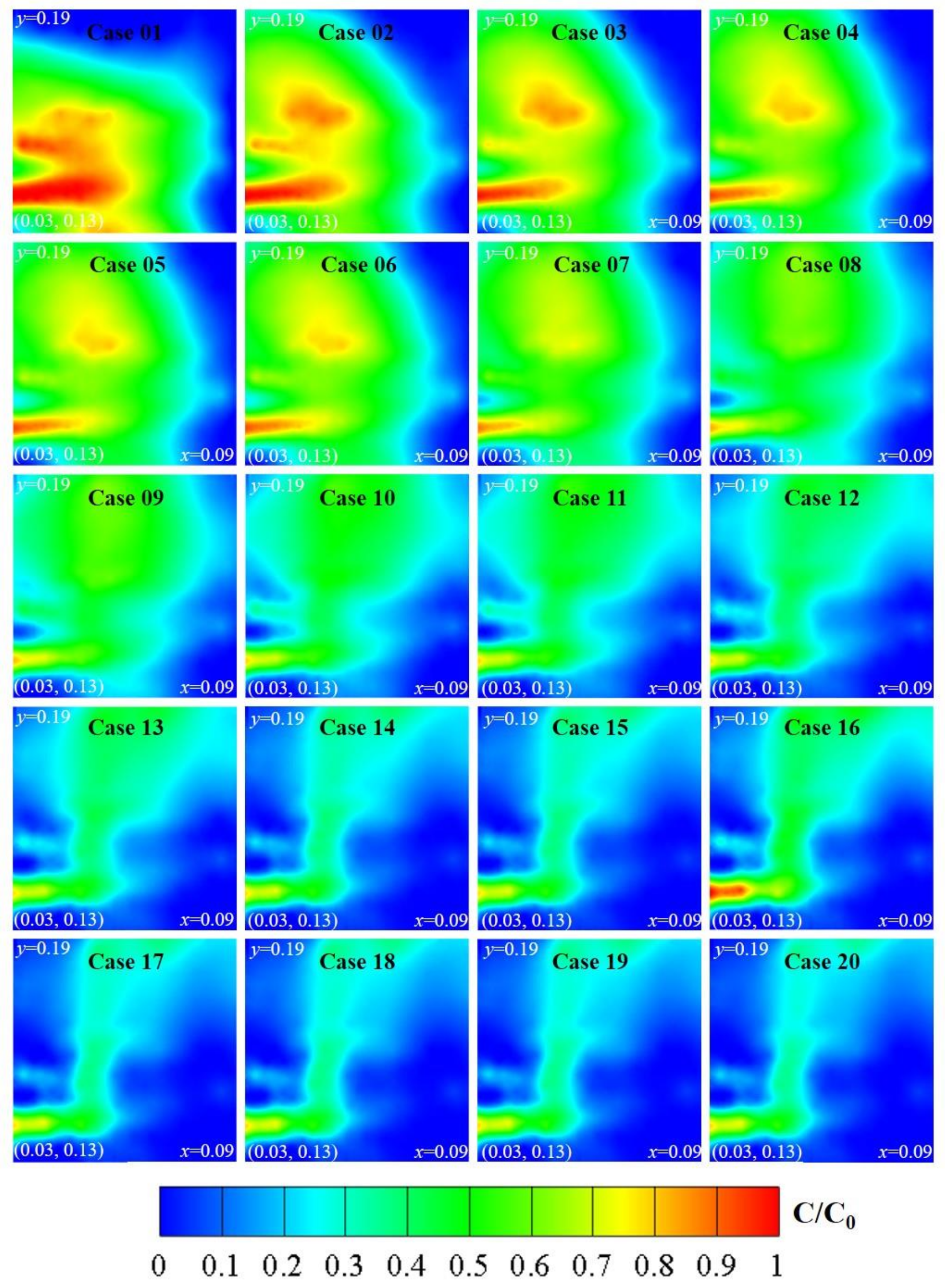
3.1. CFD Results
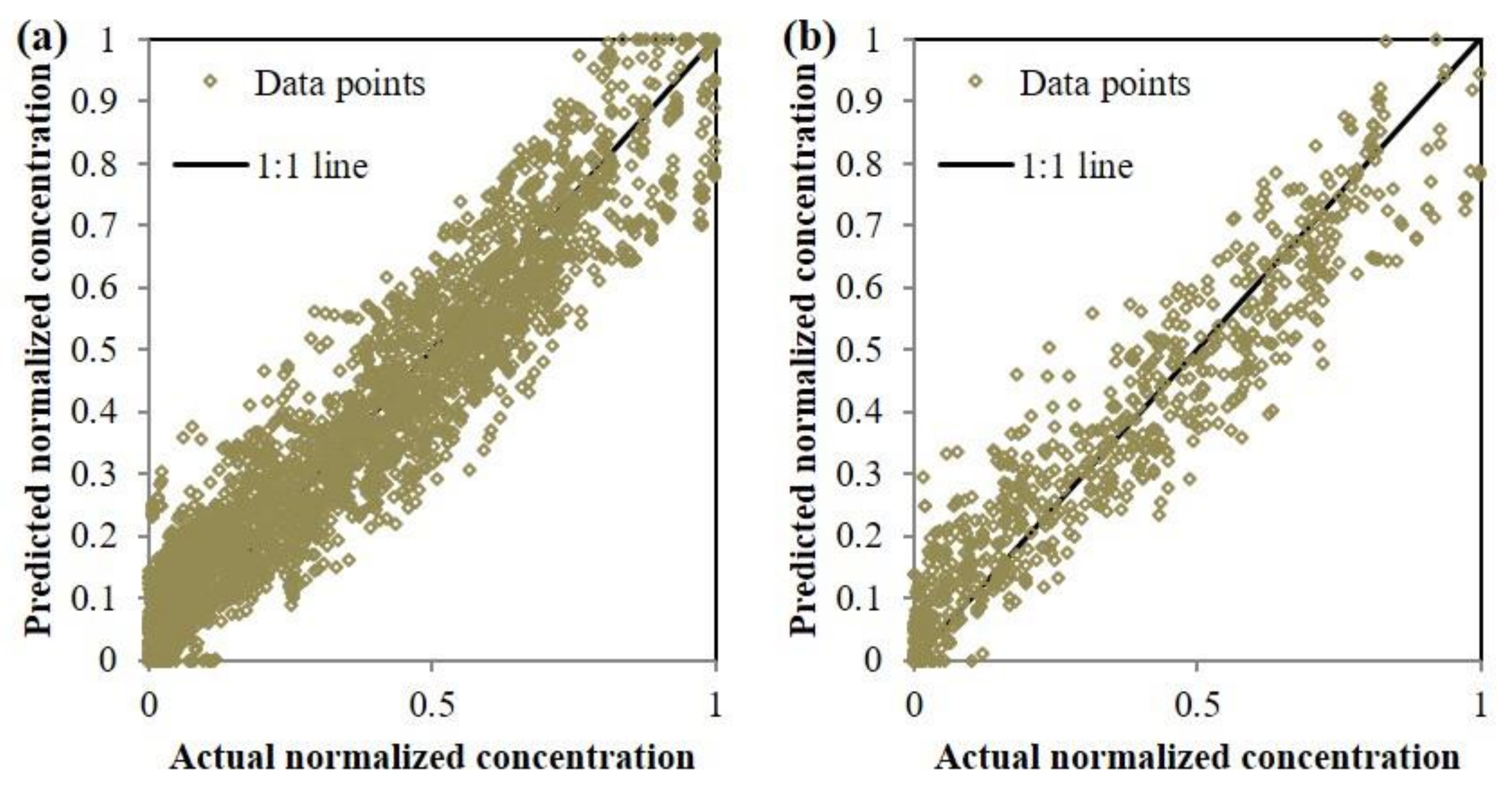
3.2. Results Obtained by the Combined Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Mohammadian, A.; Kheirkhah Gildeh, H.; Nistor, I. CFD modeling of effluent discharges: A review of past numerical studies. Water 2020, 12, 856. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Mohammadian, A. Numerical modeling of vertical buoyant jets subjected to lateral confinement. J. Hydraul. Eng. 2016, 43, 04017016. [Google Scholar] [CrossRef] [Green Version]
- Knystautas, R. The turbulent jet from a series of holes in line. Aeronaut. Q. 2016, 15, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Mohammadian, A. Multigene genetic-programming-based models for initial dilution of laterally con-fined vertical buoyant jets. J. Mar. Sci. Eng. 2019, 7, 246. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Ghodoosipour, B.; Mohammadian, A. Three-dimensional numerical study of multiple vertical buoyant jets in stationary ambient water. J. Hydraul. Eng. 2020, 7, 146. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A.; Chen, X. Three-dimensional numerical simulations of buoyant jets discharged from a rosette-type multiport diffuser. J. Mar. Sci. Eng. 2019, 7, 409. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Mohammadian, A. Evolutionary prediction of the trajectory of a rosette momentum jet group in flowing currents. J. Coast. Res. 2020, 36, 1059–1067. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W.; Gandhi, V. Rosette diffusers for dense effluents. J. Hydraul. Eng. 2016, 143, 06016029. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W. Rosette diffusers for dense effluents in flowing currents. J. Hydraul. Eng. 2017, 144, 06017024. [Google Scholar] [CrossRef]
- Fan, W.; Bao, W.; Cai, Y.; Xiao, C.; Zhang, Z.; Pan, Y.; Chen, Y.; Liu, S. Experimental study on the effects of a vertical jet impinging on soft bottom sediments. Sustainability 2020, 12, 3775. [Google Scholar] [CrossRef]
- Lai, C.C.; Lee, J.H. Mixing of inclined dense jets in stationary ambient. J. Hydro-Environ. Res. 2012, 6, 9–28. [Google Scholar] [CrossRef]
- Lai, A.C.H.; Chan, S.N.; Law, A.W.K.; Adams, E.E. Spreading hypothesis of a particle plume. J. Hydraul. Eng. 2016, 142, 04016065. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Numerical modeling of multiple inclined dense jets discharged from moderately spaced ports. Water 2019, 11, 2077. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Mohammadian, A.; Chen, X. Numerical modeling of inclined plane jets in a linearly stratified environment. Alex. Eng. J. 2020, 59, 1857–1867. [Google Scholar] [CrossRef]
- Kheirkhah Gildeh, H.; Mohammadian, A.; Nistor, I.; Qiblawey, H. Numerical modeling of 30° and 45° inclined dense turbulent jets in stationary ambient. Environ. Fluid Mech. 2015, 15, 537–562. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.K.; Jiang, M. Large eddy simulations of 45° and 60° inclined dense jets with bottom impact. J. Hydro-Environ. Res. 2017, 15, 54–66. [Google Scholar] [CrossRef]
- Lou, Y.; Jiang, H.; Han, X. Numerical simulation of two coalescing turbulent forced plumes in linearly stratified fluids. Phys. Fluids 2019, 31, 037111. [Google Scholar] [CrossRef]
- Glaze, D.J.; Frankel, S.H. Stochastic inlet conditions for large-eddy simulation of a fully turbulent jet. AIAA J. 2003, 41, 1064–1073. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Evolutionary modeling of inclined dense jets discharged from multiport diffusers. J. Coast. Res. 2019, 36, 362–371. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V. A pareto-optimal moving average-multigene genetic programming model for rain-fall-runoff modelling. Environ. Model. Softw. 2017, 92, 239–251. [Google Scholar] [CrossRef]
- Bayazidi, A.M.; Wang, G.-G.; Bolandi, H.; Alavi, A.H.; Gandomi, A. Multigene genetic programming for estimation of elastic modulus of concrete. Math. Probl. Eng. 2014, 2014, 1–10. [Google Scholar] [CrossRef] [Green Version]
- De Paiva, G.M.; Pimentel, S.P.; Alvarenga, B.P.; Marra, E.; Mussetta, M.; Leva, S. Multiple site intraday solar irradiance forecasting by machine learning algorithms: MGGP and MLP neural networks. Energies 2020, 13, 3005. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Mehr, A.D. Multigene genetic programming for sediment transport modeling in sewers for conditions of non-deposition with a bed deposit. Int. J. Sediment Res 2018, 33, 262–270. [Google Scholar] [CrossRef]
- Sakhaei, Z.; Nikooee, E.; Riazi, M. A new formulation for non-equilibrium capillarity effect using multi-gene genetic programming (MGGP): Accounting for fluid and porous media properties. Eng. Comput. 2020. [Google Scholar] [CrossRef]
- Searson, D.P. GPTIPS 2: An Open-Source Software Platform for Symbolic Data Mining. In Handbook of Genetic Programming Applications; Springer: Cham, Switzerland, 2015; pp. 551–573. [Google Scholar]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®; Holzmann CFD: Loeben, Germany, 2016. [Google Scholar]
- OpenFOAM Fundation. OpenFOAM User Guide; Version 4.0; The OpenCFD Foundation: London, UK, 2016. [Google Scholar]
- Najafzadeh, M.; Tafarojnoruz, A.; Lim, S.Y. Prediction of local scour depth downstream of sluice gates using data-driven models. ISH J. Hydraul. Eng. 2017, 23, 1–8. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Rezaie Balf, M.; Tafarojnoruz, A. Prediction of riprap stone size under overtopping flow using data-driven models. Int. J. River Basin Manag. 2018, 16, 1–30. [Google Scholar] [CrossRef]


| σk | σε | c1ε | c2ε | cμ | η0 | β |
|---|---|---|---|---|---|---|
| 0.71942 | 0.71942 | 1.42 | 1.68 | 0.0845 | 4.38 | 0.012 |
| Cases | ρj (kg/m3) | ρa (kg/m3) | ∆ρ (kg/m3) | g’ (m/s2) | D (m) | U (m/s) | Fr (—) |
|---|---|---|---|---|---|---|---|
| Case 01 | 997 | 998.3 | 1.3 | 0.013 | 0.0044 | 0.185 | 24.676 |
| Case 02 | 997 | 999.5 | 2.5 | 0.025 | 0.0044 | 0.185 | 17.805 |
| Case 03 | 997 | 1000.2 | 3.2 | 0.031 | 0.0044 | 0.185 | 15.743 |
| Case 04 | 997 | 1001.1 | 4.1 | 0.040 | 0.0044 | 0.185 | 13.914 |
| Case 05 | 997 | 1001.3 | 4.3 | 0.042 | 0.0044 | 0.185 | 13.588 |
| Case 06 | 997 | 1001.4 | 4.4 | 0.043 | 0.0044 | 0.185 | 13.433 |
| Case 07 | 997 | 1002.5 | 5.5 | 0.054 | 0.0044 | 0.185 | 12.022 |
| Case 08 | 997 | 1004.8 | 7.8 | 0.076 | 0.0044 | 0.185 | 10.107 |
| Case 09 | 997 | 1005.9 | 8.9 | 0.087 | 0.0044 | 0.185 | 9.467 |
| Case 10 | 997 | 1009.0 | 12.0 | 0.117 | 0.0044 | 0.185 | 8.165 |
| Case 11 | 997 | 1009.9 | 12.9 | 0.125 | 0.0044 | 0.185 | 7.879 |
| Case 12 | 997 | 1013.5 | 16.5 | 0.160 | 0.0044 | 0.185 | 6.979 |
| Case 13 | 997 | 1014.4 | 17.4 | 0.168 | 0.0044 | 0.185 | 6.799 |
| Case 14 | 997 | 1020.2 | 23.2 | 0.223 | 0.0044 | 0.185 | 5.905 |
| Case 15 | 997 | 1021.0 | 24.0 | 0.231 | 0.0044 | 0.185 | 5.808 |
| Case 16 | 997 | 1021.5 | 24.5 | 0.235 | 0.0044 | 0.185 | 5.750 |
| Case 17 | 997 | 1023.1 | 26.1 | 0.250 | 0.0044 | 0.185 | 5.575 |
| Case 18 | 997 | 1023.9 | 26.9 | 0.258 | 0.0044 | 0.185 | 5.494 |
| Case 19 | 997 | 1024.3 | 27.3 | 0.261 | 0.0044 | 0.185 | 5.454 |
| Case 20 | 997 | 1025.9 | 28.9 | 0.276 | 0.0044 | 0.185 | 5.305 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Wang, Y.; Mohammadian, A.; Liu, J. Simulations of the Concentration Fields of Rosette-Type Multiport Buoyant Discharges Using Combined CFD and Multigene Genetic Programming Techniques. J. Mar. Sci. Eng. 2021, 9, 1311. https://doi.org/10.3390/jmse9111311
Yan X, Wang Y, Mohammadian A, Liu J. Simulations of the Concentration Fields of Rosette-Type Multiport Buoyant Discharges Using Combined CFD and Multigene Genetic Programming Techniques. Journal of Marine Science and Engineering. 2021; 9(11):1311. https://doi.org/10.3390/jmse9111311
Chicago/Turabian StyleYan, Xiaohui, Yan Wang, Abdolmajid Mohammadian, and Jianwei Liu. 2021. "Simulations of the Concentration Fields of Rosette-Type Multiport Buoyant Discharges Using Combined CFD and Multigene Genetic Programming Techniques" Journal of Marine Science and Engineering 9, no. 11: 1311. https://doi.org/10.3390/jmse9111311
APA StyleYan, X., Wang, Y., Mohammadian, A., & Liu, J. (2021). Simulations of the Concentration Fields of Rosette-Type Multiport Buoyant Discharges Using Combined CFD and Multigene Genetic Programming Techniques. Journal of Marine Science and Engineering, 9(11), 1311. https://doi.org/10.3390/jmse9111311








