Systematic Validation Study of an Unsteady Cavitating Flow over a Hydrofoil Using Conditional Averaging: LES and PIV
Abstract
:1. Introduction
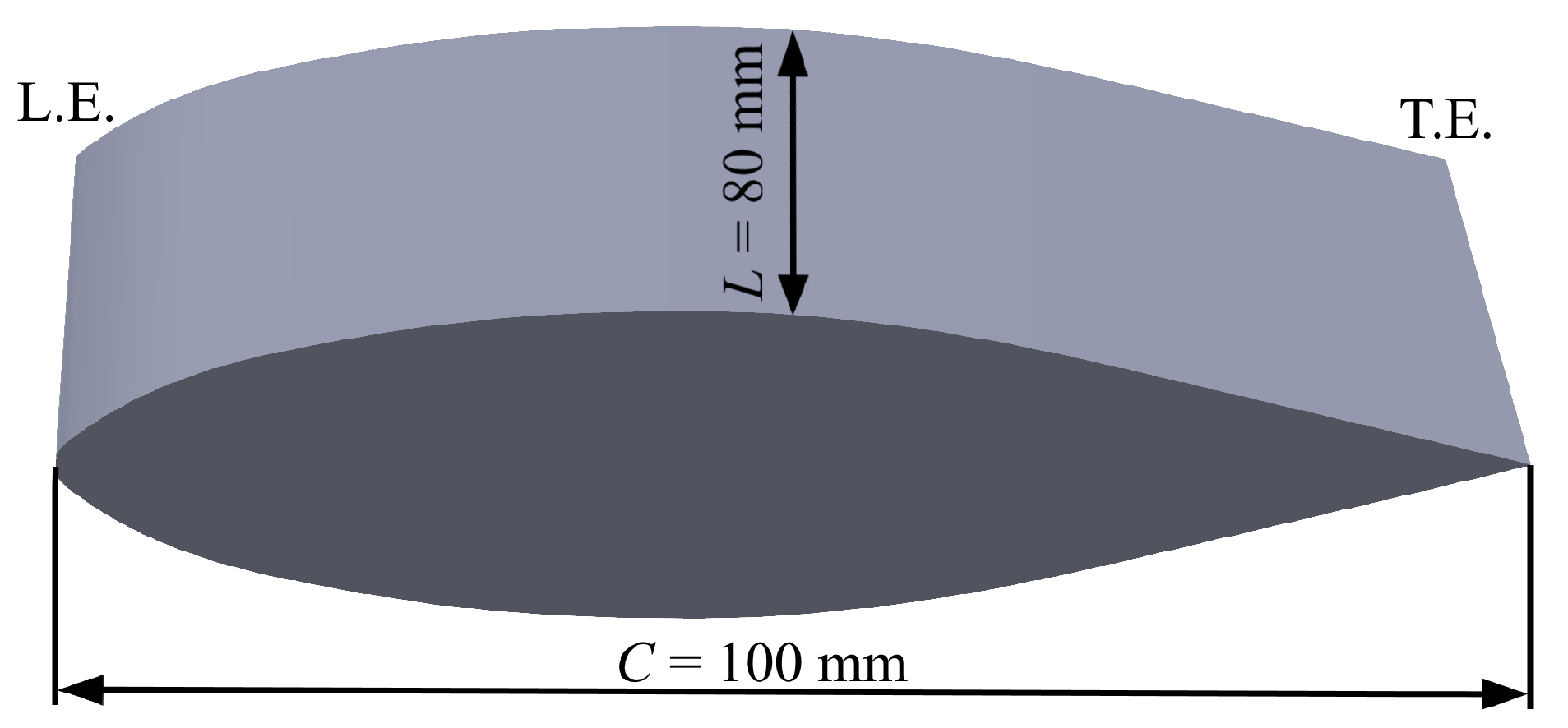
2. Experimental Setup and Flow Regimes
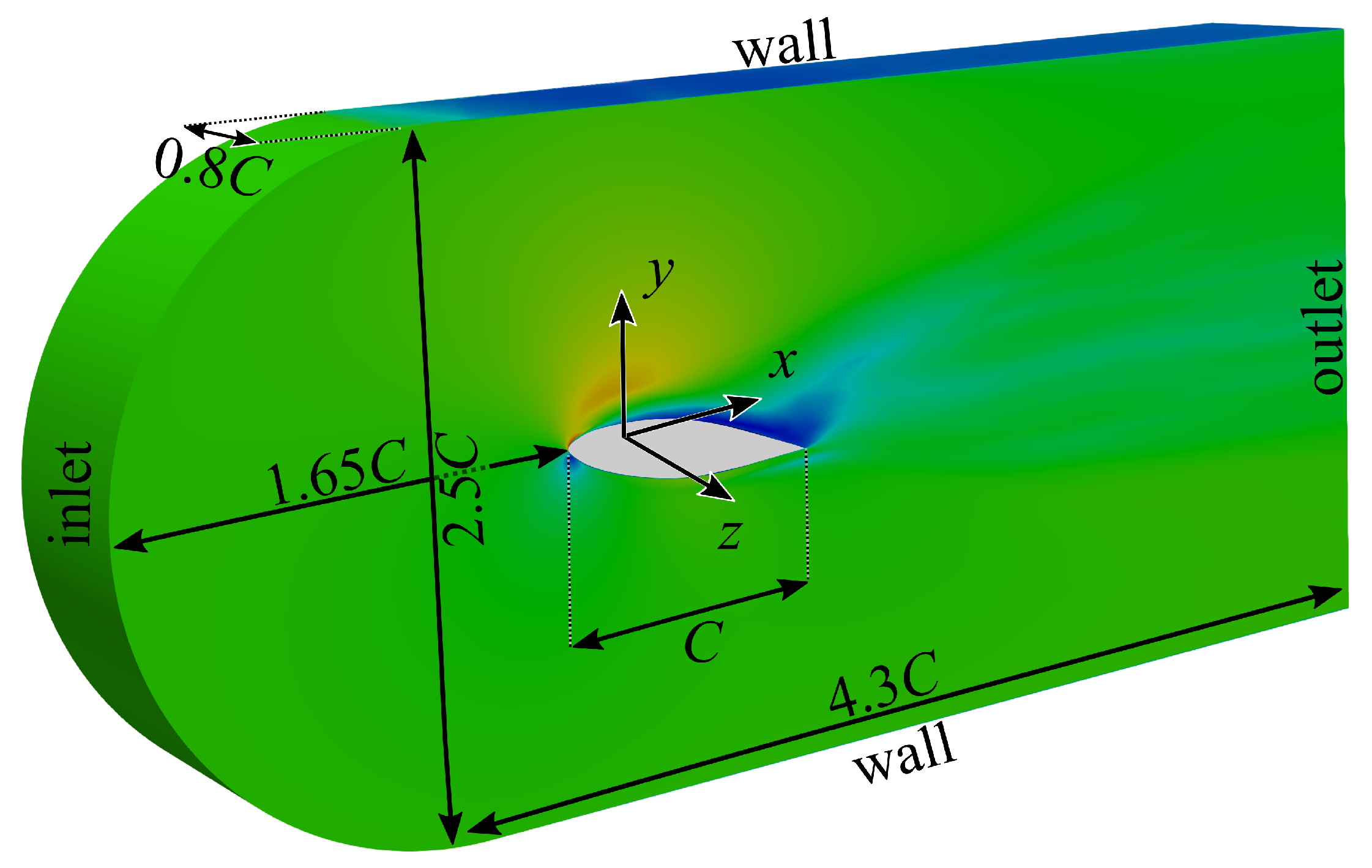
3. Modeling and Computational Details
3.1. Governing Equations
3.2. Cavitation Modeling
3.3. Large-Eddy Simulation Framework
- In a standard manner we ignore the commutation errors within the LES framework caused by the inhomogeneous mesh [12].
- We add an additional term to the left-hand-side of Equation (13), where is the relative velocity vector between the two phases, which is also called the compression velocity [61]. It is sometimes described as an artificial term added to compress the interface, but in fact is directly derived from the mass conservation equation of the vapor phase. The compression velocity is modeled as:which is based on the maximum velocity in some region of the interface, is the constant that controls intensity of the interface compression.
- The term in Equation (13) is nonlinear; thus, it has to be modeled. We ignore this fact employing the relation .
3.4. Numerical Details
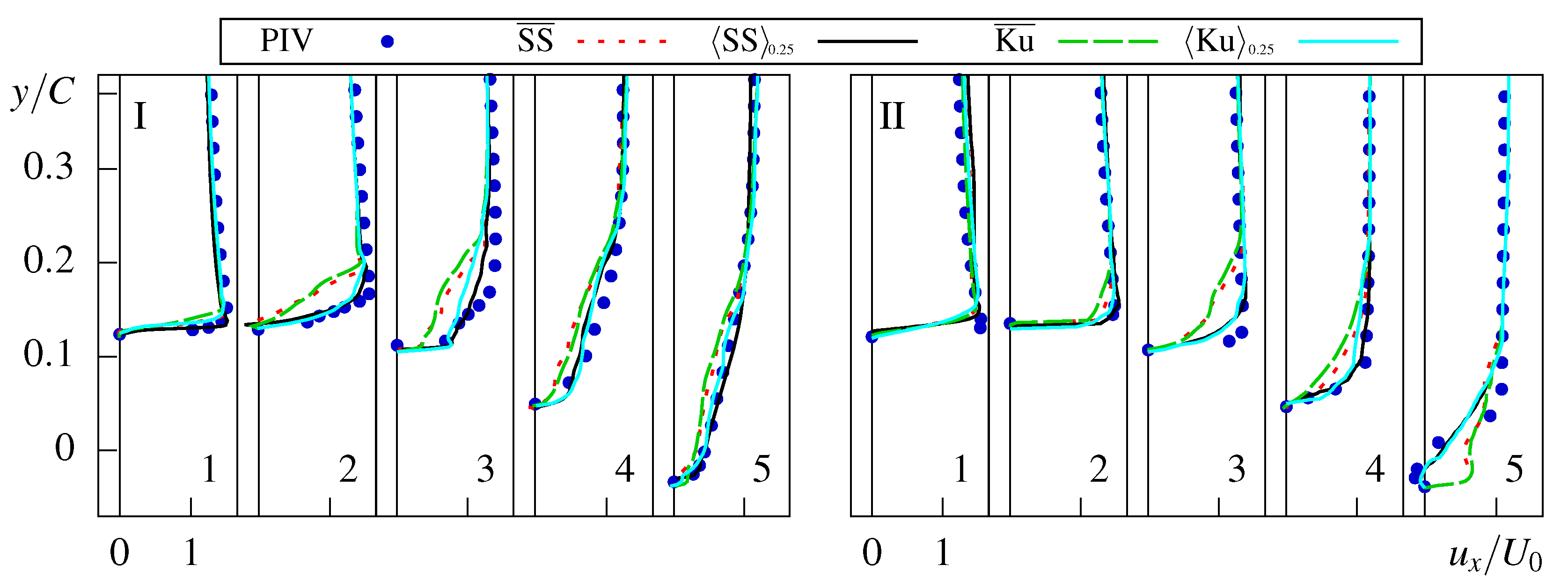
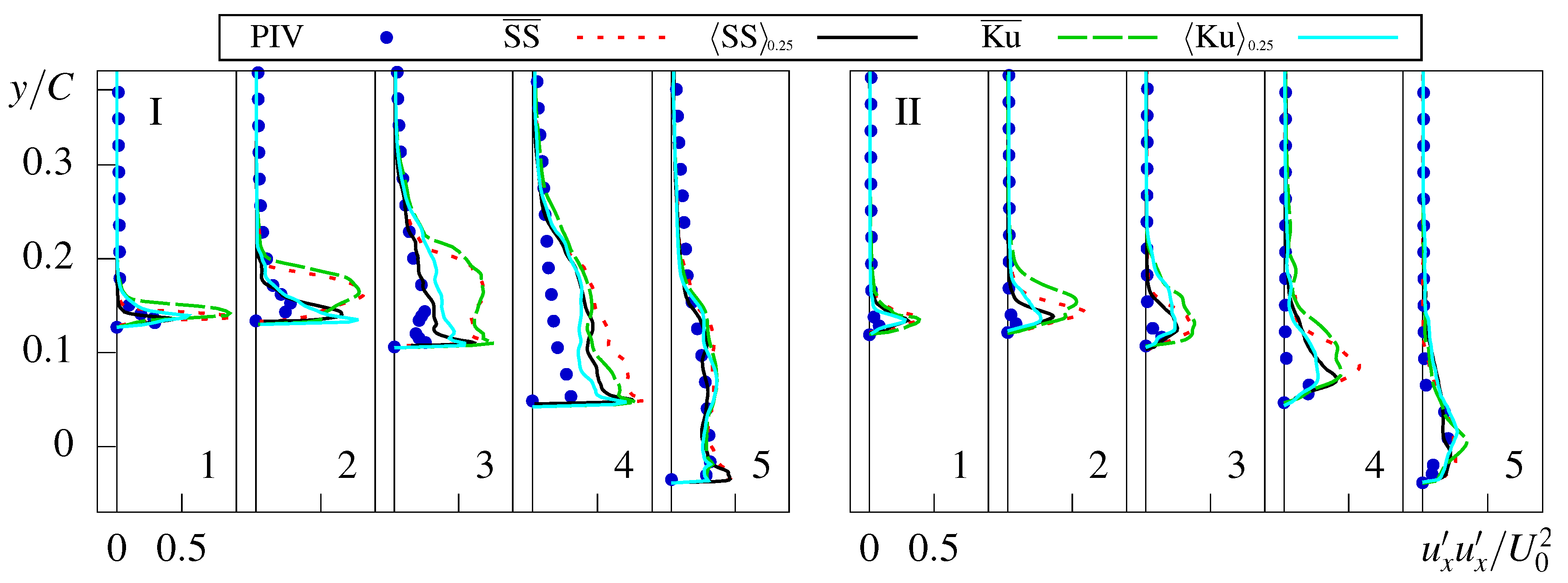
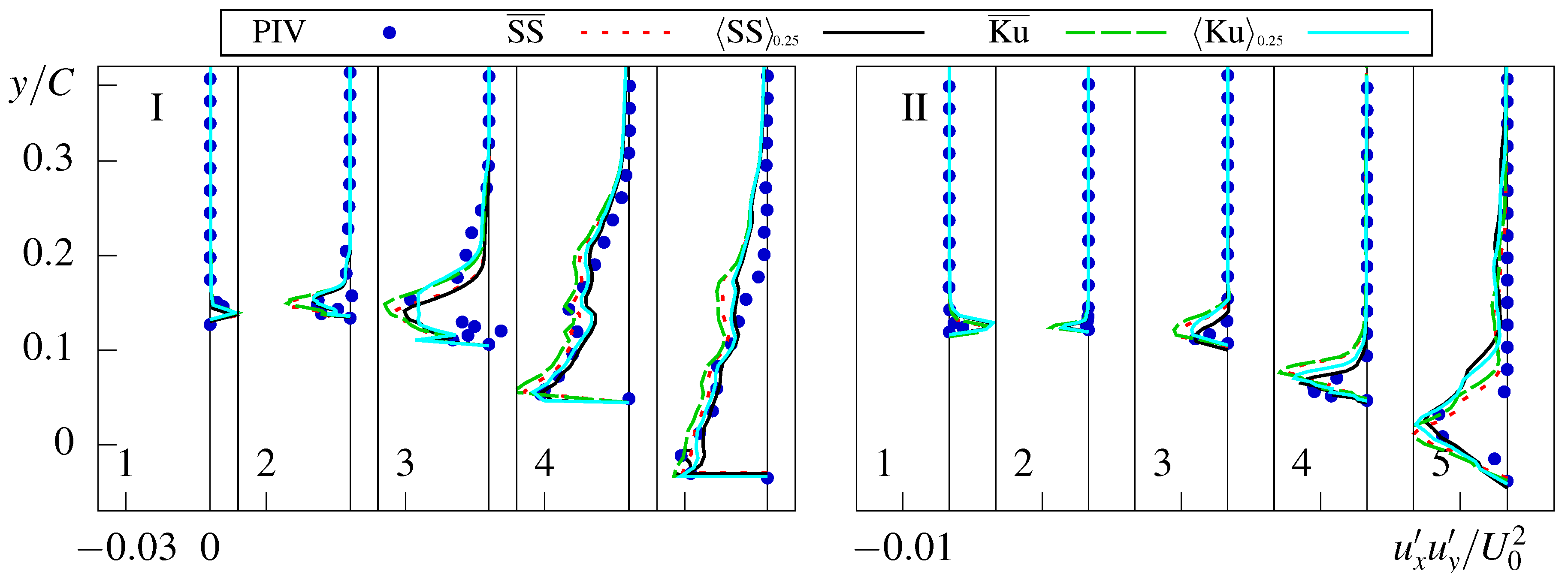
3.5. Conditional Averaging
4. Results and Discussion
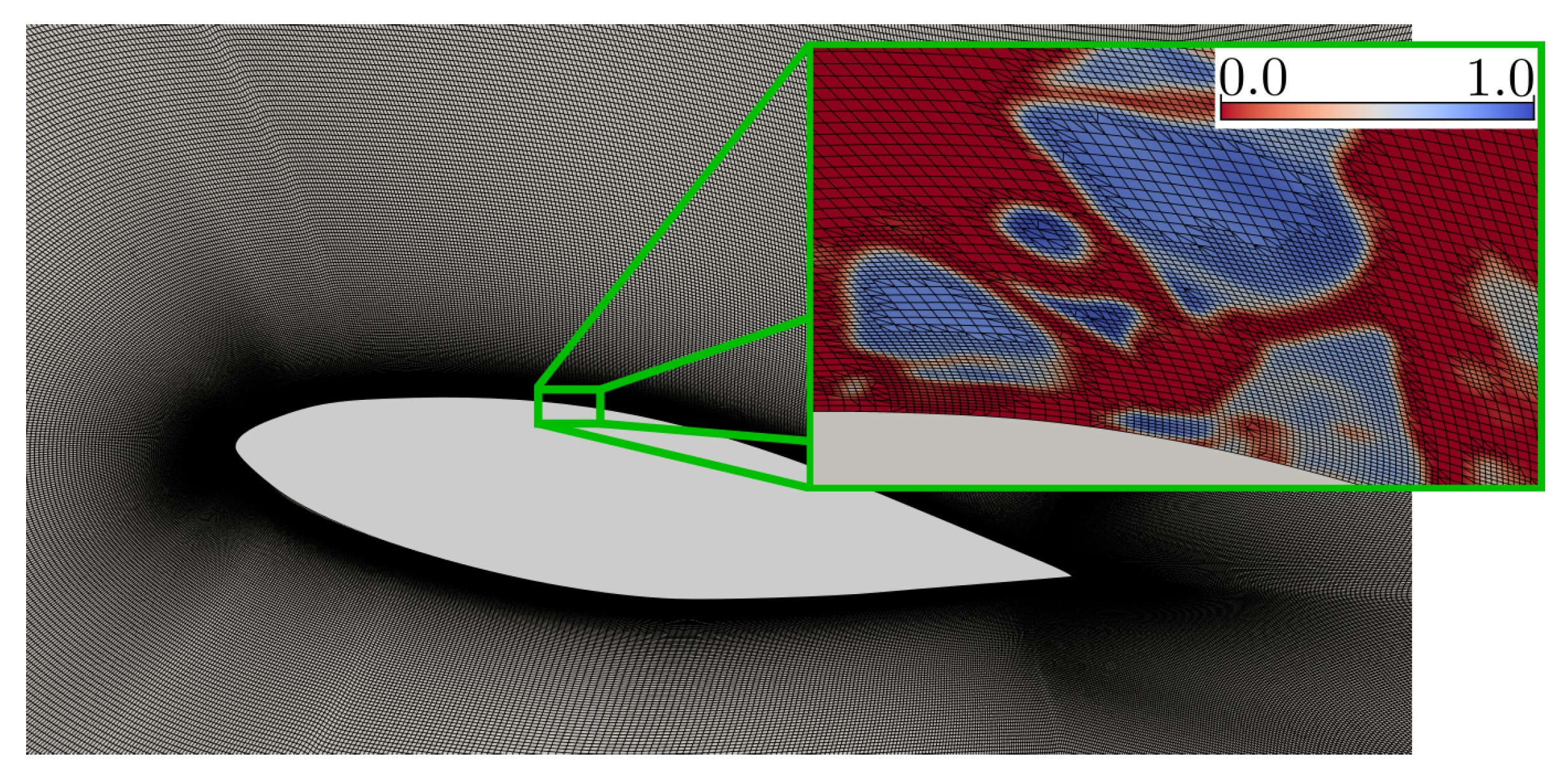
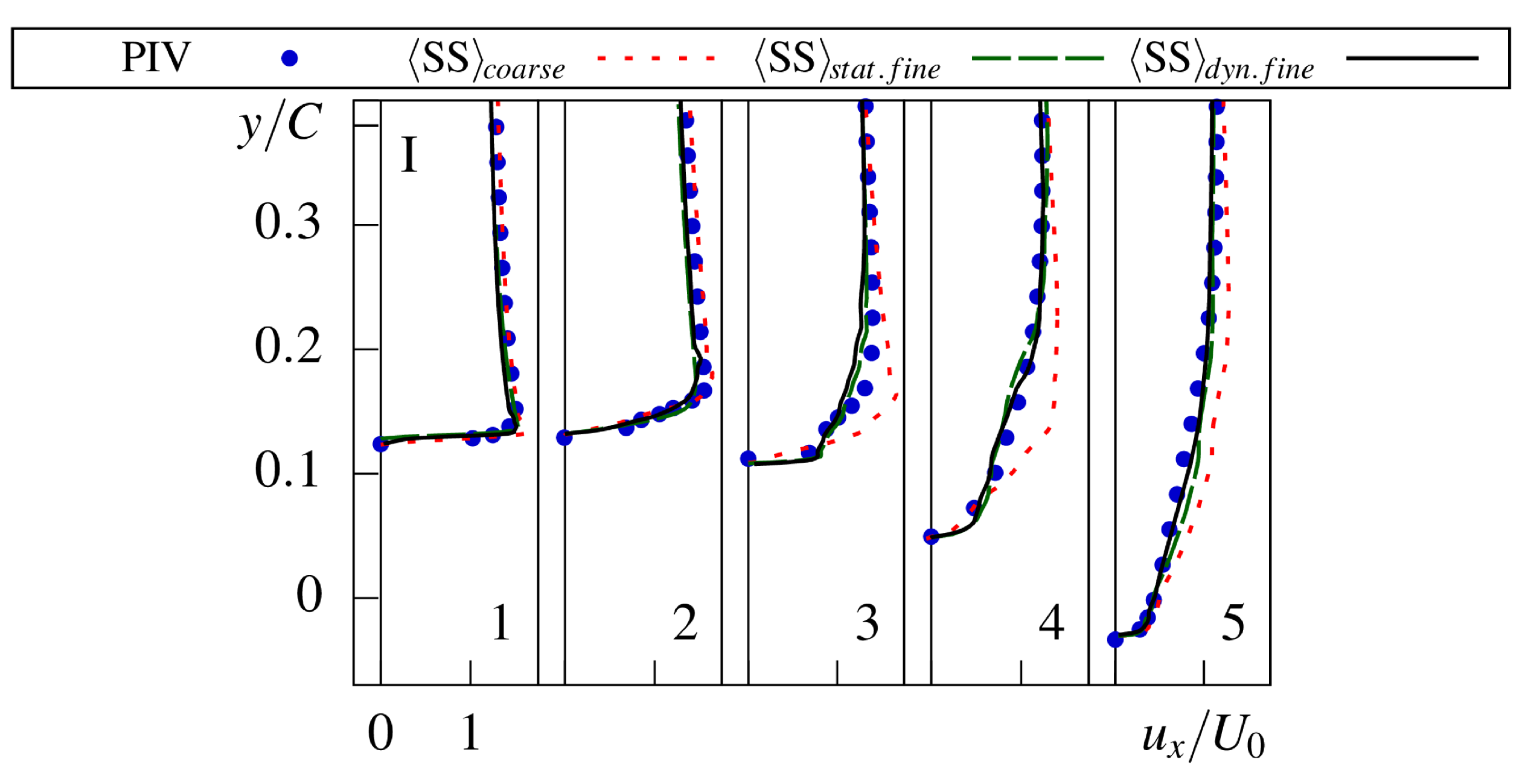
4.1. Mesh Refinement
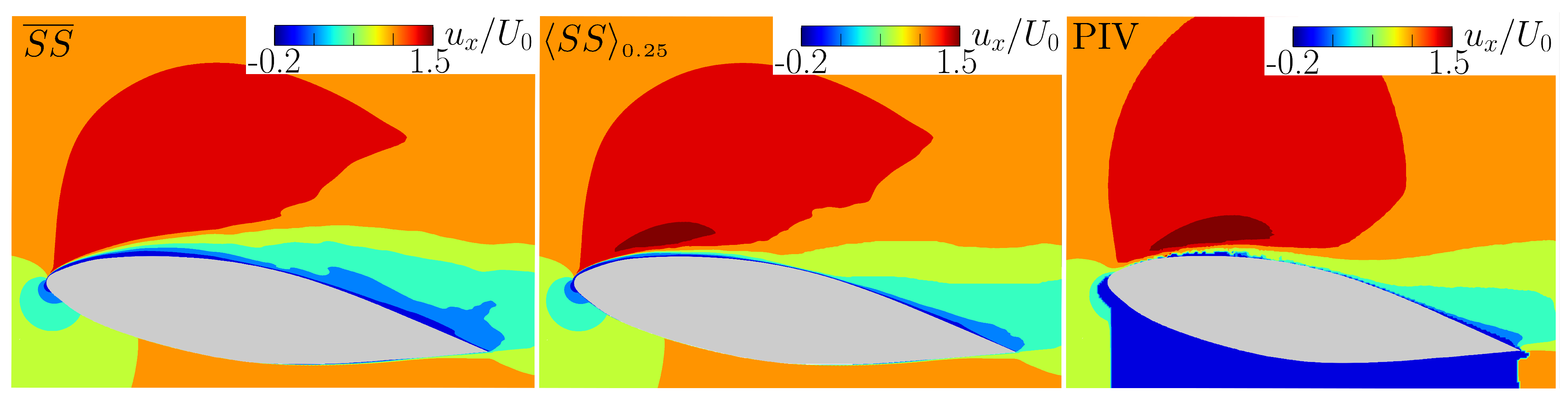
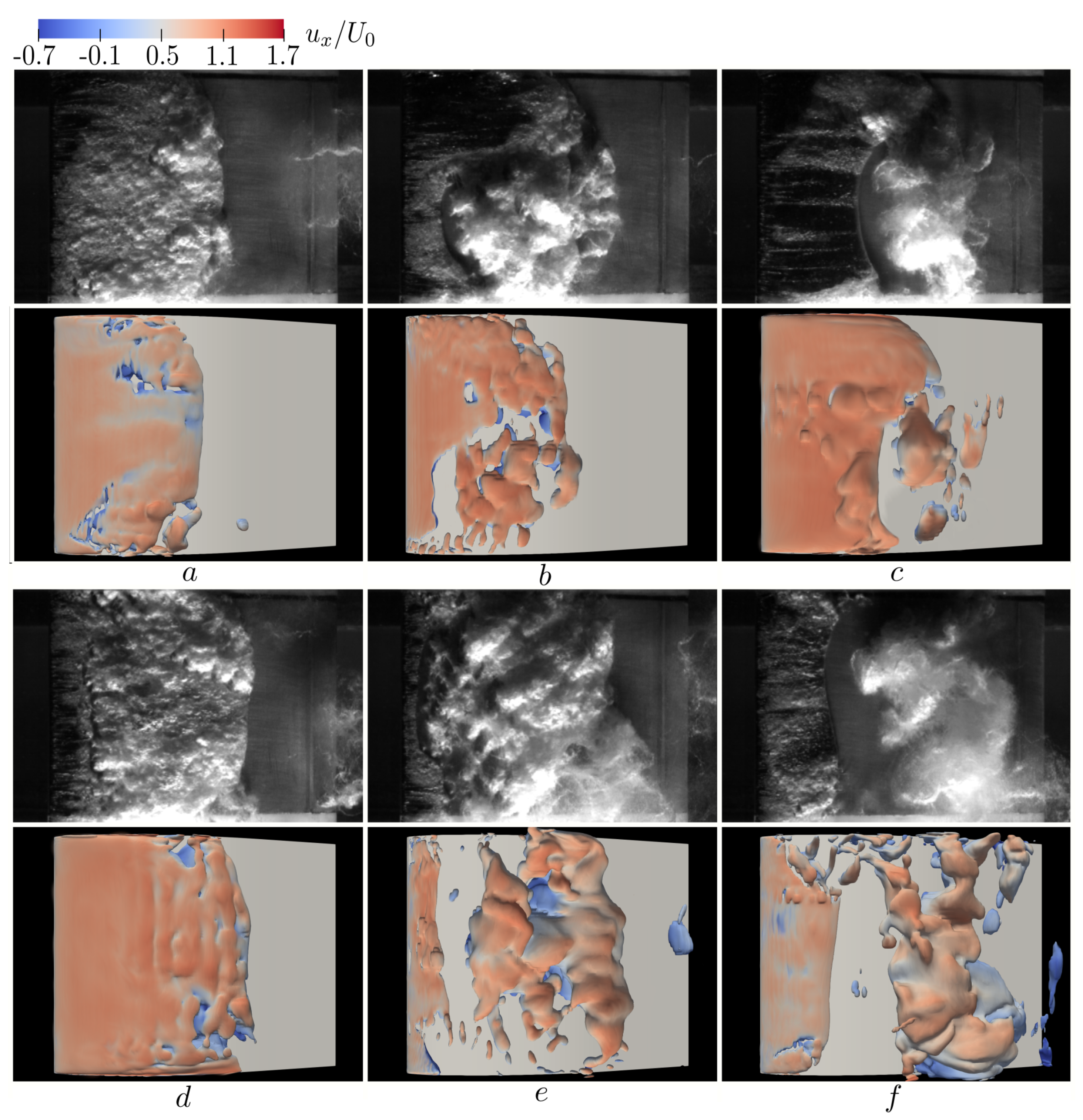
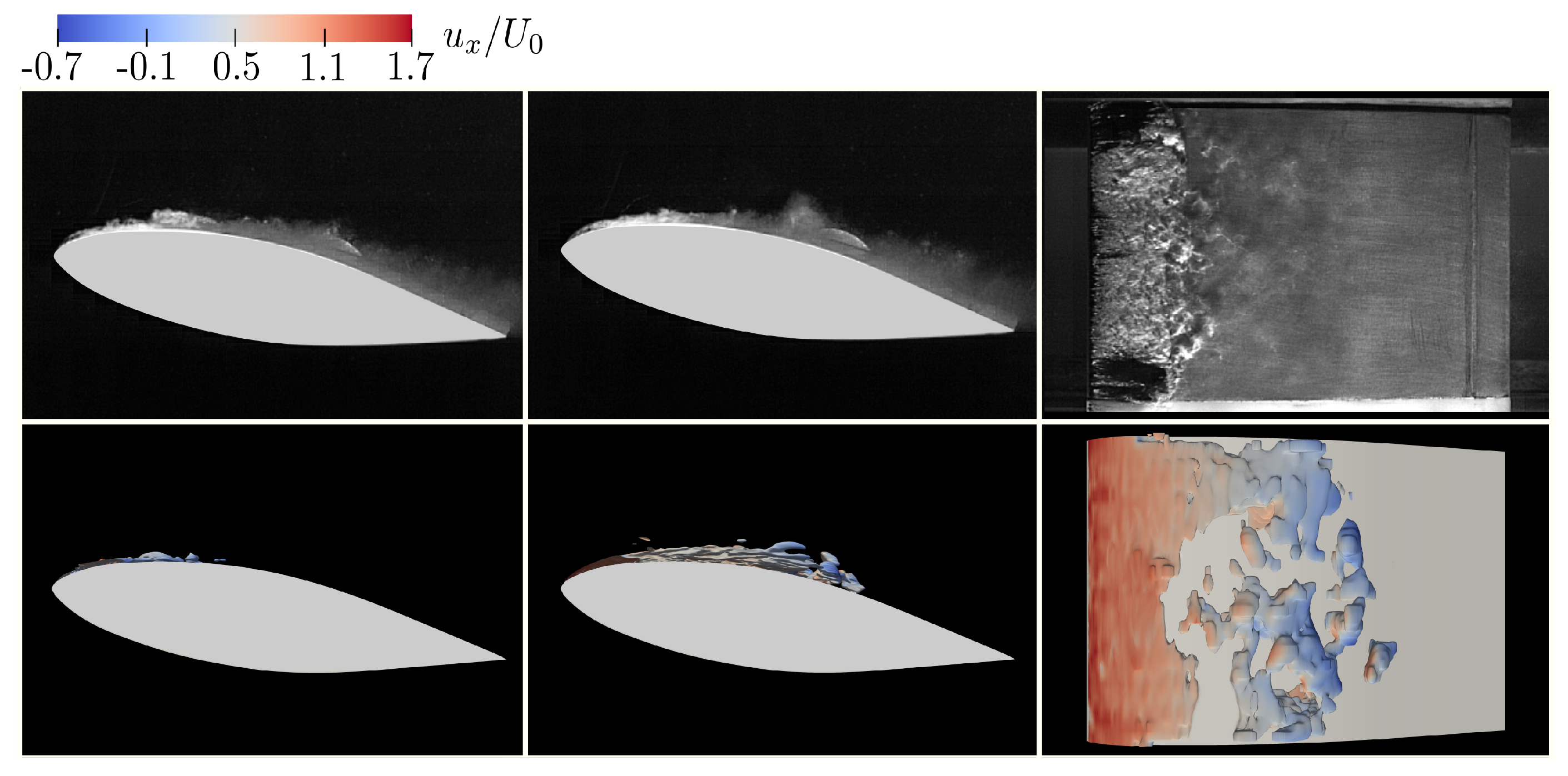
4.2. Visualization and Flow Dynamics
4.3. Comparison of Cavitation Models
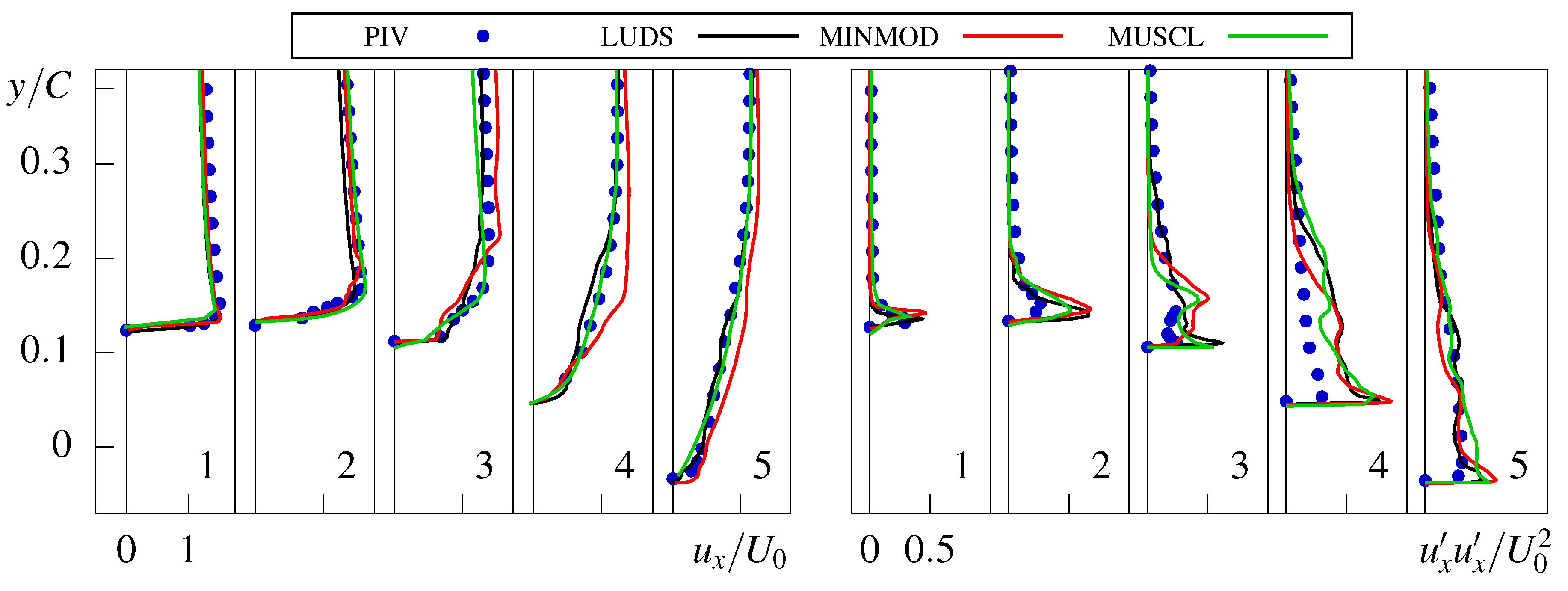
4.4. Comparison of Convective Schemes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Plesset, M. Bubble dynamics and cavitation. Annu. Rev. Fluid Mech. 1977, 9, 145–185. [Google Scholar] [CrossRef]
- Arndt, R. Cavitation in fluid machinery and hydraulic structures. Annu. Rev. Fluid Mech. 1981, 13, 273–328. [Google Scholar] [CrossRef]
- Arndt, R. Cavitation in vortical flows. Annu. Rev. Fluid Mech. 2002, 34, 143–175. [Google Scholar] [CrossRef]
- Brennen, C. Cavitation and Bubble Dynamics; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Franc, J.; Michel, J. Fundamentals of Cavitation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Li, C.; Ceccio, S. Interaction of single travelling bubbles with the boundary layer and attached cavitation. J. Fluid Mech. 1996, 322, 329–353. [Google Scholar] [CrossRef]
- Lindau, O.; Lauterborn, W. Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J. Fluid Mech. 2003, 479, 327–348. [Google Scholar] [CrossRef]
- Ausoni, P.; Zobeiri, A.; Avellan, F.; Farhat, M. The effects of a tripped turbulent boundary layer on vortex shedding from a blunt trailing edge hydrofoil. J. Fluids Eng. 2012, 134, 051207. [Google Scholar] [CrossRef]
- Gopalan, S.; Katz, J. Flow structure and modeling issues in the closure region of attached cavitation. Phys. Fluids 2000, 12, 895–911. [Google Scholar] [CrossRef]
- Huang, B.; Young, Y.; Wang, G.; Shyy, W. Combined experimental and computational investigation of unsteady structure of sheet/cloud cavitation. J. Fluids Eng. 2013, 135, 071301. [Google Scholar] [CrossRef]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Sagaut, P. Large Eddy Simulation for Incompressible Flows: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kubota, A.; Kato, H.; Yamaguchi, H. A new modelling of cavitating flows: A numerical study of unsteady cavitation on a hydrofoil section. J. Fluid Mech. 1992, 240, 59–96. [Google Scholar] [CrossRef]
- Merkle, C.; Feng, J.; Buelow, P. Computational modeling of the dynamics of sheet cavitation. In Proceedings of the Third International Symposium on Cavitation, Grenoble, France, 7–10 April 1998. [Google Scholar]
- Kunz, R.; Boger, D.; Stinebring, D.; Chyczewski, T.; Lindau, J.; Gibeling, H.; Venkateswaran, S.; Govindan, T. A preconditioned Navier–Stokes method for two-phase flows with application to cavitation prediction. Comput. Fluids 2000, 29, 849–875. [Google Scholar] [CrossRef]
- Schnerr, G.; Sauer, J. Physical and numerical modeling of unsteady cavitation dynamics. In Proceedings of the Fourth International Conference on Multiphase Flow, New Orleans, LA, USA, 27 May–1 June 2001. [Google Scholar]
- Singhal, A.; Athavale, M.; Li, H.; Jiang, Y. Mathematical basis and validation of the full cavitation model. J. Fluids Eng. 2002, 124, 617–624. [Google Scholar] [CrossRef]
- Frobenius, M.; Schilling, R.; Bachert, R.; Stoffel, B.; Ludwig, G. Three-dimensional, unsteady cavitation effects on a single hydrofoil and in a radial pump–measurements and numerical simulations, Part two: Numerical simulation. In Proceedings of the Fifth International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Coutier-Delgosha, O.; Reboud, J.; Delannoy, Y. Numerical simulation of the unsteady behaviour of cavitating flows. Int. J. Numer. Methods Fluids 2003, 42, 527–548. [Google Scholar]
- Saito, Y.; Nakamori, I.; Ikohagi, T. Numerical analysis of unsteady vaporous cavitating flow around a hydrofoil. In Proceedings of the Fifth International Symposium on Cavitation, Osaka, Japan, 1–4 November 2003. [Google Scholar]
- Zwart, P.; Gerber, A.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Senocak, I.; Shyy, W. Interfacial dynamics-based modelling of turbulent cavitating flows, Part-1: Model development and steady-state computations. Int. J. Numer. Methods Fluids 2004, 44, 975–995. [Google Scholar] [CrossRef]
- Senocak, I.; Shyy, W. Interfacial dynamics-based modelling of turbulent cavitating flows, Part-2: Time-dependent computations. Int. J. Numer. Methods Fluids 2004, 44, 997–1016. [Google Scholar] [CrossRef]
- Owis, F.; Nayfeh, A. Numerical simulation of 3-D incompressible, multi-phase flows over cavitating projectiles. Eur. J. Mech.-B/Fluids 2004, 23, 339–351. [Google Scholar] [CrossRef]
- Leroux, J.; Coutier-Delgosha, O.; Astolfi, J. A joint experimental and numerical study of mechanisms associated to instability of partial cavitation on two-dimensional hydrofoil. Phys. Fluids 2005, 17, 052101. [Google Scholar] [CrossRef] [Green Version]
- Coutier-Delgosha, O.; Stutz, B.; Vabre, A.; Legoupil, S. Analysis of cavitating flow structure by experimental and numerical investigations. J. Fluid Mech. 2007, 578, 171–222. [Google Scholar] [CrossRef] [Green Version]
- Frikha, S.; Coutier-Delgosha, O.; Astolfi, J. Influence of the cavitation model on the simulation of cloud cavitation on 2D foil section. Int. J. Rotating Mach. 2008, 2008, 146234. [Google Scholar] [CrossRef] [Green Version]
- Morgut, M.; Nobile, E.; Bilus, I. Comparison of mass transfer models for the numerical prediction of sheet cavitation around a hydrofoil. Int. J. Multiph. Flow 2011, 37, 620–626. [Google Scholar] [CrossRef]
- Yang, J.; Zhou, L.; Wang, Z. Numerical simulation of three-dimensional cavitation around a hydrofoil. J. Fluids Eng. 2011, 133, 081301. [Google Scholar] [CrossRef]
- Ducoin, A.; Huang, B.; Young, Y. Numerical modeling of unsteady cavitating flows around a stationary hydrofoil. Int. J. Rotating Mach. 2012, 2012, 215678. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Bai, X.; Long, X.; Ji, B.; Peng, X.; Farhat, M. Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence. Appl. Math. Model. 2020, 77, 788–809. [Google Scholar] [CrossRef]
- Long, Y.; Long, X.; Ji, B.; Xing, T. Verification and validation of Large Eddy Simulation of attached cavitating flow around a Clark-Y hydrofoil. Int. J. Multiph. Flow 2019, 115, 93–107. [Google Scholar] [CrossRef]
- Wang, G.; Ostoja-Starzewski, M. Large eddy simulation of a sheet/cloud cavitation on a NACA0015 hydrofoil. Appl. Math. Model. 2007, 31, 417–447. [Google Scholar] [CrossRef]
- Luo, X.; Ji, B.; Peng, X.; Xu, H.; Nishi, M. Numerical simulation of cavity shedding from a three-dimensional twisted hydrofoil and induced pressure fluctuation by large-eddy simulation. J. Fluids Eng. 2012, 134, 041202. [Google Scholar] [CrossRef]
- Ji, B.; Luo, X.; Arndt, R.; Peng, X.; Wu, Y. Large eddy simulation and theoretical investigations of the transient cavitating vortical flow structure around a NACA66 hydrofoil. Int. J. Multiph. Flow 2015, 68, 121–134. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Li, B.; Hu, Z.; Lin, Y.; Cheung, S. Large eddy simulation of unsteady shedding behavior in cavitating flows with time-average validation. Ocean. Eng. 2016, 125, 1–11. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Cavitation-vortex-turbulence interaction and one-dimensional model prediction of pressure for hydrofoil ALE15 by large eddy simulation. J. Fluids Eng. 2016, 141, 021103. [Google Scholar] [CrossRef]
- Gnanaskandan, A.; Mahesh, K. Numerical investigation of near-wake characteristics of cavitating flow over a circular cylinder. J. Fluid Mech. 2016, 790, 453–491. [Google Scholar] [CrossRef] [Green Version]
- Brandao, F.; Bhatt, M.; Mahesh, K. Numerical study of cavitation regimes in flow over a circular cylinder. J. Fluid Mech. 2020, 885, A19. [Google Scholar] [CrossRef] [Green Version]
- Bensow, R.; Bark, G. Implicit LES predictions of the cavitating flow on a propeller. J. Fluids Eng. 2010, 132, 041302. [Google Scholar] [CrossRef]
- Dittakavi, N.; Chunekar, A.; Frankel, S. Large eddy simulation of turbulent-cavitation interactions in a Venturi nozzle. J. Fluids Eng. 2010, 132, 121301. [Google Scholar] [CrossRef]
- Zhang, L.; Khoo, B. Computations of partial and super cavitating flows using implicit pressure-based algorithm (IPA). Comput. Fluids 2013, 73, 1–9. [Google Scholar] [CrossRef]
- Yu, X.; Huang, C.; Du, T.; Liao, L.; Wu, X.; Zheng, Z.; Wang, Y. Study of characteristics of cloud cavity around axisymmetric projectile by large eddy simulation. J. Fluids Eng. 2014, 136, 051303. [Google Scholar] [CrossRef] [Green Version]
- Orley, F.; Trummler, T.; Hickel, S.; Mihatsch, M.; Schmidt, S.; Adams, N. Large-eddy simulation of cavitating nozzle flow and primary jet break-up. Phys. Fluids 2015, 27, 086101. [Google Scholar] [CrossRef] [Green Version]
- Gnanaskandan, A.; Mahesh, K. Large eddy simulation of the transition from sheet to cloud cavitation over a wedge. Int. J. Multiph. Flow 2016, 83, 86–102. [Google Scholar] [CrossRef] [Green Version]
- Bhatt, M.; Mahesh, K. Numerical investigation of partial cavitation regimes over a wedge using large eddy simulation. Int. J. Multiph. Flow 2020, 122, 103155. [Google Scholar] [CrossRef]
- Warming, R.; Beam, R. Upwind second-order difference schemes and applications in aerodynamic flows. AIAA J. 1976, 14, 1241–1249. [Google Scholar] [CrossRef]
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1996. [Google Scholar]
- Harten, A. High resolution schemes for hyperbolic conservation laws. J. Comput. Phys. 1997, 135, 260–278. [Google Scholar] [CrossRef] [Green Version]
- Ferziger, J.; Perić, M.; Street, R. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2002; Volume 3. [Google Scholar]
- Sagaut, P.; Adams, N.; Garnier, E. Large-Eddy Simulation for Compressible Flows; Springer: Berlin/Heidelberg, Germany, 2009; Volume 276. [Google Scholar]
- Kravtsova, A.; Markovich, D.; Pervunin, K.; Timoshevskiy, M.; Hanjalić, K. High-speed visualization and PIV measurements of cavitating flows around a semi-circular leading-edge flat plate and NACA0015 hydrofoil. Int. J. Multiph. Flow 2014, 60, 119–134. [Google Scholar] [CrossRef]
- Kravtsova, A.; Pervunin, K.; Timoshevskiy, M.; Churkin, S.; Markovich, D.; Hanjalić, K. Cavitating flow around a scaled-down model of guide vanes of a high-pressure turbine. Int. J. Multiph. Flow 2016, 78, 75–87. [Google Scholar]
- Arndt, R.; Song, C.; Kjeldsen, M.; He, J.; Keller, A. Instability of Partial Cavitation: A Numerical/Experimental Approach; National Academies Press: Washington, DC, USA, 2000. [Google Scholar]
- Huang, B.; Zhao, Y.; Wang, G. Large eddy simulation of turbulent vortex-cavitation interactions in transient sheet/cloud cavitating flows. Comput. Fluids 2014, 92, 113–124. [Google Scholar] [CrossRef]
- Decaix, J.; Goncalves, E. Investigation of three-dimensional effects on a cavitating venturi flow. Int. J. Heat Fluid Flow 2013, 44, 576–595. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, W.; Chen, J.; Qiu, L.; Sun, D. Validation of dynamic cavitation model for unsteady cavitating flow on NACA66. Sci. China Technol. Sci. 2014, 57, 819–827. [Google Scholar] [CrossRef]
- Wu, Q.; Huang, B.; Wang, G.; Gao, Y. Experimental and numerical investigation of hydroelastic response of a flexible hydrofoil in cavitating flow. Int. J. Multiph. Flow 2015, 74, 19–33. [Google Scholar] [CrossRef]
- Timoshevskiy, M.; Ilyushin, B.; Pervunin, K. Statistical structure of the velocity field in cavitating flow around a 2D hydrofoil. Int. J. Heat Fluid Flow 2020, 85, 108646. [Google Scholar] [CrossRef]
- Arabnejad, M.; Amini, A.; Farhat, M.; Bensow, R. Numerical and experimental investigation of shedding mechanisms from leading-edge cavitation. Int. J. Multiph. Flow 2019, 119, 123–143. [Google Scholar] [CrossRef]
- Berberović, E.; van Hinsberg, N.; Jakirlić, S.; Roisman, I.; Tropea, C. Drop impact onto a liquid layer of finite thickness: Dynamics of the cavity evolution. Phys. Rev. E 2009, 79, 036306. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Horiuti, K. A statistically-derived subgrid-scale kinetic energy model for the large-eddy simulation of turbulent flows. J. Phys. Soc. Jpn. 1985, 54, 2834–2839. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef] [Green Version]
- Lilly, D. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- OpenFOAM. Project Site. 2004. Available online: http://www.openfoam.com (accessed on 20 October 2021).
- Van Leer, B. Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. J. Comput. Phys. 1974, 14, 361–370. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1947; Volume 43, pp. 50–67. [Google Scholar]
- Moukalled, F.; Mangani, L.; Darwish, M. The Finite Volume Method in Computational Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2016; Volume 113. [Google Scholar]
- OpenFOAM. Dynamic Mesh Refine Library. 2019. Available online: https://holzmann-cfd.com/community/training-cases/adaptive-mesh-refinement (accessed on 20 October 2021).


| [m/s] | [kPa] | [kPa] | [-] | [-] | |
|---|---|---|---|---|---|
| I | |||||
| II |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivashchenko, E.; Hrebtov, M.; Timoshevskiy, M.; Pervunin, K.; Mullyadzhanov, R. Systematic Validation Study of an Unsteady Cavitating Flow over a Hydrofoil Using Conditional Averaging: LES and PIV. J. Mar. Sci. Eng. 2021, 9, 1193. https://doi.org/10.3390/jmse9111193
Ivashchenko E, Hrebtov M, Timoshevskiy M, Pervunin K, Mullyadzhanov R. Systematic Validation Study of an Unsteady Cavitating Flow over a Hydrofoil Using Conditional Averaging: LES and PIV. Journal of Marine Science and Engineering. 2021; 9(11):1193. https://doi.org/10.3390/jmse9111193
Chicago/Turabian StyleIvashchenko, Elizaveta, Mikhail Hrebtov, Mikhail Timoshevskiy, Konstantin Pervunin, and Rustam Mullyadzhanov. 2021. "Systematic Validation Study of an Unsteady Cavitating Flow over a Hydrofoil Using Conditional Averaging: LES and PIV" Journal of Marine Science and Engineering 9, no. 11: 1193. https://doi.org/10.3390/jmse9111193
APA StyleIvashchenko, E., Hrebtov, M., Timoshevskiy, M., Pervunin, K., & Mullyadzhanov, R. (2021). Systematic Validation Study of an Unsteady Cavitating Flow over a Hydrofoil Using Conditional Averaging: LES and PIV. Journal of Marine Science and Engineering, 9(11), 1193. https://doi.org/10.3390/jmse9111193







