The Improved Localized Equivalent-Weights Particle Filter with Statistical Observation in an Intermediate Coupled Model
Abstract
1. Introduction
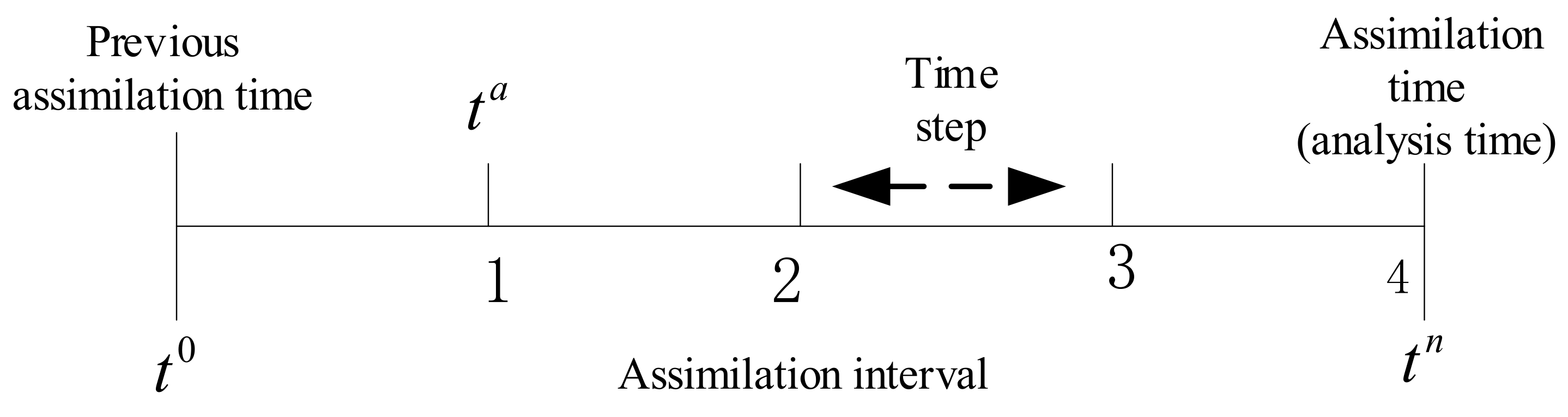
2. Materials and Methods
2.1. The Local Particle Filter
2.2. Classical Localized Equivalent-Weights Particle Filter with Statistical Observation
- (1)
- Calculate the accumulated weight of each particle ωi until the last time step tn, the equivalent-weight may be written as:where represents the proposal density weights ωi accumulated over the assimilation interval.
- (2)
- The final target weights which is chosen based on the maximum weight each particle can achieve. so the target weight is given by:This choice would make all weights equal to the minimum weights. However, the algorithm can compromise between retaining the particles and the weight, and particles are still returned by resampling [22].
- (3)
- Determined the new particles that have equal weighs, the model state at time tn can be written as [23]:where K = QHT(HQHT + R)−1, , and the .
- (1)
- Calculate the proposal density weights based on the statistical observation and Equation (10):
- (2)
- The particles are moved towards the statistical historical reanalysis observation and updated the model equation Equation (11) at time tb:
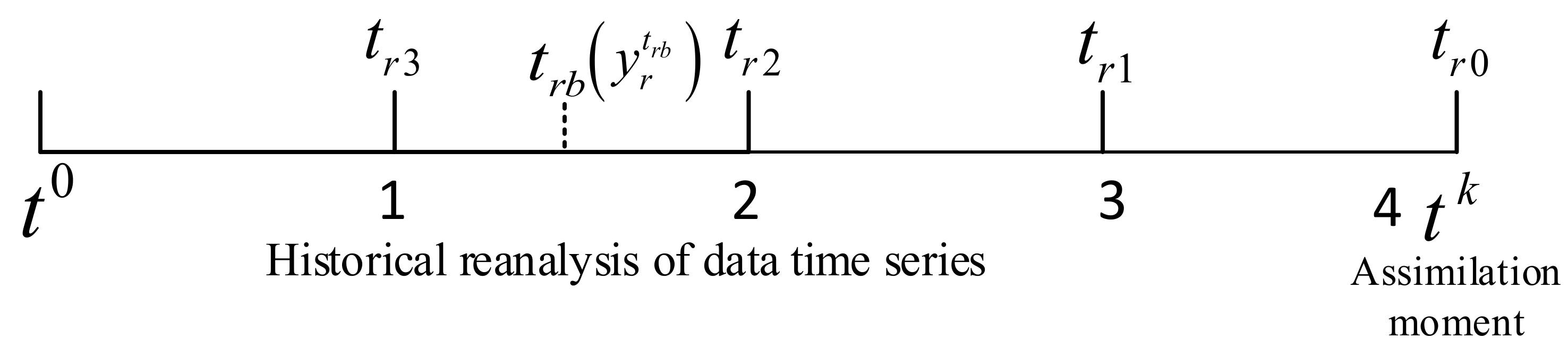
2.3. Refining Statistical Observation and Localization Scheme
- (1)
- Before the moment of assimilation tn. Use the statistical historical reanalysis observation and Equation (19) to determine the statistical observation which used in the proposal density. Using the Equations (17) and (18) to determine the proposal density’s weights ωi and update particles.
- (2)
- In the moment of assimilation tn. Based on the proposal density weighs and use Equations (13)–(15) to calculate the final models states which correspond to the observation position .
- (3)
- In the moment of assimilation tn. The particles without observations in the radius of influence c. The historical reanalysis data of is the observation of the corresponding position of these particles at history moment tra and using them to adjust the particles close to the historical observations according to Equation (11) to obtain the adjusted particles .
- (4)
- Assimilate moment tn application localization schemes. Using the and Equation (1) calculate the weight of particles around the observation based on a given observation and get the resampling indices k1,k2,…,kNe and the particles are shown as ;
- (5)
- In the moment of assimilation tn according to the observation . We refer to the localization scheme state update equations (3)–(6) and (20) of LPF. Combine the particles and resampled particles using the formula to update the particles within the localization radius c.
3. Cycling Data Assimilation Experiments Set Up
3.1. An Intermediate Atmosphere-Ocean-Land Coupled Model
3.2. Simulation Experiments Setup
4. The Numerical Experimental Results
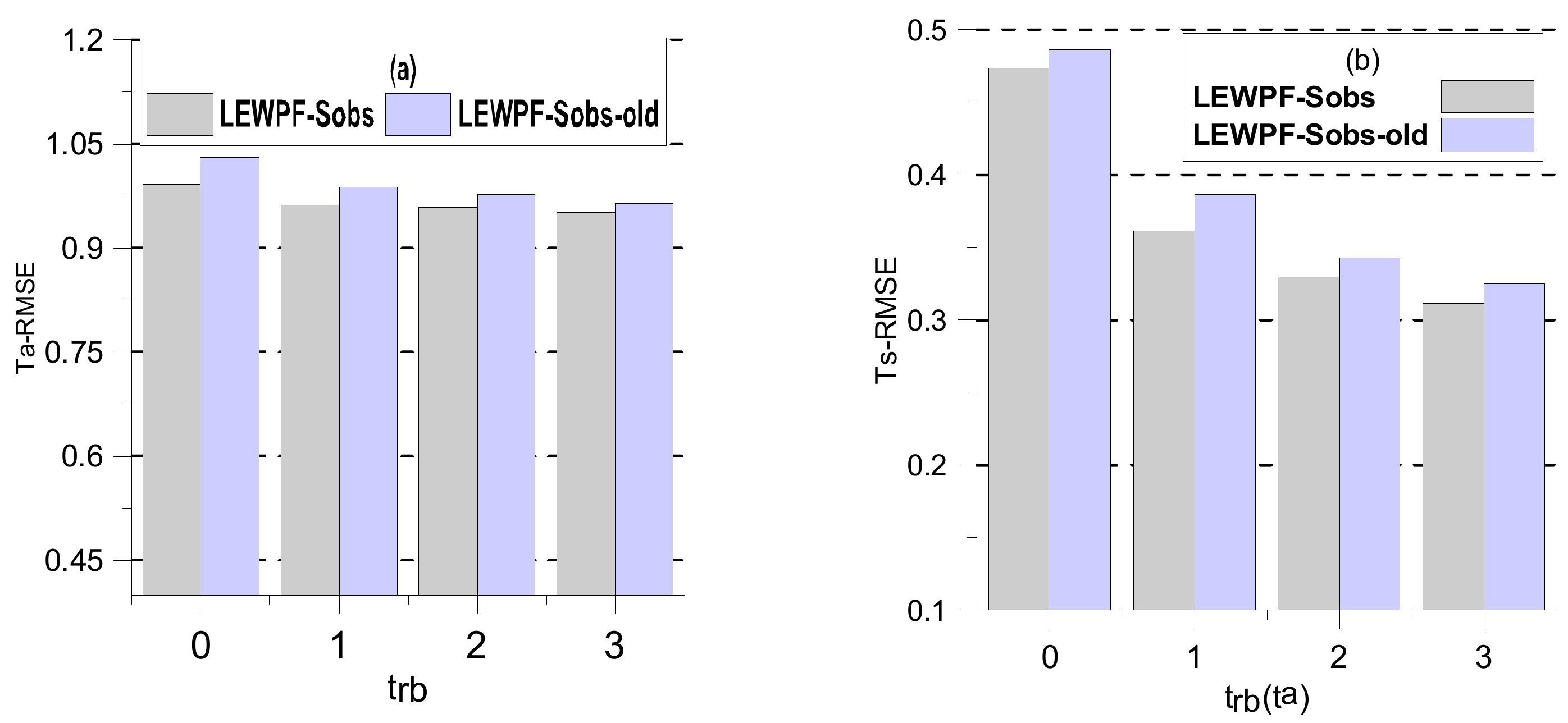
4.1. Standard Observation Distribution Experiment
4.2. Sparse Observational Distribution Experiments
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Nichols, N.K. Data Assimilation: Aims and Basic Concepts. In Data Assimilation for the Earth System; Springer: Berlin/Heidelberg, Germany, 2003; pp. 9–20. [Google Scholar]
- Evensen, G.; Leeuwen, P.V. Assimilation of Geosat Altimeter Data for the Agulhas Current using the Ensemble Kalman Filter with a Quasi-Geostrophic Model. Mon. Weather Rev. 1995, 124, 85–96. [Google Scholar] [CrossRef]
- Jadidoleslam, N.; Mantilla, R.; Krajewski, W.F. Data Assimilation of Satellite-Based Soil Moisture into a Distributed Hydrological Model for Streamflow Predictions. Hydrology 2021, 8, 52. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, W.; Zhu, M. A localized weighted ensemble Kalman filter for high-dimensional systems. Q. J. R. Meteorol. Soc. 2020, 146, 438–453. [Google Scholar] [CrossRef]
- Wu, P.Y.; Yang, S.C.; Tsai, C.C.; Cheng, H.W. Convective-Scale Sampling Error and Its Impact on the Ensemble Radar Data Assimilation System: A Case Study of a Heavy Rainfall Event on 16 June 2008 in Taiwan. Mon. Weather Rev. 2020, 148, 3631–3652. [Google Scholar] [CrossRef]
- Pires, C.A.; Talagrand, O.; Bocquet, M. Diagnosis and impacts of non-Gaussianity of innovations in data assimilation. Phys. D Nonlinear Phenom. 2010, 239, 1701–1717. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J.; Künsch, H.R.; Nerger, L.; Potthast, R.; Reich, S. Particle filters for high-dimensional geoscience applications: A review. Q. J. R. Meteorol. Soc. 2019, 145, 2335–2365. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J. Particle filtering in geophysical systems. Mon. Wather Rev. 2009, 137, 4089–4114. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J.; Cheng, Y.; Reich, S. Nonlinear Data Assimilation; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Potthast, R.; Walter, A.; Rhodin, A. A localized adaptive particle filter within an operational NWP framework. Mon. Weather Rev. 2019, 147, 345–362. [Google Scholar] [CrossRef]
- Brajard, J.; Carrassi, A.; Bocquet, M.; Bertino, L. Combining data assimilation and machine learning to infer unresolved scale parametrization. Philos. Trans. R. Soc. A 2021, 379, 20200086. [Google Scholar] [CrossRef]
- Khan, R.S.; Bhuiyan, M.A.E. Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets. Atmosphere 2021, 12, 1239. [Google Scholar] [CrossRef]
- van Leeuwen, P.J. Aspects of Particle Filtering in High-Dimensional Spaces. In Dynamic Data-Driven Environmental Systems Science; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 251–262. [Google Scholar]
- Zhao, Y.; Yang, S.; Jia, R.; Zhou, D.; Deng, X.; Liu, C.; Wu, X. The statistical observation localized equivalent-weights particle filter in a simple nonlinear model. Acta Oceanol. Sin. 2021. [Google Scholar] [CrossRef]
- Poterjoy, J.; Wicker, L.; Buehner, M. Progress toward the application of a localized particle filter for numerical weather prediction. Mon. Weather Rev. 2018, 147, 1107–1126. [Google Scholar] [CrossRef]
- Poterjoy, J. A localized particle filter for high-dimensional nonlinear systems. Mon. Weather Rev. 2016, 144, 59–76. [Google Scholar] [CrossRef]
- Poterjoy, J.; Anderson, J.L. Efficient Assimilation of Simulated Observations in a High-Dimensional Geophysical System Using a Localized Particle Filter. Mon. Weather Rev. 2016, 144, 2007–2020. [Google Scholar] [CrossRef]
- van Leeuwen, P.J. Nonlinear data assimilation in geosciences: An extremely efficient particle filter. Q. J. R. Meteorol. Soc. 2010, 136, 1991–1999. [Google Scholar] [CrossRef]
- Poterjoy, J.; Anderson, J.L. Particle filters for high-dimensional geoscience applications: A review. Q. J. R. Meteorol. Soc. 2018, 723, 2335–2365. [Google Scholar]
- Ades, M.; Van Leeuwen, P.J. An exploration of the equivalent weights particle filter. Q. J. R. Meteorol. Soc. 2013, 139, 820–840. [Google Scholar] [CrossRef]
- Zhu, M.; Van Leeuwen, P.J.; Amezcua, J. Implicit equal-weights particle filter. Q. J. R. Meteorol. Soc. 2016, 142, 1904–1919. [Google Scholar] [CrossRef]
- Van Leeuwen, P.J. Efficient nonlinear data-assimilation in geophysical fluid dynamics. Comput. Fluids 2011, 46, 52–58. [Google Scholar] [CrossRef][Green Version]
- Chen, Y.; Zhang, W.; Wang, P. An application of the localized weighted ensemble Kalman filter for ocean data assimilation. Q. J. R. Meteorol. Soc. 2020, 146, 3029–3047. [Google Scholar] [CrossRef]
- Gaspari, G.; Cohn, S.E. Construction of correlation functions in two and three dimensions. Q. J. R. Meteorol. Soc. 1999, 125, 723–757. [Google Scholar] [CrossRef]
- Shen, Z.; Tang, Y.; Li, X. A new formulation of vector weights in localized particle filters. Q. J. R. Meteorol. Soc. 2017, 143, 3269–3278. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, S.; Liu, Z.; Rosati, A.; Delworth, T.L.; Liu, Y. Impact of Geographic-Dependent Parameter Optimization on Climate Estimation and Prediction: Simulation with an Intermediate Coupled Model. Mon. Weather Rev. 2011, 140, 3956–3971. [Google Scholar] [CrossRef]
- Robert, A. The integration of a spectral model of the atmosphere by the implicit method. In Proceedings of the WMO/IUGG Symposium on NWP, Tokyo, Japan, 26 November–4 December 1968. [Google Scholar]
- Liu, Z. Interannual positive feedbacks in a simple extratropical air-sea coupling system. J. Atmos. Sci. 1993, 50, 3022–3028. [Google Scholar] [CrossRef][Green Version]
- Philander, S.G.H. Unstable air-sea interaction in the tropics. J. Atmos. 1984, 41, 604–613. [Google Scholar] [CrossRef]
- Zhang, X.F.; Zhang, S.; Liu, Z. Parameter optimization in an intermediate coupled climate model with biased physics. J. Clim. 2015, 28, 1227–1247. [Google Scholar] [CrossRef]
- Dommenget, D.; Flöter, J. Conceptual understanding of climate change with a globally resolved energy balance model. Clim. Dyn. 2011, 37, 2143–2165. [Google Scholar] [CrossRef]
- Thompson, S.L.; Warren, S.G. Parameterization of outgoing infrared radiation derived from detailed radiative calculations. J. Atmos. Sci. 1982, 39, 2667–2680. [Google Scholar] [CrossRef]


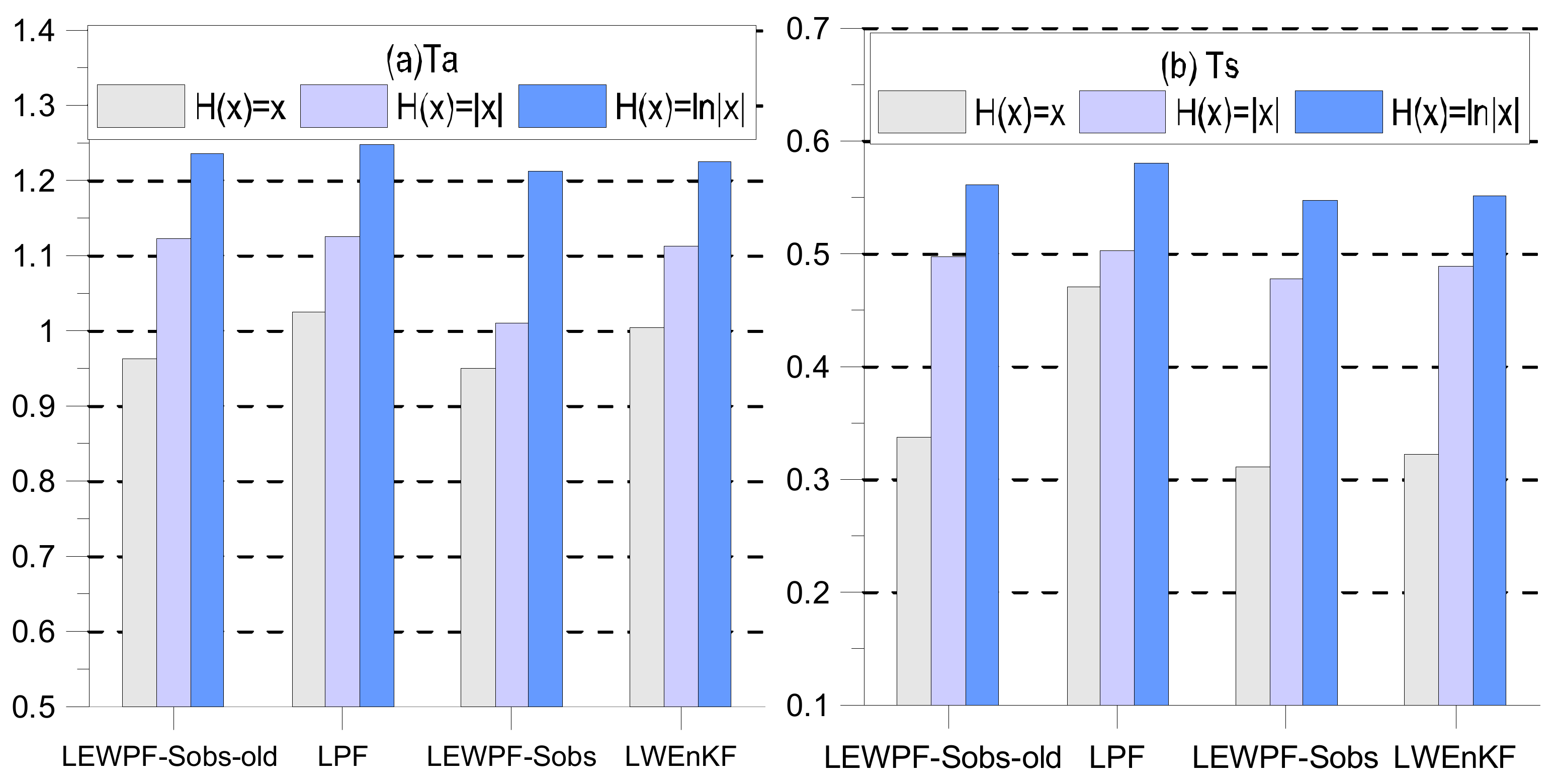
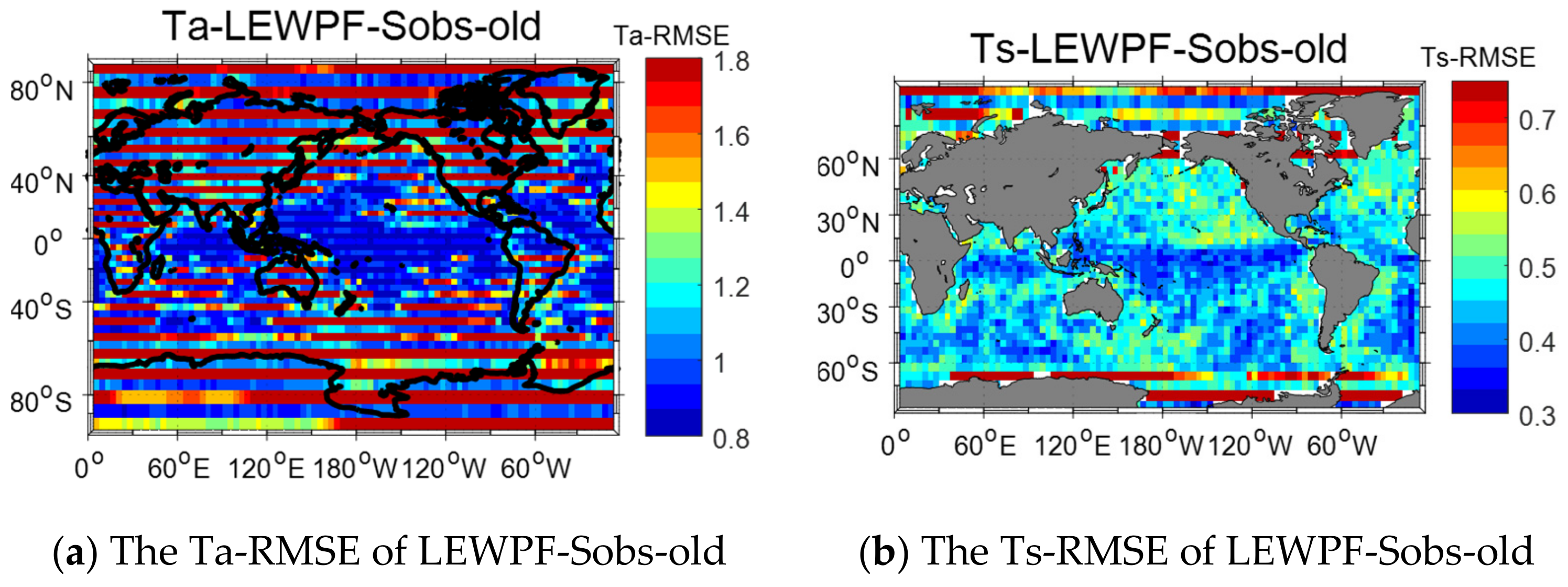
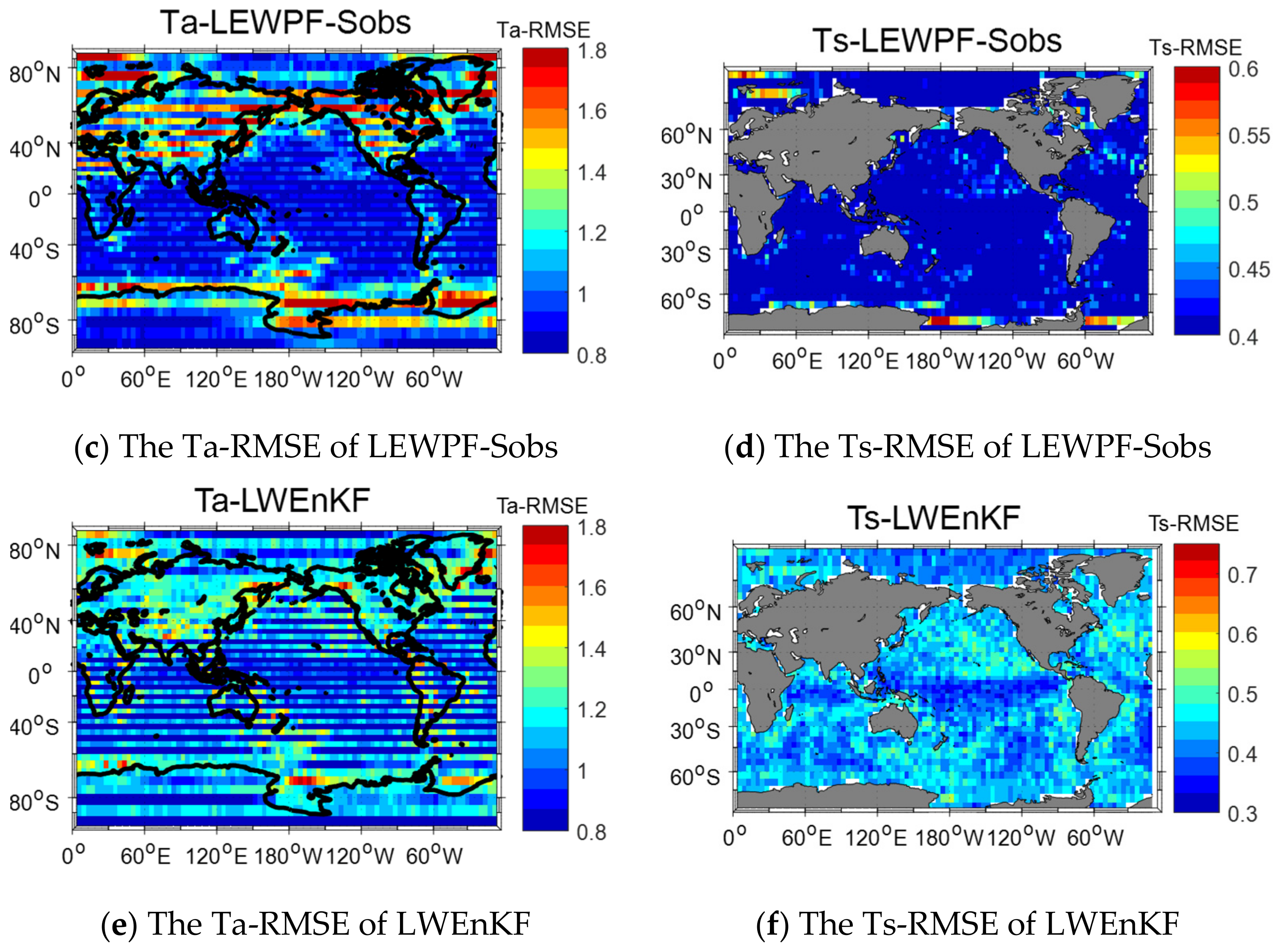
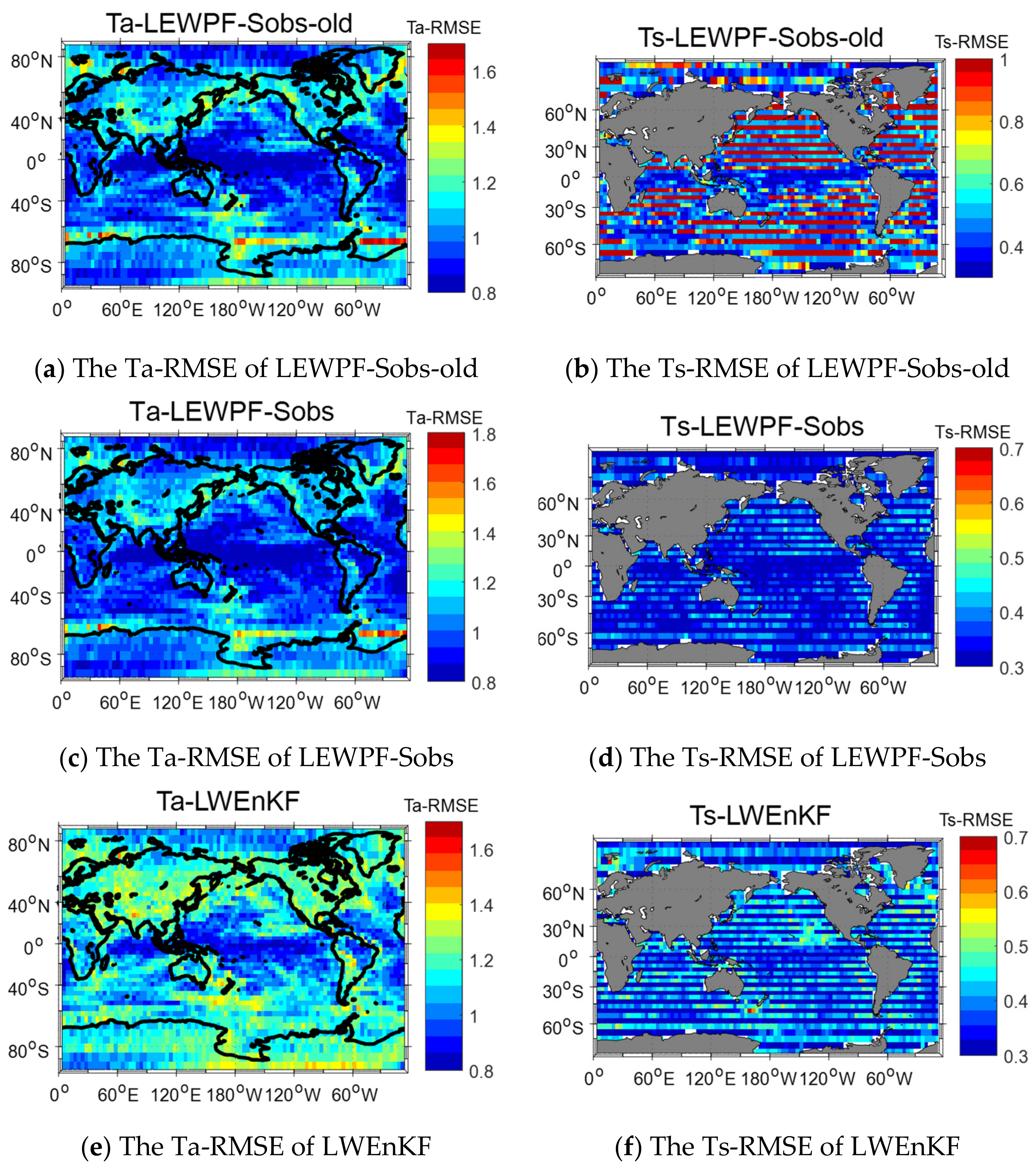

| Standard Observation | Spare Observation | |||
|---|---|---|---|---|
| Spatial Distribution | RMSE Histogram | Spatial Distribution | RMSE Histogram | |
| LEWPF-Sobs | √ | √ | √ | √ |
| LEWPF-Sobs-old | √ | √ | √ | √ |
| LWEnKF | √ | √ | √ | √ |
| LPF | √ | √ | ||
| H(x) = x | H(x) = |x| | H(x) = ln(|x|) | ||||
|---|---|---|---|---|---|---|
| RMSE | Spread | RMSE | Spread | RMSE | Spread | |
| Atmospheric temperature (Ta) | ||||||
| LPF | 1.024866 | 0.89107 | 1.1214 | 0.9105 | 1.24840 | 0.8889 |
| LEWPF-Sobs-old | 0.960692 | 0.30691 | 1.1184 | 0.314 | 1.23545 | 0.4399 |
| LEWPF-Sobs | 0.951810 | 0.32541 | 1.0215 | 0.421 | 1.2124 | 0.456 |
| LWEnKF | 1.0048 | 0.296 | 1.114 | 0.301 | 1.2254 | 0.412 |
| Ocean temperature (Ts) | ||||||
| LPF | 0.47064 | 0.421315 | 0.503 | 0.5031 | 0.58093 | 0.45319 |
| LEWPF-Sobs-old | 0.356783 | 0.357434 | 0.497 | 0.478 | 0.56165 | 0.47837 |
| LEWPF-Sobs | 0.3310 | 0.34756 | 0.4786 | 0.487 | 0.5487 | 0.4863 |
| LWEnKF | 0.3229 | 0.3341 | 0.4885 | 0.469 | 0.551 | 0.464 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yang, S.; Zhou, D.; Deng, X.; Zhu, M. The Improved Localized Equivalent-Weights Particle Filter with Statistical Observation in an Intermediate Coupled Model. J. Mar. Sci. Eng. 2021, 9, 1153. https://doi.org/10.3390/jmse9111153
Zhao Y, Yang S, Zhou D, Deng X, Zhu M. The Improved Localized Equivalent-Weights Particle Filter with Statistical Observation in an Intermediate Coupled Model. Journal of Marine Science and Engineering. 2021; 9(11):1153. https://doi.org/10.3390/jmse9111153
Chicago/Turabian StyleZhao, Yuxin, Shuo Yang, Di Zhou, Xiong Deng, and Mengbin Zhu. 2021. "The Improved Localized Equivalent-Weights Particle Filter with Statistical Observation in an Intermediate Coupled Model" Journal of Marine Science and Engineering 9, no. 11: 1153. https://doi.org/10.3390/jmse9111153
APA StyleZhao, Y., Yang, S., Zhou, D., Deng, X., & Zhu, M. (2021). The Improved Localized Equivalent-Weights Particle Filter with Statistical Observation in an Intermediate Coupled Model. Journal of Marine Science and Engineering, 9(11), 1153. https://doi.org/10.3390/jmse9111153







