Abstract
This paper starts with surveying the state-of-the-art knowledge of breaching flow slides, with an emphasis on the relevant fluid mechanics. The governing physical processes of breaching flow slides are explained. The paper highlights the important roles of the associated turbidity current and the frequent surficial slides in increasing the erosion rate of sediment. It also identifies the weaknesses of the current breaching erosion models. Then, the three-equation model of Parker et al. is utilised to describe the coupled processes of breaching and turbidity currents. For comparison’s sake, the existing breaching erosion models are considered: Breusers, Mastbergen and Van Den Berg, and Van Rhee. The sand erosion rate and hydrodynamics of the current vary substantially between the erosion models. Crucially, these erosion models do not account for the surficial slides, nor have they been validated due to the scarcity of data on the associated turbidity current. This paper motivates further experimental studies, including detailed flow measurements, to develop an advanced erosion model. This will improve the fidelity of numerical simulations.
1. Introduction
Submerged slope failure is a common problem in both geotechnical and hydraulic engineering, causing worldwide significant damages. The phenomenon of flow slide takes place when a large amount of underwater sediment moves downslope and eventually redeposits, creating a milder slope. The term "flow slide" stems from the fact that the sediment failing from the slope is transported as a sediment-water mixture and not as a sediment mass [1]. Flow slides pose a severe risk for submerged infrastructure, and coastal and river flood defences, as they can completely undermine a hydraulic structure (see Figure 1). Besides, flow slides of submerged slopes are an important production mechanism in dredging activities, possibly threatening the stability of nearby infrastructure or foreshores. The assessment of the risk of flow slides is important for the construction and reinforcement of flood defences [2].

Figure 1.
Damage to a river dike caused by a flow slide, from US Army Corps of Engineers, with the permission from Rogers, J.D. 2018 (left) [9]. A large collapse of beach at Inskip Point in Queensland due to a breaching event, with the permission from Rainbow Beach Helicopters Australia, 2019 (right) [10].
The existing literature reports many historical cases of large submarine flow slides worldwide (e.g., [3,4,5,6]). There is a long history of flow slide events in the Netherlands [7], particularly in the southwestern estuary of the Netherlands (Zeeland), where hundreds of flow slides have been observed since 1800 [8]. However, the observations were made after the flow slides had already occurred, as their timing is unpredictable, implying that the temporal development of the failure was not monitored. Flow slides have been widely studied through post-event field observations, lab experiments, and numerical models, but are still not sufficiently understood. This is because they exhibit a complicated failure mechanism, including both geotechnical and hydraulic processes.
It was common to consider flow slides to be caused by soil liquefaction occurring in loose sand. In recent years, however, flow slides have also been observed in dense sand induced by a less-known failure mechanism termed breaching. Liquefaction is a process by which the soil structure collapses abruptly after an increase in pore water pressure, which in turn results in a dramatic reduction of the effective stress and the associated shear resistance. Consequently, the soil body flows downslope, behaving as a viscous fluid. Fine, loosely-packed sand is more susceptible to static liquefaction due to its contracting behaviour under shear forces. When loosely-packed sand is subjected to shear force, the grains tend to a denser packing, forcing the pore water out of the pores (Figure 2 left), which increases the pore pressure and reduces the effective stress [11]. Liquefaction usually starts near the slope toe, leading to a retrogressive failure of the entire slope [12]. The time scale of a static-liquefaction flow slide is short, probably a matter of seconds or minutes [13]. In contrast, breaching occurs slowly and perhaps lasts for several hours or even longer than one day, depending on the slope geometry [14].

Figure 2.
Behaviour of loosely-packed sand (left) versus densely-packed sand (right) under shear force.
Even though the two sub-mechanisms, liquefaction and breaching, are fundamentally different and the failure evolution over time is also different, they both result in a flowing soil-water mixture and a very similar post-event morphology. This implies that it is challenging to know the extent to which the two sub-mechanisms played a role in any flow slide event observed. Recent studies, however, have indicated that the dominant failure process in submerged slopes of fine sand [15] and the main trigger of observed flow slides is breaching [1]. This conclusion suggests that it is important to gain a deeper insight into the breaching failure mechanism.
This paper sheds light on breaching flow slides and presents a detailed explanation for the main associated physical processes, from the triggering mechanism up to the end of the failure event. The aim is to provide a better insight into the physics and to identify the relevant knowledge gaps. Existing breaching erosion models were employed in combination with the three-equation model of [16] and applied to a typical case of a breaching subaqueous slope. That shows the implications of using different breaching erosion models for the sand erosion rate and the hydrodynamics of breaching-generated turbidity currents. As a result, this paper provides evidence that advanced breaching erosion models are required, and thus, suggests further experimental studies on breaching flow slides. Finally, some open questions are posed and key future directions are defined for research on this fascinating topic.
2. Phenomenology
2.1. Breaching Flow Slides
Breaching is a common term in hydraulic engineering, mostly referring to the ultimate failure caused by the overtopping of dams, embankments, and sand barriers [17], but it is used here in a more restrictive manner. Specifically, it is a gradual retrogressive failure of a very steep subaqueous slope, which is steeper than the angle of repose [18]. The Dutch dredging industry in the 1970s first identified breaching as an important production mechanism for stationary suction hopper dredgers. Currently, breaching is incorporated into corresponding safety assessments of dikes in the Netherlands, as it is an important failure mechanism [8].
Breaching takes place in dense sand, as it shows dilative behaviour under shear forces [18,19]. Dilatancy refers to the volume increase of a granular material, during shear deformation, resulting from the increase in pore volume. This leads to a negative pore pressure, and hence an increase in the effective stress. Consequently, the erosion process is significantly retarded. An inward hydraulic gradient is generated due to the pressure difference, forcing the ambient water to flow into the pores (Figure 2 right). This restores the hydrostatic pressure, and thus only the particles located at the sand–water interface are destabilised and fall downslope one by one. These particles are suspended in water and form a turbulent, sand-water mixture flow, referred to as a turbidity current, propagating over and interacting with the breach face [17,20].
During the particle-by-particle failure, the negative pore pressure dissipates locally, weakening the sand near the sand–water interface and leading to a thin surficial slide (a collapse of a coherent sand wedge), which leads to an abrupt drop in the pore pressure. This reinforces the sand deposit and converts the failure process back to particle-by-particle failure. In large-scale flume experiments on breaching, [19] observed the occurrence of surficial slides. The variant involving particle-by-particle failure and surficial slides was termed "dual-mode slope failure" by [21]. However, Van den Berg et al. [15] did not agree with this term and considered it misleading, debating that the particle-by-particle failure and surficial slides are inherent properties of breaching and strongly linked to each other.
Experimental investigation carried out by [19] showed that two types of breaching can be distinguished: stable and unstable (Figure 3). The breaching process is considered unstable when the face of the steepening slope increases in height over time, leading to uncontrolled retrogressive failure of the slope. Stable breaching is characterised by the fact that the height of the breaching face decreases over time and disappears quickly. Whether the breaching is stable or unstable relies on the initial breach height and slope angle, and the sand characteristics [13].
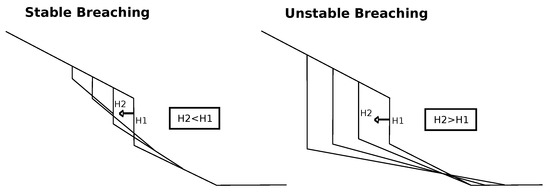
Figure 3.
Schematic illustration of the two types of breaching, stable breaching (left) and unstable breaching (right); H is the breach height and the horizontal axis represents time, with the permission from Van Rhee, C. 2015 (adapted from [13]).
If the subaqueous slope is steeper than the angle of repose, the downslope component of gravitational force is greater than the sand’s shear resistance. In such a case, retrogressive erosion occurs until a slope milder than the angle of repose is formed, even if the flow-induced shear stress is negligible. Due to the generation of a turbidity current, an extra bed-shear stress develops and the erosion rate increases [22]. The following subsection presents an overview of turbidity currents and their importance in sediment transport, in order to pave the way for the description of the role of turbidity currents in breaching flow slides and identifying the relevant knowledge gaps.
2.2. Turbidity Current
Turbidity currents belong to the greater group of gravity-driven flows, the overarching term for flows driven by gravitational forces resulting from the density gradient in a fluid. Traditionally, turbidity currents are defined as sediment-laden gravity-driven underflows in which the particles are largely or entirely suspended due to fluid turbulence. This turbulence is generated due to the ongoing travel of current over the lower boundary of sediment bed and the shear stress generated at the upper boundary of the current. The motion of this current is generated by the density difference between the sediment-water mixture and the ambient water [23].
Turbidity currents can be encountered in the oceans, lakes, estuaries, and reservoirs [24,25]. They are an important consideration for the management of siltation and water quality in reservoirs and lakes [26]. In fact, turbidity currents represent an important sediment transport mechanism, as they carry sediment from the continental shelves towards the deep sea [27]. Therefore, these currents are considered to be the reason for the excavation of many submarine canyons and fans [28]. According to [29,30], the current understanding of bed erosion by turbidity currents remains very limited. These currents can travel at surprisingly swift velocities [31], up to 20 m/s [32], and are, therefore, from an engineering viewpoint, extremely dangerous for the stability of submarine structures placed at the seabed, such as oil pipelines, well heads, and telecommunication cables [33].
Very few field measurements of turbidity currents are reported in the literature (e.g., [34,35,36]), as these currents often occur unexpectedly and may also destroy the measurement instruments. This explains why current understanding of turbidity currents is based mainly on laboratory experiments and numerical modelling.
Turbidity currents are not conservative flows, because they freely exchange the suspended sediments with the bed sediments through erosion and deposition. When the current is adequately swift, it picks up more sediments from the erodible bed than it deposits, increasing the suspended sediment concentration, and thus accelerating the flow, known as ignition or self-accelerating current [16,37]. In contrast, when the turbidity current becomes weak, it starts releasing the suspended sediments at the bed, decaying the gravitational force, and thus decelerating until all the suspended material settles down.
Turbidity currents can be formed by numerous triggering mechanisms, such as submarine slope failures, storm-induced retrogressive failure of the canyon walls [38], hyperpycnal flows [39], breaking internal waves, and breaching flow slides in fine-grained sands. Breaching-generated turbidity currents were unexplored until the publication of [22], which revealed that breaching is an important triggering mechanism of turbidity currents. This fact was supported later by the work of [17]. The next section presents a detailed explanation of the physical processes of breaching flow slides, among which is the generation of turbidity currents.
3. Governing Processes of Breaching Flow Slides
Breaching flow slides involve several physical processes, starting from the initiation of the failure up to the final deposition of the sediments. These processes should be well quantified and understood in order to model them accurately. Figure 4 shows a conceptual sketch of these processes, and that is followed by a description of each one in subsequent paragraphs.

Figure 4.
Conceptual sketch of the governing physics of a breaching process.
3.1. Initial Breaching
When the underwater slope of a densely packed sand deposit becomes steeper than the angle of repose, due to a certain triggering process, the slope becomes unstable. This is because the downslope component of gravity is greater than sand’s shear resistance. In this case, due to the dilative behaviour of sand, the sand grains located at the sand–water interface drop grain by grain. This erosion process, breaching, stops once the slope reaches an angle milder than or near the angle of repose.
Many different triggering mechanisms for flow slides in general are reported in the literature, such as earthquakes, excavations, slope erosion, rapid accumulation of deposits, gas charging, tides, and waves [40]. Fluid motion in particular, plays a very important role in triggering flow slides, either by changing the geometry of the slope or the soil stresses or by destabilising the existing forces. According to [41], flow slides usually occur because the submerged slopes become gradually steeper by erosion processes due to river currents or tidal currents in estuaries. Figure 1 left shows the 213 m long section of a dike that slid into the Mississippi River in 1983 at Darrow, in Louisiana. The flow slide took place shortly after a high water level had dropped, suggesting that rapid draw-down probably contributed to the failure [9].
The current understanding of the triggering mechanisms of breaching flow slides remains very limited, showing the need for further investigations and research on this topic. It is possible that many breaching flow slides are triggered by scour at the toe of a submerged slope, which would lead to over-steepening of the submerged slope at the toe, resulting in a local instability. When the slope at the toe becomes steeper than the angle of repose, a retrogressive flow slide will take place starting from the toe [42]. A well-documented case of such a retrogressive flow slide in a relatively dense sand is the Mississippi riverbank (presented and described by [43,44]).
3.2. Generation of a Turbidity Current
The sand particles falling from the slope disperse as a sand-water mixture with a density greater than that of the ambient water, which provides the driving force for a turbidity current flowing downslope over the sand surface. This current generates turbulence which keeps the sand particles in suspension while it also increases sand–water interfacial stresses. The periodic surficial slides significantly increase sand erosion and thus augment the turbidity current. Interestingly, the influence of the turbidity current determines whether the breaching process is stable or unstable. A complete theoretical description of this influence is not yet available, but an empirical relationship can be found in [13] to predict whether the breaching process is stable or unstable.
The wall-normal velocity structure of turbidity currents shows two distinctive regions: (1) an inner, near-bed region, and (2) an outer region (Figure 5). The inner region shows a positive velocity gradient, similar to the conventional turbulent boundary layer, but the outer region shows a negative velocity gradient related to the entrainment of ambient water [45]. An experimental investigation conducted by [46] showed that the maximum velocity of the velocity profile occurs at about 0.2 times the entire height of the turbidity current. Turbulent kinetic energy reaches its maximum in the shear layer and is close to zero at the location of the velocity maximum [46,47]. The sediment concentration decays in the wall-normal direction away from the bed, and seems to follow a power law distribution [48].
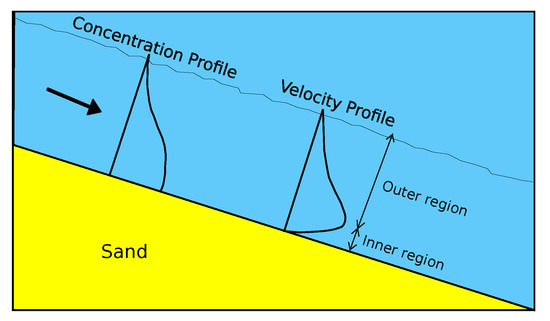
Figure 5.
Typical velocity and concentration profiles of turbidity currents.
3.3. Sediment Entrainment into Turbidity Current
Turbidity currents have the potential to keep sediments in suspension for long distances and to erode additional sediments from the bed. They pick up sediment from the bed mainly through the shear stress they exert on the mobile bed [49]. Sediment entrainment and the fate of the transported sediment are largely governed by turbulence. In the case that more sediments are picked up from bed into the turbidity current, the gravitational force that drives it boosts, which expedites the flow and enhances more sediment entrainment through a process termed ignition [16,50].
Breaching-generated turbidity currents exert additional shear stress on the breach face, leading to an increased erosion rate of the sand [22]. Steep slopes formed of fine-grained sediments are distinctive features in the breaching failure. The authors of [51] found out that steeper slopes composed of finer sediments have lower critical values of the velocity and sediment concentration, causing ignition. This suggests that breaching-generated turbidity currents begin picking up sediments from the bed at earlier evolution stages than turbidity currents formed by other triggering mechanisms.
Very few studies have focused on the entrainment of sediments from the bed by turbidity currents (e.g., [52]). The lower boundary layer of the turbidity current, the so-called near-bed region, has a relatively high concentration of sediment particles where the particle-fluid and particle-particle interactions promote the momentum and mass exchanges between the mixture flow and the sediment bed [30]. The dynamics of this lower boundary layer are still poorly understood. This implies that the estimate of the sediment entrainment by breaching-generated turbidity currents is challenging, and the use of an empirical function is required, as discussed later in this paper.
3.4. Water Entrainment into Turbidity Current
While the sand entrains into the turbidity current from the lower boundary, water entrains from the upper boundary of the current. Water entrainment is caused by the development of Kelvin–Helmholtz instabilities at the interface between the turbidity current and ambient water [53]. The dynamics of the current are affected by the amount of the entrained ambient water. This entrainment contributes to the dilution of the current. Additionally, it increases the overall thickness of the current and generates a shear stress along its upper surface, thereby reducing the net driving force and flow velocity [54].
Based on laboratory experimental studies on steady gravity currents, water entrainment was parametrised in terms of the densimetric Froude number (e.g., [55,56]) and in terms of both the Froude and Reynolds numbers [57]. The water entrainment coefficient —defined as the entrainment velocity normalised by the mean downstream velocity—proposed by [56], reads
where (-) is the bulk Richardson number defined as
in which (-) is the relative submerged density of the sediment, g (m/s) is the gravitational acceleration, h (m) is the current height, c (-) is the layer-averaged, volumetrically-suspended sediment concentration, and u (m/s) is the depth-averaged stream-wise velocity.
Stagnaro and Pittaluga [58] validated the empirical relation suggested by [56] using their experimental values of the entrainment coefficient and found that it provides a good estimate.
3.5. Sedimentation and Erosion on Downstream Soil Bed
Once the turbidity current reaches the lowest point of the slope and begins flowing over the downstream bed, sediment exchange with the bed may take place through deposition and erosion processes. This means that the amount of suspended particles in the current changes with time. Whether erosion or deposition processes dominate the region at the bottom boundary is dependent on the magnitude of the shear stress at the lower boundary layer [59]. The balance of sediment exchange with the erodible bed determines whether the current is self-accelerating or decelerating, implying that any mechanism affecting the sediment exchange would affect the dynamics of the current [60]. Complex topography may result when sediments are eroded, which may hinder or promote further sediment erosion. The dynamics of the sediment exchange are usually complicated and the mechanisms behind the interaction between the highly turbulent gravity current and the bed are not yet sufficiently understood. Therefore, empirical models for sediment entrainment and deposition are usually used in numerical computations.
3.6. Deposition of Suspended Material
When the breaching process ceases, the sediment supply driving the turbidity current diminishes. Accordingly, the turbidity current loses momentum and the suspended particles start settling down at the bed. When the current releases sand grains, it becomes more diluted and moves slower, which further diminishes the processes of sediment deposition and deceleration. The heaviest (coarsest) grains settle first and the lightest (finest) grains settle last, leading to deposits with an upward-fining character [49]. The final post-failure angle of the breach face is usually near the maximum angle of repose.
In conclusion, the estimate of sediment erosion during breaching flow slides is not trivial, as many parameters govern the erosion process, such as breach height, slope angle, soil characteristics, and the accompanied turbidity current. Yet, prediction of the erosion rate along the slope during breaching is required to assess the evolution of the sediment morphology and the turbidity current, which, owing to the previously described feed back mechanism, are coupled phenomena. This will determine whether or not the erosion or the associated turbidity current could potentially threaten the stability of nearby hydraulic structures. Furthermore, this can be used to estimate dredging production when a breaching failure is triggered deliberately as a means of sand mining. To this end, the next section addresses and discusses existing modelling approaches for breaching.
4. Modelling Slope Erosion During Breaching
4.1. Slope Erosion in Stagnant Water
Breusers [61] introduced the term “active wall velocity”, which is defined as the horizontal travelling speed of a vertical submerged slope due to the breaching process. The expression of wall velocity can readily be derived by balancing the forces acting on a sand particle present on a slope (for a detailed derivation, the reader is referred to [62]). For the sake of consistency, this paper presents the resulting expression for the sand erosion velocity perpendicular to the breach face, (m/s), which reads
where is the internal friction angle, is the slope angle, (-) is the in situ porosity of the sand, (m/s) is the sand permeability at the loose state, (kg/m) is the density of the particles, (kg/m) is the density of water, and is the relative change in porosity, in which (-) is the maximum porosity of the sand.
The erosion rate calculated using Equation (3) only takes into account the gravity-induced particle-by-particle failure resulting from the over-steepening of the slope. Van Rhee and Bezuijen [19] found that this expression was invalid for the large-scale experiment they conducted, arguing that the reasons behind the mismatch are the sediment entrainment by the turbidity current and the periodic surficial slides. Results of small-scale experiments even indicate that the expression of wall velocity could not be suited for small breach heights, where weak turbidity current would be expected. Therefore, direct application of Equation (3) in practical events is somewhat limited.
Figure 6 depicts the failure evolution in two small-scale breaching experiments, clearly showing that the erosion rate is non-uniform along the breach face, in contrast to the notion of a uniform wall velocity. The erosion rate increases in the downstream direction due to the acceleration of the turbidity current. Additionally, periodic surficial slides considerably boost sediment erosion, and thus provide the associated turbidity current with a higher capacity to erode the sand [1].
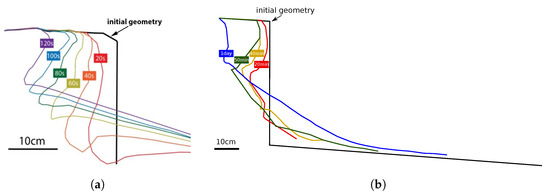
Figure 6.
Development of the breach face showing nonuniform erosion along the sand–water interface: (a) breach height = 30 cm, = 140 m (adapted from [63], with the permission from You, Y. 2013); (b) breach height = 70 cm, =70 m (adapted from [64], with the permission from Eke, E.C. 2008).
In conclusion, breaching erosion models should incorporate sediment entrainment by the turbidity current and surficial slides to better predict the total sediment erosion rate along the breach face, and improve predictions of the failure evolution. The next section discusses some sediment entrainment functions relevant to breaching flow slides.
4.2. Sediment Entrainment
A complete theoretical description of sediment entrainment by fluid motion is not yet available, due to the complexity of the erosion phenomena, and erosion by turbidity current is not an exception. As a consequence, sediment pick-up functions are usually developed by conducting experimental studies under special conditions in order to estimate the sediment fluxes (e.g., [65,66]). Most of the proposed pick-up functions in the literature consider a horizontal mobile bed over which a steady uniform flow propagates. The conditions of the breaching-generated turbidity current are different from these typical conditions. It is an unsteady, non-uniform, sediment-laden current which travels over a sloping, dilative bed, which retards the erosion rate.
Generally speaking, the rate of sediment transport is dependent on the flow-induced bed shear stress, flow turbulence, the characteristics of the sediment particles, and in some conditions, on the bulk properties of sediments. Initiation of motion of non-cohesive sediment grains occurs once the Shields parameter exceeds a critical value defined by
where (Pa) is the critical bed shear stress and (m) is the median grain size. Sediment grains begin to move along the bed by saltation, rolling, or shearing, but are not at that point entrained into the main flow. The pick-up process initiates once the sediment grains are entrained into the body of the flow, which is generally characterised by an empirical non-dimensional pickup rate defined as [67],
where (kg/(s m)) is the sediment pick-up rate perpendicular to the bed surface. Empirical relations are needed to express this non-dimensional pick-up rate in terms of the sediment and fluid properties, and the bed shear stress.
Several of these so-called “pick-up functions” can be found in the literature on the erosion of granular sediment. Most studies on sediment pick-up were conducted for horizontal and mild stream-wise bed slopes in a steady uniform flow. Accordingly, the available erosion models for granular material at high flow velocities, where dilatancy is important, were only validated for a horizontal bed (e.g., [68,69]).
The focus of this paper is on the most common pick-up functions and on those accounting for the dilatancy effect, which, for steady and uniform conditions, are attended to in the following subsection. The sediment entrainment in gravity currents is typically an unsteady phenomenon, which means that the inner density distribution and current kinematics are time varying, motivating a treatment in a separate subsection.
4.2.1. Steady and Uniform Flows
One of the most widely used sediment pick-up functions is that of [65]. Based on experiments with a very low sediment concentration, sand particles ranging from 0.13 to 1.5 mm and mean flow velocities ranging from 0.5 to 1 m/s matching bed shear stress ranging between 0.5 and 2 Pa, [65] derived the following pick-up function
where (-) is a dimensionless particle diameter defined by , in which (m/s) is the kinematic viscosity of water.
Winterwerp et al. [66] conducted erosion experiments at a higher bed shear stress than Van Rijn [65] ranging between 5 and 130 Pa. The investigation and analysis of their experimental data yielded an empirical pick-up function suited to this erosion regime where the erosion rate is reduced by the dilative behaviour of the sand. The pick-up function reads
It is worth mentioning that this function does not account explicitly for the effect of inflow of water into the pores. However, the effect is implicitly accounted for through the fitting procedure with the experimental data.
The experimental data of [65,66] was used in [22] to develop an empirical pick-up function including the effect of the dilative behaviour of sand to describe the breaching process in fine-grained sands. The dilative behaviour was taken into account by including the bulk properties of sand, such as permeability and porosity in their pick-up function
The experimental data presented in [22] are partly in line with this pick-up rate.
The work of [70] showed that the pick-up function of [65] overestimates the erosion in the case of high concentrations. They presented an empirical pick-up function based on experiments of highly concentrated flows with subcritical flow velocity. This function includes the effect of the near-bed volume concentration (-) based on the argument that sediments are entrained by the turbulent eddies. If an eddy transports a certain volume of both sediment and water from the bed, the same volume of water should flow back to the bed due to continuity. If the sediment concentration is low, this backflow will contain few particles, but if it is high, the backflow will transport more particles. Following this argument, a reduction factor was introduced to include the effect of the near-bed concentration. However, no reference level above the bed was defined for the near-bed concentration, nor was a formula provided to estimate it. The resulting pick-up function presented by [70] reads
This empirical pick-up function can also be written in terms of the critical Shields parameter, as presented in [13]
The work of [68,71] showed that using the pick-up function of [65] results in overestimation of the erosion in the presence of dilatancy effect. The inward flow of water resulting from dilatancy amplifies the magnitude of the critical Shields parameter. Van Rhee [68] adapted the conventional critical Shields parameter to include the influence of a sloping bed, and the influence of dilatancy considering the hydraulic gradient as an additional stabilising force acting on sand grains:
where is the modified critical Shields parameter, and is the erosion velocity perpendicular to the slope surface. For a horizontal bed, this expression reduces to
Bisschop [69] performed erosion experiments and validated the pick-up function developed by [68] (Equation (12)). It was concluded that this pick-up function provides a good estimate of the pick-up flux for the finest sand types used in the experiments ( = 51 m, 125 m), while it overestimates the pick-up flux for the coarsest sand types used in the experiments ( = 262 m, 561 m).
4.2.2. Turbidity Currents
Although there is abundant literature on turbidity currents, limited knowledge is available on the dynamics of sediment erosion by turbidity currents. Several relationships are proposed in the literature for the estimation of the associated entrainment rate of sediment. In the field of turbidity currents, it is common to use a non-dimensional sediment entrainment coefficient (-); see for instance [72].
where (m/s) is the particle settling velocity. In equilibrium suspensions, equals the volumetric near-bed sediment concentration.
Akiyama and Fukushima [73] utilised measurements for open-channel suspensions in rivers and flumes to develop the following relation for the sediment entrainment coefficient.
where , in which is the shear velocity, is the particle Reynolds number, and D is the particle diameter. The parameter (-) is a critical value for the onset of significant entrainment, and 13.2 (-) represents a maximum value of Z beyond which becomes constant with a value of approximately 0.3 (-).
Garcia and Parker [72] also developed a sediment entrainment function for suspensions of uniform material in an open-channel flow. This function was compared in the work of [52] with experimental results for turbidity currents. The estimated values by the empirical function followed the trend of the experimental data, but the scatter was large. Therefore, [52] modified the function to take the form
where (-) and , in which
Yi and Imran [51] implemented different sediment entrainment relations in the four-equation model of Parker et al. (see [52,73,74]). For the same input conditions, the computed results showed a different behaviour of the turbidity current depending on the particular relation used for the sediment entrainment. In other words, a turbidity current predicted to be depositing when using a certain entrainment function could be ignited when using another one. This result explains the need for a better insight into the sediment transport mechanism by turbidity currents, as to derive advanced erosion models.
4.3. Discussion
Based on the overview above, the following discussion points were raised:
- Van Rhee [68] stated that the adapted critical Shields parameter can be used in any existing pick-up function as long as it includes the critical Shields parameter. Nevertheless, the existing pick-up functions are empirical and the effect of dilatancy could be already included (maybe to a certain extent) in the function. Having this effect in the empirical pick-up function and also in the critical Shields parameter may result in underestimation of the erosion rate.
- All the pick-up functions presented above require an estimate of the flow-induced shear stress. As a result, estimating sediment erosion is highly sensitive to the method by which the bed shear stress is computed.
- The existing relationships proposed to estimate the sediment entrainment by turbidity currents are mainly expressed in terms of the local shear stress. Nonetheless, boundary shear stress is just one of several impelling forces that result in sediment erosion [30]. Other hydrodynamic quantities, such as turbulent stresses, and turbulent and mean velocities, also govern the mechanisms of sediment entrainment and transport [75].
- The existing sediment entrainment relations of turbidity currents were developed for a current propagating over a bed covered with loose sediment. Very little is known about the interaction of turbidity currents with densely-packed particles. In this case, dilatancy plays a major role in retarding the erosion process. Therefore, a sediment entrainment function for turbidity currents accounting for dilatancy effects is required to describe the breaching process properly.
In conclusion, the conventional sediment entertainment relations of turbidity currents (e.g., [52,73]) are inappropriate for breaching flow slides, as they do not account for the dilatation effect. Therefore, they will not be considered further in this paper.
The next section outlines the existing numerical models coupling the breaching failure with the generated turbidity current, with an emphasis on the incorporated breaching erosion models and to what extent they deviate from each other.
5. Numerical Assessment of Breaching-Generated Turbidity Current
To study the implications of using different breaching erosion models for the hydrodynamics of the generated turbidity current, the existing erosion closure models are presented here, and followed by a comparison between the obtained numerical results. The existing breaching erosion models are the wall-velocity model of [61], the model of [22], and the model of [13]: Equations (3), (23), and (24) respectively. These were employed in combination with the three-equation model of [16] and applied to a typical case of a breaching subaqueous slope. The three-equation model is a layer-averaged model based on the conservation of momentum, water mass, and suspended sediment in the turbidity current. More sophisticated numerical models can be used for computations of turbidity currents; however, a simple model was used here, as the purpose was to check to what extent the results of the model may deviate once different erosion models are adopted, rather than to obtain precise results.
5.1. Three-Equation Model
The approximate, layer-averaged, three-equation model of [16] is obtained by integrating the conservation equations for momentum, fluid mass, and sediment mass over height of the turbidity current, including the bed shear stress, water entrainment, and sediment erosion, respectively, as source terms. Using the layer thickness h (m), the layer-averaged velocity in the stream-wise direction u (m/s), and the layer-averaged volume suspended sediment concentration c (-) as independent variables, and assuming a steady state, the equations read as follows,
where s [m] is the stream-wise coordinate along the slope, (-) is the relative submerged density of sediment, g (m/s) is the gravitational acceleration, (-) is the bed slope angle, (-) is the water entrainment coefficient, and is the net erosion velocity perpendicular to the breach face resulting from the combined effects of erosion and sedimentation. The bed shear velocity (m/s) is calculated by the relation , where (-) is a dimensionless bed friction coefficient.
After rearrangement, Equations (17)–(19) are conveniently formulated as “backwater” flow equations taking the form
where is the Richardson number, as defined in Equation (2).
After providing closure relations for and , the set of backwater equations is solved using a forward space marching procedure where the layer thickness, flow velocity, and sediment concentration at the top of the slope need to be specified as initial conditions; see also Section 5.3.2.
5.2. Water Entrainment and Sediment Exchange
For the dimensionless water entrainment coefficient , the relation from [56] is adopted; see Equation (1). For the erosion velocuity , existing breaching erosion models can be considered: the wall-velocity model of [61], the model of [22], and the model of [13]. These models are introduced below with a brief evaluation of their suitability to breaching flow slides.
5.2.1. Breusers (1977)
Using [61], the erosion velocity is taken as equal to the wall velocity in Equation (3). Since the wall velocity only describes the initial stage of the breaching process, this erosion model does not account for the influence of the turbidity current. This erosion model was incorporated into the numerical model of [17] to estimate the erosion rate at the breach face.
Based on the work of [16,76], Eke et al. [17] developed a three-equation, layer-averaged numerical model for breaching-generated turbidity current. The governing equations of this model are the conservation of momentum and mass of the turbidity current. The results of this numerical model confirmed that breaching can be an important trigger of turbidity currents in submerged canyons. However, the model is subject to some limitations. The predicted slope profiles were not in line with the experimental data, as the model predicted much steeper slopes at the breach face than those observed in the experiments. The model also over-predicted the sediment deposition rates at the toe of the breach face [64]. This could be due to the assumption that the erosion rate along the breach face is uniform and equal to the wall velocity.
5.2.2. Mastbergen and Van den Berg (2003)
Mastbergen and Van Den Berg [22] developed a numerical model for breaching-generated turbidity currents based on one-dimensional, steady state, depth-averaged equations: momentum, water continuity, and sediment continuity. This model incorporated a formula modified from the work of [66] to estimate the erosion rate .
where it has been assumed that the sediment deposition is negligible compared to the erosion.
The data presented by [22] were too limited for proper validation by these authors. In addition, the formula does not account for the frequent surficial slides. The authors also reported that there was insufficient data for an accurate calibration of all needed parameters for field conditions. However, the model revealed that the breaching mechanism can generate a strong turbidity current, which is capable of excavating a submarine canyon [22].
5.2.3. Van Rhee (2015)
Van Rhee (2015) [13] developed a computational fluid dynamics, two-dimensional, drift-flux model based on the Reynolds averaged Navier–Stokes equations (RANS) to investigate the stability of the breaching process. This model is hydrodynamic (non-hydrostatic) and incorporates a formula modified from the work of [68,70] to estimate the erosion rate as
This relation accounts for the added effect of sedimentation, but does not account for the frequent surficial slides. Validation of this model is still missing.
5.3. Comparison of Results
To explore the deviations between the breaching erosion models, the breaching erosion rate was calculated for a typical situation, a 60-degree slope of fine sand, ignoring slope deformation and considering two different median grain diameters. The various parameters characterising the sand are listed in Table 1. The settling velocity of a single grain was computed using the formula of Budryck [77], and the effect of the hindered settling was taken into account according to [78] to calculate the settling velocity . The permeability has been computed using the Kozeny–Carman equation (a semi-empirical expression).

Table 1.
Sand parameters used in the calculations of the erosion rate.
Two different situations are considered here: a uniform flow and a developing turbidity current, respectively. As the near-bed volume concentration is not clearly defined in [70], a value of 0.2 was assumed in the calculations. Regarding the bed friction coefficient, studies have revealed that for turbidity currents, varies between 0.002 and 0.05, with the lower values corresponding to observations in reservoirs and the higher values to laboratory experiments [56]. The estimates suggest that is inversely proportional to the case scale. Therefore, for the uniform flow case, the calculations were performed using a value for of 0.008, while for the case with a developing turbidity current it was chosen to be in the range of 0.015–0.025; see Table 2.

Table 2.
Values of , u, c, h, and computed 10 m downstream from the origin, using the three different erosion formulas.
5.3.1. Uniform Flow
Erosion rates resulting from the different erosion models are presented here, assuming a uniform flow, where the coupling between the sediment pick-up and the dynamics of the flow is ignored. A median grain diameter of 0.135 mm is used. Figure 7 shows the calculated erosion velocity as a function of the flow velocity in the sediment layer.

Figure 7.
Comparison between breaching erosion formulations based on a uniform flow velocity; 0.135 mm (see Table 1).
As expected, the wall-velocity model renders the same erosion rate irrespective of the magnitude of flow velocities, since it is independent of the flow dynamics. The model of [22] results in higher erosion rates than the model of [13], and the difference is amplified at high flow velocities. This difference in the estimate of erosion rate may have critical implications for the numerical modelling of breaching-generated turbidity currents, since there is a direct feedback between the morphological changes of the breach face and the hydrodynamics of the turbidity current. These implications are described in the next section.
5.3.2. Developing Turbidity Current
The development of a turbidity current over a steep subaqueous slope of fine sand was considered, as depicted in Figure 8. Experience shows that a flow slide can occur spontaneously in fine sands if the slope steepness is at least 1:3 over a breach height of at least 5 m [7]. Thus, a breach face of 10 m was considered in all the executed model runs, satisfying breach heights of more than 5 m. For the sake of simplicity, the deformation of the slope due to erosion was ignored by assuming that the slope angle remains 60 degrees along the entire breach face. Additionally, the turbidity current was considered to be purely erosive, since the slope simulated was very steep and eroded irrespective of the sediment transport capacity of the generated turbidity current.

Figure 8.
Sketch for the case considered in the numerical runs. is the erosion velocity; is the slope angle.
The ordinary differential Equations (20)–(22) are discretised using first-order backward differences. The resulting system of discrete equations is solved using a simple forward space marching procedure using the layer thickness, flow velocity, and suspended sediment concentration at the crest of the breach face as initial conditions. The initial conditions have a local effect only—hardly affecting the overall steady state solution—as the turbidity current adjusts rapidly to the local conditions. The stream-wise coordinate is denoted as s, and the origin of this coordinate is the crest of the breach face. The different breaching erosion models were explored and compared for various input parameters as illustrated in Table 2. Besides, the values of u, c, h, , and (the volumetric suspended sediment transport rate per unit width) just before the toe of the slope are documented. The evolution of the turbidity current along the entire slope for Run 4 is shown in Figure 9. Unfortunately, there are no data in the literature for breaching-generated turbidity currents to compare with the results of our numerical simulations.
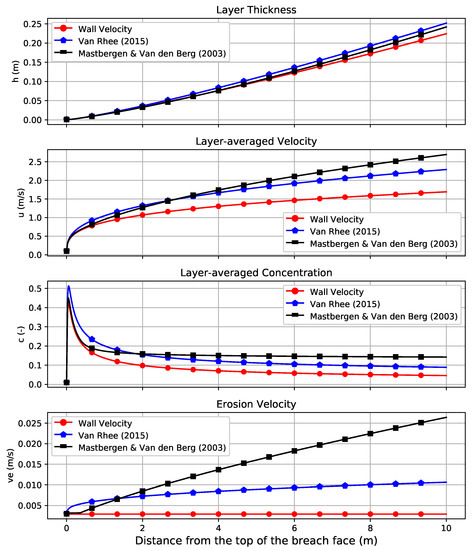
Figure 9.
Comparison of the numerical steady-state results using different erosion formulas; = 0.100 mm, , , (Run 4 from Table 2).
Figure 9 shows that the behaviour of the turbidity current does not vary with the erosion model; the layer thickness increases downstream, the layer-averaged concentration decreases downstream, and the turbidity current accelerates downstream. This acceleration is due to the sediment entrainment, which makes the current denser, and thus faster. This in turn increases the sediment erosion rate downstream the breach face. It is also obvious that using different erosion formulas renders very different erosion rates, and thus, different estimates of the hydrodynamic characteristics of the generated turbidity current. Using the expression of the wall velocity renders the weakest turbidity current with substantial deviation from the other two models. This makes sense, as this expression does not include the entrainment of sediment by the turbidity current, resulting in low uniform sediment supply along the slope, in contrast to the other two models. Accordingly, the focus was set on the deviation between [22], Model(b), and [13], Model(c). To have a better insight into the variation of results for these two models, the percentages of the differences between the results were computed. Considering Run 4 (see Table 2), for example, it is clear that the value of the sediment transport flux () yielded by Model(b) is more than two times of that yielded by Model(c) with deviations of 31% and 70% in the velocity and concentration respectively.
5.4. Discussion
Comparison of numerical results shows that the sediment entrainment relation has important implications for the modelling of turbidity currents, since the model can give different predictions based on which relation is utilised.
In particular, model results at the toe of the slope are important, since they are the main information for determining the upstream boundary conditions for the turbidity current propagating over the bed of the downstream region. This could result in a different behaviour of the turbidity current over the downstream bed concerning erosion and sedimentation. Another crucial implication is that different predictions of the hydrodynamics of the turbidity current may lead to different predictions of the stability of the breaching process, as the turbidity current is the main parameter influencing breaching stability.
The results also reveal that numerical results are more sensitive to the value of when the erosion formula of [22] is used.
6. Conclusions and Outlook
In the course of this methodical review and analysis of the state-of-the-art knowledge and current modelling approaches, the most relevant physical processes and models to breaching flow slides have been discussed. This resulted in the identification of some knowledge gaps and weaknesses of the current models.
It is important to further investigate the breaching failure mechanism, as recent studies have revealed that breaching, rather than liquefaction, is the main driver of the observed flow slides in nature. It is quite difficult to conduct controlled in situ experiments on breaching and the associated turbidity currents. This emphasises the importance of laboratory studies and numerical modelling for gaining a better understanding of the nature of breaching flow slides and their associated sediment transport.
Turbidity currents at laboratory scale are usually depositional, but breaching-generated turbidity currents are primarily erosive as they propagate over the failing slope, due to the over-steepening of the slope. It was shown that using the same input parameters and computational grid in a numerical model while employing different sediment entrainment relationships yields very different sediment erosion rates and hydrodynamics of turbidity currents. Therefore, the development of advanced erosion models accounting for sediment entrainment by the turbidity current and frequent surficial slides will be instrumental to improving the accuracy of numerical computations. To that end, it is helpful to conduct breaching experiments, which include detailed measurements of flow and turbulence, particularly measurements of sediment concentration, as it is the critical parameter controlling turbidity currents. Such measurements are quite scarce in the literature. Therefore, laboratory breaching experiments are being currently conducted in the water lab of Delft University of Technology.
On the modelling part, there are also significant challenges which should be addressed. A deeper understanding of the triggering mechanisms by which a breaching flow slide takes place is required to develop convenient initial and boundary conditions. Given that soil is rarely homogeneous in reality, it would be beneficial to couple the simulation of the turbidity current to an advanced soil model that accounts for the spatial variation in soil characteristics, such as packing density, permeability, particle size, and porosity. Pursuing the above goals requires the incorporation of complementary research methodologies from the fields of soil and fluid mechanics.
Author Contributions
S.A. ran the numerical simulations, analysed the results, and wrote the manuscript. R.J.L. and W.U. contributed to supervising, editing, and improving this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This study was conducted as a part of the MPM-Flow project “Understanding flow slides in flood defences”. This project is funded by The Netherlands Organisation for Scientific Research (NWO) (grant number 13889).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beinssen, K.; Mastbergen, D.R. Flow Slides: Understanding their geo-mechanical mechanisms, the threats they pose and how these threats can be managed. In Proceedings of the 13th Hydraulics in Water Engineering Conference, Sydney, NSW, Australia, 13–16 November 2017; p. 132. [Google Scholar]
- Alhaddad, S.; Labeur, R.J.; Uijttewaal, W. The need for experimental studies on breaching flow slides. In Proceedings of the Second International Conference on the Material Point Method for Modelling Soil-Water-Structure Interaction, Cambridge, UK, 8–10 January 2019; pp. 166–172. [Google Scholar]
- Koppejan, A.; Van Wamelen, B.; Weinberg, L. Coastal Flow Slides in the Dutch Province of Zeeland. In Proceedings of the Second International Conference on Soil Mechanics and Foundation Engineering, Rotterdam, The Netherlands, 21–23 June 1948; pp. 89–96. [Google Scholar]
- Kramer, S. Triggering of liquefaction flow slides in coastal soil deposits. Eng. Geol. 1988, 26, 17–31. [Google Scholar] [CrossRef]
- Silvis, F.; Groot, M.D. Flow slides in the Netherlands: Experience and engineering practice. Can. Geotech. J. 1995, 32, 1086–1092. [Google Scholar] [CrossRef]
- Mastbergen, D.R.; Beinssen, K.; Nédélec, Y. Watching the Beach Steadily Disappearing: The Evolution of Understanding of Retrogressive Breach Failures. J. Mar. Sci. Eng. 2019, 7, 368. [Google Scholar] [CrossRef]
- Mastbergen, D.; van den Ham, G.; Cartigny, M.; Koelewijn, A.; de Kleine, M.; Clare, M.; Hizzett, J.; Azpiroz, M.; Vellinga, A. Multiple flow slide experiment in the Westerschelde Estuary, The Netherlands. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2015; pp. 241–249. [Google Scholar]
- Van Duinen, A.; Bezuijen, A.; van den Ham, G.; Hopman, V. Field measurements to investigate submerged slope failures. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 13–21. [Google Scholar]
- Rogers, J.D. Levees. Available online: http://web.mst.edu/~rogersda/levees/Mississippi%20Delta%20Region.htm (accessed on 30 October 2018).
- BBC. Inskip Point: Section of Australian Beach Collapses into Sea. Available online: https://www.bbc.com/news/world-australia-45622385 (accessed on 30 November 2019).
- Schiereck, G.J.; Verhagen, J.H. Introduction to Bed, Bank and Shore Protection; VSSD: Delft, The Netherlands, 2012. [Google Scholar]
- Torrey, V.H., III. Retrogressive Failures in Sand Deposits of the Mississippi River. Report 2. Empirical Evidence in Support of the Hypothesized Failure Mechanism and Development of the Levee Safety Flow Slide Monitoring System; Technical Report; Army Engineer Waterways Experiment Station Vicksburg Ms Geotechnical Lab.: Vicksburg, MS, USA, 1988. [Google Scholar]
- Van Rhee, C. Slope failure by unstable breaching. In Proceedings of the Institution of Civil Engineers-Maritime Engineering; Thomas Telford Ltd.: London, UK, 2015; Volume 168, pp. 84–92. [Google Scholar]
- Weij, D.; Keetels, G.; Goeree, J.; van Rhee, C. An Approach to research of the Breaching Process. In Proceedings of the WODCON XXI, Miami, FL, USA, 13–17 June 2016. [Google Scholar]
- Van den Berg, J.; Martinius, A.; Houthuys, R. Breaching-related turbidites in fluvial and estuarine channels: Examples from outcrop and core and implications to reservoir models. Mar. Pet. Geol. 2017, 82, 178–205. [Google Scholar] [CrossRef]
- Parker, G.; Fukushima, Y.; Pantin, H.M. Self-accelerating turbidity currents. J. Fluid Mech. 1986, 171, 145–181. [Google Scholar] [CrossRef]
- Eke, E.; Viparelli, E.; Parker, G. Field-scale numerical modeling of breaching as a mechanism for generating continuous turbidity currents. Geosphere 2011, 7, 1063–1076. [Google Scholar] [CrossRef]
- Van Den Berg, J.H.; Van Gelder, A.; Mastbergen, D.R. The importance of breaching as a mechanism of subaqueous slope failure in fine sand. Sedimentology 2002, 49, 81–95. [Google Scholar]
- Van Rhee, C.; Bezuijen, A. The breaching of sand investigated in large-scale model tests. In Proceedings of the 26th International Conference on Coastal Engineering, Copenhagen, Denmark, 22–26 June 1998; pp. 2509–2519. [Google Scholar]
- Van den Ham, G.A.; de Groot, M.B.; Mastbergen, D.R. A Semi-empirical Method to Assess Flow-Slide Probability. In Submarine Mass Movements and Their Consequences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 213–223. [Google Scholar]
- You, Y.; Flemings, P.; Mohrig, D. Mechanics of dual-mode dilative failure in subaqueous sediment deposits. Earth Planet. Sci. Lett. 2014, 397, 10–18. [Google Scholar] [CrossRef]
- Mastbergen, D.R.; Van Den Berg, J.H. Breaching in fine sands and the generation of sustained turbidity currents in submarine canyons. Sedimentology 2003, 50, 625–637. [Google Scholar] [CrossRef]
- Meiburg, E.; Kneller, B. Turbidity currents and their deposits. Annu. Rev. Fluid Mech. 2010, 42, 135–156. [Google Scholar] [CrossRef]
- Islam, M.A.; Imran, J.; Pirmez, C.; Cantelli, A. Flow splitting modifies the helical motion in submarine channels. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Liu, J.T.; Wang, Y.H.; Yang, R.J.; Hsu, R.T.; Kao, S.J.; Lin, H.L.; Kuo, F.H. Cyclone-induced hyperpycnal turbidity currents in a submarine canyon. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Hu, P.; Cao, Z. Fully coupled mathematical modeling of turbidity currents over erodible bed. Adv. Water Resour. 2009, 32, 1–15. [Google Scholar] [CrossRef]
- Piper, D.J.; Normark, W.R. Processes that initiate turbidity currents and their influence on turbidites: A marine geology perspective. J. Sediment. Res. 2009, 79, 347–362. [Google Scholar] [CrossRef]
- Pirmez, C.; Imran, J. Reconstruction of turbidity currents in Amazon Channel. Mar. Pet. Geol. 2003, 20, 823–849. [Google Scholar] [CrossRef]
- Talling, P.J.; Allin, J.; Armitage, D.A.; Arnott, R.W.; Cartigny, M.J.; Clare, M.A.; Felletti, F.; Covault, J.A.; Girardclos, S.; Hansen, E.; et al. Key Future Directions For Research On Turbidity Currents and Their Deposits. J. Sediment. Res. 2015, 85, 153–169. [Google Scholar] [CrossRef]
- Zordan, J.; Juez, C.; Schleiss, A.J.; Franca, M.J. Experimental Results on Sediment Entrainment By Gravity Currents. In Proceedings of the 37th IAHR World Congress, Kuala Lumpur, Malaysia, 13–18 August 2017; pp. 1453–1458. [Google Scholar]
- Krause, D.C.; White, W.C.; Piper, D.J.W.; Heezen, B.C. Turbidity currents and cable breaks in the western New Britain Trench. Geol. Soc. Am. Bull. 1970, 81, 2153–2160. [Google Scholar] [CrossRef]
- Hsu, S.K.; Kuo, J.; Lo, C.L.; Tsai, C.H.; Doo, W.B.; Ku, C.Y.; Sibuet, J.C. Turbidity Currents, Submarine Landslides and the 2006 Pingtung Earthquake off SW Taiwan. Terr. Atmos. Ocean. Sci. 2008, 19, 7. [Google Scholar] [CrossRef]
- Meiburg, E.; Radhakrishnan, S.; Nasr-Azadani, M. Modeling gravity and turbidity currents: computational approaches and challenges. Appl. Mech. Rev. 2015, 67, 040802. [Google Scholar] [CrossRef]
- Xu, J.; Noble, M.; Rosenfeld, L.K. In-situ measurements of velocity structure within turbidity currents. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Andrieux, O.; Cooper, C.K.; Wood, J. Turbidity Current Measurements in the Congo Canyon. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 9 May 2013. [Google Scholar]
- Azpiroz-Zabala, M.; Cartigny, M.J.; Talling, P.J.; Parsons, D.R.; Sumner, E.J.; Clare, M.A.; Simmons, S.M.; Cooper, C.; Pope, E.L. Newly recognized turbidity current structure can explain prolonged flushing of submarine canyons. Sci. Adv. 2017, 3, e1700200. [Google Scholar] [CrossRef] [PubMed]
- Sequeiros, O.E.; Mosquera, R.; Pedocchi, F. Internal Structure of a Self-Accelerating Turbidity Current. J. Geophys. Res. Oceans 2018, 123, 6260–6276. [Google Scholar] [CrossRef]
- Salaheldin, T.; Imran, J.; Chaudhry, M.; Reed, C. Role of fine-grained sediment in turbidity current flow dynamics and resulting deposits. Mar. Geol. 2000, 171, 21–38. [Google Scholar] [CrossRef]
- Mulder, T.; Migeon, S.; Savoye, B.; Faugères, J.C. Inversely graded turbidite sequences in the deep Mediterranean: A record of deposits from flood-generated turbidity currents? Geo-Mar. Lett. 2001, 21, 86–93. [Google Scholar]
- Locat, J.; Lee, H.J. Submarine landslides: Advances and challenges. Can. Geotech. J. 2002, 39, 193–212. [Google Scholar] [CrossRef]
- Jonkman, S.; Schweckendiek, T. Flood Defences. In Lecture Notes CIE5314; Delft University of Technology: Delft, The Netherlands, 2015. [Google Scholar]
- Chu, J.; Ho, M.; Loke, W.; Leong, W. Effects of scour and hydraulic gradient on the stability of granular soil slope. In Proceedings of the Second International Conference on Scour and Erosion, Singapore, 14–17 November 2004. [Google Scholar]
- Hadala, P.F.; Torrey, V. Mississippi riverbank flowslides. In The Art and Science of Geotechnical Engineering; Prentice-Hall Inc.: Englewood Cliffs, NJ, USA, 1989; pp. 13–30. [Google Scholar]
- Torrey, V.H., III; Dunbar, J.B.; Peterson, R.W. Retrogressive Failures in Sand Deposits of the Mississippi River; Report 1: Field Investigations, Laboratory Studies, and Analysis of Hypothesized Failure Mechanism; Army Engineer Waterways Experiment Station Vicksburg MS Geotechnical Lab.: Vicksburg, MS, USA, 1988. [Google Scholar]
- Simpson, J.E. Gravity Currents: In the Environment and the Laboratory; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Kneller, B.C.; Bennett, S.J.; McCaffrey, W.D. Velocity structure, turbulence and fluid stresses in experimental gravity currents. J. Geophys. Res. Oceans 1999, 104, 5381–5391. [Google Scholar] [CrossRef]
- Gray, T.E.; Alexander, J.; Leeder, M.R. Quantifying velocity and turbulence structure in depositing sustained turbidity currents across breaks in slope. Sedimentology 2005, 52, 467–488. [Google Scholar] [CrossRef]
- Middleton, G.; Southard, J. Mechanics of sediment movement. Soc. Econ. Paleontol. Mineral. Short Course 1984, 3, 401. [Google Scholar]
- Pratson, L.F.; Imran, J.; Parker, G.; Syvitski, J.P.; Hutton, E. AAPG Memoir 72/SEPM Special Publication No. 68, Chapter 6: Debris Flows vs. Turbidity Currents: A Modeling Comparison of Their Dynamics and Deposits; American Association of Petroleum Geologists (AAPG): Tulsa, OK, USA, 2000; pp. 57–72. [Google Scholar]
- Sequeiros, O.E.; Naruse, H.; Endo, N.; Garcia, M.H.; Parker, G. Experimental study on self-accelerating turbidity currents. J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Yi, A.; Imran, J. The role of erosion rate formulation on the ignition and subsidence of turbidity current. In Proceedings of the 4th IAHR symposium on River, Coastal and Estuarine Morphodynamics, Urbana, IL, USA, 4–7 October 2006; pp. 543–551. [Google Scholar]
- Garcia, M.; Parker, G. Experiments on the entrainment of sediment into suspension by a dense bottom current. J. Geophys. Res. Oceans 1993, 98, 4793–4807. [Google Scholar] [CrossRef]
- Ottolenghi, L.; Adduce, C. LES Investigation on Entrainment in Gravity Currents, River Flow 2016: Iowa City, USA, July 11–14, 2016; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Mulder, T.; Syvitski, J.P.; Skene, K.I. Modeling of erosion and deposition by turbidity currents generated at river mouths. J. Sediment. Res. 1998, 68, 124–137. [Google Scholar] [CrossRef]
- Turner, J. Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 1986, 173, 431–471. [Google Scholar] [CrossRef]
- Parker, G.; Garcia, M.; Fukushima, Y.; Yu, W. Experiments on turbidity currents over an erodible bed. J. Hydraul. Res. 1987, 25, 123–147. [Google Scholar] [CrossRef]
- Cenedese, C.; Adduce, C. A new parameterization for entrainment in overflows. J. Phys. Oceanogr. 2010, 40, 1835–1850. [Google Scholar] [CrossRef]
- Stagnaro, M.; Pittaluga, M.B. Velocity and concentration profiles of saline and turbidity currents flowing in a straight channel under quasi-uniform conditions. Earth Surf. Dyn. 2014, 2, 167. [Google Scholar] [CrossRef]
- Cossu, R.; Wells, M.G. A comparison of the shear stress distribution in the bottom boundary layer of experimental density and turbidity currents. Eur. J. Mech.-B/Fluids 2012, 32, 70–79. [Google Scholar] [CrossRef]
- Dutta, S.; Pantano-Rubino, C.; Cantaero, M.I.; Garcia, M.H.; Parker, G. Effects of self-stratification on turbidity currents: A large eddy simulation approach. In Proceedings of the XIX International Conference on Water Resources, Urbana-Champaign, IL, USA, 17–22 June 2012. [Google Scholar]
- Breusers, H. Hydraulic excavation of sand. In Proceedings of the International Course in Modern Dredging, The Hague, The Netherlands, 5–10 June 1977. [Google Scholar]
- Van der Schrieck, G. Lecture Notes Dredging Technology; Delft University of Technology: Delft, The Netherlands, 2012. [Google Scholar]
- You, Y. Dynamics of Dilative Slope Failure. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2013. [Google Scholar]
- Eke, E.C. Breaching as a Mechanism for Generating Sustained Turbidity Currents. Master’s Thesis, University of Illinois at Urbana-Champaign, Urbana-Champaign, IL, USA, 2008. [Google Scholar]
- Van Rijn, L.C. Sediment pick-up functions. J. Hydraul. Eng. 1984, 110, 1494–1502. [Google Scholar] [CrossRef]
- Winterwerp, J.C.; Bakker, W.T.; Mastbergen, D.R.; van Rossum, H. Hyperconcentrated sand-water mixture flows over erodible bed. J. Hydraul. Eng. 1992, 118, 1508–1525. [Google Scholar] [CrossRef]
- Einstein, H.A. The Bed-Load Function for Sediment Transportation in Open Channel Flows; United States Department of Agriculture: Washington, DC, USA, 1950; Volume 1026.
- Van Rhee, C. Sediment entrainment at high flow velocity. J. Hydraul. Eng. 2010, 136, 572–582. [Google Scholar] [CrossRef]
- Bisschop, F. Erosion of Sand at High Flow Velocities: An Experimental Study. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2018. [Google Scholar]
- Van Rhee, C.; Talmon, A. Sedimentation and erosion of sediment at high solids concentration. In Proceedings of the 18th International Conference on Hydrotransport, Rio de Janeiro, Brazil, 22–24 September 2010; BHR Group: Cranfield, UK, 2010; pp. 211–222. [Google Scholar]
- Bisschop, F.; Visser, P.; van Rhee, C.; Verhagen, H.J. Erosion due to high flow velocities: A description of relevant processes. Coast. Eng. Proc. 2010, 1, 24. [Google Scholar] [CrossRef]
- Garcia, M.; Parker, G. Entrainment of bed sediment into suspension. J. Hydraul. Eng. 1991, 117, 414–435. [Google Scholar] [CrossRef]
- Akiyama, J.; Fukushima, Y. Entrainment of Noncohesive Bed Sediment into Suspension, External Memorandom No. 195, St.; Anthony Falls Hydraulic Laboratory, U. of Minnessota: Minneapolis, MN, USA, 1985. [Google Scholar]
- Smith, J.D.; McLean, S. Spatially averaged flow over a wavy surface. J. Geophys. Res. 1977, 82, 1735–1746. [Google Scholar] [CrossRef]
- Zordan, J.; Juez, C.; Schleiss, A.J.; Franca, M.J. Entrainment, transport and deposition of sediment by saline gravity currents. Adv. Water Resour. 2018, 115, 17–32. [Google Scholar] [CrossRef]
- Fukushima, Y.; Parker, G.; Pantin, H. Prediction of ignitive turbidity currents in Scripps Submarine Canyon. Mar. Geol. 1985, 67, 55–81. [Google Scholar] [CrossRef]
- Miedema, S.A. OE4607 Introduction Dredging Engineering, 2nd ed.; MSc Offshore and Dredging Engineering Delft University of Technology: Delft, The Netherlands, 2016. [Google Scholar]
- Richardson, J.; Zaki, W. Fluidization and sedimentation—Part I. Trans. Inst. Chem. Eng. 1954, 32, 38–58. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).