Effect of Top Tension on Vortex-Induced Vibration of Deep-Sea Risers

Abstract

With the increase of water depth, the design and use of the top-tensioned risers (TTR) are facing more and more challenges. This research presents the effect of top tension on dynamic behavior of deep-sea risers by means of numerical simulations and experiments. First, the governing equation of vortex-induced vibration (VIV) of TTR based on Euler-Bernoulli theory and Van der Pol wake-oscillator model was established, and the effect of top tension on natural vibration of TTR was discussed. Then, the dynamic response of TTR in shear current was calculated numerically by finite difference method. The displacement, bending stress and vibration frequency of TTR with the variation of top tension were investigated. Finally, a VIV experiment of a 5 m long flexible top-tensioned model was carried out at the towing tank of Tianjin University. The results show that the vibration displacement of TTR increases and the bending stress decreases as the top tension increases. The dominant frequency of VIV of TTR is controlled by the current velocity and is barely influenced by the top tension. With the increase of top tension, the natural frequency of TTR increases, the lower order modes are excited in the same current.

1. Introduction

In recent years, owing to the large demand of crude oil, offshore oil and gas explorations have been shifted to deeper water regions. Risers are one of the basic elements of offshore installations that are usually used for drilling and production. The riser is installed between wellhead at the sea bed and floating platform. Actually, the riser has suffered the strong influences of environmental conditions in unshielded deep-water region, hence it has complicated dynamic behavior under the influence of platform’s motions, wind, waves and sea current, as shown in Figure 1. One of the most famous phenomena is vortex-induced vibration (VIV). When the riser moves under the action of sea current, vortices are shed along its surface, resulting in the formation of an unstable wake region behind it. Vortex shedding normally takes place with different frequencies and amplitudes, thus induces a periodically varying transverse force on the riser (i.e., perpendicular to the direction of the current), resulting in a periodically transverse vibration known as the VIV [1,2,3,4].

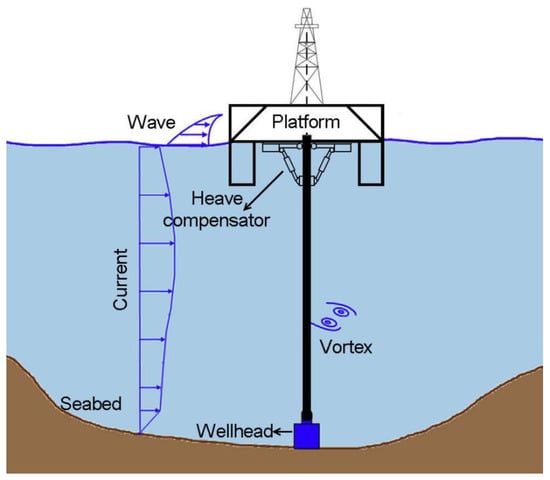
Figure 1. Schematic of a top-tensioned riser in ocean environment.

Drilling and production risers are mostly affected by VIV, which leads to increases in their hydrodynamic loading and reduction in their service life due to fatigue. In the past, to ensure the safety and to enhance the productivity of riser systems, many investigations on VIV of marine risers have been reported. Srinil [5] studied dynamic behavior of a variable tension vertical riser placed in a linearly sheared current by using numerical methods and experiments. He concluded that the current velocity and the variable tension had great influence on VIV response of a deep-sea riser. The prediction of VIV of a deep-sea riser was a challenging task since the incident current was practically non-uniform and the associated fluid-structure interaction (FSI) phenomena was highly complex. Wang and Xiao [6] presented an investigation on the VIV of the riser in uniform and linearly sheared current by means of a fully 3D FSI simulation. They pointed out that the dominating modes of the riser in uniform and linearly sheared current with the same surface velocity had no great difference. However, the lock-in frequency range of the riser was wider in the sheared current, and the maximum stress was smaller than in the uniform current. The contribution from in-line vibration has been noticed by many researchers [7,8,9,10,11]. The coupled model of In-Line (IL) and Cross-Flow (CF) VIV was established, and the results showed that IL VIV would affect the mode of the vortex and the amplitude of the CF VIV. As the water depth increases, the IL-VIV was more easily excited than CF VIV, and IL VIV had a significant contribution to fatigue on the deep-sea riser for the low-order modes. Duan et al. [12] presented a numerical study on VIV of a riser with internal flow. Guo and Lou [13] performed an experiment in water with a pipe made of rubber to investigate the effect of internal flow on VIV. The results indicated that the internal flow would reduce the natural frequency of the riser system, and the response amplitude increases while the vibration frequency decreases. Chen et al. [14] studied the dynamic response of the riser suffering both the floating top-end and VIV. An integrated system with both platform and riser was established by means of finite element numerical simulations. The result showed that the displacement of the riser was multiple times larger than that of the case without moving top-end. Wang et al. and Yin et al. [15,16] performed experiments in towing tank for the riser which was excited at the top by platform surge motion, and the results showed that the platform surge had a great influence on VIV of the riser.

The top-tensioned risers (TTR) are widely deployed by FPSOs, Semi-submersible platforms, Spar or Tensioned-leg platforms for drilling and production. The bottom end of TTR is connected with the wellhead by ball joint, and the top end is connected with the platform by heave compensator (or tensioner, see Figure 1). The compensator provides a large static tensile tension at the top end of TTR (known as “top tension” for short in this paper), which can keep TTR vertical and avoid buckling due to its large length. TTR is very sensitive to heave movements due to waves and to VIV caused by sea current, since the rotation at the top and bottom connections is limited. The heave movement also requires top tension equipment to compensate for the lack of tension. Therefore, the compensator has the buffering function as a spring on the riser to reduce the heave motion effect [17,18]. The top tension is generally 1.1~1.6 times of the submerged weight of TTR. Insufficient top tension might cause buckling failure of the riser, while excessive top tension might result in stress concentration at the top or bring about failure of the lower flexible joint. Yang et al. [19] pointed out that the stress and displacement of TTR was controlled by the tensioners which provided constant axial tension to the riser. Moghiseh et al. [20] concluded that increasing the pretension in the middle of the riser could effectively reduce the displacement of the riser. Fujiwara et al. [21] performed a large-scale experiment in deep-sea basin with a Teflon tube of 28.5 m long that was tensioned at the top end, and they found out that the displacement of VIV of TTR was increased as the top tension increased.

Unlike the shallow sea risers, the deep-sea riser has a large slenderness ratio (around 10⁴). In order to study how VIV response of TTR changes with the change of top tension, this research presents the effect of top tension on VIV of deep-sea risers by means of numerical simulations and experiments.

2. Governing Equations

In this research, TTR is modeled as simply-supported beam, as shown in Figure 2. The sea current is in y direction and simplified as shear current. The influence of IL VIV is neglected, since the IL VIV is an order of magnitude smaller than the CF VIV [22].

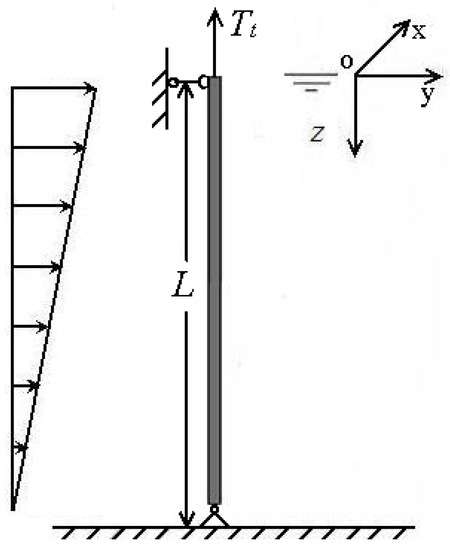
Figure 2. Simply supported TTR.

The Euler-Bernoulli theory is applicable for description of TTR dynamic bending. The motion equation governing the transverse displacement $x(z,t)$ of TTR from its straight vertical equilibrium as a function of depth $z$ and time $t$ can be written as:

$$EI\frac{{\partial }^{4}x(z,t)}{\partial z^4}-\frac{\partial }{\partial z}\left[(T_t-wz)\frac{\partial x(z,t)}{\partial z}\right]+\overline{m}\frac{{\partial }^{2}x(z,t)}{\partial t^2}=f_x(z,t)$$

(1)

where $EI$ is the bending stiffness. $\overline{m}$ is the mass per unit length of the system (riser with internal fluid and added mass). $w$ is the submerged weight of TTR per unit length. $T_t$ is the top tension of TTR.

$$T_t=f_{top}\cdot w\cdot L$$

(2)

where $f_{top}$ is a dimensionless pretension factor which generally varies between 1.1 and 1.6. $L$ is the length of TTR.

$f_x(z,t)$ is the hydrodynamic force per unit length of the riser. Generally, $f_x(z,t)$ is calculated by Morison’s Equation:

$$f_x(z,t)=\frac{1}{2}{\rho }_{w}D{C}_L{U}^2-\frac{1}{2}{\rho }_{w}D{C}_d\left|\dot{x}\right|\dot{x}$$

(3)

where ${\rho }_w$ is the density of seawater, $D$ is the outer diameter of the riser, $C_L$ is the lift force coefficient. $U$ is the current velocity in any depth, $U=(1-\frac{z}{L})U_0$, $U_0$ is the current velocity at sea level. $C_d$ is the drag coefficient.

A forced Van der Pol oscillator equation is used to describe the dynamics of the riser’s wake [23]:

$$\ddot{q}+\epsilon {\mathsf{\Omega }}_f(q^2-1)\dot{q}+{\mathsf{\Omega }}_f^{2}q=F$$

(4)

where the variable $q$ is defined as the local fluctuating lift coefficient, $q=2C_L/C_{L0}$, the reference lift coefficient $C_{L0}$ is that observed on a fixed structure subjected to vortex shedding. ${\mathsf{\Omega }}_f$ is the vortex-shedding frequency, which is related to the non-dimensional Strouhal number $S_t$, ${\mathsf{\Omega }}_f=2\pi S_{t}U/D$. It is common practice to assume $S_t=0.2$ in the sub-critical range, $300\prec R_e\prec 1.5\times {10}^5$. The reference lift coefficient $C_{L0}$ being usually taken as $C_{L0}=0.3$ in the large range of $R_e$. The right-hand side forcing term $F$ models the effect of the cylinder motion on the near wake, $F=A\ddot{x}/D$. $\epsilon$ and $A$ are given parameters, and the values are estimated through experimental data on free and forced vortex shedding behind cylinders, $\epsilon =0.3$, $A=12$ [23].

The boundary conditions at the ends of the riser are given as

$$x(z,t)=0,\frac{{\partial }^{2}x(z,t)}{\partial z^2}=0(z=0,z=L)$$

(5)

The bending stress is dependent on the second derivative of displacement of TTR:

$${\sigma }_{\mathrm{b}}(\mathrm{z})=\frac{ED{x}^{″}(z,t)}{2}$$

(6)

3. Effect of Top Tension on Natural Vibration of TTR

3.1. Natural Frequencies and Mode Shapes

The natural vibration characteristics of TTR mainly include natural frequencies and mode shapes, which are the basis of complex vibration analysis. The natural frequency directly affects the excitation of vortex-induced resonance for deep-sea risers, and the mode shape can be used to analyze the vibration response.

For the deep-sea riser, an accepted conclusion is that the low order natural frequencies and mode shapes can be expressed by simplified formulas which depend on the tension in the riser [24,25].

$${\omega }_n=\frac{n\pi }{2L\sqrt{\overline{m}}}(\sqrt{T_t}+\sqrt{T_b})$$

(7)

$${\phi }_n(z)={\left(\frac{T_b}{T_t-wz}\right)}^{1/4}\sin \left(\frac{n\pi \left(\sqrt{T_t-wz}-\sqrt{T_b}\right)}{\sqrt{T_t}-\sqrt{T_b}}\right)$$

(8)

where ${\omega }_n$ is the $n$th natural frequency of TTR. ${\phi }_n(z)$ is the $n$th mode function. $T_b$ is the tension at the bottom end of TTR, $T_b=(f_{top}-1)wL$.

It shows that the deep-sea riser is like a cable owing to the large slenderness ratio, the lower order modes are mainly affected by tension and unrelated to the bending stiffness. The natural frequency of TTR will increase with the increase of top tension, it is equivalent to increasing the stiffness of TTR. The $n$th natural frequency is about $n$ times of the first frequency (i.e., ${\omega }_n=n{\omega }_1$), this is typical phenomenon of deep-sea risers. Meanwhile, the axial tension in riser gradually decreases with the increase of water depth due to the self-weight; the mode shape is no longer a standard sine function.

The mode curvature is obtained by finding the second derivative of the variable z in Equation (8):

$${\varphi }_n(z)={\phi }_n^{\text{'}\text{'}}(z)$$

(9)

3.2. System Parameters and Basic Calculations

The adopted values of the system parameters are shown in Table 1. It should be pointed out that the data in Table 1 are from the Truss Spar (named Horn Mountain) servicing in the Gulf of Mexico [26].

Table 1. Base set of system parameters.

No.	Property	Symbol	Value	Unit
1	Riser length	$L$	1500	m
2	Outer diameter	$D$	0.3048	m
3	Wall thickness	$t$	0.0136	m
4	Young’s modulus	$E$	2.1E11	Pa
5	Density of steel	${\rho }_s$	7850	kg/m3
6	Density of seawater	${\rho }_w$	1025	kg/m3
7	Density of internal fluid	${\rho }_f$	800	kg/m3
8	Added mass coefficient	$C_a$	1.0	-
9	Drag coefficient	$C_d$	1.0	-

The natural frequencies of TTR are shown in Table 2. It shows that the low order natural frequencies of TTR are small. The current velocity at sea level generally varies between 0.1 m/s and 1 m/s without considering influence of waves in South China Sea [27], and the range of vortex-shedding frequencies will be concentrated in the low order mode frequencies of TTR.

Table 2. Natural frequencies of TTR (rad/s).

	${\mathit{\omega }}_1$	${\mathit{\omega }}_2$	${\mathit{\omega }}_3$	${\mathit{\omega }}_4$	${\mathit{\omega }}_5$
$f_{top}=1.1$	0.1075	0.2149	0.3224	0.4298	0.5373
$f_{top}=1.3$	0.1329	0.2658	0.3986	0.5315	0.6644
$f_{top}=1.5$	0.1521	0.3042	0.4563	0.6083	0.7604

The 4th mode shape and mode curvature of TTR are shown in Figure 3 and Figure 4. Under the same condition, with the increase of top tension, the nodes and anti-nodes of the mode shape move up, and the mode shape more conforms to the standard sine function. The amplitude of mode shape decreases as the top tension decreases. However, the smaller the top tension, the larger amplitude of mode curvature at the bottom of TTR.

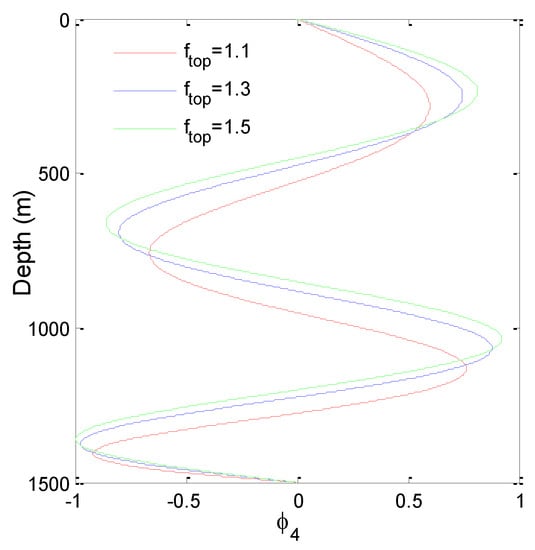
Figure 3. The 4th mode shape of TTR.

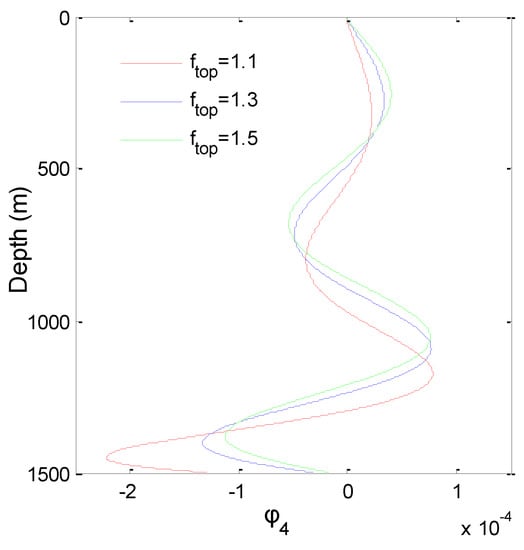
Figure 4. The 4th mode shape curvature of TTR.

4. Effect of Top Tension on VIV of TTR

The VIV response of TTR can be calculated numerically by finite difference method (FDM) according to Equations (1)–(6). The time history of VIV of TTR at each depth are obtained. Figure 5 shows the displacement and bending stress of TTR at midpoint (z = 750 m). It can be seen that the change trend of displacement is not obvious under different top tensions, while the bending stress decreases significantly with the increase of top tension.

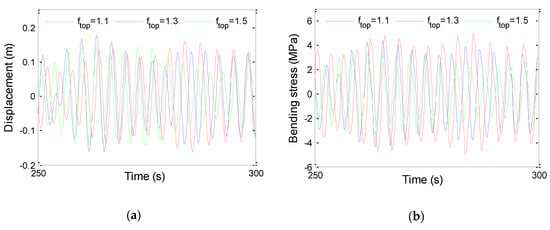
Figure 5. Dynamic response of TTR (U₀ = 0.5 m/s, z = 750 m). (a) Time history of displacement. (b) Time history of bending stress.

The frequency spectrum of TTR is shown in Figure 6. The dominant frequency of TTR decreases slightly with the increase of top tension. It indicates that the dominant frequency is mainly controlled by vortex-shedding frequency, which is related to the current velocity and the riser’s outer diameter.

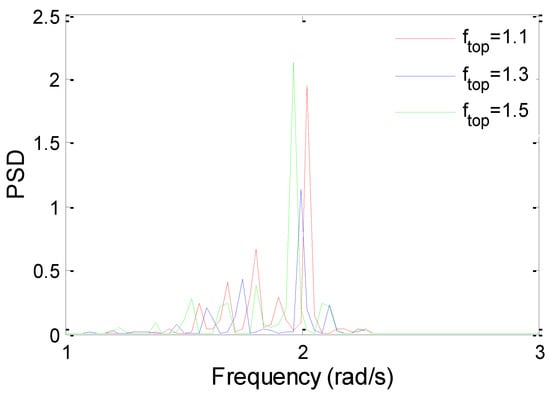
Figure 6. Frequency spectrum of TTR (U₀ = 0.5 m/s).

According to the time history of displacement and bending stress of each depth, the maximum displacement and the maximum bending stress of TTR are obtained, as shown in Figure 7 and Figure 8.

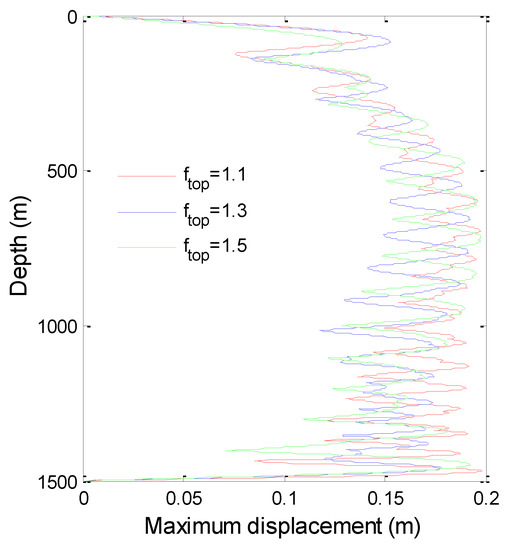
Figure 7. The maximum displacement of TTR(U₀ = 0.5 m/s).

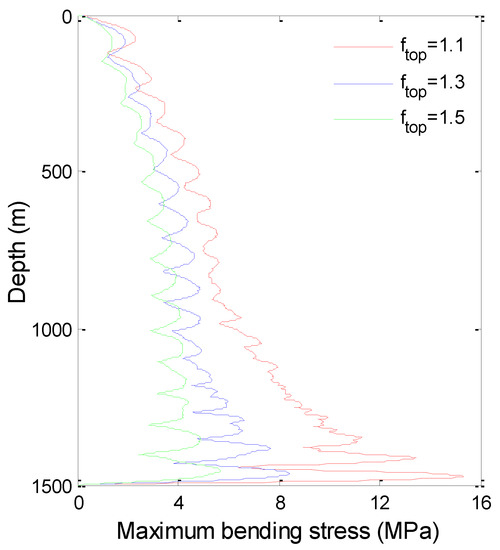
Figure 8. The maximum bending stress of TTR (U₀ = 0.5 m/s).

It shows that, with the increase of top tension, the maximum displacement increases slightly and the bending stress decreases significantly. This phenomenon is especially apparent at the bottom of TTR, since the axial tension in a riser decreases with the increase of water depth, the effective tension at the bottom of TTR is small, and the top pretension has a greater influence on the effective tension at the bottom of TTR.

This is a typical phenomenon of deep-sea risers, which is different from the conventional beam or shallow sea riser. The reason for this phenomenon is that: increasing the top tension is equivalent to increasing the stiffness of TTR, leading to the increase of the riser’s natural frequency. However, the vortex-shedding frequency does not change under the same conditions, resulting in the lower modes of TTR becoming excited (or it can be equivalent to the stiffness staying the same but the current velocity decreasing). When the low-order modes of TTR are excited, the displacement is generally large but the stress is small.

5. VIV Experiment

5.1. Test Introduction

This experiment was carried out at the towing tank of Tianjin University (137 × 7 × 3 m). The TTR model was placed horizontally due to the limitation of the depth of tank, and the riser was hung at the bottom and moved at a constant speed in the towing tank. The top tension is presented by hanging weights at the top end of TTR, as shown in Figure 9. The stress of TTR at the midpoint was monitored by use of strain gauges.

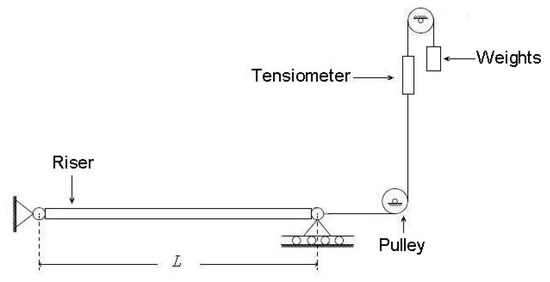
Figure 9. VIV test of TTR.

The TTR model was made of Teflon. The parameters of the model are shown in Table 3. The test conditions are shown in Table 4.

Table 3. Specifications of riser model.

No.	Property	Value	Unit
1	Length	5	m
2	Outer diameter	0.016	m
3	Wall thickness	0.001	m
4	Young’s modulus	7.38 × 108	Pa
5	Material	Teflon	-
6	Density of Teflon	2178	kg/m3
7	Density of seawater	1000	kg/m3
8	Density of internal fluid	1000	kg/m3

Table 4. Test conditions.

No.	Current Velocity (U)	$\mathbf{Pretension}\left({\mathit{T}}_{\mathit{t}}\right)$
1	0.3 m/s	80 N
2	0.3 m/s	100 N
3	0.3 m/s	120 N
4	0.5 m/s	80 N
5	0.5 m/s	100 N
6	0.5 m/s	120 N

The first five natural frequencies of the riser model under different pretension are shown in Table 5.

Table 5. Natural frequencies of TTR test model (Hz).

	${\mathit{\omega }}_1$	${\mathit{\omega }}_2$	${\mathit{\omega }}_3$	${\mathit{\omega }}_4$	${\mathit{\omega }}_5$
T = 80 N	1.3273	2.6738	4.0579	5.4976	7.0093
T = 100 N	1.4858	2.9887	4.5253	6.1119	7.7637
T = 120 N	1.6198	3.2552	4.9217	6.6342	8.4069

5.2. Verification for Numerical Simulation

The bending stress, frequency and displacement of VIV of TTR are obtained by means of numerical simulations and tests. The comparisons are shown in Figure 10, Figure 11 and Figure 12. It should be pointed out that the displacement data of TTR were from Fujiwara et al. [21], since the displacement was not measured in this experiment.

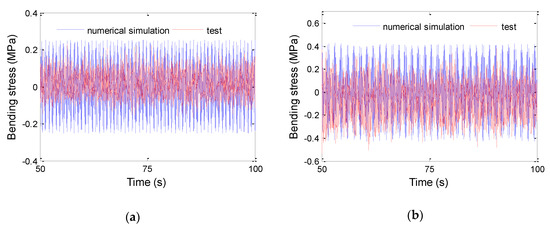
Figure 10. Bending stress time history of riser at midpoint. (a) U = 0.3 m/s, $T_t$ = 100 N. (b) U = 0.5 m/s, $T_t$ = 100 N.

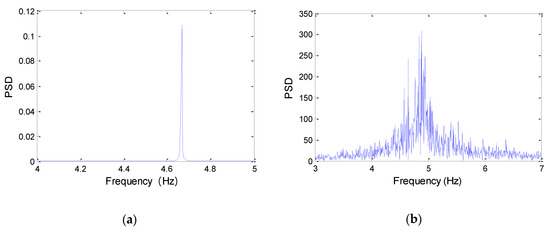
Figure 11. Frequency spectrum of TTR (U = 0.5 m/s). (a) numerical simulation. (b) experiment.

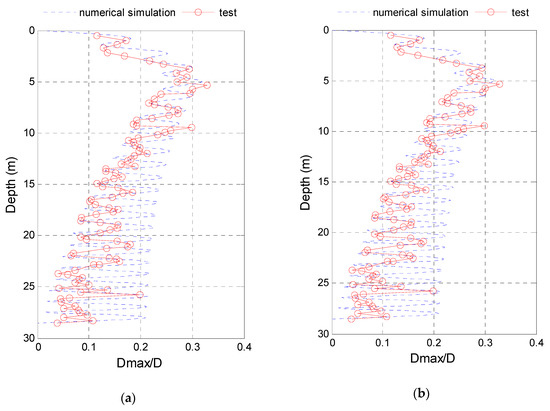
Figure 12. The maximum displacement of TTR (test data were from [21]). (a) Self-weight balanced in water. (b) Add-tens./Self-weight = 0.58.

After a lot of comparisons between the numerical simulations and experiments, it is proved that the prediction model of VIV of TTR in this paper is reasonable, and the calculating program is reliable.

5.3. Effect of Top Tension on VIV of TTR

The bending stress time history of TTR at midpoint and the frequency spectrum are shown in Figure 13 and Figure 14. It can be found that the larger the top tension, the smaller the bending stress. However, increasing the top tension has little influence on the dominant frequency of VIV of TTR. This indicates that the VIV frequency of TTR is controlled by the current velocity, but it is also related to the natural frequency of TTR. In general, the low order modes of TTR are more easily excited than the high order modes.

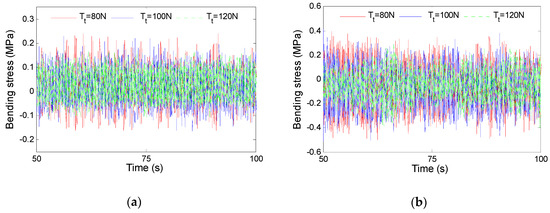
Figure 13. Bending stress time history of TTR at midpoint. (a) U = 0.3 m/s. (b) U = 0.5 m/s.

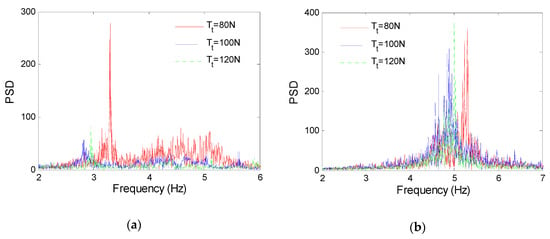
Figure 14. Frequency spectrum of TTR. (a) U = 0.3 m/s. (b) U = 0.5 m/s.

The maximum displacement of VIV of TTR is shown in Figure 15. The higher the top tension, the larger the displacement of TTR. It indicates that the natural frequency of TTR increases with the increase of the top tension, and the lower order modes of TTR are excited at the same current velocity. Therefore, the displacement is larger but the stress is smaller when the top tension is increasing.

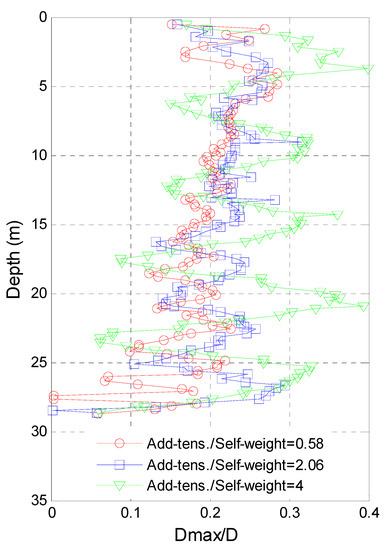
Figure 15. The maximum displacement of TTR (test data were from [21]).

6. Conclusions

Unlike the shallow sea risers, there will be some new dynamic phenomena of deep-sea risers under the complex ocean environment. In order to study the effect of top tension on VIV of TTR, the governing equation of VIV of TTR is established, and the dynamic response of TTR is calculated numerically by FDM based on Van der Pol wake-oscillator model. In addition, a validation experiment in the towing tank of Tianjin University is presented. The following conclusions can be drawn:

The natural frequency of TTR increases as the top tension increases, and it is equivalent to increasing the stiffness of TTR.

With the increase of top tension, the lower order modes are excited in the same current, and the vibration displacement of TTR increases and the bending stress decreases.

The dominant frequency of VIV of TTR is controlled by the current velocity and is barely influenced by the top tension.