Influence of Bending Stiffness on Snap Loads in Marine Cables: A Study Using a High-Order Discontinuous Galerkin Method
Abstract
1. Introduction
Scope of the Paper
2. Numerical Method
2.1. Preliminaries
2.2. Governing Equations
2.3. External Forces
2.4. Shear Force Modelling
2.5. Tension-Strain Relations
3. Finite Element Method
3.1. Boundary Conditions
3.2. Time Integration
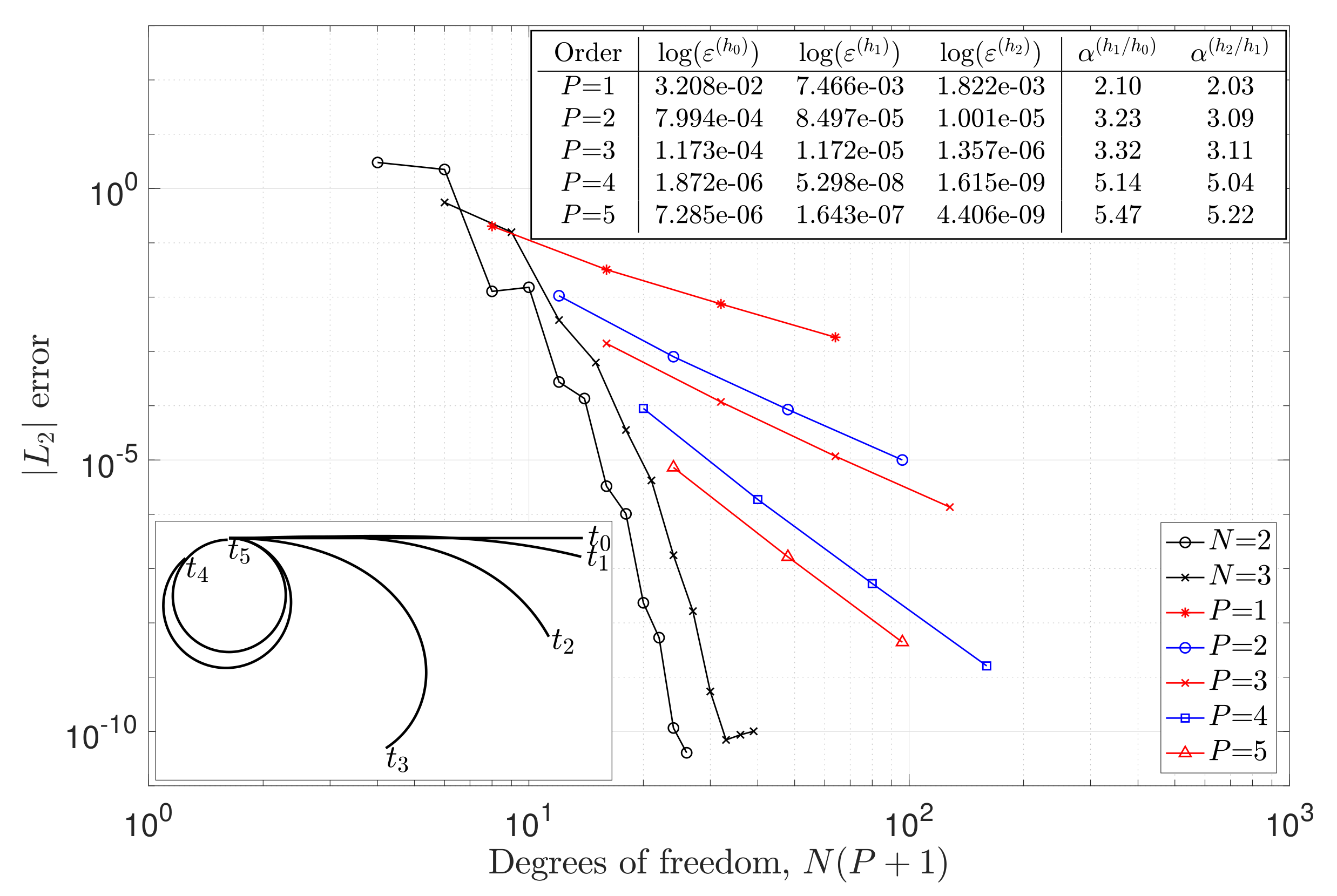
4. Verification
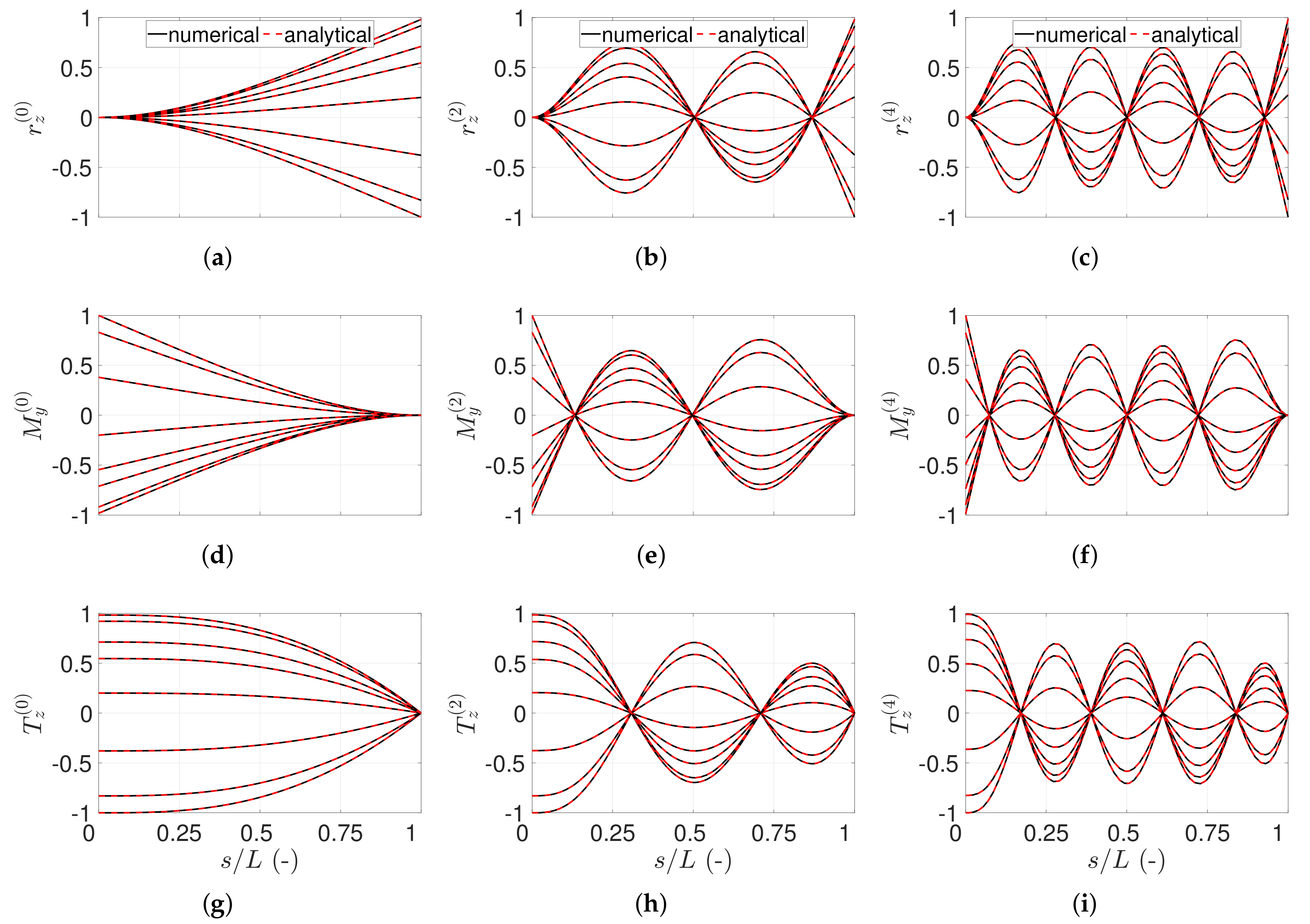
4.1. Ring-Shaped Beam
4.2. Vibrating Cantilever
5. A Swinging Cable
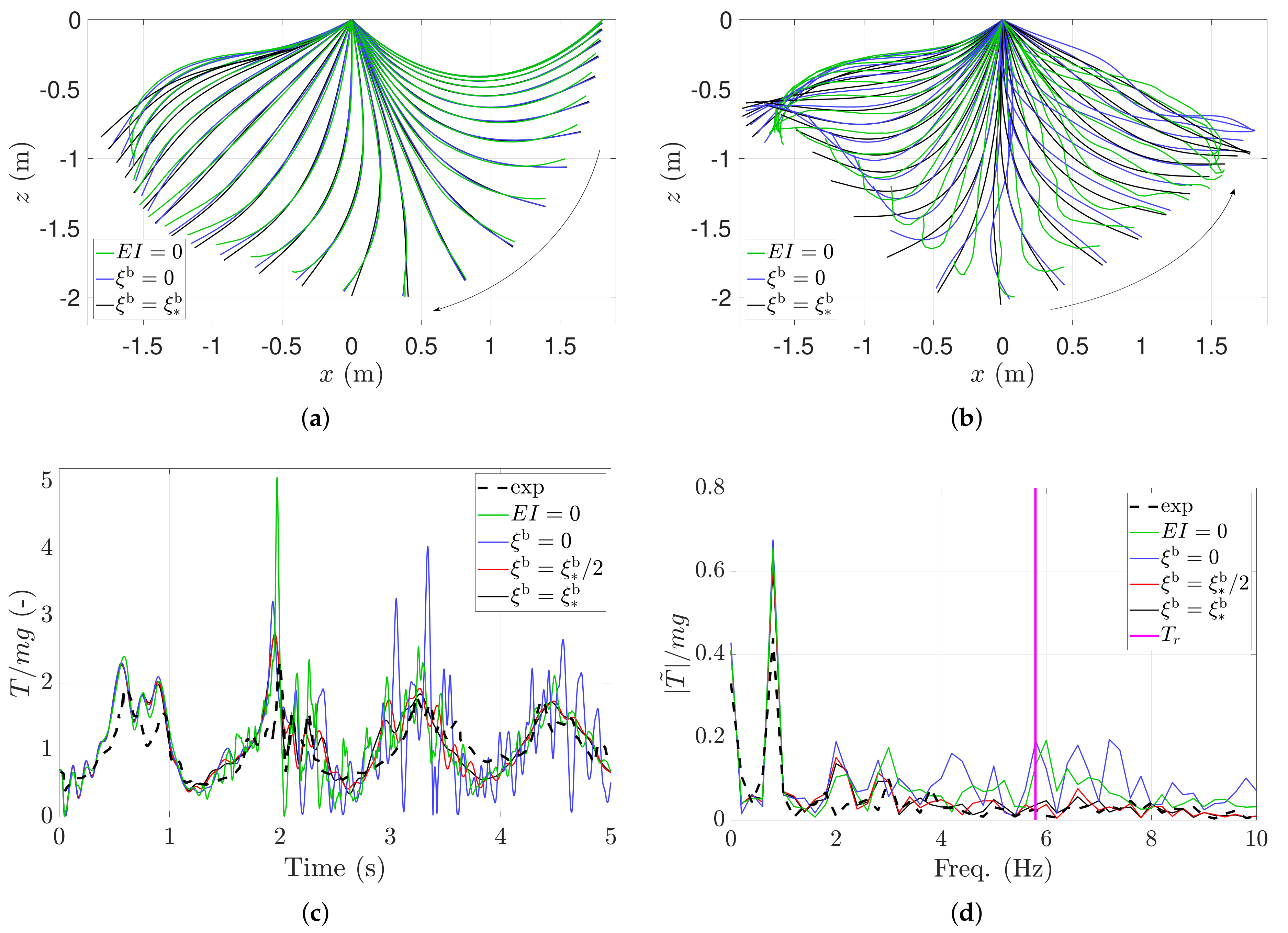
- The bending stiffness is important for the cable response. During the first swing in Figure 3a, mostly the end of the cable is affected, but on the return swing in Figure 3b, the cable deviates significantly from the simulations with bending stiffness. In particular, we highlight the “whipping” behaviour of the case, which results in a significant overestimation of the tension force at s compared to the experiments; see Figure 3c. The whipping is effectively avoided by the addition of bending stiffness for all configurations studied.
- Experimental results are reproduced well in the simulations. The peak frequencies match well in all cases studied (see Figure 3d), and the two simulations with bending damping provide a very good approximation to the experimental force reading in Figure 3c. The primary experimental loss factor is probably the frictional losses at the pivot pin, which were not taken into account in the numerical model. This can to some extent account for the overestimation of the primary snap load at s.
- The simulations with bending stiffness require a damping mechanism to reduce the transient bending modes. This is particularly important for the high-frequency response. In Figure 3d, both and simulations show significant forces around the return period of longitudinal waves in the cable , which are not present in the experimental readings. Please note that the high-frequency oscillation of, e.g., in Figure 3c is not numerical noise. It is the long-lived elastic response of the bending modes due to insufficient damping properties. The results are much improved by the addition of , and less sensitive to its value. Cable experiments in air are known to be sensitive to the damping properties of the setup and behave very differently from experiments in water [45]. We therefore expect the importance of parameter to be small to negligible in marine application of cables.
6. Snap Loading in a Deep Water ROV System
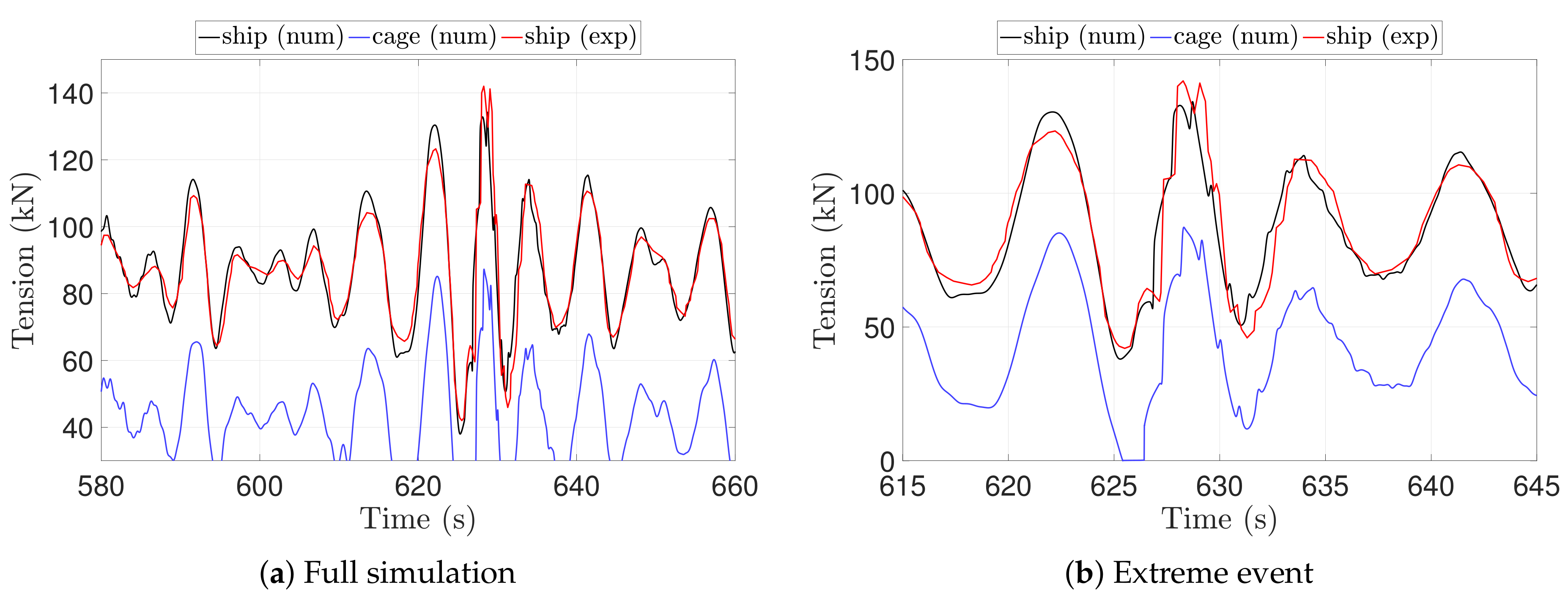
6.1. Calibration and Validation
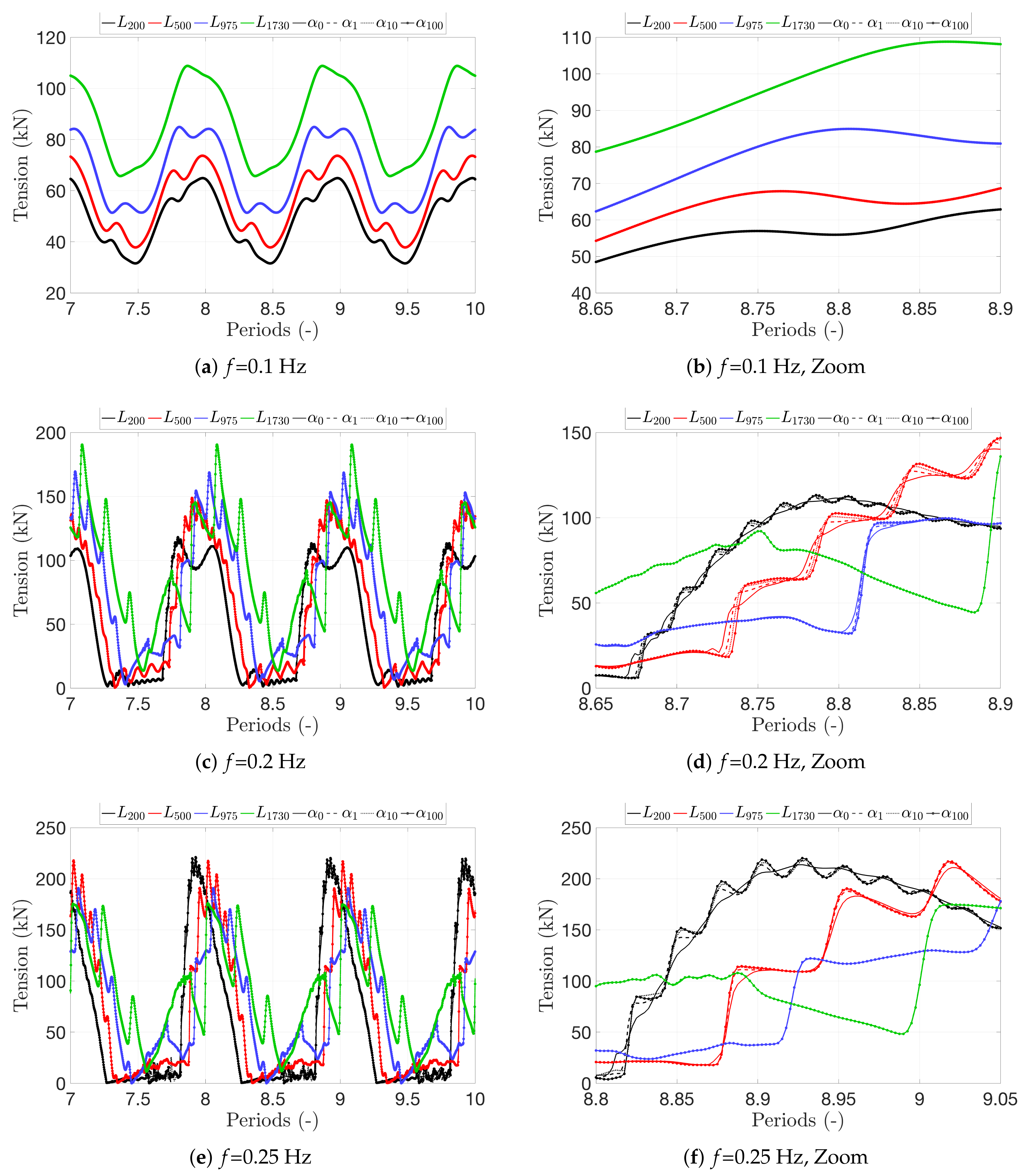
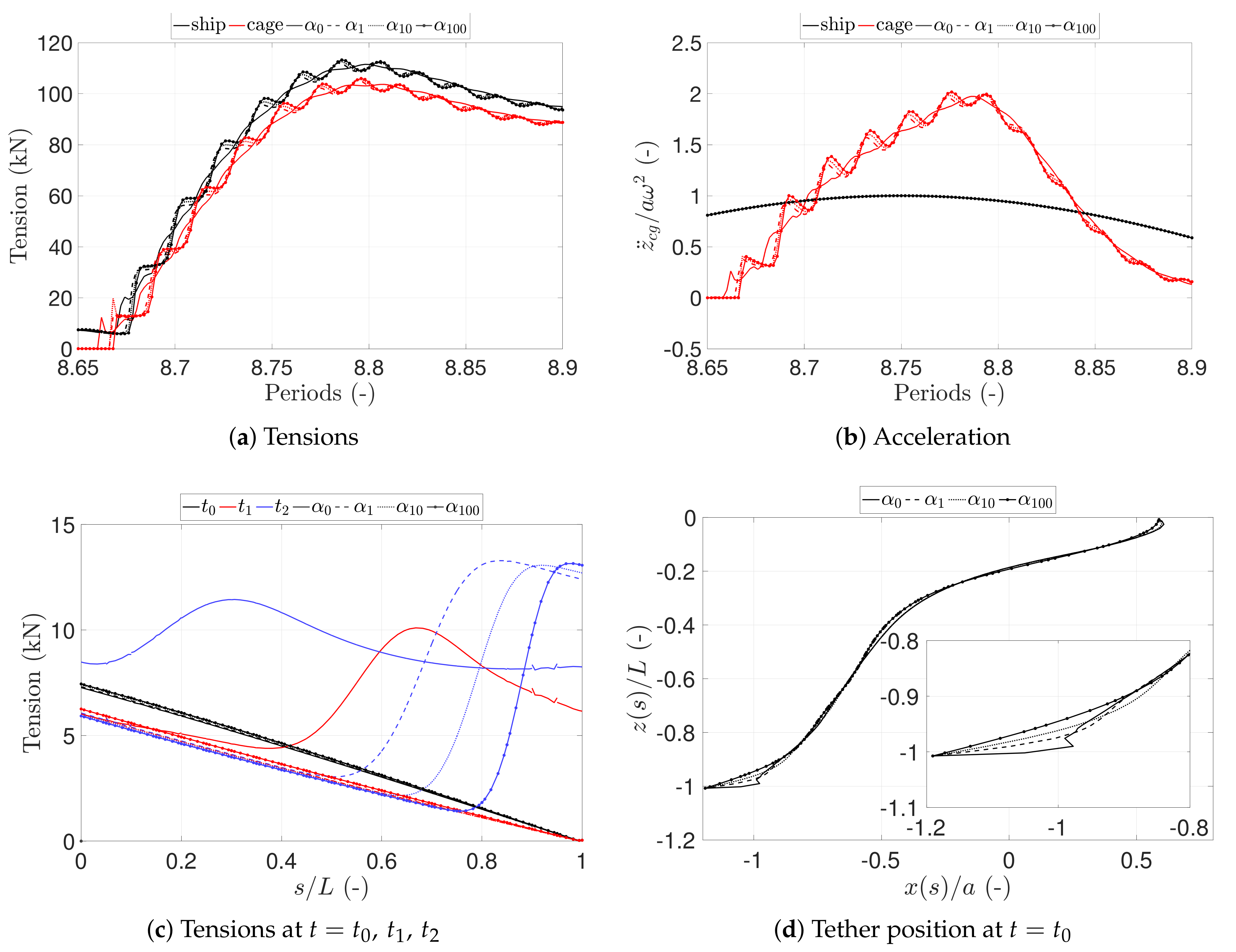
6.2. Bending Influence
- We confirm the predictions of the analytical model in [16] that slack-snap occurs at and Hz with this amplitude, while the Hz case remains in tension.
- There is no noticeable difference in system response due to bending stiffness for the largest operational depths and . For and , a small but increasing difference can be seen in the snap load generation.
- The small effect of bending stiffness can be observed in Figure 5d,f. The lower the bending stiffness value becomes, the earlier the generated snap load appears at the ship after each period of slack. The difference between the simulations increases with decreasing cable length.
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DG | Discontinuous Galerkin |
| LDG | Local Discontinuous Galerkin |
| RK | Runge–Kutta |
| RKDG | Runge–Kutta Discontinuous Galerkin |
| ROV | Remotely Operated Vehicle |
| ROPOS | Remotely Operated Platform for Oceanographic Science |
Appendix A. Deep Water ROV Simulation: Mesh Resolution
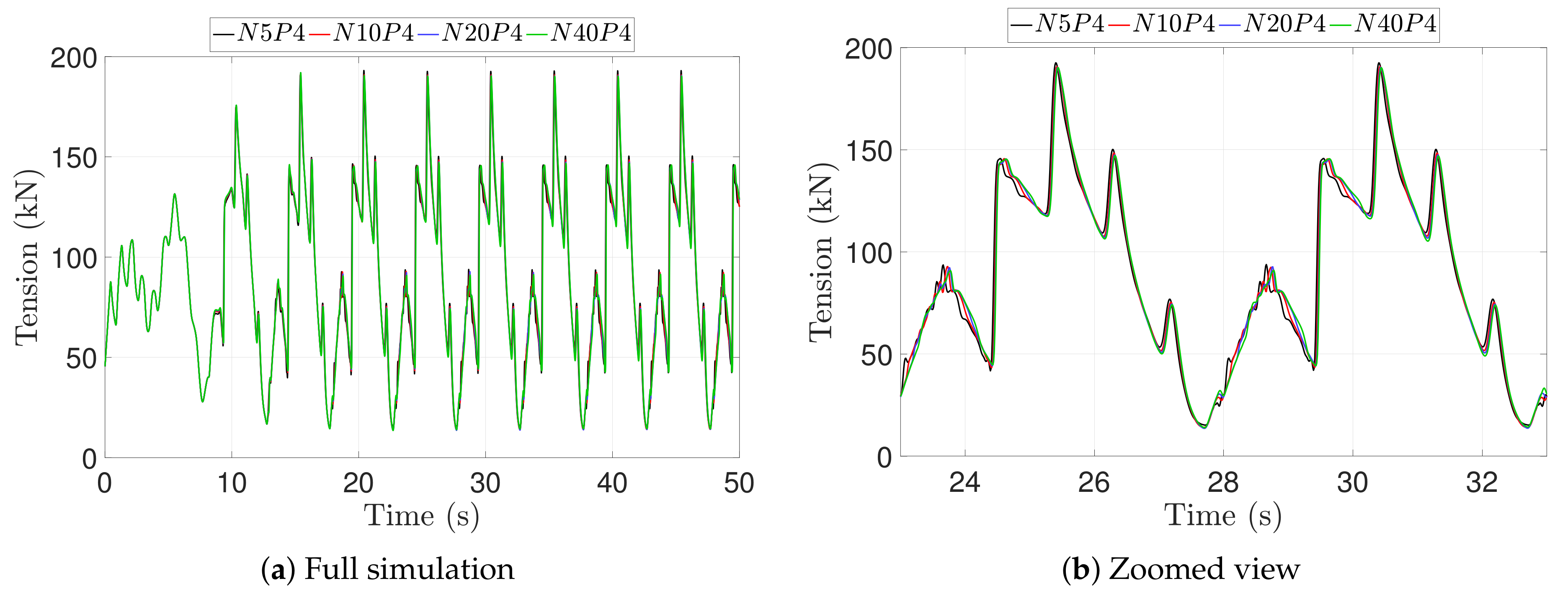
References
- The Hazards of Snap-Back: Initial Learnings from a Serious Incident of Mooring Line Failure; Technical Report; Oil Companies International Marine Forum: London, UK, 2015.
- Tjavaras, A. The Dynamics of Highly Extensible Cables. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1996. [Google Scholar]
- DNV, G.L. Position Mooring; Offshore standard DNVGL-OS-301; DNV GL AS: Oslo, Norway, 2015. [Google Scholar]
- Fitzgerald, J.; Bergdahl, L. Including moorings in the assessment of a generic offshore wave energy converter: A frequency domain approach. Mar. Struct. 2008, 21, 23–46. [Google Scholar] [CrossRef]
- Savin, A.; Svensson, O.; Leijon, M. Azimuth-inclination angles and snatch load on a tight mooring system. Ocean Eng. 2012, 40, 40–49. [Google Scholar] [CrossRef]
- Hann, M.; Greaves, D.; Raby, A. Snatch loading of a single taut moored floating wave energy converter due to focussed wave groups. Ocean Eng. 2015, 96, 258–271. [Google Scholar] [CrossRef]
- Hsu, W.; Thiagarajan, K.P.; Manuel, L. Extreme mooring tensions due to snap loads on a floating offshore wind turbine system. Mar. Struct. 2017, 55, 182–199. [Google Scholar] [CrossRef]
- Harnois, V. Analysis of Highly Dynamic Mooring Systems: Peak Mooring Loads in Realistic Sea Conditions. Ph.D. Thesis, University of Exeter, UK, 2014. [Google Scholar]
- Moura Paredes, G.; Eskilsson, C.; Engsig-Karup, A.P. Uncertainty quantification in mooring cable dynamics using polynomial chaos expansions. J. Mar. Sci. Eng. 2020, 8, 162. [Google Scholar] [CrossRef]
- Barrera, C.; Guanche, R.; Rodriguez, A.; Armesto, J.A.; Losada, I.J. On the importance of mooring system parametrisation for accurate floating structure designs. Mar. Struct. 2020, 72, 102765. [Google Scholar] [CrossRef]
- Goeller, J.; Laura, P. Analytical and experimental study of the dynamic response of segmented cable systems. J. Sound Vib. 1971, 18, 311–324. [Google Scholar] [CrossRef]
- Hennessey, C.; Pearson, N.; Plaut, R. Experimental snap loading of synthetic ropes. Shock Vib. 2005, 12, 163–175. [Google Scholar] [CrossRef]
- Driscoll, F.R.; Lueck, R.G.; Nahon, M. The motion of a deep-sea remotely operated vehicle system. Part 1: Motion observations. Ocean Eng. 2000, 27, 29–56. [Google Scholar] [CrossRef]
- Bergdahl, L.; Palm, J.; Eskilsson, C.; Lindahl, J. Dynamically Scaled Model Experiment of a Mooring Cable. J. Mar. Sci. Eng. 2016, 4, 5. [Google Scholar] [CrossRef]
- Triantafyllou, M.; Bliek, A.; Shin, H. Dynamic analysis as a tool for open-sea mooring system design. SNAME Trans. 1985, 93, 302–324. [Google Scholar]
- Driscoll, F.R.; Lueck, R.G.; Nahon, M. The motion of a deep-sea remotely operated vehicle system. Part 2: Analytical model. Ocean Eng. 2000, 27, 57–76. [Google Scholar] [CrossRef]
- Shin, H. Analysis of extreme tensions in a snapping cable. In Proceedings of the 1st International Offshore and Polar Engineering Conference, Edinburgh, UK, 11–16 August 1991. [Google Scholar]
- Vassalos, D.; Kourouklis, A. Experimental, Theoretical and Full-Scale Investigation on the Snap Loading of Marine Cables; Main Report OTH 558; University of Strathclyde: Glasgow, Scotland, 1998; ISBN 0-7176-1595-2. [Google Scholar]
- Driscoll, F.R.; Lueck, R.G.; Nahon, M. Development and validation of a lumped-mass dynamics model of a deep-sea ROV system. Appl. Ocean Res. 2000, 22, 169–182. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C.; Bergdahl, L. An hp-adaptive discontinuous Galerkin method for modelling snap loads in mooring cables. Ocean Eng. 2017, 144, 266–276. [Google Scholar] [CrossRef]
- Howell, C.T. Investigation of the Dynamics of Low-Tension Cables. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1992. [Google Scholar]
- Triantafyllou, M.; Howell, C. Nonlinear impulsive motion of low-tension cables. J. Eng. Mech. 1992, 118, 807–830. [Google Scholar] [CrossRef]
- Gobat, J.; Grosenbaugh, M.A.; Triantafyllou, M. Generalised alpha time integration solutions for hanging chain dynamics. J. Eng. Mech. 2002, 128, 677–687. [Google Scholar] [CrossRef]
- Chatjigeorgiou, I.K.; Mavrakos, S.A. Cable dynamics for marine applications. In Springer Handbook of Ocean Engineering; Dhanak, M., Xiros, N., Eds.; Springer Handbooks; Springer: Cham, UK, 2016; pp. 875–906. [Google Scholar]
- Grosenbaugh, M.A.; Howell, C.; Moxnes, S. Simulating the dynamics of underwater vehicles with low-Tension tethers. Int. J. Offshore Polar Eng. 1993, 3, 213–218. [Google Scholar]
- Buckham, B.; Driscoll, F.; Nahon, M. Development of a finite element cable model for use in low-tension dynamics simulations. J. Appl. Mech. 2004, 71, 476–485. [Google Scholar] [CrossRef]
- Buckham, B.; Nahon, M.; Cote, G. Validation of a finite element model for slack ROV tethers. In Proceedings of the OCEANS 2000 MTS/IEEE Conference and Exhibition. Conference Proceedings (Cat. No.00CH37158), Providence, RI, USA, 11–14 September 2000; Volume 2, pp. 1129–1136. [Google Scholar]
- Koh, C.; Zhang, Y.; Quek, S. Low-tension cable dynamics: Numerical and experimental studies. J. Eng. Mech. 1999, 125, 347–354. [Google Scholar] [CrossRef]
- Koh, C.; Rong, Y. Dynamic analysis of large displacement cable motion with experimental verification. J. Sound Vib. 2004, 272, 187–206. [Google Scholar] [CrossRef]
- Fried, I. Large deformation static and dynamic finite element analysis of extensible cables. Comp. Struct. 1982, 15, 315–319. [Google Scholar] [CrossRef]
- Davidson, J.; Ringwood, J.V. Mathematical modelling of mooring systems for wave energy converters—A review. Energies 2017, 10, 666. [Google Scholar] [CrossRef]
- Orcina Inc. OrcaFlex Manual—Version 9.6a; Orcina Ltd.: Ulverston, UK, 2012. [Google Scholar]
- DNV GL. SESAM Theory Manual for DeepC 3.0; DNV GL AS: Oslo, Norway, 2014. [Google Scholar]
- Garrett, D.L. Dynamic analysis of slender rods. J. Energy Resour. Technol. 1982, 104, 302–306. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Meguid, S.A. Elastodynamic analysis of low tension cables using a new curved beam element. J. Solids Struct. 2006, 43, 1490–1504. [Google Scholar] [CrossRef][Green Version]
- Raknes, S.; Deng, X.; Bazilevs, Y.; Benson, D.; Mathisen, M.; Kvamsdal, T. Isogeometric rotation-free bending-stabilized cables: Statics, dynamics, bending strips and coupling with shells. Comp. Meth. Appl. Mech. Eng. 2013, 263, 127–143. [Google Scholar] [CrossRef]
- Tasora, A.; Benatti, S.; Mangoni, D.; Garziera, R. A geometrically exact isogeometric beam for large displacements and contacts. Comput. Methods Appl. Mech. Eng. 2020, 358, 112635. [Google Scholar] [CrossRef]
- Morison, J.; O’Brien, M.; Johnson, J.; Schaaf, S. The Force Exerted by Surface Waves on Piles. Pet. Trans. Amer. Inst. Min. Eng. 1950, 186, 149–154. [Google Scholar] [CrossRef]
- Palm, J.; Eskilsson, C. MOODY, User’s Manual Version 1.0. 2018. Available online: www.github.com/johannep/moodyAPI/releases (accessed on 1 September 2020).
- Cockburn, B.; Shu, C. The local discontinuous Galerkin method for time-dependent convection-dominated systems. SIAM J. Numer. Anal. 1998, 35, 2440–2463. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C. The Runge-Kutta local projection P1-discontinuous Galerkin method for scalar conservation laws. Math. Model. Numer. Anal. 1991, 25, 337–361. [Google Scholar] [CrossRef]
- Cockburn, B.; Shu, C. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems. J. Sci. Comp. 2001, 16, 173–261. [Google Scholar] [CrossRef]
- Wu, J.S.; Lin, T.L. Free vibration analysis of a uniform cantilever beam with point masses by an analytical-and-numerical-combined method. J. Sound Vib. 1990, 136, 201–213. [Google Scholar] [CrossRef]
- Luis, A.R.; Armesto, J.A.; Guanche, R.; Barrera, C.; Vidal, C. Simulation of marine towing cable dynamics using a finite elements method. J. Mar. Sci. Eng. 2020, 8, 140. [Google Scholar] [CrossRef]
- Papazoglou, V.J.; Mavrakos, S.A. Non-linear cable response and model testing in water. J. Sound Vib. 1990, 140, 103–115. [Google Scholar] [CrossRef]
- Zhu, K.; Zheng, D.; Cai, Y.; Yu, C.; Wang, R.; Liu, Y.; Zhang, F. Nonlinear hydrodynamic response of marine cable-body system under random dynamic excitations. J. Hydrodyn. 2009, 21, 851–855. [Google Scholar] [CrossRef]
| Description | |||||
|---|---|---|---|---|---|
| Prescribed motion, pinned | |||||
| Pinned joint | |||||
| Free cable end | |||||
| Clamped fixed end | |||||
| Point force and moment | |||||
| Rigid body connection at point P |
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Unit | (N) | (Ns) | (Nm) | (Nms) | (kg/m) | (-) | (m) |
| Value | 1541 | 4.079 | 0.060 | 0.020 | 0.702 | 1 | 2.022 |
| Cage | Tether | ||||
|---|---|---|---|---|---|
| Parameter | Label | Value | Parameter | Label | Value |
| Mass (kg) | 4995 | Mass (kg/m) | 3.01 | ||
| Density (kg/m) | 8448 | Density (kg/m) | 7153 | ||
| Diameter (m) | 3.01 | Diameter (m) | D | 0.03 | |
| Added mass coeff., surge (-) | 7.1 | Normal added mass coeff. (-) | CMn | 1 | |
| Added mass coeff., heave (-) | 7.1 | Tangential added mass coeff. (-) | CMt | 0 | |
| Drag coeff., surge (-) | 1.3 | Drag coeff. | CDn | 1.0 | |
| Drag coeff., heave (-) | 2.7 | Tangential drag coeff., | CDt | 0.02 | |
| Height (m) | 4.2 | Elasticity (GPa) | E | 65.9 | |
| Pitch moment of inertia (kgm) | Internal damping (kNs/m) | 45.5 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palm, J.; Eskilsson, C. Influence of Bending Stiffness on Snap Loads in Marine Cables: A Study Using a High-Order Discontinuous Galerkin Method. J. Mar. Sci. Eng. 2020, 8, 795. https://doi.org/10.3390/jmse8100795
Palm J, Eskilsson C. Influence of Bending Stiffness on Snap Loads in Marine Cables: A Study Using a High-Order Discontinuous Galerkin Method. Journal of Marine Science and Engineering. 2020; 8(10):795. https://doi.org/10.3390/jmse8100795
Chicago/Turabian StylePalm, Johannes, and Claes Eskilsson. 2020. "Influence of Bending Stiffness on Snap Loads in Marine Cables: A Study Using a High-Order Discontinuous Galerkin Method" Journal of Marine Science and Engineering 8, no. 10: 795. https://doi.org/10.3390/jmse8100795
APA StylePalm, J., & Eskilsson, C. (2020). Influence of Bending Stiffness on Snap Loads in Marine Cables: A Study Using a High-Order Discontinuous Galerkin Method. Journal of Marine Science and Engineering, 8(10), 795. https://doi.org/10.3390/jmse8100795






