Large Eddy Simulation of Flow over Wavy Cylinders with Different Twisted Angles at a Subcritical Reynolds Number
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equations
2.2. Numerical Method
3. Numerical Setting
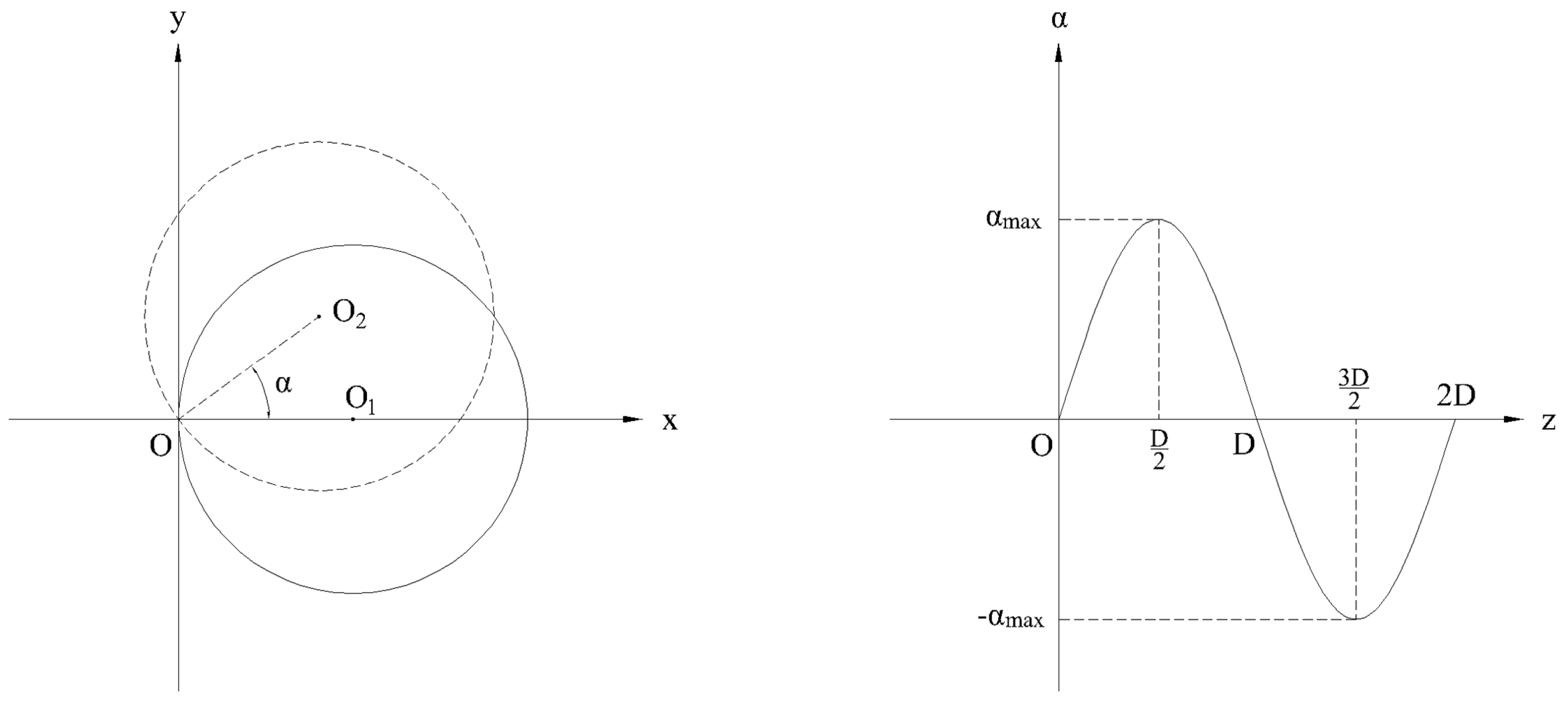
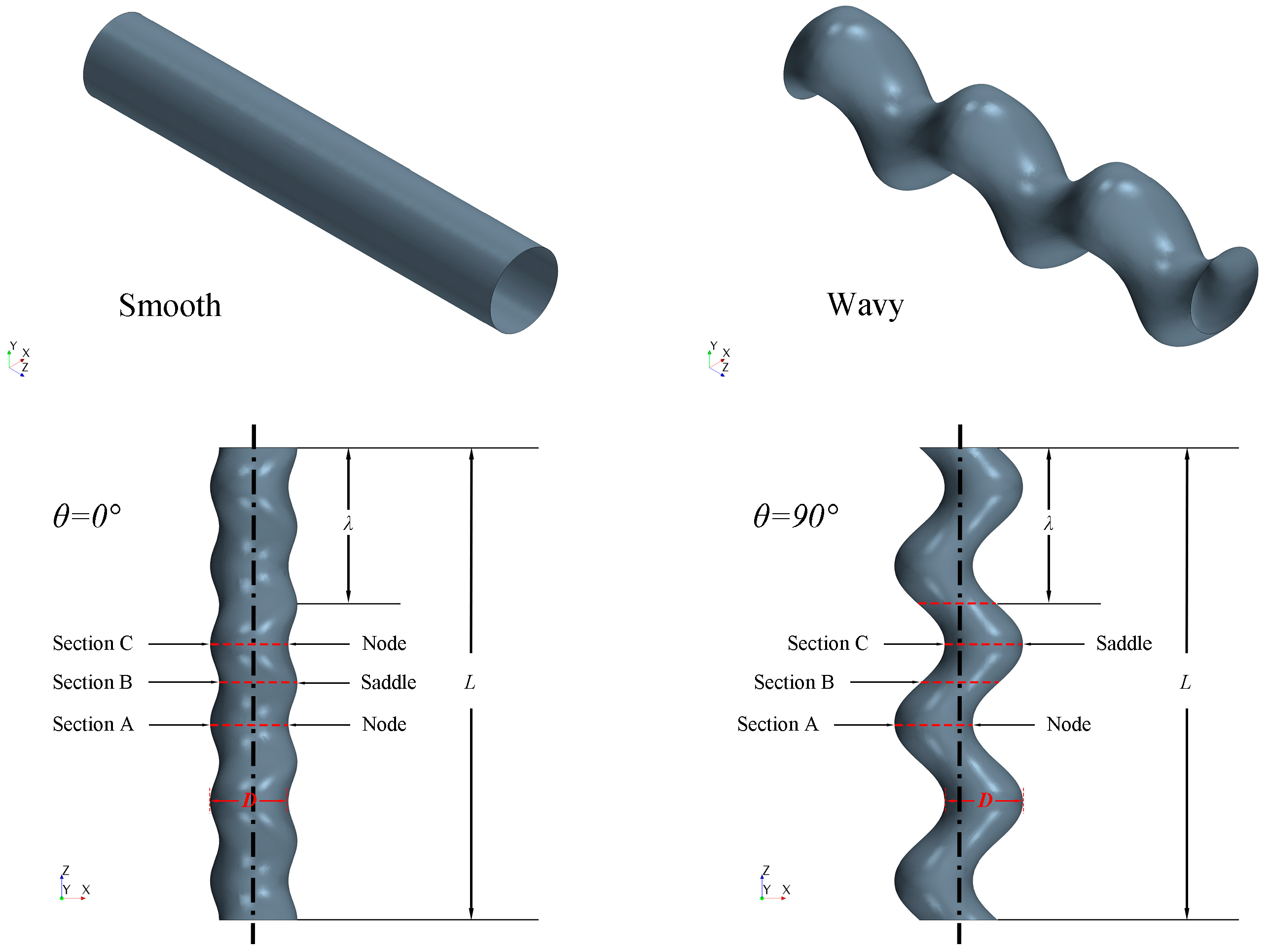
3.1. Computational Model
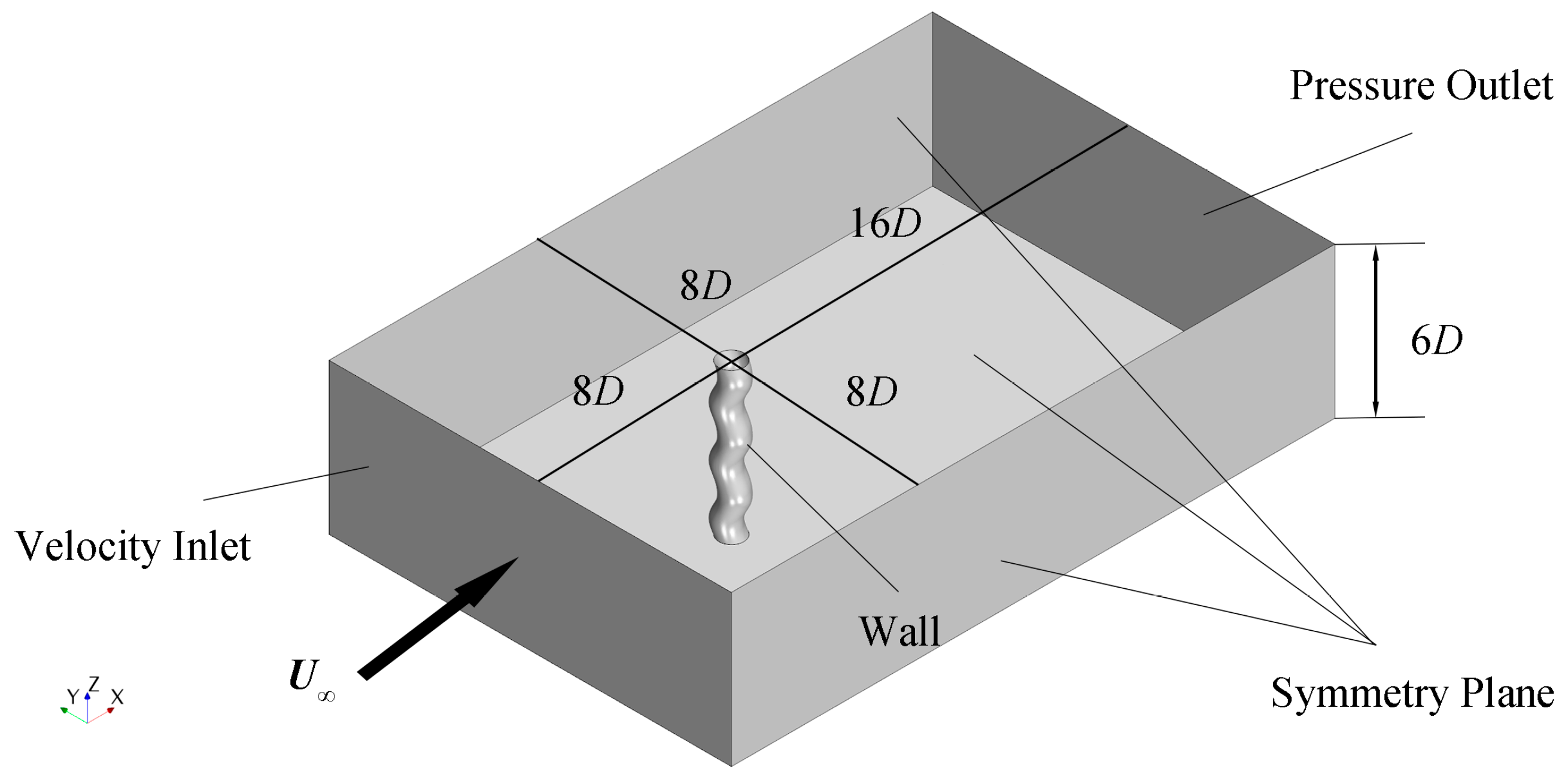
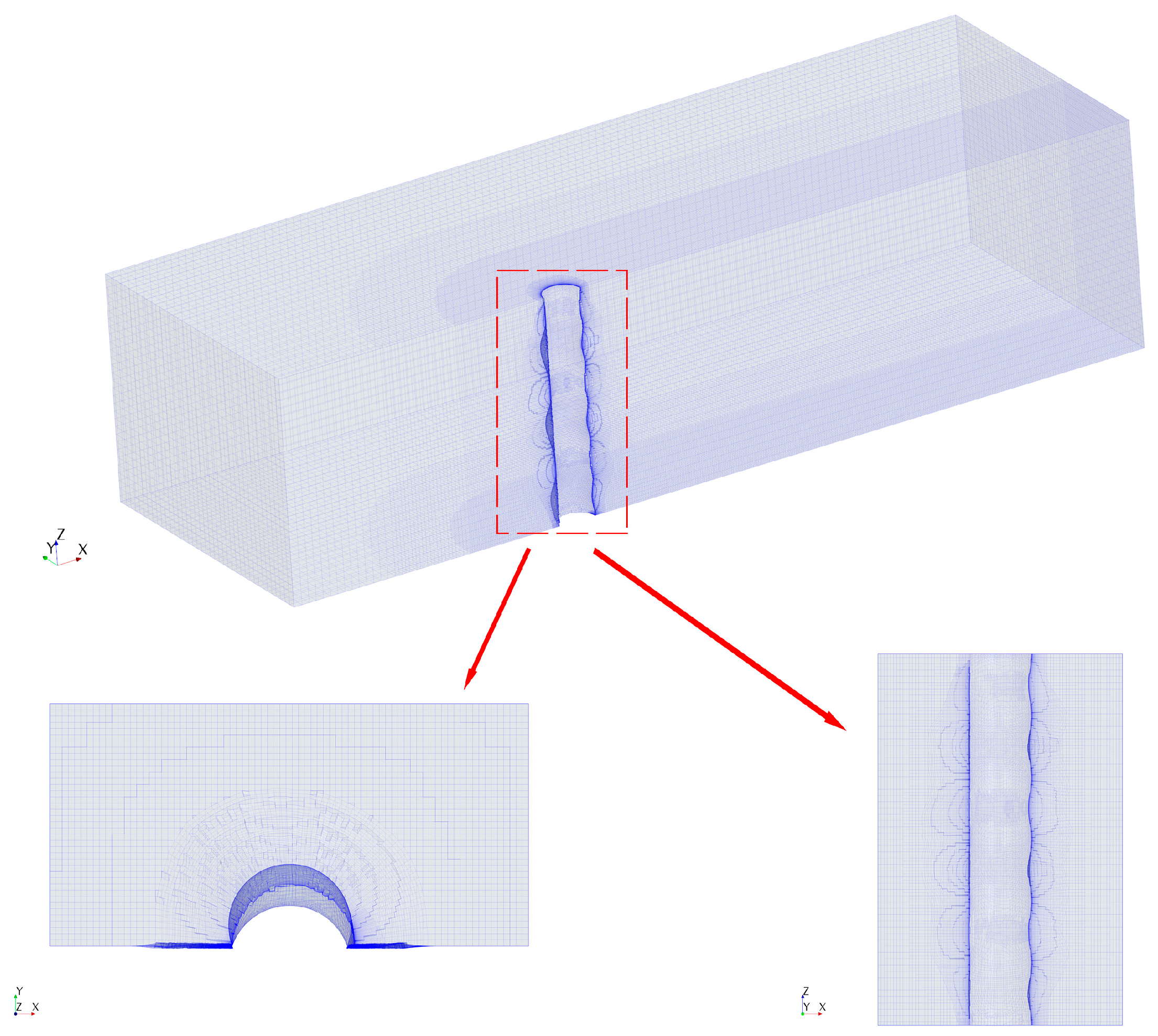
3.2. Computational Domain and Boundary Conditions
4. Numerical Model Validation
4.1. Validation for Smooth Cylinder
4.2. Validation for Wavy Cylinder
5. Results and Analysis
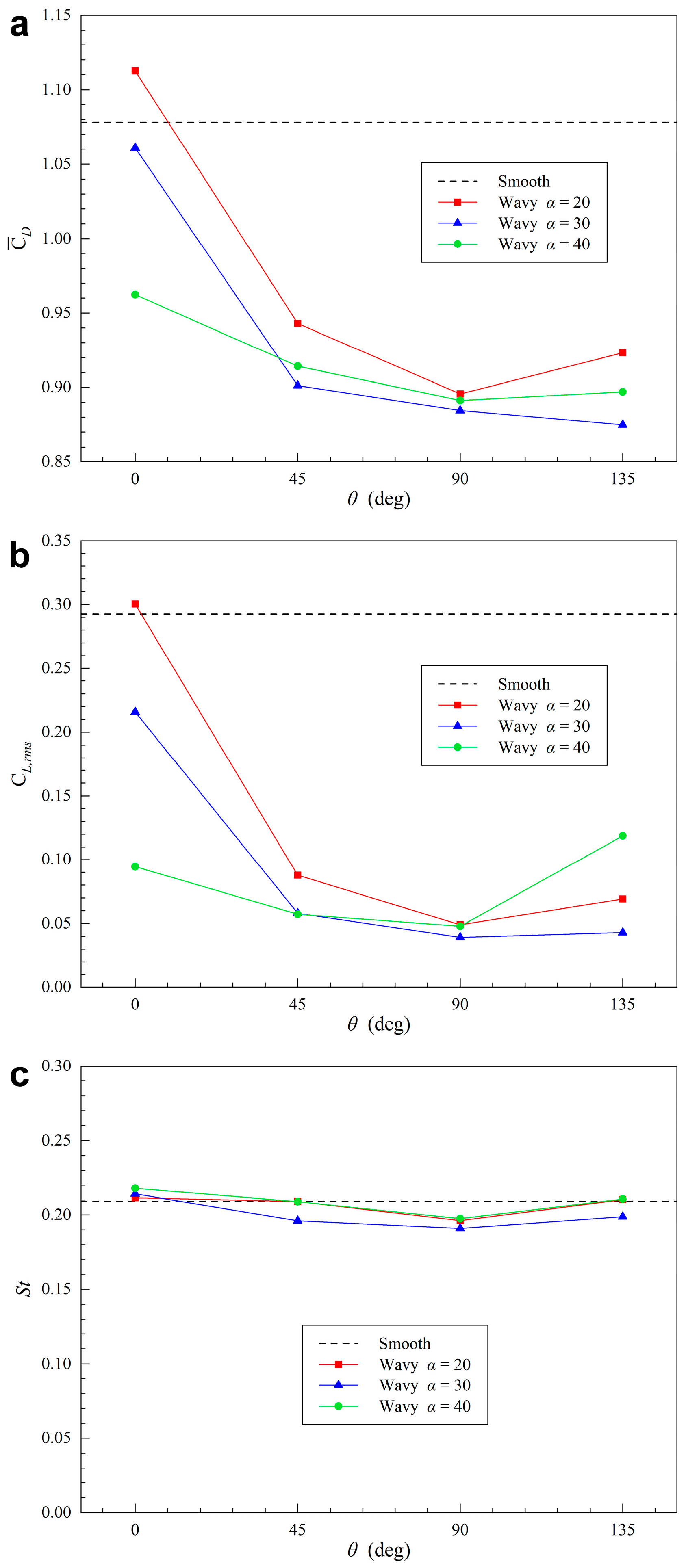
5.1. Force and Strouhal Number
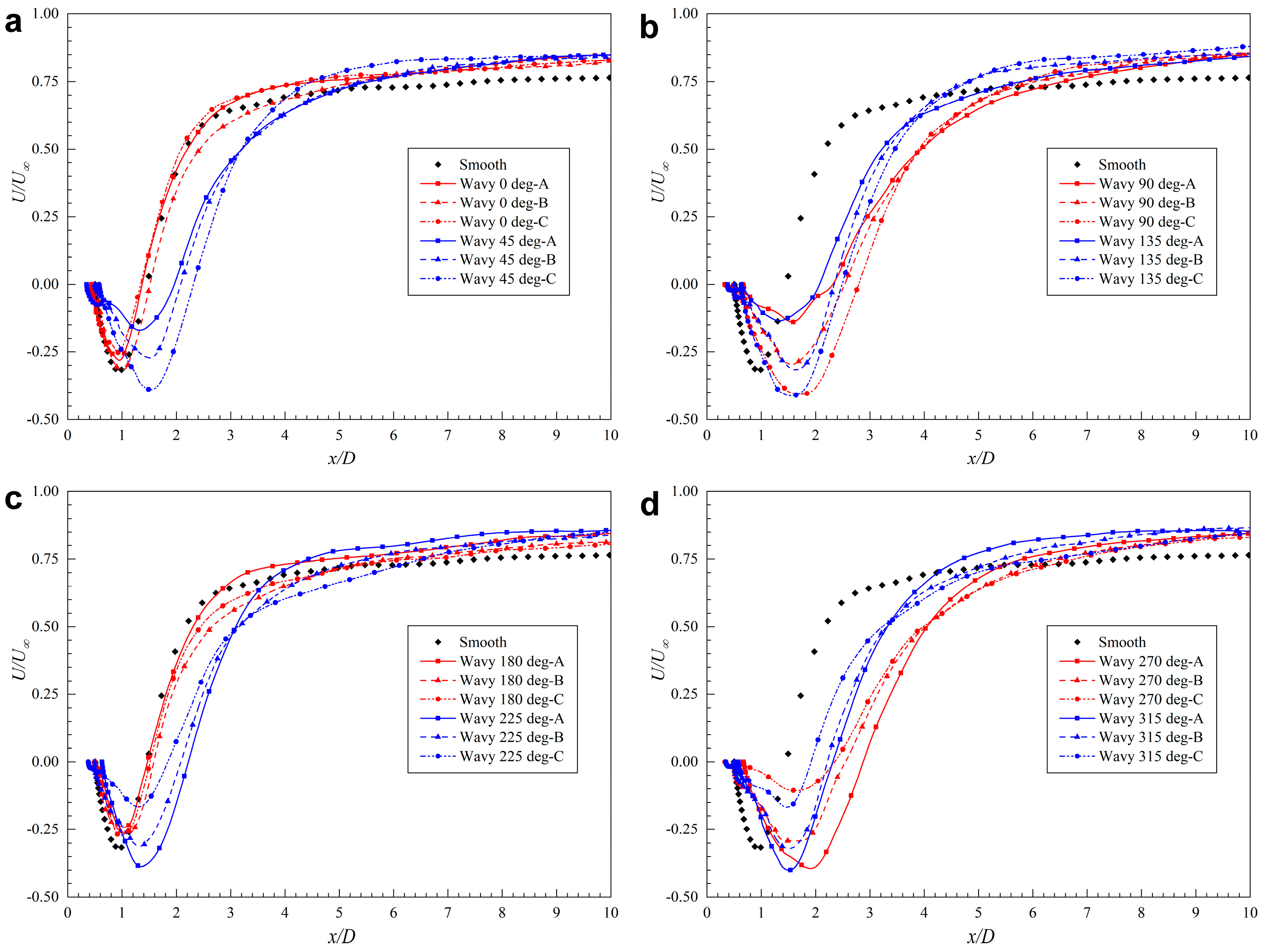
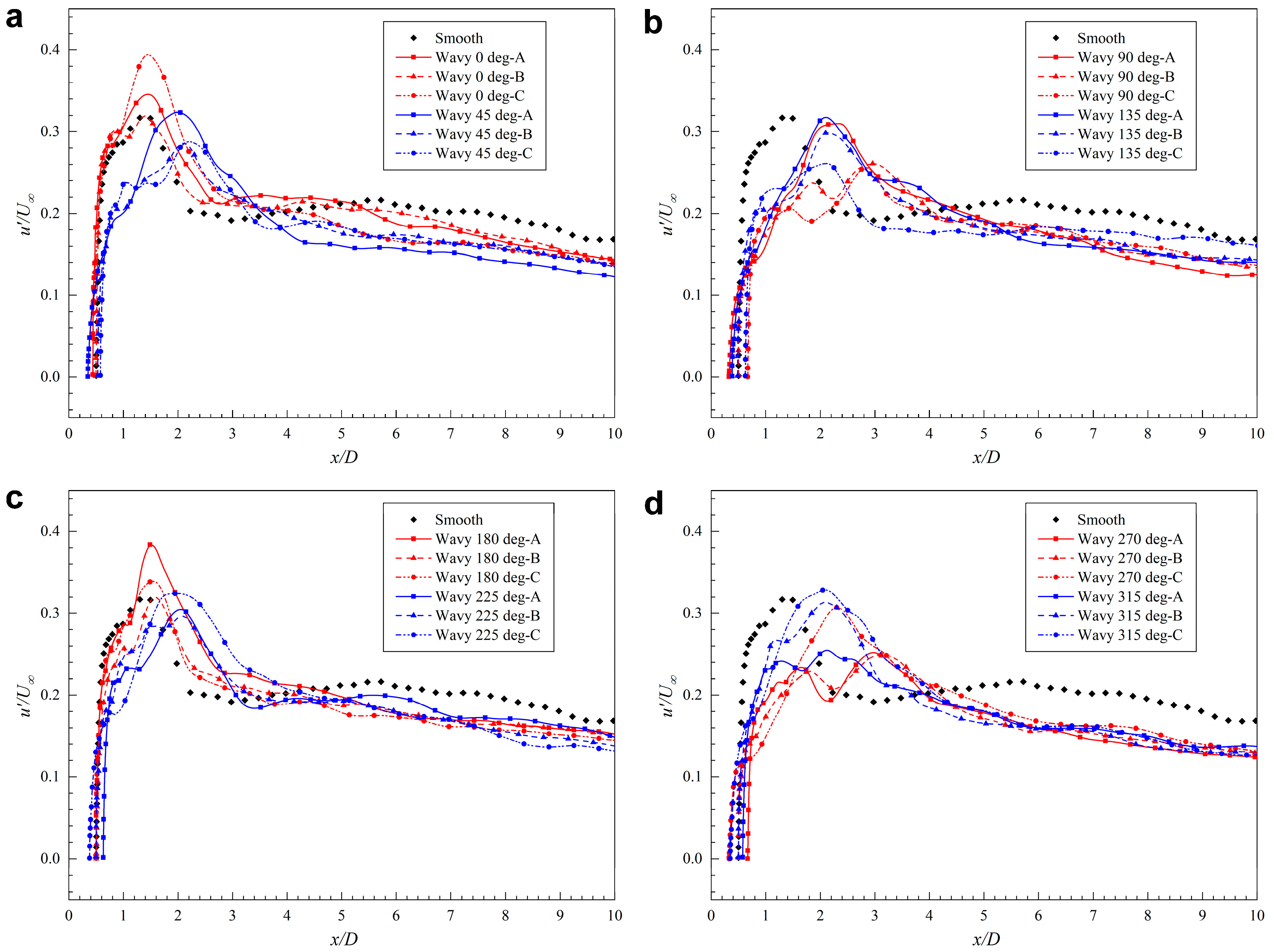
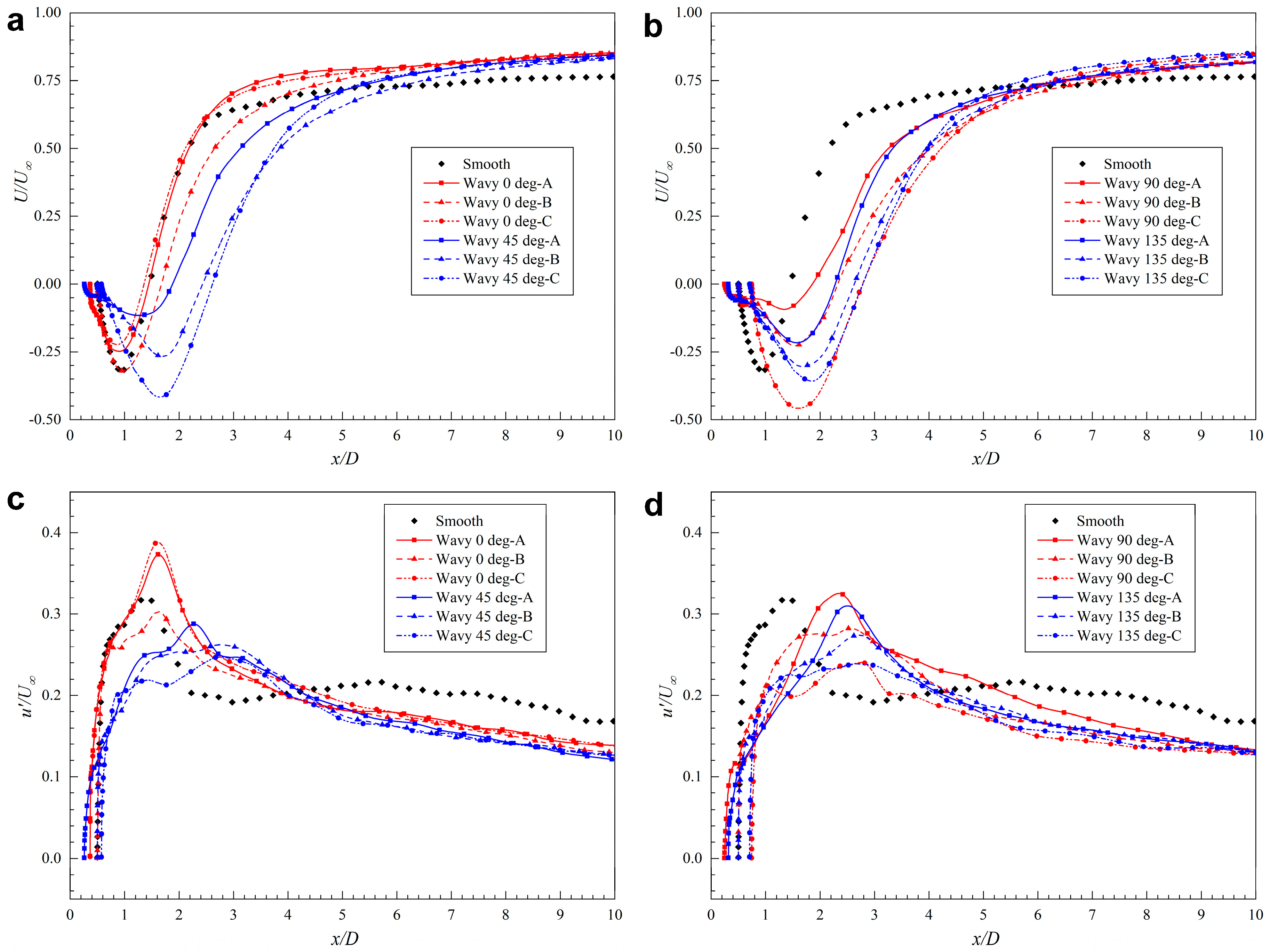
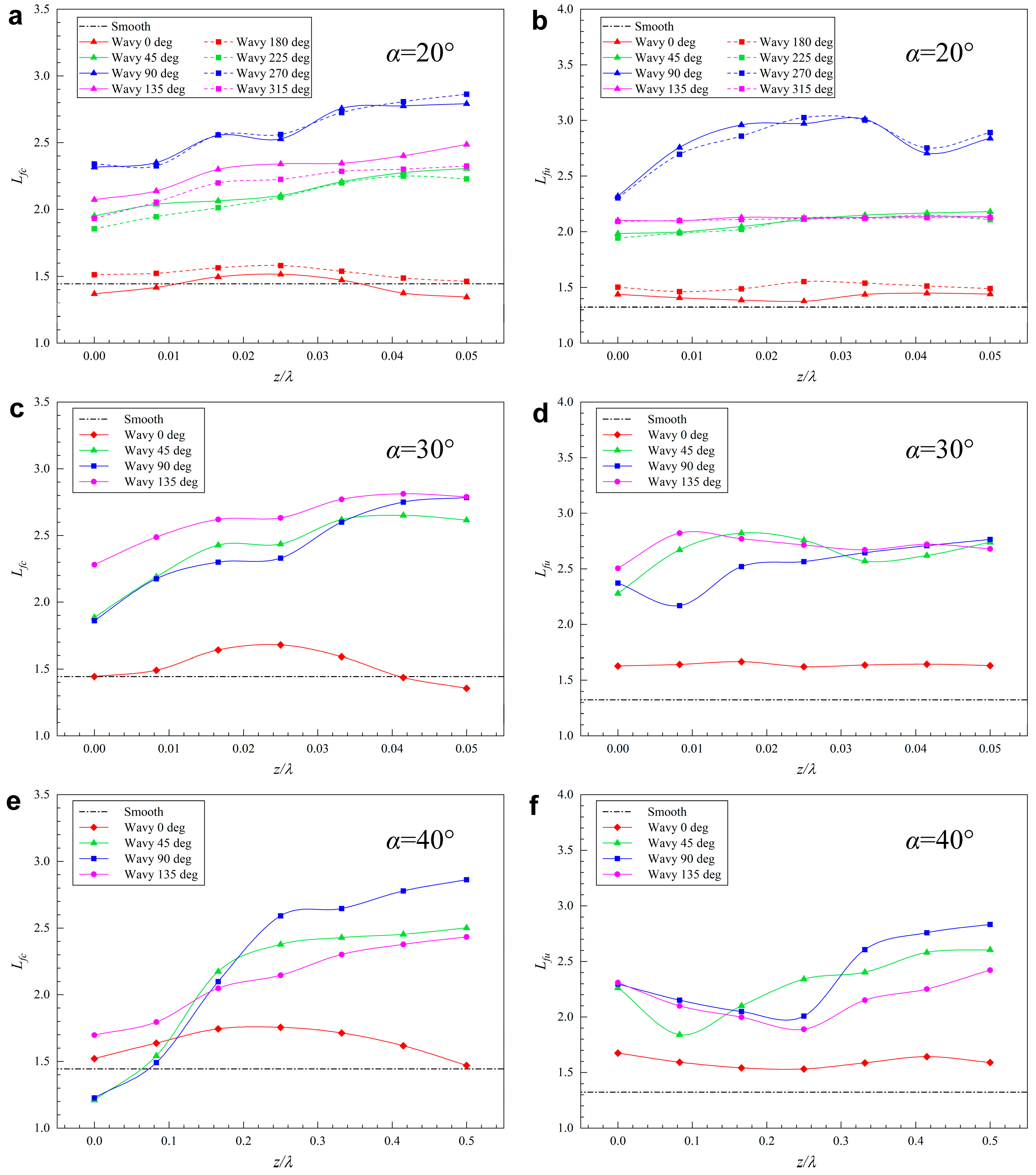
5.2. Velocity Distribution and Vortex Formation Length
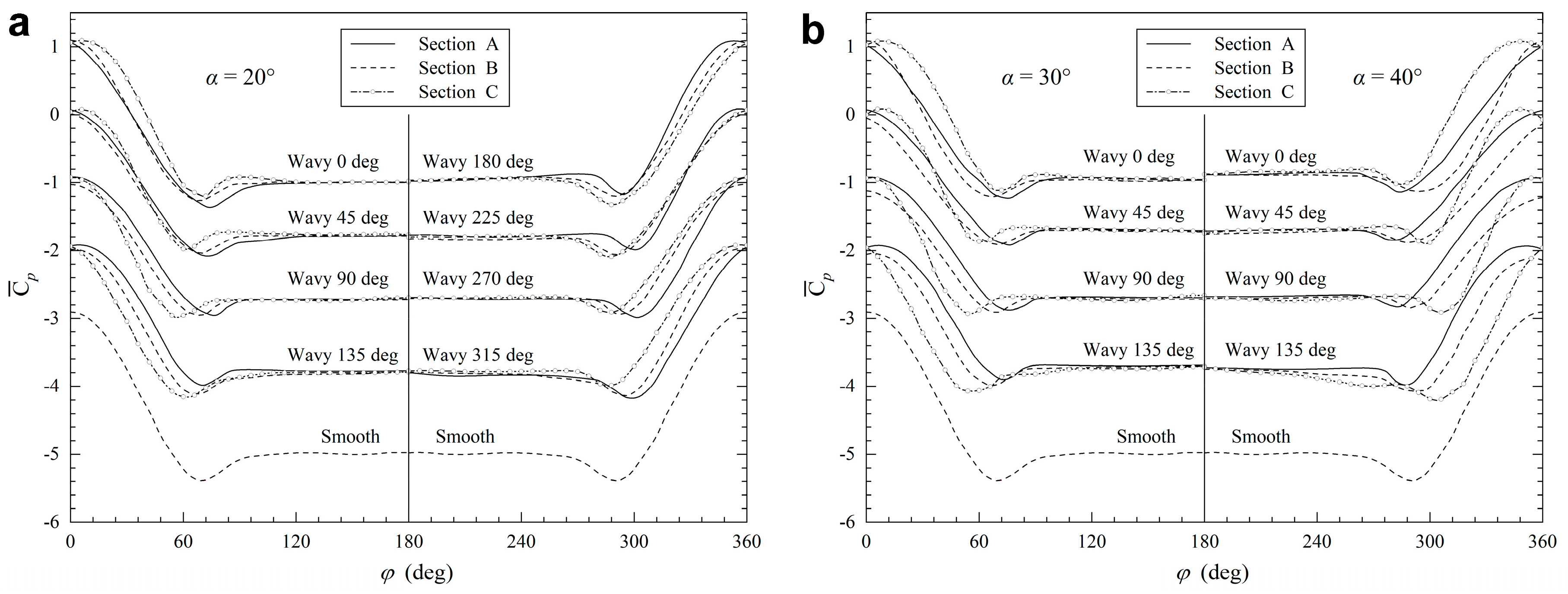
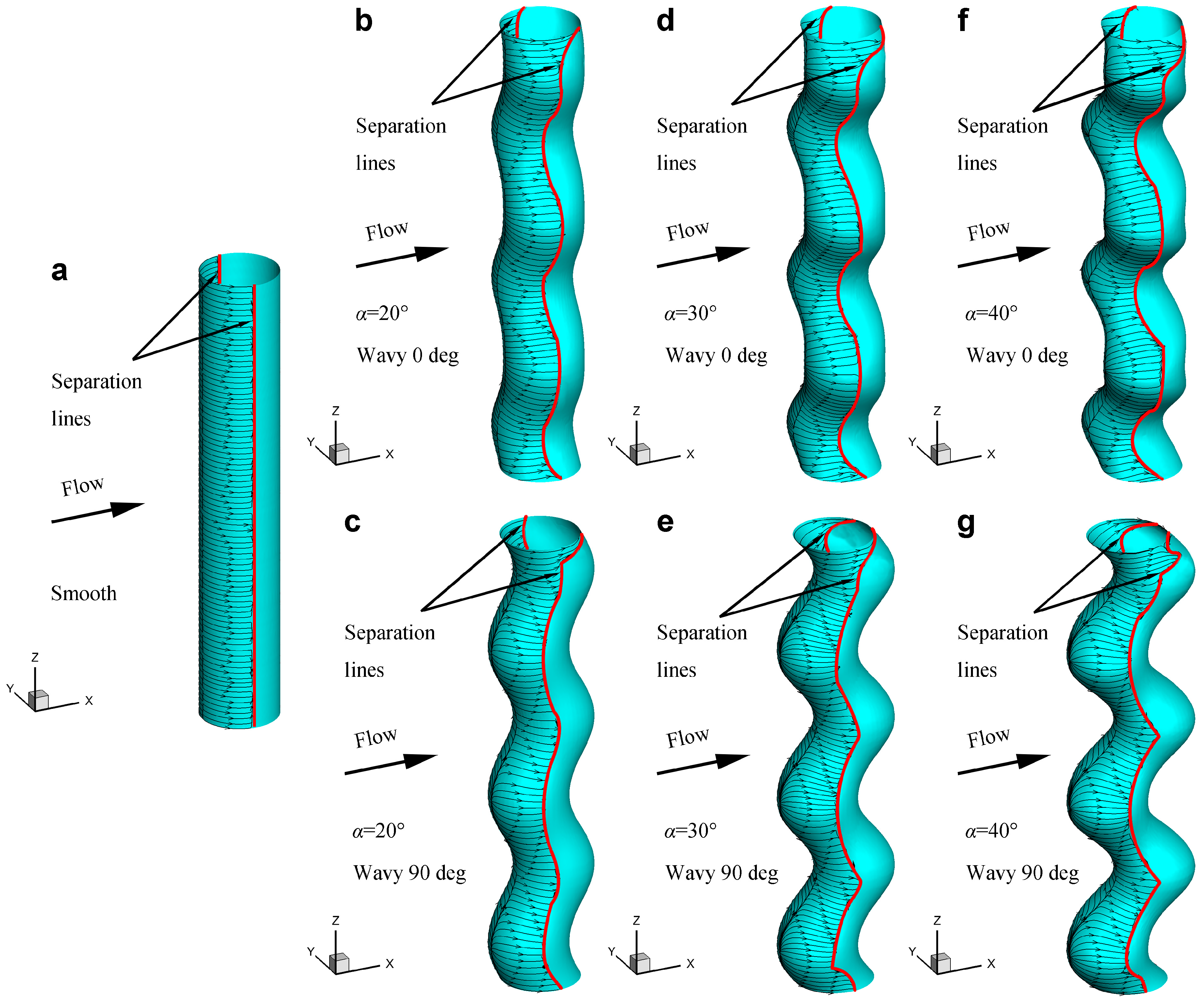
5.3. Pressure Coefficient and 3D Separation
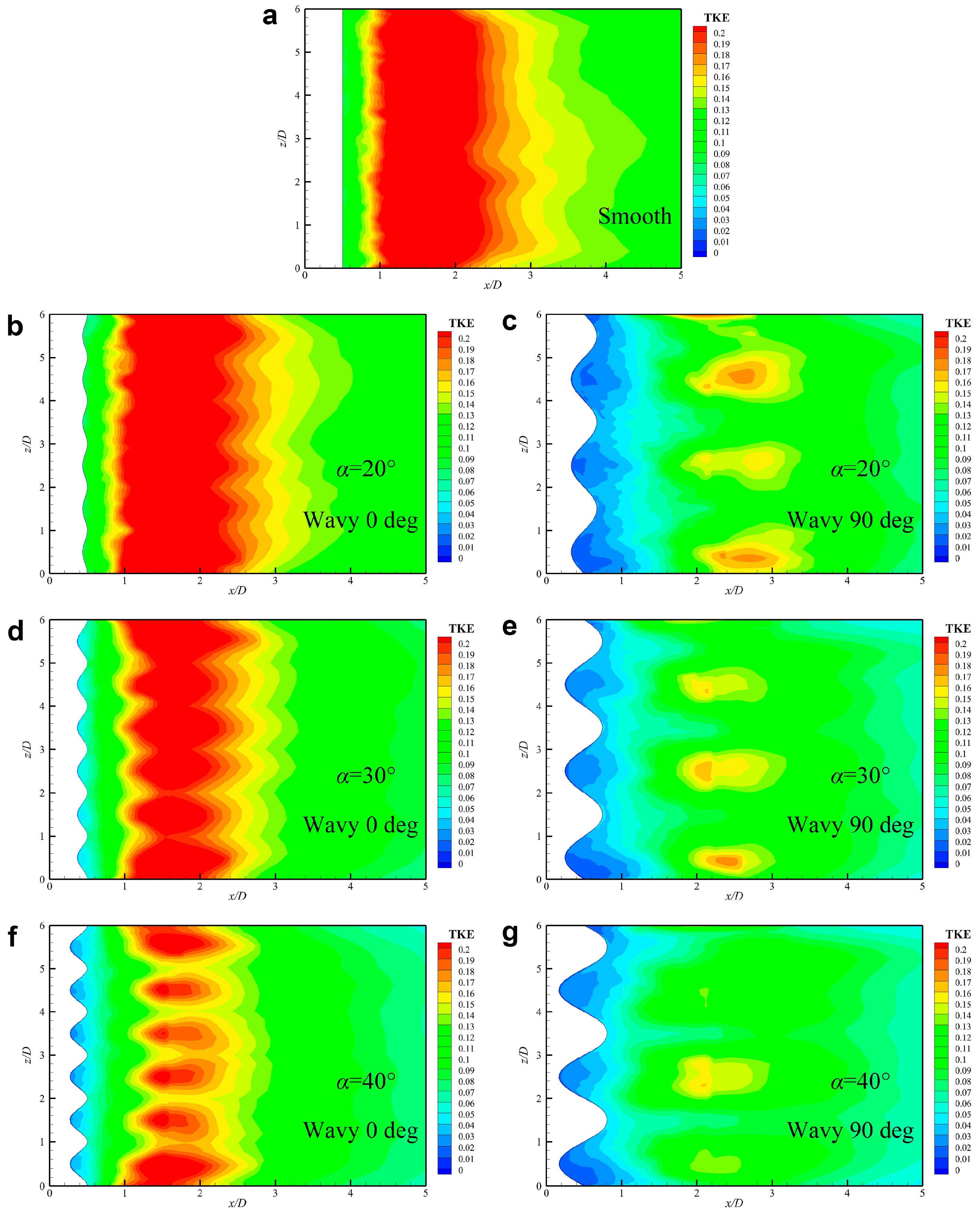
5.4. Turbulent Kinetic Energy
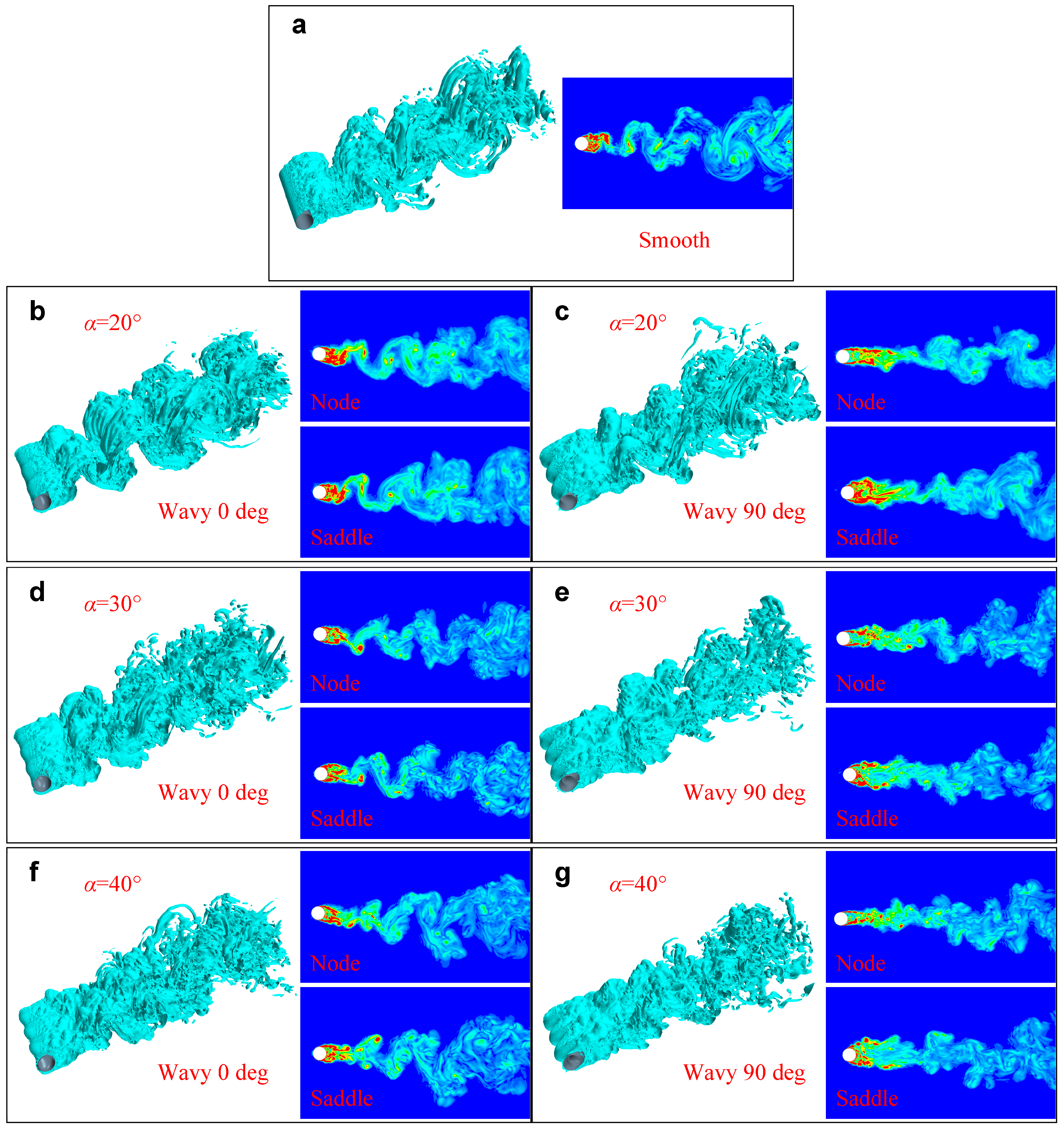
5.5. Three-Dimensional Vortex Structures
6. Conclusions and Prospect
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Placzek, A.; Sigrist, J.F.; Hamdouni, A. Numerical simulation of an oscillating cylinder in a cross-flow at low Reynolds number: Forced and free oscillations. Comput. Fluids 2009, 38, 80–100. [Google Scholar] [CrossRef] [Green Version]
- Pastò, S. Vortex-induced vibrations of a circular cylinder in laminar and turbulent flows. J. Fluids Struct. 2008, 24, 977–993. [Google Scholar] [CrossRef]
- Zhao, M.; Cheng, L. Vortex-induced vibration of a circular cylinder of finite length. Phys. Fluids 2014, 26, 015111. [Google Scholar] [CrossRef]
- Wang, R.; Xin, D.; Ou, J. Experimental investigation on suppressing circular cylinder VIV by a flow control method based on passive vortex generators. J. Wind Eng. Ind. Aerodyn. 2019, 187, 36–47. [Google Scholar] [CrossRef]
- Zhu, H.; Yao, J.; Ma, Y.; Zhao, H.; Tang, Y. Simultaneous CFD evaluation of VIV suppression using smaller control cylinders. J. Fluids Struct. 2015, 57, 66–80. [Google Scholar] [CrossRef]
- Kang, Z.; Zhang, C.; Ma, G.; Ni, W. A numerical investigation of two-degree-of-freedom VIV of a circular cylinder using the modified turbulence model. Ocean Eng. 2018, 155, 211–226. [Google Scholar] [CrossRef]
- Belloli, M.; Giappino, S.; Morganti, S.; Muggiasca, S.; Zasso, A. Vortex induced vibrations at high Reynolds numbers on circular cylinders. Ocean Eng. 2015, 94, 140–154. [Google Scholar] [CrossRef]
- Zou, L.; Lin, Y. Force reduction of flow around a sinusoidal wavy cylinder. J. Hydrodyn. 2009, 21, 308–315. [Google Scholar] [CrossRef]
- Zhuang, Y.Q.; Sun, X.J.; Huang, D.G. Numerical study of unsteady flows past a rotating wavy cylinder. Eur. J. Mech. B Fluids 2018, 72, 538–544. [Google Scholar] [CrossRef]
- Xu, C.Y.; Ni, Z.Q. Novel characteristics of wavy cylinder in supersonic turbulent flow. Eur. J. Mech. B Fluids 2018, 67, 158–167. [Google Scholar] [CrossRef]
- Lam, K.; Wang, F.H.; So, R.M.C. Three-dimensional nature of vortices in the near wake of a wavy cylinder. J. Fluids Struct. 2004, 19, 815–833. [Google Scholar] [CrossRef]
- Lam, K.; Lin, Y.F. Large eddy simulation of flow around wavy cylinders at a subcritical Reynolds number. Int. J. Heat Fluid Flow 2008, 29, 1071–1088. [Google Scholar] [CrossRef]
- Jung, J.H.; Yoon, H.S. Large eddy simulation of flow over a twisted cylinder at a subcritical Reynolds number. J. Fluid Mech. 2014, 759, 579–611. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, X.; Guo, W.; Gho, W.M.; Tan, S.K. Experimental study on flow past a circular cylinder with rough surface. Ocean Eng. 2015, 109, 7–13. [Google Scholar] [CrossRef]
- Wong, K.W.L.; Zhao, J.; LoJacono, D.; Thompson, M.C.; Sheridan, J. Experimental investigation of flow-induced vibration of a rotating circular cylinder. J. Fluid Mech. 2017, 829, 486–511. [Google Scholar] [CrossRef] [Green Version]
- Jie, H.; Liu, Y.Z. Large eddy simulation and proper orthogonality decomposition of turbulent flow around a vibrissa-shaped cylinder. Int. J. Heat Fluid Flow 2017, 67, 261–277. [Google Scholar] [CrossRef]
- Yeon, S.M.; Yang, J.; Stern, F. Large-eddy simulation of the flow past a circular cylinder at sub- to super-critical Reynolds numbers. Appl. Ocean Res. 2016, 59, 663–675. [Google Scholar] [CrossRef] [Green Version]
- Deardorff, J.W. The use of subgrid transport equations in a three-dimensional model of atmospheric turbulence. J. Fluids Eng. 1973, 95, 429. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-scale stress modelling based on the square of the velocity gradient tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Deardoff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- CD-Adapco, S. STAR CCM+ User Guide Version 12.04; CD-Adapco: New York, NY, USA, 2017. [Google Scholar]
- Leonard, B.P. The ultimate conservative difference scheme applied to unsteady one-dimensional advection. Comput. Methods Appl. Mech. Eng. 1991, 88, 17–74. [Google Scholar] [CrossRef]
- Baek, D.G.; Yoon, H.S.; Jung, J.H.; Kim, K.S.; Paik, B.G. Effects of the advance ratio on the evolution of a propeller wake. Comput. Fluids 2015, 118, 32–43. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Hydrodynamics Around Cylindrical Structures; World Scientific Publishing: Singapore, 1997. [Google Scholar]
- Bloor, S. The transition to turbulence in the wake of a circular cylinder. J. Fluid Mech. 1966, 19, 290–304. [Google Scholar] [CrossRef]
- Gerrard, J.H. The wakes of cylindrical bluff bodies at low Reynolds number. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1978, 288, 351–382. [Google Scholar] [CrossRef]
- Woo, H.G.C.; Cermak, J.E.; Peterka, J.A. On vortex locking-on phenomenon for a cable in linear shear-flow. J. Wind Eng. Ind. Aerodyn. 1983, 14, 289–300. [Google Scholar] [CrossRef]
- Norberg, C. LDV-measurements in the near wake of a circular cylinder. In Proceedings of the 1998 ASME Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: Washington, DC, USA, 1998; FED-Volume 245, FEDSM98-5202. [Google Scholar]
- Govardhan, R.; Williamson, C.H.K. Mean and fluctuating velocity fields in the wake of a freely-vibrating cylinder. J. Fluids Struct. 2001, 15, 489–501. [Google Scholar] [CrossRef]
- Bearman, P.W. Investigation of the flow behind a two-dimensional model with a blunt trailing edge and fitted with splitter plates. J. Fluid Mech. 1965, 21, 241–255. [Google Scholar] [CrossRef]
- Zhang, W.; Dai, C.; Lee, S.J. PIV measurements of the near-wake behind a sinusoidal cylinder. Exp. Fluids 2005, 38, 824–832. [Google Scholar] [CrossRef]
- Xu, C.Y.; Chen, L.-W.; Lu, X.Y. Large-eddy simulation of the compressible flow past a wavy cylinder. J. Fluid Mech. 2010, 665, 238–273. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.-Z.; Lu, X.-Y.; Zhuang, L.-X. Integral force acting on a body due to local flow structures. J. Fluid Mech. 2007, 576, 265–286. [Google Scholar] [CrossRef]
- Chyu, C.K.; Rockwell, D. Near-wake flow structure of a cylinder with a helical surface perturbation. J. Fluids Struct. 2002, 16, 263–269. [Google Scholar] [CrossRef]

| Smooth Cylinder | T | Grid | Error (%) | Error (%) | St | Error (%) | ||
|---|---|---|---|---|---|---|---|---|
| EFD | - | - | 1.1356 | 0.2995 | 0.2046 | |||
| coarse (S1) | 0.02 | 2.42M | 1.0325 | 9.08 | 0.3206 | 7.05 | 0.2105 | 2.88 |
| medium (S2) | 0.02 | 4.18M | 1.0781 | 5.06 | 0.2925 | 2.34 | 0.209 | 2.15 |
| fine (S3) | 0.02 | 7.22M | 1.1151 | 1.81 | 0.3073 | 2.60 | 0.2087 | 2.00 |
| Smooth Cylinder | T | Grid | Error (%) | Error (%) | St | Error (%) | ||
|---|---|---|---|---|---|---|---|---|
| EFD | - | - | 1.1356 | 0.2995 | 0.2046 | |||
| small (S4) | 0.01 | 4.18M | 1.1081 | 2.42 | 0.3063 | 2.27 | 0.2089 | 2.10 |
| medium (S5) | 0.02 | 4.18M | 1.0781 | 5.06 | 0.2925 | 2.34 | 0.209 | 2.15 |
| large (S6) | 0.04 | 4.18M | 0.9007 | 20.69 | 0.1729 | 42.27 | 0.2137 | 4.45 |
| Wavy Cylinder | T | Grid | St | ||
|---|---|---|---|---|---|
| coarse (W1) | 0.02 | 2.42M | 1.0728 | 0.2758 | 0.2075 |
| medium (W2) | 0.02 | 4.18M | 1.1125 | 0.3003 | 0.2115 |
| fine (W3) | 0.02 | 7.22M | 1.1359 | 0.3213 | 0.2125 |
| Wavy Cylinder | T | Grid | St | ||
|---|---|---|---|---|---|
| small (W4) | 0.01 | 4.18M | 1.1149 | 0.3101 | 0.2114 |
| medium (W5) | 0.02 | 4.18M | 1.1125 | 0.3003 | 0.2115 |
| large (W6) | 0.04 | 4.18M | 1.1191 | 0.3149 | 0.2127 |
| θ | St | ||
|---|---|---|---|
| 0 | 1.1125 | 0.3003 | 0.2115 |
| 45 | 0.943 | 0.0877 | 0.209 |
| 90 | 0.8956 | 0.0489 | 0.1962 |
| 135 | 0.9232 | 0.0692 | 0.2103 |
| 180 | 1.0735 | 0.2671 | 0.211 |
| 225 | 0.9318 | 0.0844 | 0.2064 |
| 270 | 0.8864 | 0.0463 | 0.1911 |
| 315 | 0.9271 | 0.0659 | 0.2102 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, C.; Guo, H.; Hu, J.; Song, K.; Zhang, W.; Wang, W. Large Eddy Simulation of Flow over Wavy Cylinders with Different Twisted Angles at a Subcritical Reynolds Number. J. Mar. Sci. Eng. 2019, 7, 227. https://doi.org/10.3390/jmse7070227
Guo C, Guo H, Hu J, Song K, Zhang W, Wang W. Large Eddy Simulation of Flow over Wavy Cylinders with Different Twisted Angles at a Subcritical Reynolds Number. Journal of Marine Science and Engineering. 2019; 7(7):227. https://doi.org/10.3390/jmse7070227
Chicago/Turabian StyleGuo, Chunyu, Hang Guo, Jian Hu, Kewei Song, Weipeng Zhang, and Wei Wang. 2019. "Large Eddy Simulation of Flow over Wavy Cylinders with Different Twisted Angles at a Subcritical Reynolds Number" Journal of Marine Science and Engineering 7, no. 7: 227. https://doi.org/10.3390/jmse7070227
APA StyleGuo, C., Guo, H., Hu, J., Song, K., Zhang, W., & Wang, W. (2019). Large Eddy Simulation of Flow over Wavy Cylinders with Different Twisted Angles at a Subcritical Reynolds Number. Journal of Marine Science and Engineering, 7(7), 227. https://doi.org/10.3390/jmse7070227





