Stochastic Modeling of Forces on Jacket-Type Offshore Structures Colonized by Marine Growth
Abstract
1. Introduction
2. Materials and Methods
2.1. Requirements for a Meta-Model
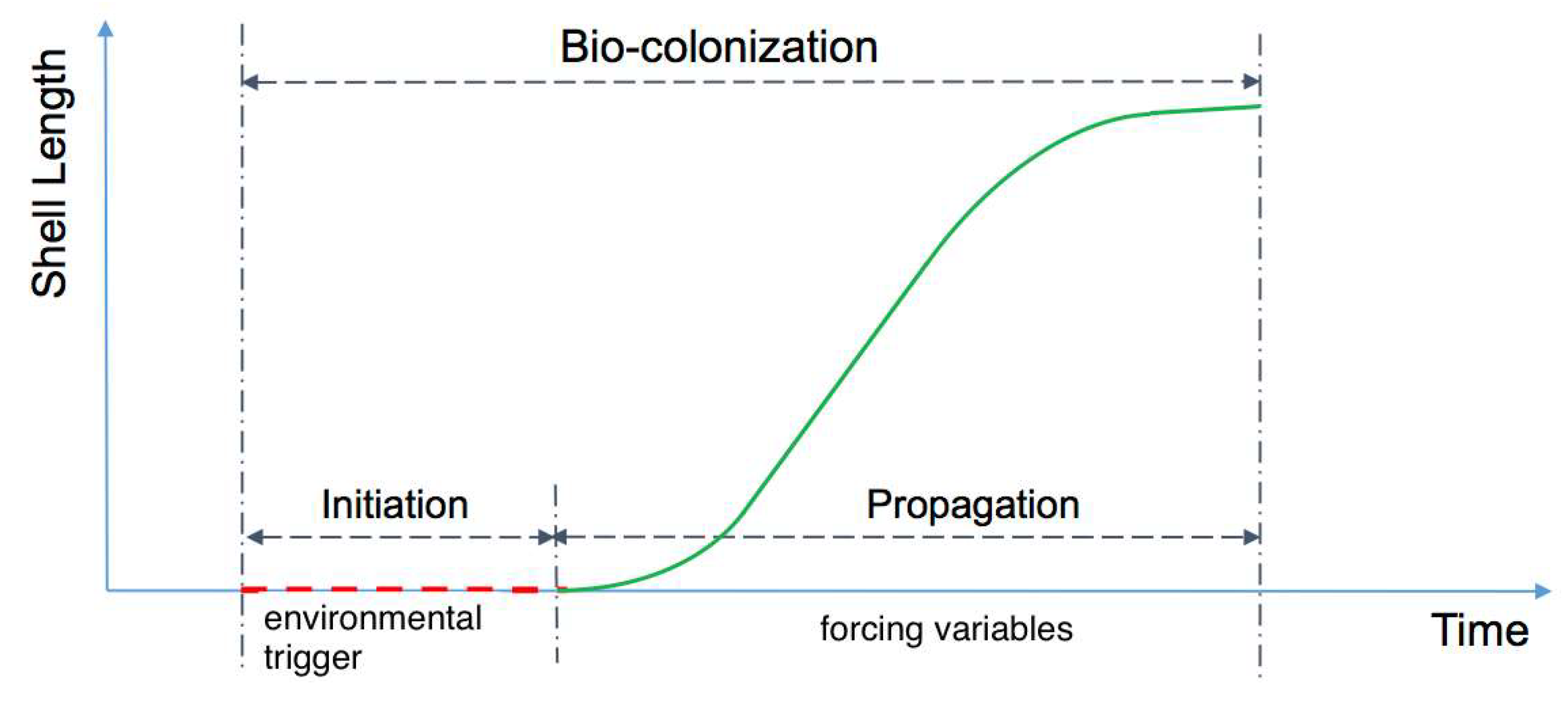
2.2. Description of Bio-Colonization Temporal Dynamic
2.3. Description of Bio-Colonization Temporal Dynamic
2.4. Initiation Phase and Propagation Phases
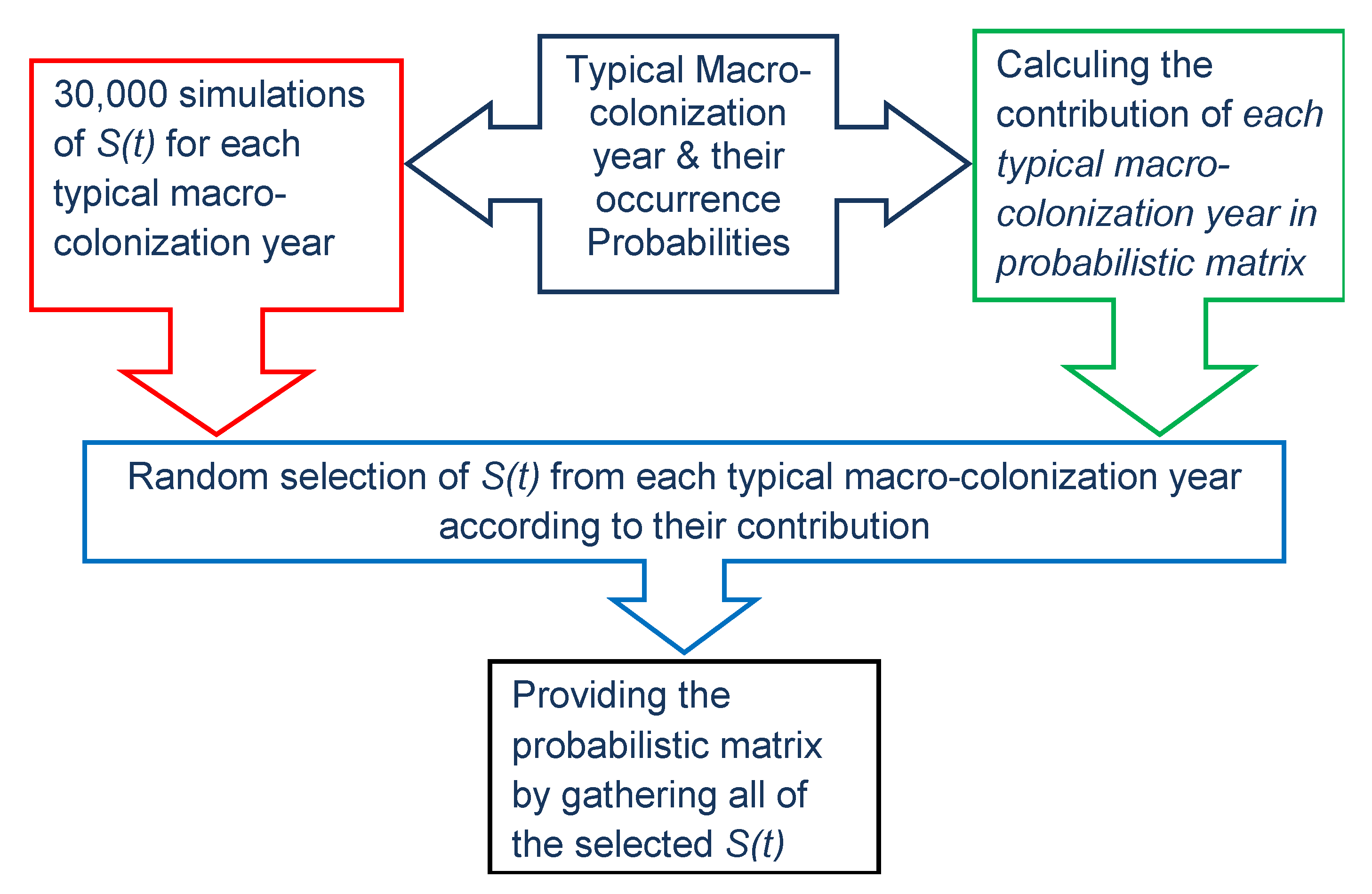
2.5. Database Post-Treatment, Virtual Database, and Aggregation of Influencing Factors
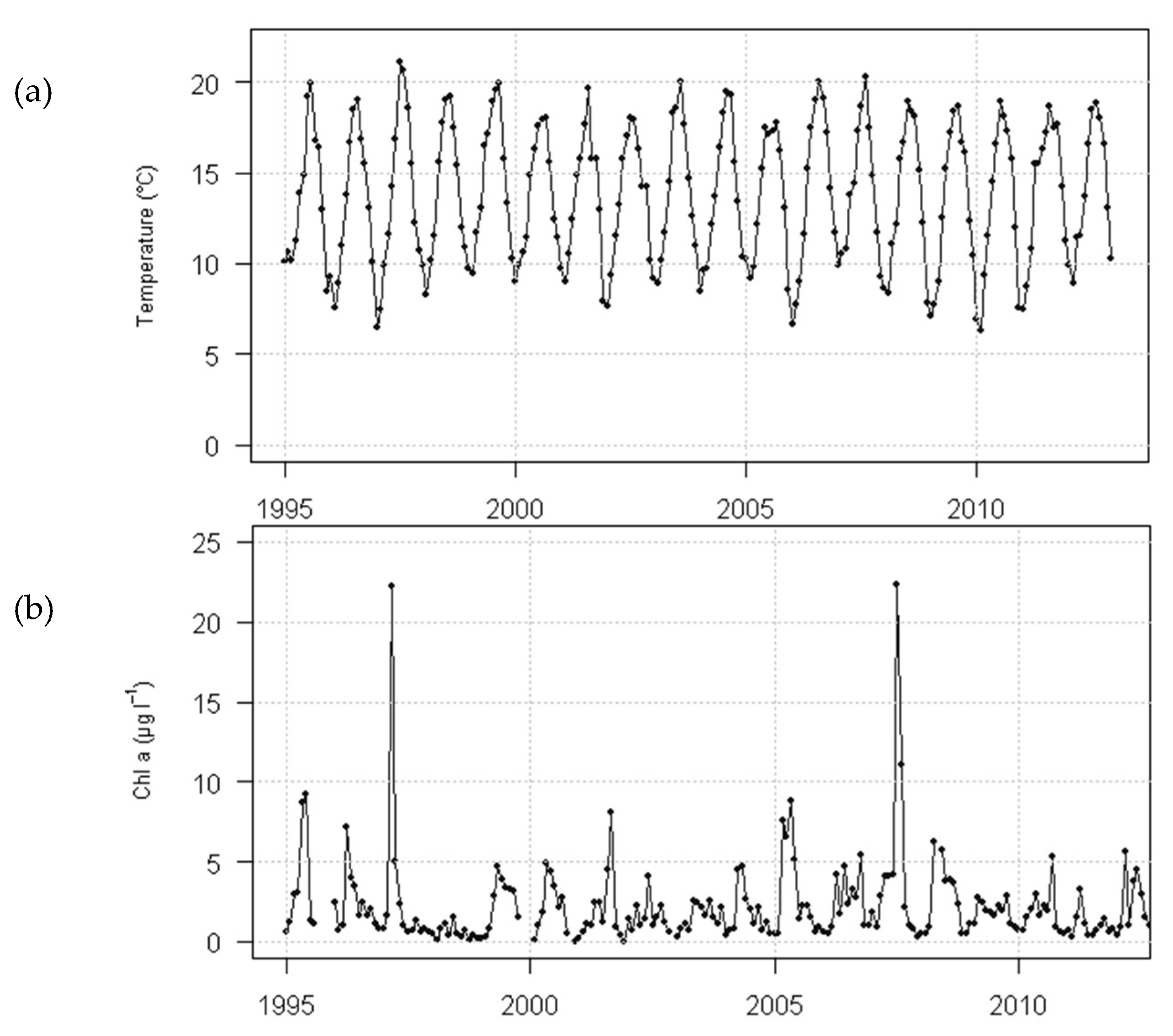
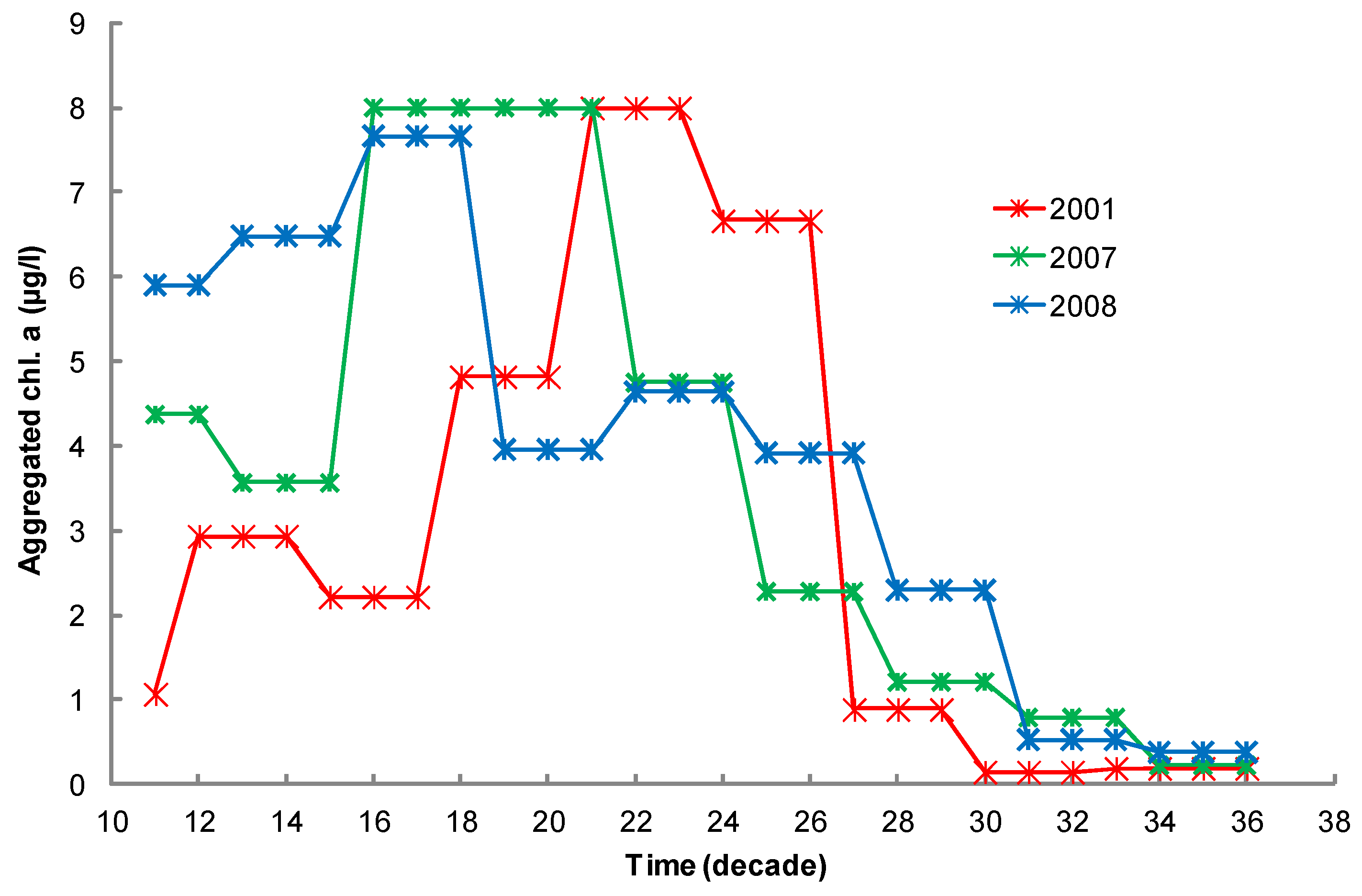
2.5.1. Environmental Data at the Case-Study Site
2.5.2. Environmental Data at the Case-Study Site
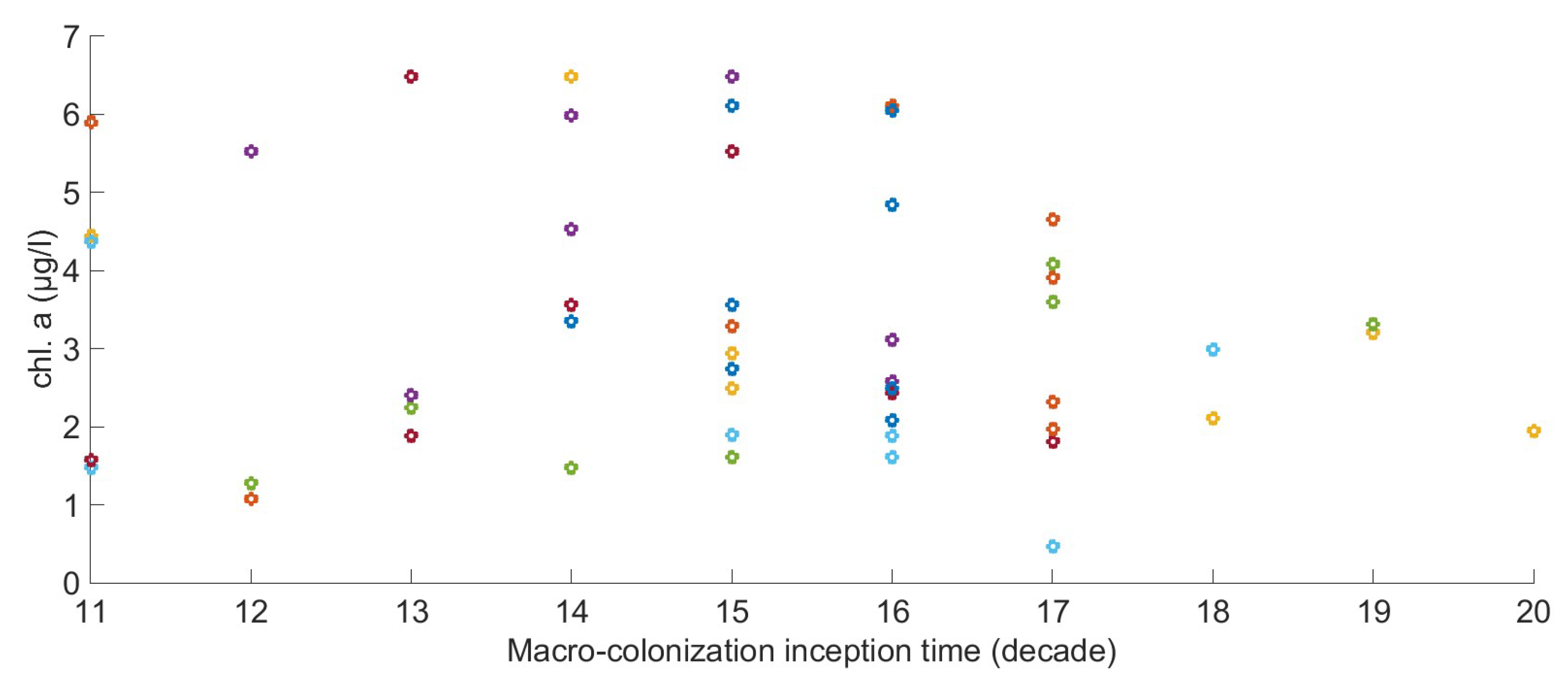
2.6. The Relation between Environmental Factors, Growth, and the Start of Macro-Colonization
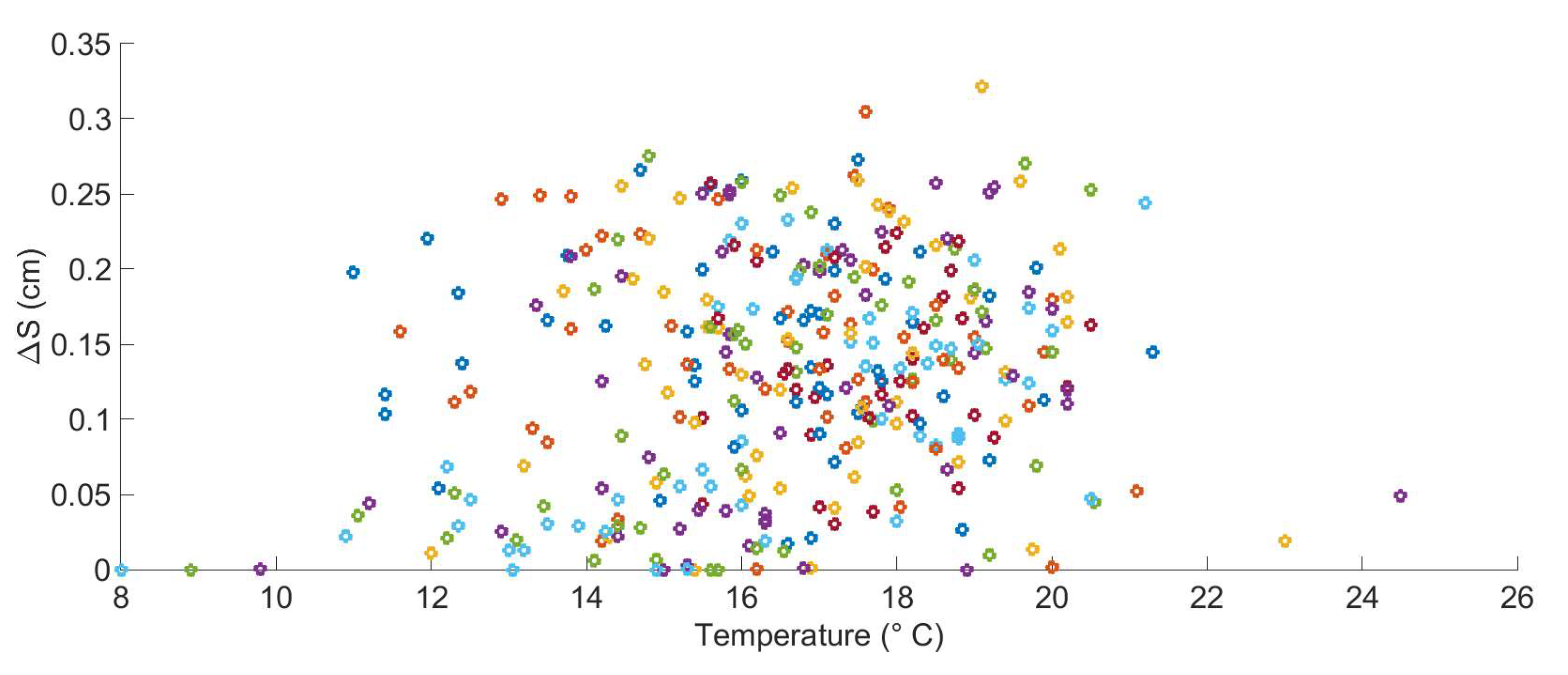
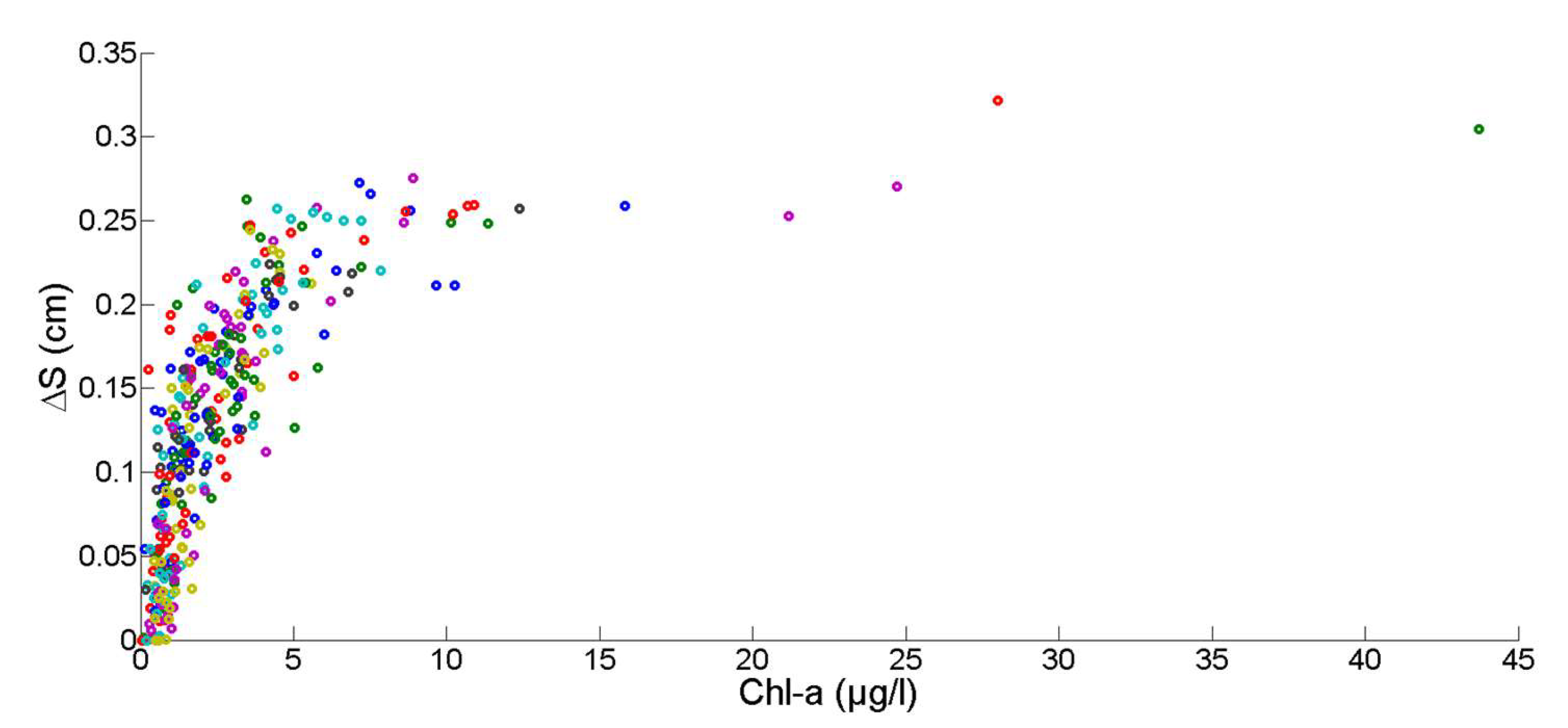
2.7. Chlorophyll Data Aggregation for Growth Computation
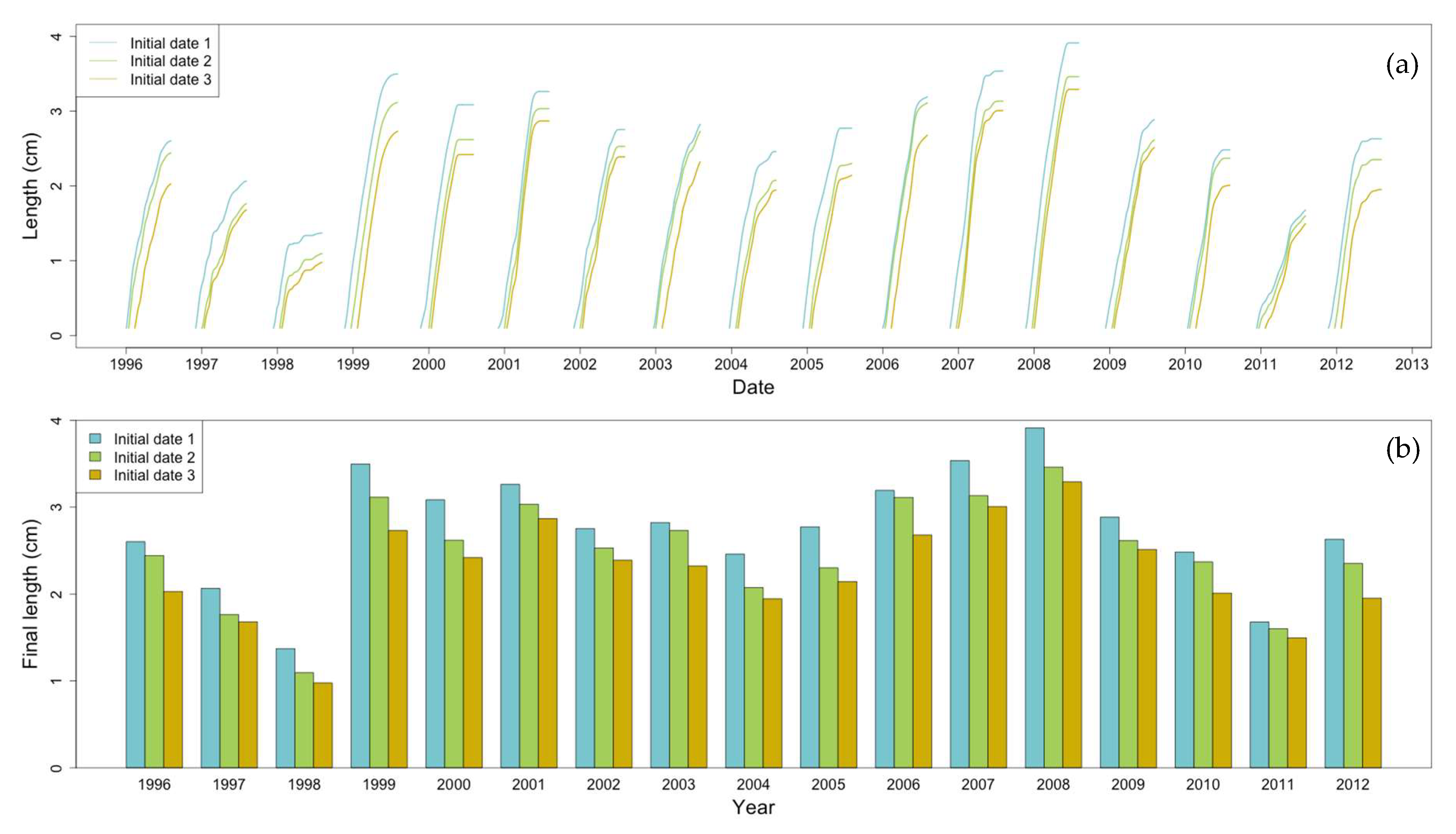
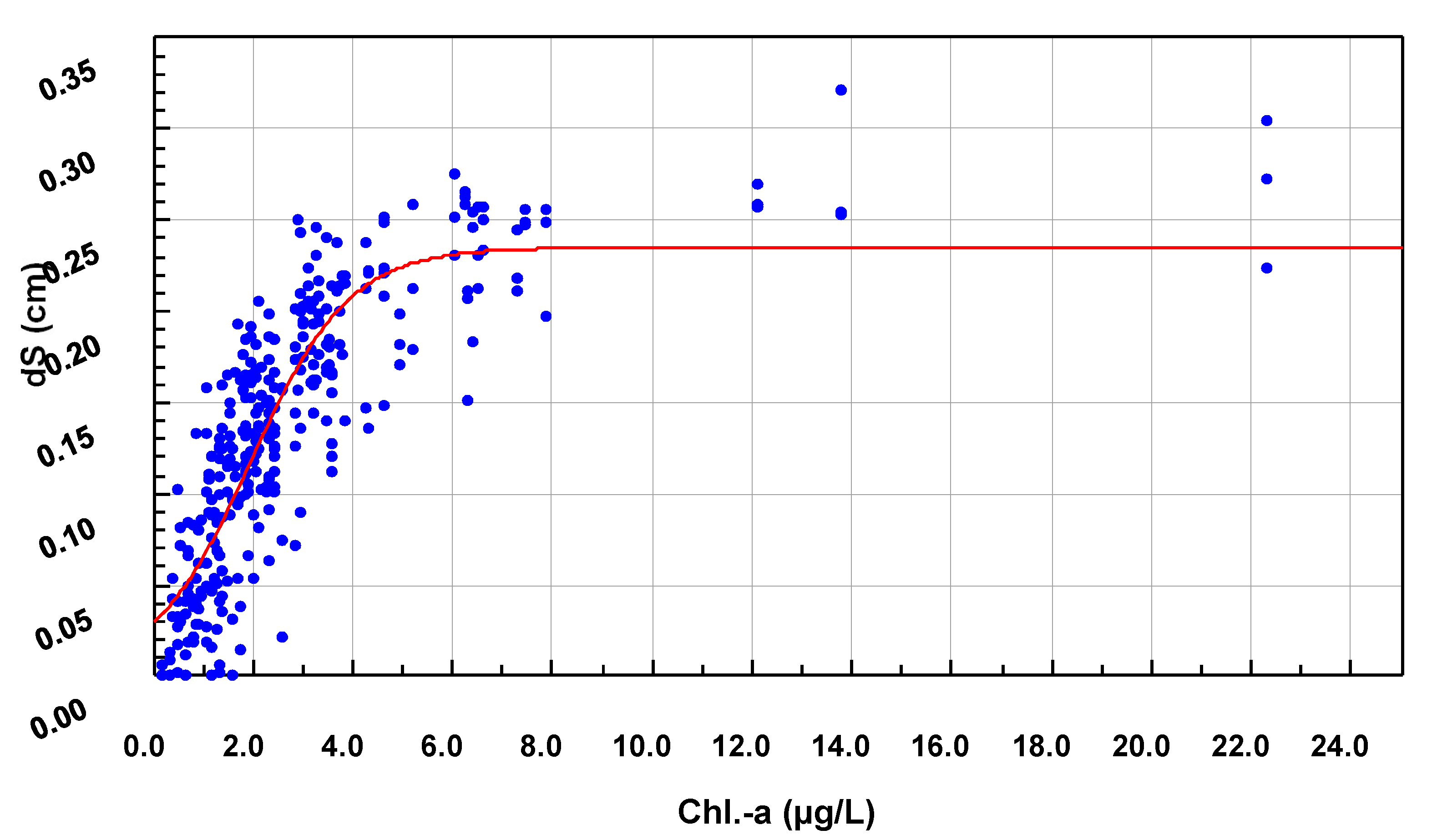
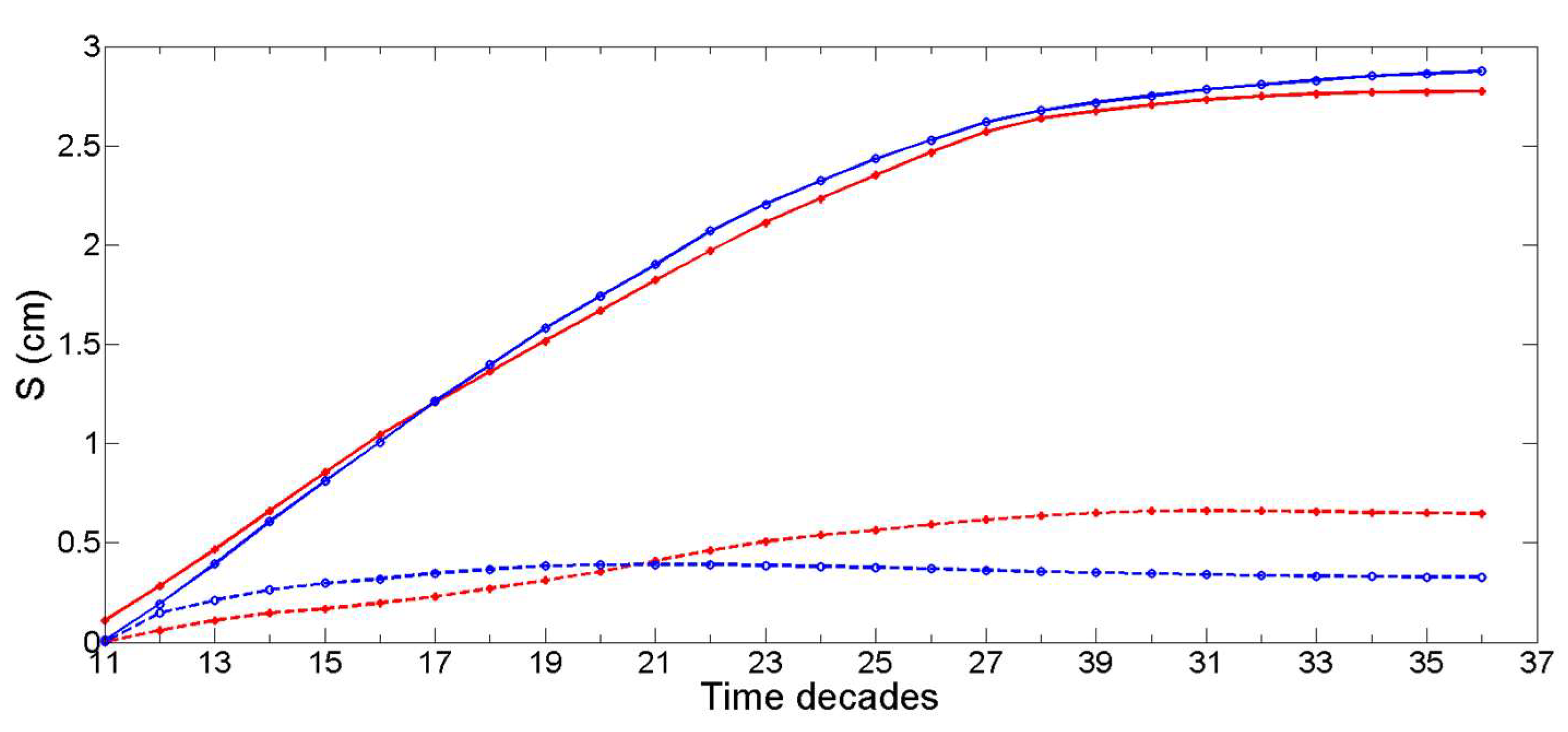
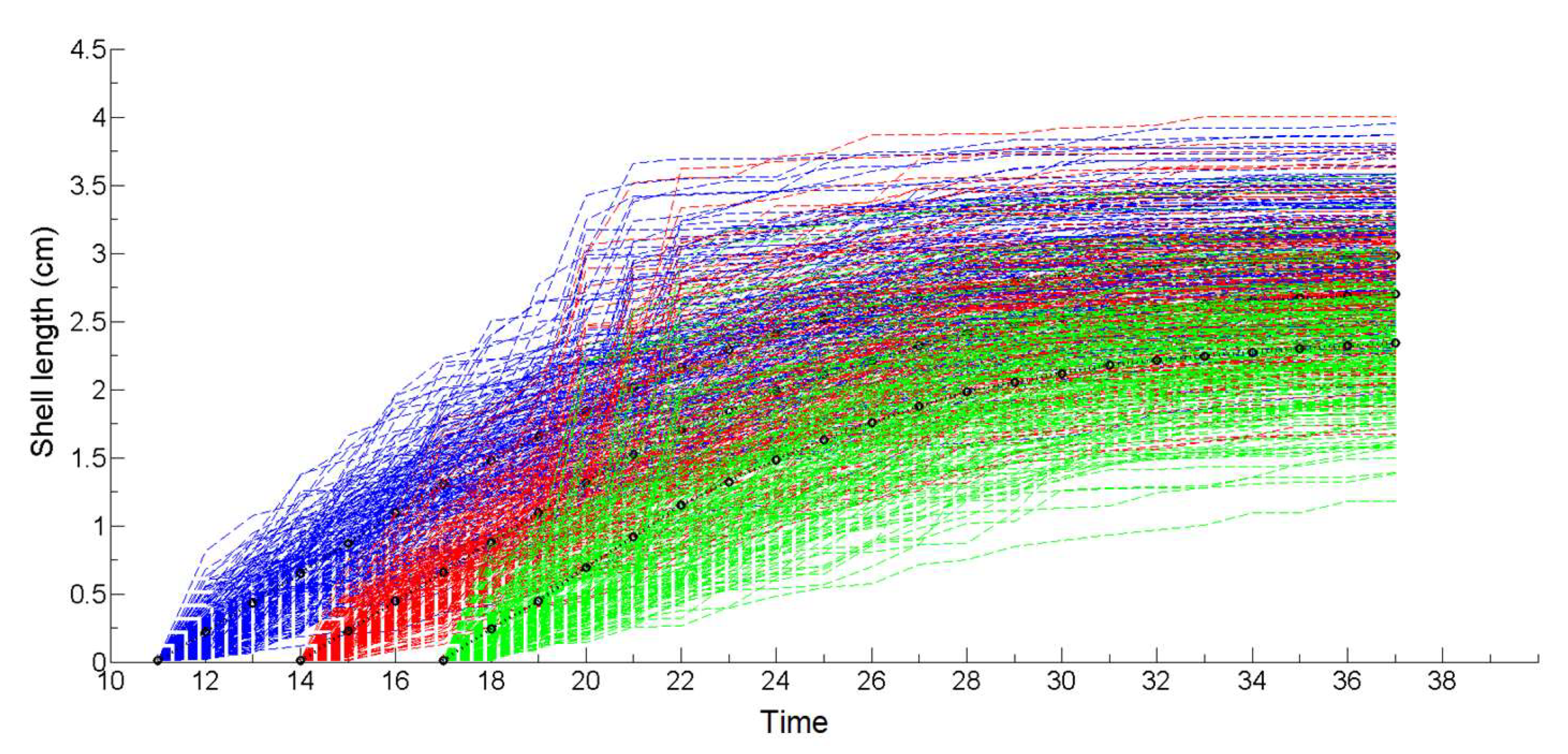
2.8. Non-Stationary Modeling of Shell Growth through Stochastic Gamma Process
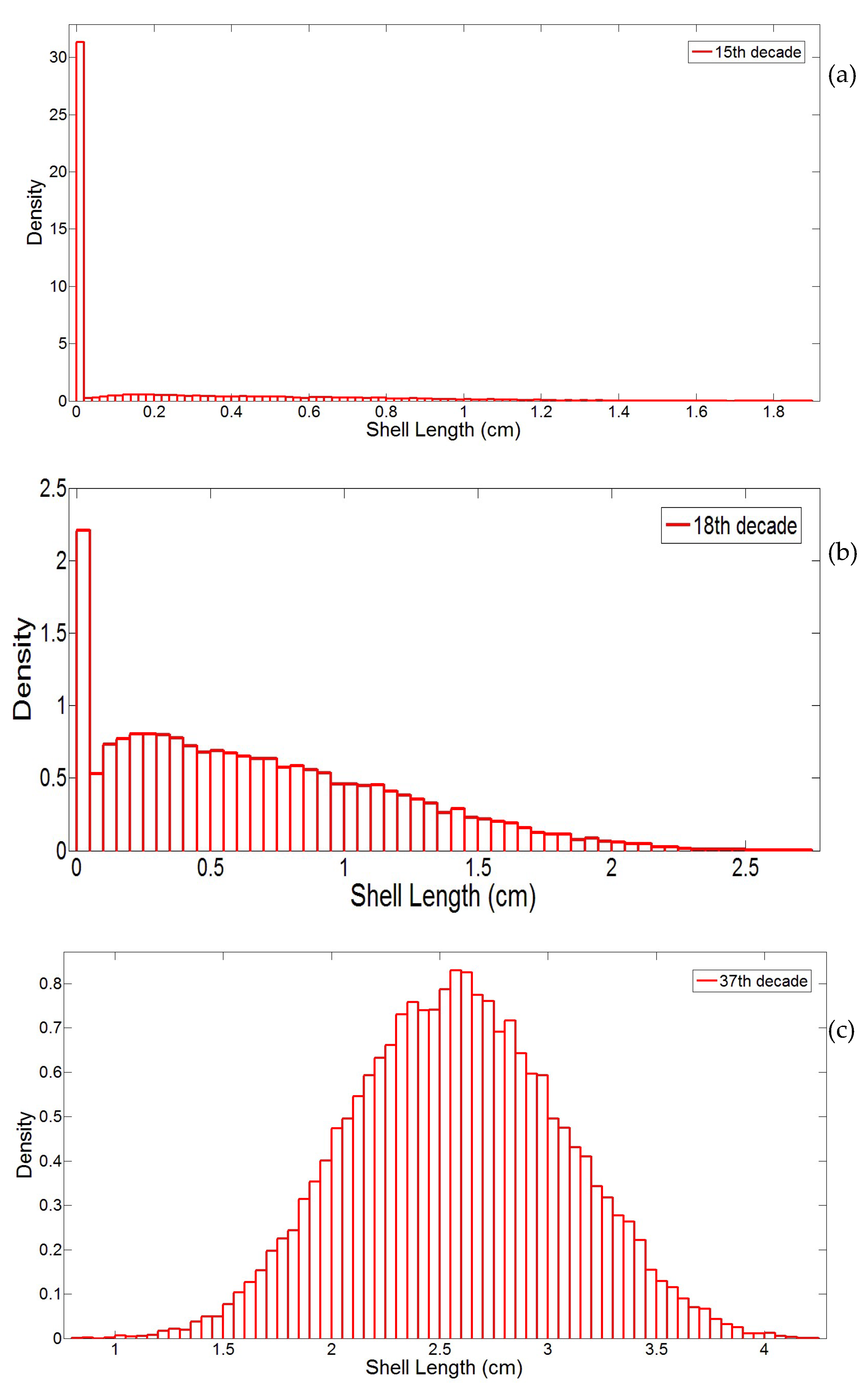
2.8.1. Growth Approximation through Gamma Processes Meta-Models
2.8.2. Parameter Estimation of the Gamma Process (Learning Phase)
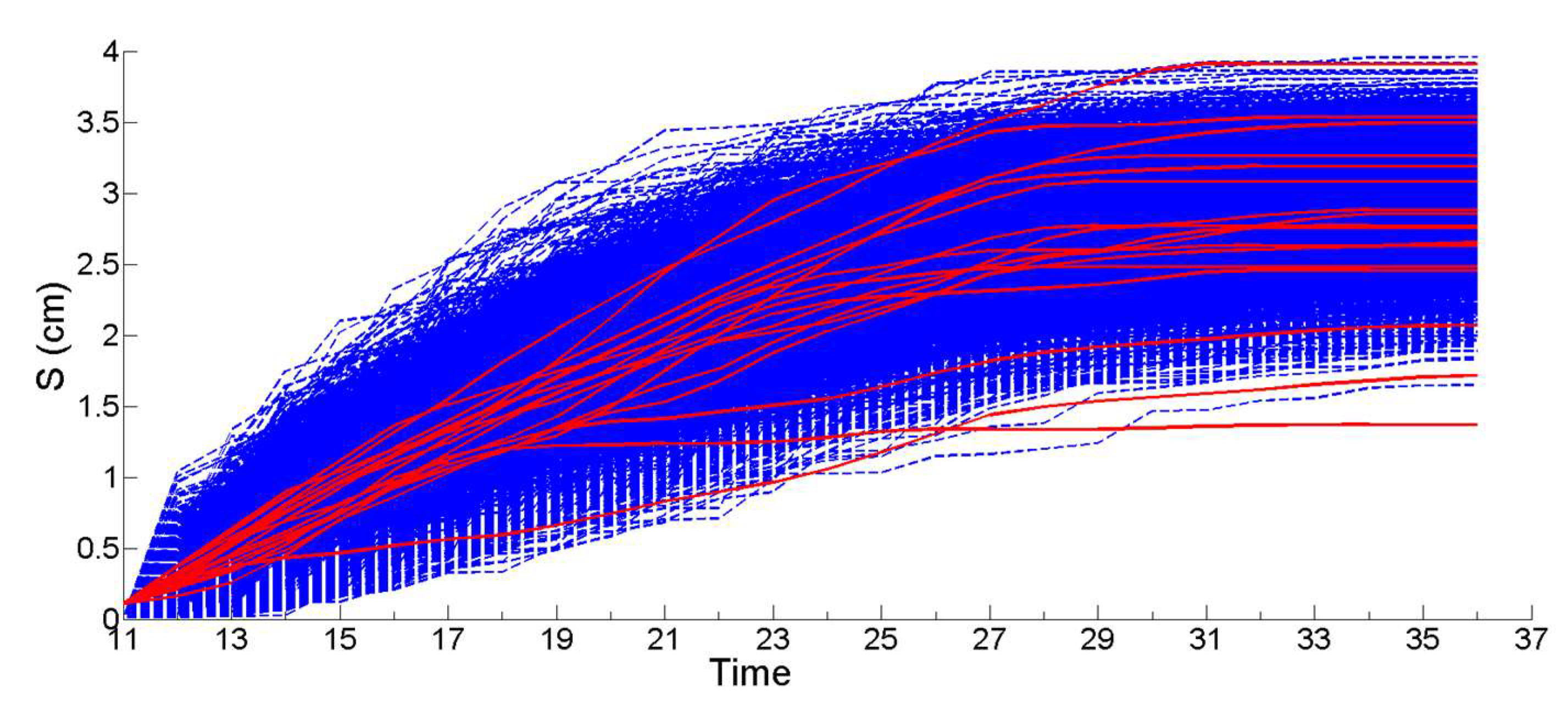
2.8.3. Stochastic Simulation from Gamma Process (Propagation Phase)
2.9. Effect of Marine Growth and Hydrodynamic Forces on Jackets
- (i)
- (ii)
- evaluation of hydrodynamic forces by the physical modeling of marine growth characteristics obtained from in-situ measurements [6,48]. These studies were based on inspections carried out during survey campaigns. They advocate guidelines for the probabilistic modeling of hydrodynamic forces at a given time. The biofouling database has been analyzed to propose a model of marine growth evolution and to update the design criterion. A physical response surface matrix has been proposed in order to provide a probabilistic modeling of the environmental loading on jacket type offshore structures. The key parameter is the increase of the structural diameter due to the marine growth thickness.
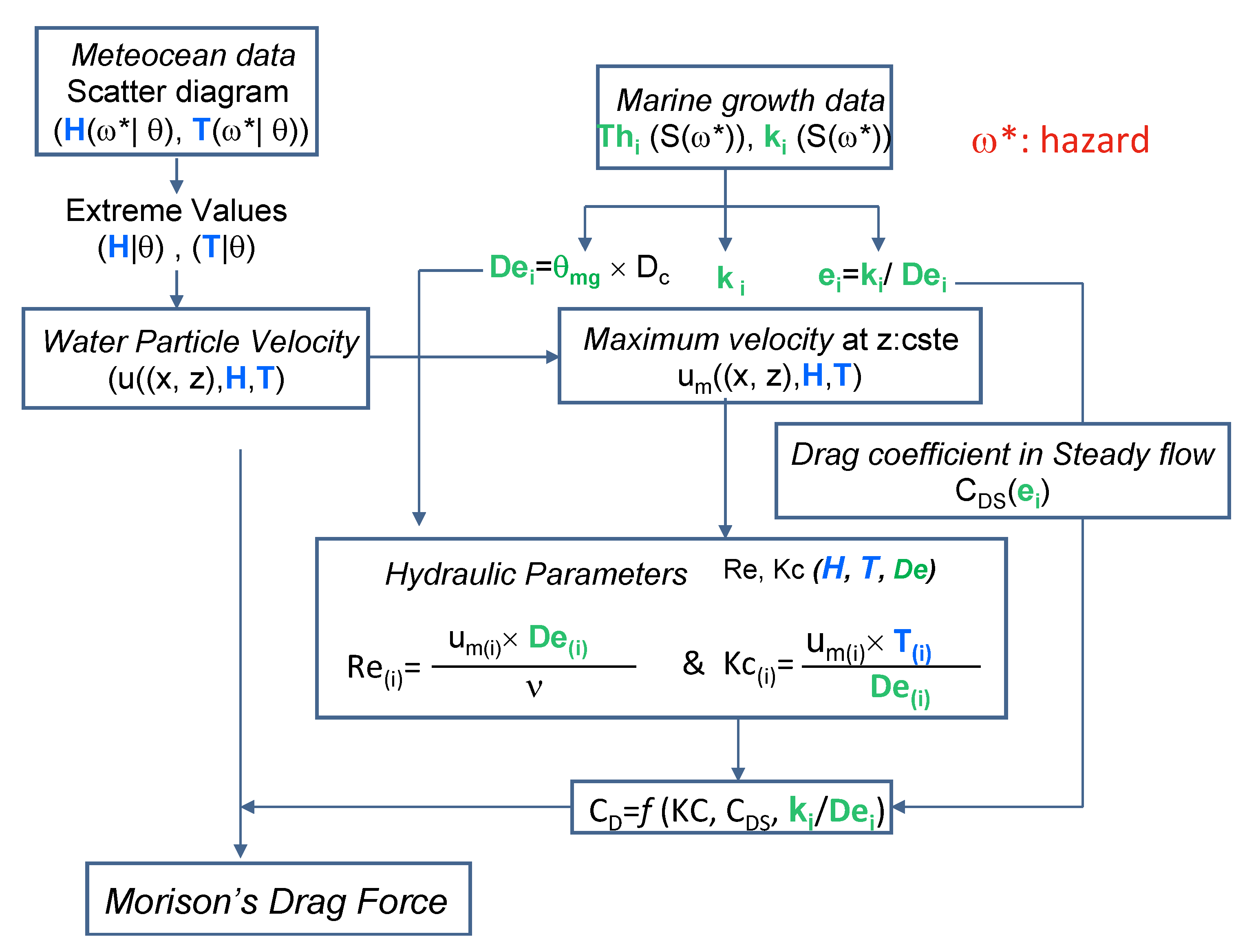
2.9.1. Effect of Marine Growth on Morison’s Equation
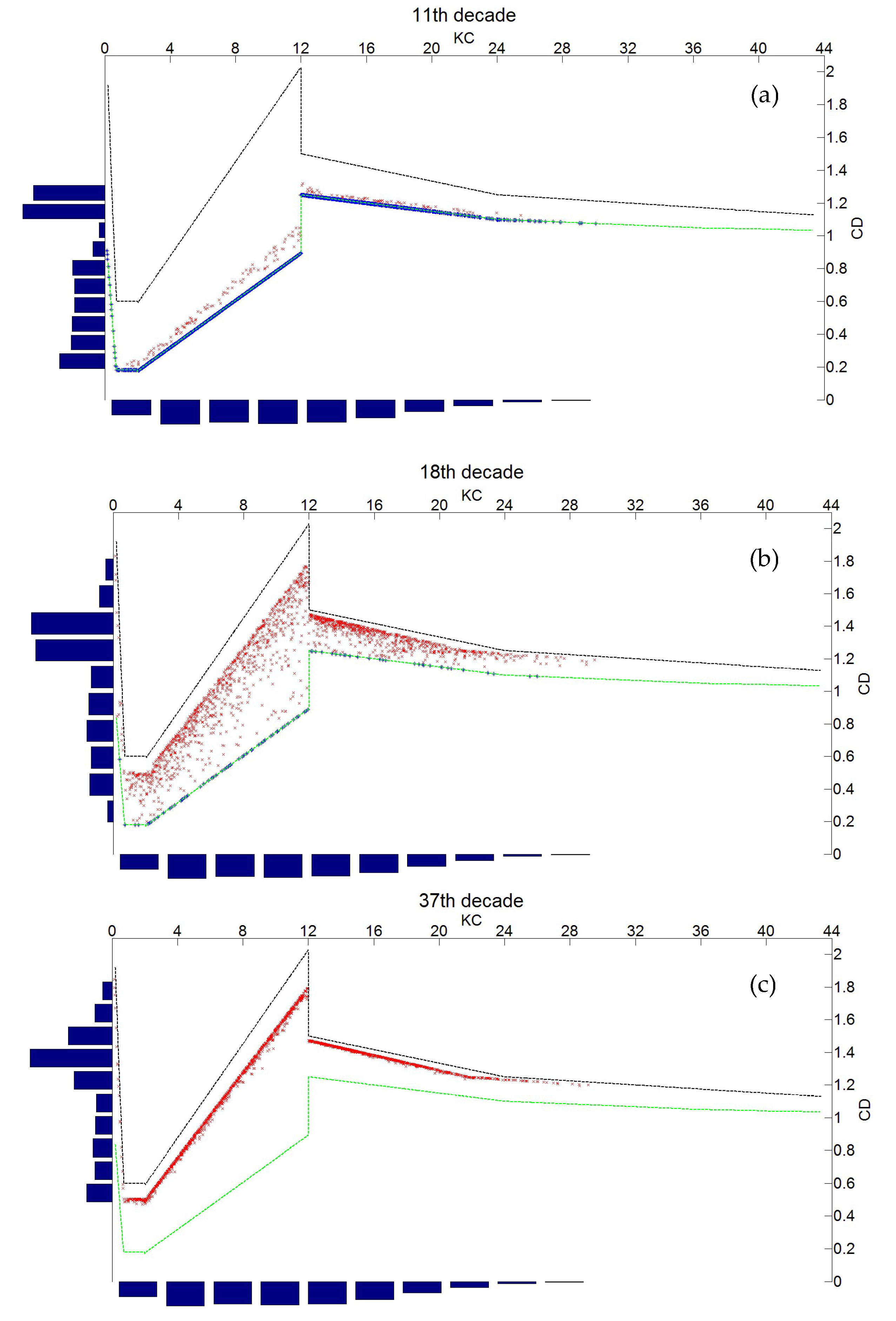
2.9.2. Stochastic Modeling of Marine Growth and Hydrodynamic Parameters
2.9.3. The Stochastic Modeling Wave Loading in the Presence of Marine Growth
- (#1) Statistical Identification: the employed parameters are the heights of extreme waves H and associated periods T. They are modeled with a random variable, whose probability is conditioned by the wave direction θ;
- (#2) A kinematic model for the fluid for computation of water particle velocity: the Stokes model [50] is used. It assumes that the fluid is Newtonian and irrotational and the trajectory of the fluid particles is elliptical. The kinematics field deduced from the velocity potential can be defined at any point M of coordinates x and z. The maximum velocity um (#5) is deduced and is used in the computation of KC and Re (#6).
- (#3) The fluid-structure Interaction model: this level is involved in the hydrodynamic coefficients determined by using the recommendation of [3].
- For the probabilistic modeling of CD, in order to avoid multiplying the case studies, only vertical elements under the wave crest are analyzed. This implies high horizontal speeds and accelerations that generate very small forces, which means that the inertia forces in (7) are very low and will be neglected in the following.
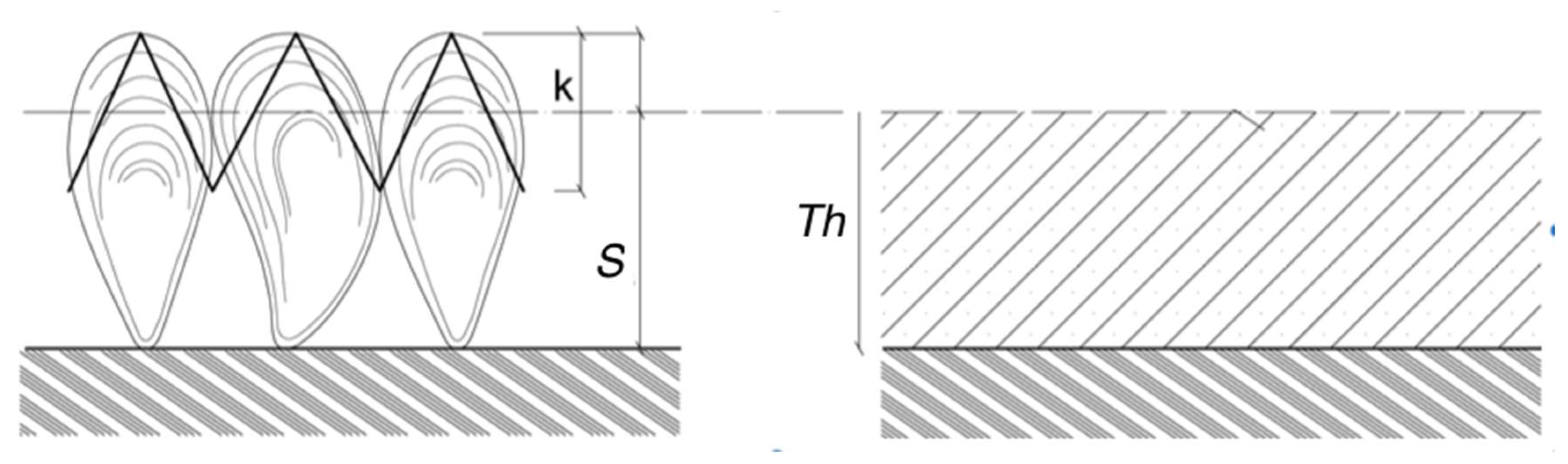
- (#4) The colonized diameter De(t) is a stochastic process that results from the increase Th(t) of the initial radius of the clean component. Starting from (8), the diameter is computed by multiplying Dc by the factor θmg. The latter is computed from the thickness Th(t) (12):
3. Results
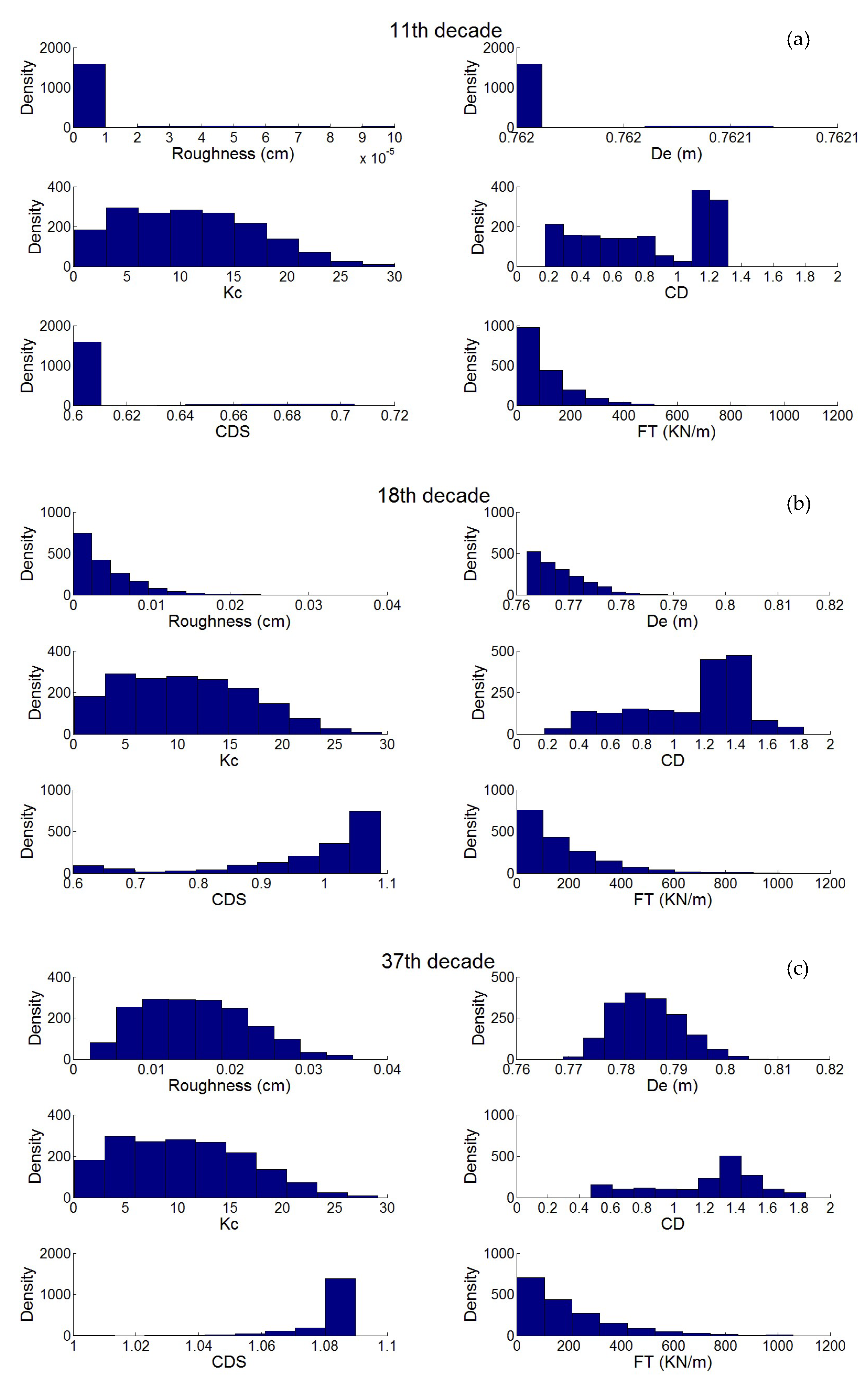
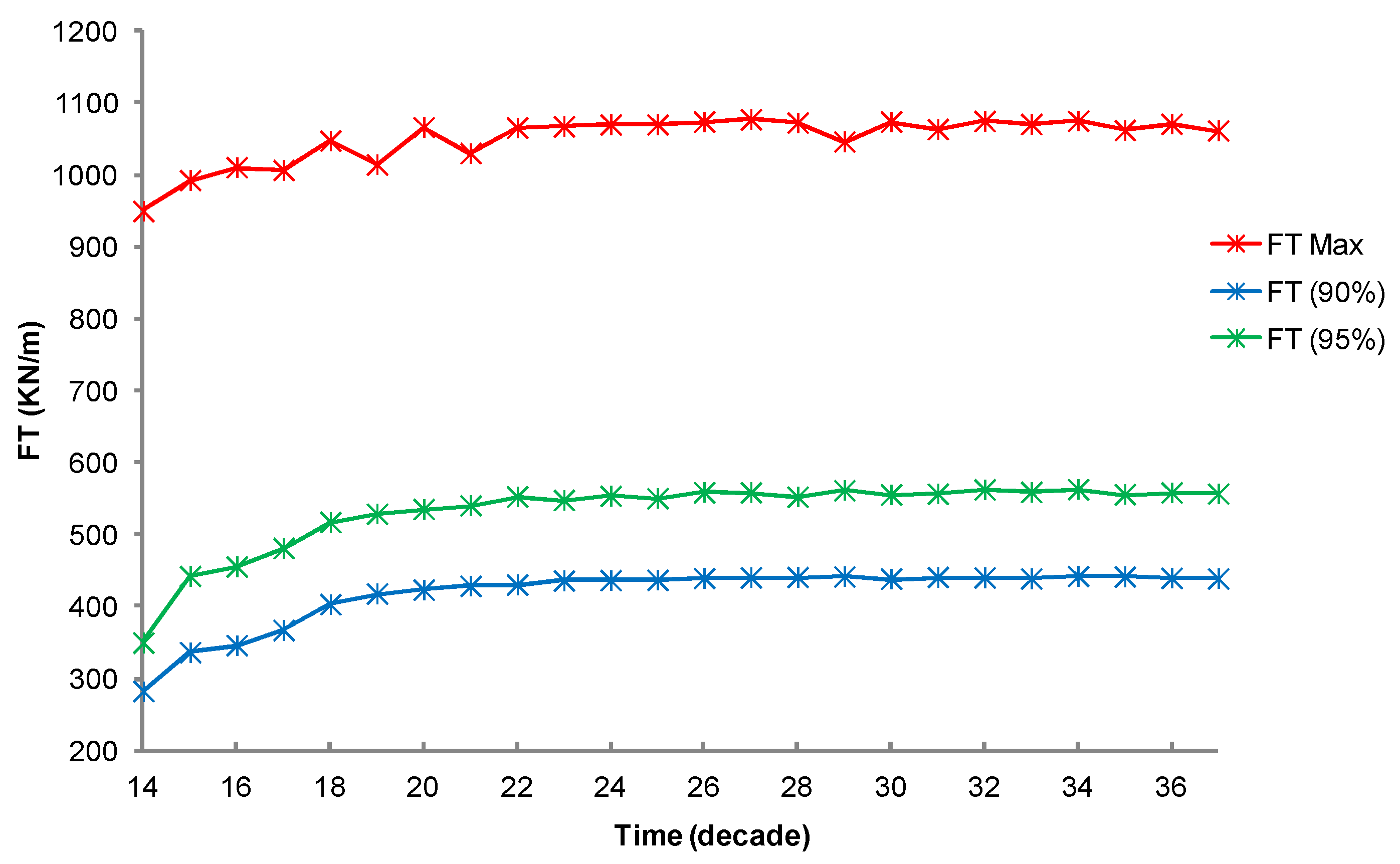
3.1. Simulation of the Drag Force Evolution from the Stochastic Time-Series of blue Mussels
3.2. Statistical Analysis of the Transfer of Distributions
4. Discussion
5. Conclusions
- -
- Environmental: due both to the physics of waves (height, period) and water parameters (temperature and chlorophyll-a).
- -
- Modeling: with an uncertainty of modeling from the shell size to the thickness and the roughness in the sense of API regulation.
- -
- Biological: accounting for the inter-individual variability.
- -
- Moreover, calculation of hydrodynamic forces due to the biocolonization using meteo-ocean data as well as biological data is a complex task and generates two types of difficulties.
- -
- First, the distribution of input variables that can be multi-modal (e.g., individual shell length) due to the various macro-colonization inception times.
- -
- Second, the nonlinear transfer from the Keulegan Carpenter number to drag coefficient generates bimodal distributions from mono-modal ones.
- -
- A single species was studied in a place where we can find barnacles and even algae. For the latter, relationships for the computation of drag coefficients are less developed and research is required.
- -
- There is uncertainty in the definition of roughness and its use by engineers, which is the reason why an uncertainty of modeling is added in this paper. Recent works [60] have proposed some improvements, but this is still an open area of study. Quantification from on site inspections is possible [54], thereby opening a new area for more representative tests in laboratories.
- -
- The probability of the occurrence of storms depends on seasons and could be introduced to reduce the conservatism.
- -
- Effects of the Cd variations on dynamics should be introduced to expand the method to fatigue assessment.
- -
- In the same manner, inertia forces and current could be added to get a more global influence of marine growth.
6. Patents
Author Contributions
Funding
Conflicts of Interest
Appendix A. Additional Information about the Growth of Blue Mussels


References
- Heaf, N.J. The Effect of Marine Growth on The Performance of Fixed Offshore Platforms in The North Sea. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 30 April–3 May 1979; p. 14. [Google Scholar] [CrossRef]
- Jusoh, I.; Wolfram, J. Effects of marine growth and hydrodynamic loading on offshore structures. J. Mek. 1996, 1, 77–98. [Google Scholar]
- API RP 2A WSD. Recommended Practice for Planning, Designing, and Constructing Fixed Offshore Platforms, 21st ed.; American Petroleum Institute: Washington, DC, USA, 2005; Volume 2. [Google Scholar]
- DNV. Recommended Practice Det Norske Veritas; DNV-RP-C20; DNV: Oslo, Norway, 2010. [Google Scholar]
- Faber, M.H.; Hansen, P.F.; Jepsen, F.D.; Moller, H.H. Reliability-Based Management of Marine Fouling. J. Offshore Mech. Arct. Eng. 2001, 123, 76. [Google Scholar] [CrossRef]
- Schoefs, F.; Boukinda, M.L. Sensitivity Approach for Modeling Stochastic Field of Keulegan–Carpenter and Reynolds Numbers Through a Matrix Response Surface. J. Offshore Mech. Arct. Eng. 2010, 132, 011602. [Google Scholar] [CrossRef]
- Boukinda, M.L. Surface de Réponse des Efforts de Houle des Structures Jackets Colonisées par des Bio-salissures. Ph.D. Thesis, Université de Nantes, Nantes, France, 2007. [Google Scholar]
- Schoefs, F.; Boukinda, M.L. Modelling of Marine Growth Effect on Offshore Structures Loading Using Kinematics Field of Water Particle. In Proceedings of the Fourteenth International Offshore and Polar Engineering Conference, Toulon, France, 23–28 May 2004; pp. 419–427. [Google Scholar]
- Joschko, T.J.; Buck, B.H.; Gutow, L.; Schröder, A. Colonization of an artificial hard substrate by Mytilus edulis in the German Bight. Mar. Biol. Res. 2008, 4, 350–360. [Google Scholar] [CrossRef]
- Maar, M.; Bolding, K.; Petersen, J.K.; Hansen, J.L.S.; Timmermann, K. Local effects of blue mussels around turbine foundations in an ecosystem model of Nysted off-shore wind farm, Denmark. J. Sea Res. 2009, 62, 159–174. [Google Scholar] [CrossRef]
- El Hajj, B.; Schoefs, F.; Castanier, B.; Yeung, T. A condition-based deterioration model for the stochastic dependency of corrosion rate and crack propagation in a submerged concrete structure. Comput. Aided Civ. Infrastruct. Eng. 2014, 32, 18–33. [Google Scholar] [CrossRef]
- Ameryoun, H. Probabilistic Modeling of Wave Actions on Jacket Type Offshore Wind Turbines in Presence of Marine Growth. Ph.D. Thesis, Université de Nantes, Nantes, France, 2015. [Google Scholar]
- Koojiman, S. Dynamic Energy and Mass Budgets in Biological Systems; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Koojiman, S. Dynamic Energy Budget Theory for Metabolic Organization. Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Dürr, S.; Thomason, J. Biofouling; Wiley-Blackwell: New York, NY, USA, 2009; Available online: http://eu.wiley.com/WileyCDA/WileyTitle/productCd-1405169265.html (accessed on 18 December 2009).
- Railkin, A.I. Marine Biofouling: Colonization Processes and Defenses; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Liu, Y. Modeling the Time-to-Corrosion Cracking of the Cover Concrete in Chloride Contaminated Reinforced Concrete Structures. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 1996. [Google Scholar]
- Newell, R.I.E. Species Profiles: Life Histories and Environmental Requirements of Coastal Fishes and Invertebrates (North and Mid-Atlantic); Biological Report, 82(11.102) TR EL-82-4 June; US dept of Interior/US Army Corps of Engineers: Baltimore, MD, USA, 1989. [Google Scholar]
- Bruijs, M.C.M. Biological Fouling Survey of Marine Fouling on Turbine Support Structures of the Offshore Windfarm Egmond aan Zee. Report Prepared for Noordzeewind; 50863511-TOS/PCW 10-4207, OWEZ_R_112_T1_20100226; KEMA Nederland, B.V.: Arnhem, The Netherlands, 2010. [Google Scholar]
- Langhamer, O.; Wilhelmsson, D.; Engström, J. Artificial reef effect and fouling impacts on offshore wave power foundations and buoys—A pilot study. Estuarine. Coast. Shelf Sci. 2009, 82, 426–432. [Google Scholar] [CrossRef]
- Gosling, E. Bivalve Molluscs: Biology, Ecology and Culture; Wiley-Blackwel: Hoboken, NJ, USA, 2003. [Google Scholar]
- Barillé Boyer, A.-L. Contribution à l’étude des potentialités conchylicoles du Pertuis Breton. Ph.D. Thesis, Université d’Aix-Marseille II, Marseille, France, 1996. [Google Scholar]
- Garen, P.; Robert, S.; Bougrier, S. Comparison of growth of mussel, Mytilus edulis, on longline, pole and bottom culture sites in the Pertuis Breton, France. Aquaculture 2004, 232, 511–524. [Google Scholar] [CrossRef]
- Rosland, R.; Strand, Ø.; Alunno-bruscia, M.; Bacher, C.; Strohmeier, T. Applying Dynamic Energy Budget (DEB) theory to simulate growth and bio-energetics of blue mussels under low seston conditions. J. Sea Res. 2009, 62, 49–61. [Google Scholar] [CrossRef]
- Widdows, J. Physiological ecology of mussel larvae. Aquaculture 1991, 94, 147–163. [Google Scholar] [CrossRef]
- Dutertre, M.; Beninger, P.G.; Barillé, L.; Papin, M.; Rosa, P.; Barillé, A.-L.; Haure, J. Temperature and seston quantity and quality effects on field reproduction of farmed oysters, Crassostrea gigas, in Bourgneuf Bay, France. Aquat. Living Resour. 2009, 22, 319–329. [Google Scholar] [CrossRef]
- Bayne, B.L. Growth and the delay of metamorphosis of the larvae of Mytilus edulis (L.). Ophelia 1965, 2, 1–47. [Google Scholar] [CrossRef]
- Bayne, B.L.; Worrall, C.M. Growth and Production of Mussels Mytilus edulis from Two Populations. Mar. Ecol. 1980, 3, 317–328. [Google Scholar] [CrossRef]
- Van Harden, R.; Koojiman, S. Application of a Dynamic Energy Budget Model to Mytilus edulis (L.). Neth. J. Sea Res. 1993, 31, 119–133. [Google Scholar] [CrossRef]
- Page, H.M.; Hubbard, D.M. Temporal and spatial patterns of growth in mussels Mytihs edulis on an offshore platform: Relationships to water temperature and food availability. Exp. Mar. Biol. Ecol. 1987, 111, 159–179. [Google Scholar] [CrossRef]
- Thomas, Y.; Mazurié, J.; Alunno-Bruscia, M.; Bacher, C.; Bouget, J.-F.; Gohin, F.; Pouvreau, S.; Struski, C. Modelling spatio-temporal variability of Mytilus edulis (L.) growth by forcing a dynamic energy budget model with satellite-derived environmental data. J. Sea Res. 2011, 66, 308–317. [Google Scholar] [CrossRef]
- Thompson, R. Production, reproductive effort, reproductive value and reproductive cost in a population of the blue mussel Mytilus edulis from a subarctic environment. Mar. Ecol. Prog. Ser. 1984, 16, 249–257. [Google Scholar] [CrossRef]
- REPHY dataset. French Observation and Monitoring program for Phytoplankton and Hydrology in coastal waters. 1987–2016. Metrop. Data 2017. [Google Scholar] [CrossRef]
- Hernandez-Farinas, T.; Soudant, D.; Barille, L.; Belin, C.; Lefebvre, A.; Bacher, C. Temporal changes in the phytoplankton community along the French coast of the eastern English Channel and the southern Bight of the North Sea. Mar. Sci. 2013, 70, 1439–1450. [Google Scholar] [CrossRef]
- Barillé, L.; Lerouxel, A.; Dutertre, M.; Haure, J.; Barillé, A.L.; Pouvreau, S.; Alunno-Bruscia, M. Growth of the Pacific oyster (Crassostrea gigas) in a high-turbidity environment: Comparison of model simulations based on scope for growth and dynamic energy budgets. J. Sea Res. 2011, 66, 392–402. [Google Scholar] [CrossRef]
- Handå, A.; Alver, M.; Edvardsen, C.V.; Halstensen, S.; Olsen, A.J.; Øie, G.; Reinertsen, H. Growth of farmed blue mussels (Mytilus edulis L.) in a Norwegian coastal area; comparison of food proxies by DEB modeling. J. Sea Res. 2011, 66, 297–307. [Google Scholar]
- Pouvreau, S.; Bourles, Y.; Lefebvre, S.; Gangnery, A.; Alunno-Bruscia, M. Application of a dynamic energy budget model to the Pacific oyster, Crassostrea gigas, reared under various environmental conditions. J. Sea Res. 2006, 56, 156–167. [Google Scholar] [CrossRef]
- Ren, J.S.; Ross, A.H. Environmental influence on mussel growth: A dynamic energy budget model and its application to the greenshell mussel Perna canaliculus. Ecol. Model. 2005, 189, 347–362. [Google Scholar] [CrossRef]
- Barillé, L.; Prou, J.; Héral, M.; Razet, D. Effects of high natural seston concentrations on the feeding, selection, and absorption of the oyster Crassostrea gigas (Thunberg). J. Exp. Mar. Biol. Ecol. 1997, 212, 149–172. [Google Scholar] [CrossRef]
- Bayne, B.L.; Newell, R.C. Physiological energetics of marine molluscs. Mollusca 1983, 4, 407–515. [Google Scholar]
- Van Noortwijk, J.M. A survey of the application of gamma processes in maintenance. Reliab. Eng. Syst. Saf. 2009, 94, 2–21. [Google Scholar] [CrossRef]
- Abdel-Hameed, M. A Gamma Wear Process. IEEE Trans. Reliab. 1975, R-24, 152–153. [Google Scholar] [CrossRef]
- Cheng, T.; Pandey, M.D.; Van Der Weide, J.A.M. The probability distribution of maintenance cost of a system affected by the gamma process of degradation: Finite time solution. Reliab. Eng. Syst. Saf. 2012, 108, 65–76. [Google Scholar] [CrossRef]
- Van Noortwijk, J.M.; Van der Weide, J.A.M.; Kallen, M.J.; Pandey, M.D. Gamma processes and peaks-over-threshold distributions for time-dependent reliability. Reliab. Eng. Syst. Saf. 2007, 92, 1651–1658. [Google Scholar] [CrossRef]
- Guida, M.; Postiglione, F.; Pulcini, G. A time-discrete extended gamma process for time-dependent degradation phenomena. Reliab. Eng. Syst. Saf. 2012, 105, 73–79. [Google Scholar] [CrossRef]
- Sarpkaya, T. On the Effect of Roughness on Cylinders. J. Offshore Mech. Arct. Eng. 1990, 112, 334. [Google Scholar] [CrossRef]
- Theophanatos, A. Marine Growth and the Hydrodynamic Loading of Offshore Structures. Ph.D. Thesis, University of Srathclyde, Glasgow, UK, 1988. [Google Scholar]
- Schoefs, F. Sensitivity approach for modelling the environmental loading of marine structures through a matrix response surface. Reliab. Eng. Syst. Saf. 2008, 93, 1004–1017. [Google Scholar] [CrossRef][Green Version]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The Force Exerted by Surface Waves on Piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Stokes, G.G. On the theory of oscillatory waves. Trans. Camb. Phil. Soc. 1847, 8, 441–455. [Google Scholar]
- Wolfram, J.; Jusoh, I.; Sell, D. Uncertainty in the Estimation of Fluid Loading Due to the Effects of Marine Growth, Safety and Reliability Symposium. In Proceedings of the 12th International Conference on Offshore Mechanics and Arctic Engineering (O.M.A.E’93), Glasgow, Scotland, UK, 20–24 June 1993; Volume II, pp. 219–228. [Google Scholar]
- Kasahara, Y.; Koterayama, W.; Shimazaki, K. Wave Forces Acting on Rough Circular Cylinders at High Reynolds Numbers. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2013; p. 12. [Google Scholar] [CrossRef]
- Troesch, A.W.; Kim, S.K. Hydrodynamic forces acting on cylinders oscillating at small amplitudes. J. Fluids Struct. 1991, 5, 113–126. [Google Scholar] [CrossRef]
- O’Byrne, M.; Schoefs, F.; Pakrashi, V.; Ghosh, B. An underwater lighting and turbidity image repository for analysing the performance of image based non-destructive techniques. Struct. Infrastruct. Eng. 2018, 14, 104–123. [Google Scholar] [CrossRef]
- O’Byrne, M.; Schoefs, F.; Pakrashi, V.; Ghosh, B. A Stereo-Matching Technique for Recovering 3D Information from Underwater Inspection Imagery. Comput. Aided Civ. Infrastruct. Eng. 2018, 33, 193–208. [Google Scholar] [CrossRef]
- O’Byrne, M.; Pakrashi, V.; Schoefs, F.; Ghosh, B. Semantic Segmentation of Underwater Imagery Using Deep Networks. J. Mar. Sci. Eng. 2018, 6, 93. [Google Scholar] [CrossRef]
- Zeinoddini, M.; Bakhtiari, A.; Schoefs, F.; Zandi, A.P. Towards an Understanding of the Marine Fouling Effects on VIV of Circular Cylinders: Partial Coverage Issue. Biofouling 2017, 33, 268–280. [Google Scholar] [CrossRef]
- Bakhtiari, A.; Schoefs, F.; Ameryoun, H. Unified Approach for Estimating of The Drag Coefficient In Offshore Structures In Presence Of Bio-Colonization. In Proceedings of the 37th International Conference on Offshore Mechanics and Arctic Engineering (O.M.A.E’18), Madrid, Spain, 17–22 June 2018; p. 78757. [Google Scholar]
- Nerzic, R.; Prevosto, M.; Frelin, C.; Quiniou, V. Joint Distributions for Wind/waves/current in West Africa and derivation of Multi Variate Extreme I-FORM Contours. In Proceedings of the 17th International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007; pp. 81–88. [Google Scholar]
- Schoefs, F.; Bakhtiari, A.; Hameryoun, H.; Quillien, N.; Damblans, G.; Reynaud, M.; Berhault, C.; O’Byrne, M. Assessing and modeling the thickness and roughness of marine growth for load computation on mooring lines. In Proceedings of the Floating Offshore Wind Turbine Conference (FOWT 2019), Montpellier, France, 24–26 April 2019. [Google Scholar]
| Development Type | Occurrence | Probability |
|---|---|---|
| SSS | 2 | 0.12 |
| SSF | 10 | 0.59 |
| SFS | 0 | 0.00 |
| SFF | 5 | 0.29 |
| Start of Macro-Colonization | Occurrence | Probability | ||
|---|---|---|---|---|
| 11 | 14 | 15 | 2 | 0.12 |
| 11 | 14 | 17 | 2 | 0.12 |
| 11 | 15 | 16 | 1 | 0.06 |
| 12 | 15 | 16 | 3 | 0.18 |
| 13 | 14 | 17 | 1 | 0.06 |
| 13 | 16 | 17 | 3 | 0.18 |
| 14 | 15 | 18 | 1 | 0.06 |
| 14 | 17 | 18 | 1 | 0.06 |
| 15 | 16 | 19 | 2 | 0.12 |
| 16 | 17 | 20 | 1 | 0.06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ameryoun, H.; Schoefs, F.; Barillé, L.; Thomas, Y. Stochastic Modeling of Forces on Jacket-Type Offshore Structures Colonized by Marine Growth. J. Mar. Sci. Eng. 2019, 7, 158. https://doi.org/10.3390/jmse7050158
Ameryoun H, Schoefs F, Barillé L, Thomas Y. Stochastic Modeling of Forces on Jacket-Type Offshore Structures Colonized by Marine Growth. Journal of Marine Science and Engineering. 2019; 7(5):158. https://doi.org/10.3390/jmse7050158
Chicago/Turabian StyleAmeryoun, Hamed, Franck Schoefs, Laurent Barillé, and Yoann Thomas. 2019. "Stochastic Modeling of Forces on Jacket-Type Offshore Structures Colonized by Marine Growth" Journal of Marine Science and Engineering 7, no. 5: 158. https://doi.org/10.3390/jmse7050158
APA StyleAmeryoun, H., Schoefs, F., Barillé, L., & Thomas, Y. (2019). Stochastic Modeling of Forces on Jacket-Type Offshore Structures Colonized by Marine Growth. Journal of Marine Science and Engineering, 7(5), 158. https://doi.org/10.3390/jmse7050158






