1. Introduction
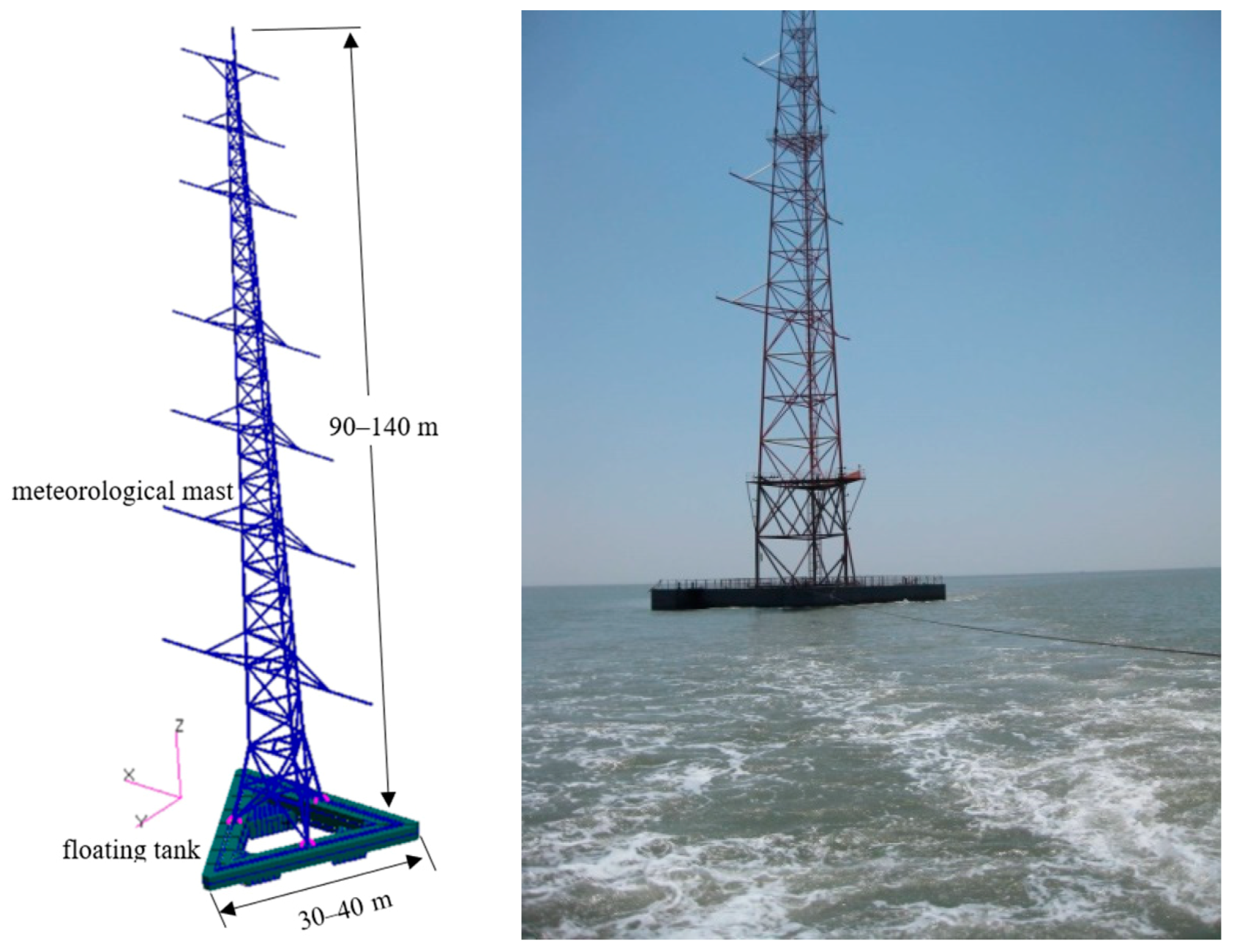
The development of offshore wind turbine power characteristics is based on the anemometer technology including both meteorological mast structures and measurement devices [
1]. While the primary problem for an offshore meteorological mast is associated with the structure design. Offshore meteorological masts are usually required to be installed on a fixed or a floating foundation. It can be expensive to install such a foundation or platform and maintain the instrument in an offshore location [
1]. Tianjin University and Dao Da Heavy Industry Company (DDHI) developed an offshore meteorological mast with an innovative foundation as an integrated structure (OIMM) that reduces costs by shortening the installation process and narrowing down the required amount of marine operation equipment [
2,
3]. This offshore integrated meteorological mast (OIMM) is shown in
Figure 1 with the transporting operation. The OIMM excels in two aspects: the integrated construction and the integrated installation. It can be manufactured onshore, hoisted into the sea and wet towed to an installation site. Since the structure has a big triangular floating tank, thus it can be self-floating and wet towed. As can be seen in
Figure 1, the OIMM has three major components: the upper meteorological mast, the floating tank, and the anti-slide skirt plates (bottom).
The design concept of this OIMM is based on many former research [
4,
5,
6] about the one-step-installation technology applied in the lager-scale composite bucket foundation (CBF). However, the construction and installation process for the OIMM are more simplified and different, because it has a relatively small dimensional size of infrastructure and a much higher superstructure. Generally, the entire OIMM weights about 300 t, and it has a height varying from 90–140 m, which can be adjusted based on specific requirements. The huge floating tank usually has multiple subdivisions inside to function as individual ballast compartments and to facilitate the stability adjustment during the wet-towing. It can also function as a gravity type foundation during the service life. The upper structure is a meteorological mast that carries many wind measurement devices. The bottom anti-slide skirt plates penetrate the sea bed working as suction caissons, and providing horizontal righting moment by the lateral resistance.
Many publications are focused on the offshore structure installation technology to understand the behavior of the structure and estimate the feasibility of this installation process. The basic dynamics of a subsea template, assembled system, were studied by calculating the dynamic forces and displacements by using time integration in SIMO (simulation of marine operations, SESAM package) [
7,
8]. They estimated the tension of a lift wire by SIMO and a simplified method simulating this dynamic system which agreed well with the experimental investigation. The feasibility of dry transport a TLP (tension leg platform) by a heavy lift transport vessel was studied, and the motion behavior of TLP structure and its transport vessel were evaluated [
9]. Eriksson and Kullander [
10] conducted a wet towing of a substructure with special equipment and vessels in Sweden. Some researchers focus on the towing stability feature and important influence factors in terms of the different sea conditions for a floating platform and offshore wind turbines [
11,
12,
13,
14]. A dynamic analysis of the wet tow for a floating wind turbine based on a multi-body model in SESAM has been performed by Ding et al., and the towline force and the stability features are studied [
15]. While a comparison of the cost estimation between the dry towing and the wet towing for a semisubmersible platform, conducted by Kim et al. [
16], suggests that the wet towing is more cost-saving for this structure. More installation solutions, especially for deepwater structures, backed by engineering tools and numerical simulation methods are discussed by Wang et al. [
17] with main characteristics and critical challenges.
Little research has been done on the offshore meteorological mast, especially for the transport operation. Based on the above research, this paper adopts two special wet towing methods to the innovative OIMM and compares the corresponding dynamic performance by using the numerical simulation software MOSES (offshore platform design and installation software). The purpose is to obtain the feasibility of the two towing methods with respect to its reliability and operability.
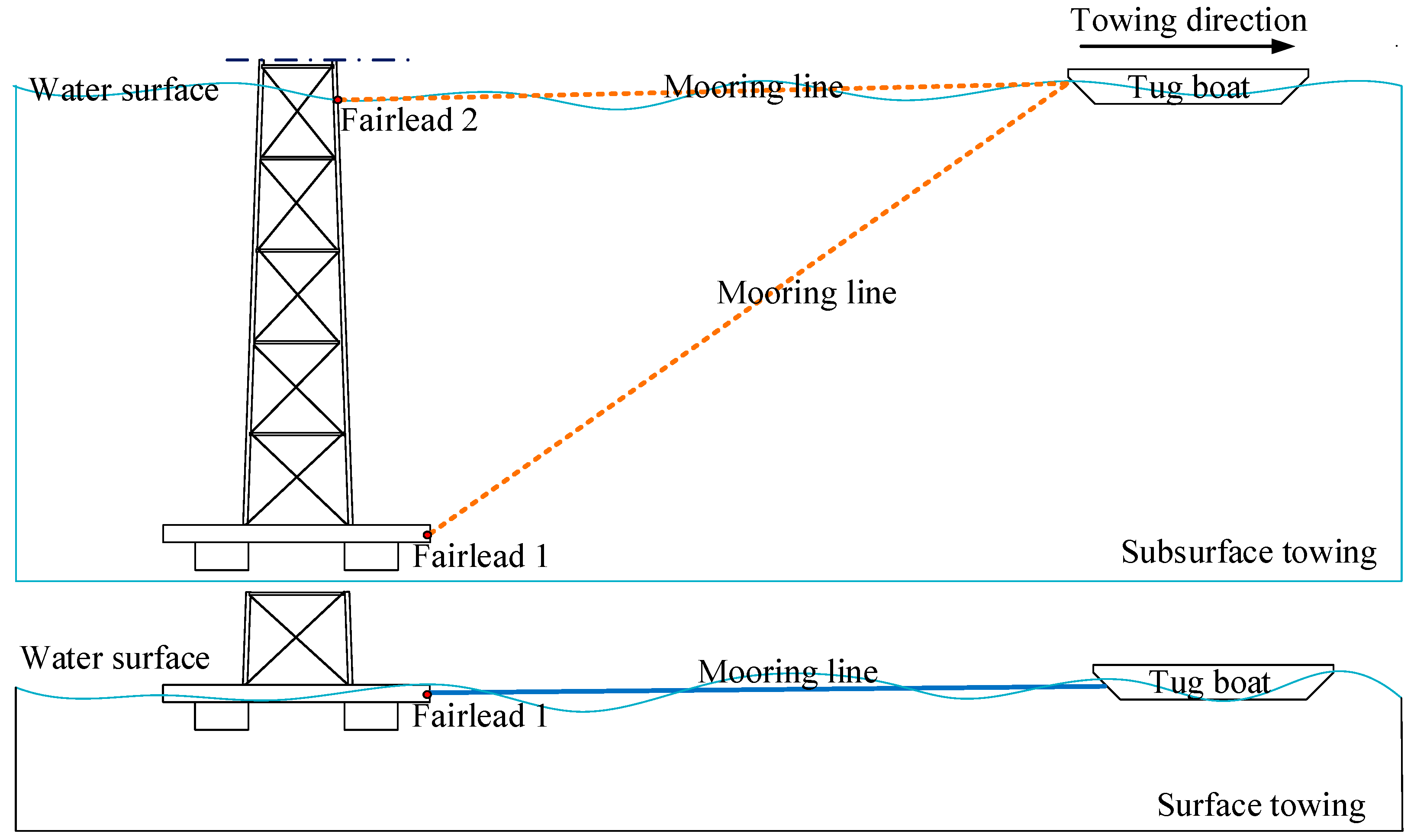
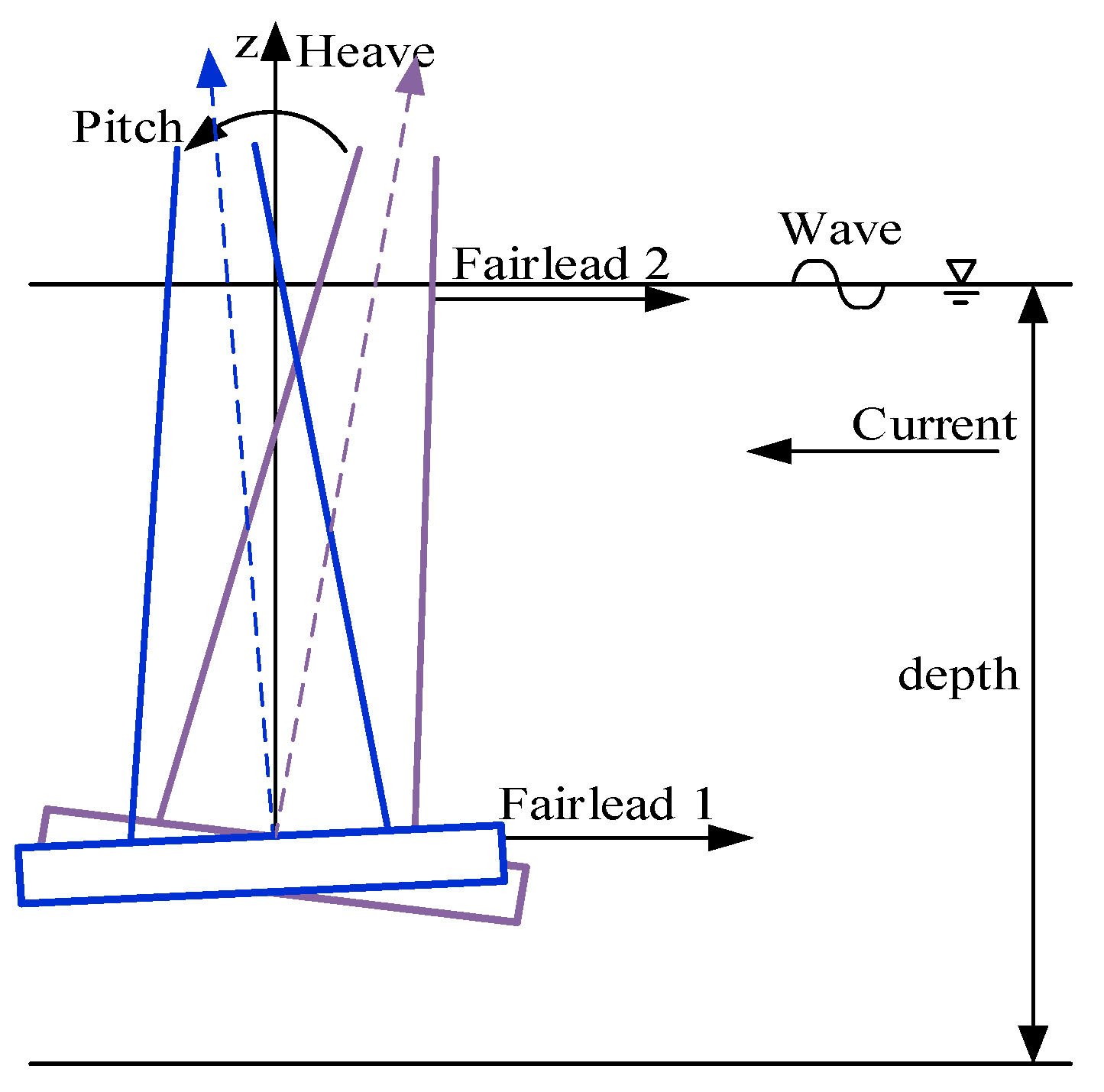
Figure 2 demonstrates the detailed information of the applied towing methods: the surface towing and the submerged towing (or subsurface towing). As for the submerged towing method, the mooring point can either be attached to the floating tank (fairlead 1) or to the mast (fairlead 2). While for the surface towing method, the mooring point is attached to the floating tank (fairlead 1). The OIMM is designed to be suitable for a water depth around 50 m. Therefore, when performing a submerged towing simulation, the submerged depth of the OIMM is defined varying within 0–40 m. For the surface towing method, it is simple with only one submerged depth (draft). The towing resistance based on these two methods is obtained and compared between the MOSES simulation and the manual computation method. The towing speed and hydrodynamic motion responses relating to the mooring positions are also considered and compared. The results can provide recommendations and references for the estimation of the feasibility of the two methods and on the optimization of the towing operation for OIMM.
The paper is organized as follows.
Section 2 introduces the relevant methods for the computation of the towing resistance and the hydrodynamic theory. A comparison of towing resistance between the numerical method and manual method is shown in
Section 3, as well as the detailed explanations about the towing speed and the mooring positions.
Section 4 illustrates the results based on the discussion in
Section 3, and conclusions are drawn in
Section 5.
2. Theory Background
The towing resistance is a basic parameter, on which the towing system depends. The estimation methods have been investigated by many researchers [
18,
19] in terms of the speed reduction and numerical calculation. The total resistance for different sea states can be described by four different types of resistance: surface friction, energy loss due to wave generating, energy loss due to current, wind resistance. For low speed towing, the surface friction counts for a majority. According to DNV-RP-H103 [
20], the tug will have the maximum towing force at zero velocity and in the absence of wind, waves and current, and the available towing force decreases with forward velocity. In this paper, the towing resistance is obtained from two methods: the numerical computation by MOSES, and the manual computation by the Guidelines for Towage at Sea (CCS code) [
21].
2.1. Towing Resistance By MOSES
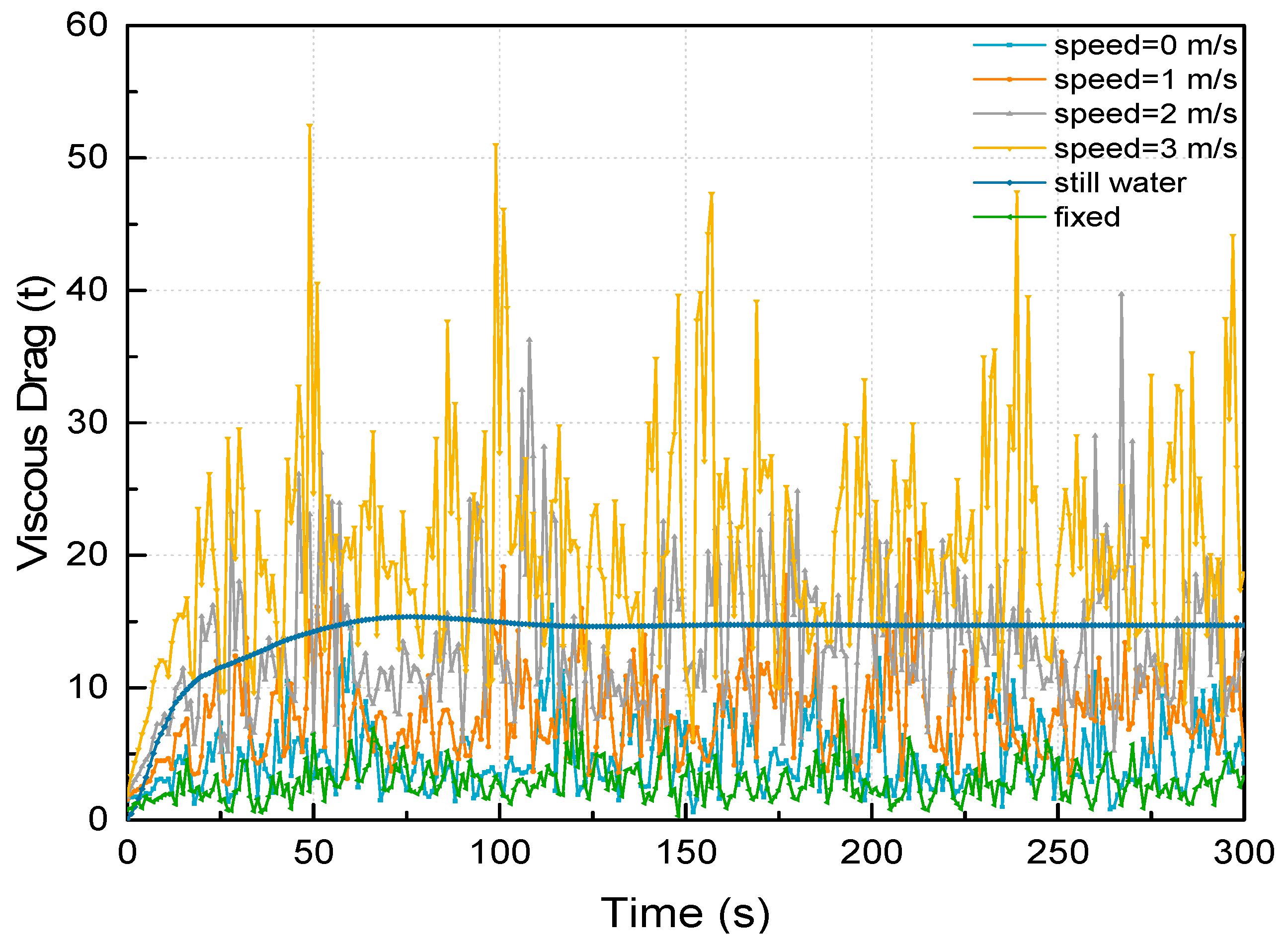
In MOSES, the towing resistance is primarily influenced by the wind force and the viscous drag force. The viscous drag force is illustrated as a portion of the system which is the velocity squared term in Morison’s equation, the viscous roll damping, or the viscous drag on a piece. This can be either an excitation due to wave or current, or a damping in still water [
22]. Generally, MOSES employs three hydrodynamic theories: Morison’s equation, strip theory, and 3D-diffraction theory. The Morison’s Equation is used for beam element and the viscous drag will be computed. For panel model, the 3D-diffraction theory is applied.
The drag force on a cylinder in an unsteady viscous flow is determined by Morison’s Equation, which consists of a combination of an inertia term and a drag term:
where
is the force per unit length of a cylinder [N/m],
is the diameter of cylinder [m],
is the density of fluid [kg/m
3],
is the mass coefficient,
is the drag coefficient,
is the acceleration [m/s
2].
Drag force on submerged element consists mainly of friction resistance and pressure resistance. Friction resistance can be expressed as:
where
is the friction resistance on object [N] and
is the towing velocity [m/s].
is the dimensionless friction coefficient depended on the Reynolds number.
is the wet surface area of the object [m
2].
The pressure distribution on panel element can be found by velocity potential function and Bernoulli’s equation with boundary conditions [
23].
where
is the pressure in Bernoulli’s equation,
is an arbitrary function of time.
2.2. Towing Resistance By Code
As for the manual computation, the Guidelines for Towage at Sea (CCS code) provides an estimation of ocean towage resistance considering the towing speed, by the following empirical equation:
where:
Rf and
RB are the friction and the residual resistance of towed vessel, in kN;
Rft and
RBt are the friction and the residual resistance of towing vessel, in kN;
A1 is the wetted surface area under waterline of vessel or surface structure, in m
2;
V is the towage velocity, in m/s;
is the block coefficient;
A2 is the submerged transverse section area amidships, in m
2.
Rf is the residual resistance of towing vessel, in kN.
For drilling units or other surface structures with huge wind area, the towage resistance is also to be calculated as follows, taken whichever is greater:
where:
Rf and
RB are the same as (1) above, and the
Ra is the air resistance;
is the air density, to be taken as 1.22 kg/ m
3;
is the wind velocity, to be taken as 20.6 m/s;
is the wind area, to be taken as upwind, in m
2;
is the configuration coefficient of wind area.
Equations (5)–(9) are applied to compute the total towing resistance of the floating tank and the upper meteorological mast. The resistance of the towing vessel (tugboat) is not included in the total resistance so that it can be compared with numerical results for which the towing resistance is given separately.
The sea states in MOSES are defined according to the items in CCS guidelines. The wind velocity is 20.6 m/s, and the current velocity is 0.5 m/s. The towing speed is 3 m/s with a significant wave height of 2 m.
The results of towing resistance based on this code will be analyzed in
Section 3.
2.3. The Hydrodynamic Theory
The motion of the OIMM is featured by the free surface boundary condition, which is nonlinear and makes the description of the body motion complex. Based on the potential theory, the dynamic responses of marine structures are widely studied. The problem of hydrodynamics can be formulated in terms of potential theory based on the following assumptions:
The sea water is assumed incompressible and inviscid. The fluid motion is irrotational. Viscous effects are neglected and the fluid is assumed to be incompressible. The depth h is finite and constant and the free surface is infinite in all directions. Assumed the motion of the body and the fluid to be small for a linearization of the boundary condition and free surface condition.
A velocity potential
can be used to describe the fluid velocity vector
V (
x, y, z) = (
u, v, w) at time
t at the point X = (
x, y, z) in a cartesian coordinate system fixed in space [
23].
It is convenient to decompose the total velocity potential in the alternative forms [
24]:
where
is the velocity potential of the incident wave system;
is the scattered field due to the presence of the body; the diffraction problem can be solved by considering the
and the
together;
,
= 1–6, is the contribution to the velocity potential from the
th mode of motion. Therefore the
(
= 1–6) is called the radiation potential.
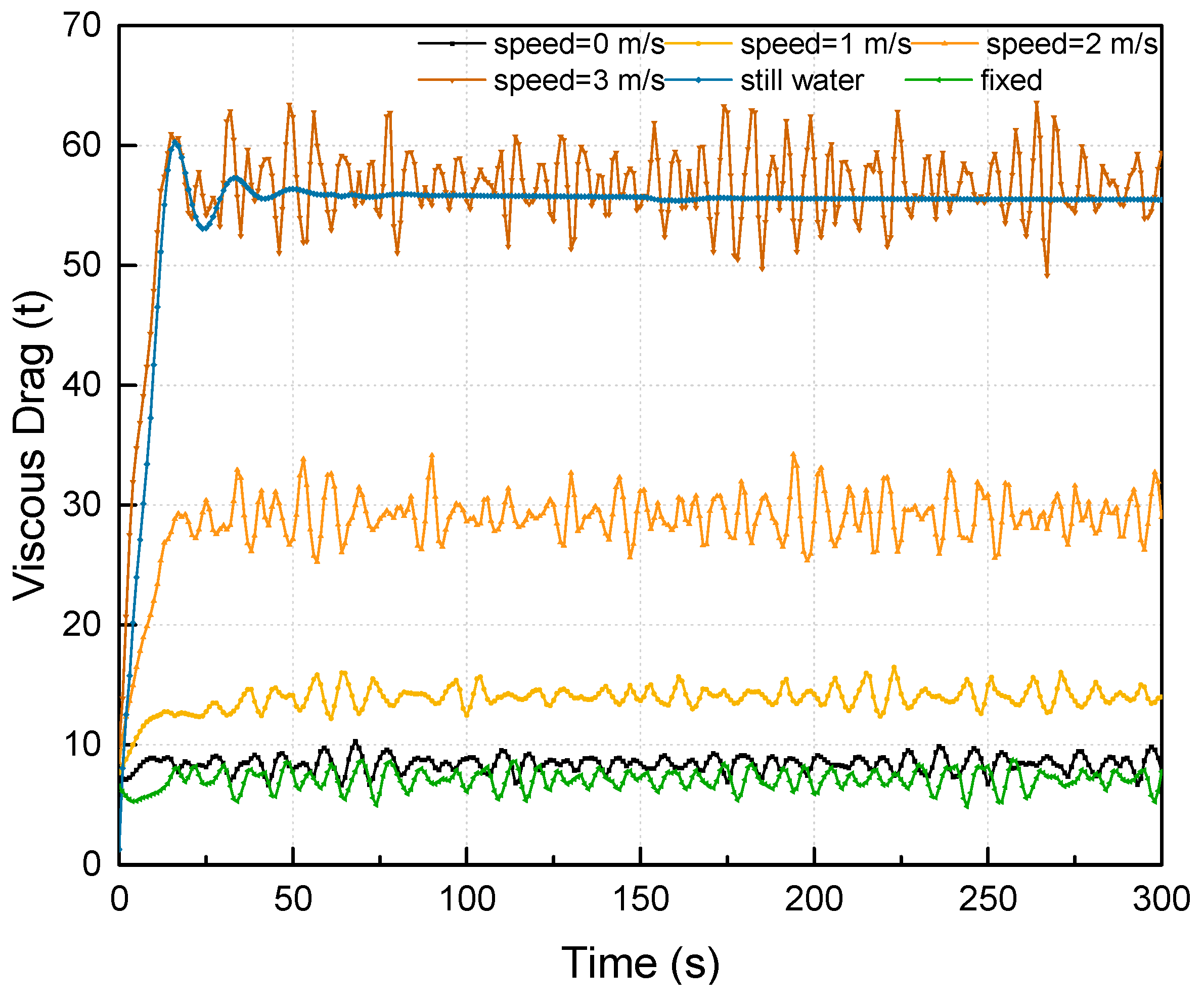
The towing dynamic problem in this paper is analyzed separately by whether or not considering the forward speed. To achieve that, we change the forward speed by applying different towing force. In two ways, the system has no forward speed. One is to tow the structure with a limited force and keep the OIMM to its initial position without moving forward. Another way is that the towing tugboat is fixed in the global system and the OIMM connected with the tugboat by a mooring line, and then the OIMM can oscillate under the environment loadings.
5. Conclusions
This study deals with the dynamic characteristics of an innovative integrated offshore structure OIMM in terms of the towing resistance and motion responses. Two special towing methods are adopted for this high-rise structure and the hydrodynamic software MOSES is applied to simulate the towing process in time domain. This paper estimates the feasibility of the towing operations and provides suggestions for potential problems when conducting an offshore wet towing for the OIMM.
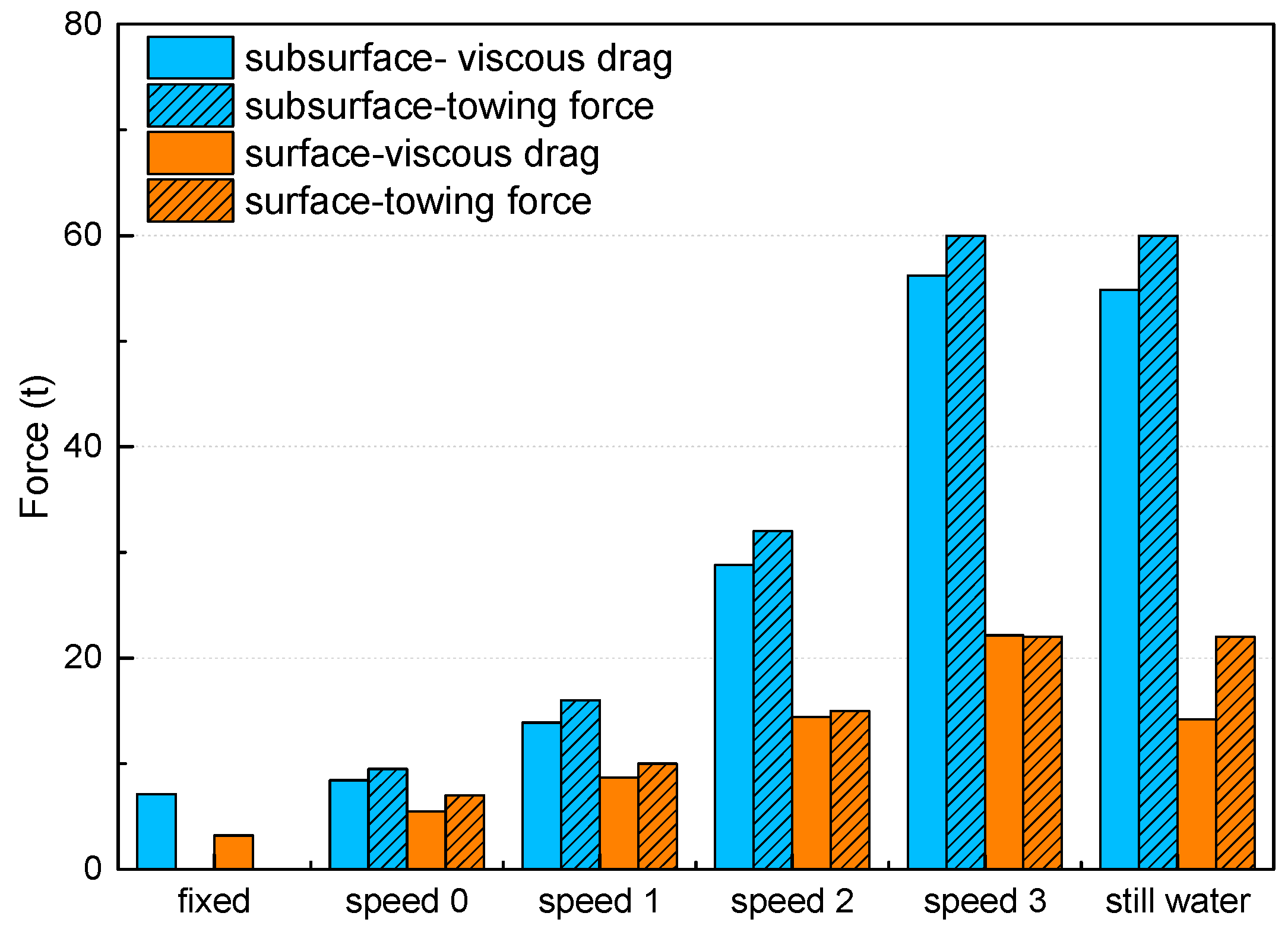
First, the towing resistance is obtained by MOSES and CCS code. The numerical result is verified with manual computation. The manual result of towing resistance is agreed with the result by MOSES for surface towing and shallow submerged towing. For deep submerged towing, the difference between two methods is caused by the applied theory in MOSES and CCS. The potential theory and Morison equation are applied in numerical method, while empirical equations are used by CCS code. The current impact is the most important component since the induced speed is closest to the overall induced speed.
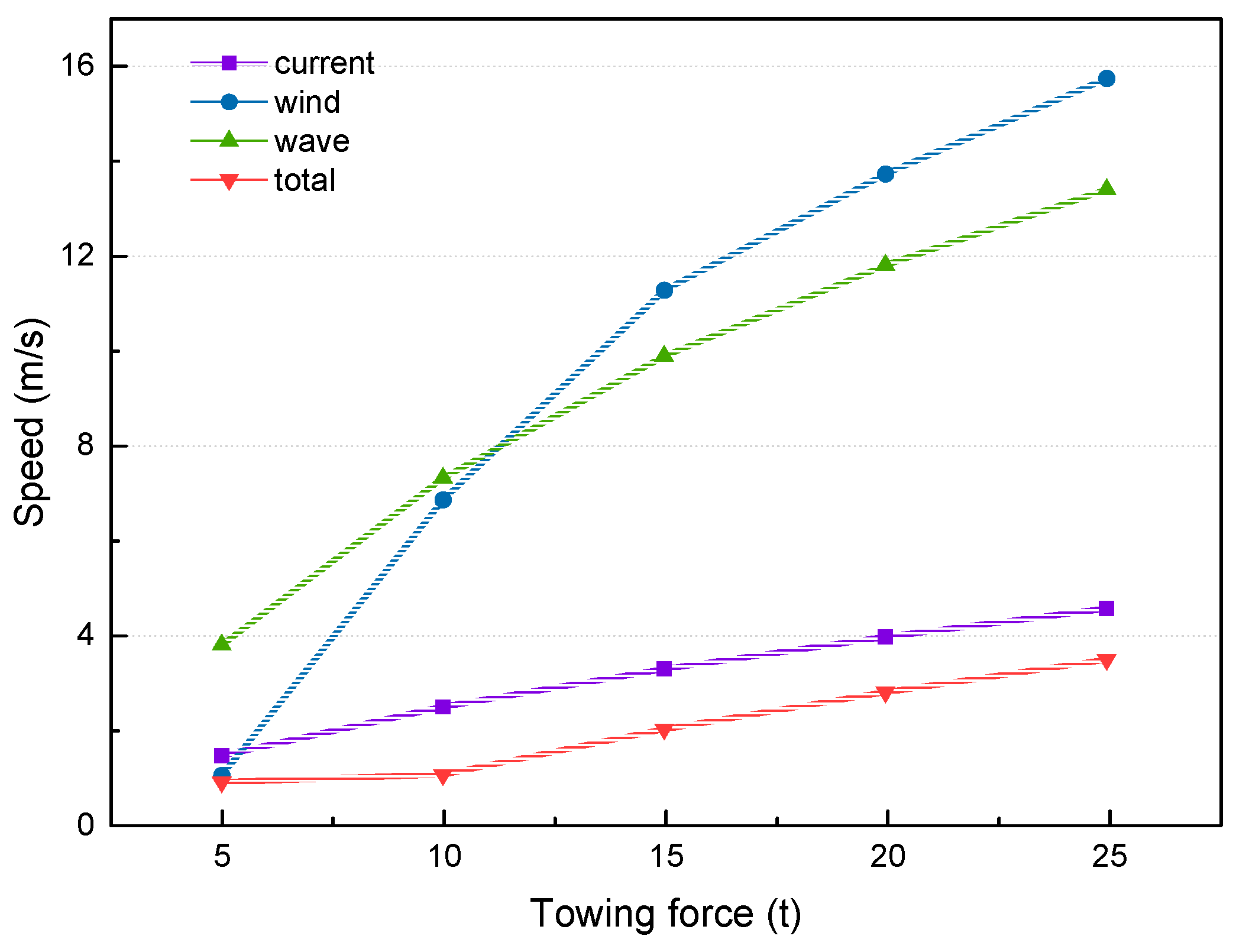
Secondly, the surface and submerged towing methods are compared in terms of different forward speeds and the results suggest that to obtain a higher speed by increasing the towing force is unreasonable with respect to the transportation cost, since the towing resistance increases much higher. Larger towing force is required for submerged towing to achieve the same speed level as surface towing, particularly when the towing speed becomes higher.
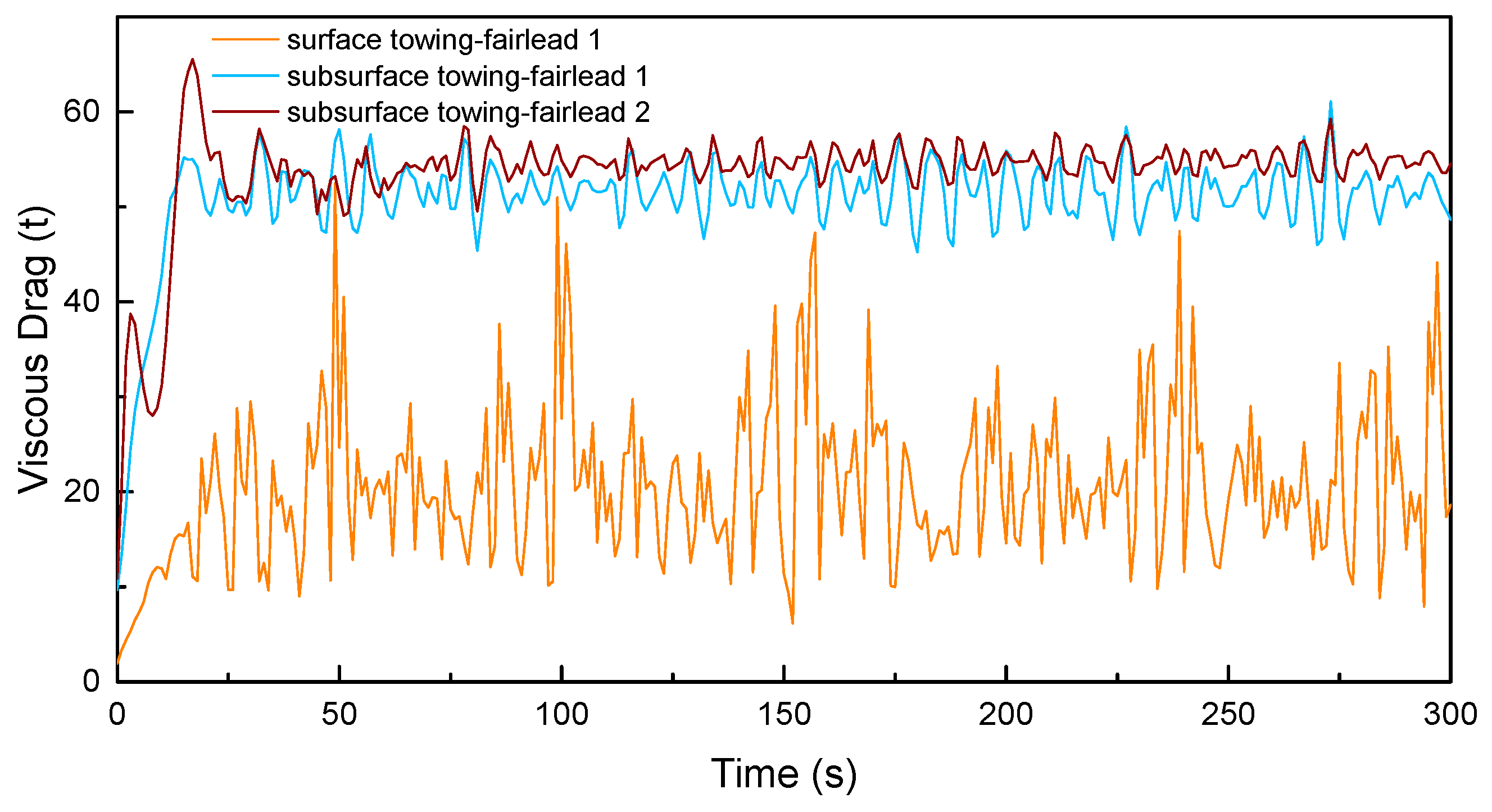
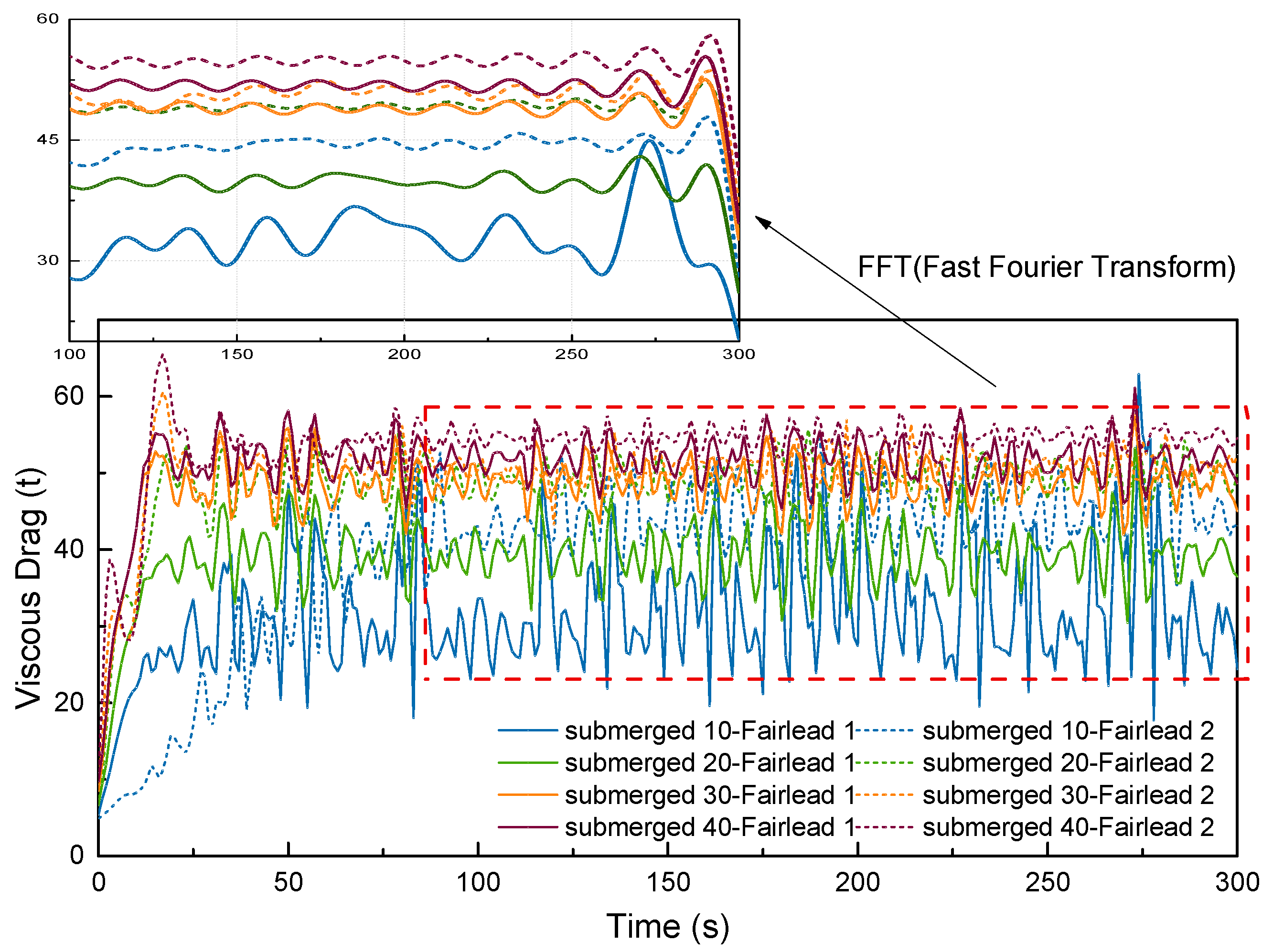
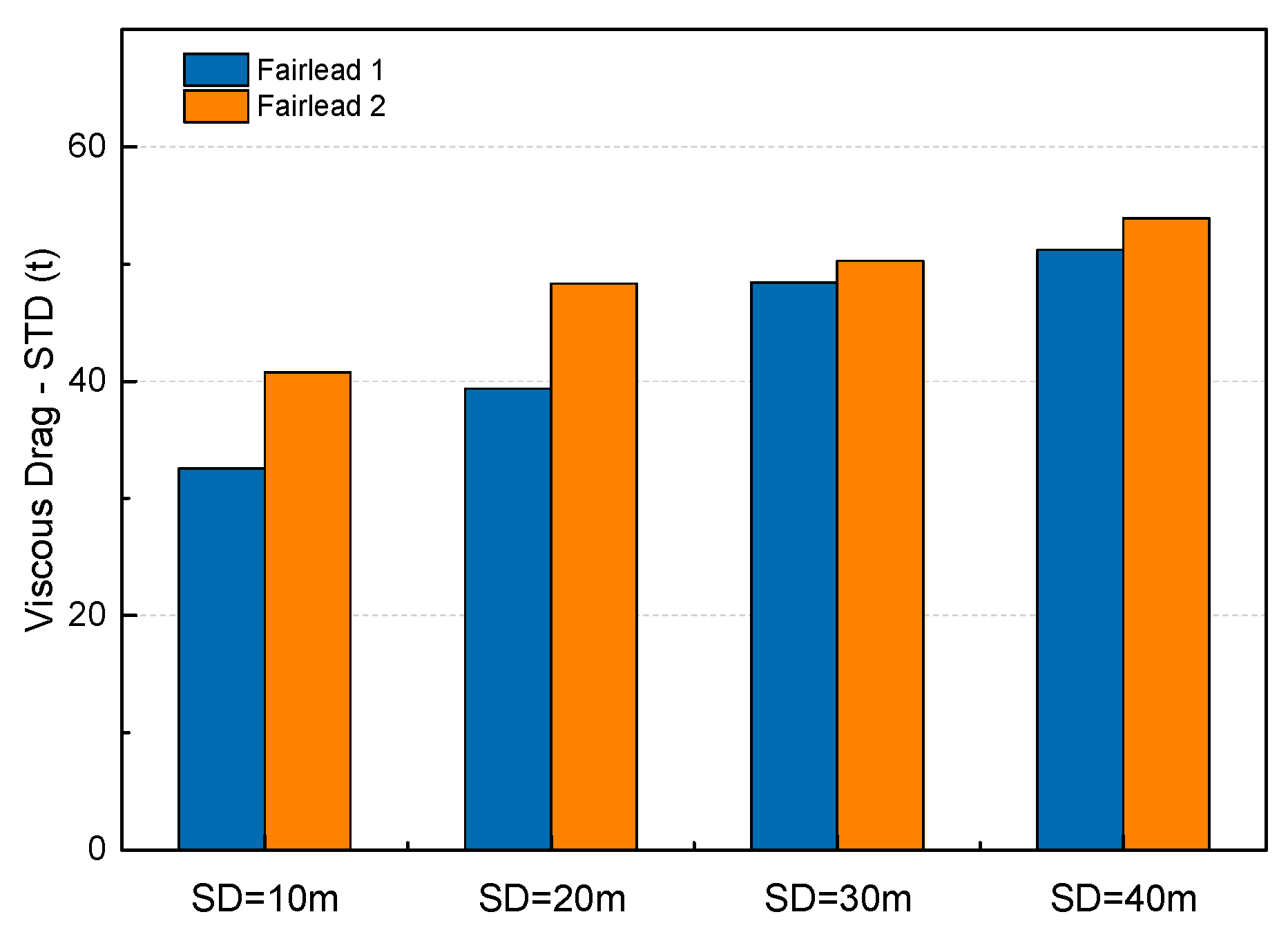
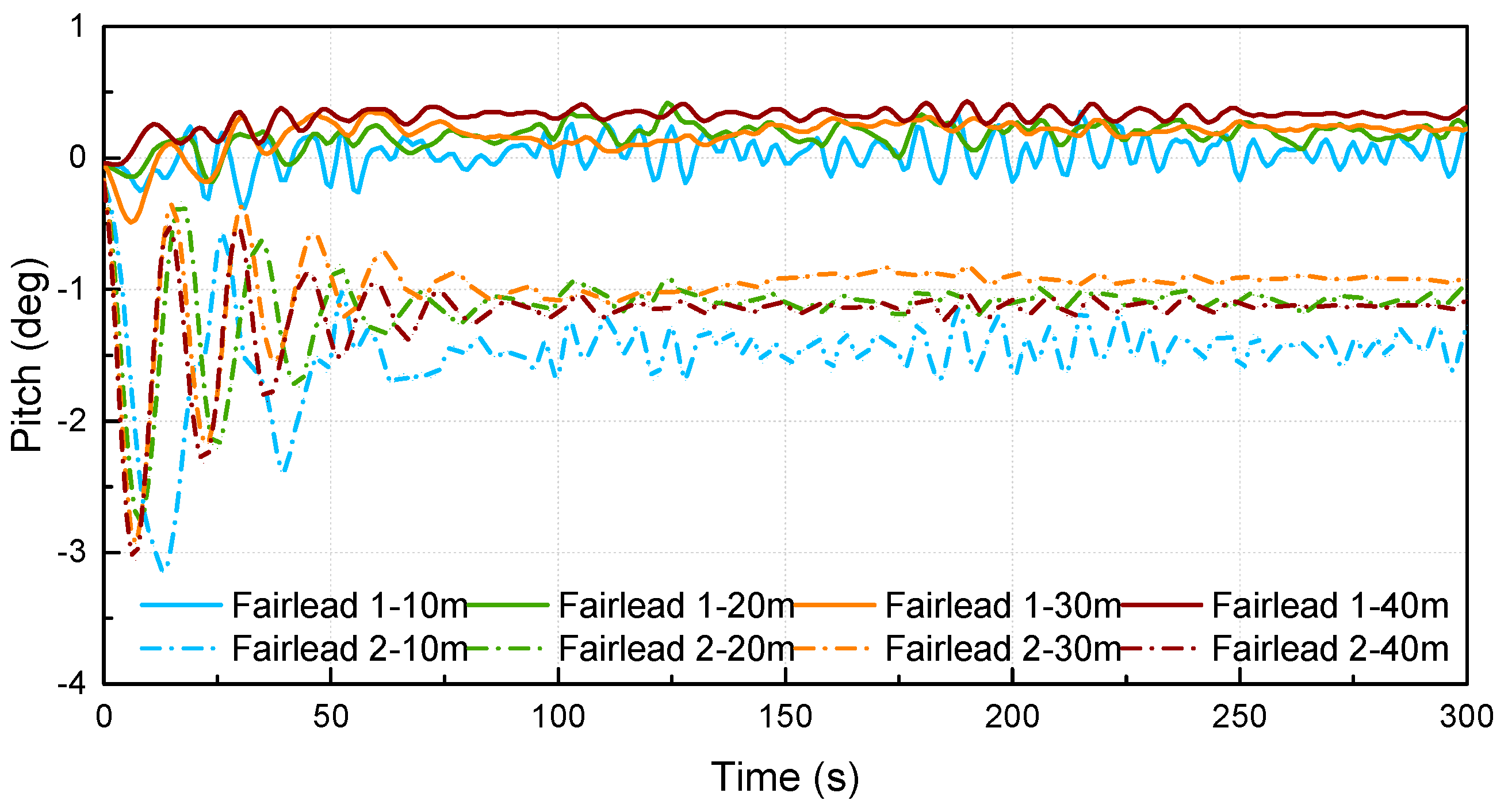
Thirdly, based on the fairlead positions, time domain simulations are conducted to estimate the surface and the submerged towing methods with respect to the resistance and dynamic responses. It suggests that higher mooring position is likely to result in larger viscous resistance. Deeper submerged depth is preferred when the lower motion amplitude is required. Fairlead 1 excels in two aspects: lower resistance and lower motion responses. The submerged towing should be performed with sufficient distance away from the seabed because the OIMM is likely to descend by a large distance.
Finally, it can be concluded that the numerical method by MOSES can be applied for the preliminary estimation of the towing operations for OIMM considering complex sea environment. More accurate and detailed estimation will require to consider the properties of the mooring line and the impacts of the tugboat in the system. These conclusions can provide recommendations and references for the estimation of the feasibility of the towing methods and on the optimization of the towing operation for OIMM and resembling structures.