Numerical Analysis of Leading-Edge Vortex Effect on Tidal Current Energy Extraction Performance for Chord-Wise Deformable Oscillating Hydrofoil
Abstract
:1. Introduction
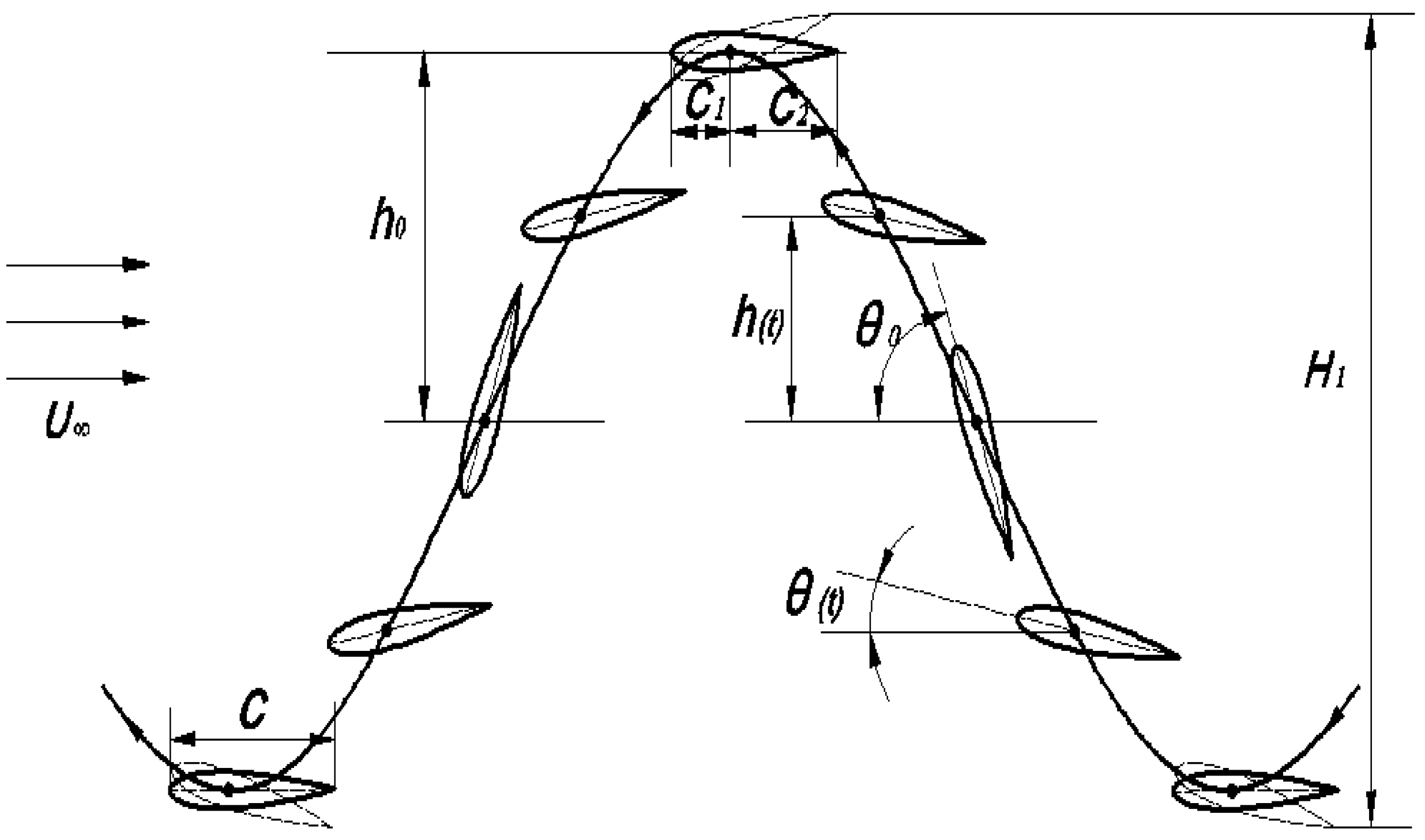
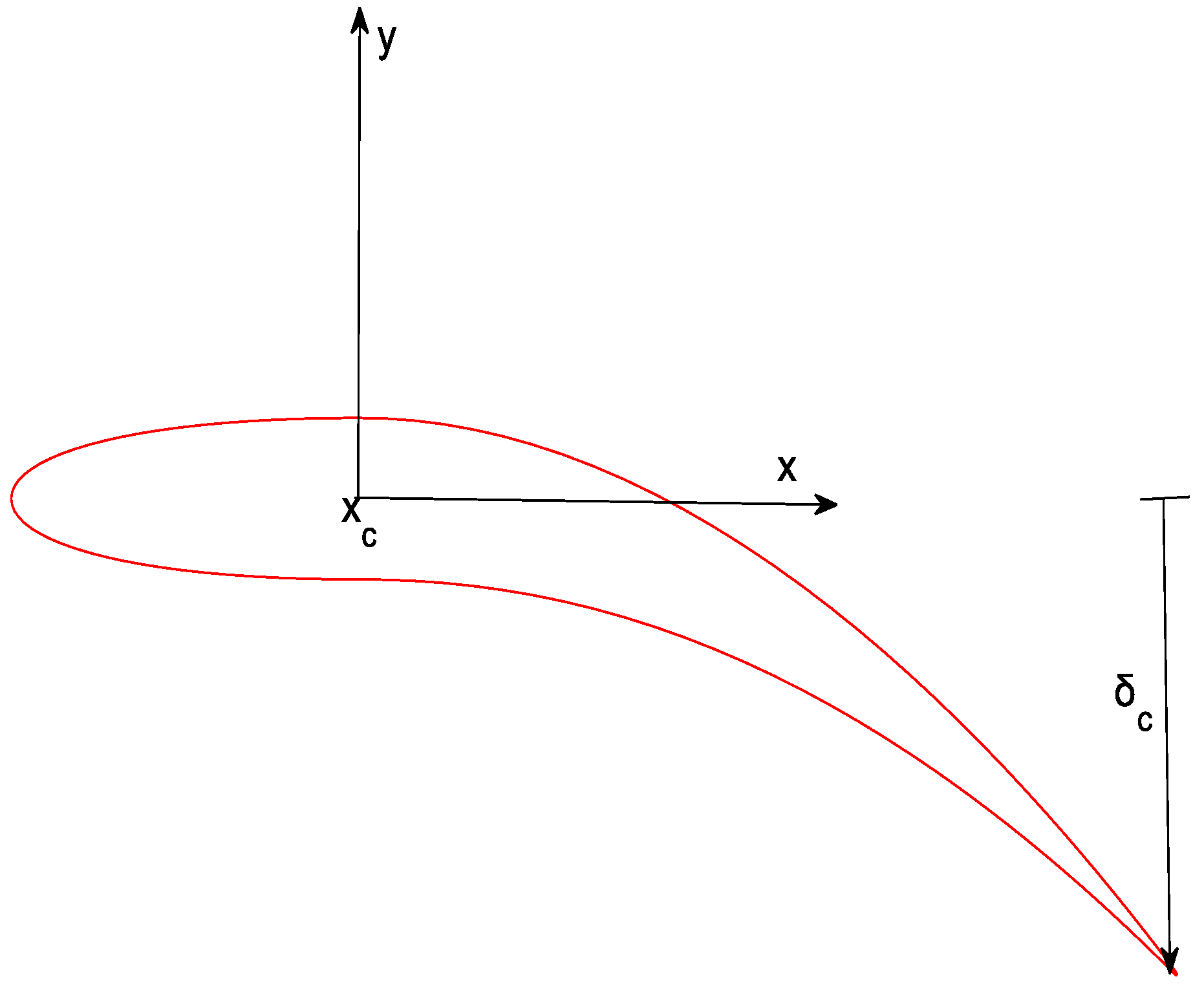
2. Hydrofoil Motion and Deformation Equation
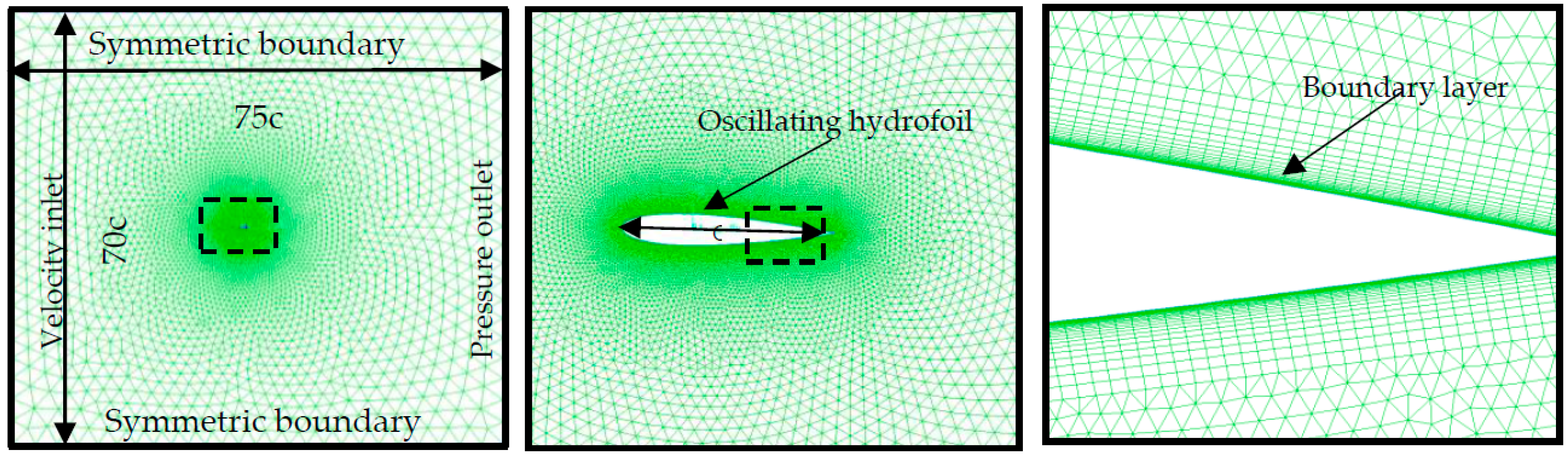
3. Numerical Calculation Method
4. Energy Extraction Parameter
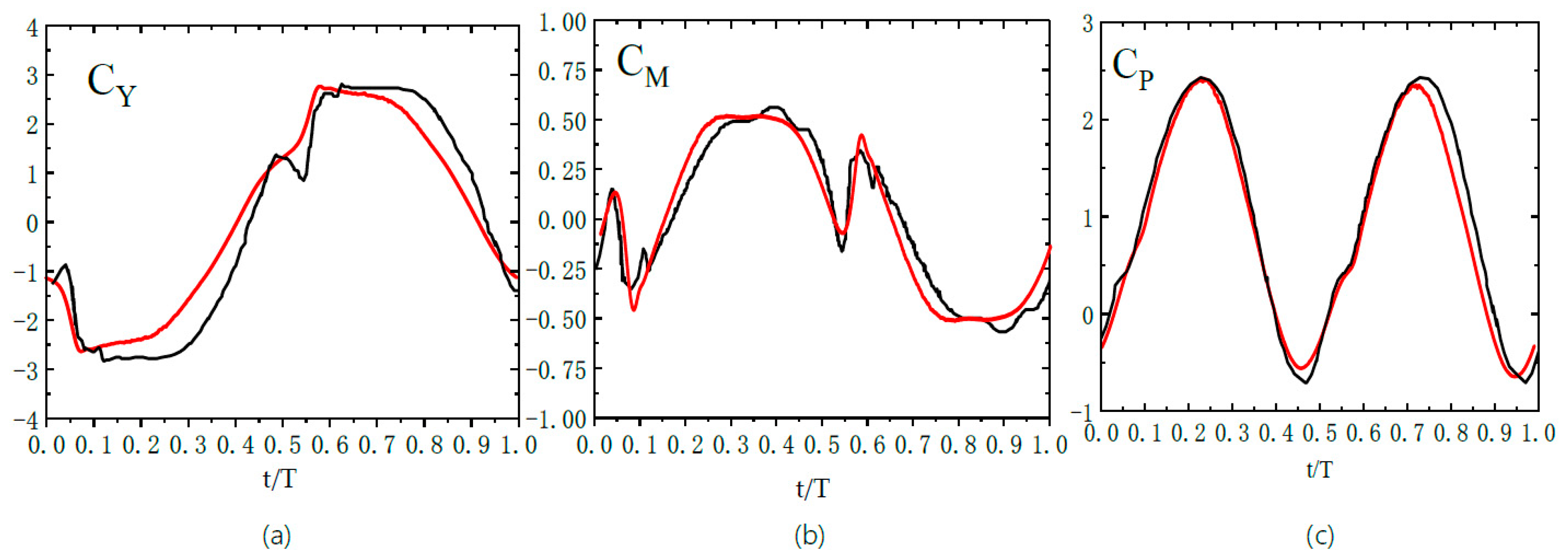
5. Validation of the Numerical Results
6. Results and Discussion
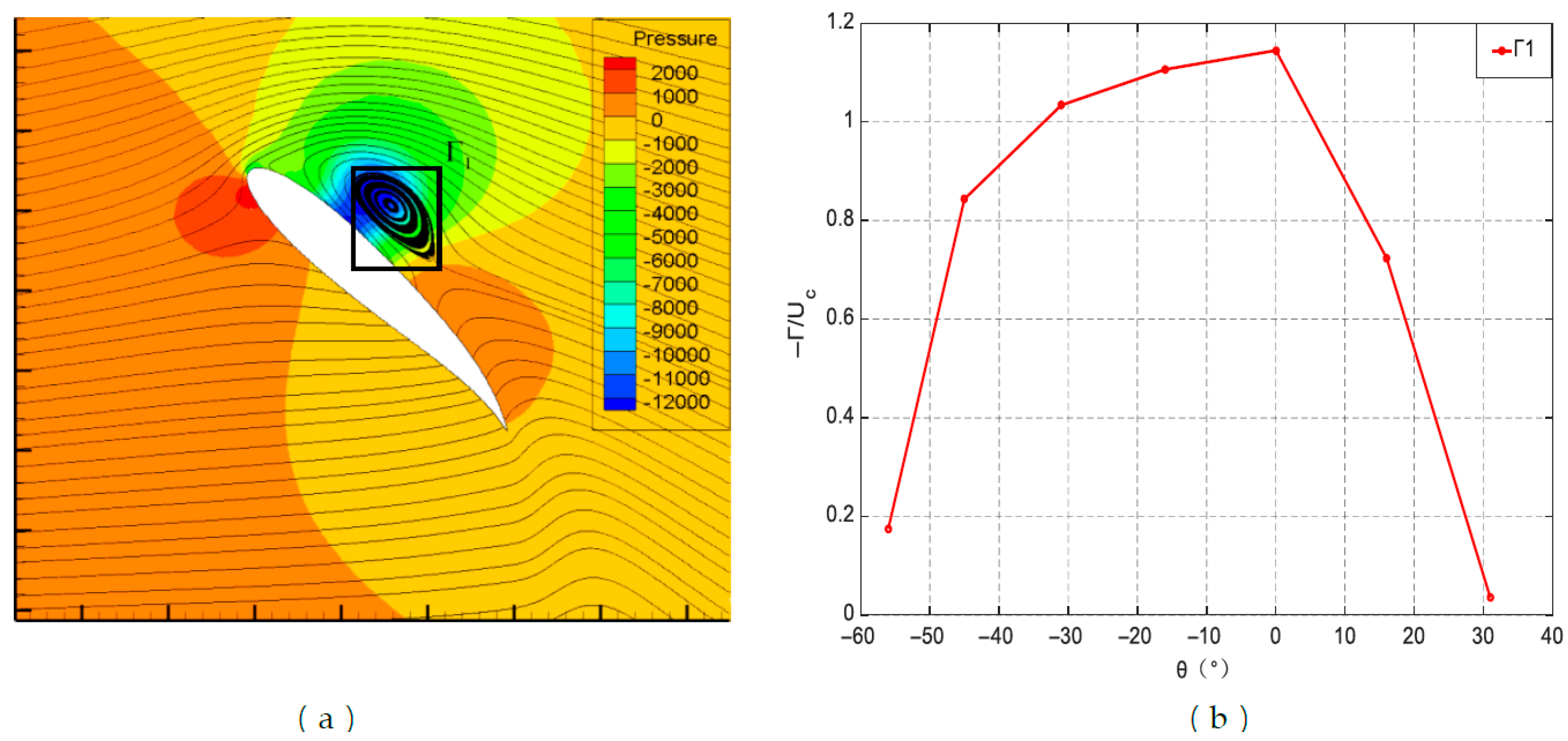
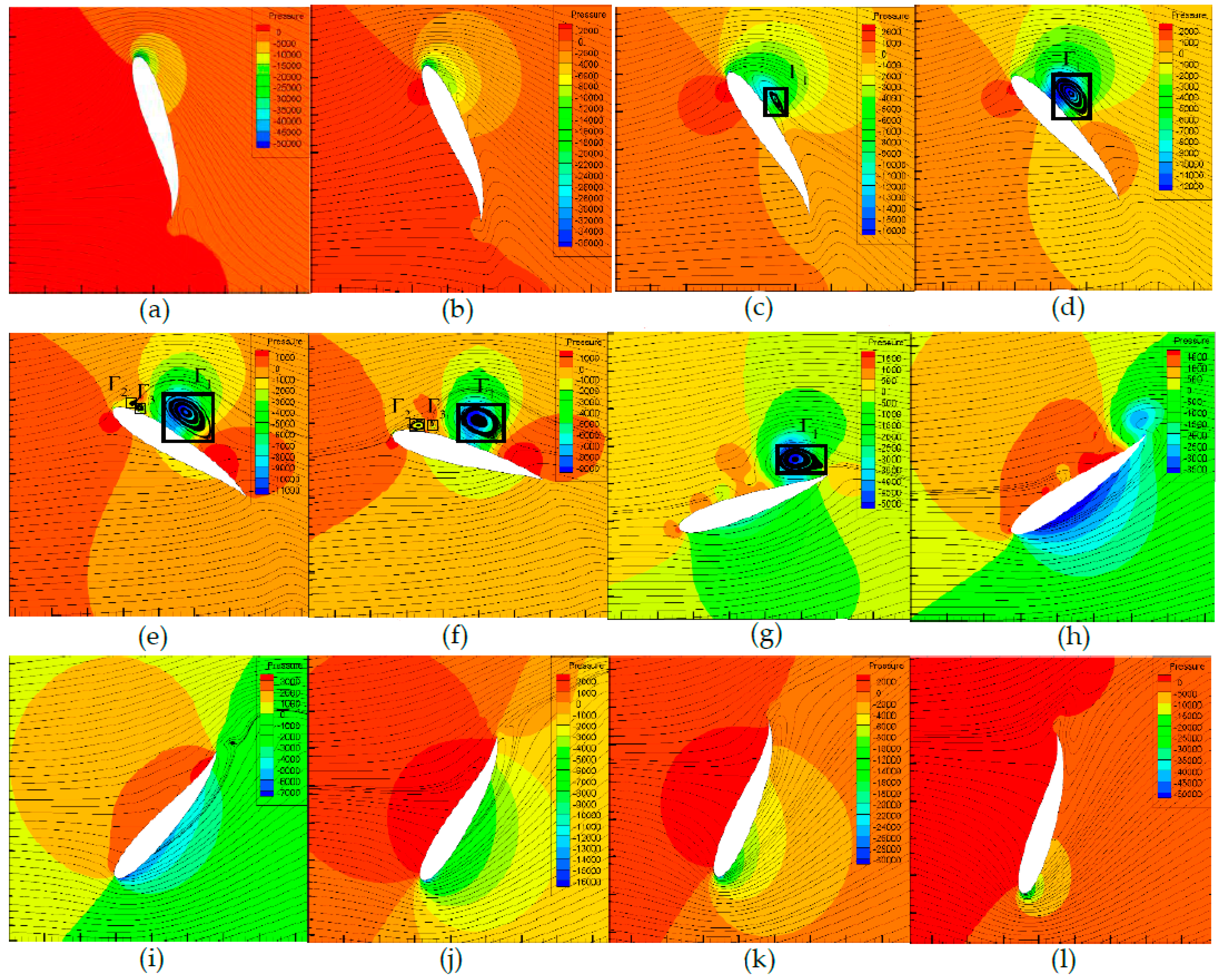
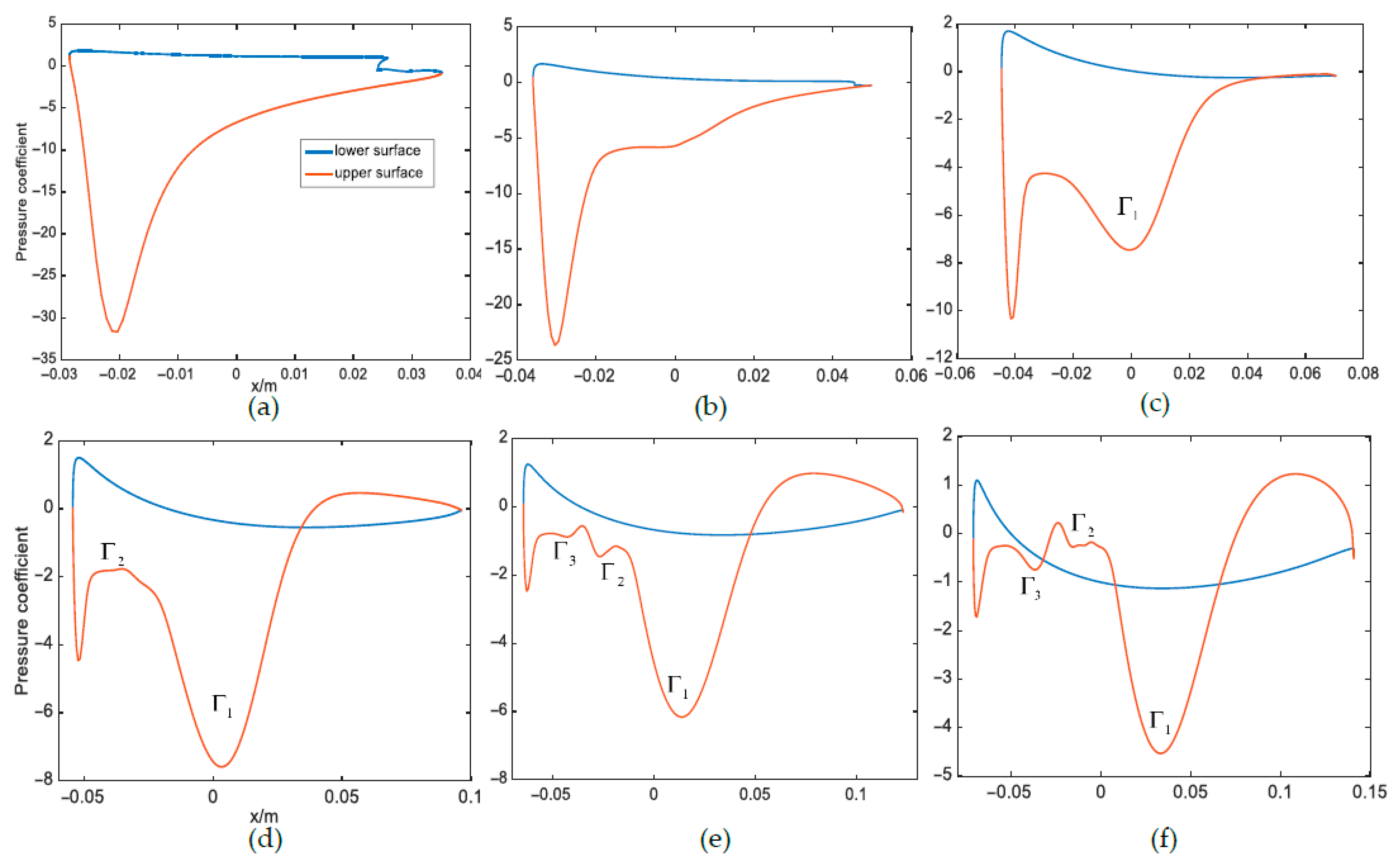
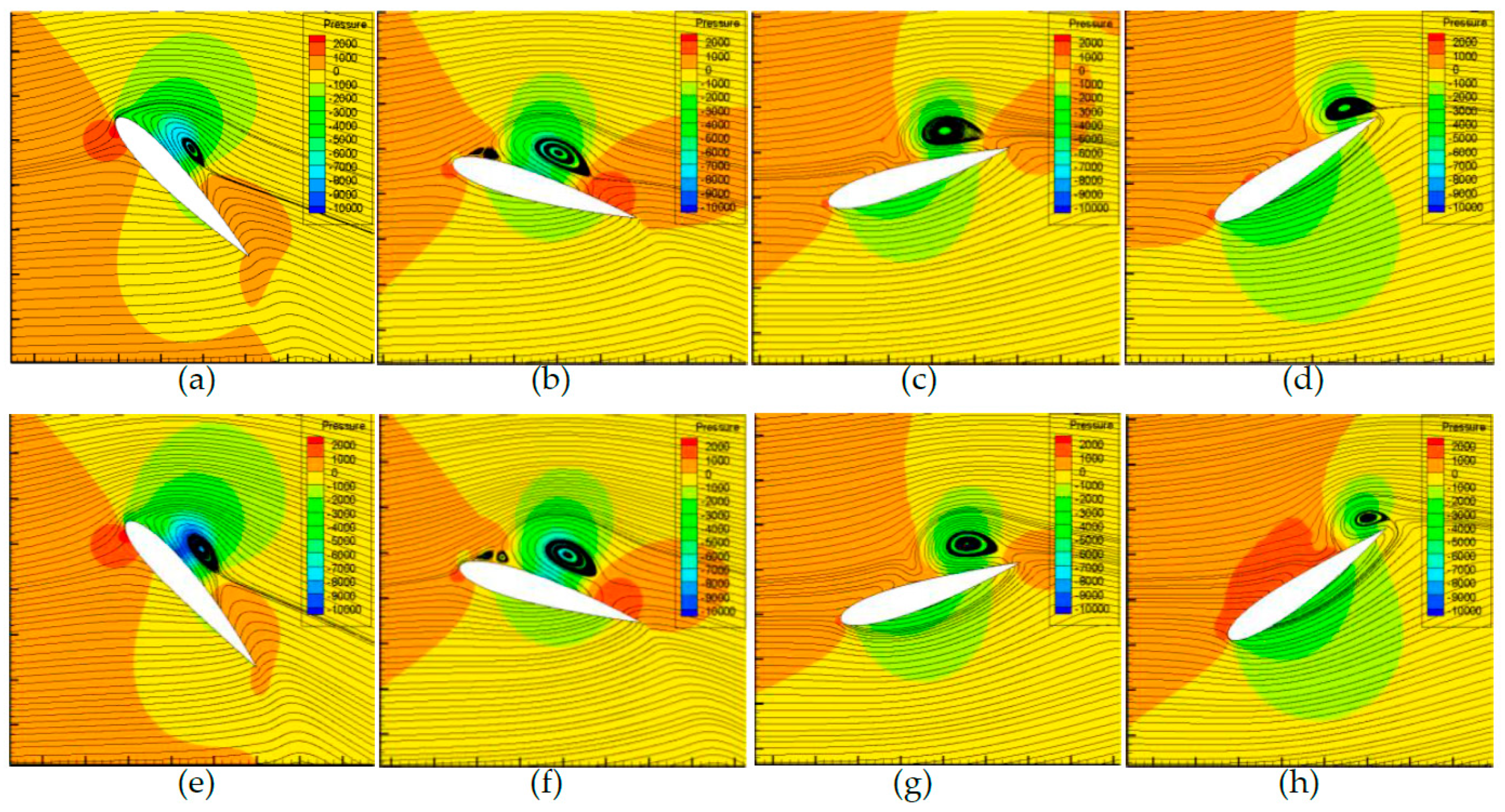
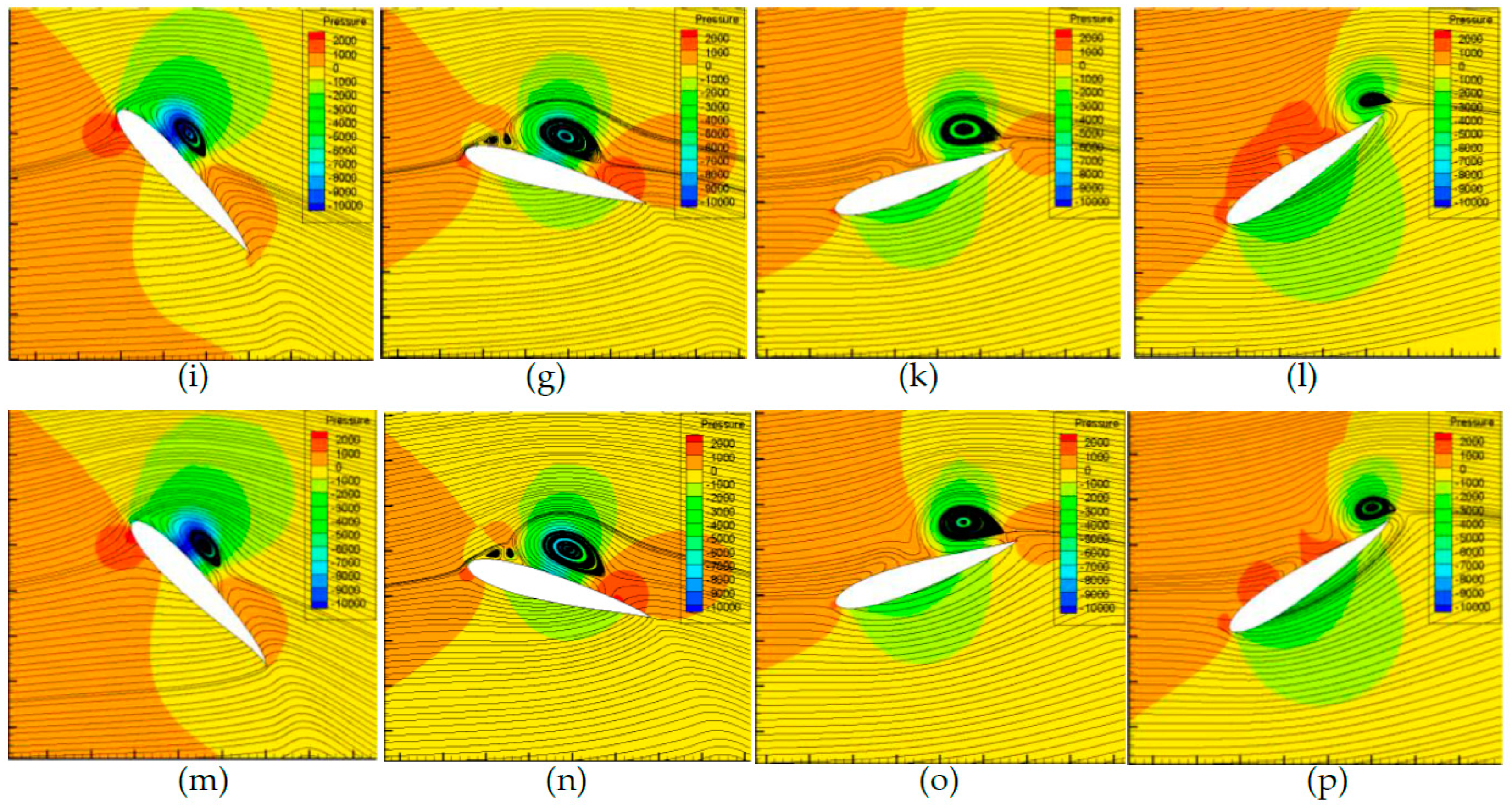
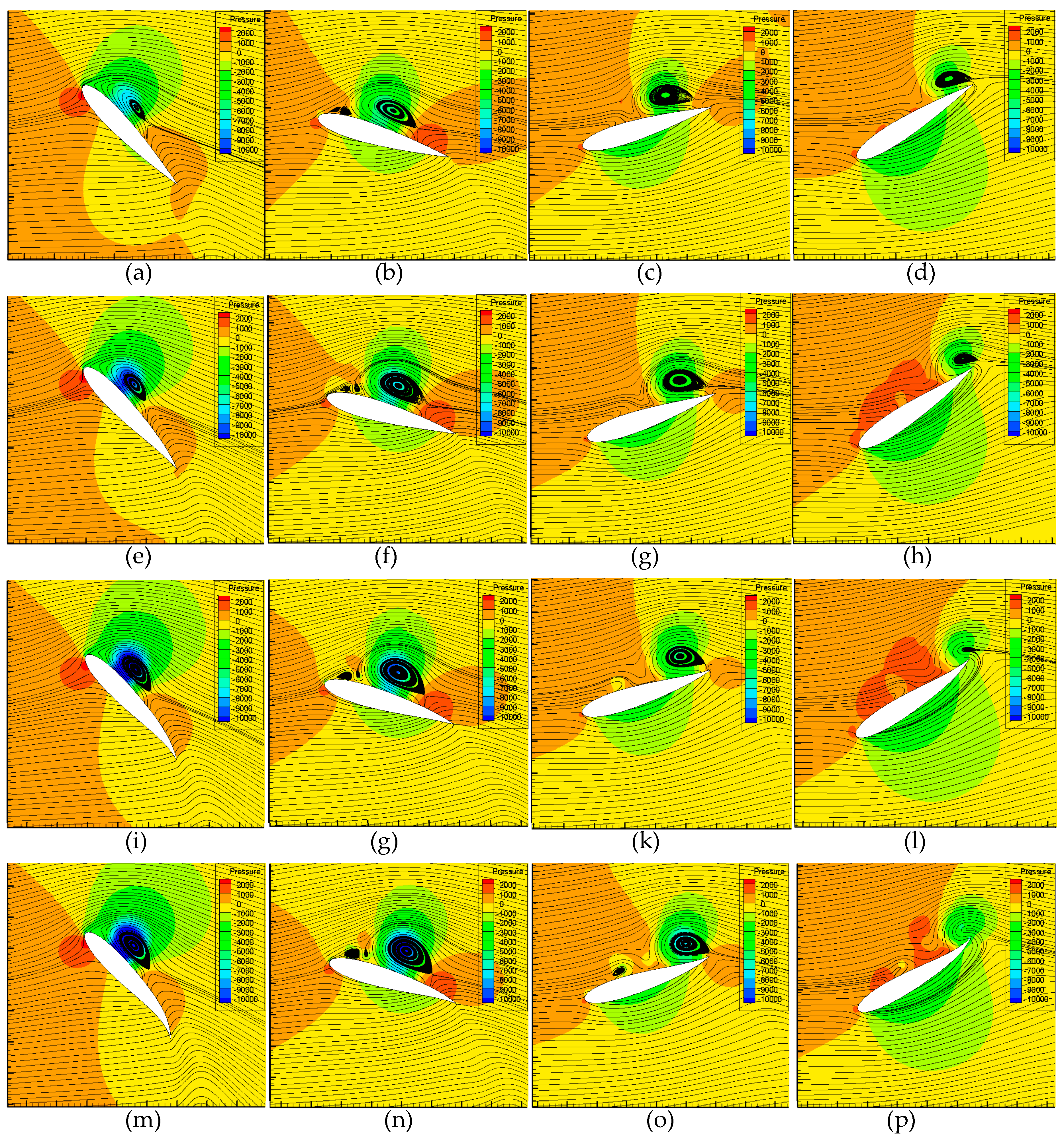
6.1. Quantification of the Attached Vortex and Its Relationship with Hydrofoil Pressure Distribution
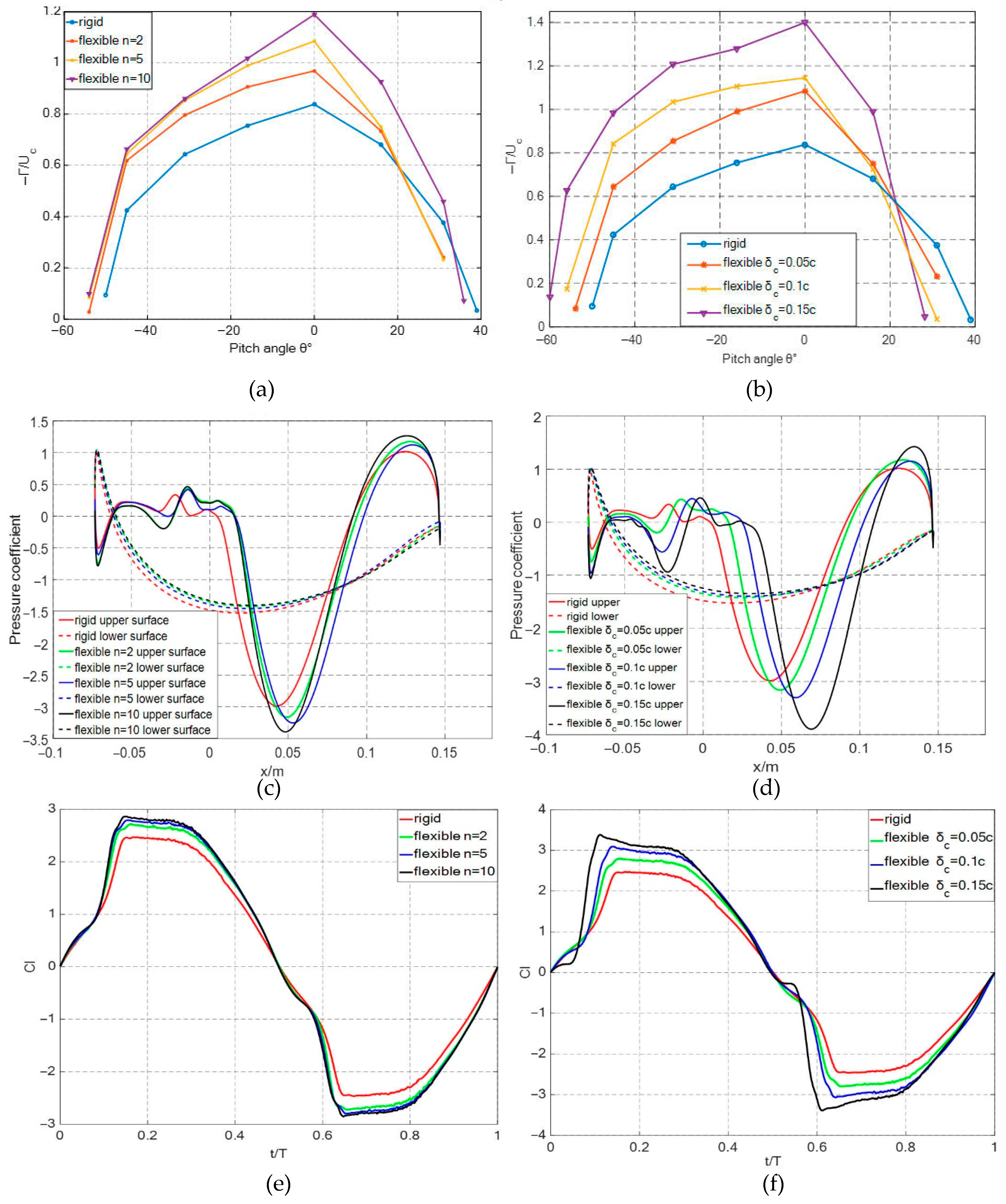
6.2. The Effect of Chord-Wise Flexure on Hydrofoil Lift
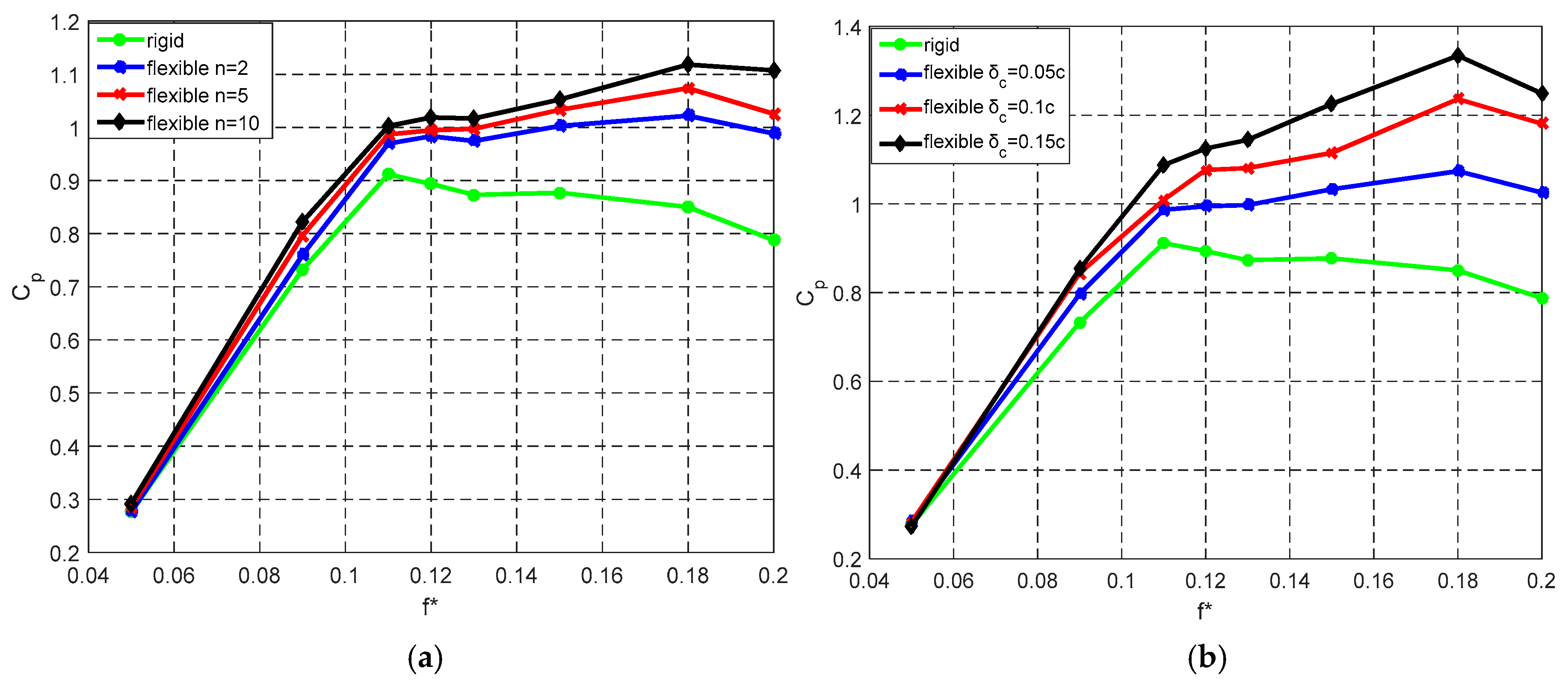
6.3. The Effect of Chord-Wise Flexure on Hydrofoil Energy Extraction
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McKinney, W.; DeLaurier, J. Wingmill: An oscillating-wing windmill. J. Energy 1981, 5, 109–115. [Google Scholar] [CrossRef]
- Platzer, M.; Ashraf, M.; Young, J. Development of a new oscillating-wing wind and hydropower generator. In 47th Aerospace Sciences Meeting; AIAA: Reston, VA, USA, 2013. [Google Scholar]
- Ashraf, M.; Young, J.; Lai, J.C.S.; Platzer, M.F. Numerical analysis of an oscillating-wing wind and hydropower generator. AIAA J. 2011, 49, 1374–1386. [Google Scholar] [CrossRef]
- Zhu, Q. Optimal frequency for flow energy harvesting of a flapping foil. J. Fluid Mech. 2011, 675, 495–517. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Optimal operating parameters for an oscillating foil turbine at Reynolds number 500,000. AIAA J. 2014, 52, 1885–1895. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Three-dimensional effects on an oscillating-foil hydrokinetic turbine. J. Fluids Eng. 2012, 134, 071105. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G.; Lalande, G.; Ruel, J.; Mehut, A. Prototype testing of a hydrokinetic turbine based on oscillating hydrofoils. Renew. Energy 2011, 36, 1710–1718. [Google Scholar] [CrossRef]
- Kinsey, T.; Dumas, G. Computational fluid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils. J. Fluids Eng. 2012, 134, 021104. [Google Scholar] [CrossRef]
- Xu, J.A.; Sun, H.Y.; Tan, S.L. Wake vortex interaction effects on energy extraction performance of tandem oscillating hydrofoils. J. Mech. Sci. Technol. 2016, 30, 4227–4237. [Google Scholar] [CrossRef]
- Xu, J.A.; Tan, S.L.; Guan, D.T. Energy extraction performance of motion constrained tandem oscillating hydrofoils. J. Renew. Sustain. Energy 2017, 9, 044501. [Google Scholar] [CrossRef]
- Lindsey, K. A Feasibility Study of Oscillating-Wing Power Generation; United States Naval Postgraduate School: Monterey, CA, USA, 2002. [Google Scholar]
- Usoh, C.O.; Young, J.; Lai, J.C.S. Numerical analysis of a non-profiled plate for flapping wing turbines. In Proceedings of the 18th Australian Fluid Mechanics Conference, Launceston, Australia, 3–7 December 2012. [Google Scholar]
- Wei, S.; Liu, H. Flapping wings and aerodynamic lift: The role of leading edge vortices. AIAA J. 2007, 45, 2817–2819. [Google Scholar]
- Ellington, C.P.; van den Berg, C.; Willmott, A.P.; Thomas, A.L.R. Leading-edge vortices in insect flight. Nature 1996, 384, 626. [Google Scholar] [CrossRef]
- Huang, B.; Wu, Q.; Wang, G.Y. Numerical simulation of unsteady cavitating flows around a transient pitching hydrofoil. Sci. China Technol. Sci. 2014, 57, 101–116. [Google Scholar] [CrossRef]
- Kevin, D.J.; Lindsey, K.; Platzer, M.F. An investigation of the fluid-structure interaction in an oscillating-wing micro-hydropower generator. WIT Trans. Built Environ. 2003, 71, 10. [Google Scholar]
- Kinsey, T.; Dumas, G. Parametric study of an oscillating airfoil in a power-extraction regime. AIAA J. 2008, 46, 1318–1330. [Google Scholar] [CrossRef]
- Liu, W.D.; Xiao, Q.; Cheng, F. A bio-inspired study on tidal energy extraction with flexible flapping wings. Bioinspir. Biomim. 2013, 8, 1–11. [Google Scholar] [CrossRef]
- Zhu, B.; Xia, P.; Huang, Y.; Zhang, W. Energy extraction properties of a flapping wing with an arc-deformable airfoil. J. Renew. Sustain. Energy 2019, 11, 023302. [Google Scholar] [CrossRef]
- Hoke, C.M.; Young, J.; Lai, J.C.S. Effects of time-varying camber deformation on flapping foil propulsion and power extraction. J. Fluids Struct. 2015, 56, 152–176. [Google Scholar] [CrossRef]
- Wu, Y.J.; Wu, J.; Tian, F.B. How a flexible tail improves the power extraction efficiency of a semi-activated flapping foil system: A numerical study. J. Fluids Struct. 2015, 54, 886–899. [Google Scholar] [CrossRef]
- Bose, N. Performance of chord-wise flexible oscillating propulsors using a time-domain panel method. Int. Shipbuild. Prog. 1995, 42, 281–294. [Google Scholar]


| Hydrofoil | c (m) | Re | θo | n | δc | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| NACA0015 | c/3 | 10−6 | 0.5π | 0.22 | 1.8 | c | 500,000 | 720 | 1, 2, 5, 10 | 0, 0.05c, 0.1c, 0.15c |
| Hydrofoil | c (m) | f* | Re | θo | |||||
|---|---|---|---|---|---|---|---|---|---|
| NACA0015 | c/3 | 10−6 | 0.5π | 0.25 | 2.0 | 0.14 | c | 500,000 | 750 |
| Hydrofoil | Total Average Power Coefficient | Average Power Coefficient of the Heave Motion | Average Power Coefficient of the Pitch Motion |
|---|---|---|---|
| Rigid hydrofoil | 0.8731 | 0.9744 | −0.1013 |
| Flexibility coefficient n = 2 | 0.9743 | 1.0947 | −0.1204 |
| Flexibility coefficient n = 5 | 0.9972 | 1.1304 | −0.1332 |
| Flexibility coefficient n = 10 | 1.0168 | 1.1547 | −0.1379 |
| Maximum offset = 0.05c | 0.9972 | 1.1304 | −0.1332 |
| Maximum offset = 0.1c | 1.0808 | 1.2345 | −0.1537 |
| Maximum offset = 0.15c | 1.1441 | 1.3258 | −0.1817 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Zhu, H.; Guan, D.; Zhan, Y. Numerical Analysis of Leading-Edge Vortex Effect on Tidal Current Energy Extraction Performance for Chord-Wise Deformable Oscillating Hydrofoil. J. Mar. Sci. Eng. 2019, 7, 398. https://doi.org/10.3390/jmse7110398
Xu J, Zhu H, Guan D, Zhan Y. Numerical Analysis of Leading-Edge Vortex Effect on Tidal Current Energy Extraction Performance for Chord-Wise Deformable Oscillating Hydrofoil. Journal of Marine Science and Engineering. 2019; 7(11):398. https://doi.org/10.3390/jmse7110398
Chicago/Turabian StyleXu, Jianan, Haiyang Zhu, Daitao Guan, and Yong Zhan. 2019. "Numerical Analysis of Leading-Edge Vortex Effect on Tidal Current Energy Extraction Performance for Chord-Wise Deformable Oscillating Hydrofoil" Journal of Marine Science and Engineering 7, no. 11: 398. https://doi.org/10.3390/jmse7110398
APA StyleXu, J., Zhu, H., Guan, D., & Zhan, Y. (2019). Numerical Analysis of Leading-Edge Vortex Effect on Tidal Current Energy Extraction Performance for Chord-Wise Deformable Oscillating Hydrofoil. Journal of Marine Science and Engineering, 7(11), 398. https://doi.org/10.3390/jmse7110398




