Prediction of Seabed Scour Induced by Full-Scale Darrieus-Type Tidal Current Turbine
Abstract
:1. Introduction
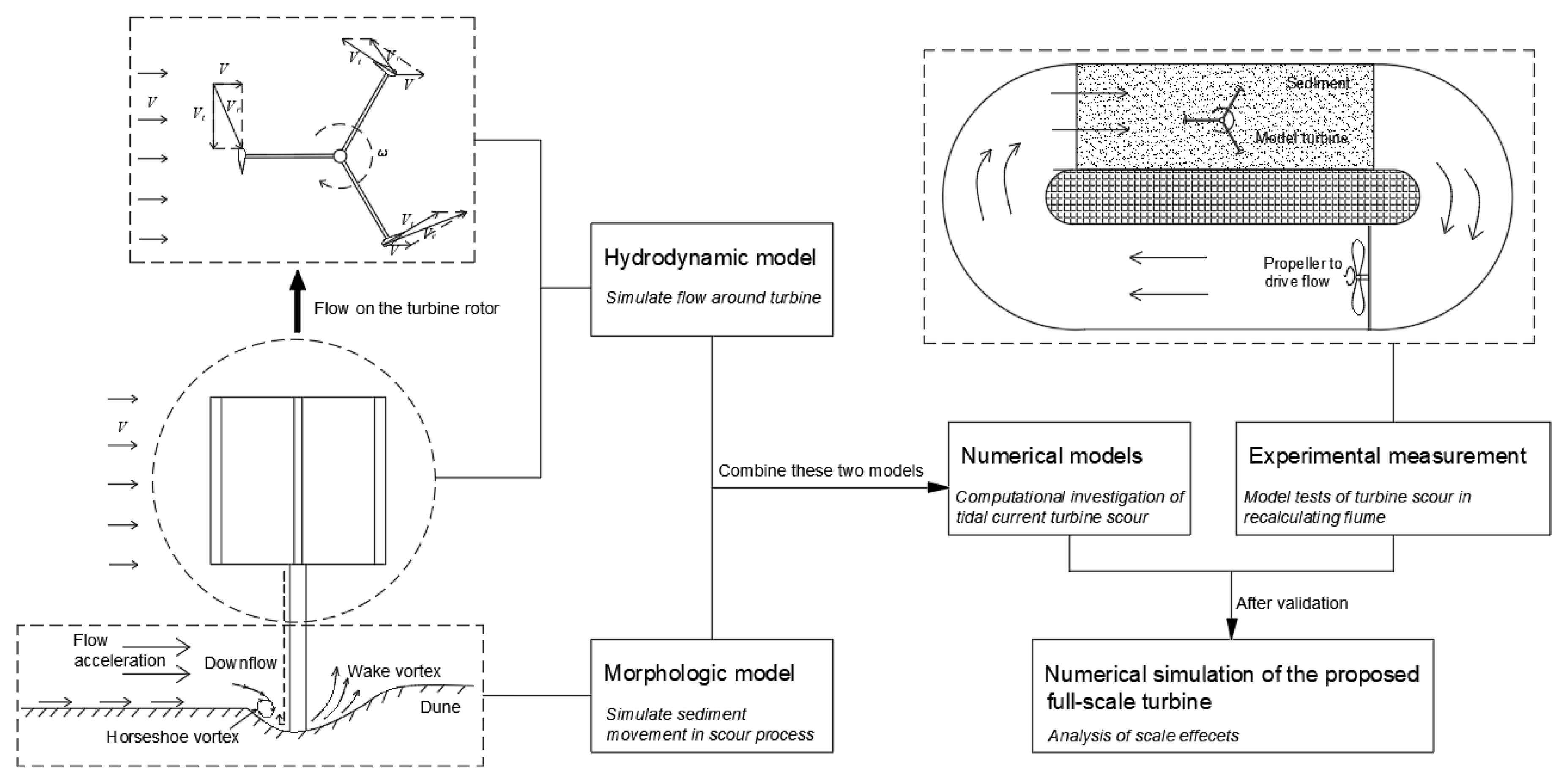
2. Methodology
2.1. Hydrodynamic Model
2.1.1. Governing Equations
2.1.2. Turbulence Model
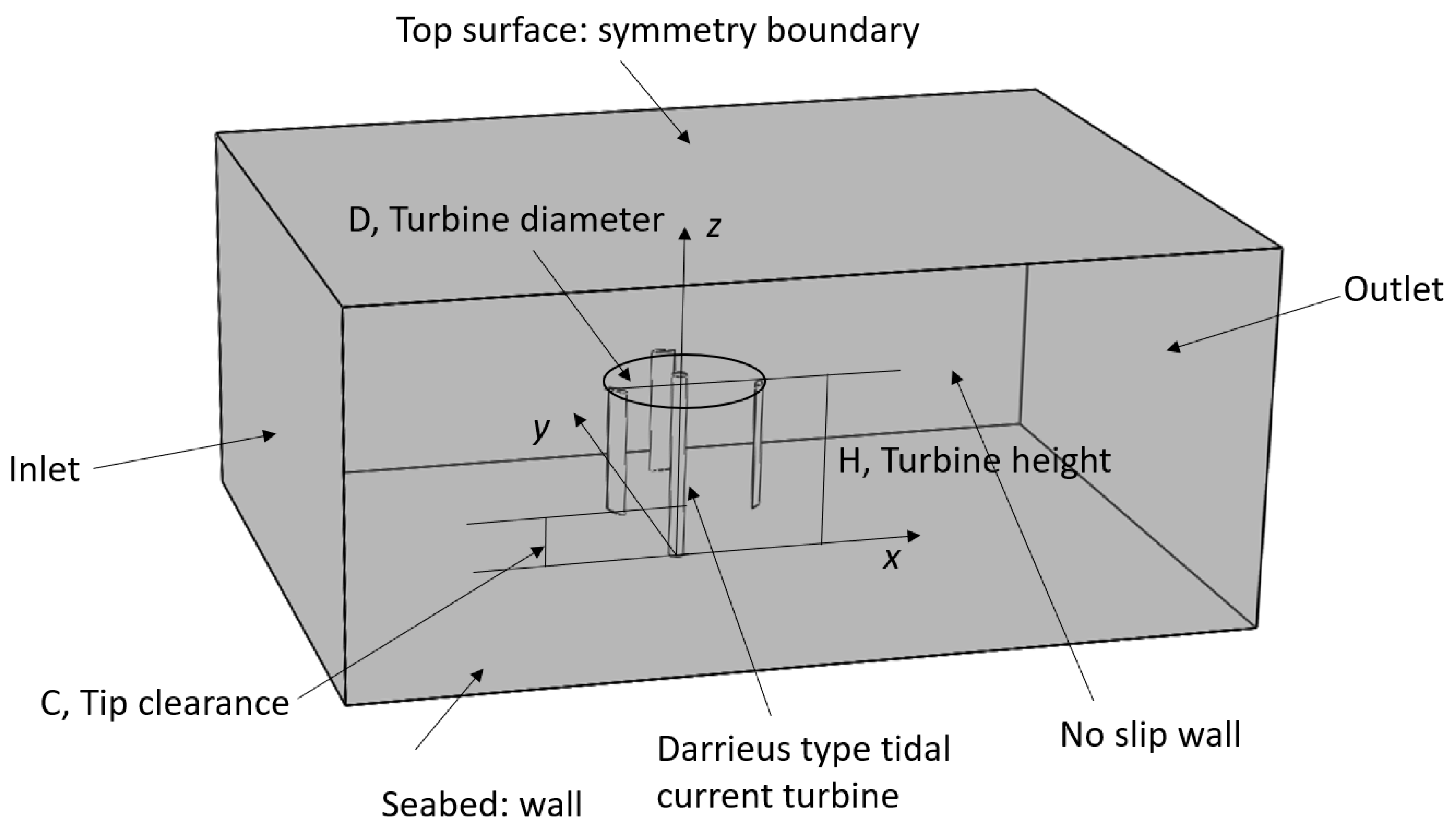
2.1.3. Boundary Conditions
- (1)
- Inlet and outlet boundary conditions: For the inlet boundary, the uniform velocity inlet condition was used, and the initial pascal pressure was set as 0. The outlet boundary pressure outlet was applied for all quantities. The turbulence intensity at the inlet/outlet boundaries was 5% for medium intensity as a default value, which is suggested in Fluent Help [21];
- (2)
- Symmetry boundaries: The symmetry boundary was applied to simulate the free surface condition. At the symmetry boundaries, Neumann conditions were applied for variables in the k- turbulence model. It was assumed that a “lid” was on the top surface. The symmetry boundary condition is an effective method to simulate the free surface, and it has been applied in many scour simulations, such as in References [12] and [23];
- (3)
- Walls: The sides of the computational domain, surfaces of foundation, and turbine blades were set as no-slip wall boundaries. The roughness height was set as zero to simulate a smooth surface. The sediment bottom was set as a rough wall boundary. The roughness height of the sediment bottom was set as 2.5, which can simulate the true sediment bed (as suggested by Roulund) [12].
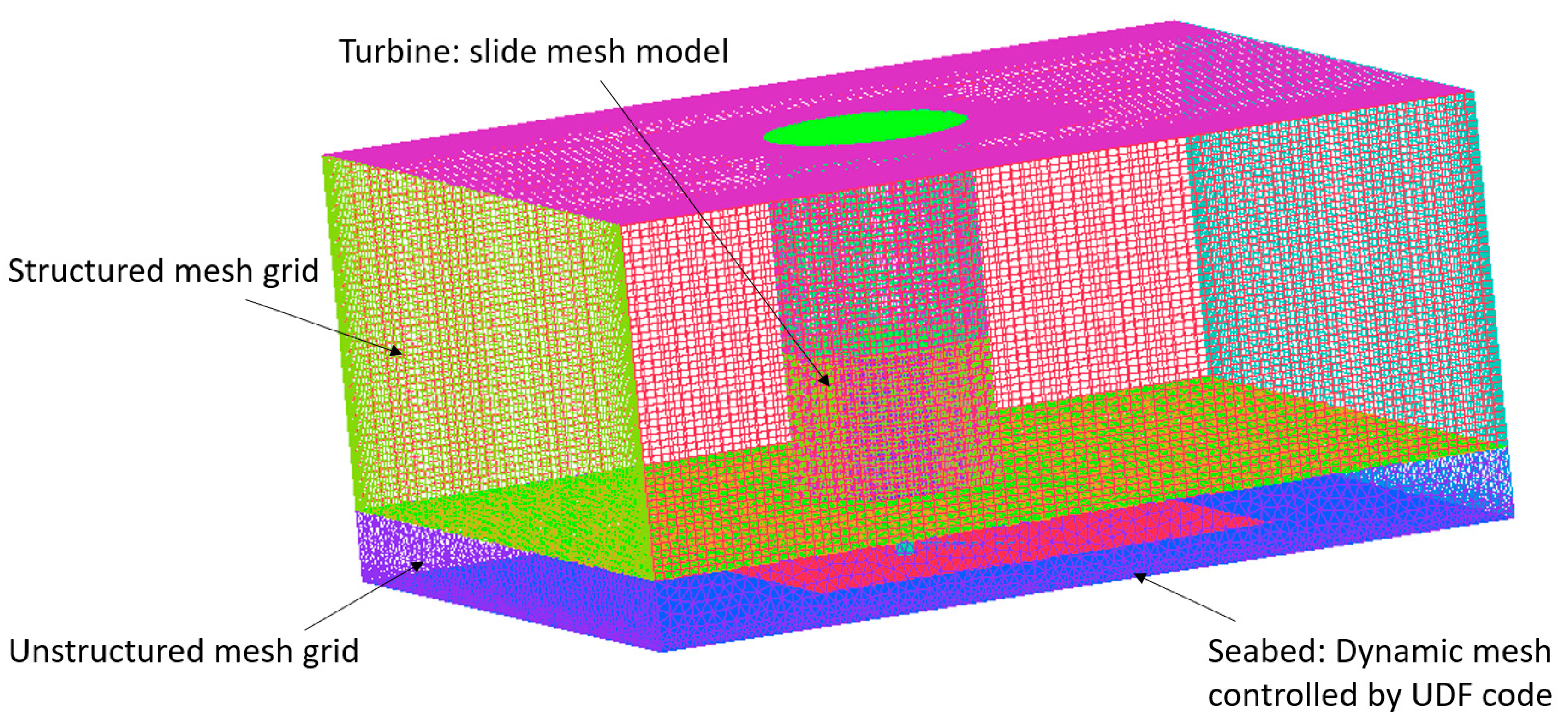
2.1.4. Computational Mesh
2.1.5. Grid Independence Analysis
2.2. Morphological Model
2.2.1. Sediment Transport Model
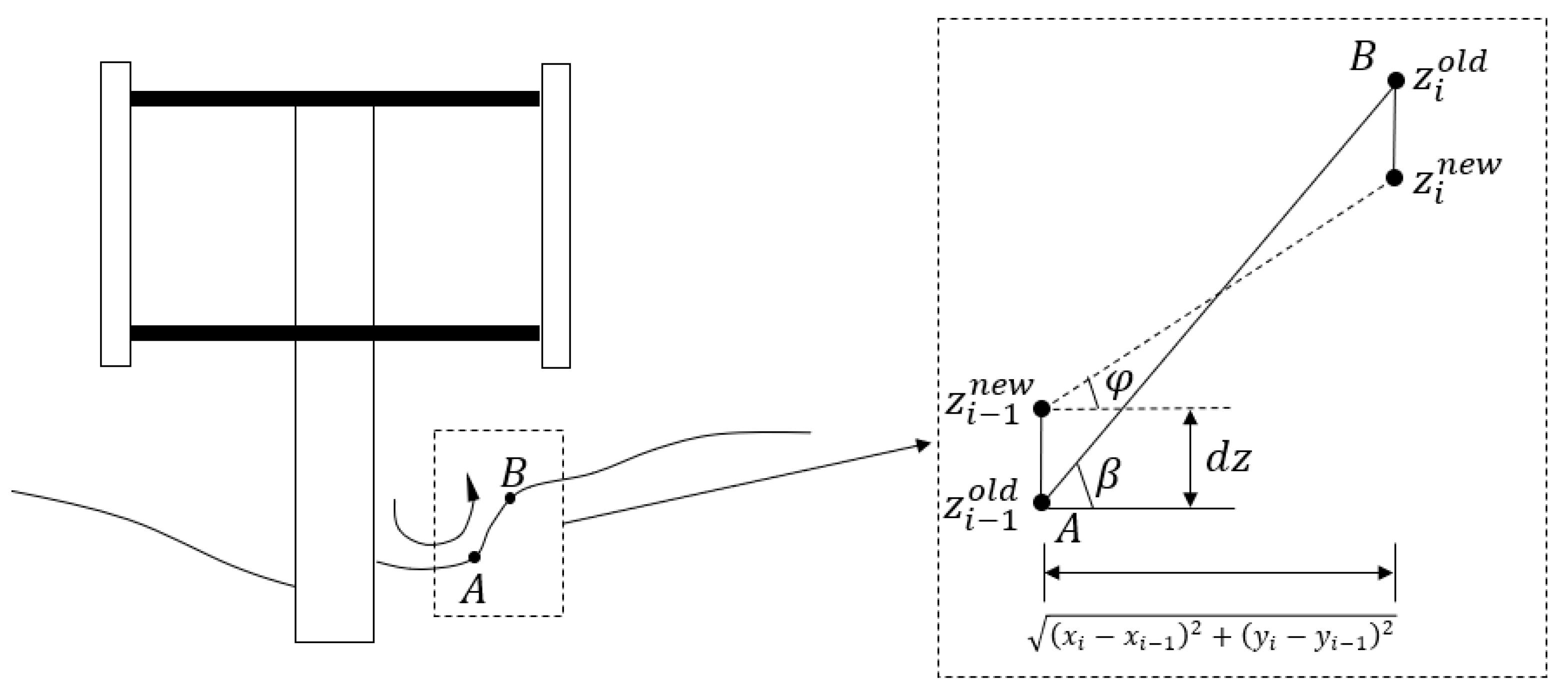
2.2.2. Sand Slide
- (1)
- Update the seabed elevation change based on the sediment transport model at each time step. After that, scan all the nodes and center points of the mesh grid on the seabed boundary;
- (2)
- If the angle between grid node A() and grid node B() is greater than the bed slope angle of repose , then the model raises or reduces the z coordinate of grid node A and B, making sure the slope angle is less than . The vertical displacements of A and B are the same, which ensures the conservation of sediment in the scour process. Equation (11) is
- (3)
- Repeat the above process 6–10 times, ensuring all of the inclination angles are under .
2.2.3. Updating Strategy
- (1)
- Calculate the flow field;
- (2)
- Calculate the sediment transport due to bed load;
- (3)
- Update the seabed boundary;
- (4)
- Check the sand slide and use the sand slide model to correct the slope angle;
- (5)
- Turn to the next time step and return to step 1.
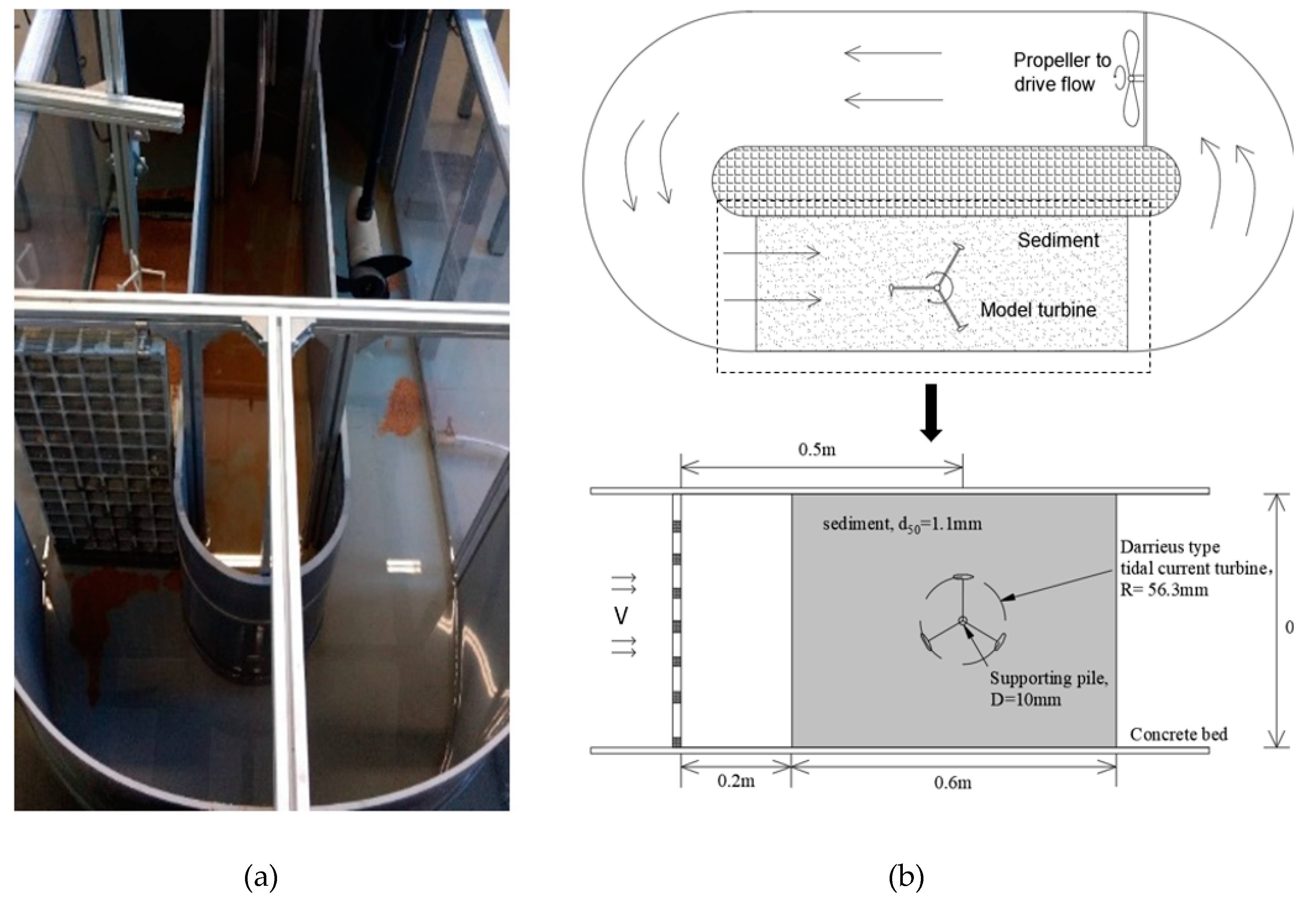
2.3. Experimental Setup
3. Numerical Test and Application of Turbine Scour
3.1. Numerical Model Setup
3.2. Model Validation through First Group
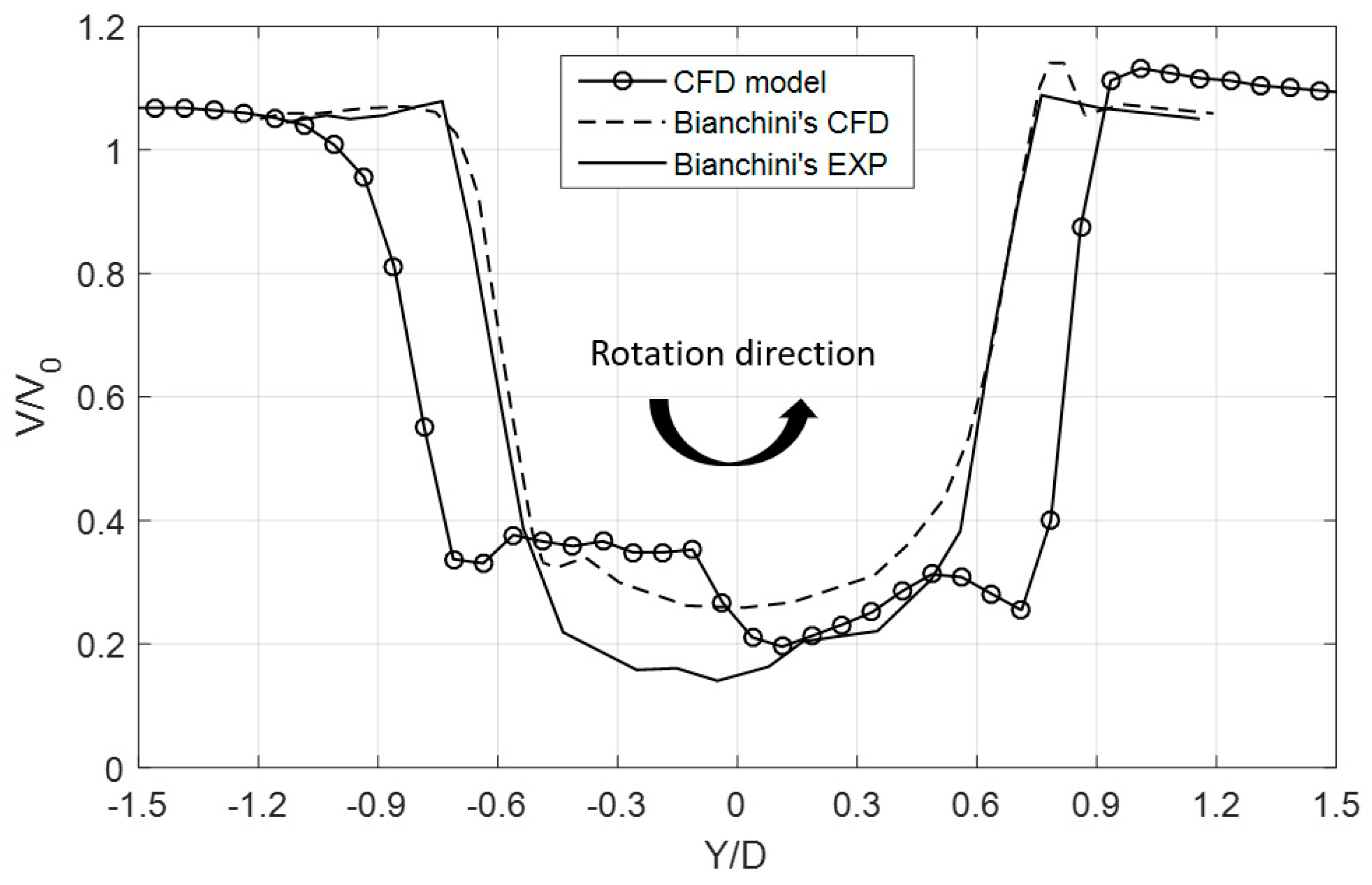
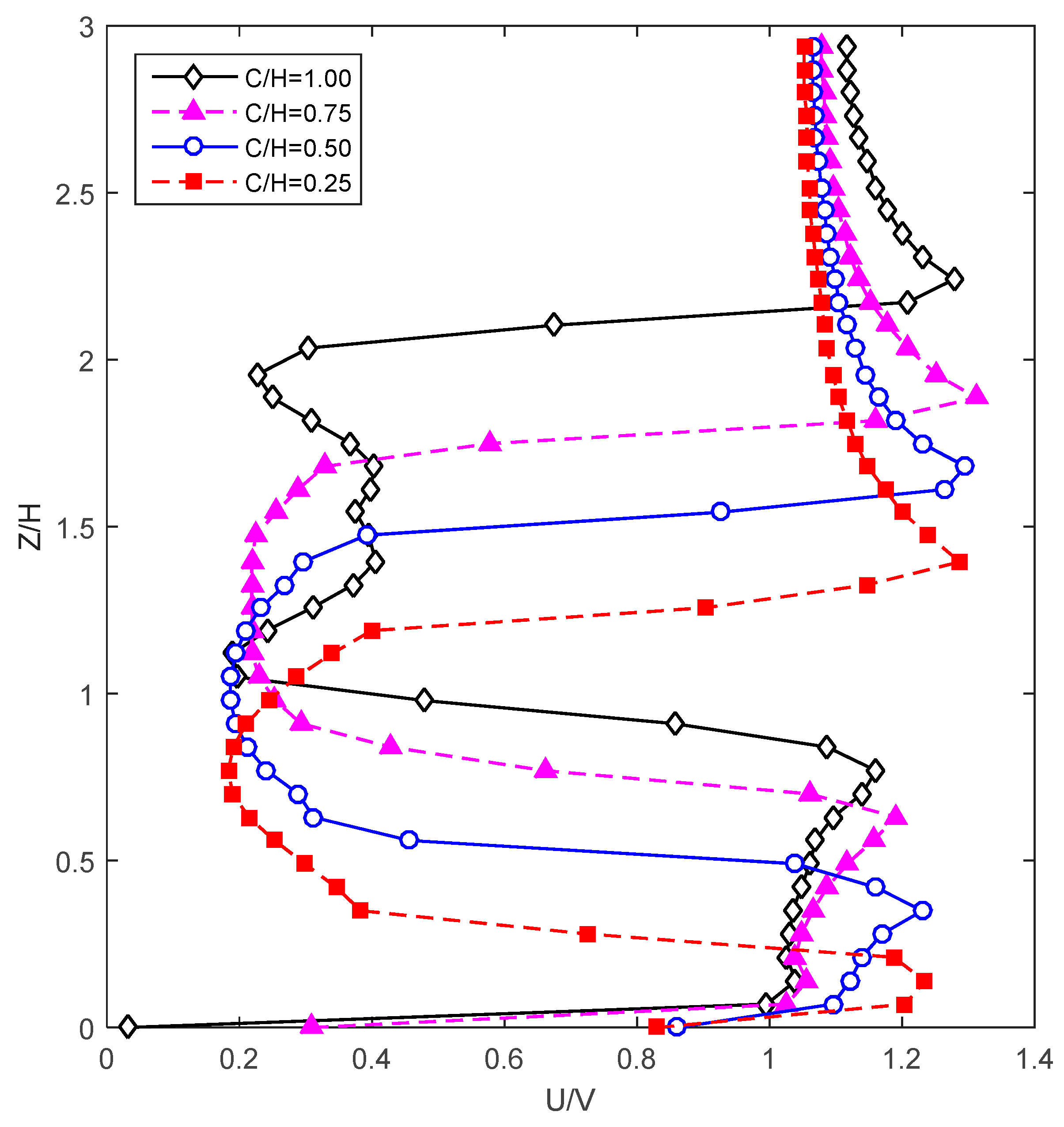
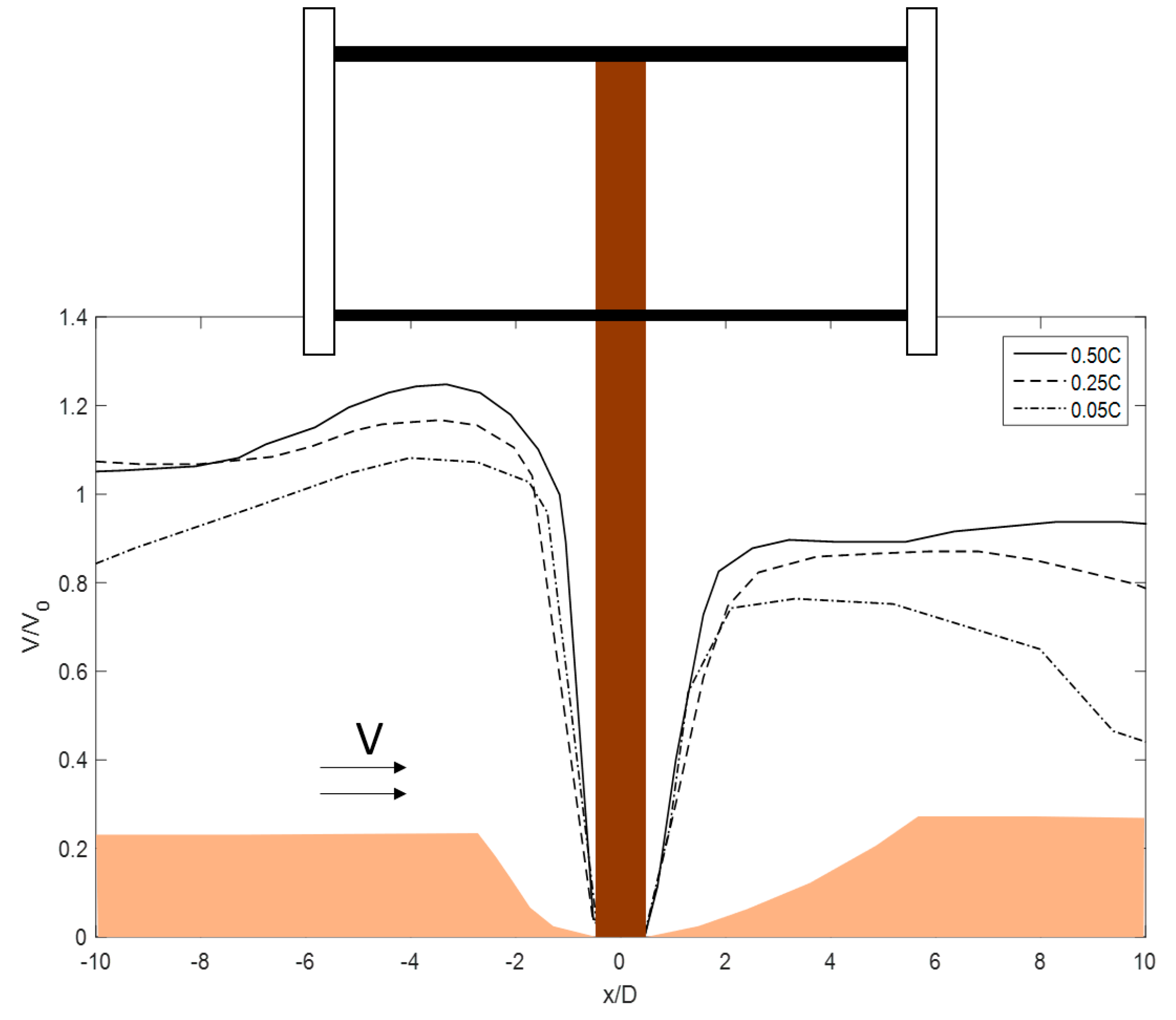
3.2.1. Flow Field Validation
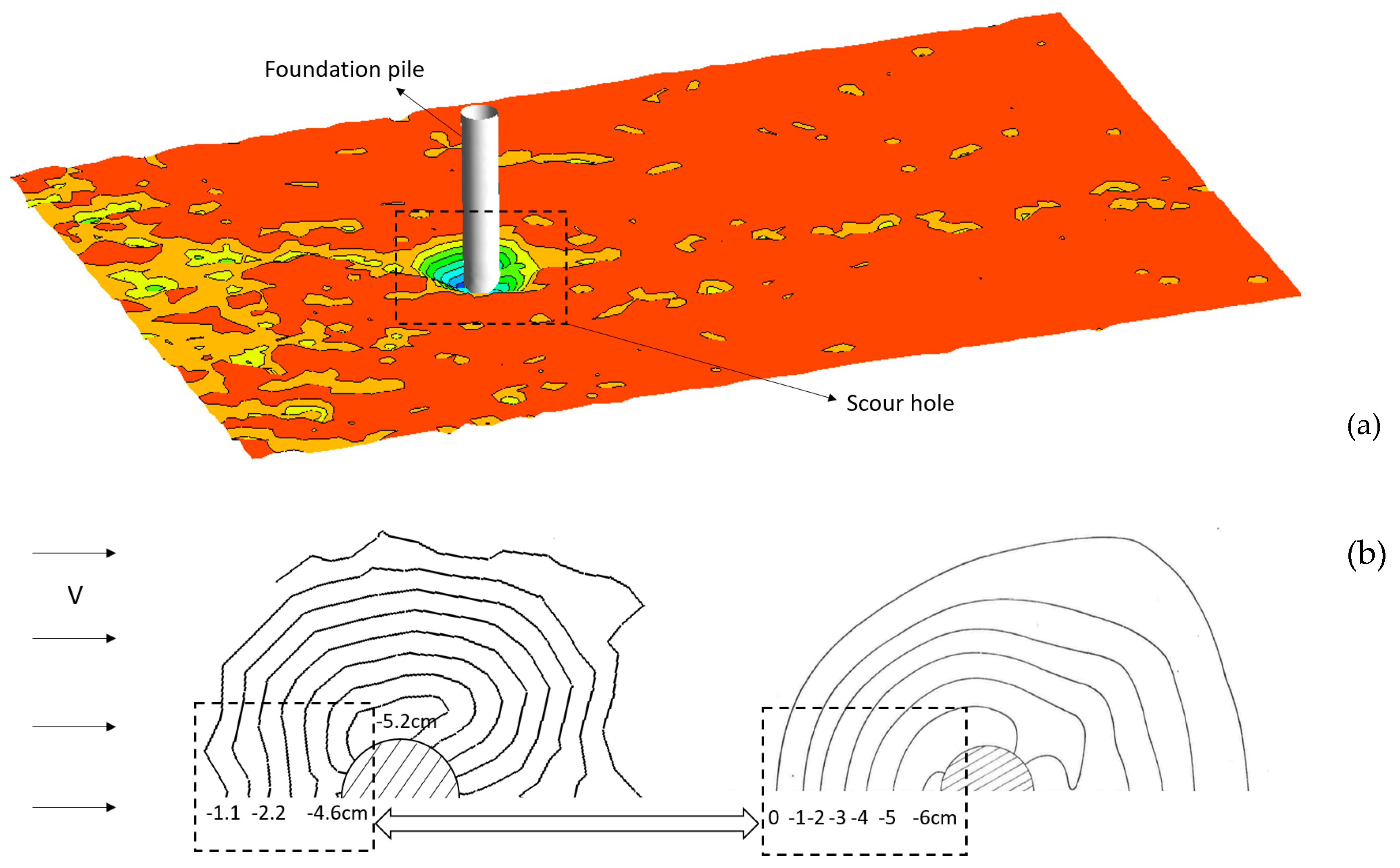
3.2.2. Scour Shape Validation
- (i)
- A semicircular shape (in plan view) of the upstream part of the scour hole with a slope equal to the angle of repose;
- (ii)
- The formation of a gentler slope on the downstream side of the scour hole;
- (iii)
- A maximum scour depth occurring on the near sides of the foundation pile.
3.3. Model Validation through Second Group
3.3.1. Scour Depth Validation
3.3.2. Scour Profile Validation
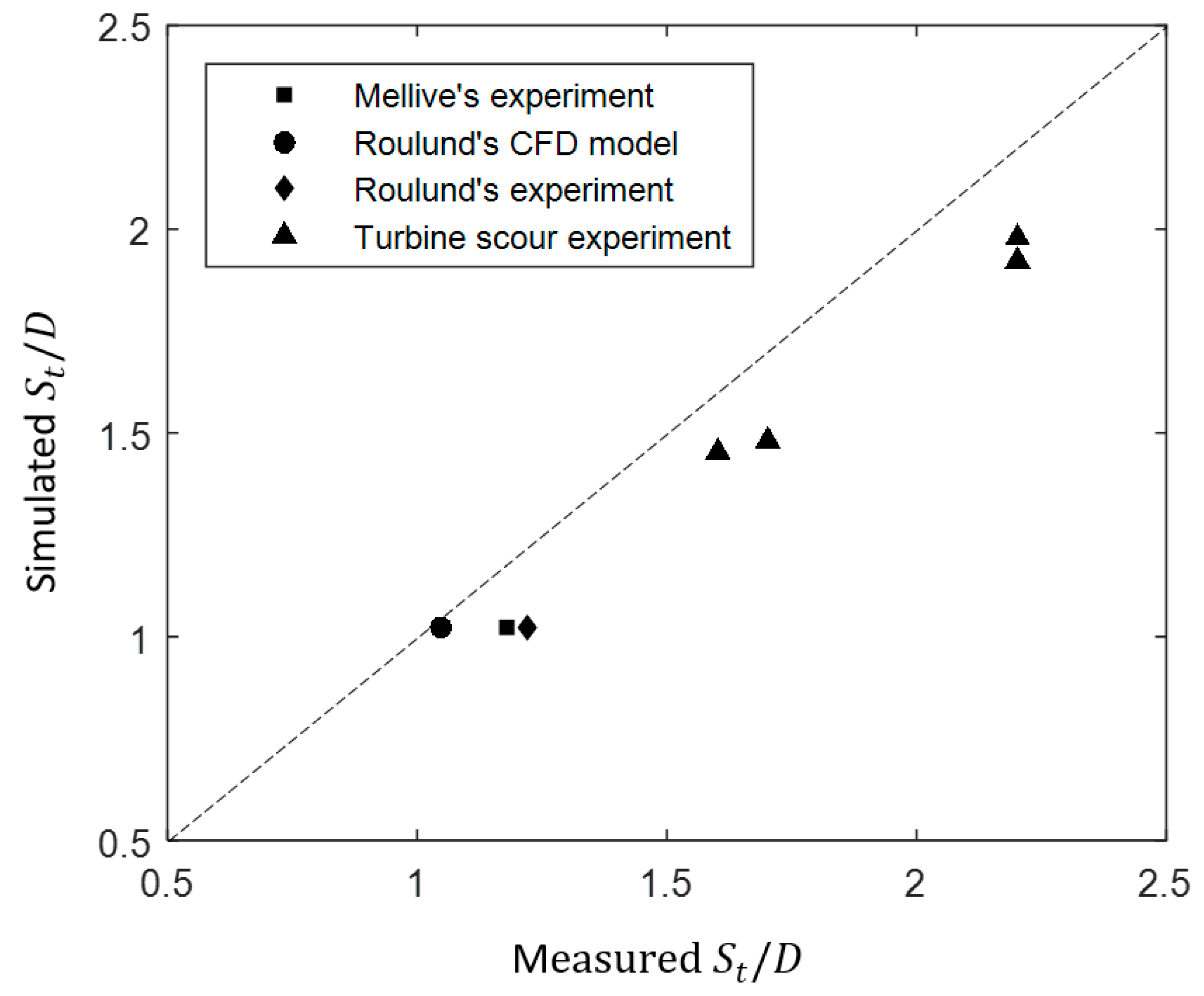
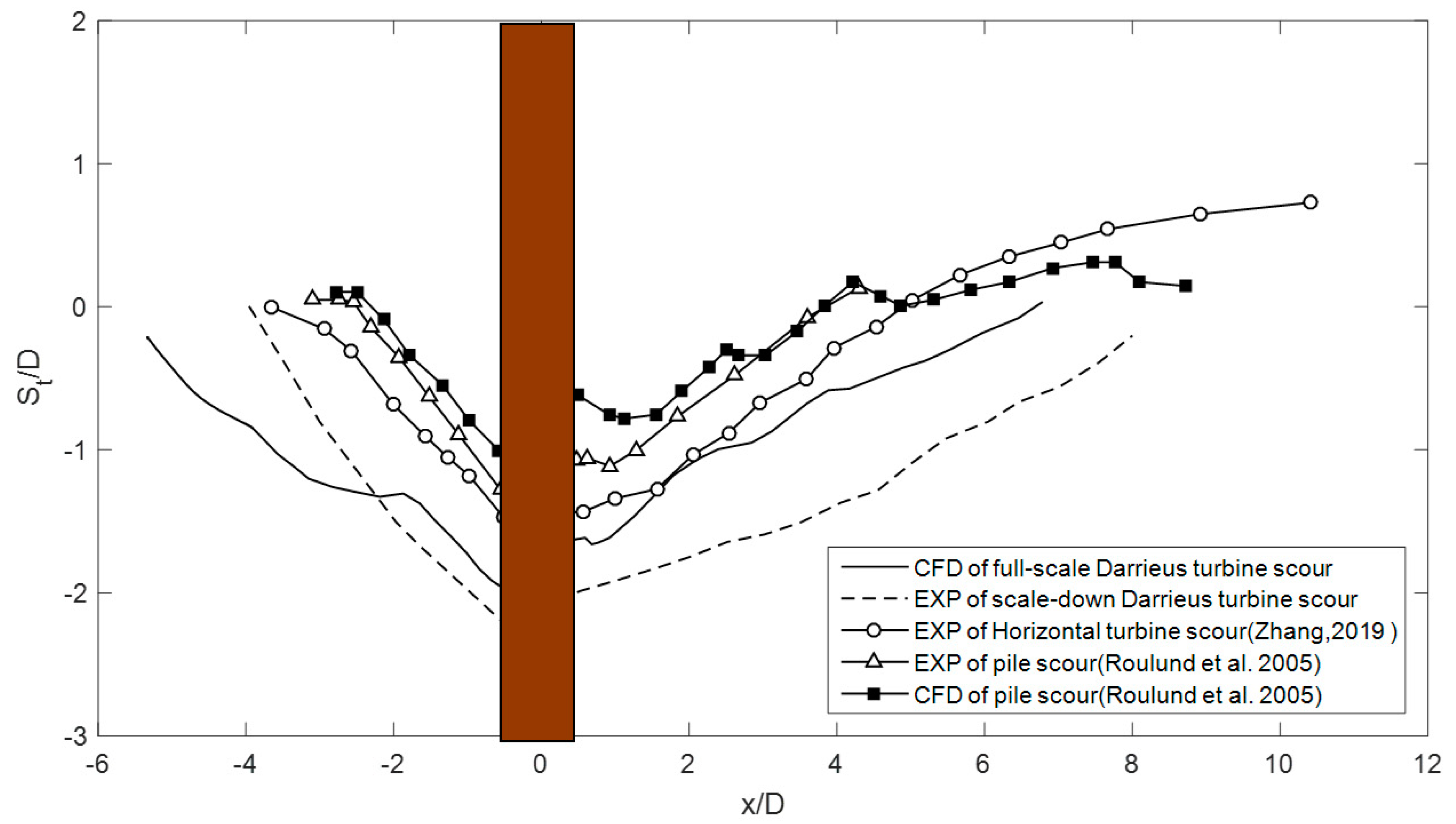
3.4. Error Analysis of the Proposed Model
4. Numerical Investigation of Full-Scale Turbine Scour
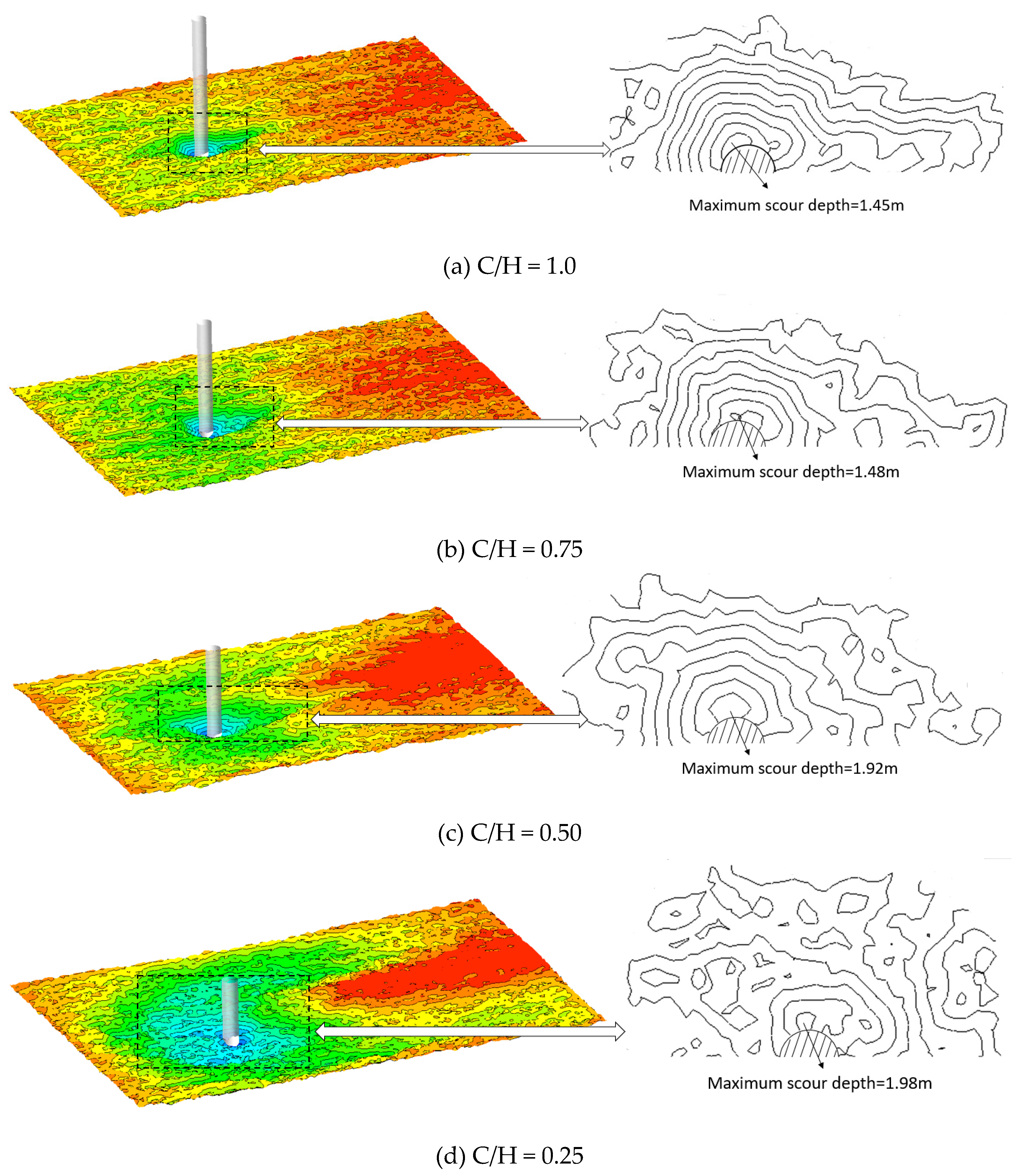
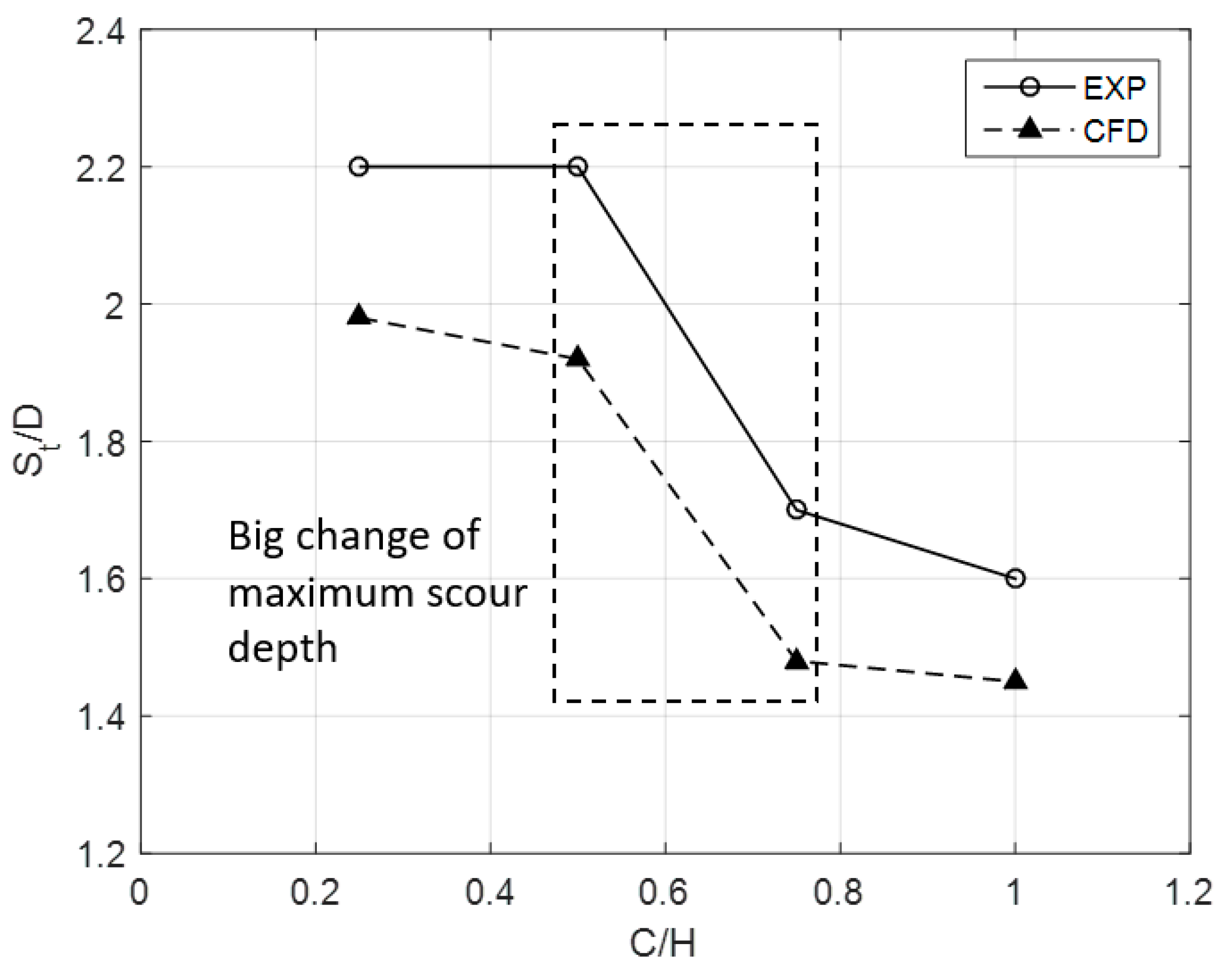
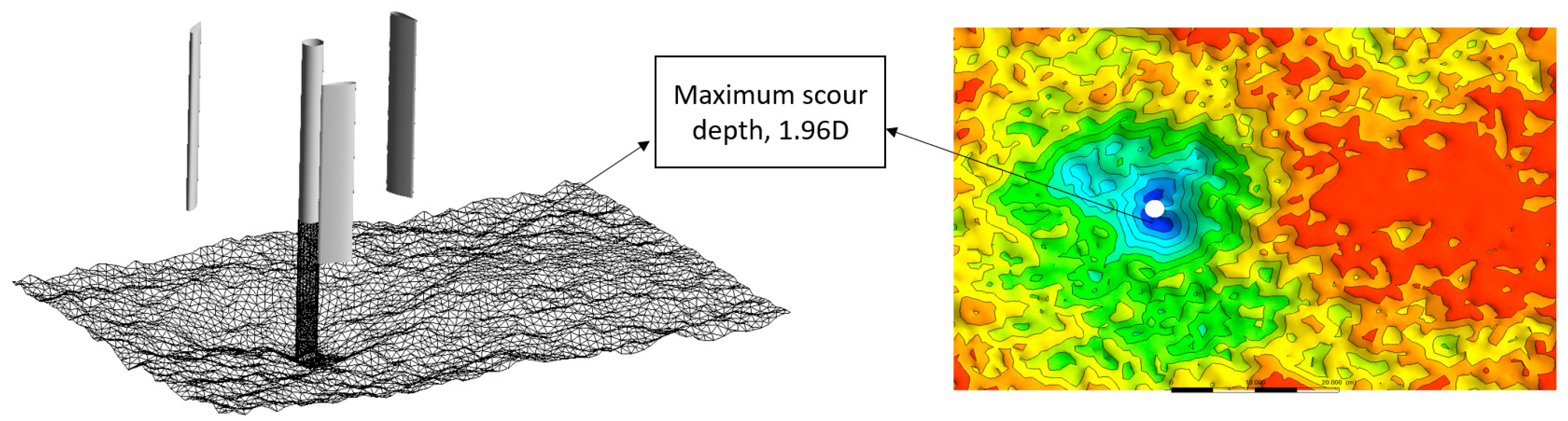
4.1. Maximum Scour Depth
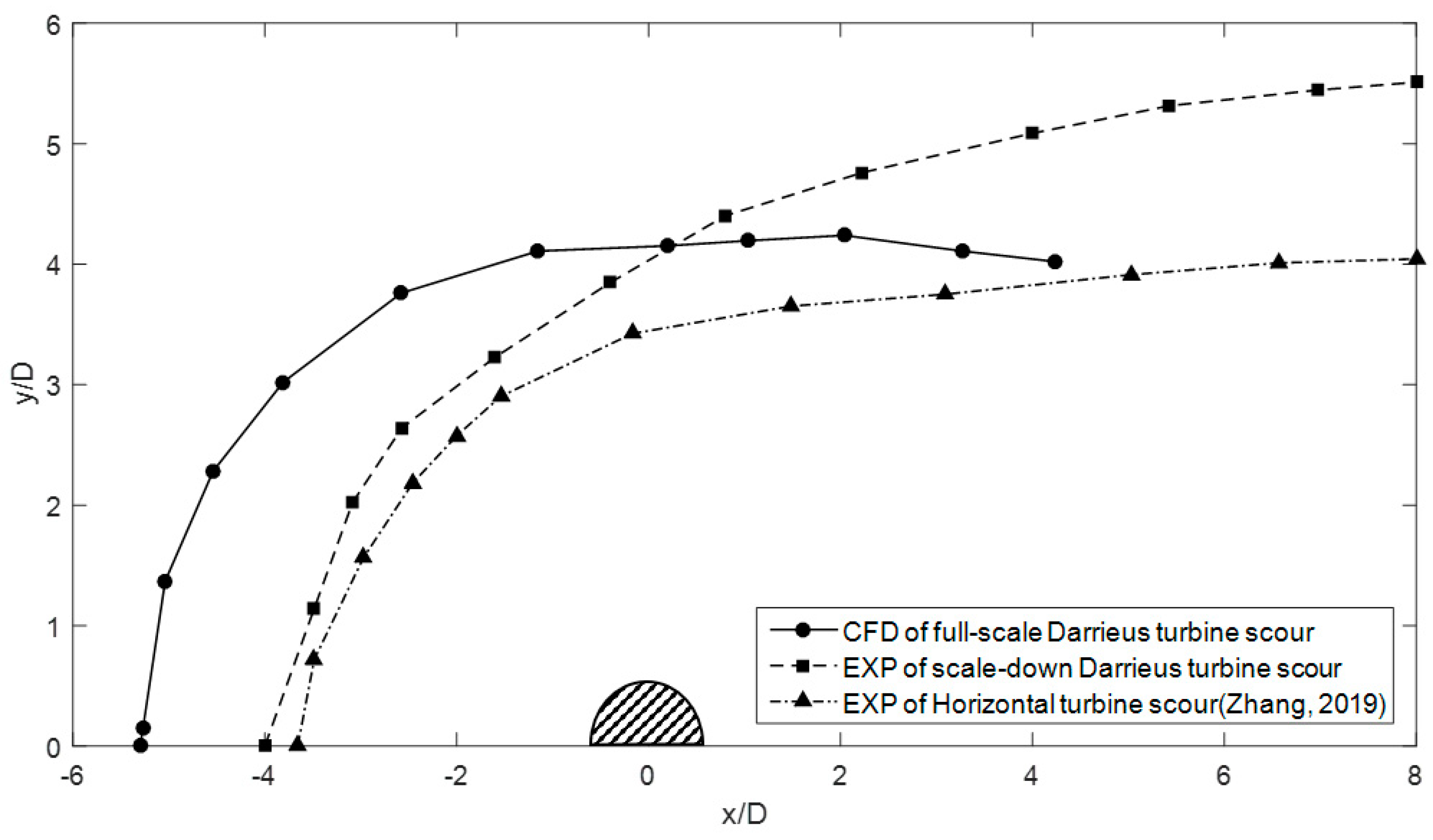
4.2. Horizontal Extent of Scour Hole
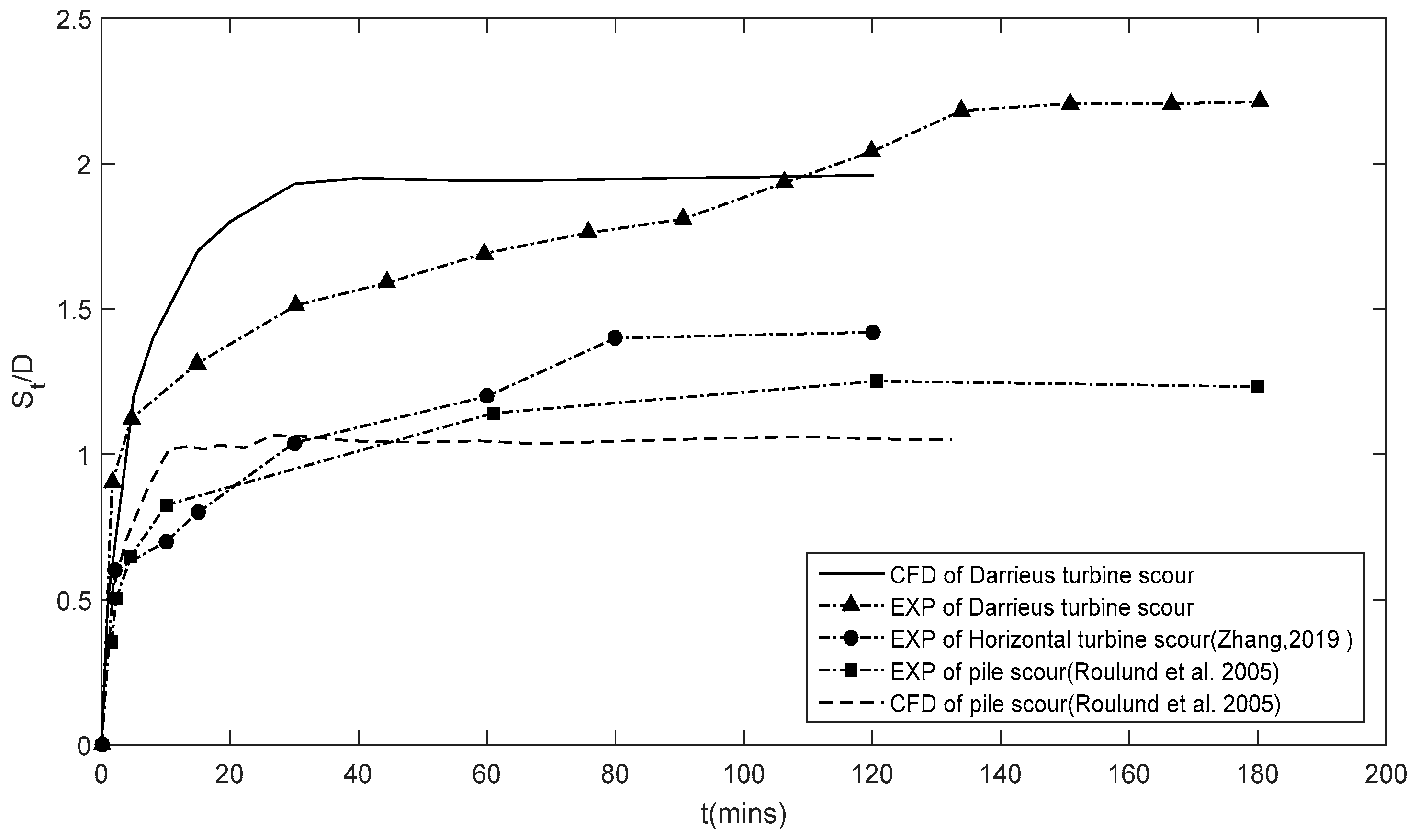
4.3. Temporal Development of Scour Depth
4.4. Turbine Scour Mechanism
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sumer, M.B. Mathematical modelling of scour: A review. J. Hydraul. Res. 2007, 45, 723–735. [Google Scholar] [CrossRef]
- Melikoglu, M. Current status and future of ocean energy sources: A global review. Ocean Eng. 2018, 148, 563–573. [Google Scholar] [CrossRef]
- Musa, M.; Hill, C.; Sotiropoulos, F.; Guala, M. Performance and resilience of hydrokinetic turbine arrays under large migrating fluvial bedforms. Nat. Energy 2018, 3, 839–846. [Google Scholar] [CrossRef]
- Chen, L.; Lam, W.H. Methods for predicting seabed scour around marine current turbine. Renew. Sustain. Energy Rev. 2014, 29, 683–692. [Google Scholar] [CrossRef]
- Sun, C.; Lam, W.H.; Cui, Y.; Zhang, T.; Jiang, J.; Guo, J.; Ma, Y.; Wang, S.; Tan, T.H.; Chuah, J.H.; et al. Empirical model for Darrieus-type tidal current turbine induced seabed scour. Energy Convers. Manag. 2018, 171, 478–490. [Google Scholar] [CrossRef] [Green Version]
- Breusers, H.N.C.; Nicollet, G.; Shen, H.W. Local Scour Around Cylindrical Piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Wang, D.; Atlar, M.; Sampson, R. An experimental investigation on cavitation, noise, and slipstream characteristics of ocean stream turbines. Proc. Inst. Mech. Eng. Part A J. Power Energy 2007, 221, 219–231. [Google Scholar] [CrossRef]
- Hill, C.; Musa, M.; Chamorro, L.P.; Ellis, C. Local Scour around a Model Hydrokinetic Turbine in an Erodible Channel. J. Hydraul. Eng. 2014, 140, 04014037. [Google Scholar] [CrossRef]
- Zhang, T.; Lam, W.H.; Cui, Y.; Jang, J.; Sun, C.; Guo, J.; Ma, Y.; Wang, S.; Lam, S.S. Tip-Bed Velocity and Scour Depth of Horizontal-Axis Tidal Turbine with Consideration of Tip Clearance. Energies 2019, 12, 2450. [Google Scholar] [CrossRef]
- Sun, C.; Lam, W.H.; Lam, S.S.; Dai, L.M.; Hamill, G. Temporal Evolution of Seabed Scour Induced by Darrieus-Type Tidal Current Turbine. Water 2019, 11, 896. [Google Scholar] [CrossRef]
- Chen, L.; Lam, W.H. Slipstream between marine current turbine and seabed. Energy 2014, 68, 801–810. [Google Scholar] [CrossRef]
- Roulund, A.; Sumer, B.M.; Fredsoe, J.; Michelsen, J. Numerical and experimental investigation of flow and scour around a circular pile. J. Fluid Mech. 2005, 534, 351–401. [Google Scholar] [CrossRef]
- Ettema, R.; Melville, B.W.; Barkdoll, B. Scale Effect in Pier-Scour Experiments. J. Hydraul. Eng. 1998, 124, 639–642. [Google Scholar] [CrossRef]
- Huang, W.; Yang, Q.; Xiao, H. CFD modeling of scale effects on turbulence flow and scour around bridge piers. Comput. Fluids 2009, 38, 1050–1058. [Google Scholar] [CrossRef]
- Dai, Y.M.; Lam, W. Numerical study of straight-bladed Darrieus-type tidal turbine. Proc. Inst. Civ. Eng. Energy 2009, 162, 67–76. [Google Scholar] [CrossRef]
- Jeffcoate, P.; Starzmann, R.; Elsaesser, B.; Scholl, S.; Bischoff, S. Field measurements of a full scale tidal turbine. Int. J. Mar. Energy 2015, 12, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Neill, S.P.; Litt, E.J.; Couch, S.J.; Davies, A.G. The impact of tidal stream turbines on large-scale sediment dynamics. Renew. Energy 2009, 34, 2803–2812. [Google Scholar] [CrossRef]
- Burkow, M.; Griebel, M. A full three dimensional numerical simulation of the sediment transport and the scouring at a rectangular obstacle. Comput. Fluids 2016, 125, 1–10. [Google Scholar] [CrossRef]
- Zhang, J.S.; Gao, P.; Zheng, J.H.; Wu, X.G.; Peng, Y.X.; Zhang, T.T. Current-Induced seabed scour around a pile-supported horizontal-axis tidal stream turbine. J. Mar. Sci. Technol. 2015, 23, 929–936. [Google Scholar]
- Patankar, S.V. Numerical heat transfer and fluid flow. In Series in Computational Methods in Mechanics and Thermal Sciences; Taylor & Francis: Didcot, UK, 1980. [Google Scholar]
- Fluent User Manual. In Fluent User’s Guide; Fluent Inc.: Lebanon, PA, USA, 2003.
- Wilcox, D.C. Turbulence Modelling for, C.F.D., 2nd ed.; DCW Industries: La Canada, CA, USA, 1993. [Google Scholar]
- Baykal, C.; Sumer, B.M.; Fuhrman, D.R.; Jacobsen, N.G.; Fredsøe, J. Numerical investigation of flow and scour around a vertical circular cylinder. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 373, 20140104. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Chien, N.; Wan, Z. Mechanics of Sediment Transport; Science Press: Beijing, China, 1983; ISBN 978-0-7844-0400-3. [Google Scholar]
- Lagasse, P.F.; Zevenbergen, L.W.; Spitz, W.J.; Arneson, L.A. Stream Stability at Highway Structures, 4th ed.; National Technical Information Service: Springfield, VA, USA, 2012. [Google Scholar]
- Nagata, N.; Hosoda, T.; Nakato, T.; Muramoto, Y. Three-dimensional numerical model for flow and bed deformation around river hydraulic structures. J. Hydraul. Eng. 2005, 131, 1074–1087. [Google Scholar] [CrossRef]
- Brørs, B. Numerical modeling of flow and scour at pipelines. J. Hydraul. Eng. 1999, 125, 511–523. [Google Scholar] [CrossRef]
- Xiong, W.; Cai, C.S.; Kong, B.; Kong, X. CFD simulations and analyses for bridge-scour development using a dynamic-mesh updating technique. J. Comput. Civ. Eng. 2014, 30, 04014121. [Google Scholar] [CrossRef]
- Liang, D.; Cheng, L.; Li, F. Numerical modeling of flow and scour below a pipeline in currents: Part, I.I. Scour simulation. Coast. Eng. 2005, 52, 43–62. [Google Scholar] [CrossRef]
- Ballio, F.; Radice, A.; Dey, S. Temporal scales for live-bed scour at abutments. J. Hydraul. Eng. 2009, 136, 395–402. [Google Scholar] [CrossRef]
- Rajaratnam, N. Erosion by plane turbulent jets. J. Hydraul. Res. 1981, 19, 339–358. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Sites. Ph.D. Thesis, School of Engineering, University of Auckland, Auckland, New Zealand, 1975. [Google Scholar]
- Bianchini, A.; Balduzzi, F.; Ferrara, G.; Ferrari, L.; Persico, G.; Dossena, V.; Battisti, L. Detailed Analysis of the Wake Structure of a Straight-Blade H-Darrieus Wind Turbine by Means of Wind Tunnel Experiments and Computational Fluid Dynamics Simulations. J. Eng. Gas Turbines Power 2018, 140, 032604. [Google Scholar] [CrossRef]
- Kolekar, N.; Banerjee, A. Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and blockage effects. Appl. Energy 2015, 148, 121–133. [Google Scholar] [CrossRef]
- Hahn, E.M.; Lyn, D.A. Anomalous contraction scour? Vertical-contraction case. J. Hydraul. Eng. 2010, 136, 137–141. [Google Scholar] [CrossRef]



| Variables | Case 1 | Case 2 | Case 3 (Selected) | Case 4 |
|---|---|---|---|---|
| Mesh grid numbers | 1,285,567 | 1,679,654 | 2,046,678 | 2,442,236 |
| Cp | 16.4% | 18.8% | 19.7% | 19.9% |
| Additional cells | - | 394,087 | 367,024 | 395,558 |
| Validation | - | 14.6% | 4.8% | 1.0% |
| Parameters | Values |
|---|---|
| Rotor radius R (mm) | 56.3 |
| Rotor height H (mm) | 87.5 |
| Chord length c (mm) | 20.4, |
| Dimensionless tip clearance C/H | 0.25, 0.5, 0.75, 1 |
| Monopile diameter D (mm) | 10 |
| (rpm) | 110 |
| Depth of water h (m) | 0.3 |
| Width of flume b (m) | 0.35 |
| (mm) | 1.1 |
| (m/s) | 0.23 |
| Number | Scale-Up Ratio Based on Physical Models | Tip Clearance, (C/H) | Sediment Diameter (mm) | Inlet Velocity (m/s) | Rotational Speed (rpm) |
|---|---|---|---|---|---|
| T1 | 5.08 | - | 0.385 | 0.25 | - |
| T2 | 5.08 | 0.5 | 0.385 | 0.25 | 15 |
| T3 | 100 | 0.25 | 8.0 | 2.3 | 11 |
| T4 | 100 | 0.5 | 8.0 | 2.3 | 11 |
| T5 | 100 | 0.75 | 8.0 | 2.3 | 11 |
| T6 | 100 | 1.0 | 8.0 | 2.3 | 11 |
| Statistical Functions | MAE | RMSE | SI | |
|---|---|---|---|---|
| Value | 0.98 | 0.11 | 0.12 | 0.05 |
| Parameters | Values |
|---|---|
| Rotor radius R(m) | 13.5 |
| Rotor height H (m) | 21 |
| Chord length c (m) | 4.9 |
| Dimensionless tip clearance C/H | 0.5 |
| Monopile diameter D (m) | 2.4 |
| (rpm) | 14 |
| (mm) | 8 |
| (m/s) | 3.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, C.; Lam, W.H.; Dai, M.; Hamill, G. Prediction of Seabed Scour Induced by Full-Scale Darrieus-Type Tidal Current Turbine. J. Mar. Sci. Eng. 2019, 7, 342. https://doi.org/10.3390/jmse7100342
Sun C, Lam WH, Dai M, Hamill G. Prediction of Seabed Scour Induced by Full-Scale Darrieus-Type Tidal Current Turbine. Journal of Marine Science and Engineering. 2019; 7(10):342. https://doi.org/10.3390/jmse7100342
Chicago/Turabian StyleSun, Chong, Wei Haur Lam, Ming Dai, and Gerard Hamill. 2019. "Prediction of Seabed Scour Induced by Full-Scale Darrieus-Type Tidal Current Turbine" Journal of Marine Science and Engineering 7, no. 10: 342. https://doi.org/10.3390/jmse7100342
APA StyleSun, C., Lam, W. H., Dai, M., & Hamill, G. (2019). Prediction of Seabed Scour Induced by Full-Scale Darrieus-Type Tidal Current Turbine. Journal of Marine Science and Engineering, 7(10), 342. https://doi.org/10.3390/jmse7100342






