The DeepWater Horizon Oil Slick: Simulations of River Front Effects and Oil Droplet Size Distribution
Abstract
1. Introduction
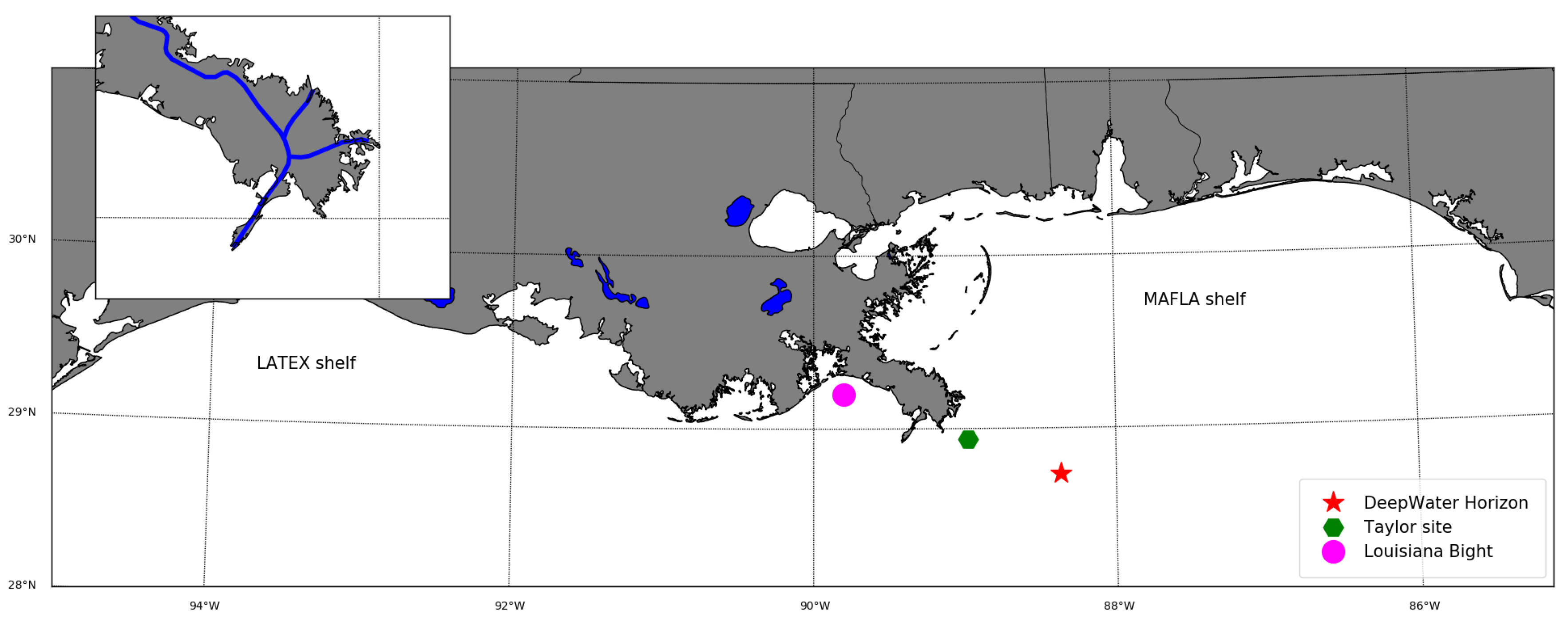
2. Materials and Methods
2.1. Shapefiles of Surface Oil Patch
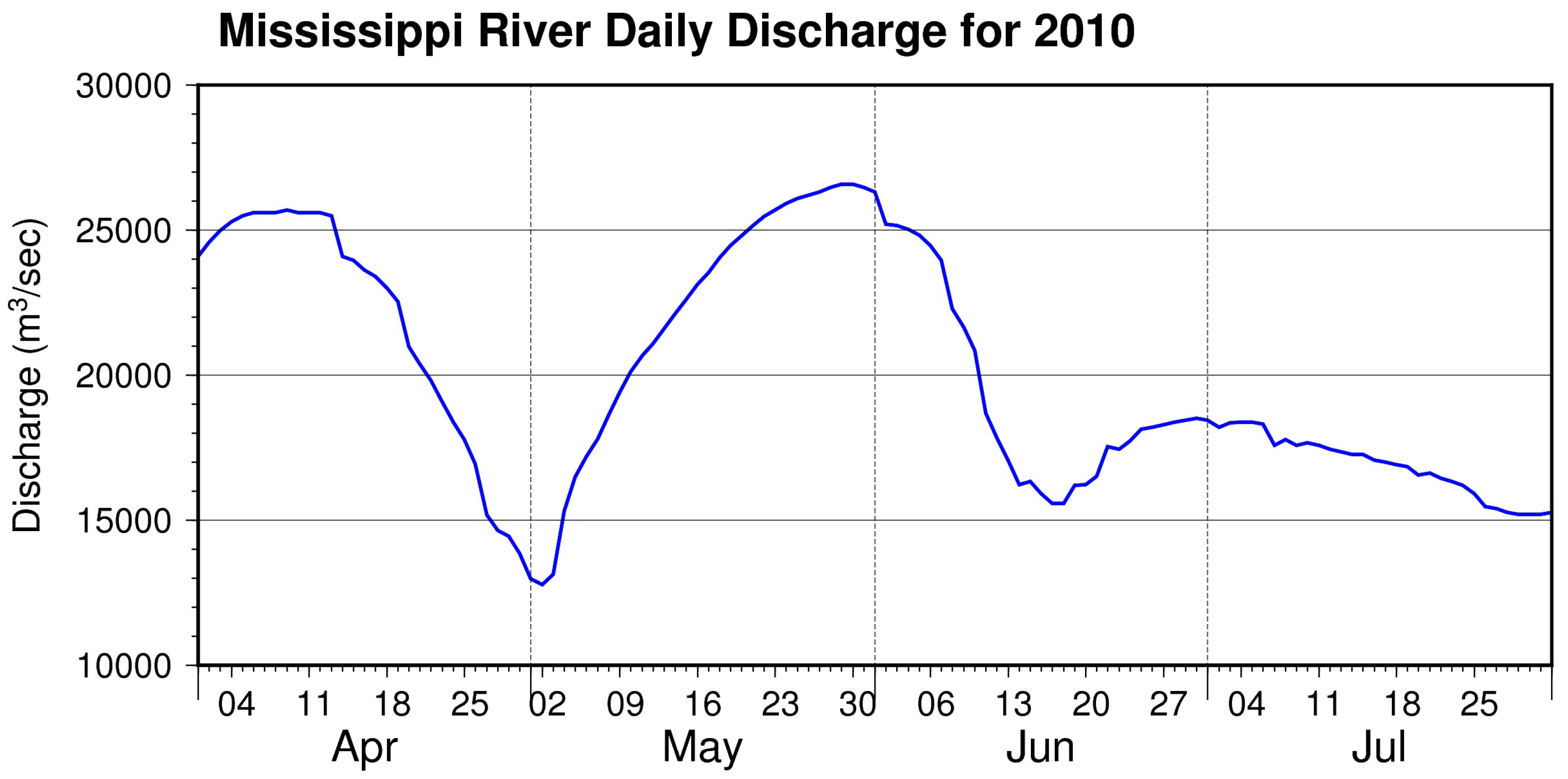
2.2. Metocean Forcing
2.3. The Oil Drift Model OpenOil
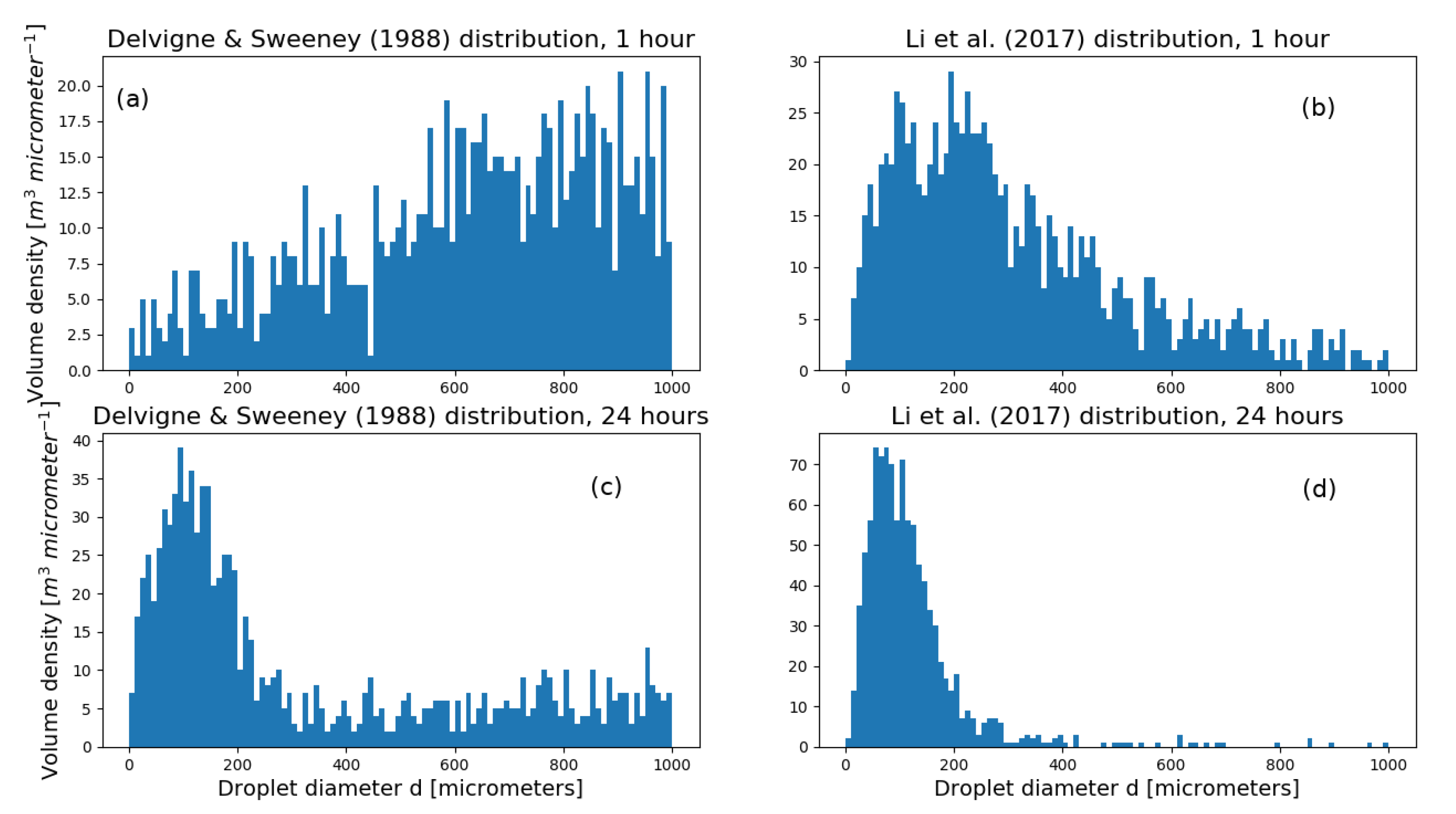
2.3.1. Oil Droplet Size Distribution
2.3.2. Droplet Size Distribution During Deep Blowouts
2.3.3. Horizontal Transport
2.3.4. Vertical Transport
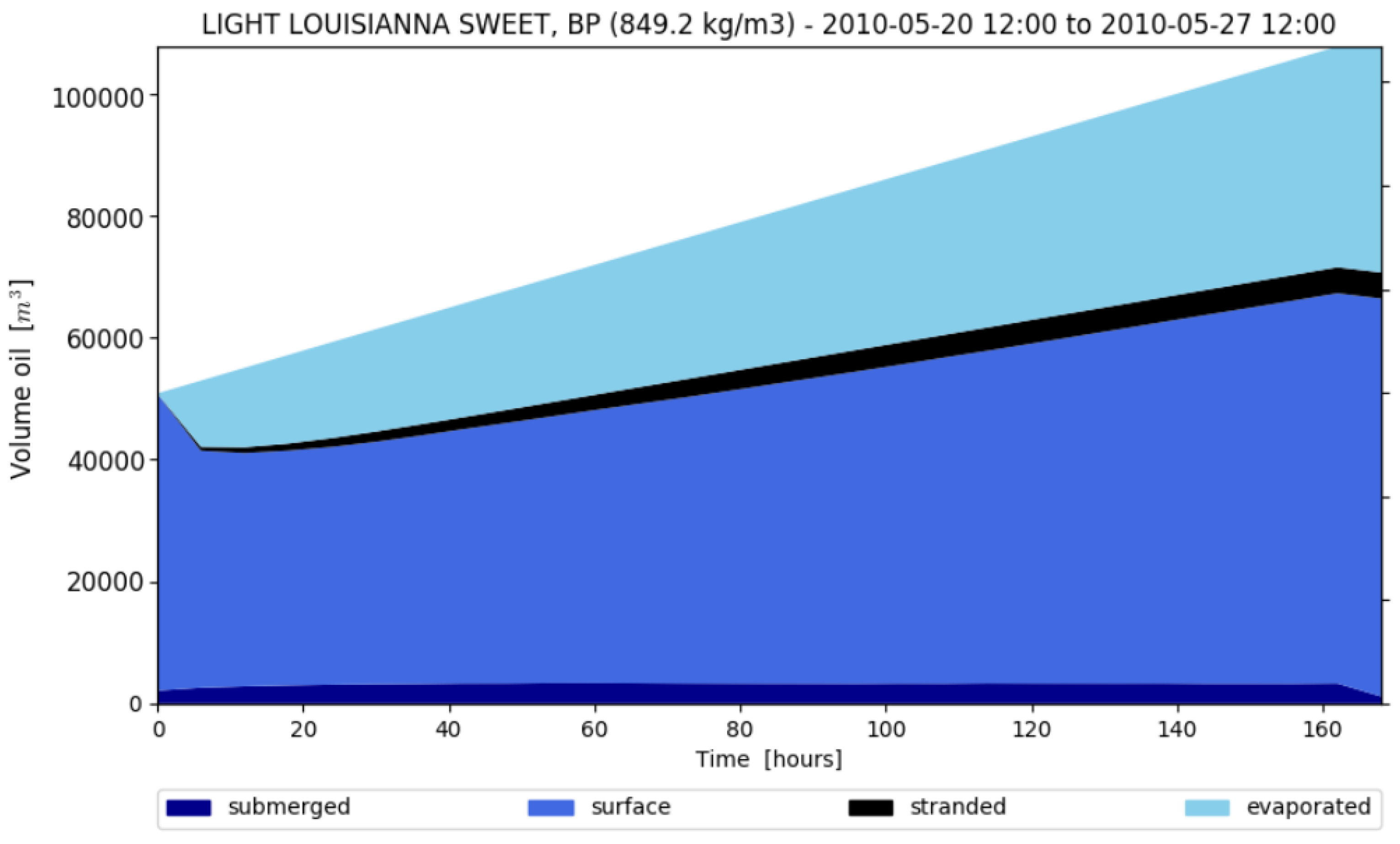
2.3.5. Weathering
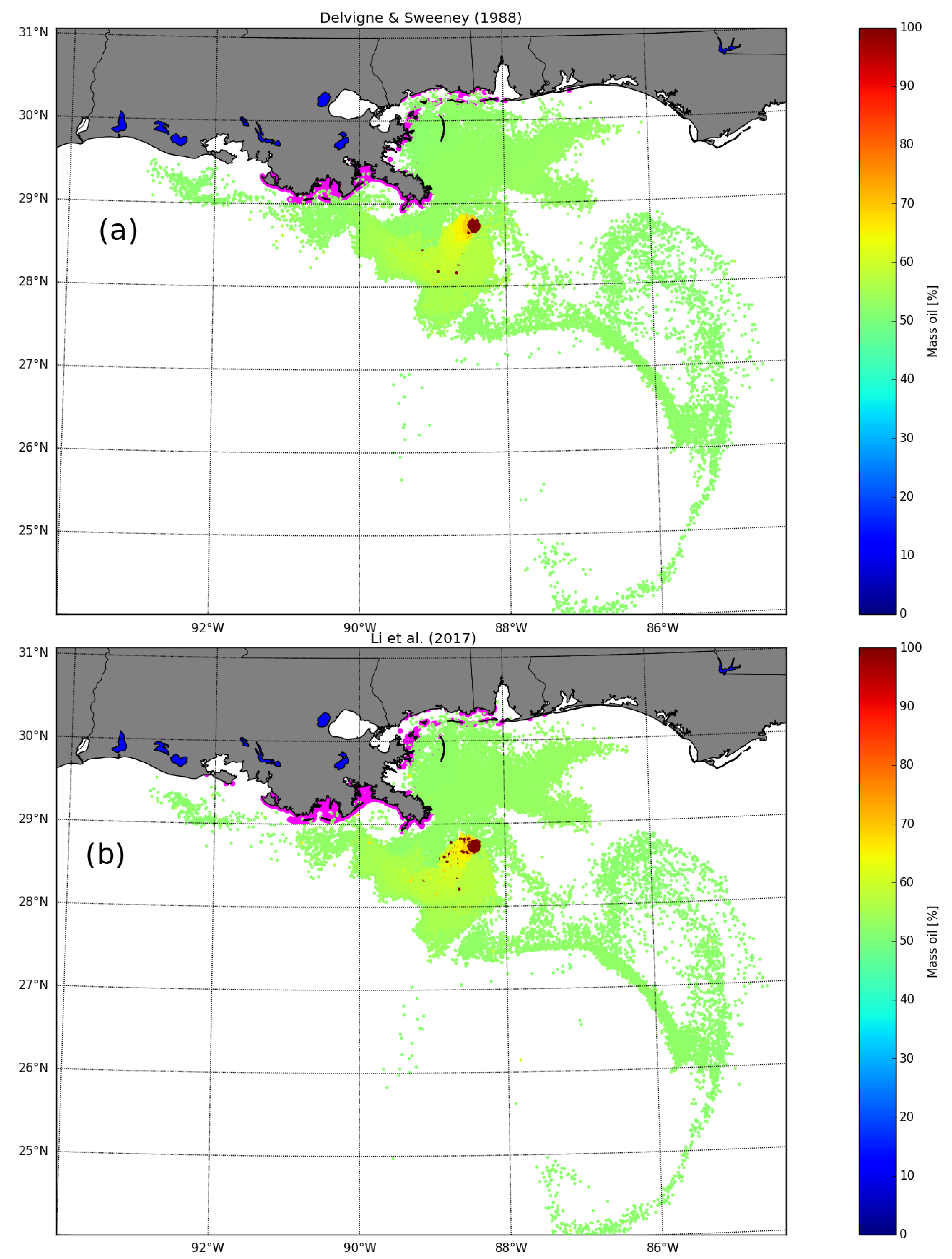
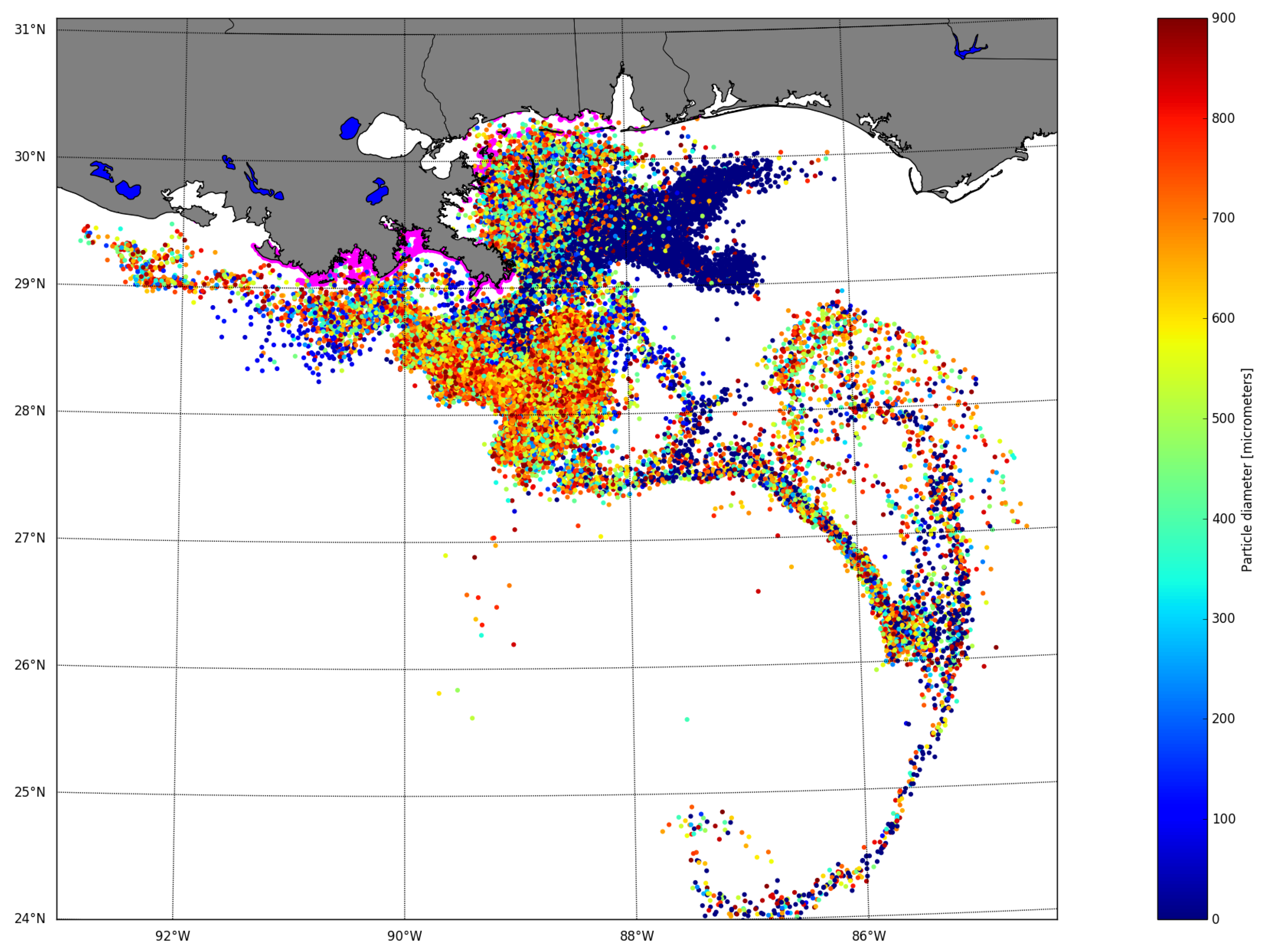
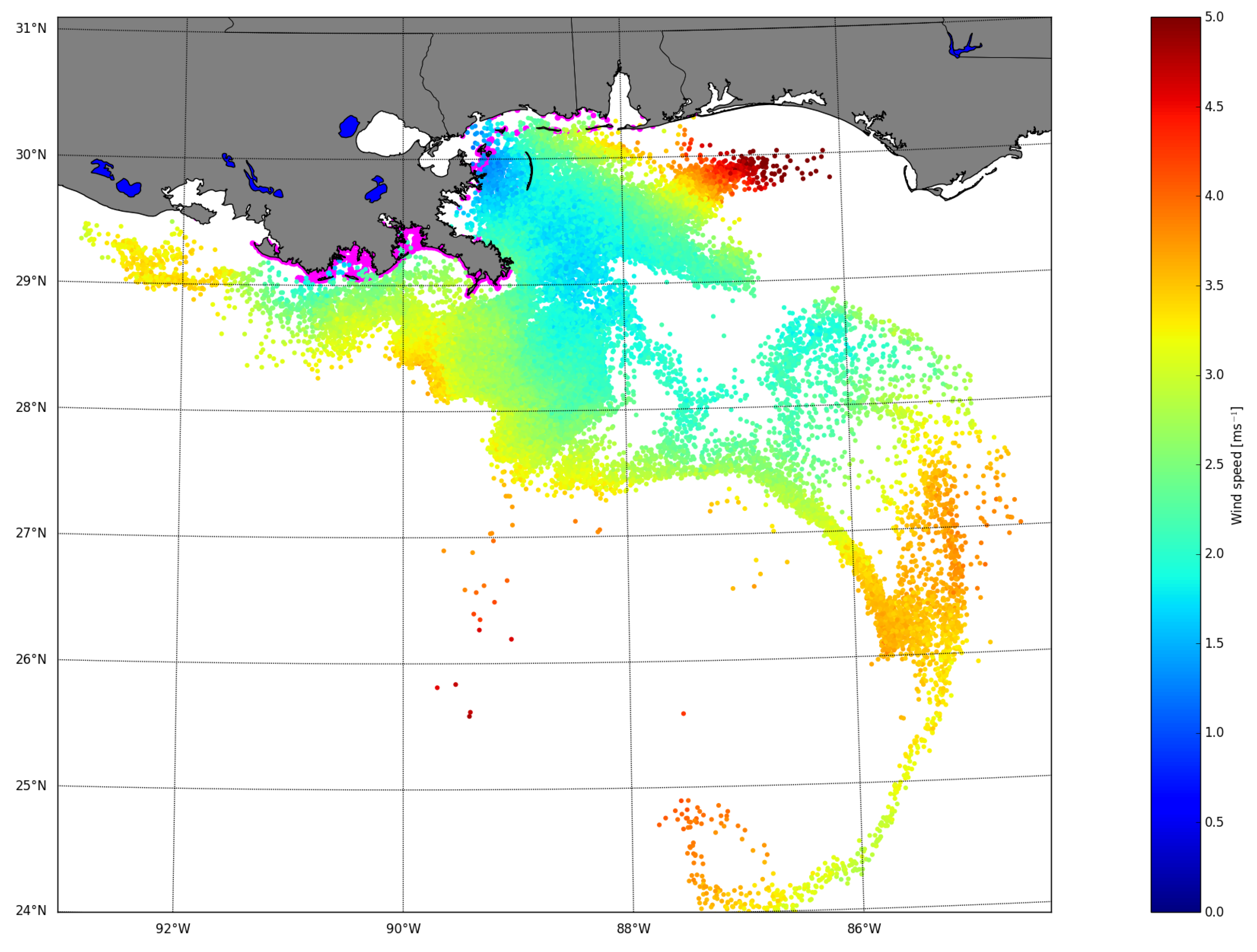
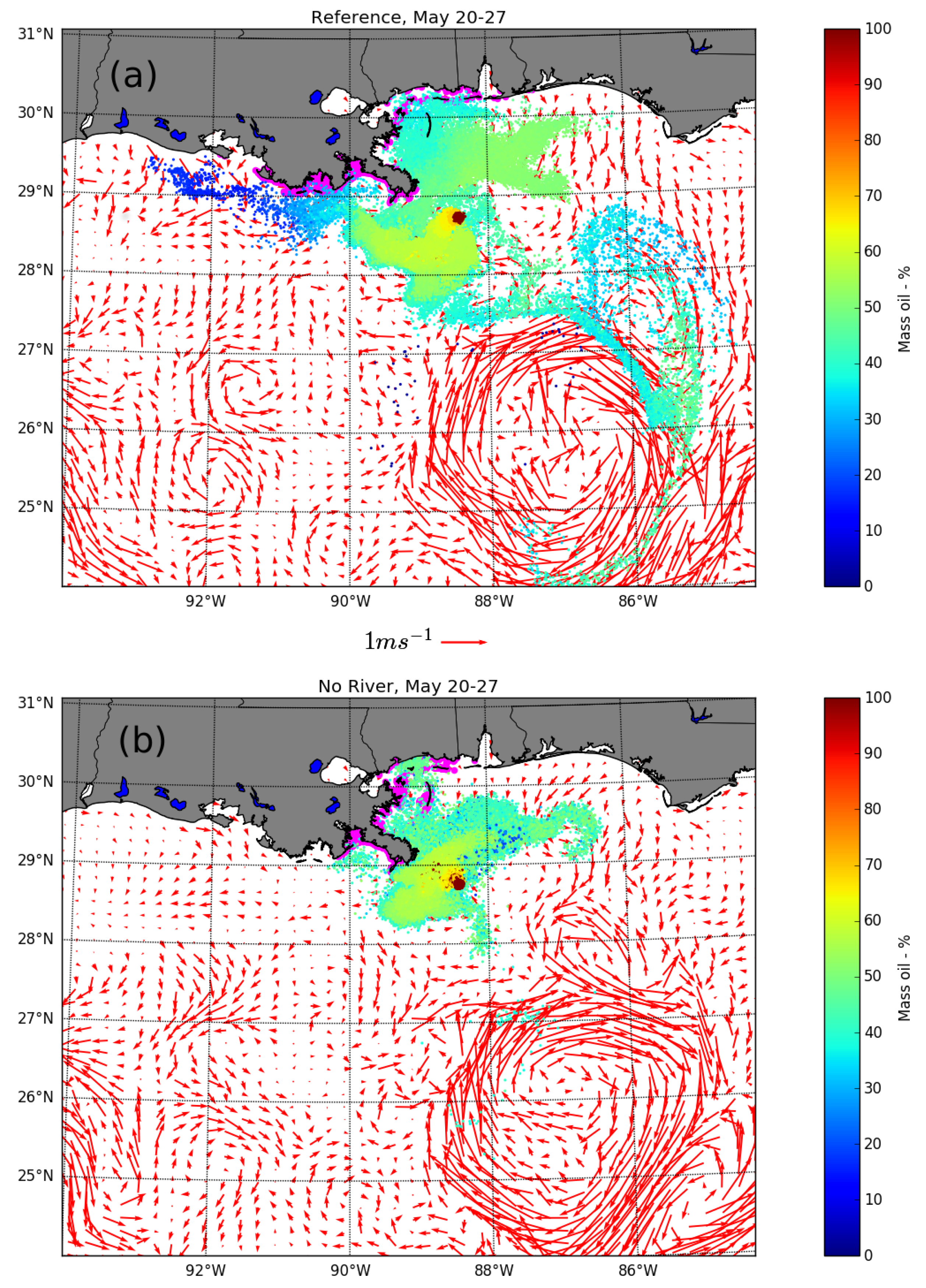
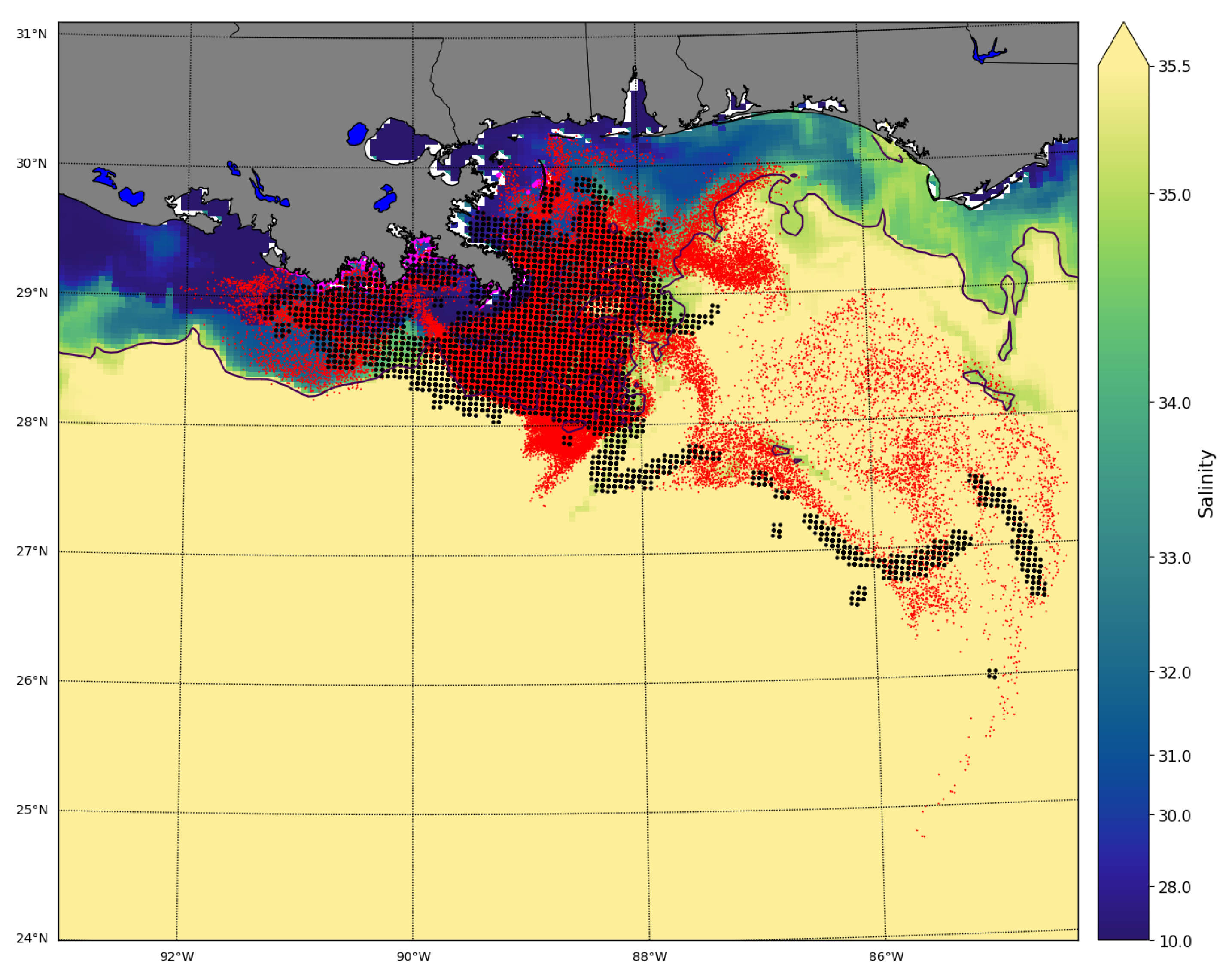
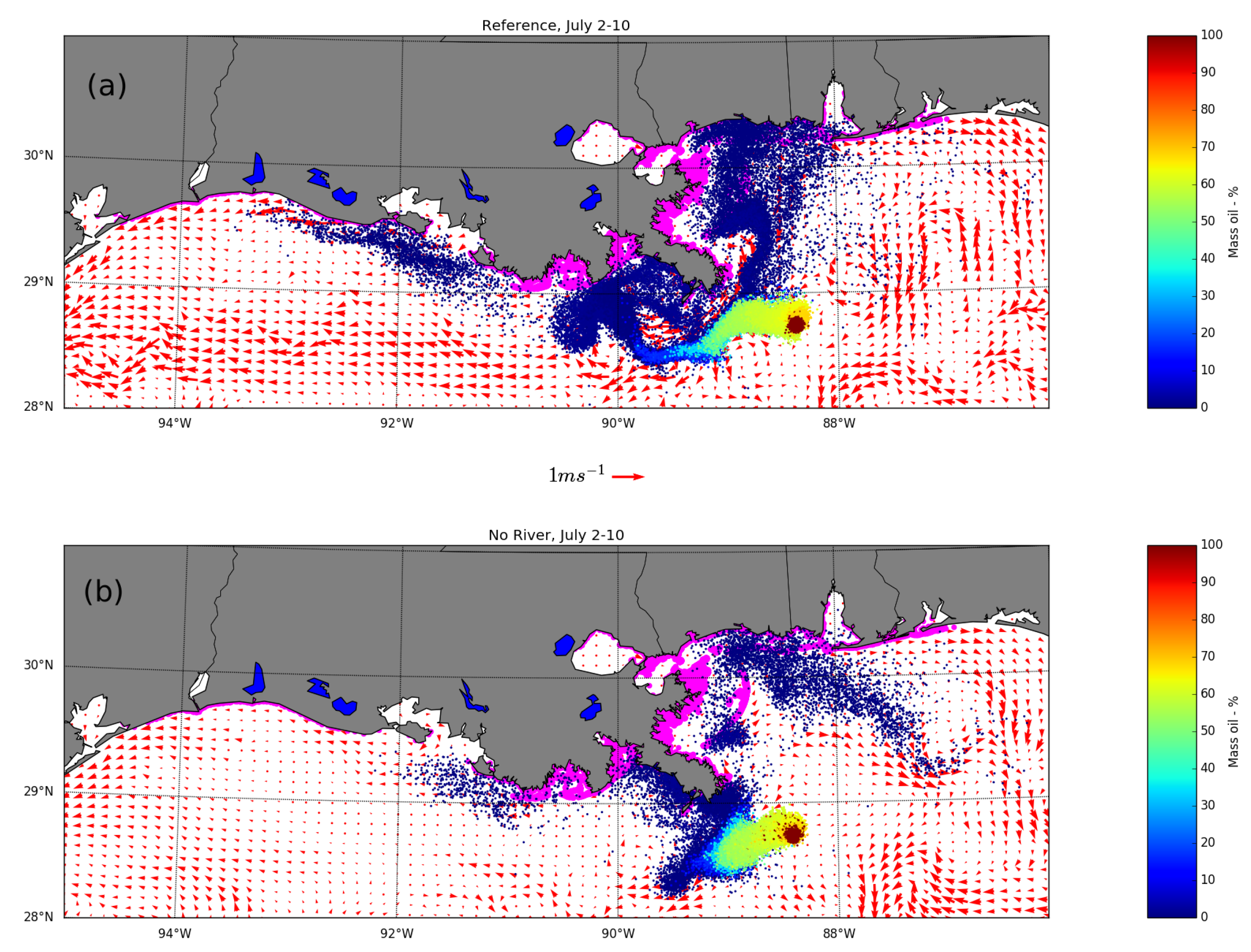
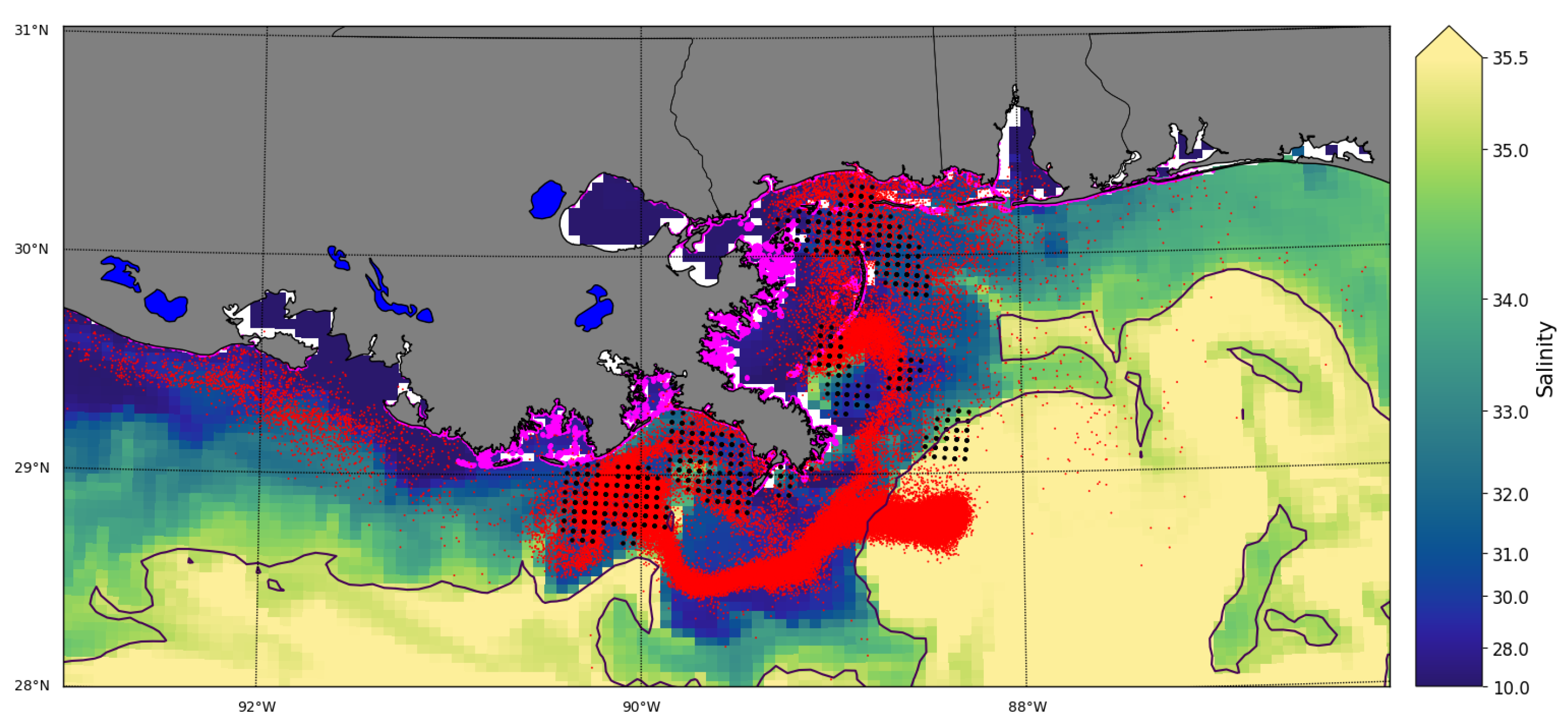
3. Results
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| (N)GoM | (Northern) Gulf of Mexico |
| DWH | DeepWater Horizon |
| HYCOM | HYbrid Coordinate Ocean Model |
| ECMWF | European Center for Medium-Range Weather Forecasts |
| ADIOS | Automated Data Inquiry for Oil Spills |
| MR | Mississippi River |
| LC | Loop Current |
| LATEX | LouisianA TEXas shelf |
| MAFLA | Mississippi Alabama FLoridA shelf |
| NOAA | National Oceanic and Atmospheric Administration |
| USGS | US Geological Survey |
References
- Joye, S.B.; Bracco, A.; Özgökmen, T.M.; Chanton, J.P.; Grosell, M.; MacDonald, I.R.; Cordes, E.E.; Montoya, J.P.; Passow, U. The Gulf of Mexico ecosystem, six years after the Macondo oil well blowout. Deep Sea Res. Part II Top. Stud. Oceanogr. 2016, 129, 4–19. [Google Scholar] [CrossRef]
- Beyer, J.; Trannum, H.C.; Bakke, T.; Hodson, P.V.; Collier, T.K. Environmental effects of the Deepwater Horizon oil spill: A review. Mar. Pollut. Bull. 2016, 110, 28–51. [Google Scholar] [CrossRef] [PubMed]
- Kourafalou, V.H.; Androulidakis, Y.S. Influence of Mississippi River induced circulation on the Deepwater Horizon oil spill transport. J. Geophys. Res. Ocean. 2013, 118, 3823–3842. [Google Scholar] [CrossRef]
- Le Hénaff, M.; Kourafalou, V.H.; Paris, C.B.; Helgers, J.; Aman, Z.M.; Hogan, P.J.; Srinivasan, A. Surface evolution of the Deepwater Horizon oil spill patch: Combined effects of circulation and wind-induced drift. Environ. Sci. Technol. 2012, 46, 7267–7273. [Google Scholar] [CrossRef] [PubMed]
- Gulf of Mexico Fact Sheet-U.S. Energy Information Administration. Available online: www.eia.gov/special/gulf_of_mexico/ (accessed on 26 June 2019).
- Crone, T.J.; Tolstoy, M. Magnitude of the 2010 Gulf of Mexico oil leak. Science 2010, 330, 634. [Google Scholar] [CrossRef] [PubMed]
- McNutt, M.K.; Camilli, R.; Guthrie, G.D.; Hsieh, P.A.; Labson, V.F.; Lehr, W.J.; Maclay, D.; Ratzel, A.C.; Sogge, M.K. Assessment of Flow Rate Estimates for the Deepwater Horizon/Macondo Well Oil Spill; US Department of the Interior: Washington, DC, USA, 2011. [Google Scholar]
- Androulidakis, Y.; Kourafalou, V.; Özgökmen, T.; Garcia-Pineda, O.; Lund, B.; Le Hénaff, M.; Hu, C.; Haus, B.K.; Novelli, G.; Guigand, C.; et al. Influence of River-Induced Fronts on Hydrocarbon Transport: A Multiplatform Observational Study. J. Geophys. Res. Ocean. 2018. [Google Scholar] [CrossRef]
- Kourafalou, V.H.; Lee, T.N.; Oey, L.Y.; Wang, J.D. The fate of river discharge on the continental shelf: 2. Transport of coastal low-salinity waters under realistic wind and tidal forcing. J. Geophys. Res. Ocean. 1996, 101, 3435–3455. [Google Scholar] [CrossRef]
- Schiller, R.V.; Kourafalou, V.H. Modeling river plume dynamics with the HYbrid Coordinate Ocean Model. Ocean Model. 2010, 33, 101–117. [Google Scholar] [CrossRef]
- Hickey, B.M.; Shillington, F.A.; Strub, P.; Brink, K.H.; Barton, E.D.; Thomas, A.C. Eastern ocean boundaries. Sea Reg. Stud. Synth. 1998, 11, 29. [Google Scholar]
- Walker, N.D.; Huh, O.K.; Rouse, L.J.; Murray, S.P. Evolution and structure of a coastal squirt off the Mississippi River delta: Northern Gulf of Mexico. J. Geophys. Res. Ocean. 1996, 101, 20643–20655. [Google Scholar] [CrossRef]
- Schiller, R.; Kourafalou, V.; Hogan, P.; Walker, N. The dynamics of the Mississippi River plume: Impact of topography, wind and offshore forcing on the fate of plume waters. J. Geophys. Res. Ocean. 2011, 116. [Google Scholar] [CrossRef]
- Hu, C.; Nelson, J.R.; Johns, E.; Chen, Z.; Weisberg, R.H.; Müller-Karger, F.E. Mississippi River water in the Florida Straits and in the Gulf Stream off Georgia in summer 2004. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Schiller, R.; Kourafalou, V. Loop Current impact on the transport of Mississippi River waters. J. Coast. Res. 2014, 30, 1287–1306. [Google Scholar] [CrossRef]
- Androulidakis, Y.; Kourafalou, V.; Le Hénaff, M.; Kang, H.; Sutton, T.; Chen, S.; Hu, C.; Ntaganou, N. Offshore spreading of Mississippi waters: pathways and vertical structure under eddy influence. J. Geophys. Res. Ocean. 2019. [Google Scholar] [CrossRef]
- North, E.W.; Adams, E.E.; Schlag, Z.; Sherwood, C.R.; He, R.; Hyun, K.H.; Socolofsky, S.A. Simulating oil droplet dispersal from the Deepwater Horizon spill with a Lagrangian approach. Geophys. Monogr. Ser. 2011, 195, 217–226. [Google Scholar]
- Mariano, A.J.; Kourafalou, V.H.; Srinivasan, A.; Kang, H.; Halliwell, G.; Ryan, E.; Roffer, M. On the modeling of the 2010 Gulf of Mexico oil spill. Dyn. Atmos. Ocean. 2011, 52, 322–340. [Google Scholar] [CrossRef]
- MacFadyen, A.; Watabayashi, G.; Barker, C.; Beegle-Krause, C. Tactical modeling of surface oil transport during the Deepwater Horizon spill response. Monit. Model. Deep. Horiz. Oil Spil. 2011, 195, 167–178. [Google Scholar]
- Barker, C. A statistical outlook for the Deepwater Horizon oil spill. Monit. Model. Deep. Horiz. Oil Spil. 2011, 195, 237–244. [Google Scholar]
- Paris, C.B.; Hénaff, M.L.; Aman, Z.M.; Subramaniam, A.; Helgers, J.; Wang, D.P.; Kourafalou, V.H.; Srinivasan, A. Evolution of the Macondo well blowout: Simulating the effects of the circulation and synthetic dispersants on the subsea oil transport. Environ. Sci. Technol. 2012, 46, 13293–13302. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Hu, C.; Zheng, L. Trajectory forecast as a rapid response to the Deepwater Horizon oil spill. Monit. Model. Deep. Horiz. Oil Spil. 2011, 195, 153–165. [Google Scholar]
- Liu, Y.; Weisberg, R.H.; Hu, C.; Zheng, L. Tracking the Deepwater Horizon oil spill: A modeling perspective. Eos Trans. Am. Geophys. Union 2011, 92, 45–46. [Google Scholar] [CrossRef]
- Androulidakis, I.; Kourafalou, V.; Le Hénaff, M.; Kang, H.S.; Ntaganou, N. Loop Current evolution during the Deepwater Horizon oil spill period: The role of mesoscale dynamics over Northwestern Cuba. Submitt. J. Mar. Syst. 2018. [Google Scholar]
- Li, Z.; Johnson, W. An Improved Method to Estimate the Probability of Oil Spill Contact to Environmental Resources in the Gulf of Mexico. J. Mar. Sci. Eng. 2019, 7, 41. [Google Scholar] [CrossRef]
- Dagestad, K.F.; Röhrs, J.; Breivik, Ø.; Ådlandsvik, B. OpenDrift v1. 0: A generic framework for trajectory modelling. Geosci. Model Dev. 2018, 11, 1405–1420. [Google Scholar] [CrossRef]
- NOAA-Environmental Response Management Application (ERMA). Available online: https://erma.noaa.gov/gulfofmexico/erma.html#/layers=1+35410+10717+9816+16973+13763+38385+28055&x=-88.09771&y=28.81982&z=8&panel=layer (accessed on 26 June 2019).
- Hybrid Coordinate Ocean Model. Available online: www.hycom.org (accessed on 30 May 2019).
- Bleck, R. An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Model. 2002, 4, 55–88. [Google Scholar] [CrossRef]
- Le Hénaff, M.; Kourafalou, V.H. Mississippi waters reaching South Florida reefs under no flood conditions: Synthesis of observing and modeling system findings. Ocean Dyn. 2016, 66, 435–459. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts. Available online: https://www.ecmwf.int/en/forecasts/accessing-forecasts (accessed on 26 June 2019).
- Ehard, B.; Malardel, S.; Dörnbrack, A.; Kaifler, B.; Kaifler, N.; Wedi, N. Comparing ECMWF high resolution analyses to lidar temperature measurements in the middle atmosphere. Q. J. R. Meteorol. Soc. 2016, 144, 633–640. [Google Scholar] [CrossRef]
- Haiden, T.; Janousek, M.; Bidlot, J.; Ferranti, L.; Prates, F.; Vitart, F.; Bauer, P.; Richardson, D. Evaluation of ECMWF Forecasts, Including the 2016 Resolution Upgrade; European Centre for Medium Range Weather Forecasts: Reading, UK, 2016. [Google Scholar]
- Luo, H.; Bracco, A.; Cardona, Y.; McWilliams, J.C. Submesoscale circulation in the northern Gulf of Mexico: Surface processes and the impact of the freshwater river input. Ocean Model. 2016, 101, 68–82. [Google Scholar] [CrossRef]
- ECMWF Wave Forecasts. Available online: http://apps.ecmwf.int/mars-catalogue/?class=od&stream=wave (accessed on 30 May 2019).
- Group, T.W. The WAM model—A third generation ocean wave prediction model. J. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Breivik, Ø.; Bidlot, J.R.; Janssen, P.A. A Stokes drift approximation based on the Phillips spectrum. Ocean Model. 2016, 100, 49–56. [Google Scholar] [CrossRef]
- OpenDrift-Open Source Framework for Ocean Trajectory Modelling. Available online: www.github.com/opendrift (accessed on 26 June 2019).
- Jones, C.E.; Dagestad, K.F.; Breivik, Ø.; Holt, B.; Röhrs, J.; Christensen, K.H.; Espeseth, M.; Brekke, C.; Skrunes, S. Measurement and modeling of oil slick transport. J. Geophys. Res. Ocean. 2016, 121, 7759–7775. [Google Scholar] [CrossRef]
- Röhrs, J.; Dagestad, K.F.; Asbjørnsen, H.; Nordam, T.; Skancke, J.; Jones, C.; Brekke, C. The effect of vertical mixing on the horizontal drift of oil spills. Ocean Sci. Discuss. 2018. [Google Scholar] [CrossRef]
- Abascal, A.J.; Castanedo, S.; Minguez, R.; Medina, R.; Liu, Y.; Weisberg, R.H. Stochastic Lagrangian trajectory modeling of surface drifters deployed during the Deepwater Horizon oil spill. In Thirty-Eighth AMOP Technical Seminar; Environment Canada: Ottawa, ON, Canada, 2015; pp. 77–91. [Google Scholar]
- Li, Z.; Spaulding, M.L.; French-McCay, D. An algorithm for modeling entrainment and naturally and chemically dispersed oil droplet size distribution under surface breaking wave conditions. Mar. Pollut. Bull. 2017, 119, 145–152. [Google Scholar] [CrossRef]
- Nordam, T.; Kristiansen, R.; Nepstad, R.; Röhrs, J. Numerical analysis of boundary conditions in a Lagrangian particle model for vertical mixing, transport and surfacing of buoyant particles in the water column. Ocean Model. 2019, 136, 107–119. [Google Scholar] [CrossRef]
- Tkalich, P.; Chan, E.S. Vertical mixing of oil droplets by breaking waves. Mar. Pollut. Bull. 2002, 44, 1219–1229. [Google Scholar] [CrossRef]
- Lehr, W.; Jones, R.; Evans, M.; Simecek-Beatty, D.; Overstreet, R. Revisions of the ADIOS oil spill model. Environ. Model. Softw. 2002, 17, 189–197. [Google Scholar] [CrossRef]
- Delvigne, G.A.L.; Sweeney, C. Natural dispersion of oil. Oil Chem. Pollut. 1988, 4, 281–310. [Google Scholar] [CrossRef]
- Li, Z.; Spaulding, M.; McCay, D.F.; Crowley, D.; Payne, J.R. Development of a unified oil droplet size distribution model with application to surface breaking waves and subsea blowout releases considering dispersant effects. Mar. Pollut. Bull. 2017, 114, 247–257. [Google Scholar] [CrossRef]
- Johansen, Ø.; Reed, M.; Bodsberg, N.R. Natural dispersion revisited. Mar. Pollut. Bull. 2015, 93, 20–26. [Google Scholar] [CrossRef]
- Li, C.; Miller, J.; Wang, J.; Koley, S.S.; Katz, J. Size Distribution and Dispersion of Droplets Generated by Impingement of Breaking Waves on Oil Slicks. J. Geophys. Res. Ocean. 2017, 122, 7938–7957. [Google Scholar] [CrossRef]
- Johansen, Ø. DeepBlow—A Lagrangian plume model for deep water blowouts. Spill Sci. Technol. Bull. 2000, 6, 103–111. [Google Scholar] [CrossRef]
- Schwartzberg, H.G. The movement of oil spills. In International Oil Spill Conference; American Petroleum Institute: Washington, DC, USA, 1971; pp. 489–494. [Google Scholar]
- Weisberg, R.H.; Lianyuan, Z.; Liu, Y. On the movement of Deepwater Horizon Oil to northern Gulf beaches. Ocean Model. 2017, 111, 81–97. [Google Scholar] [CrossRef]
- Liu, Y.; MacFadyen, A.; Ji, Z.G.; Weisberg, R.H. Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record Breaking Enterprise; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 195. [Google Scholar]
- Sundby, S. A one-dimensional model for the vertical distribution of pelagic fish eggs in the mixed layer. Deep Sea Res. Part A. Oceanogr. Res. Papers 1983, 30, 645–661. [Google Scholar] [CrossRef]
- NOAA-Oil Library. Available online: github.com/NOAA-ORR-ERD/OilLibrary (accessed on 26 June 2019).
- NOAA-Oil Drift Model. Available online: github.com/NOAA-ORR-ERD/PyGnome (accessed on 26 June 2019).
- Boufadel, M.C.; Abdollahi-Nasab, A.; Geng, X.; Galt, J.; Torlapati, J. Simulation of the landfall of the deepwater horizon oil on the shorelines of the Gulf of Mexico. Environ. Sci. Technol. 2014, 48, 9496–9505. [Google Scholar] [CrossRef]
- Walker, N.D.; Pilley, C.T.; Raghunathan, V.V.; D’Sa, E.J.; Leben, R.R.; Hoffmann, N.G.; Brickley, P.J.; Coholan, P.D.; Sharma, N.; Graber, H.C.; et al. Impacts of Loop Current frontal cyclonic eddies and wind forcing on the 2010 Gulf of Mexico oil spill. Monit. Model. Deep. Horiz. Oil Spil. 2011, 195, 103–116. [Google Scholar]
- Short, J.W. Advances in understanding the fate and effects of oil from accidental spills in the United States beginning with the Exxon Valdez. Arch. Environ. Contam. Toxicol. 2017, 73, 5–11. [Google Scholar] [CrossRef]
- Carroll, J.; Vikebø, F.; Howell, D.; Broch, O.J.; Nepstad, R.; Augustine, S.; Skeie, G.M.; Bast, R.; Juselius, J. Assessing impacts of simulated oil spills on the Northeast Arctic cod fishery. Mar. Pollut. Bull. 2018, 126, 63–73. [Google Scholar] [CrossRef]
- Giarrusso, C.; Carratelli, E.P.; Spulsi, G. On the effects of wave drift on the dispersion of floating pollutants. Ocean Eng. 2001, 28, 1339–1348. [Google Scholar] [CrossRef]
- Caratelli, E.; Dentale, F.; Reale, F. On the effects of wave-induced drift and dispersion in the Deepwater Horizon oil spill. Monit. Model. Deep. Horiz. Oil Spil. 2011, 195, 197–204. [Google Scholar]
- Adcroft, A.; Hallberg, R.; Dunne, J.P.; Samuels, B.L.; Galt, J.A.; Barker, C.H.; Payton, D. Simulations of underwater plumes of dissolved oil in the Gulf of Mexico. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]

| Model | Resolution: | |||
|---|---|---|---|---|
| Model | Parameters | Horizontal | Vertical | Temporal |
| NOAA shape files | initial location | |||
| GOM Hycom | horizontal current | 1/50° | 32 layers | 3 h |
| ECMWF atmospheric model | wind velocity, air temperature | 1/8° | surface | 3 h |
| ECMWF wave model | Stokes drift, wave height and period | 1/8° | surface | 12 h |
| Reference Simulation | no river Simulation | |
|---|---|---|
| West of MR Delta | 6.9 | 0.5 |
| MR Delta area | 4.0 | 3.4 |
| East of MR Delta | 1.2 | 2.1 |
| Total | 12.1 | 6.0 |
| Reference Simulation | no river Simulation | |
|---|---|---|
| West of MR Delta | 10.6 | 7.8 |
| MR Delta area | 16.7 | 27.2 |
| East of MR Delta | 20.8 | 20.1 |
| Total | 48.1 | 55.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hole, L.R.; Dagestad, K.-F.; Röhrs, J.; Wettre, C.; Kourafalou, V.H.; Androulidakis, Y.; Kang, H.; Le Hénaff, M.; Garcia-Pineda, O. The DeepWater Horizon Oil Slick: Simulations of River Front Effects and Oil Droplet Size Distribution. J. Mar. Sci. Eng. 2019, 7, 329. https://doi.org/10.3390/jmse7100329
Hole LR, Dagestad K-F, Röhrs J, Wettre C, Kourafalou VH, Androulidakis Y, Kang H, Le Hénaff M, Garcia-Pineda O. The DeepWater Horizon Oil Slick: Simulations of River Front Effects and Oil Droplet Size Distribution. Journal of Marine Science and Engineering. 2019; 7(10):329. https://doi.org/10.3390/jmse7100329
Chicago/Turabian StyleHole, Lars Robert, Knut-Frode Dagestad, Johannes Röhrs, Cecilie Wettre, Vassiliki H. Kourafalou, Yannis Androulidakis, Heesook Kang, Matthieu Le Hénaff, and Oscar Garcia-Pineda. 2019. "The DeepWater Horizon Oil Slick: Simulations of River Front Effects and Oil Droplet Size Distribution" Journal of Marine Science and Engineering 7, no. 10: 329. https://doi.org/10.3390/jmse7100329
APA StyleHole, L. R., Dagestad, K.-F., Röhrs, J., Wettre, C., Kourafalou, V. H., Androulidakis, Y., Kang, H., Le Hénaff, M., & Garcia-Pineda, O. (2019). The DeepWater Horizon Oil Slick: Simulations of River Front Effects and Oil Droplet Size Distribution. Journal of Marine Science and Engineering, 7(10), 329. https://doi.org/10.3390/jmse7100329






