Analysis of Different Methods for Wave Generation and Absorption in a CFD-Based Numerical Wave Tank
Abstract
1. Introduction
2. Numerical Modeling
2.1. General Equations
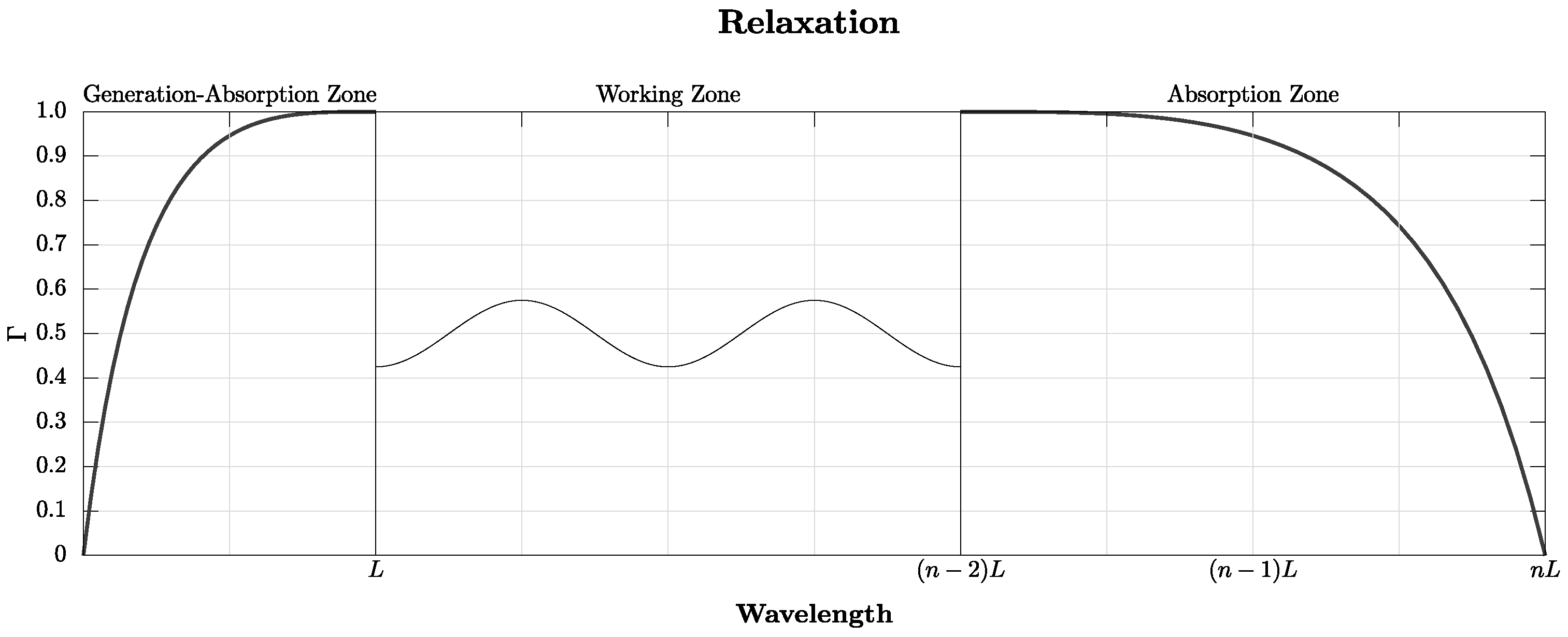
2.2. Wave Generation and Absorption
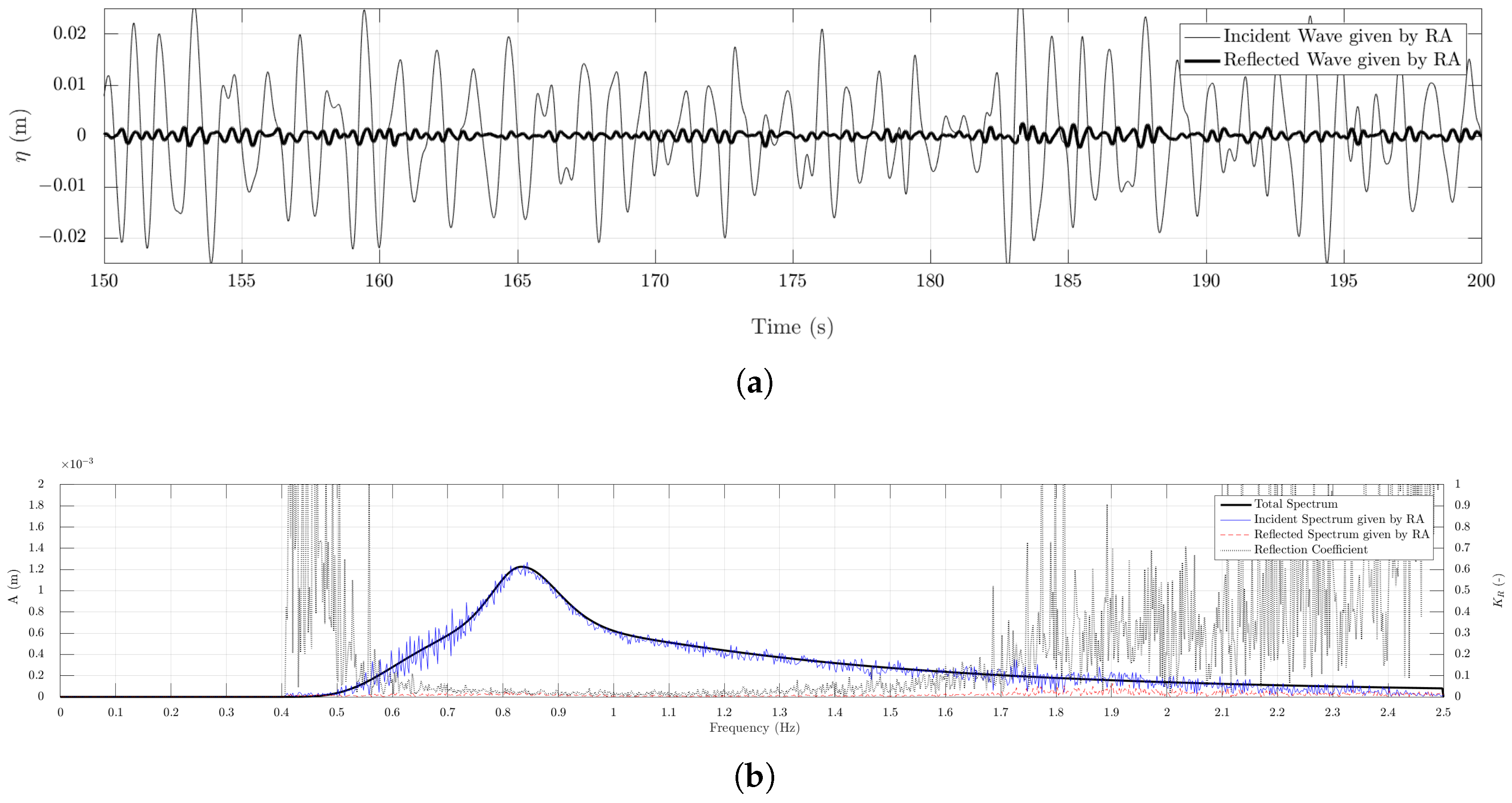
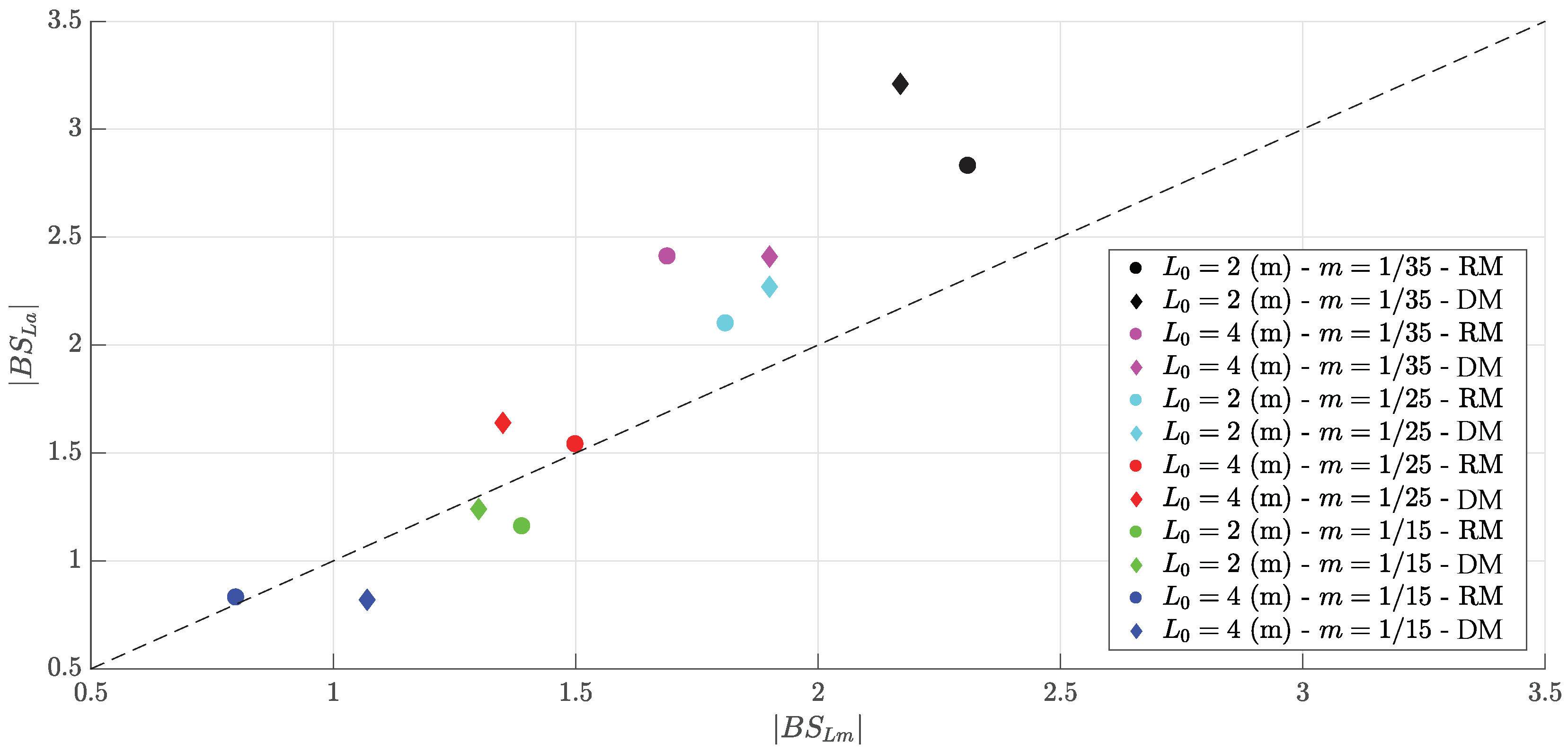
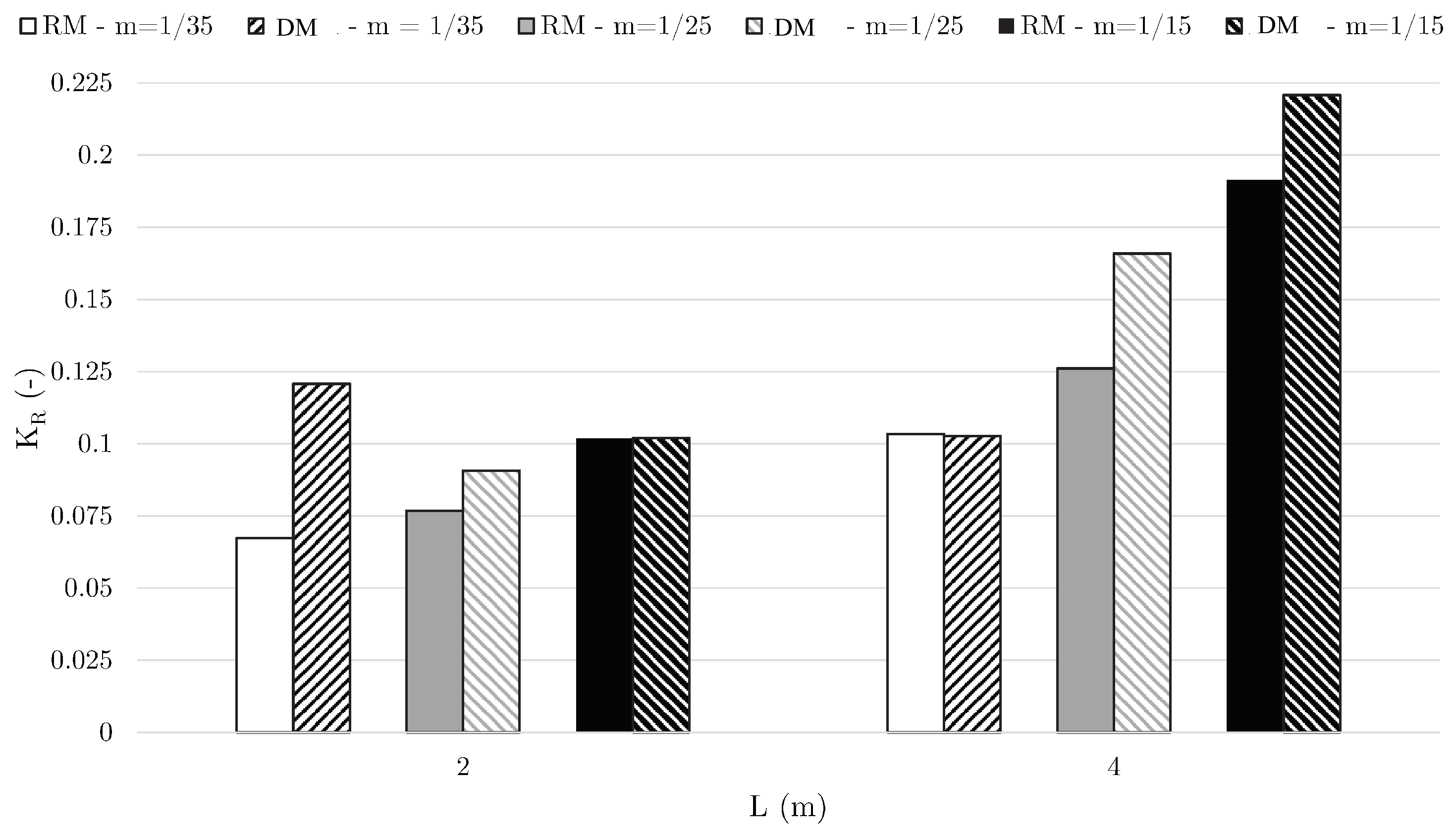
2.3. Reflection Analysis
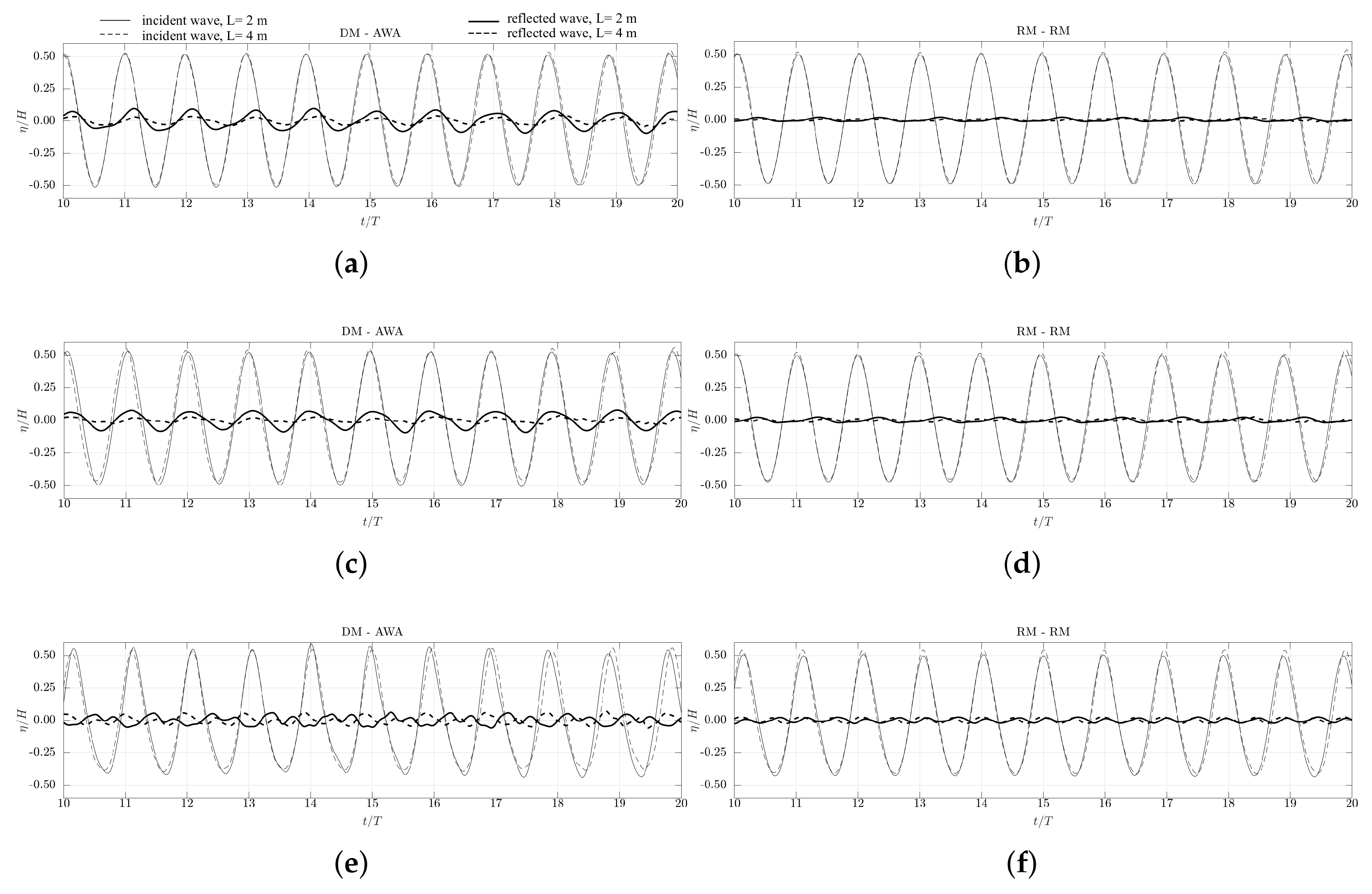
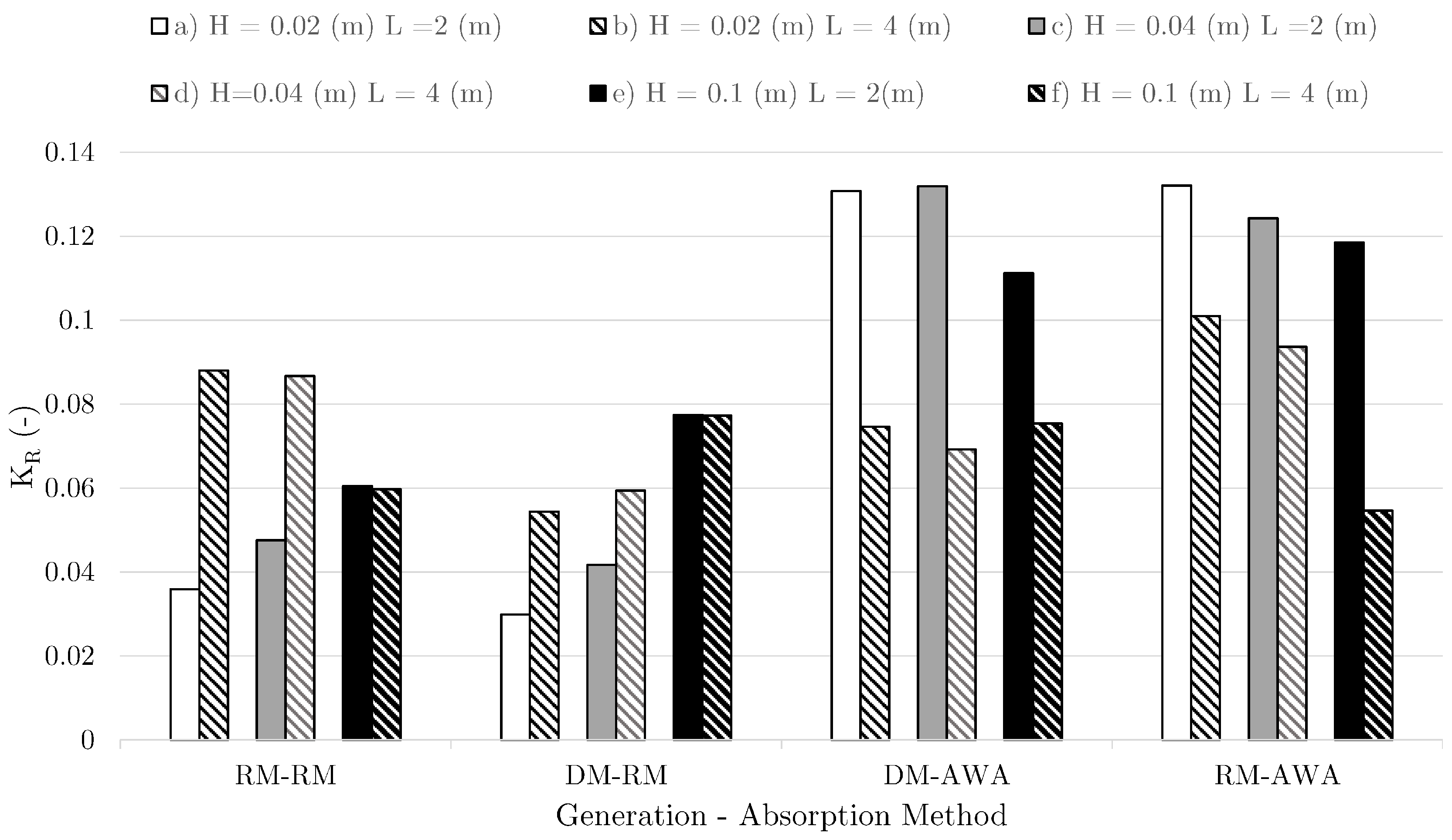
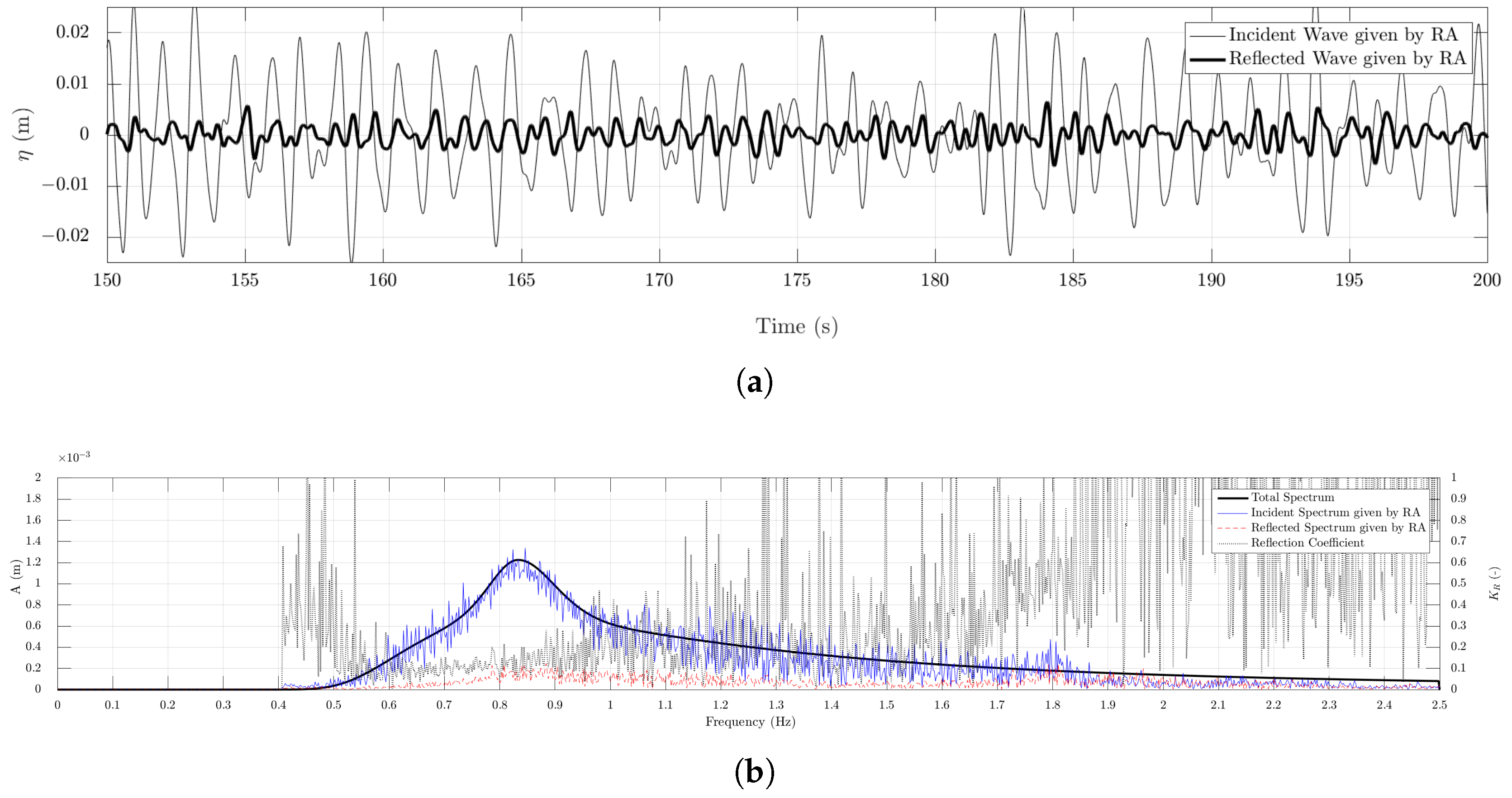
3. Results and Discussion
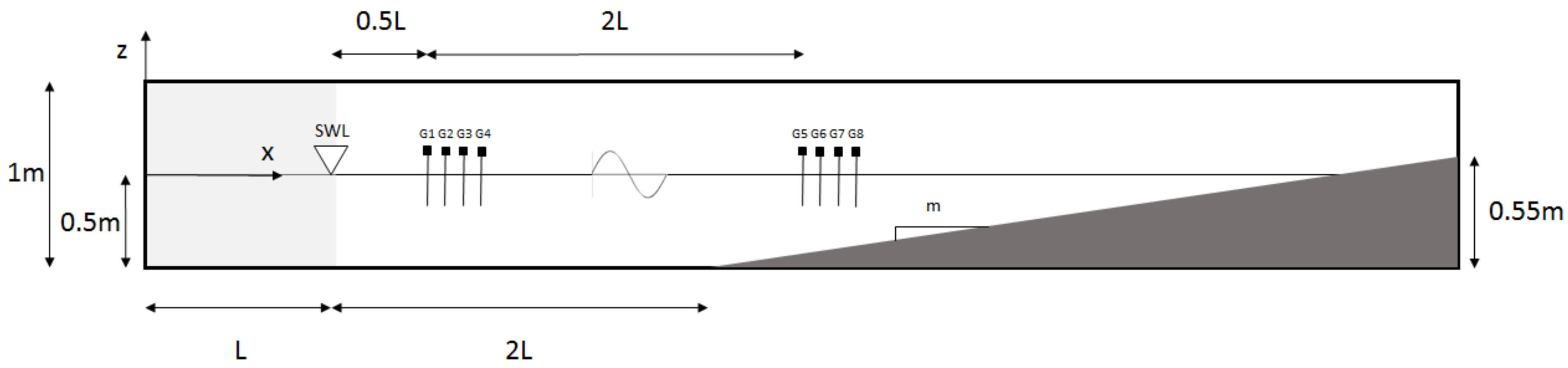
3.1. NWT without Structure
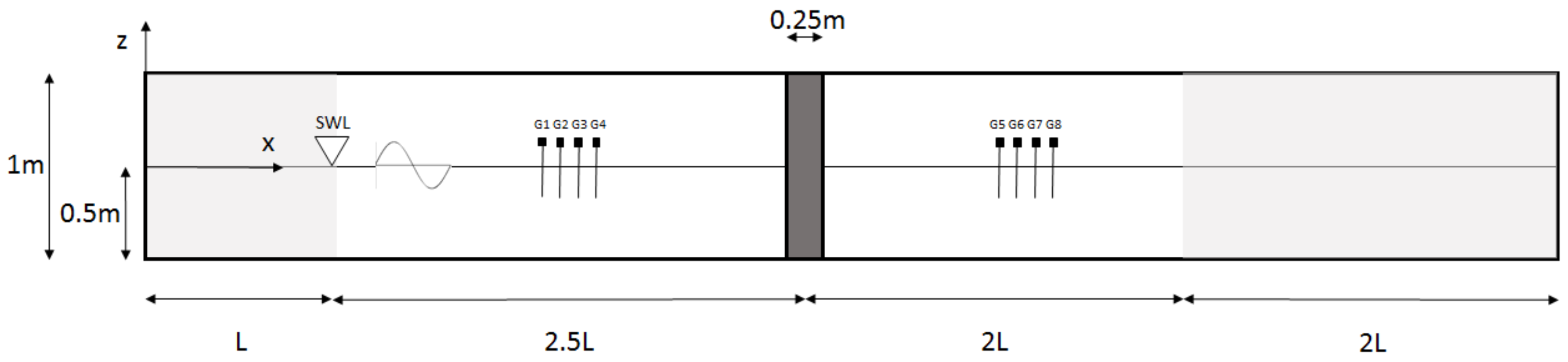
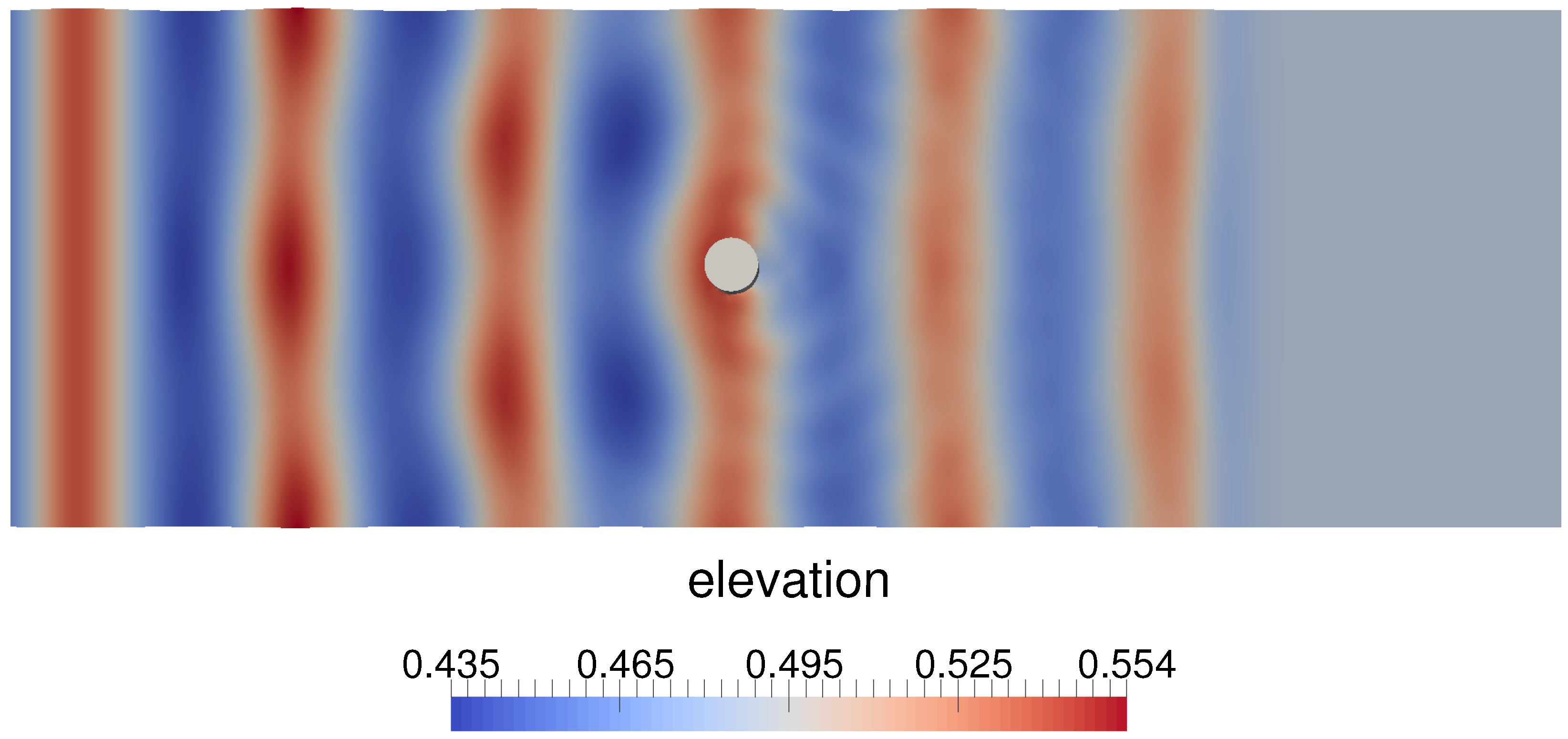
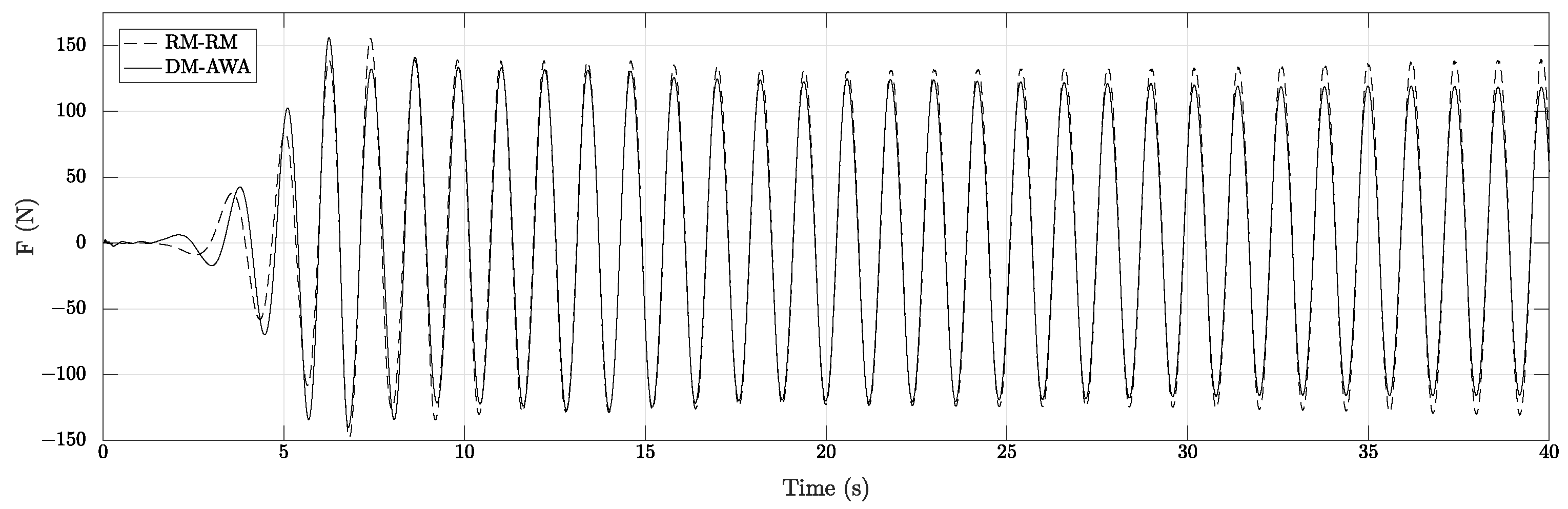
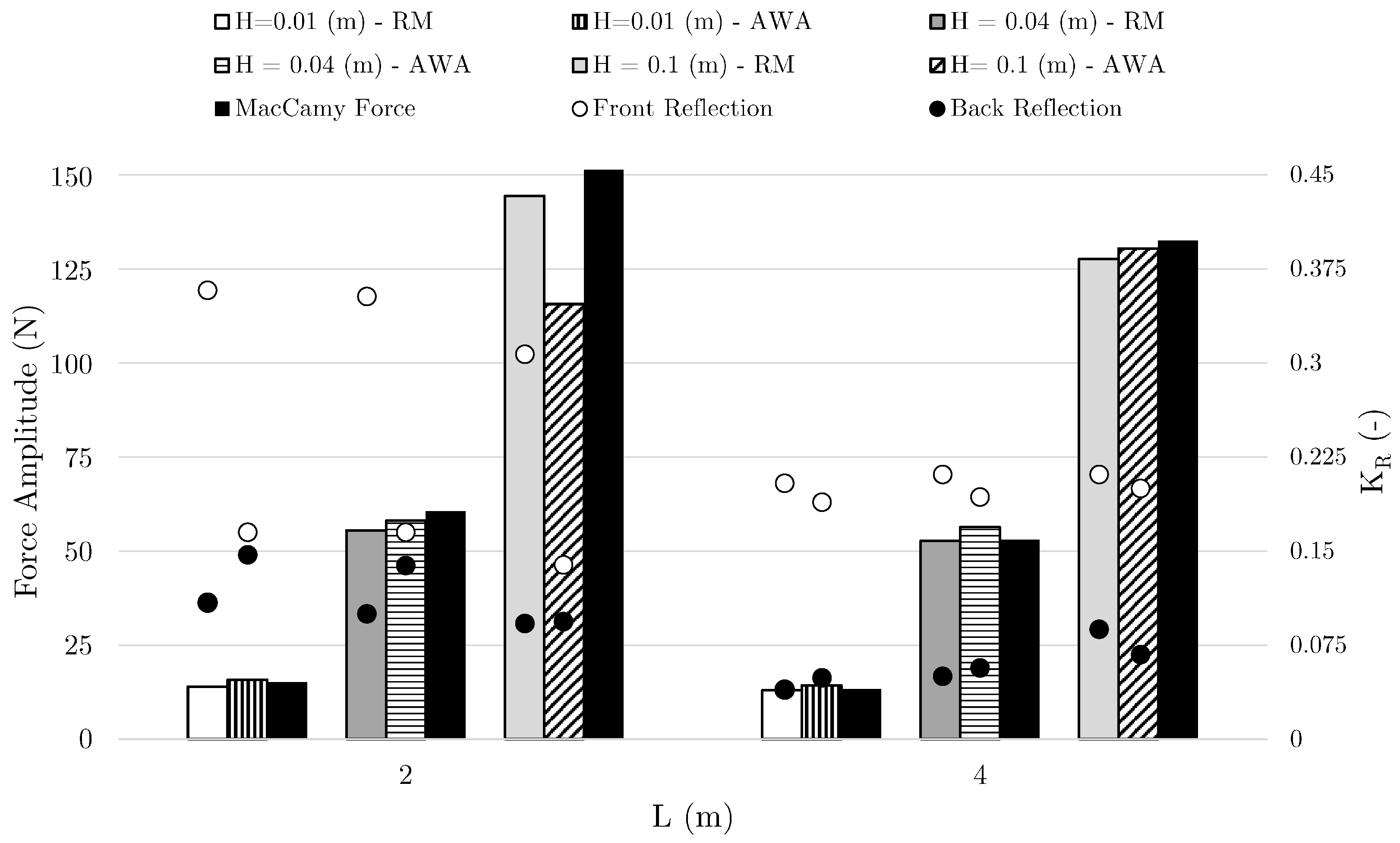
3.2. Wave Interaction with a Cylinder
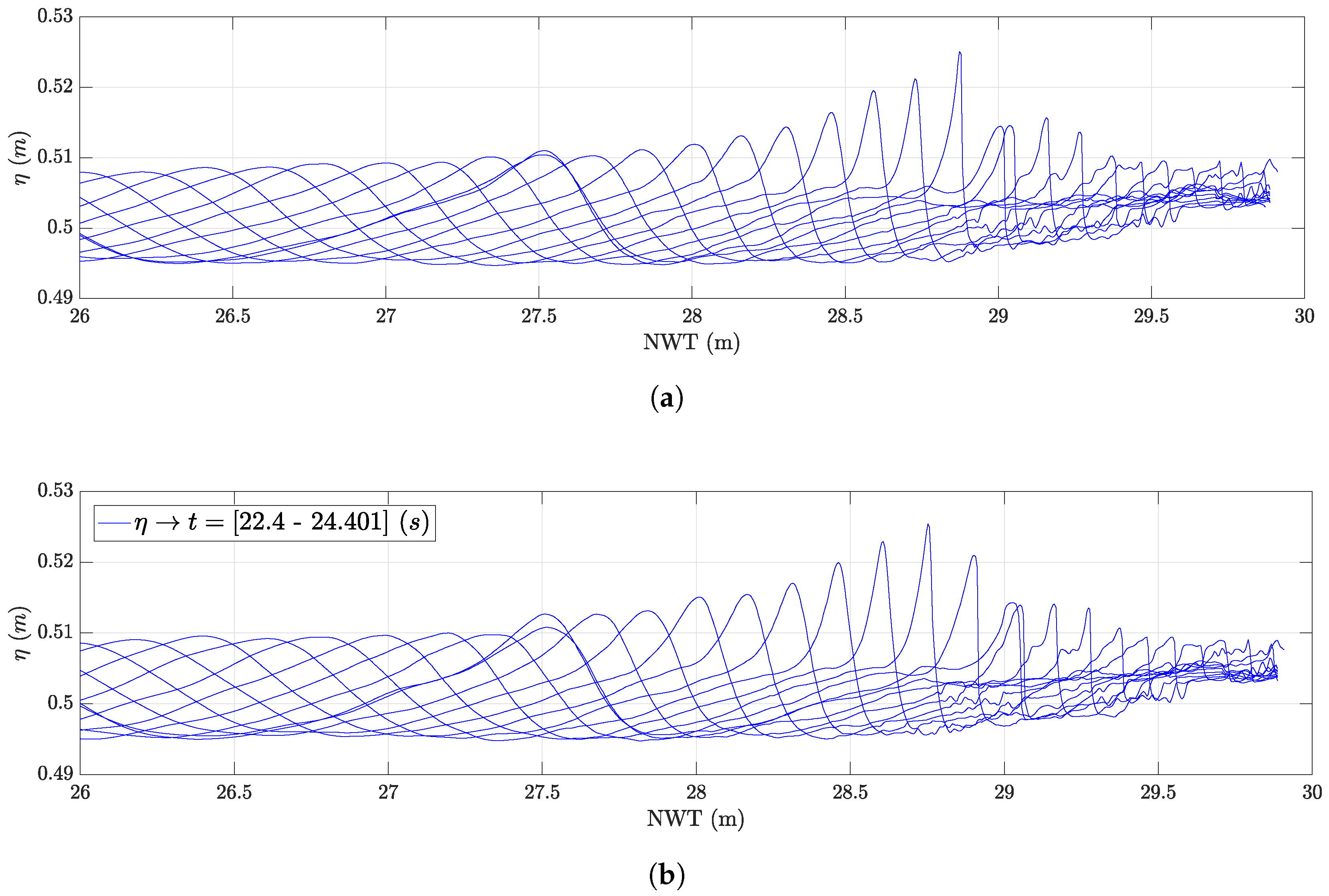
3.3. Effect of Wave Generation Methods on Wave Breaking on a Sloped Bottom
3.4. Comparison to the IHFOAM Adaptation of OpenFOAM
4. Conclusions
- The relaxation method provides better quality wave generation and absorption at a higher computational cost especially for short and steep waves.
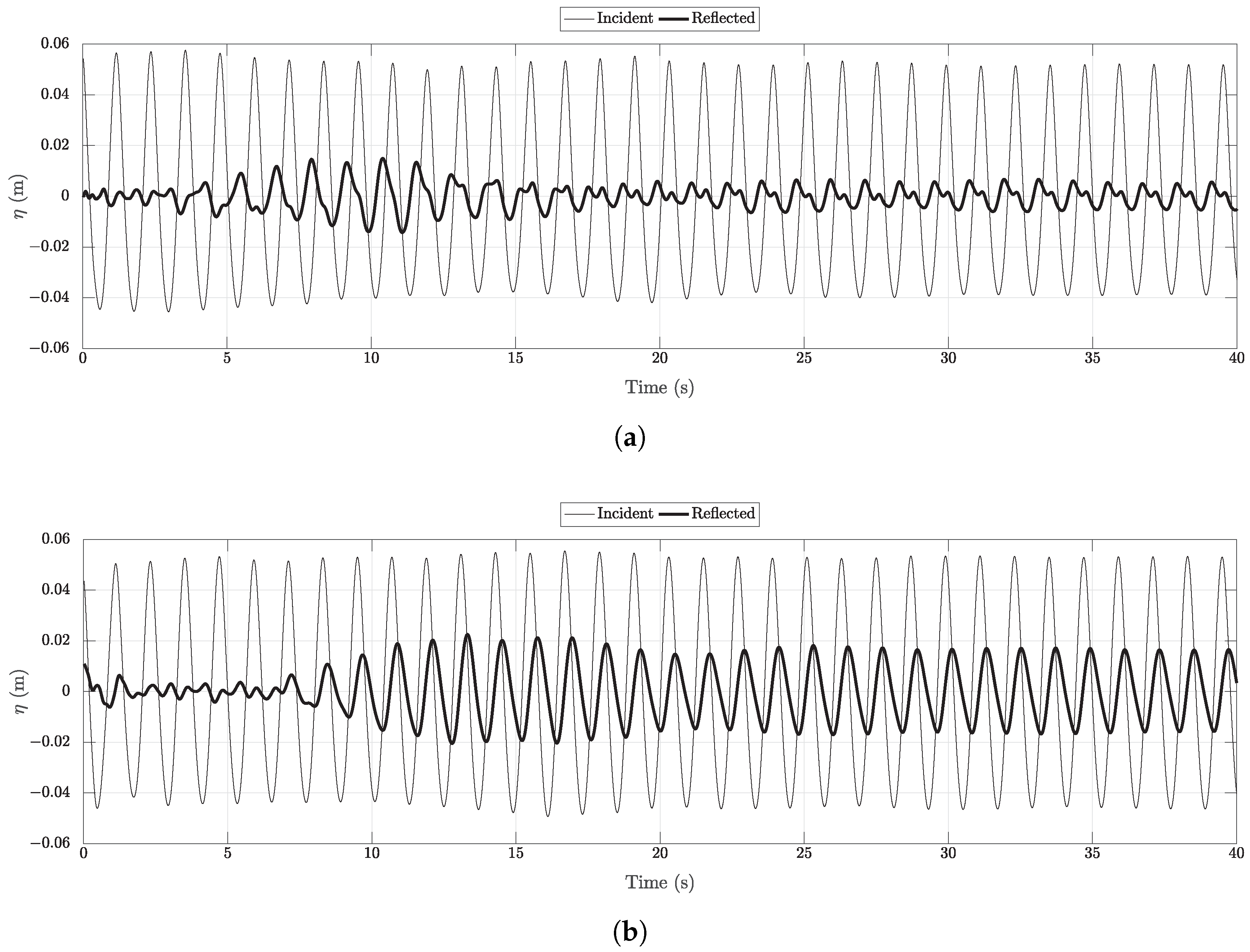
- The effect of re-reflections from the structure in the tank is seen more clearly in the free surface elevations, but its influence on the calculated wave forces is not very significant.
- The use of the Dirichlet method for wave generation results in a shift of the breaking point towards the wave generation boundary by up to of the incident wavelength.
- The generation and absorption of solitary waves are handled better using the active absorption method due to the shallow water assumption in the method.
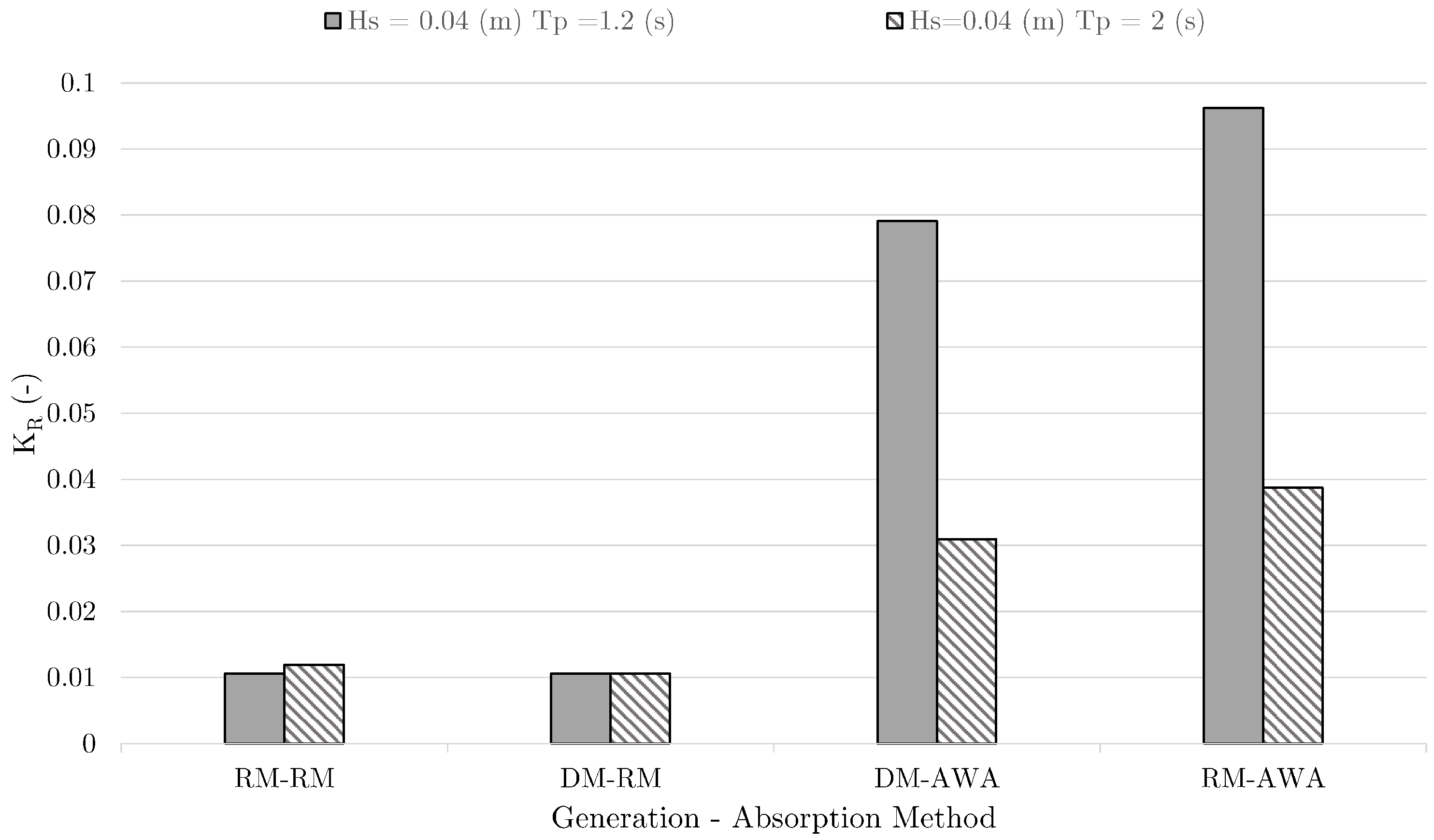
- Results from the current numerical study provide generally lower reflection coefficients in comparison to the previous study with the active wave absorption method, and the relaxation method generally provides further lower reflections.
- Different combinations of wave generation and absorption methods can be employed to achieve computational efficiency without compromising the quality of the results.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Yang, J.; Stern, F. A simple and efficient direct forcing immersed boundary framework for fluid–structure interactions. J. Comput. Phys. 2012, 231, 5029–5061. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; Fuhrman, D.R.; Fredsøe, J. A wave generation toolbox for the open-source CFD library: OpenFOAM®. Int. J. Numer. Meth. Fluids 2012, 70, 1073–1088. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, L.J.; Losada, I.J. Realistic wave generation and active wave absorption for Navier-Stokes models Application to OpenFOAM®. Coast. Eng. 2013, 71, 102–118. [Google Scholar] [CrossRef]
- Bihs, H.; Kamath, A.; Alagan Chella, M.; Aggarwal, A.; Arntsen, ∅.A. A new level set numerical wave tank with improved density interpolation for complex wave hydrodynamics. Comput. Fluids 2016, 140, 191–208. [Google Scholar] [CrossRef]
- Rhee, S.H.; Stern, F. RANS model for spilling breaking waves. J. Fluids Eng. 2002, 124, 424–432. [Google Scholar] [CrossRef]
- Alagan Chella, M.; Bihs, H.; Myrhaug, D.; Muskulus, M. Hydrodynamic characteristics and geometric properties of plunging and spilling breakers over impermeable slopes. Ocean Model. Virtual Spec. Issue Ocean Surf. Waves 2016, 103, 53–72. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, J.; Koo, B.; Stern, F. A coupled level set and volume-of-fluid method for sharp interface simulation of plunging breaking waves. Int. J. Multiph. Flow 2009, 35, 227–246. [Google Scholar] [CrossRef]
- Kamath, A.; Alagan Chella, M.; Bihs, H.; Arntsen, ∅.A. Breaking wave interaction with a vertical cylinder and the effect of breaker location. Ocean Eng. 2016, 128, 105–115. [Google Scholar] [CrossRef]
- Bihs, H.; Kamath, A.; Alagan Chella, M.; Arntsen, ∅.A. Breaking-Wave Interaction with Tandem Cylinders under Different Impact Scenarios. J. Water. Port Coast. Ocean Eng. 2016, 142. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Mai, T.; Greaves, D.; Raby, A. Investigations of offshore breaking wave impacts on a large offshore structure. J. Fluids Struct. 2017, 75, 99–116. [Google Scholar] [CrossRef]
- Li, T.; Troch, P.; De Rouck, J. Wave overtopping over a sea dike. J. Compu. Phys. 2004, 198, 686–726. [Google Scholar] [CrossRef]
- Elhanafi, A.; Macfarlane, G.; Fleming, A.; Leong, Z. Experimental and numerical measurements of wave forces on a 3D offshore stationary OWC wave energy converter. Ocean Eng. 2017, 144, 98–117. [Google Scholar] [CrossRef]
- Cavallaro, L.; Iuppa, C.; Scandura, P.; Foti, E. Wave load on a navigation lock sliding gate. Ocean Eng. 2018, 154, 298–310. [Google Scholar] [CrossRef]
- Higuera, P.; Lara, J.L.; Losada, I.J. Three-dimensional interaction of waves and porous coastal structures using OpenFOAM®. Part II: Application. Coast. Eng. 2014, 83, 259–270. [Google Scholar] [CrossRef]
- Jacobsen, N.G.; van Gent, M.R.A.; Wolters, G. Numerical analysis of the interaction of irregular waves with two dimensional permeable coastal structures. Coast. Eng. 2015, 102, 13–29. [Google Scholar] [CrossRef]
- Bihs, H.; Kamath, A. A combined level set/ghost cell immersed boundary representation for floating body simulations. Int. J. Numer. Meth. Fluids 2017, 83, 905–916. [Google Scholar] [CrossRef]
- Frigaard, P.; Brorsen, M. A time-domain method for separating incident and reflected irregular waves. Coast. Eng. 1995, 24, 205–215. [Google Scholar] [CrossRef]
- Sommerfeld, A. Lectures on Theoretical Physics; Academic Press: New York, NY, USA, 1956. [Google Scholar]
- Orlanski, I. A simple boundary condition for unbounded hyperbolic flows. J. Comput. Phys. 1976, 21, 251–269. [Google Scholar] [CrossRef]
- Engquist, B.; Majda, A. Numerical radiation boundary conditions for unsteady transonic flow. J. Comput. Phys. 1981, 40, 91–103. [Google Scholar] [CrossRef]
- Bayliss, A.; Turkel, E. Radiation Boundary Conditions for Wave-Like Equations. Commun. Pure App. Math. 1980, 33, 707–725. [Google Scholar] [CrossRef]
- Keller, J.B.; Givoli, D. Exact non-reflecting boundary conditions. J. Comput. Phys. 1989, 82, 172–192. [Google Scholar] [CrossRef]
- Madsen, P.A. Wave reflection from a vertical permeable wave absorber. Coast. Eng. 1983, 7, 381–396. [Google Scholar] [CrossRef]
- Mayer, S.; Garapon, A.; Sørensen, L.S. A fractional step method for unsteady free surface flow with applications to non-linear wave dynamics. Int. J. Numer. Meth. Fluids 1998, 28, 293–315. [Google Scholar] [CrossRef]
- Engsig-Karup, A.P. Unstructured Nodal DG-FEM Solution of High-Order Boussinesq-Type Equations. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2006. [Google Scholar]
- Schäffer, H.A.; Klopman, G. Review of multidirectional active wave absorption methods. J. Water. Port Coast. Ocean Eng. 2000, 126, 88–97. [Google Scholar] [CrossRef]
- Kamath, A.; Alagan Chella, M.; Bihs, H.; Arntsen, ∅.A. Energy transfer due to shoaling and decomposition of breaking and non-breaking waves over a submerged bar. Eng. Appl. Comput. Fluid Mech. 2017, 11, 450–466. [Google Scholar] [CrossRef]
- Kamath, A.; Alagan Chella, M.; Bihs, H.; Arntsen, ∅.A. CFD investigations of wave interaction with a pair of large tandem cylinders. Ocean Eng. 2015, 108, 738–748. [Google Scholar] [CrossRef]
- Alagan Chella, M.; Bihs, H.; Myrhaug, D.; Muskulus, M. Breaking solitary waves and breaking wave forces on a vertically mounted slender cylinder over an impermeable sloping seabed. J. Ocean Eng. Marine Energy 2017, 3, 1–19. [Google Scholar] [CrossRef]
- Bihs, H.; Alagan Chella, M.; Kamath, A.; Arntsen, ∅.A. Numerical Investigation of Focused Waves and Their Interaction With a Vertical Cylinder Using REEF3D. J. Off. Mech. Arctic Eng. 2017, 139, 041101. [Google Scholar] [CrossRef]
- Grotle, E.L.; Bihs, H.; Æsøy, V. Experimental and numerical investigation of sloshing under roll excitation at shallow liquid depths. Ocean Eng. 2017, 138, 73–85. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries Inc.: La Canada, CA, USA, 1994. [Google Scholar]
- Chorin, A. Numerical solution of the Navier-Stokes equations. Math. Comput. 1968, 22, 745–762. [Google Scholar] [CrossRef]
- Van der Vorst, H. BiCGStab: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems. SIAM J. Sci. Statist. Comput. 1992, 13, 631–644. [Google Scholar] [CrossRef]
- Center for Applied Scientific Computing. HYPRE High Performance Preconditioners–User’s Manual; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2006.
- Jiang, G.S.; Shu, C.W. Efficient implementation of weighted ENO schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Shu, C.W.; Osher, S. Efficient implementation of essentially non-oscillatory shock capturing schemes. J. Comput. Phys. 1988, 77, 439–471. [Google Scholar] [CrossRef]
- NOTUR. The Norwegian Metacenter for Computational Science. 2012. Available online: http://www.notur.no/hard ware/vilje (accessed on 15 June 2016).
- Osher, S.; Sethian, J.A. Fronts propagating with curvature- dependent speed: algorithms based on Hamilton-Jacobi formulations. J. Comput. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Sussman, M.; Smereka, P.; Osher, S. A level set approach for computing solutions to incompressible two-phase flow. J. Comput. Phys. 1994, 114, 146–159. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, Y. Estimation of incident and reflected waves in random wave experiments. In Proceedings of the 15th Conference on Coastal Engineering, Honolulu, HI, USA, 11–17 July 1976; pp. 828–845. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. The measurement of incident and reflected spectra using a least squares method. In Proceedings of the 17th Conference on Coastal Engineering, Sydney, Australia, 23–28 March 1980; pp. 154–172. [Google Scholar]
- Zelt, J.A.; Skjelbreia, J.E. Estimating incident and reflected wave fields using an arbitrary number of wave gauges. In Proceedings of the 23rd Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; pp. 777–789. [Google Scholar]
- MacCamy, R.; Fuchs, R. Wave Forces on Piles: A Diffraction Theory; US Army Corps of Engineers: Washington, DC, USA, 1954.
- Ting, F.C.; Kirby, J.T. Observation of undertow and turbulence in a laboratory surf zone. Coast. Eng. 1994, 24, 51–80. [Google Scholar] [CrossRef]
- Battjes, J.A. Surf Similarity. In Proceedings of the 14th International Conference on Coastal Engineering, Copenhagen, Denmark, 24–28 June 1974; pp. 466–480. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 1991. [Google Scholar]
- Gronbech, J.; Jensen, T.; Andersen, H. Reflection analysis with separation of cross modes. In Proceedings of the 25th Conference on Coastal Engineering, Orlando, FL, USA, 2–6 June 1996; pp. 968–980. [Google Scholar]
| Case | H (m) | L (m) | H/L | Stokes Order | |
|---|---|---|---|---|---|
| a | 0.02 | 2 | 0.01 | 1.57 | 1st |
| b | 0.02 | 4 | 0.005 | 0.785 | 1st |
| c | 0.04 | 2 | 0.02 | 1.57 | 2nd |
| d | 0.04 | 4 | 0.01 | 0.785 | 2nd |
| e | 0.10 | 2 | 0.05 | 1.57 | 5th |
| f | 0.10 | 4 | 0.025 | 0.785 | 2nd |
| No. | Generation | Beach | Notation |
|---|---|---|---|
| 1 | Relaxation method | Relaxation method | RM-RM |
| 2 | Relaxation method | Active wave absorption | RM-AWA |
| 3 | Dirichlet method | Relaxation method | DM-RM |
| 4 | Dirichlet method | Active wave absorption | DM-AWA |
| Case | (m) | (m) | m | Breaking | (m) | ||
|---|---|---|---|---|---|---|---|
| RM | DM | ||||||
| a | 0.01 | 2 | 0.40 | Spilling | 23.02 | 22.98 | |
| b | 0.01 | 4 | 0.57 | Transitional | 28.88 | 28.76 | |
| c | 0.01 | 2 | 0.57 | Transitional | 18.14 | 18.07 | |
| d | 0.01 | 4 | 0.80 | Plunging | 24.07 | 24.1 | |
| e | 0.01 | 2 | 0.94 | Plunging | 13.29 | 13.29 | |
| f | 0.01 | 4 | 1.33 | Plunging | 19.45 | 19.34 | |
| Case | (%) | (m) | ||||
|---|---|---|---|---|---|---|
| RM | DM | RM | DM | RM | DM | |
| a | 3.60 | 3.83 | 0.0210 | 0.0269 | 0.28 | 0.25 |
| b | 5.26 | 5.94 | 0.0303 | 0.0304 | 0.33 | 0.33 |
| c | 4.08 | 4.64 | 0.0225 | 0.0263 | 0.38 | 0.35 |
| d | 5.84 | 5.60 | 0.0243 | 0.0274 | 0.52 | 0.49 |
| e | 4.80 | 4.80 | 0.0191 | 0.0219 | 0.69 | 0.65 |
| f | 4.67 | 6.13 | 0.0196 | 0.0189 | 0.96 | 0.98 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miquel, A.M.; Kamath, A.; Alagan Chella, M.; Archetti, R.; Bihs, H. Analysis of Different Methods for Wave Generation and Absorption in a CFD-Based Numerical Wave Tank. J. Mar. Sci. Eng. 2018, 6, 73. https://doi.org/10.3390/jmse6020073
Miquel AM, Kamath A, Alagan Chella M, Archetti R, Bihs H. Analysis of Different Methods for Wave Generation and Absorption in a CFD-Based Numerical Wave Tank. Journal of Marine Science and Engineering. 2018; 6(2):73. https://doi.org/10.3390/jmse6020073
Chicago/Turabian StyleMiquel, Adria Moreno, Arun Kamath, Mayilvahanan Alagan Chella, Renata Archetti, and Hans Bihs. 2018. "Analysis of Different Methods for Wave Generation and Absorption in a CFD-Based Numerical Wave Tank" Journal of Marine Science and Engineering 6, no. 2: 73. https://doi.org/10.3390/jmse6020073
APA StyleMiquel, A. M., Kamath, A., Alagan Chella, M., Archetti, R., & Bihs, H. (2018). Analysis of Different Methods for Wave Generation and Absorption in a CFD-Based Numerical Wave Tank. Journal of Marine Science and Engineering, 6(2), 73. https://doi.org/10.3390/jmse6020073







