The Impact of Uncertainties in Ice Sheet Dynamics on Sea-Level Allowances at Tide Gauge Locations
Abstract
:1. Introduction
2. Data and Methodology
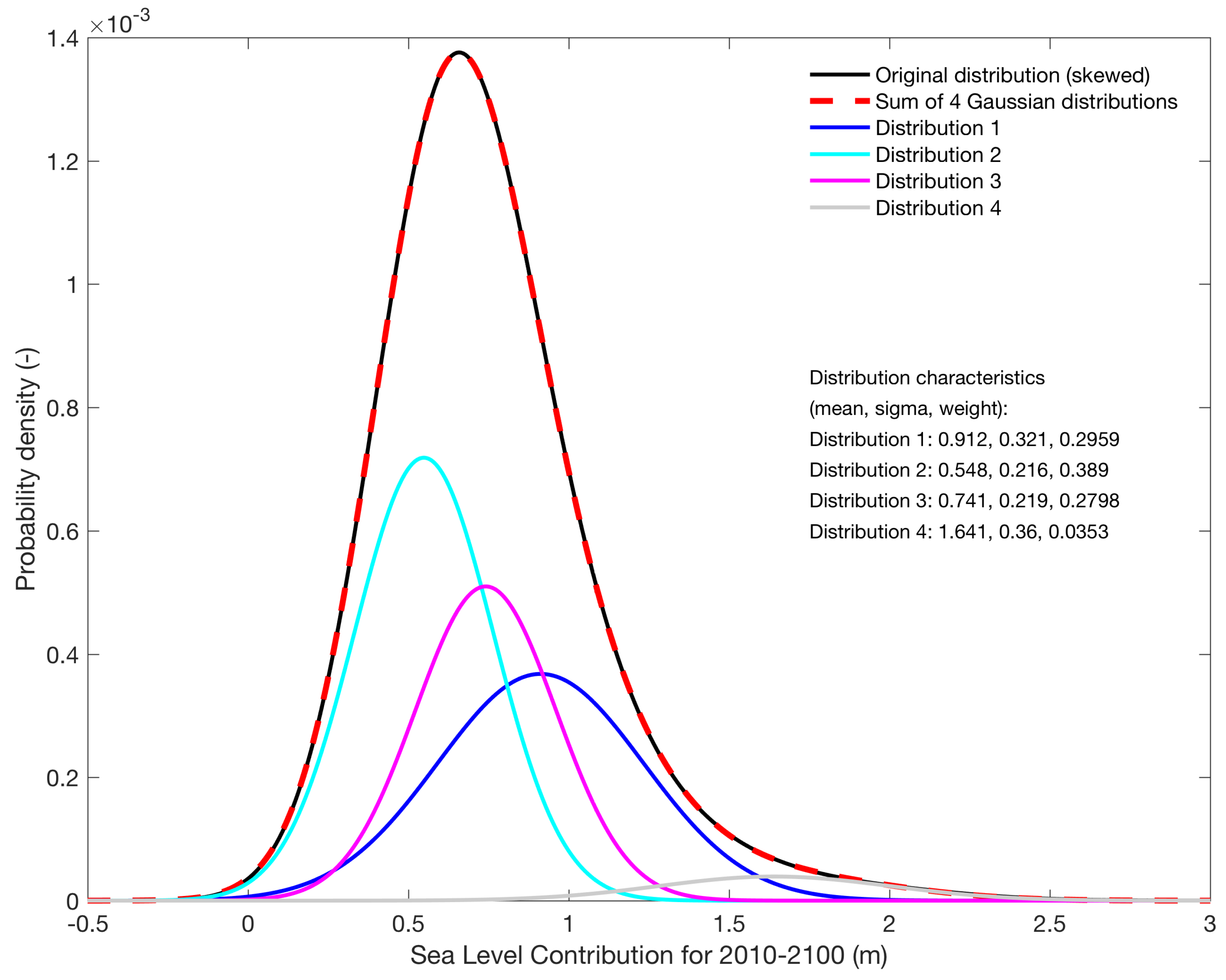
2.1. Uncertainty Distributions of Sea-Level Change
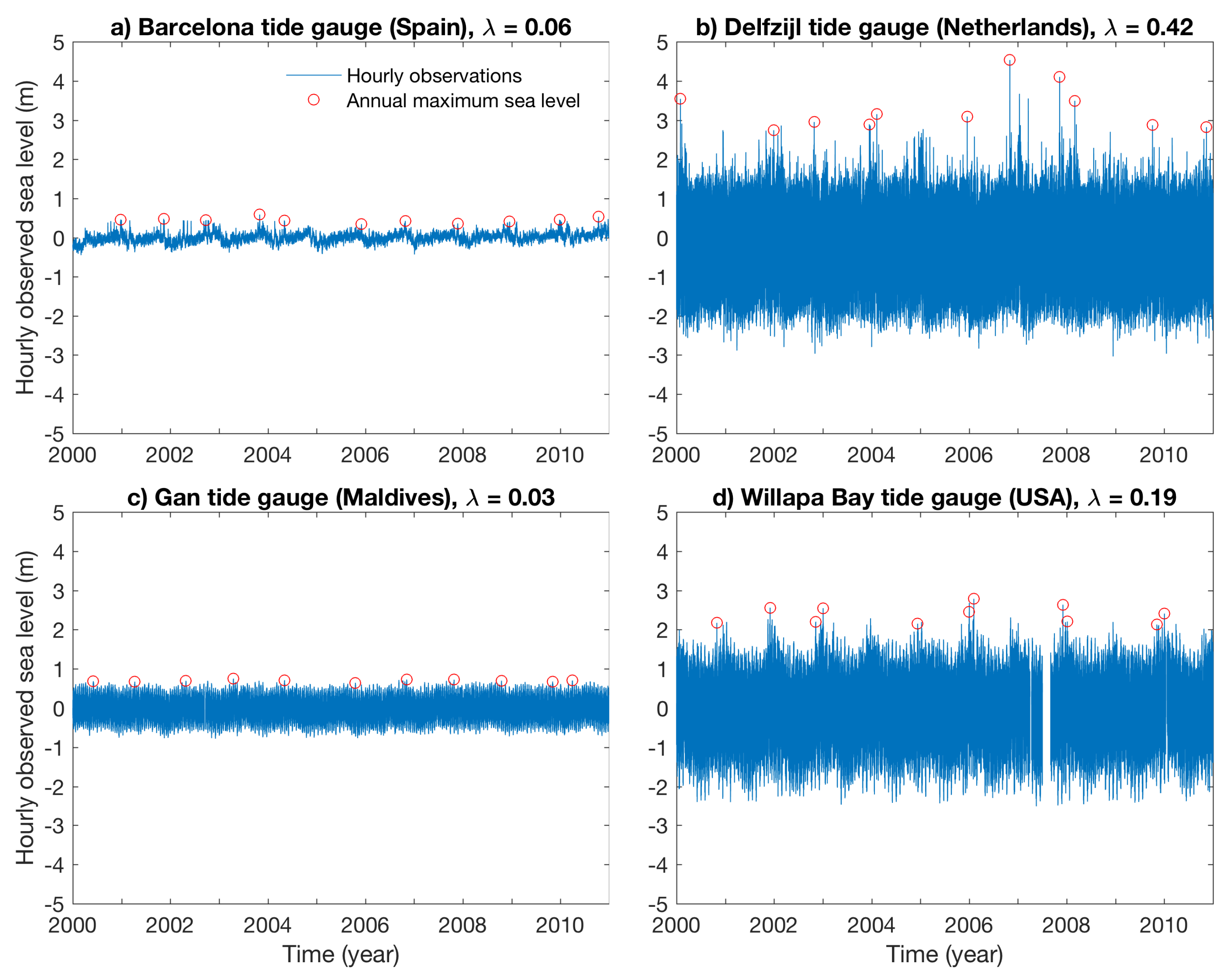
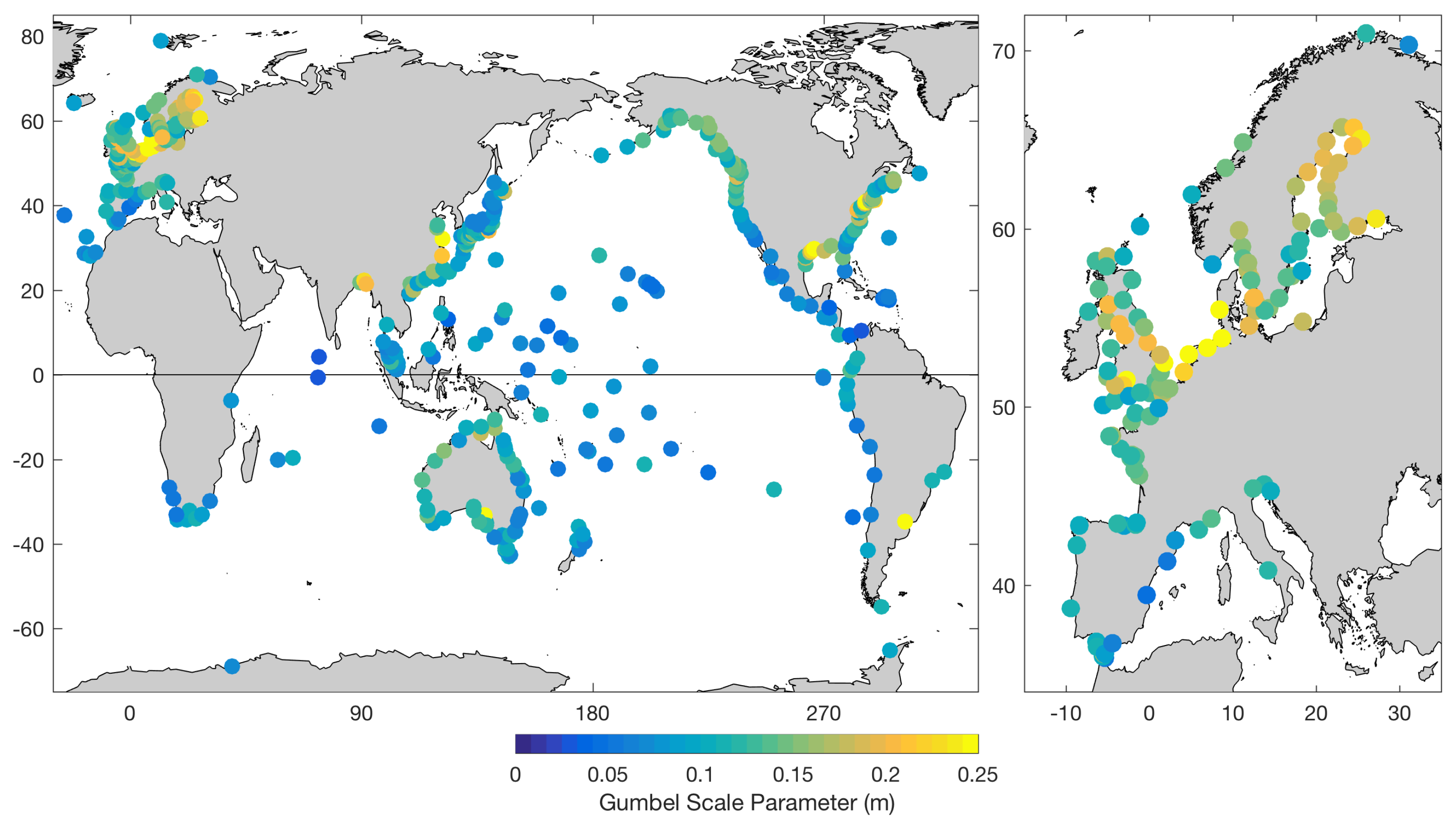
2.2. The Statistics of Sea-Level Extremes
2.3. Allowances Methodology
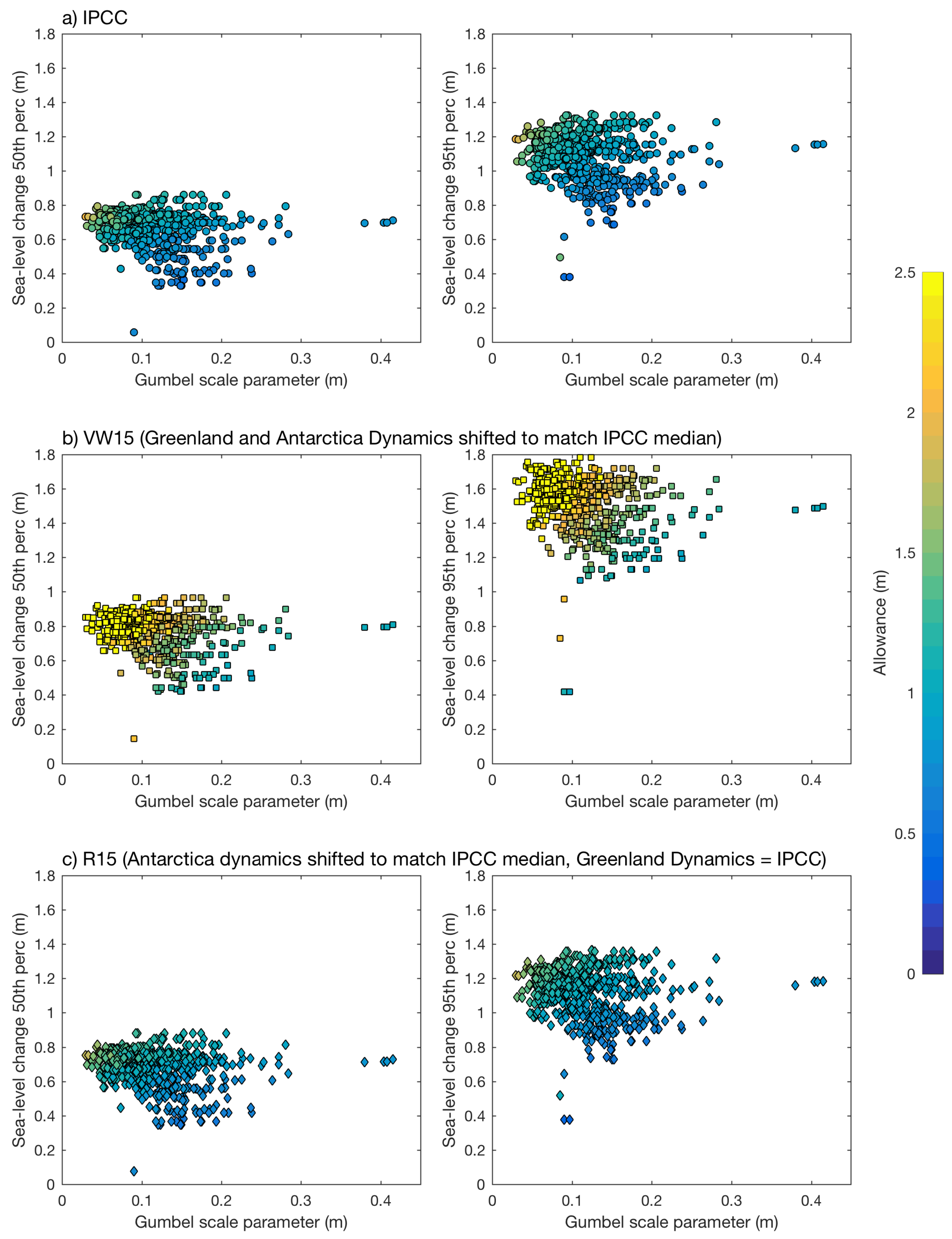
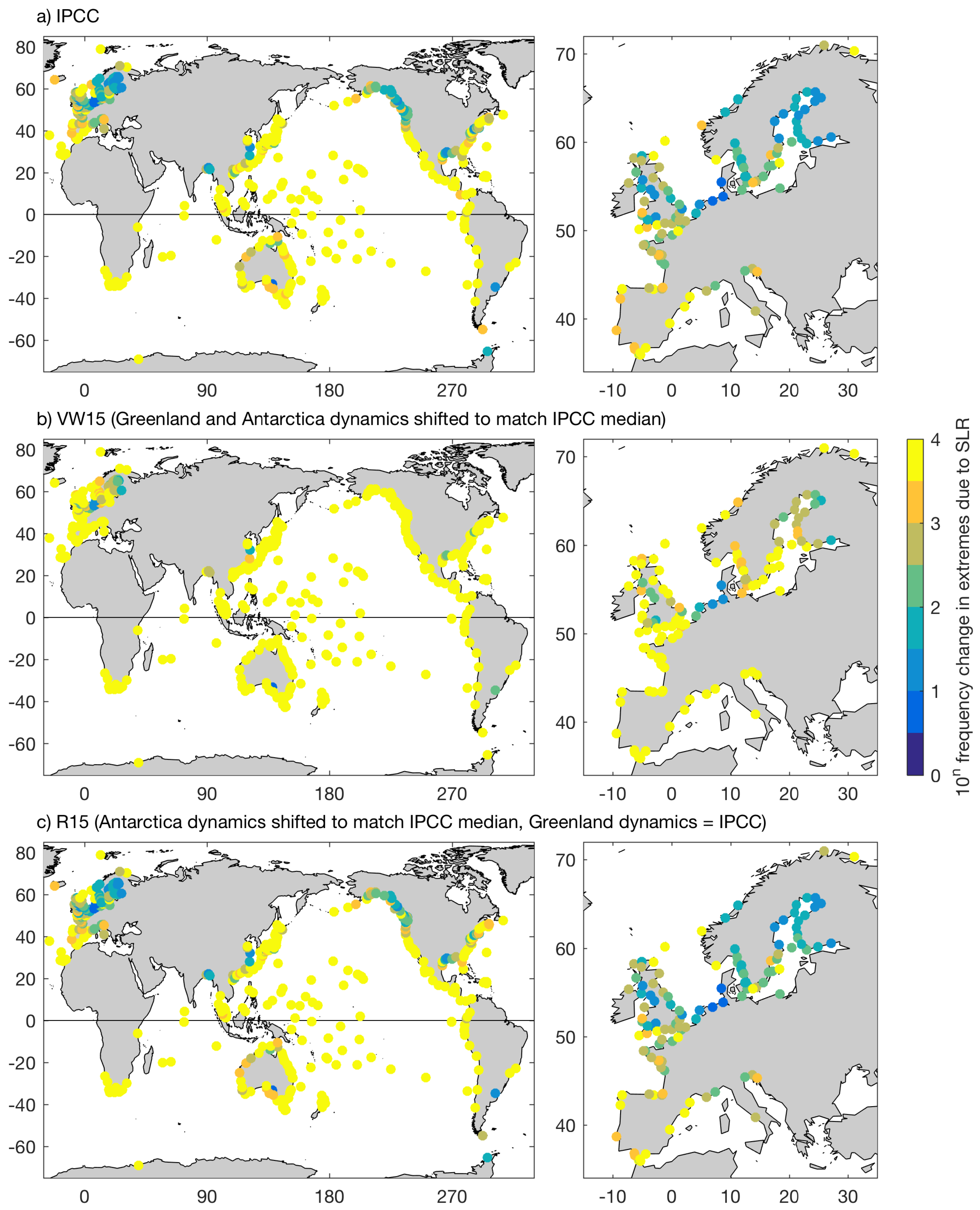
3. Results
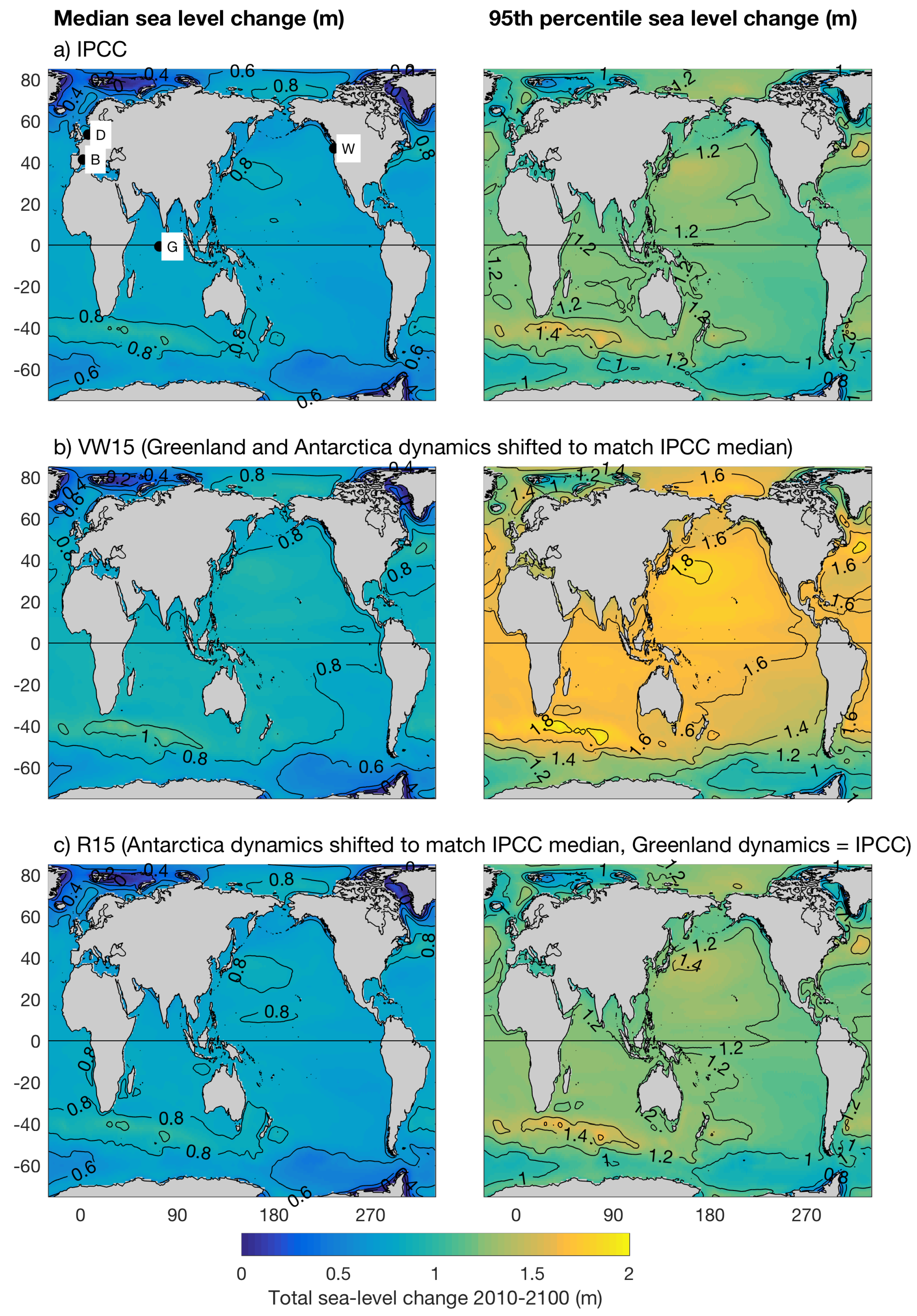
3.1. Sea-Level Projections for 2010–2100
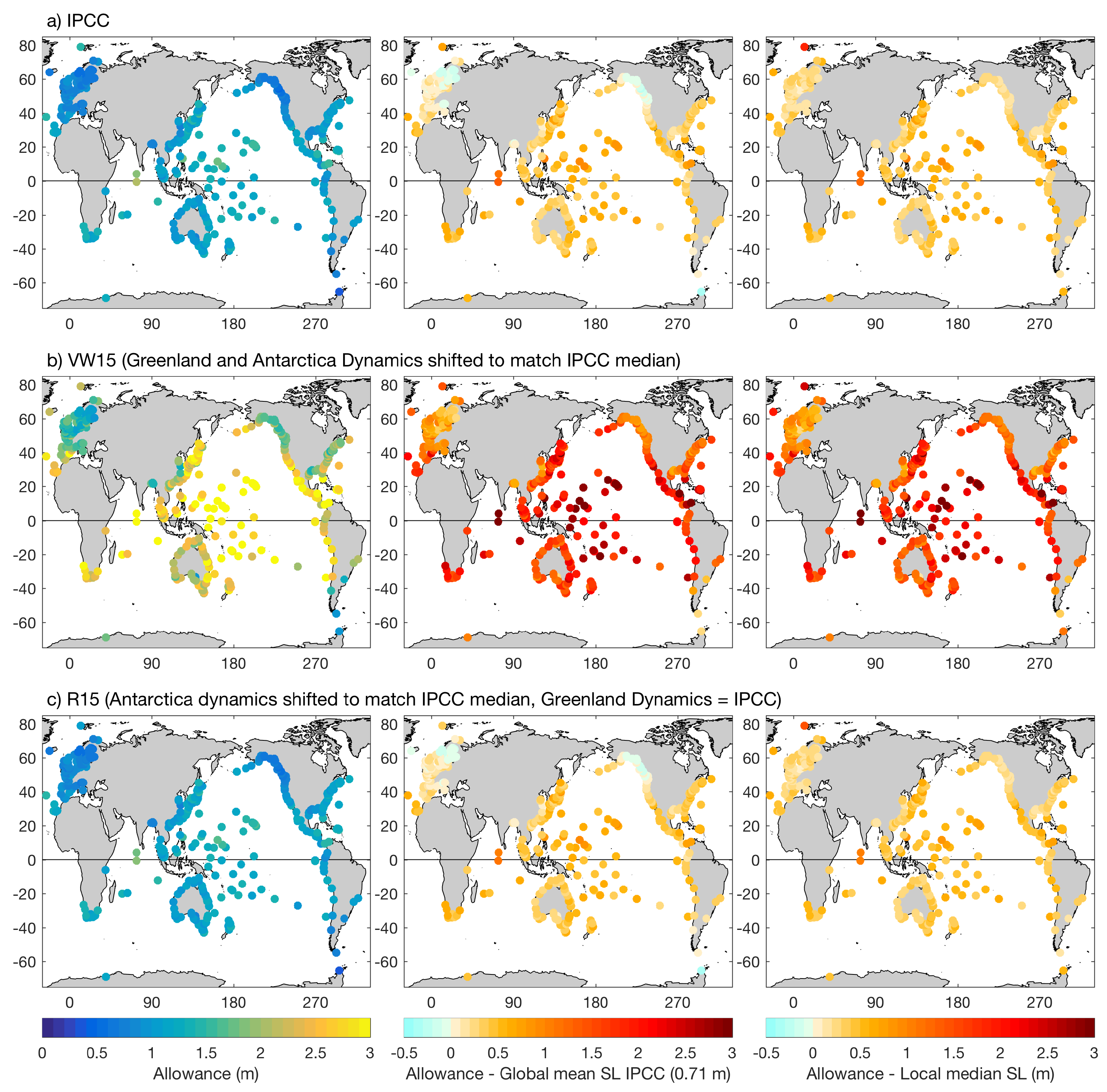
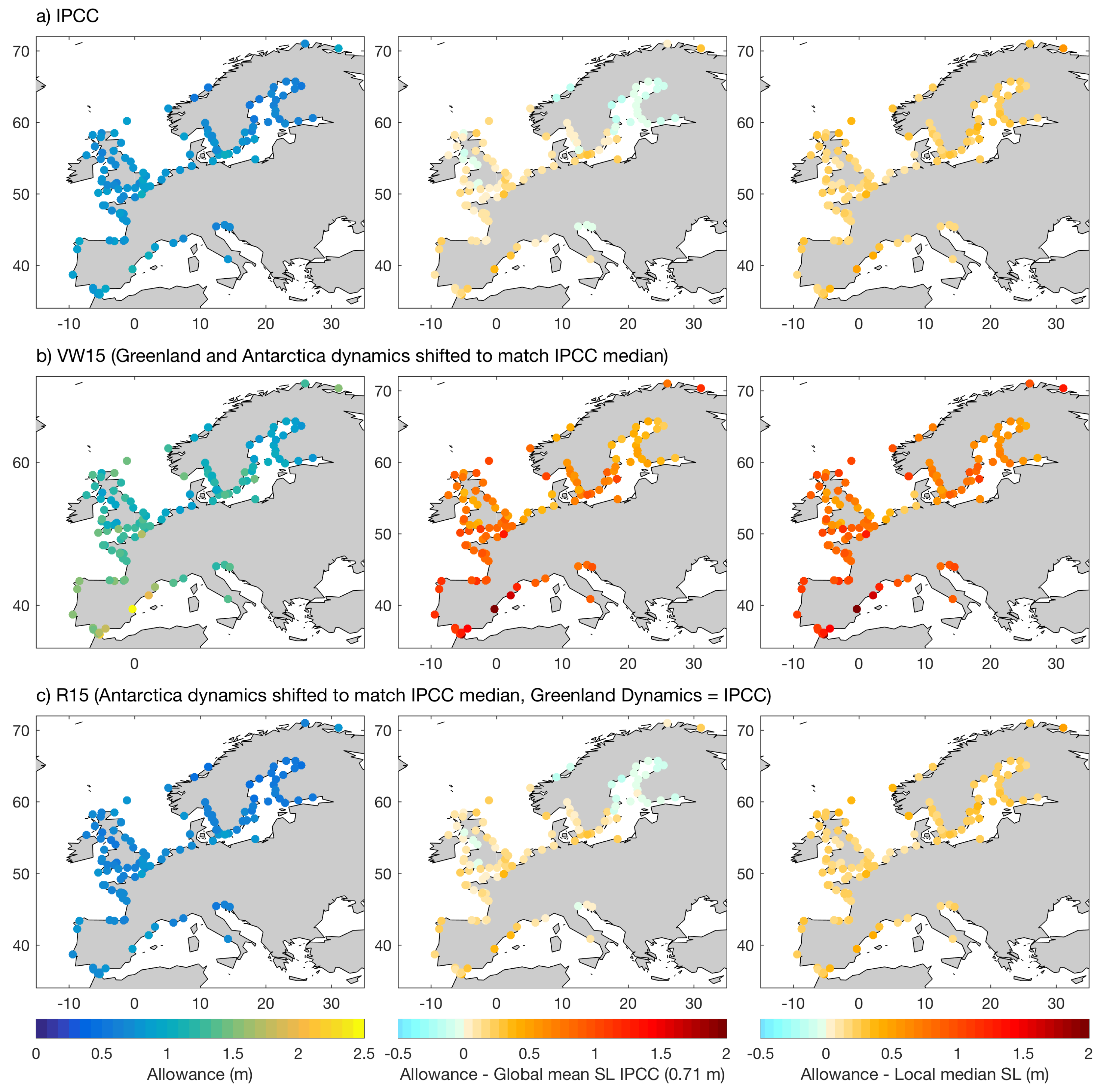
3.2. Allowances for Different Uncertainty Distributions
3.3. Changes in the Frequency of Extreme Events
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AR5 | Fifth Assessment Report |
| CMIP5 | 5th phase of the Climate Model Intercomparison Project |
| EAIS | East Antarctic Ice Sheet |
| GESLA-2 | Global Extreme Sea Level Analysis Version 2 |
| GRIS | Greenland Ice Sheet |
| IPCC | Intergovernmental Panel on Climate Change |
| RCP | Representative Concentration Pathway |
| SLR | Sea-Level Rise |
| WAIS | West Antarctic Ice Sheet |
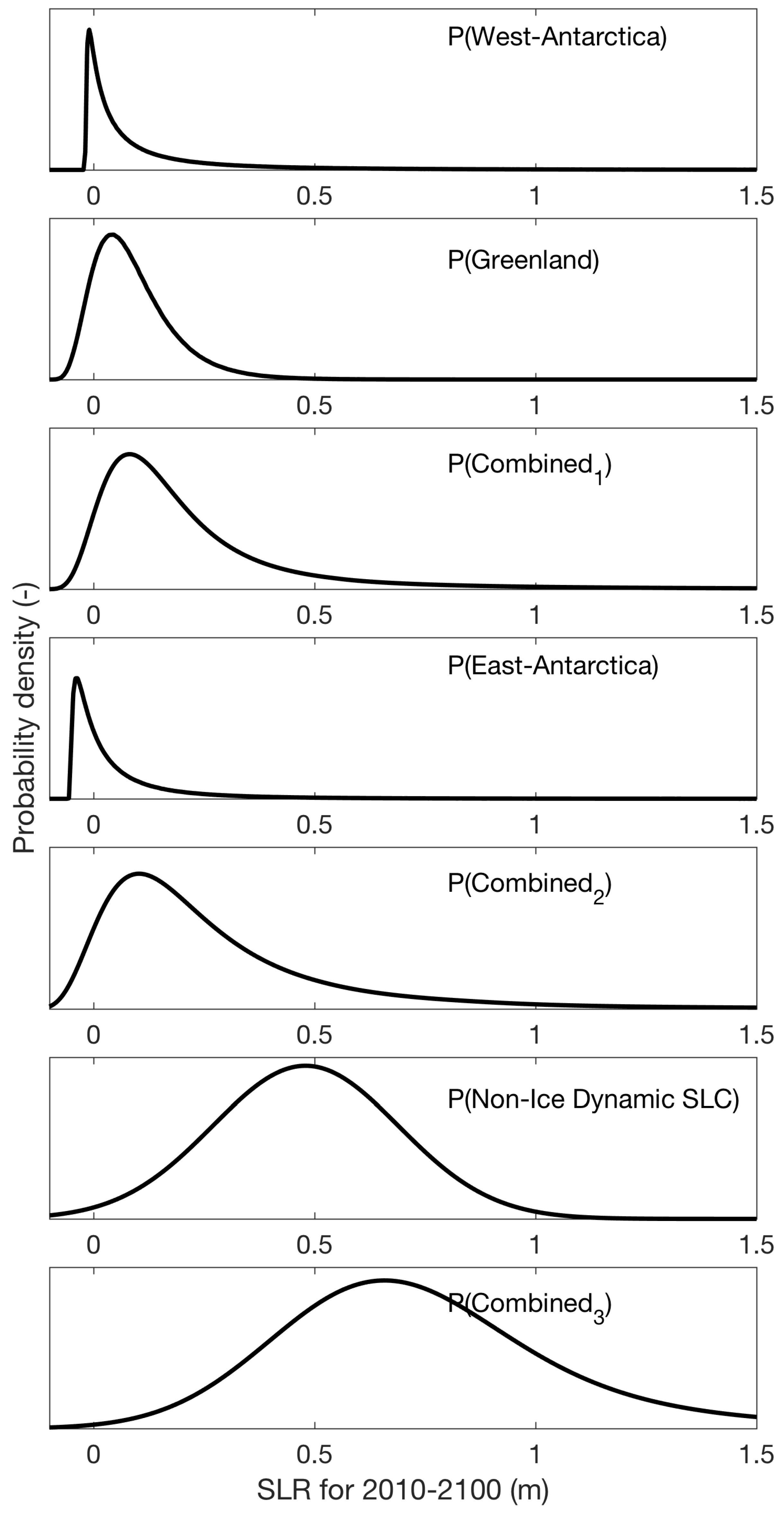
Appendix A. SEAWISE Methodology
References
- Church, J.; Clark, P.; Cazenave, A.; Gregory, J.; Jevrejeva, S.; Levermann, A.; Merrifield, M.; Milne, G.; Nerem, R.; Nunn, P.; et al. Sea Level Change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T., Qin, D., Plattner, G.K., Tignor, M., Allen, S., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Clark, P.U.; Church, J.A.; Gregory, J.M.; Payne, A.J. Recent Progress in Understanding and Projecting Regional and Global Mean Sea Level Change. Curr. Clim. Chang. Rep. 2015, 1, 224–246. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Adloff, F.; Jevrejeva, S.; Leclercq, P.W.; Marzeion, B.; Wada, Y.; Winkelmann, R. A Review of Recent Updates of Sea-Level Projections at Global and Regional Scales. Surv. Geophys. 2016, 38, 385–406. [Google Scholar] [CrossRef]
- Bamber, J.L.; Aspinall, W.P. An expert judgement assessment of future sea level rise from the ice sheets. Nat. Clim. Chang. 2013, 3, 424–427. [Google Scholar] [CrossRef]
- De Vries, H.; van de Wal, R.S.W. How to interpret expert judgment assessments of 21st century sea-level rise. Clim. Chang. 2015, 130, 87–100. [Google Scholar] [CrossRef]
- Favier, L.; Durand, G.; Cornford, S.L.; Gudmundsson, G.H.; Gagliardini, O.; Gillet-Chaulet, F.; Zwinger, T.; Payne, A.J.; le Brocq, A.M. Retreat of Pine Island Glacier controlled by marine ice-sheet instability. Nat. Clim. Chang. 2014, 4, 117–121. [Google Scholar] [CrossRef]
- Joughin, I.; Smith, B.E.; Medley, B. Marine Ice Sheet Collapse Potentially Under Way for the Thwaites Glacier Basin, West Antarctica. Science 2014, 344, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Ritz, C.; Edwards, T.L.; Durand, G.; Payne, A.J.; Peyaud, V.; Hindmarsh, R.C.A. Potential sea-level rise from Antarctic ice-sheet instability constrained by observations. Nature 2015, 528, 115–118. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J. A simple technique for estimating an allowance for uncertain sea-level rise. Clim. Chang. 2012, 113, 239–252. [Google Scholar] [CrossRef]
- Hunter, J.R.; Church, J.A.; White, N.J.; Zhang, X. Towards a global regionally varying allowance for sea-level rise. Ocean Eng. 2013, 71, 17–27. [Google Scholar] [CrossRef]
- Menéndez, M.; Woodworth, P.L. Changes in extreme high water levels based on a quasi-global tide-gauge dataset. J. Geophys. Res. 2010, 115, C10011. [Google Scholar] [CrossRef]
- Slangen, A.B.A.; Carson, M.; Katsman, C.; van de Wal, R.; Koehl, A.; Vermeersen, L.; Stammer, D. Projecting twenty-first century regional sea-level changes. Clim. Chang. 2014, 124, 317–332. [Google Scholar] [CrossRef]
- Moss, R.H.; Edmonds, J.A.; Hibbard, K.A.; Manning, M.R.; Rose, S.K.; van Vuuren, D.P.; Carter, T.R.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Kopp, R.E.; Horton, R.M.; Little, C.M.; Mitrovica, J.X.; Oppenheimer, M.; Rasmussen, D.J.; Strauss, B.H.; Tebaldi, C. Probabilistic 21st and 22nd century sea-level projections at a global network of tide-gauge sites. Earth Future 2014, 2, 383–406. [Google Scholar] [CrossRef]
- Jackson, L.P.; Jevrejeva, S. A probabilistic approach to 21st century regional sea-level projections using RCP and High-end scenarios. Glob. Planet. Chang. 2016, 146, 179–189. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Jackson, L.P.; Riva, R.E.M.; Grinsted, A.; Moore, J.C. Coastal sea level rise with warming above 2 °C. Proc. Natl. Acad. Sci. USA 2016, 113, 13342–13347. [Google Scholar] [CrossRef] [PubMed]
- De Winter, R.; Reerink, T.J.; de Vries, H.; Slangen, A.B.A.; van de Wal, R.S.W. Impact of asymmetric uncertainties in ice sheet dynamics on regional sea level projections. Nat. Hazards Earth Syst. Sci. Discuss. 2017. In Review. [Google Scholar] [CrossRef]
- Buchanan, M.K.; Kopp, R.E.; Oppenheimer, M.; Tebaldi, C. Allowances for evolving coastal flood risk under uncertain local sea-level rise. Clim. Chang. 2016, 137, 347–362. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Arns, A.; Wahl, T.; Haigh, I.D.; Jensen, J.; Pattiaratchi, C. Estimating extreme water level probabilities: A comparison of the direct methods and recommendations for best practise. Coast. Eng. 2013, 81, 51–66. [Google Scholar] [CrossRef]
- GESLA. Available online: www.gesla.org (accessed on 23 May 2017).
- Woodworth, P.; Hunter, J.; Marcos, M.; Caldwell, P.; Menendez, M.; Haigh, I. Towards a global higher-frequency sea level data set. Geosci. Data J. 2016, 3, 50–59. [Google Scholar] [CrossRef]
- Shepherd, A.; Ivins, E.R.; Geruo, A.; Barletta, V.R.; Bentley, M.J.; Bettadpur, S.; Briggs, K.H.; Bromwich, D.H.; Forsberg, R.; Galin, N.; et al. A Reconciled Estimate of Ice-Sheet Mass Balance. Science 2012, 338, 1183–1189. [Google Scholar] [CrossRef] [PubMed]
- Mitrovica, J.X.; Tamisiea, M.E.; Davis, J.L.; Milne, G.A. Recent mass balance of polar ice sheets inferred from patterns of global sea-level change. Nature 2001, 409, 1026–1029. [Google Scholar] [CrossRef] [PubMed]
- Hunter, J.R.; Woodworth, P.L.; Wahl, T.; Nicholls, R.J. Using Global Tide Gauge Data to Validate and Improve the Representation of Extreme Sea Levels in Flood Impact Studies. Glob. Planet. Chang. 2017. Under Review. [Google Scholar]
- Merrifield, M.A.; Genz, A.S.; Kontoes, C.P.; Marra, J.J. Annual maximum water levels from tide gauges: Contributing factors and geographic patterns. J. Geophys. Res. Oceans 2013, 118, 2535–2546. [Google Scholar] [CrossRef]
- De Winter, R.C.; Sterl, A.; Ruessink, B.G. Wind extremes in the North Sea Basin under climate change: An ensemble study of 12 CMIP5 GCMs. J. Geophys. Res. Atmos. 2013, 118, 1601–1612. [Google Scholar] [CrossRef]
- Press, W.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Slangen, A.B.A.; Church, J.A.; Zhang, X.; Monselesan, D. The sea-level response to external forcings in CMIP5 climate models. J. Clim. 2015, 28, 8521–8539. [Google Scholar] [CrossRef]
- Tamisiea, M.E.; Mitrovica, J.X. The moving boundaries of sea level change: Understanding the origins of geographic variability. Oceanography 2011, 24, 24–39. [Google Scholar] [CrossRef]
- Muis, S.; Verlaan, M.; Winsemius, H.C.; Aers, J.C.J.H.; Ward, P.J. A global reanalysis of storm surges and extreme sea levels. Nat. Commun. 2016, 7, 11969. [Google Scholar] [CrossRef] [PubMed]
- Wahl, T.; Haigh, I.; Nicholls, R.; Arns, A.; Dangendorf, S.; Hinkel, J.; Slangen, A. Understanding extreme sea levels for broad-scale coastal impact and adaptation analysis. Nat. Commun. 2017. Accepted. [Google Scholar]
- Haigh, I.D.; Nicholls, R.; Wells, N. A comparison of the main methods for estimating probabilities of extreme still water levels. Coast. Eng. 2010, 57, 838–849. [Google Scholar] [CrossRef]
- Dangendorf, S.; Arns, A.; Pinto, J.G.; Ludwig, P.; Jensen, J. The exceptional influence of storm ’Xaver’ on design water levels in the German Bight. Environ. Res. Lett. 2016, 11, 045001. [Google Scholar] [CrossRef]
- Erkens, G.; Bucx, T.; Dam, R.; de Lange, G.; Lambert, J.L. Sinking coastal cities. Proc. IAHS 2015, 372, 189–198. [Google Scholar] [CrossRef]
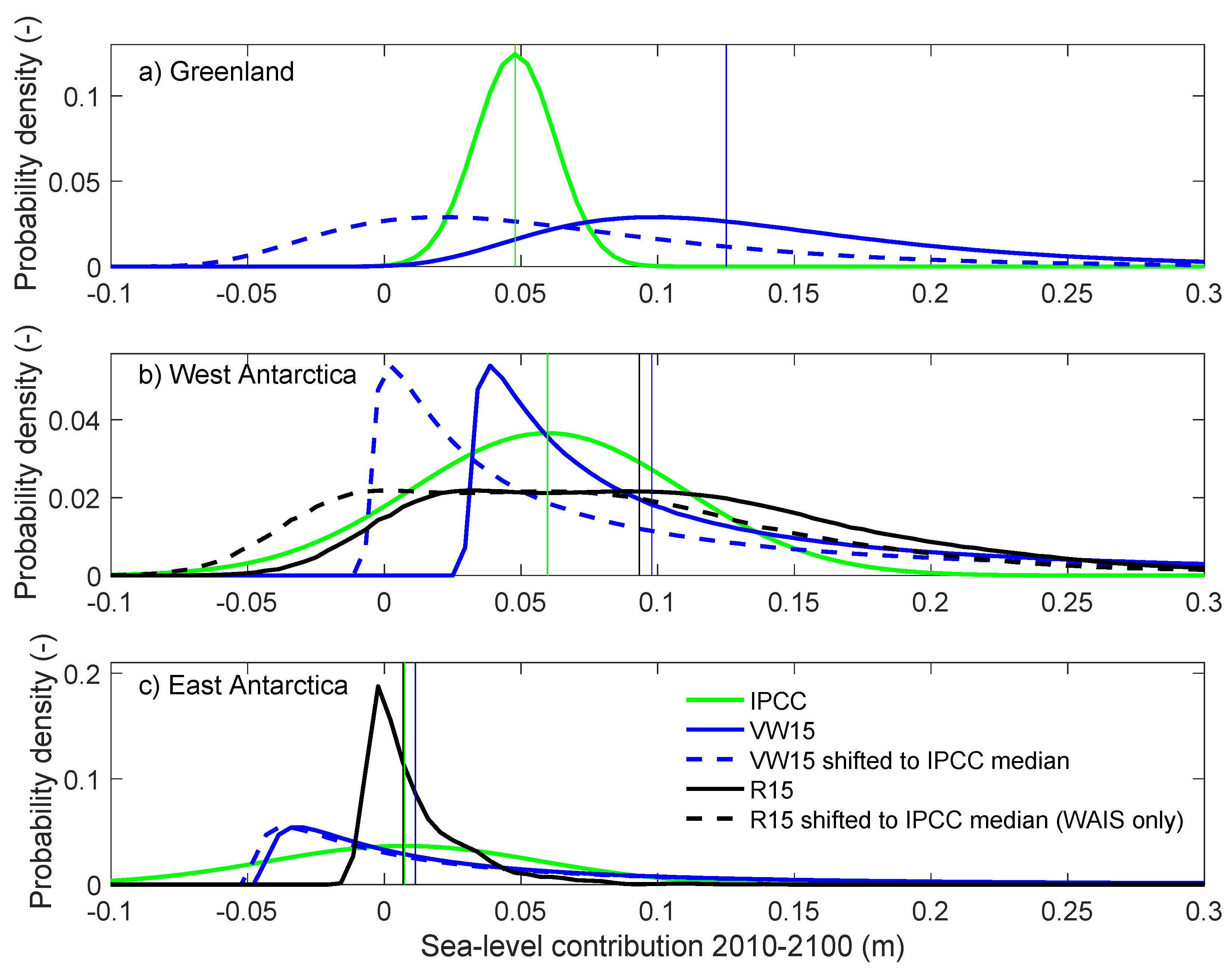
| IPCC | VW15 | R15 | |
|---|---|---|---|
| 0–1 | 1% (6) | 0% (2) | 1% (6) |
| 1–2 | 11% (73) | 1% (9) | 10% (67) |
| 2–3 | 21% (139) | 6% (37) | 21% (136) |
| 3–4 | 17% (109) | 6% (39) | 16% (105) |
| >4 | 50% (325) | 87% (565) | 52% (338) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slangen, A.B.A.; Van de Wal, R.S.W.; Reerink, T.J.; De Winter, R.C.; Hunter, J.R.; Woodworth, P.L.; Edwards, T. The Impact of Uncertainties in Ice Sheet Dynamics on Sea-Level Allowances at Tide Gauge Locations. J. Mar. Sci. Eng. 2017, 5, 21. https://doi.org/10.3390/jmse5020021
Slangen ABA, Van de Wal RSW, Reerink TJ, De Winter RC, Hunter JR, Woodworth PL, Edwards T. The Impact of Uncertainties in Ice Sheet Dynamics on Sea-Level Allowances at Tide Gauge Locations. Journal of Marine Science and Engineering. 2017; 5(2):21. https://doi.org/10.3390/jmse5020021
Chicago/Turabian StyleSlangen, Aimée B. A., Roderik S. W. Van de Wal, Thomas J. Reerink, Renske C. De Winter, John R. Hunter, Philip L. Woodworth, and Tamsin Edwards. 2017. "The Impact of Uncertainties in Ice Sheet Dynamics on Sea-Level Allowances at Tide Gauge Locations" Journal of Marine Science and Engineering 5, no. 2: 21. https://doi.org/10.3390/jmse5020021
APA StyleSlangen, A. B. A., Van de Wal, R. S. W., Reerink, T. J., De Winter, R. C., Hunter, J. R., Woodworth, P. L., & Edwards, T. (2017). The Impact of Uncertainties in Ice Sheet Dynamics on Sea-Level Allowances at Tide Gauge Locations. Journal of Marine Science and Engineering, 5(2), 21. https://doi.org/10.3390/jmse5020021






