A Hydrodynamic and Sediment Transport Model for the Waipaoa Shelf, New Zealand: Sensitivity of Fluxes to Spatially-Varying Erodibility and Model Nesting
Abstract
:1. Background
1.1. Sediment Transport Models
1.2. Study Site: Waipaoa River Continental Shelf, New Zealand
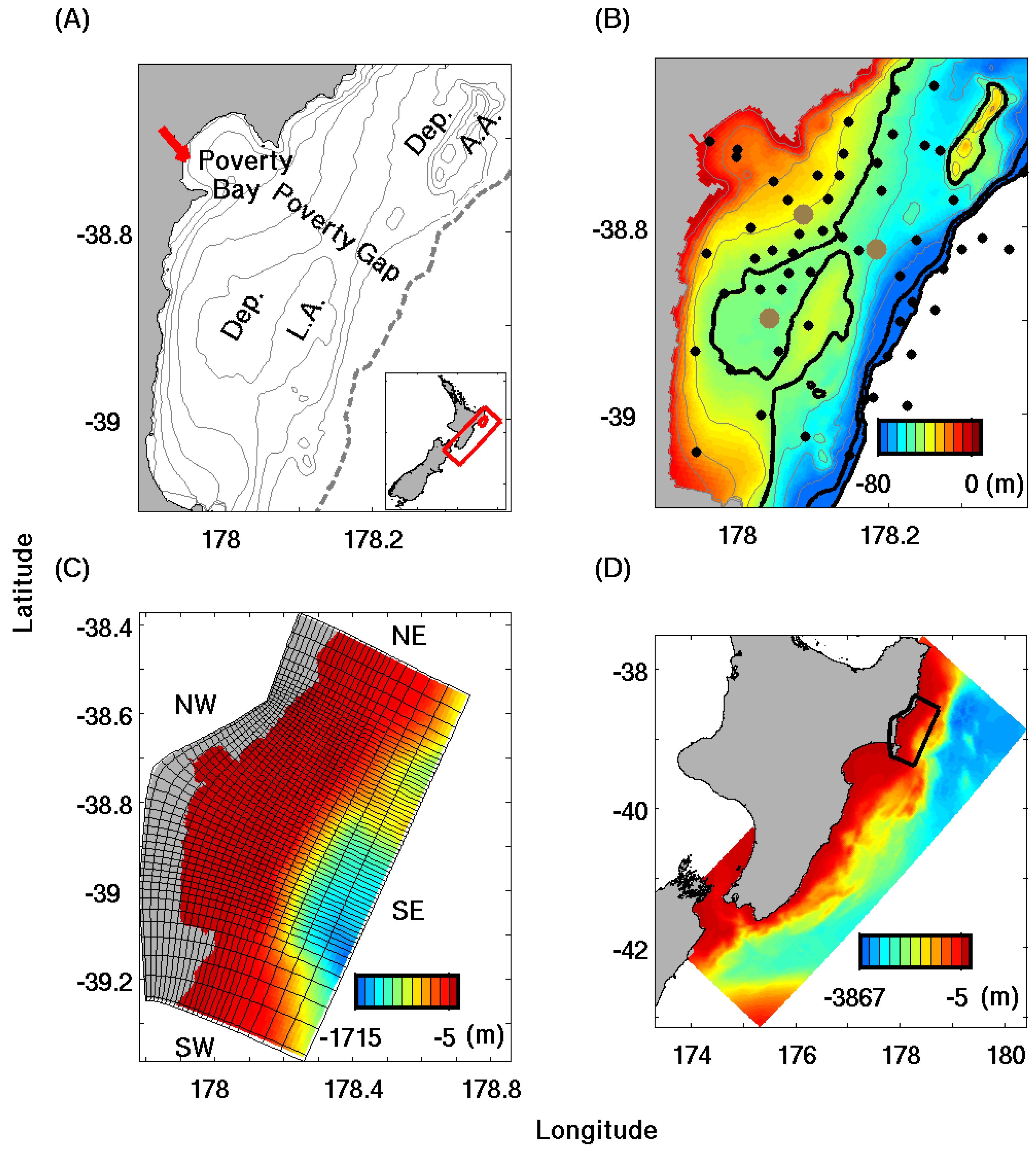
1.3. Objective
2. Model Development
2.1. Hydrodynamic Model and Numerical Schemes
| Parameter | Meaning | Unit |
|---|---|---|
| Cs,1,ised | Suspended concentration of sediment class ised in bottom water grid cell per unit area | kg m−2 |
| cx, cy | Phase speeds for oblique radiation boundary condition | m s−1 |
| D50 | Median grain diameter | M |
| Eised | Erosion for sediment class ised | kg m−2 s−1 |
| Fcs,ised | Source of sediment class ised to the water column due to seabed deposition and erosion | kg m−2 s−1 |
| Fgrid | Parameter specifying spatially-variable nudging at open boundaries | non-dimensional |
| FOBC | Parameter specifying changes to nudging at open boundaries based on current direction | non-dimensional |
| h | Water depth | m |
| htransition | Transitional water depth for erosion rate parameter parameterization | m |
| I | Number of grid cells in NW-SE direction | non-dimensional |
| i | Index for model grid in NW-SE direction | non-dimensional |
| ised | Index for modeled sediment classes | non-dimensional |
| J | Number of grid cells in SW-NE direction | non-dimensional |
| j | Index for model grid in SW-NE direction | non-dimensional |
| k1, k2 | Coefficients for active layer formulation | m2 s2 kg−1; non-dimensional |
| M | Erosion rate parameter | kg m−2 s−1 |
| Mmin | Minimum erosion rate parameter | kg m−2 s−1 |
| Mmax | Maximum erosion rate parameter | kg m−2 s−1 |
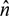 | Unit vector perpendicular to open boundary | |
| p | Seabed porosity | non-dimensional |
| S | Salinity | psu |
| S0 | Background salinity | psu |
| S0BC | Flux of freshwater through the open boundaries | m3 |
| TR,b | Relaxation timescale for nudging at open boundaries | s |
| TR,i | Relaxation timescale for nudging within model interior | s |
| TRO | Relaxation constant for nudging at open boundaries | non-dimensional |
| t | Time | s |
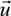 | Current velocity | m s−1 |
| ws,ised | Settling velocity for sediment class ised | m s−1 |
| x, y | Horizontal coordinates | non-dimensional |
| z | Vertical coordinate in water column | non-dimensional |
| za | Thickness of seabed active layer | m |
| zs | Vertical coordinate in seabed | m |
| ζ | Variable of interest in boundary condition equations | Same units as velocity, temperature, salinity, or sediment concentrations |
| ζ′ | Variable of interest in boundary condition equations before nudging | Same as above |
| ζobc | Prescribed value for variable of interest in open boundary condition equations | Same as above |
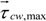 | Maximum wave-current induced bed shear stress over a wave period | Pa |
 | Magnitude of maximum wave-current induced bed shear stress over a wave period | Pa |
| τcrit | Critical shear stress for the seabed | Pa |
| Process | Numerical Scheme |
|---|---|
| Advection of momentum (Vertical, 3D) | 4th order, centered |
| Advection of momentum (Horizontal, 3D) | 3rd order, upstream |
| Advection of tracers | MPData |
| Vertical Sediment Settling | PPM |
2.2. Surface Boundary Formulation
2.3. Bottom Boundary Layer Formulation
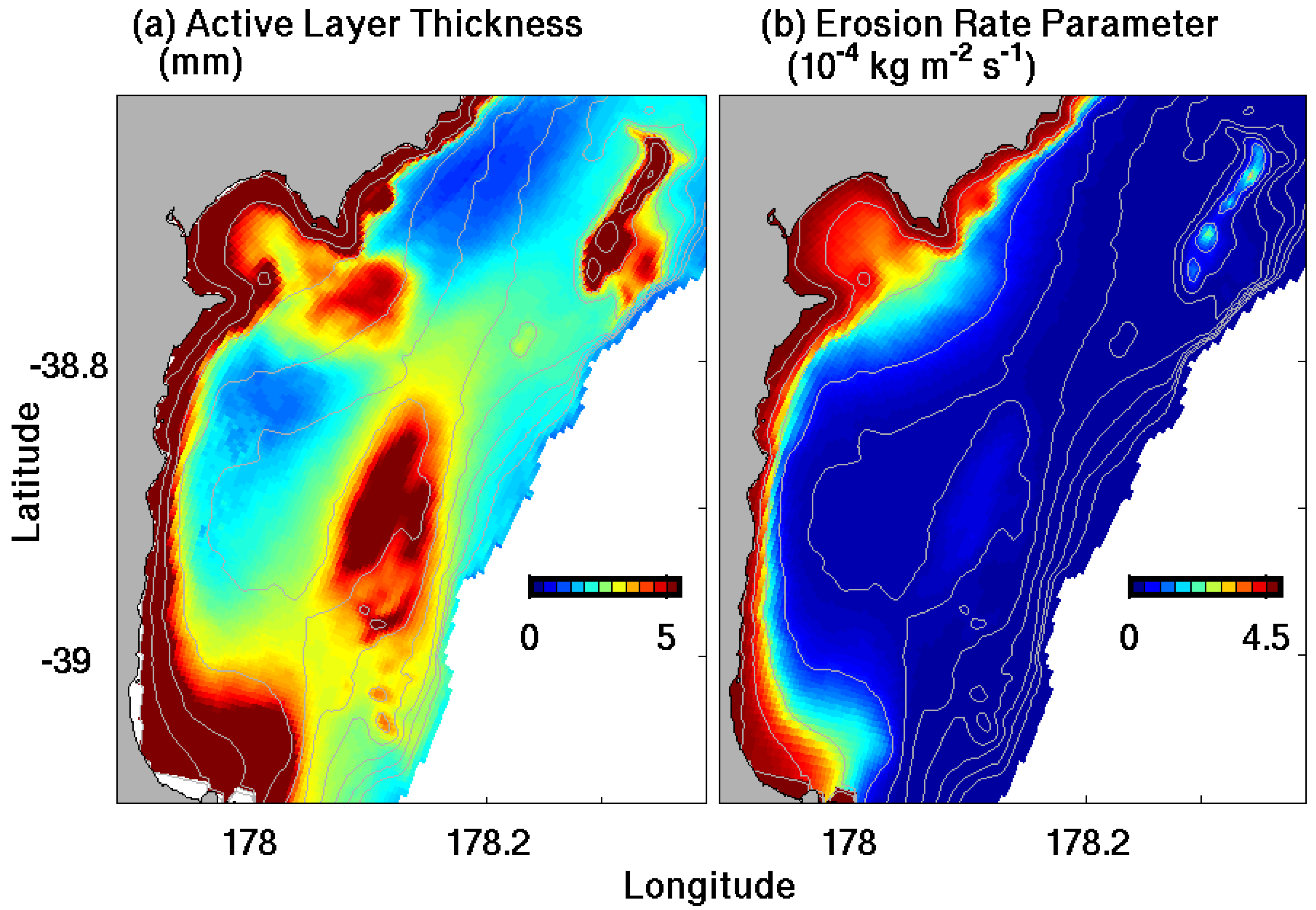
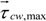 , following [54].
, following [54]. 2.4. Seabed Model


 was the magnitude of the total wave-current-bed shear stress, and τcrit was a constant critical bed shear stress. Erosion during any time step was limited to the amount of each size class available within a thin active layer whose thickness, za, was specified as:
was the magnitude of the total wave-current-bed shear stress, and τcrit was a constant critical bed shear stress. Erosion during any time step was limited to the amount of each size class available within a thin active layer whose thickness, za, was specified as:


2.5. Open Boundary Conditions

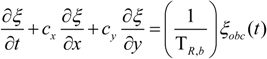 | (6) |
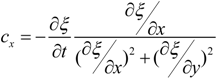 | |
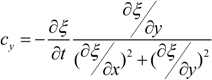 | |
 |

3. Model Initialization and Forcing
3.1. Model Grid Construction and Bathymetry
| Type of Data | Data Description and Source |
|---|---|
| Bathymetry to construct model grid | |
| Currents, temperature and salinity at open boundaries, and for model initialization | |
| Wave height, direction, and period |
|
| Wind stress |
|
| Tidal components: open boundary sea surface height and tidal velocities | |
| Meteorological data |
|
| River discharge of freshwater and sediment |
|
| Sediment properties of fluvial and seabed material (diameter, settling velocity, critical stress for erosion, erosion rate parameter) | |
| Seabed characteristics for comparison to model estimates |
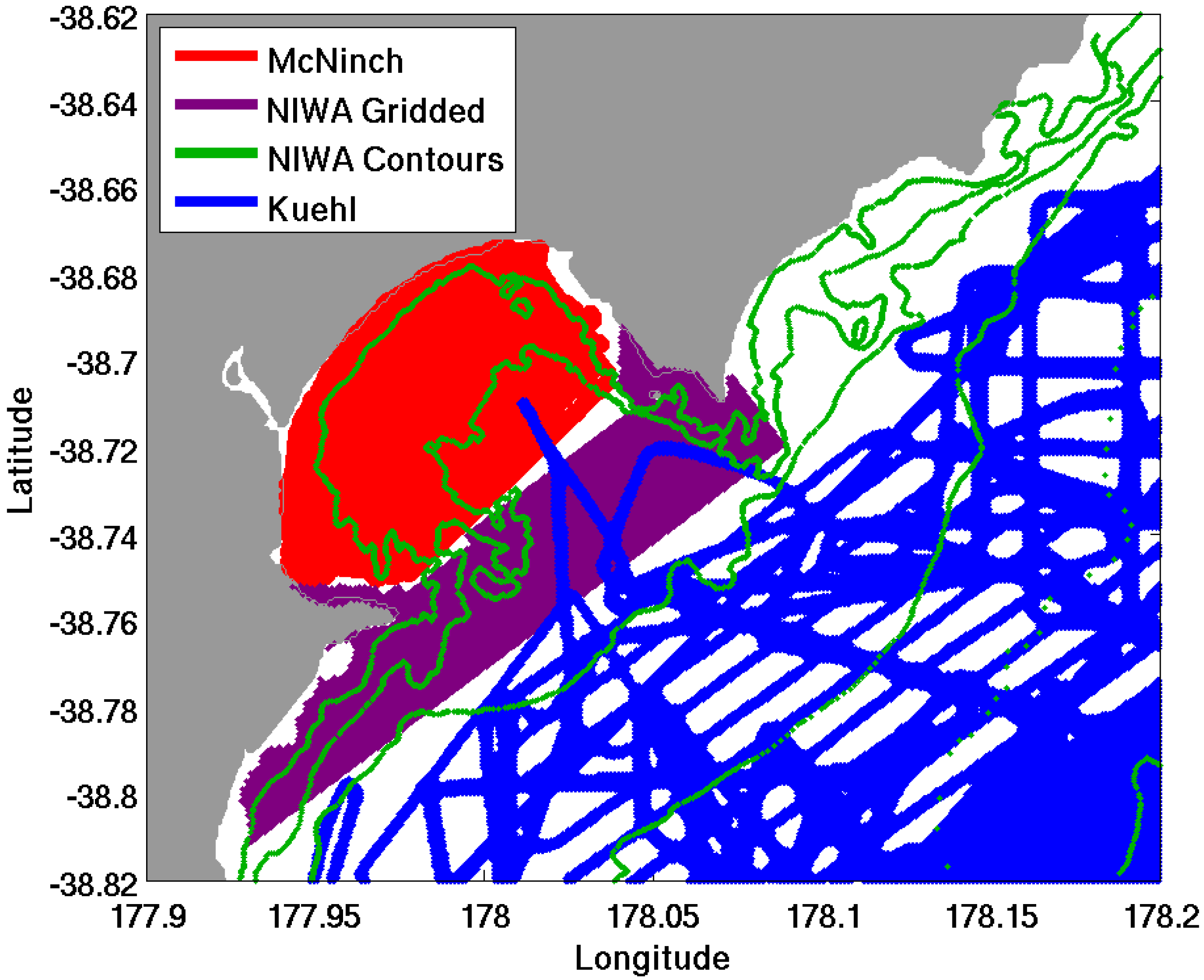
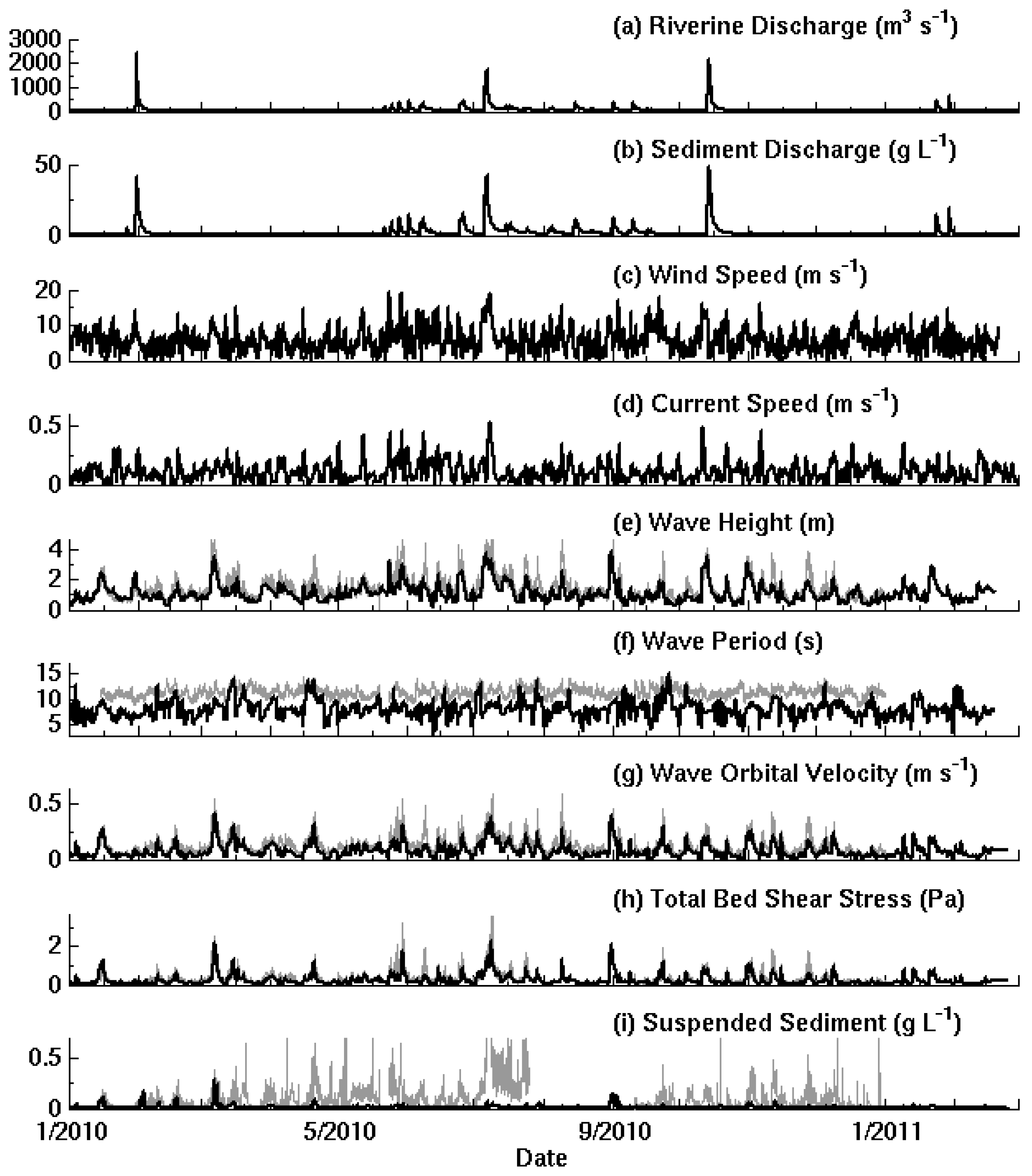
3.2. Atmospheric Forcing and Waves
3.3. River Discharge
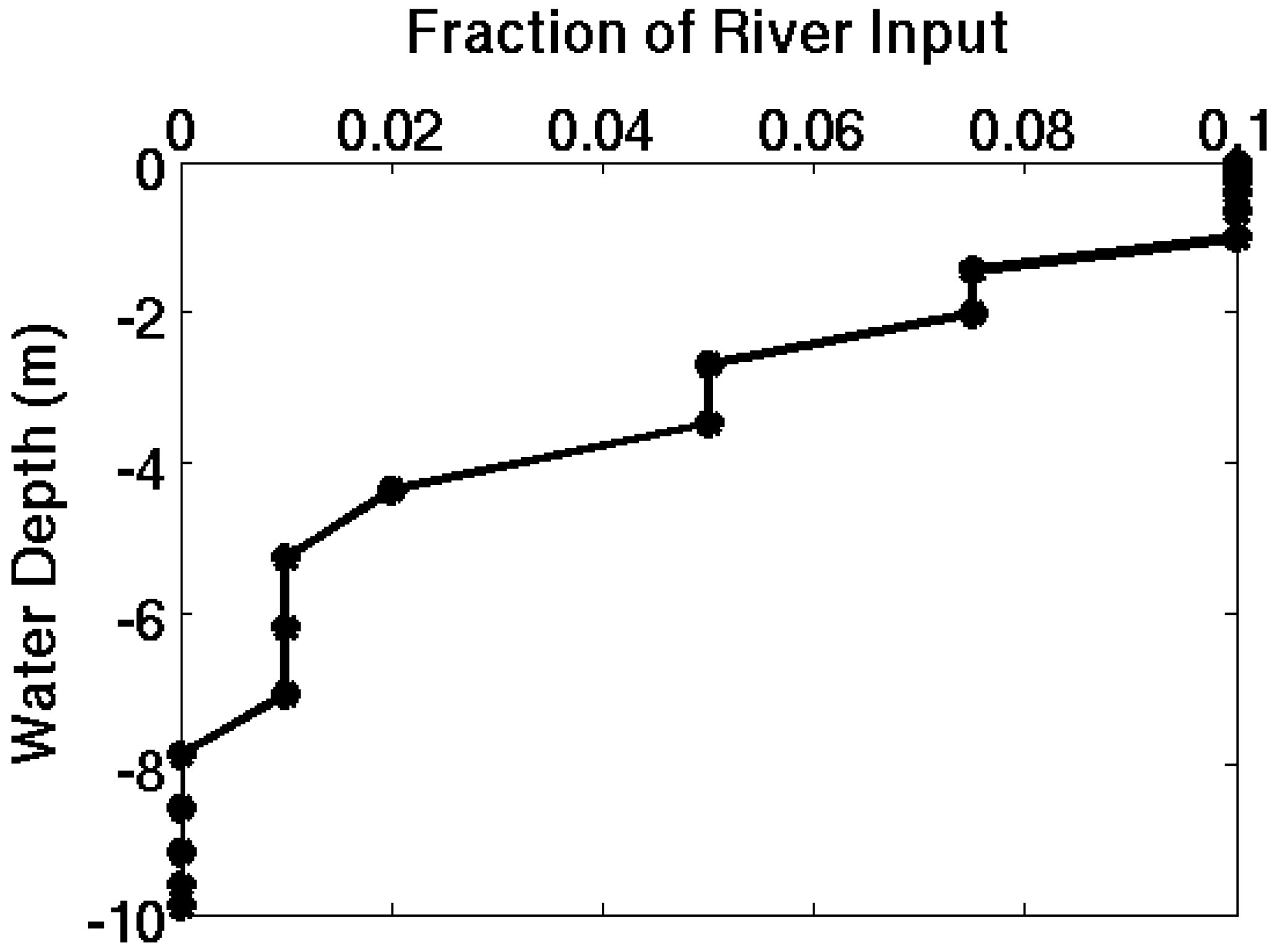
3.4. Tides
3.5. Baroclinic Currents, Temperature and Salinity
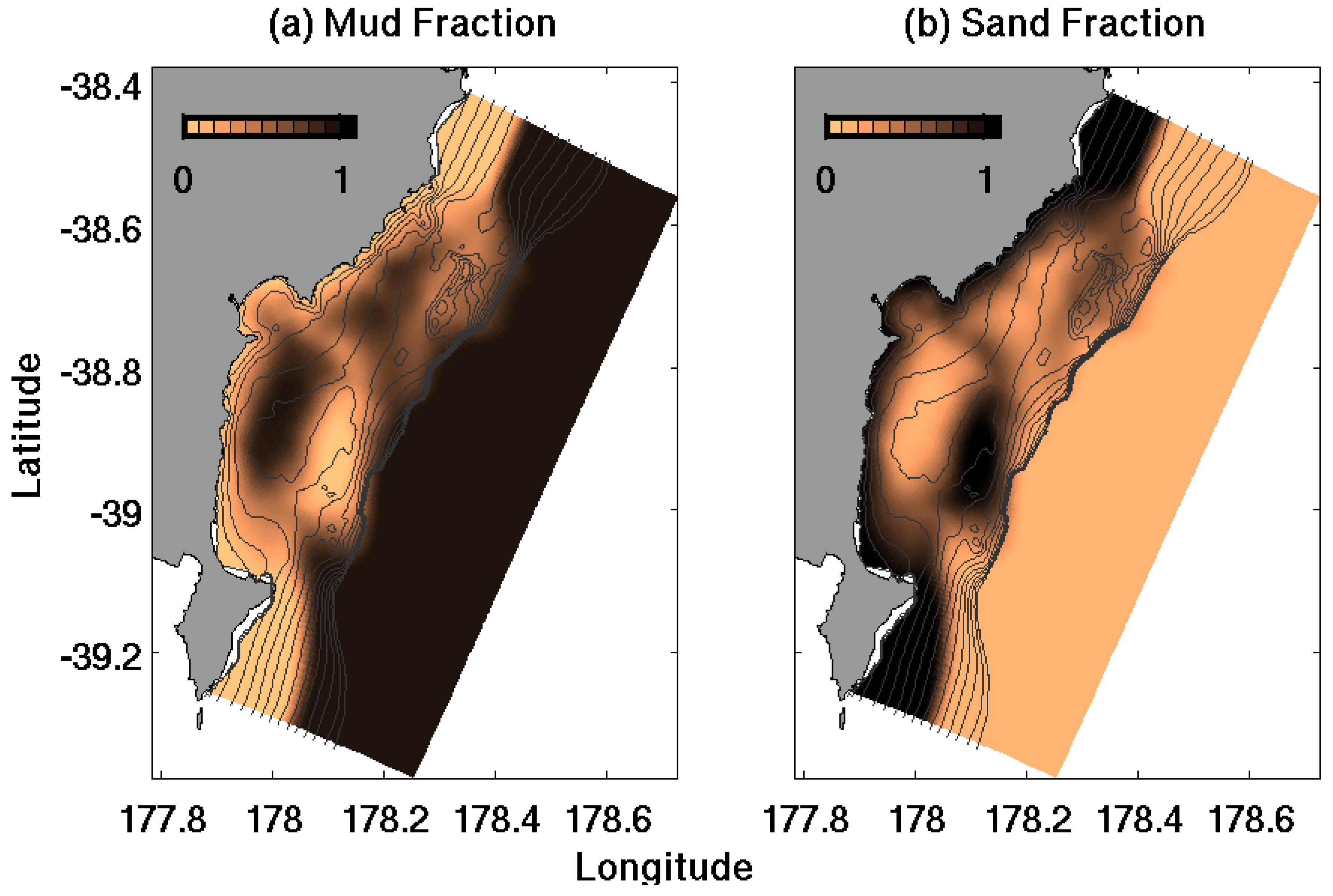
3.6. Sediment Characteristics
| Sediment Class | Source | % of Riverine Load | Settling Velocity (mm s−1) | D50(μm) |
|---|---|---|---|---|
| 1 | Seabed | − | 0.1 | 63 |
| 2 | Seabed | − | 0.5 | 500 |
| 3 | Seabed | − | 125.0 | 1000 |
| 4 | River | 53 | 0.15 | 16 |
| 5 | River | 27 | 0.3 | 22 |
| 6 | River | 13 | 0.5 | 30 |
| 7 | River | 7 | 1.0 | 40 |
3.7. Sensitivity Tests
4. Results and Discussion
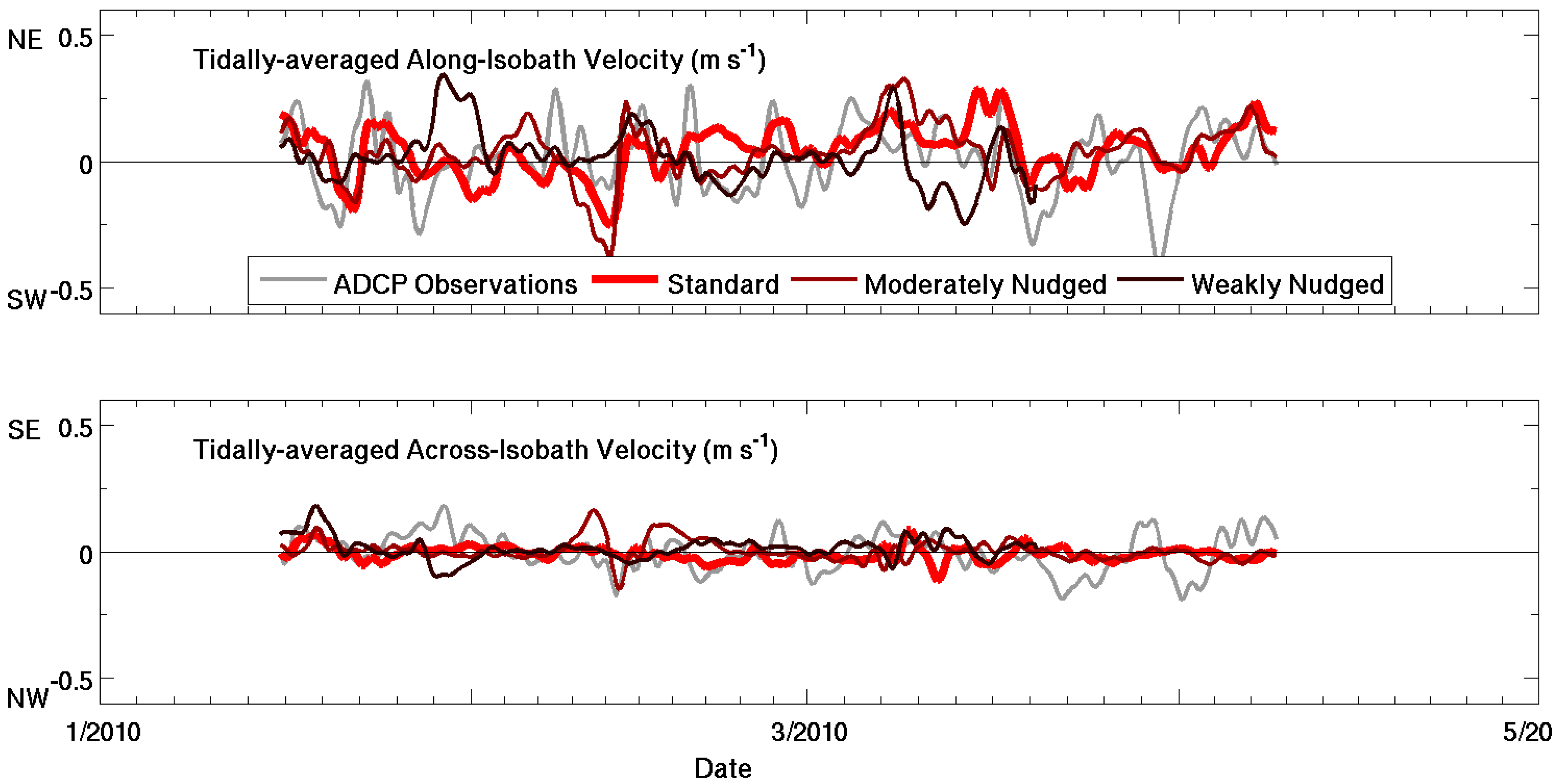
4.1. Model Evaluation

| (A) | ||||
| Parameter | R 1 | σmodel/σobservations 2 | Bias 3 | |
| Wave Orbital Velocity | 0.63–0.85 | 0.84–1.35 | −6.4–1.4 cm/s | |
| Bed Shear Stress | 0.60–0.82 | 0.72–1.79 | −0.20–0.02 Pa | |
| Depth-Averaged Currents (Along-Shelf) | 0.33–0.79 | 0.59–0.93 | −4.7–10.4 cm/s | |
| Depth-Averaged Currents (Across-Shelf) | 0.01–0.24 | 0.34–1.52 | −2.1–7.0 cm/s | |
| Suspended Sediment Concentrations | 0.27–0.52 | 0.03–0.28 | −0.22–0.01 g/L | |
| (B) | ||||
| Parameter | R 1 | σmodel/σobservations 2 | Bias 3 | |
| Depth-Averaged Currents (Along-Shelf) | Standard | 0.33–0.45 | 0.59–0.74 | 8.0–10.4 cm/s |
| Moderate Nudging | 0.40–0.41 | 0.47–0.79 | 1.2–10.0 cm/s | |
| Weak Nudging | 0.14–0.23 | 0.65–0.84 | −1.0–13.6 cm/s | |
| Depth-Averaged Currents (Across-Shelf) | Standard | 0.01–0.12 | 0.35–1.23 | −0.8–0.65 cm/s |
| Moderate Nudging | 0.02–0.07 | 0.44–1.25 | −0.64–1.0 cm/s | |
| Weak Nudging | 0.09–0.30 | 0.59–1.11 | −4.7–1.7 cm/s | |
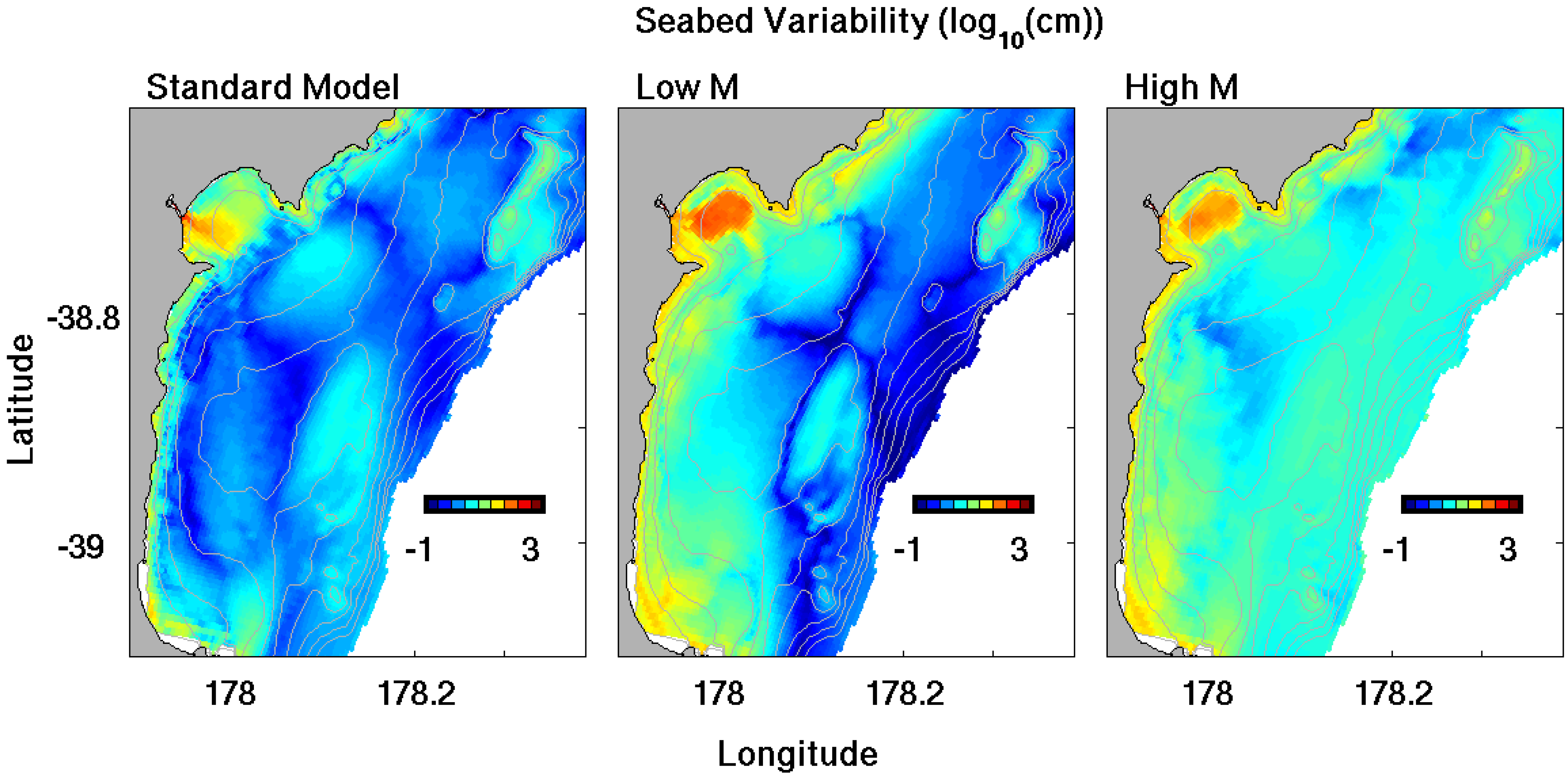

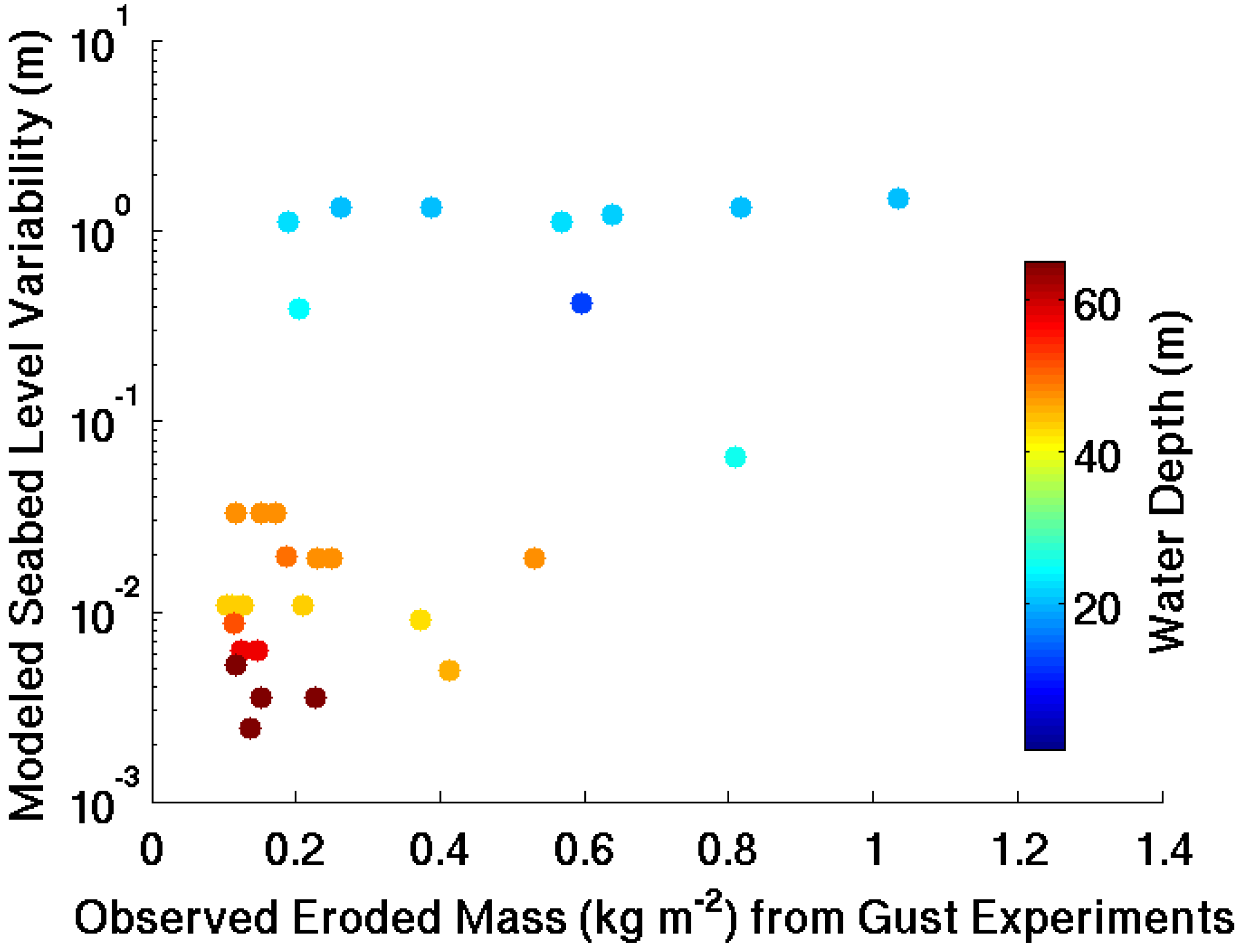
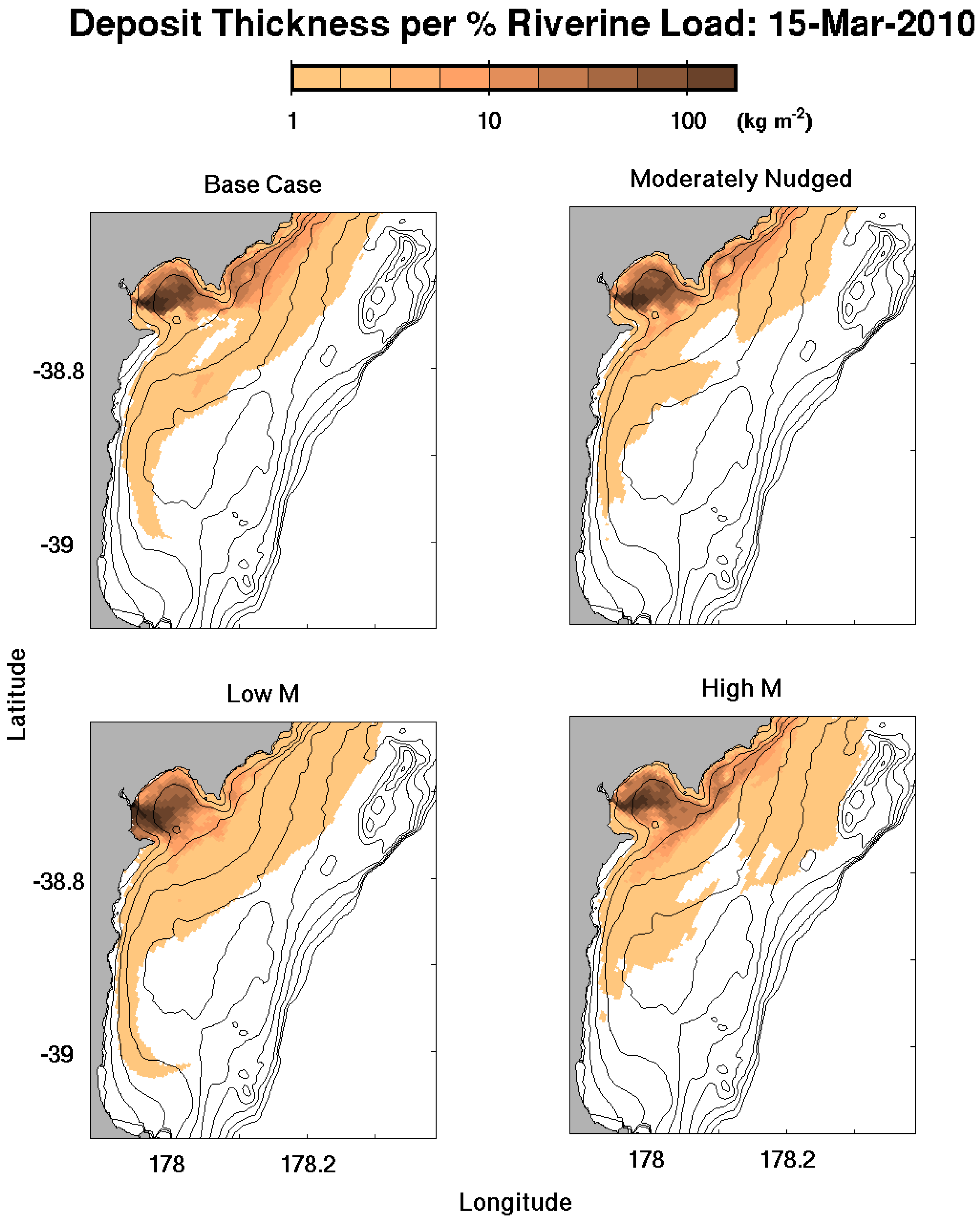
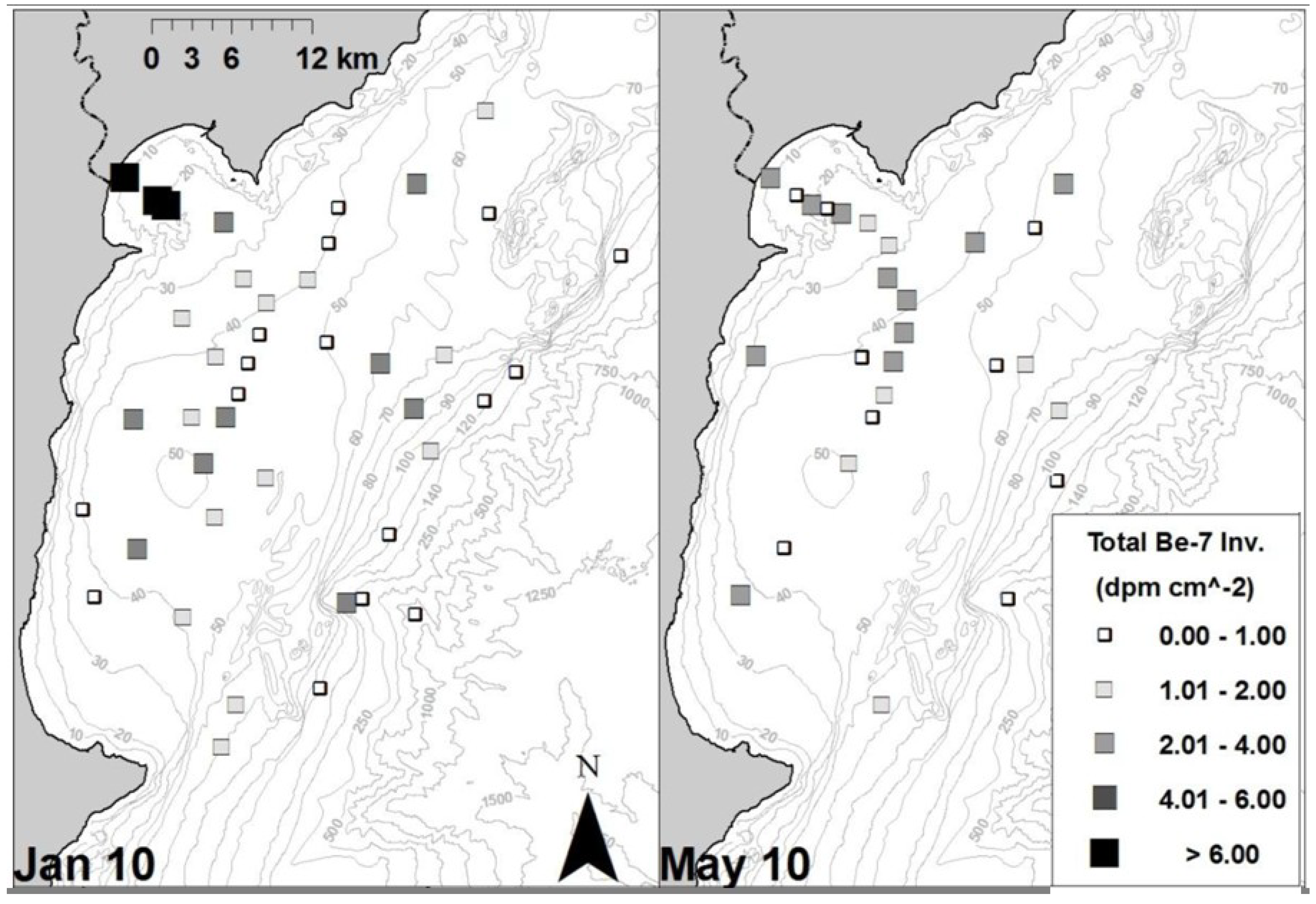
4.2. Model Nesting

 was the velocity perpendicular to an open boundary, S was salinity, and S0 was the background salinity of 35.1 psu. During the January 2010 river flood (28 January–15 February 2010), the cumulative freshwater flux through the open boundaries increased from 0.12 × 106 m3 to 0.23 × 106 m3 to 1.12 × 106 m3 when the nudging relaxation timescales, TR,i and TR0, decreased from 25 days to 5 days to 2.5 days. These fluxes of water were equivalent to about 1%, 2%, and 11% of the freshwater discharge into the grid. Note that the nudging of tracers from cells near the open boundary but within the grid (Equation (5)) removed freshwater from the grid, removing more freshwater for shorter relaxation timescales. Therefore, the estimates of freshwater flux through the boundaries represent low estimates which removed approximately double the volume of freshwater from the standard model compared to the weakly-nudged simulation.
was the velocity perpendicular to an open boundary, S was salinity, and S0 was the background salinity of 35.1 psu. During the January 2010 river flood (28 January–15 February 2010), the cumulative freshwater flux through the open boundaries increased from 0.12 × 106 m3 to 0.23 × 106 m3 to 1.12 × 106 m3 when the nudging relaxation timescales, TR,i and TR0, decreased from 25 days to 5 days to 2.5 days. These fluxes of water were equivalent to about 1%, 2%, and 11% of the freshwater discharge into the grid. Note that the nudging of tracers from cells near the open boundary but within the grid (Equation (5)) removed freshwater from the grid, removing more freshwater for shorter relaxation timescales. Therefore, the estimates of freshwater flux through the boundaries represent low estimates which removed approximately double the volume of freshwater from the standard model compared to the weakly-nudged simulation.4.3. Sediment Erodibility
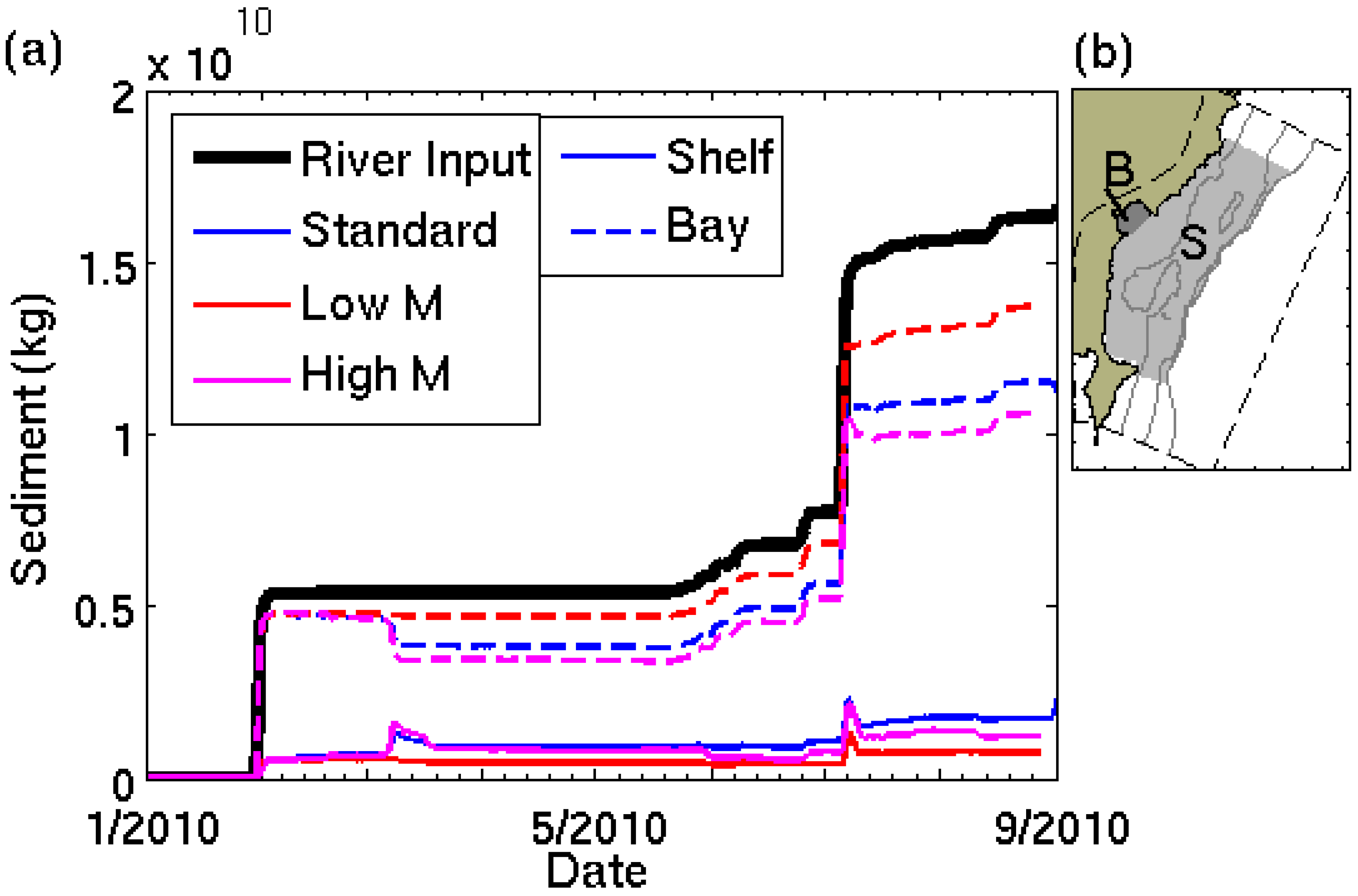
4.4. Computational Concerns
5. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Warner, J.C.; Sherwood, C.R.; Signell, R.P.; Harris, C.K.; Arango, H.G. Development of a three-dimensional, regional, coupled wave, current, and sediment-transport model. Comput. Geosci. 2008, 34, 1284–1306. [Google Scholar] [CrossRef]
- Haidvogel, D.B.; Arango, H.G.; Hedstrom, K.; Beckmann, A.; Malanotte-Rizzoli, P.; Shchepetkin, A.F. Model evaluation experiments in the North Atlantic Basin: simulations in nonlinear terrain-following coordinates. Dyn. Atmos. Ocean. 2000, 32, 239–281. [Google Scholar] [CrossRef]
- Haidvogel, D.B.; Arango, H.; Budgell, W.P.; Cornuelle, B.D.; Curchitser, E.; Di Lorenzo, E.; Fennel, K.; Geyer, W.R.; Hermann, A.J.; Lanerolle, L.; et al. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 2008, 227, 3595–3624. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The Regional Oceanic Modeling System (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. Correction and commentary for “Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the regional ocean modeling system” by Haidvogel et al., J. Comp. Phys. 227, pp. 3595–3624. J. Comput. Phys. 2009, 24, 8985–9000. [Google Scholar] [CrossRef]
- Bever, A.J.; Harris, C.K. Storm and fair-weather driven sediment-transport within Poverty Bay, New Zealand, evaluated using coupled numerical models. Cont. Shelf Res. 2013. in press.
- Ralston, D.K.; Geyer, W.R.; Traykovski, P.A.; Nidzieko, N.J. Effects of estuarine and fluvial processes on sediment transport over deltaic tidal flats. Cont. Shelf Res. 2013, 60, S40–S57. [Google Scholar] [CrossRef]
- Xu, K.; Harris, C.K.; Hetland, R.D.; Kaihatu, J.M. Dispersal of Mississippi and Atchafalaya sediment on the Texas–Louisiana shelf: Model estimates for the year 1993. Cont. Shelf Res. 2011, 31, 1558–1575. [Google Scholar] [CrossRef]
- Ganju, N.K.; Schoellhamer, D.H. Decadal-timescale estuarine geomorphic change under future scenarios of climate and sediment supply. Estuar. Coasts 2010, 33, 15–29. [Google Scholar] [CrossRef]
- Chen, S.; Sanford, L.P.; Ralston, D.K. Lateral circulation and sediment transport driven by axial winds in an idealized, partially mixed estuary. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Chapman, D.C. Numerical treatment of cross-shelf open boundaries in a barotropic coastal ocean model. J. Phys. Oceanogr. 1985, 15, 1060–1075. [Google Scholar] [CrossRef]
- Flather, R.; Proctor, R. Prediction of North Sea storm surges using numerical models: Recent developments in UK. In North Sea Dynamics; Sündermann, J., Lenz, W., Eds.; Springer: New York, NY, USA, 1983; pp. 299–317. [Google Scholar]
- Marchesiello, P.; McWilliams, J.C.; Shchepetkin, A. Open boundary conditions for long-term integration of regional oceanic models. Ocean Model. 2001, 3, 1–20. [Google Scholar] [CrossRef]
- Blaas, M.; Dong, C.; Marchesiello, P.; McWilliams, J.C.; Stolzenbach, K.D. Sediment-transport modeling on Southern Californian shelves: A ROMS case study. Cont. Shelf Res. 2007, 27, 832–853. [Google Scholar] [CrossRef]
- Xue, Z. Modeling transport and deposition of the Mekong River sediment. Cont. Shelf Res. 2012, 37, 66–78. [Google Scholar] [CrossRef]
- Dickhudt, P.J.; Friedrichs, C.T.; Schaffner, L.C.; Sanford, L.P. Spatial and temporal variation in cohesive sediment erodibility in the York River estuary, eastern USA: A biologically influenced equilibrium modified by seasonal deposition. Mar. Geol. 2009, 267, 128–140. [Google Scholar] [CrossRef]
- Sanford, L.P.; Maa, J.P. A unified erosion formulation for fine sediments. Mar. Geol. 2001, 179, 9–23. [Google Scholar] [CrossRef]
- Sanford, L.P. Modeling a dynamically varying mixed sediment bed with erosion, deposition, bioturbation, consolidation, and armoring. Comput. Geosci. 2008, 34, 1263–1283. [Google Scholar] [CrossRef]
- Amos, C.; Feeney, T.; Sutherland, T.; Luternauer, J. The stability of fine-grained sediments from the Fraser River Delta. Estuar. Coast. Shelf Sci. 1997, 45, 507–524. [Google Scholar] [CrossRef]
- Wright, L.D. Sediment transport and deposition at river mouths: A synthesis. Geol. Soc. Am. Bull. 1977, 88, 857–868. [Google Scholar] [CrossRef]
- Stevens, A.; Wheatcroft, R.; Wiberg, P. Seabed properties and sediment erodibility along the western Adriatic margin, Italy. Cont. Shelf Res. 2007, 27, 400–416. [Google Scholar] [CrossRef]
- Rinehimer, J.P.; HARRIS, C.K.; Sherwood, C.R.; Sanford, L.P. Estimating cohesive sediment erosion and consolidation in a muddy, tidally-dominated environment: Model behavior and sensitivity. In Proceedings of the 10th International Estuarine and Coastal Modeling Conference, Newport, RI, USA, 5–7 November 2007; Spaulding, M.L., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 819–838. [Google Scholar]
- Orpin, A.R.; Alexander, C.R.; Carter, L.; Kuehl, S.; Walsh, J.P. Temporal and spatial complexity in post-glacial sedimentation on the tectonically active, Poverty Bay continental margin of New Zealand. Cont. Shelf Res. 2006, 26, 2205–2224. [Google Scholar] [CrossRef]
- Hicks, D.M.; Gomez, B.; Trustrum, N.A. Erosion thresholds and suspended sediment yields, Waipaoa River Basin, New Zealand. Water Resour. Res. 2000, 36, 1129–1142. [Google Scholar] [CrossRef]
- Hicks, D.M.; Gomez, B.; Trustrum, N.A. Event suspended sediment characteristics and the generation of hyperpycnal plumes at river mouths: East Coast continental margin, North Island, New Zealand. J. Geol. 2004, 112, 471–485. [Google Scholar] [CrossRef]
- Stephens, S.A.; Bell, R.G.; Black, K.P. Complex circulation in a coastal embayment: Shelf-current, wind and density-driven circulation in Poverty Bay, New Zealand. J. Coast. Res. 2001, 17((Special issue 34)), 45–59. [Google Scholar]
- Healy, T.; Stephens, S.; Black, K.; Gorman, R.; Beamsley, B. Numerical and physical process studies for Port of Gisborne redesign for the 21st century. J. Coast. Res. 1998, 15((Special issue 26)), 304–311. [Google Scholar]
- Bever, A.J.; McNinch, J.E.; Harris, C.K. Hydrodynamics and sediment-transport in the nearshore of Poverty Bay, New Zealand: Observations of nearshore sediment segregation and oceanic storms. Cont. Shelf Res. 2011, 31, 507–526. [Google Scholar] [CrossRef]
- Ogston, A.; Hale, R.; University of Washington, Seattle, WA, USA. Unpublished data from Waipaoa shelf tripod deployments. 2013.
- Hale, R.; Ogston, A.S.; Walsh, J.P.; Orpin, A.R. Sediment transport and event deposition on the Waipaoa River Shelf, New Zealand. Cont. Shelf Res. 2014, in press. [Google Scholar]
- Chiswell, S.M. The Wairarapa Coastal Current. N. Z. J. Mar. Freshw. Res. 2000, 34, 303–315. [Google Scholar] [CrossRef]
- Chiswell, S.M.; Roemmich, D. The East Cape Current and two eddies: A mechanism for larval retention? N. Z. J. Mar. Freshw. Res. 1998, 32, 385–397. [Google Scholar] [CrossRef]
- Chiswell, S.M. Mean and variability in the Wairarapa and Hikurangi Eddies, New Zealand. N. Z. J. Mar. Freshw. Res. 2005, 39, 121–134. [Google Scholar] [CrossRef]
- Smith, R.K. Poverty Bay, New Zealand: A case of coastal accretion 1886–1975. N. Z. J. Mar. Freshw. Res. 1988, 22, 135–142. [Google Scholar] [CrossRef]
- Moriarty, J.M. Event-to-Seasonal Sediment Dispersal on the Waipaoa River Shelf, New Zealand: A Numerical Modeling Study. In Transport and Fate of Sediment on the Waipaoa River Continental Shelf: Implications for the Formation and Reworking of Flood Deposits; The Faculty of the School of Marine Science, the College of William and Mary in Virginia: Williamsburg, VA, USA, 2012. [Google Scholar]
- Kiker, J.M. Spatial and Temporal Variability in Surficial Seabed Character, Waipaoa River Margin, New Zealand. Master’s Thesis, East Carolina University, Greenville, NC, USA, 2012. [Google Scholar]
- Kniskern, T.A.; Mitra, S.; Orpin, A.R.; Harris, C.K. Characterization of flood deposition on the Waipaoa River shelf using radioisotopes and terrigenous organic matter abundance and composition. Cont. Shelf Res. 2014. submitted for publication. [Google Scholar]
- Miller, A.J.; Kuehl, S.A. Shelf sedimentation on a tectonically active margin: A modern sediment budget for Poverty continental shelf, New Zealand. Mar. Geol. 2010, 270, 175–187. [Google Scholar] [CrossRef]
- Gerber, T.P.; Pratson, L.F.; Kuehl, S.; Walsh, J.P.; Alexander, C.; Palmer, A. The influence of sea level and tectonics on Late Pleistocene through Holocene sediment storage along the high-sediment supply Waipaoa continental shelf. Mar. Geol. 2010, 270, 139–159. [Google Scholar] [CrossRef]
- Jackett, D.R.; McDougall, T.J. Minimal adjustment of hydrographic profiles to achieve static stability. J. Atmos. Ocean. Technol. 1995, 2, 381–389. [Google Scholar] [CrossRef]
- Haney, R. L. On the pressure gradient force over steep topography in sigma coordinate ocean models. J. Phys. Oceanogr. 1991, 21, 610–619. [Google Scholar] [CrossRef]
- Beckmann, A.; Haidvogel, D.B. Numerical simulation of flow around a tall isolated seamount. Part I: Formulation and model accuracy. J. Phys. Oceanogr. 1993, 23, 1736–1753. [Google Scholar] [CrossRef]
- Mellor, G.; Ezer, T.; Oey, L. The pressure gradient conundrum of sigma coordinate ocean models. J. Atmos. Ocean. Technol. 1994, 11, 1126–1134. [Google Scholar] [CrossRef]
- Mellor, G.; Oey, L.; Ezer, T. Sigma coordinate pressure gradient errors and the seamount problem. J. Atmos. Ocean. Technol. 1998, 15, 1122–1131. [Google Scholar] [CrossRef]
- Ezer, T.; Arango, H.; Shchepetkin, A.F. Developments in terrain-following ocean models: intercomparisons of numerical aspects. Ocean Model. 2002, 4, 249–267. [Google Scholar]
- Shchepetkin, A.F.; McWilliams, J.C. A method for computing horizontal pressure-gradient force in an oceanic model with a nonaligned vertical coordinate. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Huang, H.; Chen, C.; Cowles, G.W.; Winant, C.D.; Beardsley, R.C.; Hedstrom, K.S.; Haidvogel, D.B. FVCOM validation experiments: Comparisons with ROMS for three idealized barotropic test problems. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K.; Margolin, L.G. MPDATA: A finite-difference solver for geophysical flows. J. Comput Phys. 1998, 140, 459–480. [Google Scholar] [CrossRef]
- Hyatt, J.; Signell, R.P. Modeling Surface Trapped River Plumes: A sensitivity study. In Proceedings of the 6th International Estuarine and Coastal Modelling Conference, New Orleans, LA, USA, 3–5 November 1999; Spaulding, M.L., Blumberg, A.F., Eds.; American Society of Civil Engineers: Reston, VA, USA, 2000. [Google Scholar]
- Colella, P.; Woodward, P.R. The piecewise parabolic method (PPM) for gas-dynamical simulations. J. Comput. Phys. 1984, 54, 174–201. [Google Scholar] [CrossRef]
- Liu, X.; Osher, S.; Chan, T. Weighted essentially non-oscillatory schemes. J. Comput. Phys. 1994, 115, 200–212. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Rogers, D.P.; Edson, J.B.; Young, G.S. Bulk parameterization of air-sea fluxes for tropical ocean-global atmosphere coupled-ocean atmosphere response experiment. J. Geophys. Res. 1996, 101, 3747–3764. [Google Scholar] [CrossRef]
- Fairall, C.; Bradley, E.F.; Hare, J.; Grachev, A.; Edson, J. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Climate 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Madsen, O.S. Spectral Wave-Current Bottom Boundary Layer Flows. In Proceedings of the 24th International Conference on Coastal Engineering, Kobe, Japan, 23–28 October 1994; American Society of Civil Engineers: Reston, VA, USA, 1994; pp. 384–398. [Google Scholar]
- Syvitski, J.P.; Asprey, K.; Clattenburg, D.; Hodge, G.D. The prodelta environment of a fjord: Suspended particle dynamics. Sedimentology 1985, 32, 83–107. [Google Scholar] [CrossRef]
- Parchure, T.M.; Mehta, A.J. Erosion of soft cohesive sediment deposits. J. Hydraul. Eng. 1985, 111, 1308–1326. [Google Scholar] [CrossRef]
- Paterson, D.M. Biological Mediation of Sediment Erodibility: Ecology and Physical Dynamics. In Proceedings of the 4th Nearshore and Estuarine Cohesive Sediment Transport Conference, Wallingford, UK, 11–15 July 1994; Burt, N., Parker, R., Watts, J., Eds.; Wiley: Chichester, UK, 1997; pp. 215–229. [Google Scholar]
- Ariathurai, R.; Arulanandan, K. Erosion rates of cohesive soils. J. Hydraul. Div. 1978, 104, 279–283. [Google Scholar]
- Harris, C.K.; Wiberg, P.L. Approaches to quantifying long-term continental shelf sediment transport with an example from the Northern California STRESS mid-shelf site. Cont. Shelf Res. 1997, 17, 1389–1418. [Google Scholar] [CrossRef]
- Flather, R.A. A tidal model of the northwest European continental shelf. Mém. Soc. R. Sci. Liège 1976, 10, 141–164. [Google Scholar]
- Røed, L.P.; Smedstad, O.M. Open boundary conditions for forced waves in a rotating fluid. SIAM J. Sci. Stat. Comput. 1984, 5, 414–426. [Google Scholar] [CrossRef]
- Martinsen, E.A.; Engedahl, H. Implementation and testing of a lateral boundary scheme as an open boundary condition in a barotropic ocean model. Coast. Eng. 1987, 11, 603–627. [Google Scholar] [CrossRef]
- Palma, E.D.; Matano, R.P. On the implementation of passive open boundary conditions for a general circulation model: The barotropic mode. J. Geophys. Res. 1998, 103, 1319–1341. [Google Scholar] [CrossRef]
- Carter, G.S.; Merrifield, M.A. Open boundary conditions for regional tidal simulations. Ocean Model. 2007, 18, 194–209. [Google Scholar] [CrossRef]
- Hadfield, M.G.; National Institute of Water and Atmosphere, Wellington, New Zealand. Unpublished model results. 2012.
- Hadfield, M.G.; Rickard, G.J.; Uddstrom, M.J. A hydrodynamic model for Chatham Rise, New Zealand. N. Z. J. Mar. Freshw. Res. 2007, 41, 239–264. [Google Scholar] [CrossRef]
- Palma, E.D.; Matano, R.P. On the implementation of open boundary conditions for a general circulation model: The three-dimensional case. J. Geophys. Res. 2000, 105, 8605–8627. [Google Scholar] [CrossRef]
- Lavelle, J.; Thacker, W. A pretty good sponge: Dealing with open boundaries in limited-area ocean models. Ocean Model. 2008, 20, 270–292. [Google Scholar] [CrossRef]
- McNinch, J.E.; Wadman, H.M.; Perkey, D.W. Sediment segregation and dispersal across the land-sea interface: Waipaoa sedimentary system, New Zealand. In Proceedins of 2008 Ocean Sciences Meeting, Orlando, FL, USA, 2–7 March 2008; Integration and Synthesis of MARGINS Sediment Source-to-Sink Research Workshop: Gisborne, New Zealans, 2009. [Google Scholar]
- Stephens, S.; National Institute of Water and Atmosphere, Wellington, New Zealand. Personal Communication, 2006.
- National Institute of Water and Atmosphere, Viaduct Harbour, Auckland, New Zealand. Unpublished historical gridded bathymetry. 2006.
- Tolman, H.L.; Balasubramaniyan, B.; Burroughs, L.D.; Chalikov, D.V.; Chao, Y.Y.; Chen, H.S.; Gerald, V.M. Development and implementation of wind-generated ocean surface wave modelsat NCEP*. Weather Forecast. 2002, 17, 311–333. [Google Scholar] [CrossRef]
- Davies, T.; Cullen, M.; Malcolm, A.; Mawson, M.; Staniforth, A.; White, A.; Wood, N. A new dynamical core for the Met Office’s global and regional modelling of the atmosphere. Q. J. R. Meteorol. Soc. 2005, 131, 1759–1782. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Egbert, G.D.; Bennett, A.F.; Foreman, M.G. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- National Institute of Water and Atmosphere. National Climate Database Web System. Available online: http://cliflo.niwa.co.nz (accessed on 28 March 2011).
- Hall, G.; Peacock, D.; Gisborne District Council, Gisborne, New Zealand. Unpublished river observations. 2011.
- Wood, M.P. Sedimentation on a High Input Continental Shelf at the Active Hikurangi Margin. Master’s Thesis, Victoria University of Wellington, Wellington, New Zealand, 2006. [Google Scholar]
- Sikiric, M.D.; Janekovic, I.; Kuzmic, M. A new approach to bathymetry smoothing in sigma-coordinate ocean models. Ocean Model. 2009, 19, 128–136. [Google Scholar] [CrossRef]
- Wiberg, P.L.; Sherwood, C.R. Calculating wave-generated bottom orbital velocities from surface-wave parameters. Comput. Geosci. 2008, 34, 1243–1262. [Google Scholar] [CrossRef]
- Harris, C.K.; Traykovski, P.A.; Geyer, W.R. Flood dispersal and deposition by near-bed gravitational sediment flows and oceanographic transport: A numerical modeling study of the Eel River shelf, northern California. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Walsh, J.P.; East Carolina University, Greenville, NC, USA. Unpublished data from 2010 to 2011 Waipaoa shelf research cruises. 2011.
- Fall, K.A.; Harris, C.K.; Friedrichs, C.T.; Rinehimer, J.P.; Sherwood, C.R. Model behavior and sensitivity in an application of the cohesive bed component of the Community Sediment Transport Modeling System for the York River Estuary, VA. J. Mar. Sci. Eng. 2014. submitted for publication. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Moriarty, J.M.; Harris, C.K.; Hadfield, M.G. A Hydrodynamic and Sediment Transport Model for the Waipaoa Shelf, New Zealand: Sensitivity of Fluxes to Spatially-Varying Erodibility and Model Nesting. J. Mar. Sci. Eng. 2014, 2, 336-369. https://doi.org/10.3390/jmse2020336
Moriarty JM, Harris CK, Hadfield MG. A Hydrodynamic and Sediment Transport Model for the Waipaoa Shelf, New Zealand: Sensitivity of Fluxes to Spatially-Varying Erodibility and Model Nesting. Journal of Marine Science and Engineering. 2014; 2(2):336-369. https://doi.org/10.3390/jmse2020336
Chicago/Turabian StyleMoriarty, Julia M., Courtney K. Harris, and Mark G. Hadfield. 2014. "A Hydrodynamic and Sediment Transport Model for the Waipaoa Shelf, New Zealand: Sensitivity of Fluxes to Spatially-Varying Erodibility and Model Nesting" Journal of Marine Science and Engineering 2, no. 2: 336-369. https://doi.org/10.3390/jmse2020336
APA StyleMoriarty, J. M., Harris, C. K., & Hadfield, M. G. (2014). A Hydrodynamic and Sediment Transport Model for the Waipaoa Shelf, New Zealand: Sensitivity of Fluxes to Spatially-Varying Erodibility and Model Nesting. Journal of Marine Science and Engineering, 2(2), 336-369. https://doi.org/10.3390/jmse2020336





