1. Introduction
Hurricanes, earthquakes, industrial accidents, terrorist attacks and other such emergency situations pose great dangers to lives and property. Efficient evacuation during these events is one way to increase safety and avoid escalation of damages. The penalties incurred when Hurricane Katrina caught the nation off guard were severe. It is estimated that Hurricane Katrina displaced more than 1.5 million people and caused economic damages of $40–120 billion [
1]. Over the past decade, evacuation problems have been given a heightened attention and there are numerous studies available in the literature on evacuation strategies [
2,
3,
4,
5,
6,
7].
The evacuation problem has attracted significant scientific interest over the years, and mathematical models and approaches have been devised to solve it, based on network flow optimization techniques [
8]. The problem is formally stated as follows. Given a transportation network G(V,E), where each node (intersection) i ϵ V has a set demand d
i and each arc (road) has a capacity of u
ij, and a set of safe nodes S (destinations), find the optimal routes to safety. Optimality here can be defined in different ways: number of evacuees that reach safety, smallest overall time to safety, average time to safety. In this effort, we aim to maximize the number of people that are safely evacuated to one of the nodes in set S.
Maximizing the number of people that are safely evacuated to secure areas is often modeled as a quickest transshipment problem [
9]. Models for solving the problem were proposed in [
10], while a summary of recent results can be found in [
11]. In the context of evacuation, contraflow can be defined as the flow that traverses an arc in the reverse way. That is, if an arc (i,j) is reversed, then flow can travel from node j to node i. However, when we consider contraflow, the problem becomes NP-hard [
12], and as such it is inherently more difficult to solve. Hence, in large-scale, realistic transportation networks, the size of the problem renders exact approaches impractical, as significant computational time and power would be required. Decomposition schemes [
13] and heuristics are thus preferred for practical reasons.
A comprehensive survey was carried out to identify and evaluate the existing techniques for solving large-scale evacuation problems available in literature [
14]. Recognizing a reasonable level of insufficiencies in multimodal transportation, alternate evacuation routes in case of accidents and congestion, and heuristic exploration of difficult optimization problems, this survey helped explain the deficiencies in current techniques and also identified the features that significantly affect evacuation efficiency. At this moment, key approaches to solving evacuation problems (as defined previously) are optimization and simulation. In both cases, the factors that come into play are origin-destination assignments (
i.e., people that need to reach specific safe zones), arc capacities (static or dynamic, contraflow), and priorities (for sensitive groups of people or areas).
The type of optimization or simulation technique can also be used to classify the problem. The most widely used approach (and the approach adopted herein) is the maximum dynamic flow problem [
15]. Other approaches include, but are not limited to, the Dynamic Traffic Assignment Problem [
16], Macroscopic Simulation Techniques (NETVAC [
17] and MASSVAC [
18]), and techniques that utilize both optimization and simulation, as in the cell based formulation of [
19,
20]. For more information on these techniques, see [
20], where 22 evacuation models are compared.
Evacuation (and return) planning and disaster management are a vital necessity to the coastal areas of Florida where tropical storms are an ever present threat. In particular, to better understand how tropical storms impact evacuation patterns in coastal areas and to assist in coastal science, transportation, and cyberinfrastructure education, research and outreach, the Multimodal Transportation Educational Virtual Appliance (MTEVA), has been developed [
21]. The MTEVA is an application developed within the framework of the broader Coastal Science Educational Virtual Appliance (CSEVA).
The CSEVA [
22] is a unique, self-contained software environment designed to support interdisciplinary coastal science education and outreach activities, enabling active, hands-on numerical modeling experiments by researchers, stakeholders and the general public. Contained within the “virtualized” environment of the CSEVA, are the applications that cover a variety of coastal science topics. Integration of these applications into a single appliance enhances the user experience (less storage requirements, easier to install, linked application scenarios,
etc.) and provides a single collection of applications that can serve as practical and educational tools to scientists, educators and students, alike. In addition to the MTEVA, the CSEVA contains CI-TEAM [
23] and SCOOP [
24] applications as well as built-in and ready to use models and tools such as the atmospheric model WRF (Weather Research and Forecasting model) and a fully functional THREDDS Data Server (TDS) [
25]. The CI-TEAM application simulates the release of a tracer into the waters of the Indian River Lagoon estuarine system (Northeast Florida). While, the SCOOP application simulates storm surge and inundation in two different domains: a simple domain being impacted by a synthetic storm and Charlotte Harbor (southwest Florida) being impacted by various different wind forecasts for Hurricane Charley (2004).
The first generation MTEVA enabled users to perform and visualize simulations using an integrated storm surge and inundation model (CH3D-SSMS) and transportation evacuation/return modeling system that supports contraflow in a simple synthetic domain (order of tens of transportation nodes/arcs) under tropical storm conditions. In this study, the second generation MTEVA has been advanced to apply storm surge and evacuation models to the greater Jacksonville area of Northeast Florida (order tens of thousands of transportation nodes/arcs). To support solving the evacuation problem with the significantly larger transportation network, several new algorithms have been developed including a heuristic. After initial testing on several smaller stand-alone transportation networks (e.g., Anaheim, Winnipeg), the heuristic is shown to be near optimal network (average optimality gap <0.5%) for the Jacksonville transportation, while the wall clock time necessary to reach a solution decreased more than 90%, compared to the time needed to obtain a solution solving the optimization problem using an exact solver. The MTEVA’s new capability to simulate the transportation network response to a significantly larger network is demonstrated through the simulation of a Hurricane Katrina-sized storm impacting the region and studying how the evacuation patterns are affected by the closing of roads due to flooding and bridges due to high winds.
The paper is outlined as follows. First, we give a description of the Storm Surge and Inundation Modeling part within the MTEVA, and provide information on its main component, the CH3D-SSMS. Further, in
Section 3, we introduce notation and provide optimization models to describe the problem. We then describe three different methods to tackle the large-scale problem, and compare them in terms of solution quality and computational efficiency. In
Section 4, a demonstration application is presented in which a synthetic storm is bearing down on the Jacksonville area. Finally,
Section 5 summarizes the findings of this effort and aims to give further insight in future work and approaches on the field.
2. Storm Surge and Inundation Modeling within the MTEVA
The core of the MTEVA is a coupled storm surge and transportation network modeling system. These models, the optimization engine used to solve the network optimization problem, and all of the associated pre- and post-processing utilities are then packaged into the MTEVA. The main driver of the coupled modeling system is the storm surge modeling system, CH3D-SSMS (e.g., [
26]). It includes a high-resolution coastal surge model CH3D, developed by [
27,
28], which is coupled to a coastal wave model SWAN [
29] and large scale surge and wave models. Both models can receive open boundary conditions from a number of large-scale surge and wave models. Finally, a synthetic hurricane wind [
30] model is also incorporated into the system that provides wind and barometric pressure forcing in the domain. CH3D-SSMS is validated using many recent Atlantic Basin hurricanes (e.g., [
26]) and is used to produce a FIRM (Flood Insurance Rate Map) for Pinellas County, FL. CH3D-SSMS was also used to produce surge atlas which was compared with the SLOSH (the model used by the National Hurricane Center) surge atlas. Since 2004, CH3D-SSMS has been advanced to provide real-time forecast of hurricane wind, storm surge, wave, and coastal inundation for various parts of FL and Gulf coasts during hurricane seasons [
26,
31].
Also, given that the issue of sea level rise (SLR) has garnered attention recently, an option to simulate the effect of SLR is included. The SLR values chosen are: the 100-year projections derived from a continuation of the approximate local linear trend (+21 cm), the value in between of the nearby Mayport (2.40 mm/year) and Fernandina (2.02 mm/year) tide stations through 2006 [
32]; the value developed for the Intergovernmental Panel on Climate Change (IPCC) mid-range scenario A1B (+50 cm) [
33]; and an estimate near the upper SLR limits found for several IPCC scenarios in [
34] (+150 cm). Two algorithms for implementing the SLR physics on storm surge and inundation are included. In the first algorithm (“ad-hoc”), SLR is simply added onto the final simulated water level. In the second algorithm (“integrated”), SLR is added onto the water level boundary and initial conditions used in the model such that the model simulates the end effect of the SLR providing a much more realistic estimate of flooding due to SLR as it takes into consideration the hydrodynamics.
For a given storm surge and inundation simulation, CH3D-SSMS either sends the entire simulated response at the completion of the simulation or it sends the response periodically (e.g., once every 15 min of simulated time) including the current pattern of storm surge and inundation as well as the state (all roads passable, certain roads flooded, etc.) of the transportation network. The state of roads (arcs) and intersections (nodes) are based on inundation and wind conditions. Exceeding threshold inundation values will mark a road (arc or a node) as impassable and unavailable to be used in evacuation. The transportation network optimization model then reads in the state of the network along with a set of capacities, demands, etc. and determines the optimal traffic flow either using an exact solver or a heuristic approach.
During a simulation, potential nodes fall into several possible categories: (1) The node is connected to one or more other nodes via an arc; (2) The node is isolated and no longer has any connections (e.g., due to flooded roads), but may reconnect in the future; or (3) The node has been destroyed and will never again be connected to any other nodes (node becomes permanently flooded for the duration of the evacuation, so that for the remainder of the evacuation event it cannot be used). Nodes are considered destroyed if flooding exceeds some critical value, HNcr.
Each arc within the network is defined as either a “road” (considered indestructible) or a “bridge”. Roads are assumed at some height, RA, above (or below) the surrounding topography and become unusable if, during the course of a simulation, the water level at any location on the road exceeds some critical height, HAcr, above the road. If, at any point of time later the water level retreats, the road becomes usable again. Each bridge has its own elevation relative to the simulation vertical datum (e.g., NAVD88), BA. If, during the course of a simulation the water reaches the bridge, it is considered “destroyed” and permanently unusable. Additionally, regardless of water level, bridges are also assumed to be impassable during periods of high wind when the wind speed exceeds some critical value, WAcr. For practical purposes HNcr is set to 30 cm (about one foot of flooding) and WAcr to 45 mph. In reality these number can vary depending on location, but they are in line with actual values used by authorities. Critical values can be customized in the system, but not directly in the user interface.
Finally, for the optimization phase, we consider the transportation network as a graph G(V,E), where V is the set of nodes and E the set of roads. We further define two costs for the roads, namely cij and hij. The first represents the time/cost to use arc (i,j) ϵ E, while the latter the cost to reverse it, in order to allow the contraflow. It is easy to see that in order to reverse a road, some actions are necessary; police officers should be employed to control traffic, proper traffic signs should be used, etc. For simplicity, we treat every arc the same way, hence cij = hij = 1.
3. The Transportation Network Assignment (aka Evacuation) Model
Within the MTEVA, three algorithms are now available to solve the transportation network assignment (aka evacuation) problem: (1) Time Static—a fast algorithm that works with a single time instance attempting to move as many people as possible to safety (any node in the set S) and is then iterated for multiple time steps; (2) Time Dynamic—attempts a planned evacuation, however, adding the time dimension to the problem increases its size and thus takes significantly longer to solve; (3) Heuristic—a compromise between the computational time and problem complexity. Coupled to the surge model—the transportation model operates based on knowledge about flooding extents and dynamics. The mathematical models that arise within the time static, time dynamic heuristic, along with the model of the time dynamic version (exact) are all solved using the GNU Linear Programming Kit (GLPK) contained within the MTEVA.
3.1. Algorithms and Implementation
In this section, we first give the notation (
Table 1) and the necessary information we need, and then proceed to formulate the problem as a mixed-integer linear program. We also propose two heuristic approaches, and evaluate their efficiency in synthetic and real transportation networks. The two heuristic approaches can be summarized as: (1) Iteratively solve each discrete time step, updating each node’s demand and status (Time Static); (2) Heuristically solve the time dynamic version (NP-Hard) of the problem, after smartly selecting the arcs to be reversed (Time Dynamic Heuristic). Solving the NP-hard problem provides an optimal solution as to the routes that each vehicle needs to use, and the routes that need to be reversed in order to achieve maximum efficiency. On the other hand, both Time Static and Time Dynamic Heuristics provide approximate solutions that can be significantly faster to compute. The results show that the heuristics developed produce solutions within reasonable optimality gaps, and are significantly faster to compute.
Table 1.
Notation used to describe the transportation network, G(V, E), of a region and the mathematical model.
Table 1.
Notation used to describe the transportation network, G(V, E), of a region and the mathematical model.
| Sets |
| V | The set of all nodes (intersections) in the network. |
| E | The set of all arcs (roads) in the network |
| S | The set of nodes that are considered safe |
| Input Parameters |
| uij | The capacity of arc (i, j) ∈ E. For any two nodes (i, j) ∉ E, uij = 0. |
![Jmse 02 00287 i006]() | A binary input parameter that is equal to 0 if node i is destroyed at time t, or 1 otherwise. |
![Jmse 02 00287 i004]() | A binary input parameter that is equal to 0 if arc (i, j) is destroyed at time t, or 1 otherwise. |
| K | The budget of arcs that can be reversed during the evacuation process. |
| Variables to be Optimized |
![Jmse 02 00287 i008]() | The demand of node i ∈ V at time t ∈ T. ![Jmse 02 00287 i010]() is the initial demand of node i and is given. is the initial demand of node i and is given. |
![Jmse 02 00287 i001]() | The flow on arc (i, j) ∈ E at time t ∈ T. |
| yij | A binary variable that is equal to 1 if arc (i, j) ∈ E is reversed, or 0 otherwise. |
The first approach, Time Static [
21], involves the decomposition of the big, time dynamic, problem into smaller problems, each considered as one discrete time step. The final solution is essentially the collection of all partial solutions, obtained after each step. However, this approach is myopic as it does not consider future consequences. For example, evacuations are performed without any consideration of which areas are physically closer to being flooded and thus, need to be evacuated first.
On the other hand, the second approach (Time Dynamic Heuristic) considers future consequences, and selects routes and road reversals that are going to maximize the number of people that reach safety in the end, rather than at each time step. The heuristic uses model information to locate the arcs that seem to be bottlenecks for the evacuation process. This approach is based on the “shadow prices” of the capacity constraint set of the original problem. In mathematical programming, every linear program has its dual, which is typically used to extract information on the model and the solution. The capacity constraints state that the flow on any road at any time has to satisfy the capacity of the road
![Jmse 02 00287 i001]()
≤
uij without consideration of contraflow. The dual multiplier of this set of constraints represents the increase in the number of evacuees, if the capacity of the arcs were bigger. However, this assumes that the number of evacuees is much bigger (which might not be the case). Now, let
λij be the dual multipliers of the relaxed constraint. Selecting the
K arcs with the biggest
λij ∗
uji gives a greedy approach on the
K arcs that should be reversed.
After the arcs have been reversed, the remaining problem is a large-scale, time-dynamic evacuation problem that can be solved as a quickest transshipment problem [
9]. We, instead, dualize the capacity constraints, and augment them, based on an Augmented Lagrange duality iterative scheme.
The two heuristic approaches can be summarized as follows:
Time Static [
21]
- ○
Everyone evacuates simultaneously. Future events (congestion/flooding) not considered.
- ○
Decomposition into discrete, smaller problems, each considering only one time step.
Time Dynamic Heuristic (Present Study)
- ○
Evacuation is phased. Future events (congestion/flooding) are considered.
- ○
Relaxation involves the selection of the arcs to be reversed.
- ○
Locates the arcs that would benefit evacuation the most (if equal demand everywhere).
- ○
Resulting formulation of a dynamic network flow problem is solved using the Augmented Lagrange relaxation approach.
The formulation can be given as
max ∑t∈T ∑i∈N\S ∑j∈S ![Jmse 02 00287 i001]() | | (1) |
s.t. ![Jmse 02 00287 i002]() = = ![Jmse 02 00287 i008]() + ∑j∈N:(j,i)∈E + ∑j∈N:(j,i)∈E ![Jmse 02 00287 i003]() − ∑j∈N:(j,i)∈E − ∑j∈N:(j,i)∈E ![Jmse 02 00287 i001]() | ∀i ∈ V, ∀t ∈ T: ![Jmse 02 00287 i006]() = 1 = 1 | (2) |
![Jmse 02 00287 i001]() ≤ uij + yi j uj j ≤ uij + yi j uj j | ∀(i, j) ∈ E, ∀t ∈ T: ![Jmse 02 00287 i004]() = 1 = 1 | (3) |
| ∑(i, j)∈E yij ≤ K | | (4) |
![Jmse 02 00287 i001]() ≥ 0, ≥ 0, | ∀(i, j) ∈ E, ∀t ∈ T | (5) |
![Jmse 02 00287 i008]() ≥ 0, ≥ 0, | ∀i ∈ V, ∀t ∈ T | (6) |
| yi j ∈ {0,1}, | ∀(i, j) ∈ E | (7) |
The objective function in (1) ensures that the number of people exiting the “unsafe” areas of the network and entering a secure location (safe zone) is maximized. Constraint (2) is the time-dynamic counterpart of the well-known flow conservation constraint in network flow problems. Then, the capacity of the arcs is set in constraint (3). Observe that when an arc is reversed, its capacity is added to the one of the opposite direction. For simplicity, we assume that for a one-way road (i,j), there exists a reverse direction road (j,i) as well with a capacity of uij = 0. Equation (4) is a typical budget constraint that ensures no more than K arcs can be reversed. The reason for that limitation is logistical; reversing a road takes time and needs to be done carefully. Hence, it is realistic to assume a limit on that number. Last, constraints (5)–(7) define the restrictions on the variable values.
Observe that in an optimal solution, no road (i,j) can have positive values for the flows x
ij and x
ji. The proof, which is done by contradiction, can be found in Lemma 1 of [
13].
3.2. Computational Results
The key advantage of the heuristics developed herein are that they are computationally efficient. This is particularly important as events which lead to mass evacuations can be unpredictable. For example, Hurricane Charley (2004) was forecast to make landfall in Tampa Bay, FL. Within 24 h of making landfall, the storm made an abrupt turn to the right and residents of the Charlotte Harbor area (several hundred miles to the South of Tampa Bay) had little time to evacuate. In this section, we present the results of a computational study using the MTEVA to show how the heuristic performs on both synthetic and real transportation networks and show the heuristics feasibility for potential use in real-time evacuation planning. Three algorithms are compared: (1) the exact method (i.e., optimizing using GLPK); (2) the time static heuristic; and (3) the time dynamic heuristic. Findings are reported in terms of “optimality gaps” (difference between the estimated values calculated by the heuristic and the exact values) and the computational time required to reach a solution. In our approach, we measure the objective function by the number of evacuees that reached a safe node within the time horizon. Each algorithm is written in C++, and the numerical experiments were performed on a server with two AMD Opteron 6128 Eight-Core CPUs and 12 GB of RAM, running Linux x86_64, CentOS 5.9. Even though the server supports parallelization, at the moment the algorithms are not implemented in parallel.
The computational experiments were designed as follows. First, 5 synthetic networks of different sizes ranging from 20 to 10,000 nodes were created, where 5%–10% of the nodes were, at random, selected to serve as safe areas. Then, the three approaches (exact, time static, and heuristic) were tested, reporting their respective optimality gaps and computational time. In addition, real transportation networks from a set of well-known transportation network test problems (Anaheim, Austin, Philadelphia, Sioux Falls, and Winnipeg) [
35] were optimized. The safety nodes for the real networks were randomly selected and the optimization process was repeated 10 times for each network. On the other hand, for the Jacksonville transportation network, the set of safe nodes was known in advance, and hence, only one experiment was performed.
From the results of the numerical experiments, it can be seen that the optimality gap is small and the computational time was reduced significantly as compared to the exact solver. For example, for large network (10,000 nodes) simulations performed using synthetic transportation networks (
Table 2 and
Table 3), the time static heuristics is shown to decrease simulation time on average by 89% while providing a result on average within 8.11% of being optimal. For the more realistic time dynamic heuristic, simulation time is cut by 87% and optimality is within 1.99%. Similar results can be seen when simulating real transportation networks (
Table 4 and
Table 5).
Table 2.
Time Static Heuristic Statistics on Synthetic Networks.
Table 2.
Time Static Heuristic Statistics on Synthetic Networks.
| Network Size (nodes) | Average Optimality Gap (%) | Maximum Optimality Gap (%) | Average Time Decrease (%) | Maximum Time Decrease (%) |
|---|
| 20 | 0.28 | 1.27 | 81 | 89 |
| 100 | 0.41 | 3.89 | 85 | 92 |
| 500 | 0.80 | 8.02 | 87 | 93 |
| 1000 | 2.54 | 14.47 | 87 | 94 |
| 10,000 | 8.11 | 31.12 | 89 | 97 |
Table 3.
Time Dynamic Heuristic Statistics on Synthetic Networks.
Table 3.
Time Dynamic Heuristic Statistics on Synthetic Networks.
| Network Size (nodes) | Average Optimality Gap (%) | Maximum Optimality Gap (%) | Average Time Decrease (%) | Maximum Time Decrease (%) |
|---|
| 20 | 0.19 | 1.01 | 79 | 85 |
| 100 | 0.24 | 1.15 | 85 | 89 |
| 500 | 0.55 | 2.01 | 86 | 90 |
| 1000 | 1.54 | 3.60 | 87 | 90 |
| 10,000 | 1.99 | 4.41 | 87 | 91 |
Table 4.
Time Static Heuristic Statistics on Real Networks. |V| indicates the number of nodes.
Table 4.
Time Static Heuristic Statistics on Real Networks. |V| indicates the number of nodes.
| Network (nodes) | Average Optimality Gap (%) | Maximum Optimality Gap (%) | Average Time Decrease (%) | Maximum Time Decrease (%) |
|---|
Sioux Falls
(|V| = 24) | 0.00 | 0.00 | 75 | 90 |
Anaheim
(|V| = 416) | 1.08 | 1.17 | 85 | 90 |
Winnipeg
(|V| = 1057) | 3.02 | 3.66 | 86 | 92 |
Austin
(|V| = 7388) | 6.97 | 7.11 | 86 | 94 |
Philadelphia
(|V| = 13,389) | 14.90 | 20.00 | 90 | 97 |
Table 5.
Time Dynamic Heuristic Statistics on Real Networks. |V| indicates the number of nodes.
Table 5.
Time Dynamic Heuristic Statistics on Real Networks. |V| indicates the number of nodes.
| Network (nodes) | Average Optimality Gap (%) | Maximum Optimality Gap (%) | Average Time Decrease (%) | Maximum Time Decrease (%) |
|---|
Sioux Falls
(|V| = 24) | 0.00 | 0.00 | 72 | 86 |
Anaheim
(|V| = 416) | 0.00 | 0.00 | 76 | 88 |
Winnipeg
(|V| = 1057) | 0.00 | 0.00 | 76 | 88 |
Austin
(|V| = 7388) | 0.98 | 2.11 | 77 | 92 |
Philadelphia
(|V| = 13389) | 3.25 | 3.89 | 82 | 92 |
4. Demonstration Application to the NE Florida Coast
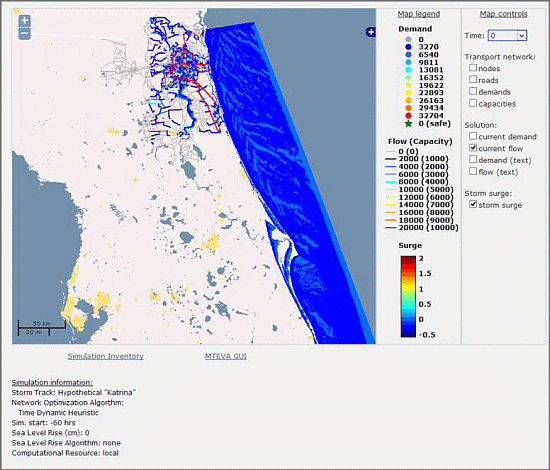
The MTEVA’s enhanced ability to simulate the evacuation patterns in significantly larger transportation networks (in a reasonable amount of time) using a heuristic are demonstrated through the simulation of a Hurricane Katrina-sized storm impacting the Northeast Florida coastal region and studying how the evacuation patterns are affected by the closing of roads due to flooding and bridges due to high winds. Results within the MTEVA are presented using high-level, standards-compliant, GUI-driven interfaces. Specifically, CH3D-SSMS output is written as NetCDF compliant with CF (climate forecasting) conventions, which enables the use of a TDS to provide access to data and simplify visualization. OpenLayers is then used to bring together the mapping of storm surge and transportation results. As part of the second generation MTEVA, the interactive interface is now developed using AJAX and PHP (
Figure 1 shows the simulation setup and
Figure 2 shows visualization of results as examples of the first generation interface).
Storm surge and inundation in the Northeast Florida region is simulated using a high resolution (100 m) CH3D-SSMS model for Northeast Florida (255 × 1201 cells), which domain spans from West Palm Beach to the Florida/Georgia border and extends ~40 km offshore. This model is then coupled with the transportation network that is based on the newest NERPM4 (NorthEast Regional Planning Model version 4, created for Northeast Florida (
Figure 3) “2005 base” MTEVA configuration. The network includes 28,585 nodes and 57,814 links. Demands at the nodes are obtained by combining different types of demands (various types of cars, public transportation,
etc.) data from the NERPM4 as the current network optimization model does not differentiate between different transportation modes.
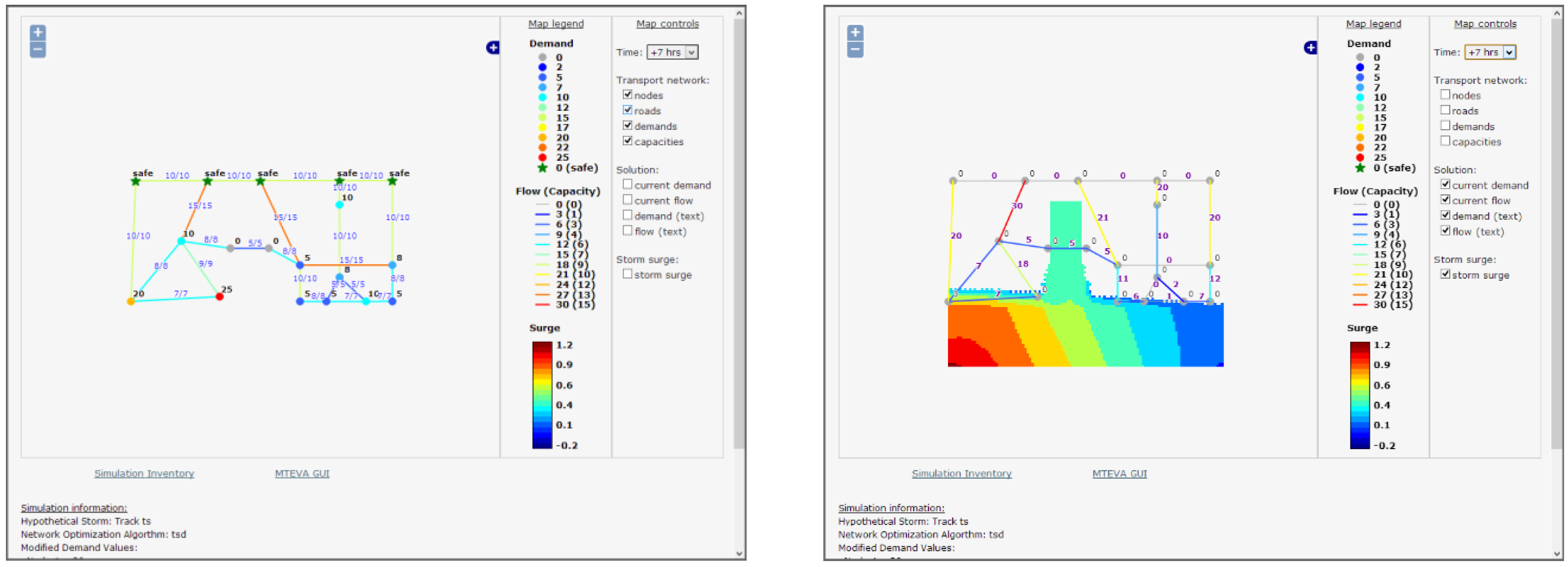
Figure 1.
User interface for the simple network MTEVA configuration featuring a synthetic tropical storm making landfall in an idealized domain with a bay.
Figure 1.
User interface for the simple network MTEVA configuration featuring a synthetic tropical storm making landfall in an idealized domain with a bay.
Figure 2.
Simulated transportation network response to the synthetic storm making landfall in an idealized domain. The initial configuration of the transportation network is shown on the left while the simulated network assignment and storm surge and inundation as the storm approaches is shown on the right.
Figure 2.
Simulated transportation network response to the synthetic storm making landfall in an idealized domain. The initial configuration of the transportation network is shown on the left while the simulated network assignment and storm surge and inundation as the storm approaches is shown on the right.
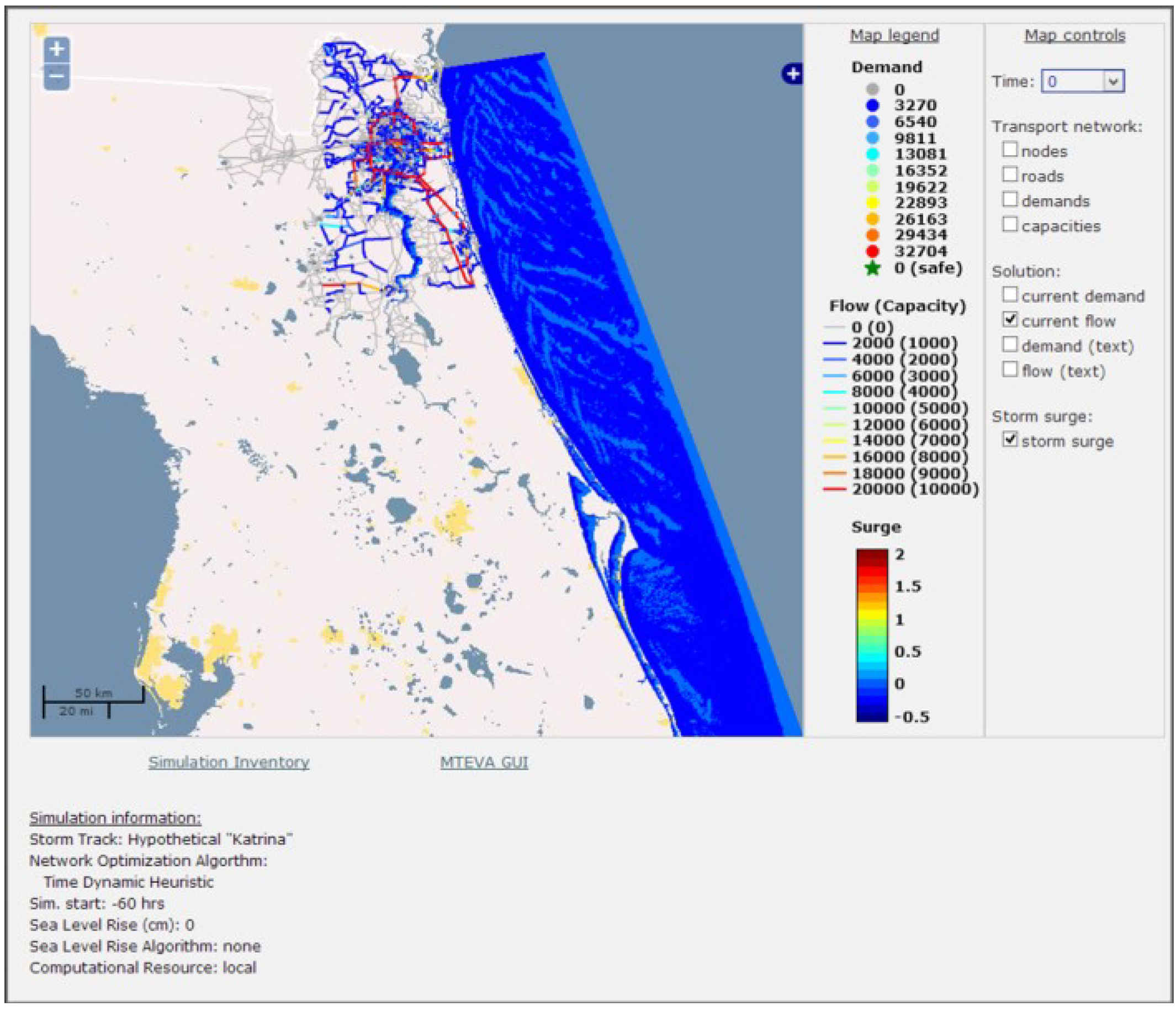
Figure 3.
NERPM4 road capacities (left) and demands (right).
Figure 3.
NERPM4 road capacities (left) and demands (right).
To assess the efficiency of the newly developed heuristic for the Northeast Florida transportation network, another set of computational experiments was performed (
Table 7). As with the experiments presented earlier, both the original and newly developed heuristics are shown to significantly improve the speed at which the evacuation problem can be solved.
Table 7.
Efficiency of the heuristics for the Northeast Florida network.
Table 7.
Efficiency of the heuristics for the Northeast Florida network.
| Heuristic | Average Optimality Gap (%) | Maximum Optimality Gap (%) | Average Time Decrease (%) | Maximum Time Decrease (%) |
|---|
| Static | 14.51 | 14.51 | 88 | 88 |
| Dynamic | 4.33 | 4.33 | 80 | 80 |
The simulation of several different Northeast Florida scenarios can be performed within the MTEVA based on a synthetic storm, similar in size to Hurricane Katrina, making landfall on the east coast of Florida in presence of varying amounts of SLR (
Figure 4). Inputs are provided through a simple interface which allows for variation of network assignment algorithm, amount of SLR, SLR algorithm,
etc. The atmospheric storm wind and pressure gradient forcing is supplied by an analytic wind model [
30] which uses a synthetic Katrina-like (size/intensity) storm track that makes landfall in the region. After completion, simulated storm surge and inundation are displayed in an interface (
Figure 5) which allows map navigation along with the ability to toggle display layers (surge and inundation, transportation network, background layers,
etc.). For reference, using relatively modern computational hardware, the evacuation model building and optimization phase, using a commercial solver, takes ~25 h to compute using the exact solver, due in part to the large-scale model and inherent difficulty of the problem.
The Northeast Florida MTEVA configuration provides an opportunity to study how timing of evacuation affects the ability to do it as well as how SLR may potentially impact evacuation plans. As a demonstration application under present day conditions (no SLR),
Figure 6 shows the use of evacuation routes at different times (5 and 2 h until landfall, respectively, with evacuation starting 48 h before landfall) and how traffic patterns change as a bridge closes due to high wind intensity and
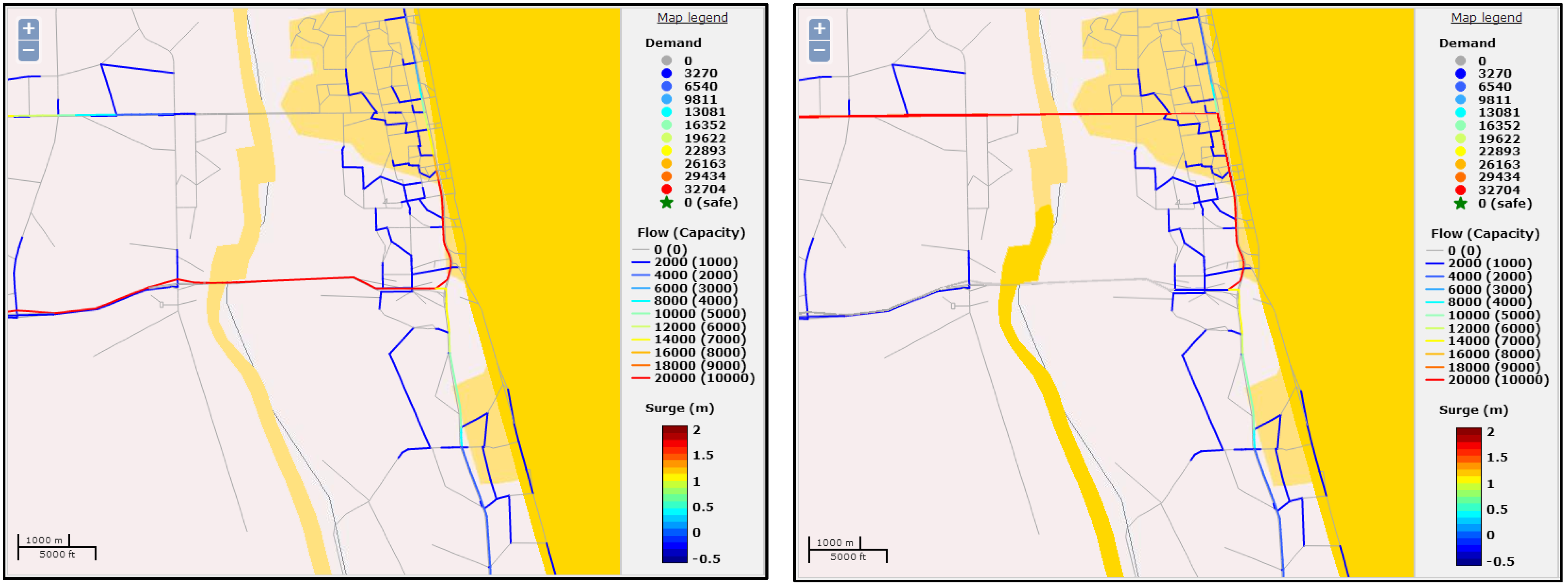
Figure 7 shows changes in local traffic routes due to flooding of roads (snapshots of traffic 3 and 2 h until landfall are shown).
Figure 4.
Interface for the Northeast Florida MTEVA configuration showing the track and intensity of the synthetic storm.
Figure 4.
Interface for the Northeast Florida MTEVA configuration showing the track and intensity of the synthetic storm.
Figure 5.
Visualization of model simulation results.
Figure 5.
Visualization of model simulation results.
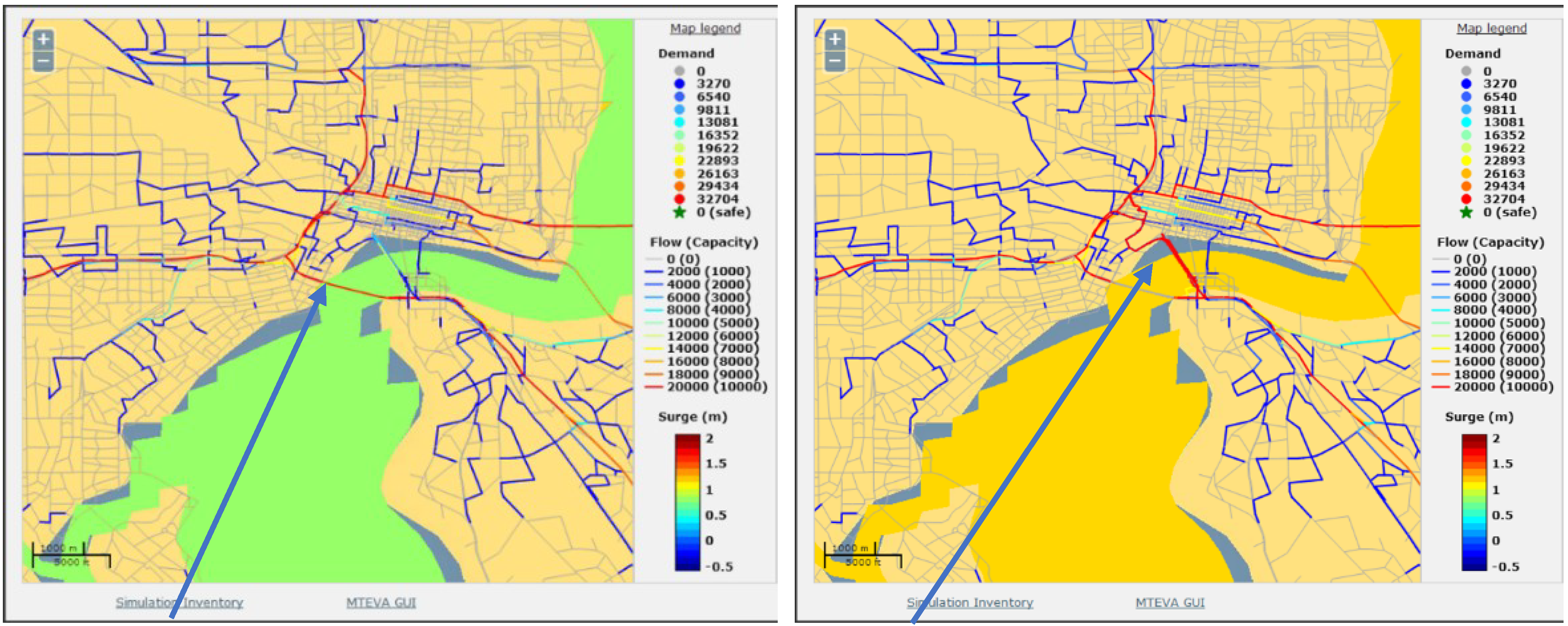
Figure 6.
Comparison of evacuation routes at different time instances three hours apart. In the second case the evacuees are forced to take Acosta Bridge (right) because of the inaccessibility of the Fuller Warren Bridge (which is otherwise the preferred route, left) due to high wind intensity.
Figure 6.
Comparison of evacuation routes at different time instances three hours apart. In the second case the evacuees are forced to take Acosta Bridge (right) because of the inaccessibility of the Fuller Warren Bridge (which is otherwise the preferred route, left) due to high wind intensity.
To determine the optimal time to begin an evacuation, a series of simulations were performed using different evacuation times.
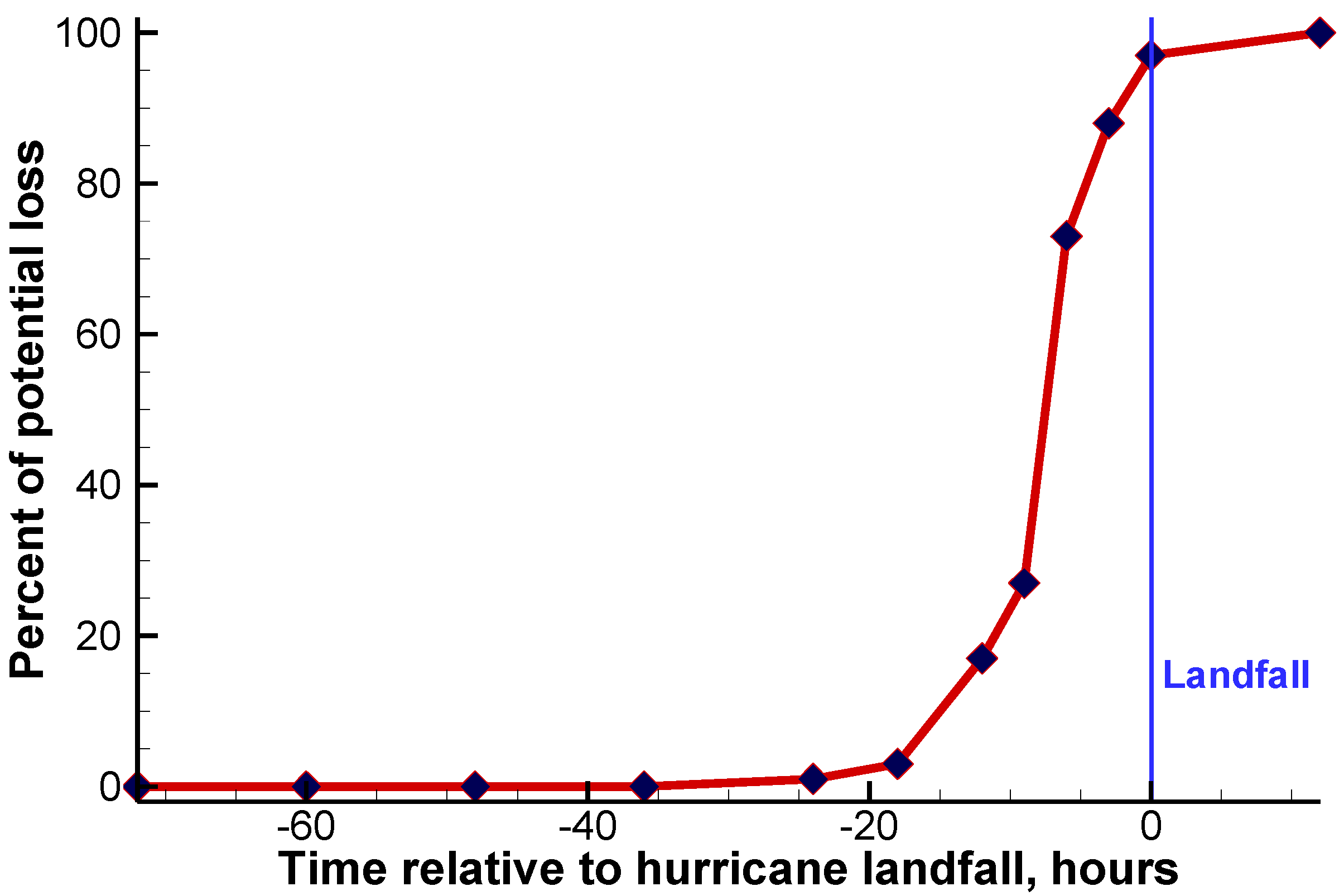
Figure 8 illustrates the number of people located in areas that flood that will not have enough time to evacuate as a function of evacuation start time. For the particular demonstration application presented, all evacuations that start at least 36 h prior to hurricane landfall are 100% successful in evacuating flooded areas. However, the number of people unable to escape increases dramatically if an evacuation has not begun at least 18 h prior to landfall with about 97% loss if evacuation starts at landfall. This is not surprising as areas near the coast that are the most prone to flooding are already cut off from the “safe” nodes of the transportation network.
Figure 7.
Raised water level alters local traffic patterns due to flooding of roads and intersections.
Figure 7.
Raised water level alters local traffic patterns due to flooding of roads and intersections.
Figure 8.
Estimated percentage of the number of people in flooded areas unable to evacuate (loss) as a function of evacuation start time.
Figure 8.
Estimated percentage of the number of people in flooded areas unable to evacuate (loss) as a function of evacuation start time.
5. Summary and Conclusions
Enhancements to a unique, self-contained, software environment, the MTEVA, have been presented. The MTEVA seeks to assist in coastal science, transportation and cyberinfrastructure research, education and outreach by creating a coupled modeling system capable of simulating the transportation network response in synthetic and real physical domains to a system subject to high winds, storm surge, and inundation. The MTEVA allows individual science components to be brought together in a simple-to-use infrastructure where users can focus on learning the science instead of trying to setup and perform simulations.
While there are countless possible uses of the MTEVA, three will be highlighted. First, the MTEVA would be well suited for use by planners and organizers of emergency preparedness exercises who need to develop (in an easy-to-use fashion) realistic scenarios of conditions and transportation network conditions before (evacuation), during, and after (return) a storm. Second, the MTEVA is now, thanks to the inclusion of a heuristic, well suited towards “real-time” use in an Emergency Operations Center (EOC) (i.e., after evacuation has occurred) to assist first responders in predicting specific transportation infrastructure which may be impassable. Finally, the MTEVA is ideally suited for deployment in educational environments where students of all skill levels can learn, through hands-on activities, about: storm surge and inundation, transportation engineering and optimization.
In summary, the MTEVA:
contains a storm surge and inundation modeling system coupled with a transportation network optimization model capable of simulating lane reversal. The coupled modeling system is then applied to both synthetic and real domains.
demonstrates and promotes interoperability through its use of a THREDDS Data Server (TDS) for distribution and visualization of results. At the most basic level, users can access the MTEVA through the web-based GUI. However, more advanced users are able to setup and perform simulations using the scheduling interfaces directly (e.g., using the “condor_submit” command).
is completely configurable, customizable and expandable. Because the tools, scripts, web interfaces, etc. are located within the MTEVA; any individual component can be altered to meet an individual user’s needs. For example, locations of nodes modified, additional network nodes/arcs can be added, or demands and capacities changed.
provides an educational environment useful for students of coastal science, cyberinfrastructure, and transportation engineering. For example, coastal science students can better understand how storm surge impacts a domain given storm strength, domain shape, etc. Cyberinfrastructure students can focus on the technical details of the MTEVA itself along with its web interfaces, databases and scripting technologies used behind the scenes. Transportation engineering students could investigate how the use of lane reversal can be optimized during a storm event. Finally, transportation practitioners in Northeast Florida could use the MTEVA to investigate how their domain responds to different synthetic tropical storms.
As part of this study, the MTEVA has been enhanced to includes three algorithms for solving the transportation network optimization problem for evacuation: (1) Time Static—a fast algorithm that works with a single time instance attempting to move as many people of possible to safety and is then iterated for multiple time steps; (2) Time Dynamic—attempts a planned evacuation, however, adding the time dimension to the problem increases its size and thus takes significantly longer to solve; (3) Heuristic—a compromise between the computational time and problem complexity.
The heuristic was shown to be able to successfully simulate large scale transportation networks with only a small optimality gap but a large decrease in computational time. For example, when using the realistic time dynamic heuristic, simulation time is cut by 87% (~3 h to obtain a heuristic solution, compared to ~25 h to solve the problem exactly) and optimality is within 1.99%, making the heuristic highly suitable for simulation of the large Northeast Florida MTEVA configuration (also implemented as part of this study) which is based on the NERPM transportation network.
Finally, a demonstration application was presented which illustrates how the MTEVA can be used to better understand how storm surge and inundation impacts key evacuation travel routes and leads to an increase in non-recurrent congestion. Through better understanding of such impacts, emergency managers and planners can better optimize evacuation/return routes increasing coastal resiliency.



 is the initial demand of node i and is given.
is the initial demand of node i and is given.
 ≤ uij without consideration of contraflow. The dual multiplier of this set of constraints represents the increase in the number of evacuees, if the capacity of the arcs were bigger. However, this assumes that the number of evacuees is much bigger (which might not be the case). Now, let λij be the dual multipliers of the relaxed constraint. Selecting the K arcs with the biggest λij ∗ uji gives a greedy approach on the K arcs that should be reversed.
≤ uij without consideration of contraflow. The dual multiplier of this set of constraints represents the increase in the number of evacuees, if the capacity of the arcs were bigger. However, this assumes that the number of evacuees is much bigger (which might not be the case). Now, let λij be the dual multipliers of the relaxed constraint. Selecting the K arcs with the biggest λij ∗ uji gives a greedy approach on the K arcs that should be reversed.
 =
=  + ∑j∈N:(j,i)∈E
+ ∑j∈N:(j,i)∈E  − ∑j∈N:(j,i)∈E
− ∑j∈N:(j,i)∈E 
 = 1
= 1 ≤ uij + yi j uj j
≤ uij + yi j uj j = 1
= 1 ≥ 0,
≥ 0, ≥ 0,
≥ 0,