Comparative Analysis of Machine Learning and Multi-View Learning for Predicting Peak Penetration Resistance of Spudcans: A Study Using Centrifuge Test Data

Abstract

Punch-through accidents pose a significant risk during the positioning of jack-up rigs. To mitigate this hazard, accurate prediction of the peak penetration resistance of spudcan foundations is essential for developing safe operational plans. Advances in artificial intelligence have spurred the widespread application of machine learning (ML) to geotechnical engineering. To evaluate the prediction effect of different algorithm frameworks on the peak resistance of spudcans, this study evaluates the feasibility of ML and multi-view learning (MVL) methods using existing centrifuge test data. Six ML models—Random Forest, Support Vector Machine (with Gauss, second-degree, and third-degree polynomial kernels), Multiple Linear Regression, and Neural Networks—alongside a Ridge Regression-based MVL method are employed. The performance of these models is rigorously assessed through training and testing across various working conditions. The results indicate that well-trained ML and MVL models achieve accurate predictions for both sand-over-clay and three-layer clay strata. For the sand-over-clay stratum, the mean relative error (MRE) across the 58-case dataset is approximately 15%. The Neural Network and MVL method demonstrate the highest accuracy. This study provides a viable and effective empirical solution for predicting spudcan peak resistance and offers practical guidance for algorithm selection in different stratigraphic conditions, ultimately supporting enhanced safety planning for jack-up rig operations.

1. Introduction

The jack-up rigs are widely used in offshore engineering, deployed for oil and gas exploration, geotechnical investigations, and installation of wind turbines. A standard rig comprises a hull, supporting legs, and spudcan foundations affixed to the base of each leg. Although the positioning of jack-up rigs is a routine operation, it entails significant geotechnical risks, particularly during spudcan penetration through multiple-layer soil, for example, punch-through events [1,2] in stratified stiff-over-soft soil layers. Such incidents can lead to structural failures, including buckling of legs and even collapse of the rig [3], posing a substantial threat to life and property.

To mitigate punch-through risks, the first concern is to predict the peak penetration resistance Q_p of spudcans in various seabed strata. Established methods for this purpose include centrifuge testing [1,4,5], large deformation finite element analysis [6,7,8,9], and limit equilibrium methods [8,10]. For stratified seabeds, such as sand-over-clay [11,12,13] and interbedded clay profiles (e.g., soft-stiff-soft [14] or stiff-soft-stiff [15]), simplified predictive models—such as the shear and load extension methods—have been developed and incorporated into international standards like ISO 19905-1 [16] and SNAME T&R Bulletin 5-5A [17]. However, in practice, the monitored Q_p during spudcan penetration frequently deviates significantly from predicted values. Cassidy et al. [18] highlight two primary factors contributing to this discrepancy: insufficient soil parameters obtained from site exploration, which leads to inaccurate soil parameterization, and the inherent limitations of deterministic calculation models themselves.

To address the uncertainties in soil parameters and the limitations of deterministic models, non-deterministic methods such as Monte Carlo simulation [19], Bayesian inference [20,21], and parameter estimation [22,23,24] have been proposed for predicting Q_p. A key advantage of these methods over conventional approaches is their capacity to incorporate real-time monitoring data from the spudcan penetration process. As penetration proceeds, this continuously updated data stream facilitates iterative optimization, progressively enhancing the accuracy of Q_p predictions. Concurrently, the rise of artificial intelligence and big data has established machine learning (ML) as a powerful tool in geotechnical engineering, valued for its robust generalization capabilities [25]. Its applications now encompass a broad spectrum, including stratum parameter estimation [26], foundation pit deformation analysis [27], slope stability assessment [28], pile foundation modeling [29], and shield tunnel excavation [30,31]. Since spudcan penetration in complex strata is governed by multiple, interdependent, and nonlinear variables, it constitutes a problem domain particularly amenable to the powerful nonlinear mapping capacities of ML. However, existing applications of ML for foundation capacity prediction have primarily focused on individual models or uniform soil conditions. The comparative effectiveness of different algorithmic approaches, particularly advanced frameworks like multi-view learning (MVL), for predicting capacity in stratified soils remains insufficiently explored.

In summary, ML provides a viable alternative to conventional theory-based methods for predicting spudcan penetration resistance, particularly when soil parameters are uncertain. However, the influence of algorithmic choice, dataset characteristics, and other modeling parameters on prediction accuracy requires further investigation. This study therefore investigates the feasibility of using ML to predict the peak penetration resistance Q_p of spudcans. Various ML and MVL methods are employed to develop predictive models for common geotechnical profiles, including clay-over-sand and three-layer clay strata. Key technical aspects, such as feature selection and training set size, are systematically examined. Furthermore, an optimized MVL method is proposed to enhance the reliability and safety of jack-up rig positioning operations.

2. Methods

2.1. Machine Learning Method

This study employs four ML algorithms—Random Forest [32,33], Support Vector Machine (SVM) [34,35], Multiple Linear Regression [36], and Neural Network [37]—to develop predictive models for the peak penetration resistance of spudcans. Below is a brief description of each algorithm:

(1)

Random Forest: An ensemble method that builds upon the decision tree algorithm. It constructs a multitude of decision trees, each trained on a distinct bootstrap sample of the data and a random subset of features. The final prediction is obtained by aggregating the outputs of all individual trees, enhancing predictive accuracy and generalization capability [32,33].

(2)

Support Vector Machine (SVM): A supervised learning model applicable for both classification and regression tasks. Its core principle is to identify the optimal hyperplane that maximizes the margin between classes in a high-dimensional space. This is achieved using kernel functions (e.g., linear, polynomial, or radial basis function), enabling the model to handle complex, nonlinearly separable data effectively [34,35].

(3)

Multiple Linear Regression: A statistical method that models the linear relationship between a single dependent variable (the target) and multiple independent variables (features). The model is fitted by determining the coefficients that minimize the sum of squared differences between the observed and predicted values [36].

(4)

Neural Network: A computational model composed of interconnected processing units (neurons), typically arranged in an input layer, one or more hidden layers, and an output layer. Each connection between neurons has an adjustable weight. Through an iterative training process, these weights are optimized, allowing the network to approximate complex nonlinear functions by applying nonlinear activation functions at each neuron [37].

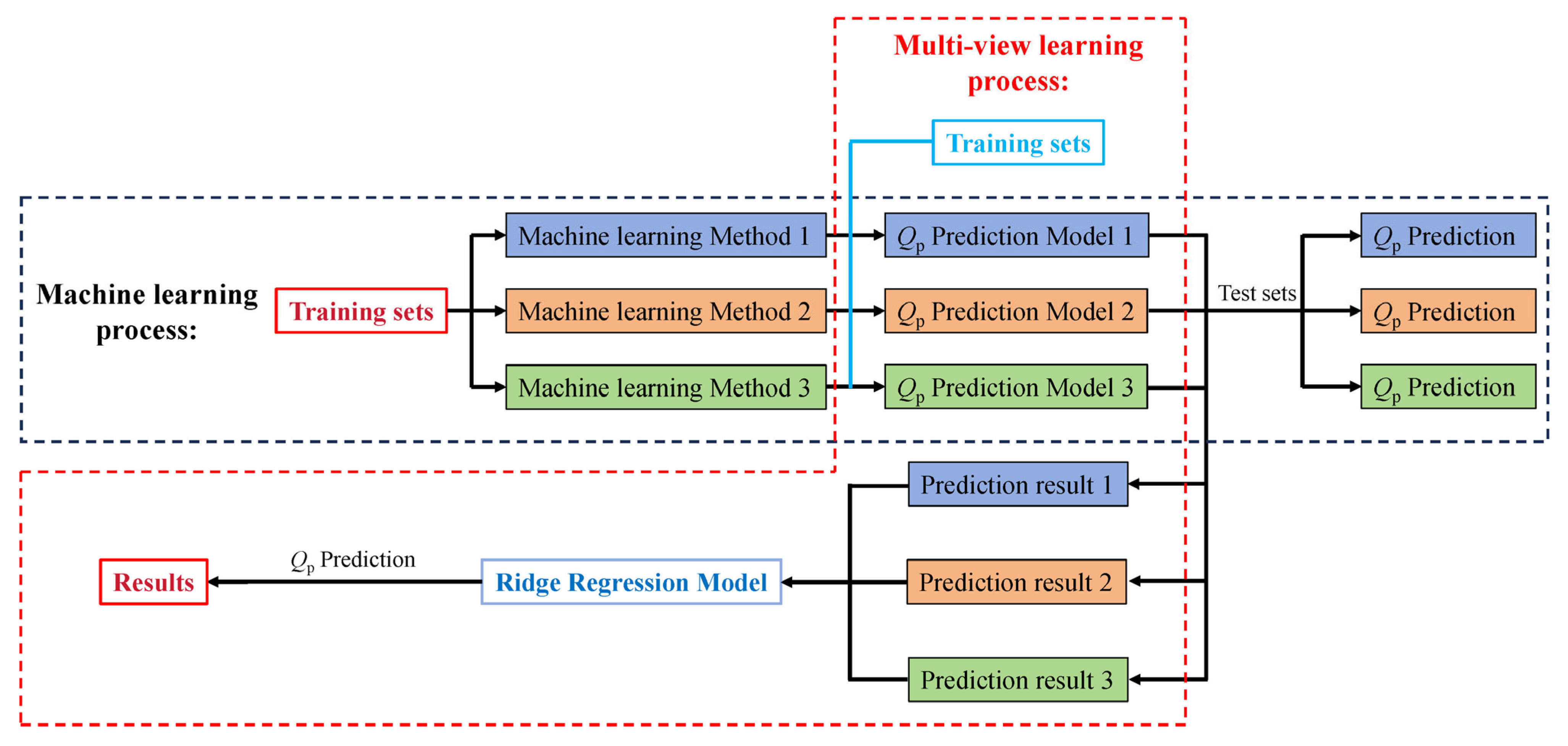
2.2. Principle of Multi-View Learning

In contrast to the single-view ML methods previously described, MVL aims to enhance predictive performance by leveraging complementary information from multiple, distinct feature sets or data sources [38]. This study employs a model-fusion MVL approach. In this framework, each ‘view’ is defined as the predictive output from a high-performing, single-view base model. These base model outputs are then integrated using a Ridge Regression-based combiner. The final ensemble prediction y_f is calculated as a weighted sum of the base model outputs:

$$y_{\mathrm{f}}=w_1\times y_1+w_2\times y_2+w_3\times y_3+\cdots +w_n\times y_n+b$$

(1)

where y_f is the final ensemble prediction, w_i are the learnable weight coefficients assigned to the prediction y_i of each base model, and b is the bias intercept. The combiner is trained on a dedicated validation set (see Section 4 for data partitioning) using the base models’ predictions as input features. Ridge regression is employed, minimizing the following loss function to determine the values of w_i and b:

$$\mathrm{L}\mathrm{o}\mathrm{s}\mathrm{s}={\sum }_{i=1}^n(y^i-{(w_1{y}_t^i+w_2{y}_s^i+w_3{y}_{st}^i+b)}^2)+\lambda {\sum }_{j=1}^l{w}_j^2$$

(2)

where n is the number of validation samples; y is the true value; l is the number of views; and the term $\lambda {\sum }_{j=1}^l{w}_j^2$ represents L2 regularization, which helps improve the model’s generalization. In this study, the regularization parameter λ is set to 0.05.

2.3. Model Construction and Accuracy Evaluation

To ensure data homogeneity, all training datasets in this study are sourced exclusively from published centrifuge test results. Due to the resource-intensive nature and relative scarcity of high-quality centrifuge data, a total of 66 representative cases are used for model training. This comprises 58 cases of sand-over-clay strata [1,10,39,40], four cases of soft-stiff-soft clay strata [14,41], and four cases of stiff-soft-stiff clay strata [15,41]. For each of these three strata types, a distinct ML model is developed. The model inputs consist of a feature set that encapsulates the most critical design parameters, while the output represents the corresponding measured peak penetration resistance Q_p. Model performance is evaluated by using the test set features to predict Q_p, and the results are discussed in the following section. The overall process is illustrated schematically in Figure 1.

The dataset is partitioned into a training set comprising 70% of the data and a test set comprising 30%. Model accuracy is quantitatively evaluated using two metrics: the mean relative error (MRE) and the root mean square error (RMSE). The MRE is prioritized as it expresses error as a direct percentage, providing an intuitive measure that aligns directly with engineering judgment and risk assessment practices. The RMSE is reported to quantify the absolute magnitude of error variance, giving greater weight to larger deviations and thus indicating prediction stability. Lower values for both metrics correspond to higher predictive accuracy and precision. The MRE and RMSE are defined as follows:

$$\mathrm{M}\mathrm{R}\mathrm{E}={\displaystyle \frac{\left|y_i-y\right|}{y}}\times 100\%$$

(3)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{\sum _{i=1}^n{(y_i-y)}^2}{n}}}$$

(4)

where y_i is the predicted value, and y is the corresponding measured (actual) value. Given the well-defined physical nature of the input parameters and the focused scope of this feasibility study, these two metrics are deemed sufficient to rigorously assess and compare model performance for the intended engineering application.

3. Machine Learning Prediction of Q_p

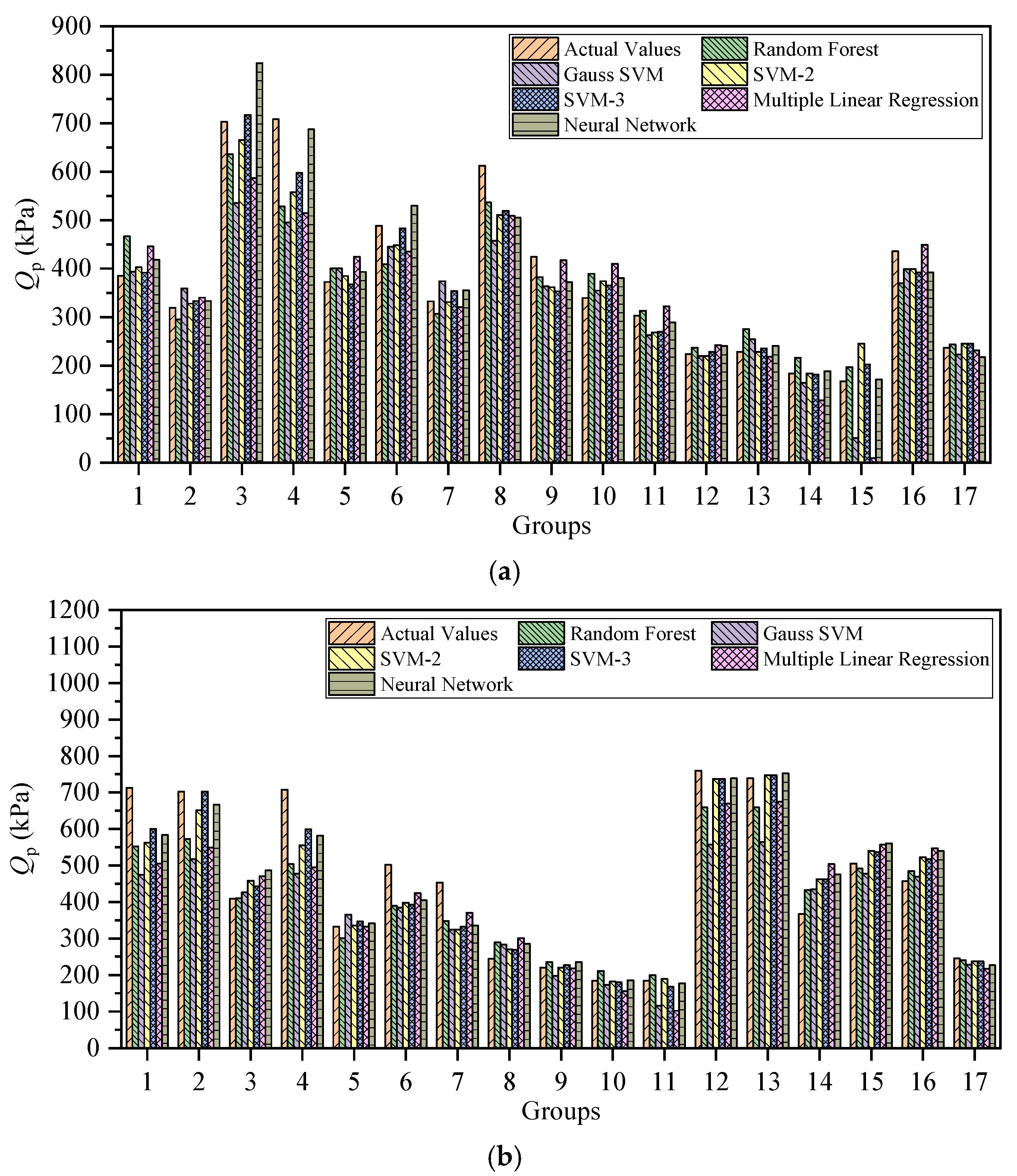
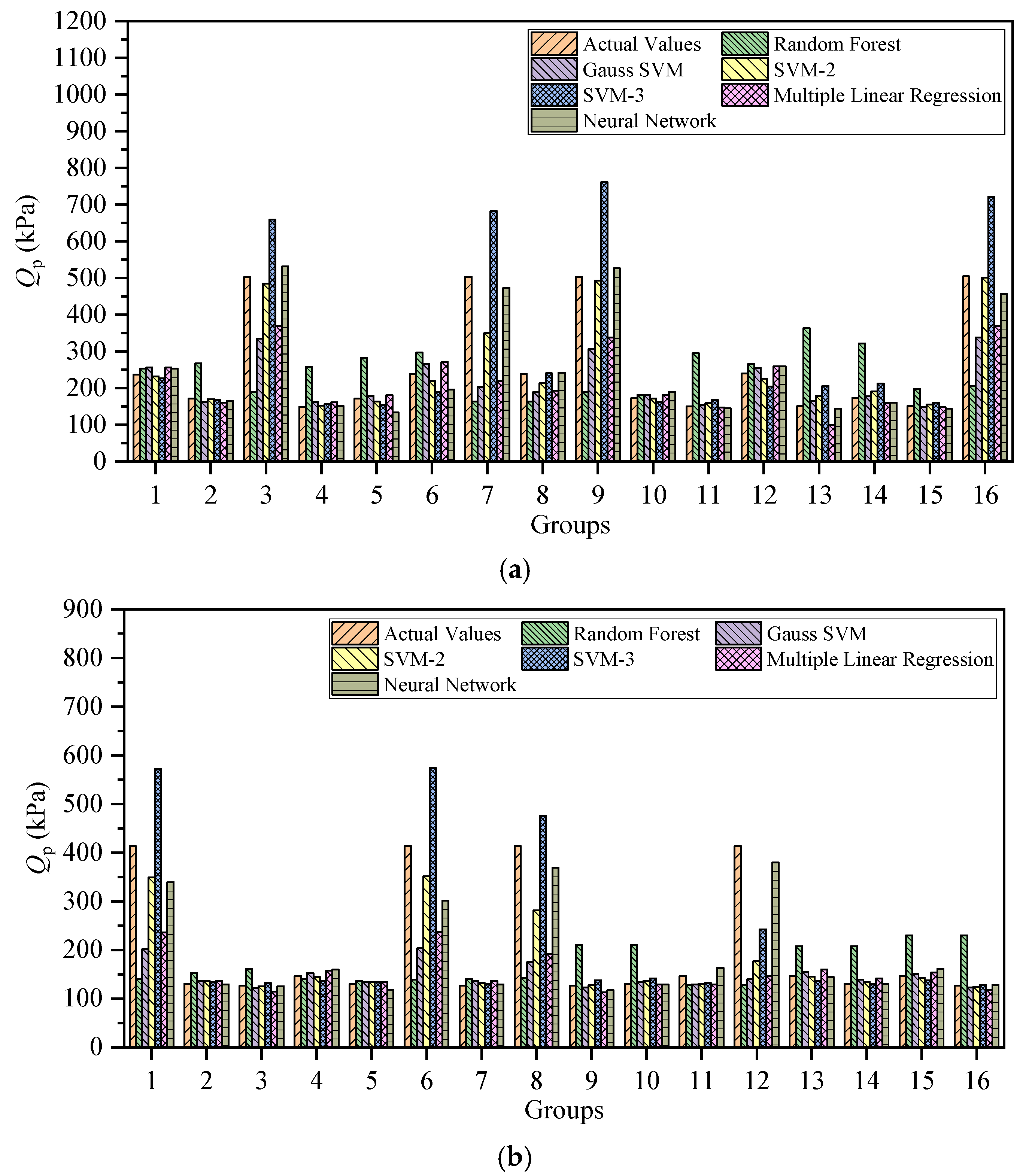
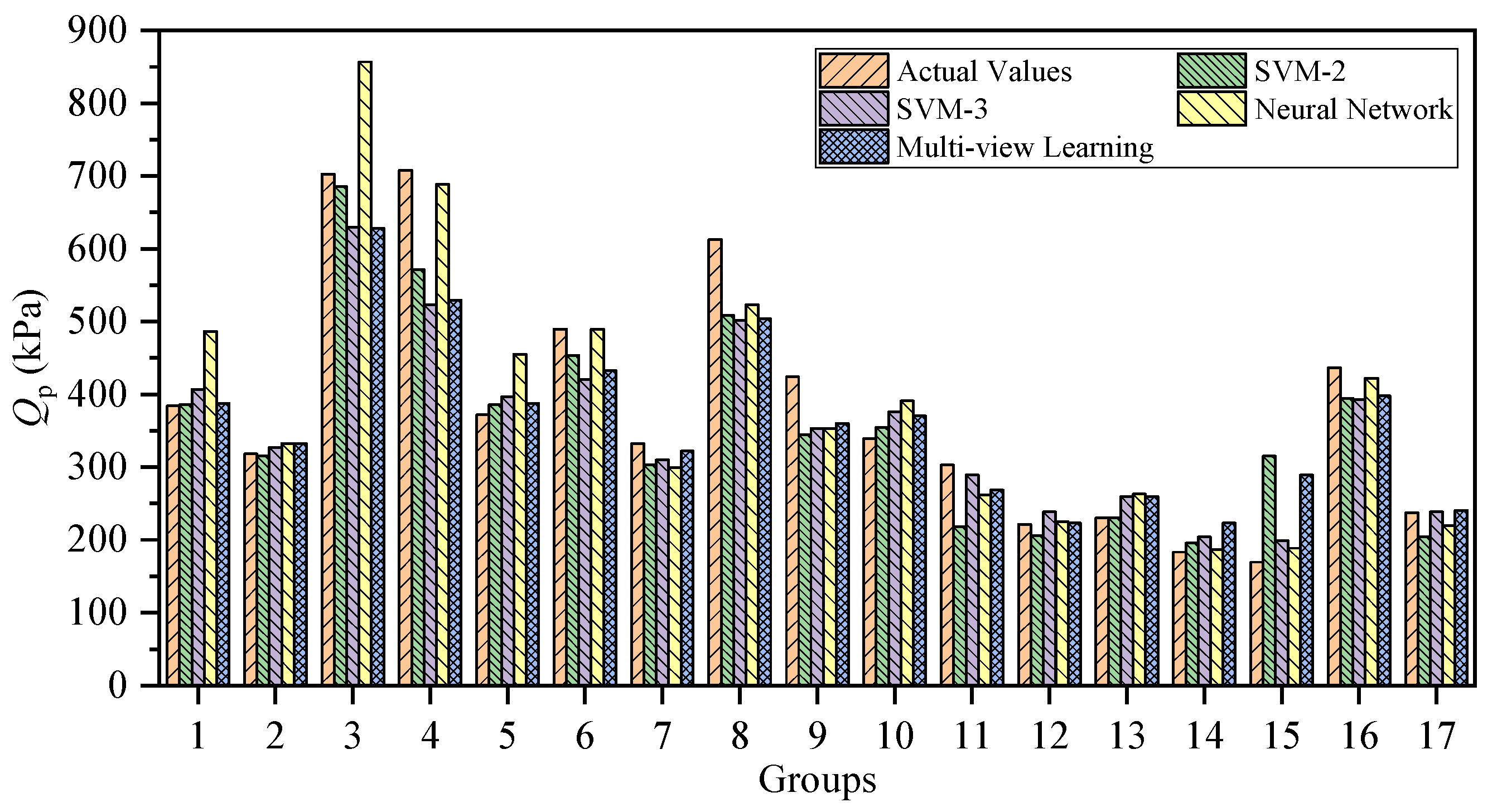
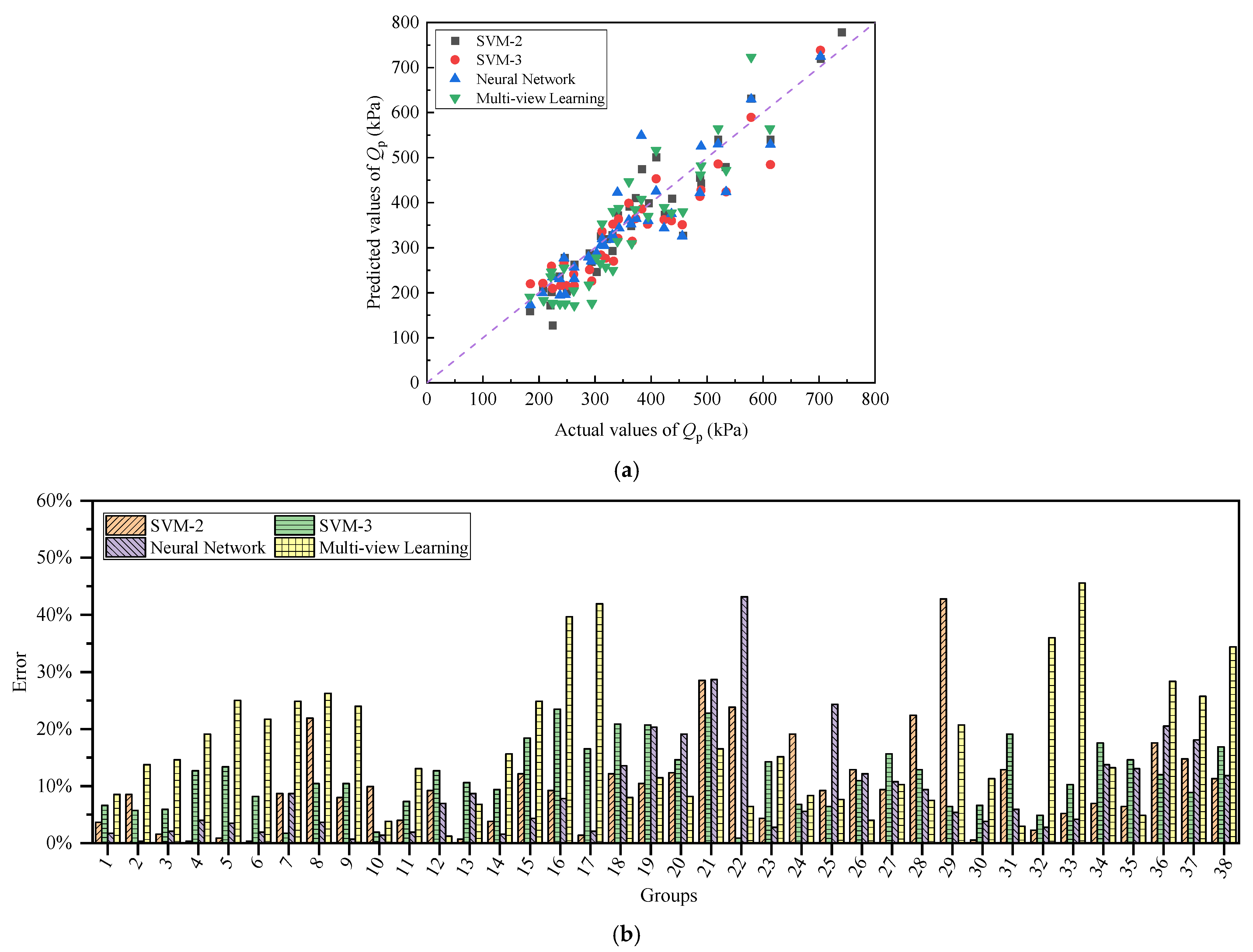
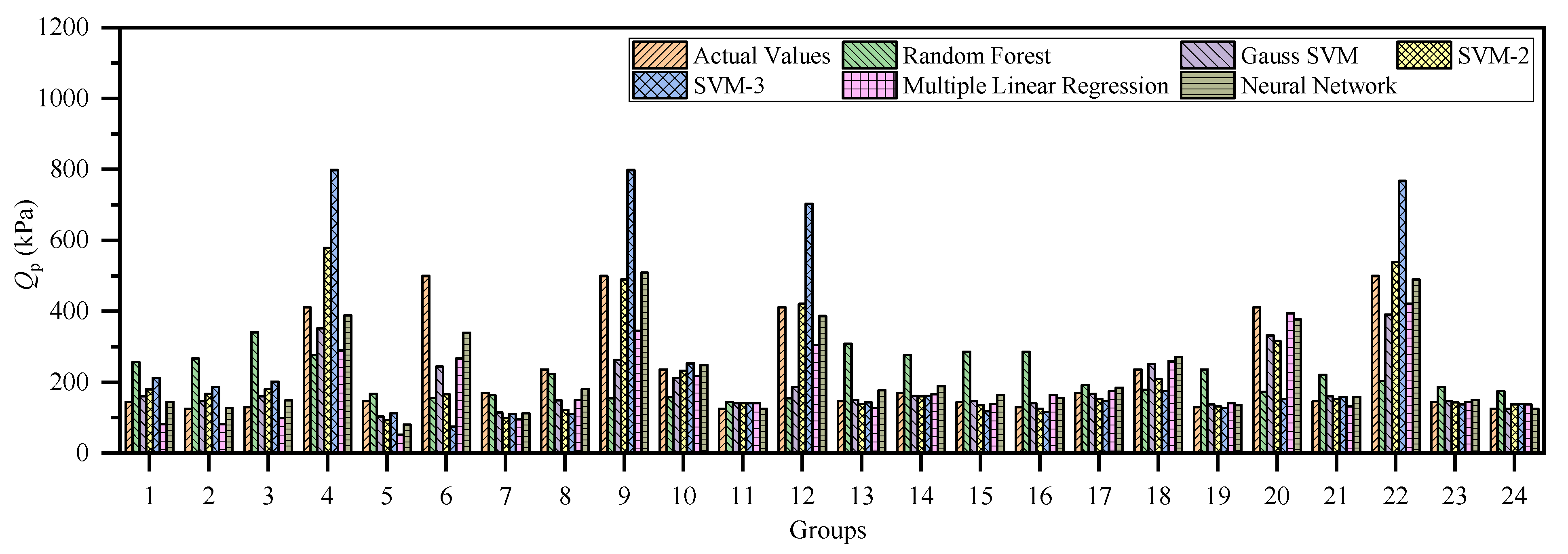
3.1. Prediction in Sand-over-Clay Strata

Based on a sensitivity analysis of the deterministic model parameters [22], key parameters are selected as input features for the training data. These features include the undrained shear strength of the clay at the sand-clay interface s_um, sand layer thickness H_s, spudcan diameter D, buoyant unit weight of the sand γ_s and clay γ_c, and the strength gradient of clay k. The corresponding peak resistance Q_p for each case is designated as the target output. The dataset of 56 cases is partitioned into a training set (39 datasets) and a test set (17 datasets) using randomized sampling to avoid bias. To ensure robustness, the modeling process was repeated with two distinct, randomized data splits. The outcomes of these two training iterations are presented in Figure 2, with detailed performance metrics detailed in

Table 1. Comparison of Q_p prediction model accuracy for sand-over-clay strata.

Methods		Random Forest	Gauss SVM	SVM-2	SVM-3	Multiple-Linear Regression	Neural Network
First training	MRE	18.9%	18.2%	13.6%	13.3%	19.8%	11.1%
	RMSE	99.19	123.35	74.87	73.21	103.37	69.34
Second training	MRE	13.5%	18.3%	11.7%	10.6%	18.9%	12.4%
	RMSE	88.6	123.37	74.09	63.33	103.34	72.34

. The analysis indicates that the average MRE for all six ML models remains below 20%. This level of accuracy surpasses the performance of the deterministic model recommended by the standard ISO 19905-1 [16] and is comparable to the model proposed by Hu et al. [13]. This margin of error is generally acceptable in practical engineering. Consequently, the predictive accuracy of the proposed models meets or exceeds the performance standards of established engineering and theoretical methods. Among the six models, the SVM with a second-degree polynomial kernel (SVM-2), the SVM with a third-degree polynomial kernel (SVM-3), and the Neural Network demonstrate the best performance, each achieving an average MRE below 15%. The Neural Network model yields the smallest RMSE, indicating superior prediction accuracy. It is therefore identified as the most effective predictor among the evaluated algorithms.

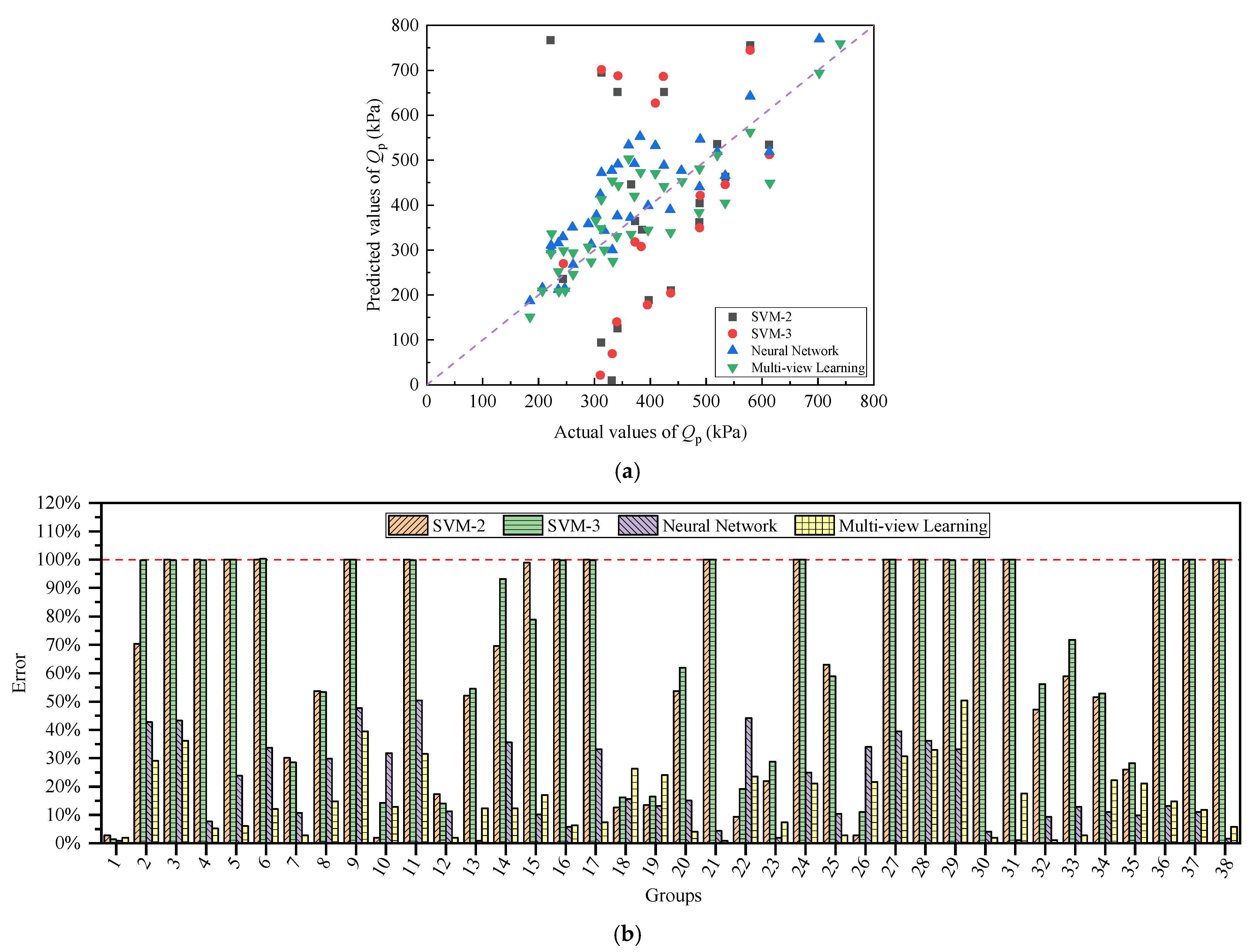
3.2. Prediction in Three-Layer Clay Strata

The ML models are trained and tested on two types of three-layer clay strata: soft-stiff-soft and stiff-soft-stiff. The input features consist of the undrained shear strengths (s_u1, s_u2, s_u3) and layer thicknesses (t₁, t₂, t₃) of the top, middle, and bottom clay layers, respectively. The analysis utilizes four datasets from each stratum (designated as Samples 1–4), resulting in a total of 16 prediction groups, as summarized in

Table 2. Training and test set composition for three-layer clay.

Group	1	2	3	4	5	6	7	8
Training sets (Samples)	1, 2, 3	1, 2, 4	1, 3, 4	2, 3, 4	1, 2	1, 2	1, 3	1, 3
Test sets (Sample)	4	3	2	1	3	4	2	4
Group	9	10	11	12	13	14	15	16
Training sets (Samples)	1, 4	1, 4	2, 3	2, 3	2, 4	2, 4	3, 4	3, 4
Test sets (Sample)	2	3	1	4	1	3	1	2

.

The prediction results for all 16 test groups (Table 2) are visualized in Figure 3, with corresponding model accuracy metrics provided in

Table 3. Comparison of Q_p predictions from different models for three-layer clay.

Methods		Random Forest	Gauss SVM	SVM-2	SVM-3	Multiple-Linear Regression	Neural Network
Soft-stiff-soft clay strata	MRE	55.4%	18.6%	7.8%	15.9%	24.8%	7.3%
	RMSE	182.08	107.69	40.46	103.35	96.30	23.52
Stiff-soft-stiff clay strata	MRE	44.5%	17.7%	9.9%	12.2%	17.9%	7.7%
	RMSE	147.42	117.6	71.38	72.28	107.43	37.11

. For both three-layer clay strata types, the SVM-2, SVM-3, and Neural Network models demonstrate superior performance, with average relative errors below 16%. Notably, both SVM-2 and the Neural Network achieve errors under 10%. In contrast, the other models, constrained by data scarcity, exhibit excessively high errors that preclude practical engineering application; for instance, the Random Forest model produces an average MRE of 50%. Consistent with its performance on sand-over-clay strata, the Neural Network model achieves the lowest MRE and RMSE, confirming its status as the optimal predictor. However, performance is consistently poor for Sample 2 in the soft-stiff-soft clay (Groups 3, 7, 9, 16; Figure 3a) and for Sample 4 in the stiff-soft-stiff clay (Groups 1, 6, 8, 12; Figure 3b). This can be attributed to the distinct geotechnical properties of these samples, which differ significantly from those of the other strata in their respective categories. When the training set lacks these specific stratum types, models primarily trained on softer strata fail to accurately predict the peak resistance Q_p for stiffer strata due to the absence of relevant features in the training data. This finding underscores the importance of having a sufficiently broad spectrum of feature values in the training dataset, representing the full range of expected stratum properties, to ensure that ML models achieve robust accuracy across diverse geotechnical conditions.

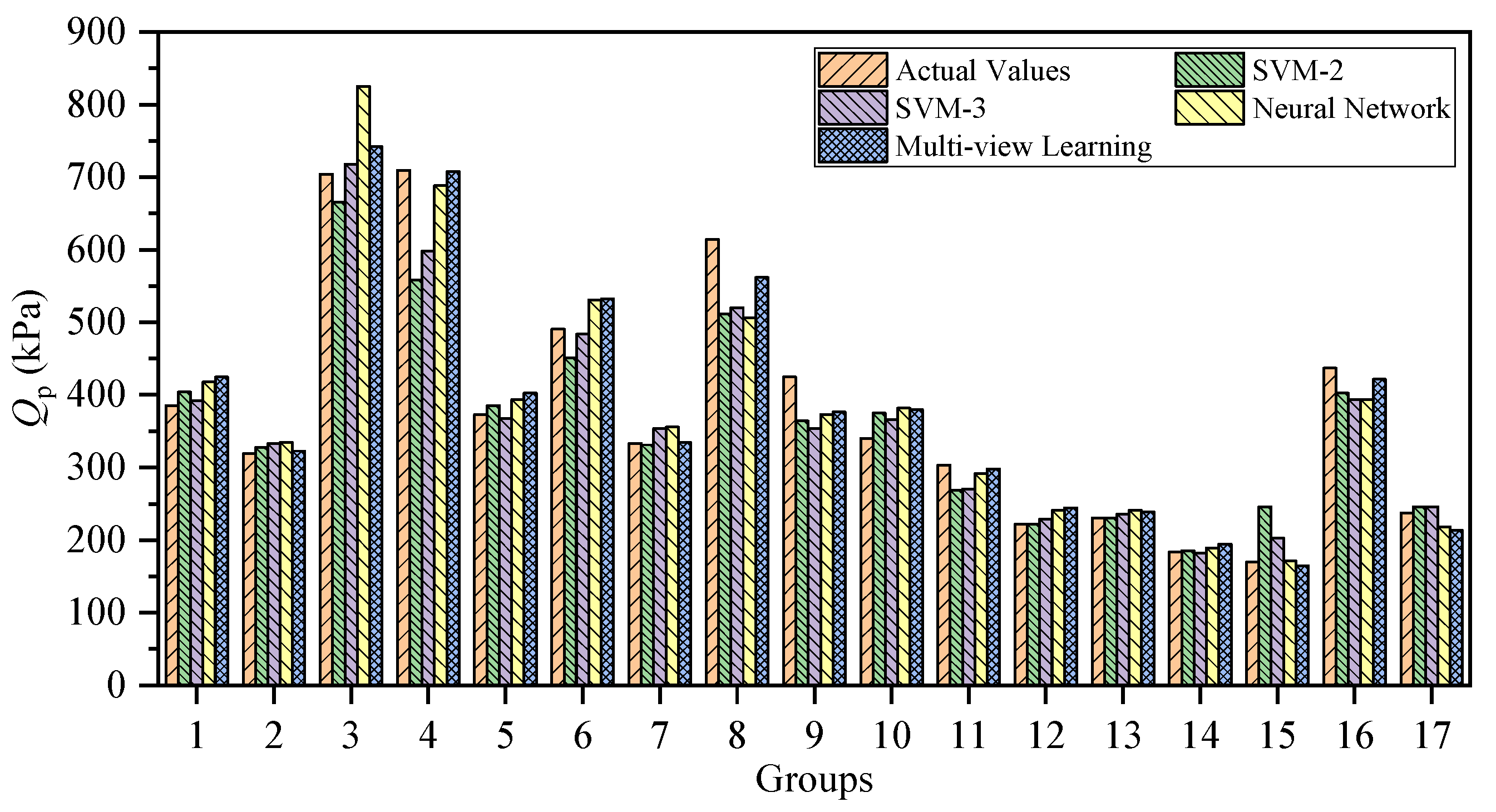
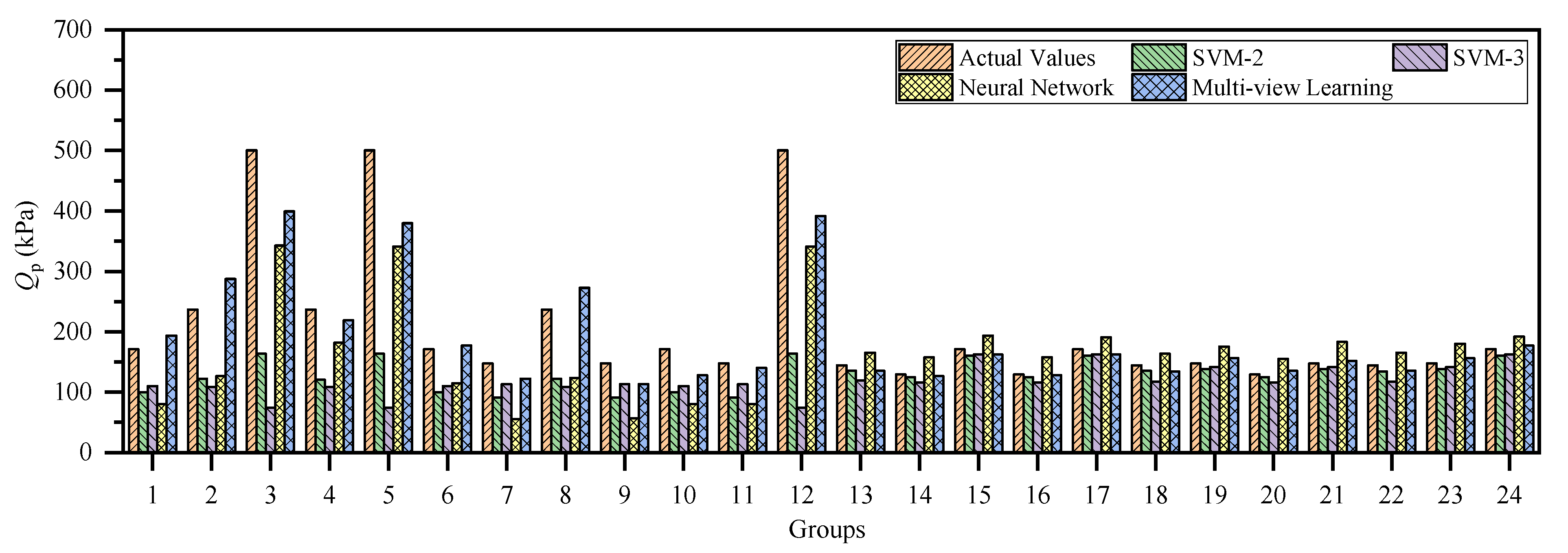
4. Q_p Prediction via Multi-View Learning

Based on the performance of the ML models for sand-over-clay strata, the top three predictors—SVM-2, SVM-3, and Neural Networks—are selected for the MVL framework, providing three distinct predictive ‘views’. The original 39 training datasets are repartitioned: twenty-six sets are allocated to train the three individual base models (SVM-2, SVM-3, Neural Network), while the remaining 13 sets form a validation partition. The trained base models are used to generate predictions for each sample in this validation set. These prediction triplets, along with the true Q_p values, are used to train the Ridge Regression combiner (Equation (1)), thereby learning the optimal fusion weights w_i and bias b. The final MVL model—the fixed base models plus the trained Ridge Regression combiner—is then evaluated on the original 17 independent test sets (Table 1) for direct comparison with the single-view models. As shown in Figure 4 and

Table 4. Comparison of Qp predictions between multi-view learning and machine learning methods.

Methods	SVM-2	SVM-3	Neural Network	Multi-View Learning
MRE	11.4%	9.5%	8.2%	6.2%
RMSE	54.33	42.87	47.18	28.59

, the MVL ensemble achieves a lower average MRE and RMSE than the individual base models. This improvement confirms that the 26-dataset training subset provides sufficient data for effective model training. The MVL ensemble demonstrates superior overall predictive performance, achieving the lowest average MRE of 6.2%. While this error is only marginally lower than that of the best individual models, the key advantage of the MVL method lies in its significantly reduced RMSE. This reduction indicates that the MVL approach offers more stable and consistent predictions, resulting in higher overall accuracy for Q_p estimation.

5. Discussion

5.1. Influence of the Number of Features

To evaluate the impact of feature selection on model performance for sand-over-clay strata, predictions are compared across different parameter combinations. The peak resistance in this stratum is governed predominantly by the bearing capacity within the sand layer and the spudcans’ geometry. The core physical parameters are therefore identified as: (1) the undrained shear strength at the clay surface (s_um), which influences the underlying support; (2) the sand layer thickness (H_s), which defines the failure wedge geometry; and (3) the spudcan diameter (D), which scales the bearing area. This simplified set reflects a priority ranking based on physical significance. The buoyant unit weights of sand (γ_s) and clay (γ_c) are excluded due to their limited variability in marine sediments and their secondary influence on the peak load relative to strength and geometric parameters. The clay strength gradient (k) is also omitted for this focused analysis because its primary influence is on penetration within the clay layer, whereas the target Q_p occurs at the sand-clay interface.

The top-performing models—SVM-2, SVM-3, and Neural Networks—are applied to predict Q_p in sand-over-clay strata. The MVL framework is implemented following the same data partitioning scheme described in Section 3.2 to ensure direct comparability. The prediction results are presented in Figure 5, with a model comparison provided in

Table 5. Comparison of Q_p Prediction in sand-over-clay strata using the three-feature model.

Methods	SVM-2	SVM-3	Neural Network	Multi-View Learning
MRE	14%	11%	11%	9%
RMSE	99.19	123.35	74.87	73.21

. Although the average MRE for all models remains below 15%, indicating acceptable performance, both the MRE and RMSE increase compared to the six-feature model. This decline in accuracy is attributed to the loss of critical information from feature reduction, which diminishes the regression model’s capability. Therefore, for practical Q_p prediction, it is recommended to utilize the complete set of characteristic parameters to maximize predictive accuracy.

5.2. Influence of the Number of Training Sets on the Prediction

A sensitivity analysis is conducted to quantify the influence of training set size on the predictive accuracy of ML and MVL models for sand-over-clay strata. Building on the baseline performance established with 26 training sets for the base model and 13 for the MVL learner, model performance is systematically evaluated using progressively smaller training subsets. The specific dataset configurations for this analysis are outlined in

Table 6. Setting of training and test sets in sand-over-clay strata.

No.	Machine Learning Training Set	Multi-View Learning Training Set	Testing Set
Training Combination 1	12	6	38
Training Combination 2	6	12	38
Training Combination 3	12	12	32

.

5.2.1. Training Combination 1

The Q_p prediction results for Training Combination 1 (Table 6) are presented in Figure 6 and summarized in

Table 7. Comparison of Q_p prediction results for Training Combination 1 in sand-over-clay strata.

Methods	SVM-2	SVM-3	Neural Network	Multi-View Learning
MRE	13.7%	14.3%	10.2%	17.5%
RMSE	46.27	51.02	51.41	90.85

. The data indicate that an ML training set of 12 samples is sufficient to effectively train the SVM-2, SVM-3, and Neural Network models, yielding predictions with an MRE below 15% and comparable RMSE values. However, Figure 6a reveals a clear performance disparity: while the models achieve high accuracy for lower Q_p values (<400 kPa), predictive performance deteriorates markedly in the higher range. Furthermore, as shown in Figure 6b, despite a satisfactory overall average error, the prediction accuracy for individual cases is highly variable. For instance, the Neural Network model for Group 22 and the SVM-2 model for Group 29 both exhibit errors exceeding 40%. In contrast, the MVL model underperformed relative to the single-model benchmarks, with both its MRE and RMSE exceeding those of the other three methods. This is likely attributable to its limited training set size, which constrained its ability to develop a robust ensemble prediction.

5.2.2. Training Combination 2

The Q_p prediction results and comparative analysis for Training Combination 2 are presented in Figure 7 and

Table 8. Comparison of Q_p prediction results for Training Combination 2 in sand-over-clay strata.

Methods	SVM-2	SVM-3	Neural Network	Multi-View Learning
MRE	138.9%	142.5%	24.7%	16.9%
RMSE	543.71	562.04	83.75	68.05

. Figure 7a illustrates that the reduced size of the ML training set severely degrades the performance of all base models. The predictive capability of both the SVM-2 and SVM-3 models deteriorates substantially, with Figure 7b indicating that the vast majority of their predictions exhibit errors exceeding 100%. In comparison, the Neural Network demonstrates greater resilience, maintaining better overall performance, although it still produces significant errors in specific instances, with MRE values surpassing 45%. Conversely, the MVL model, trained on only 12 sets, achieves reasonable predictive performance, with an average MRE of 16.9% and an RMSE of 68.5. However, this result is contingent upon the quality of its training data; the model’s performance diminishes if its dedicated training set is compromised. Since the MVL model uses the predictions of the base models as its input features, its accuracy is inherently dependent on theirs. Despite this dependency, the ensemble framework of the multi-view approach offers a key advantage: it is designed to be robust, capable of discerning and mitigating a significant portion of the error propagated from the base models, resulting in more accurate and stable final predictions.

5.2.3. Training Combination 3

The prediction results and comparative analysis for Training Combination 3 are presented in Figure 8 and

Table 9. Comparison of Q_p prediction results for Training Combination 3 in sand-over-clay strata.

Methods	SVM-2	SVM-3	Neural Network	Multi-View Learning
MRE	12.5%	28.2%	14.5%	10.1%
RMSE	46.43	124.40	66.27	40.22

. The results demonstrate that a training set of 12 samples is sufficient for both the SVM-2 and Neural Network models, each achieving an MRE below 15%. However, the Neural Network model exhibits greater prediction variance, with specific errors exceeding 30%, resulting in a higher RMSE than the SVM-2 model. In contrast, the SVM-3 model performs poorly with the limited data, yielding an average MRE of 28.2%. The MVL model demonstrates robust performance, achieving an overall MRE below 20% and producing predictions with an MRE under 10% in 24 cases. This represents a significant improvement over the performance observed in Figure 7, an enhancement attributable to the higher-quality training data generated from the outputs of the more reliable base models in this configuration.

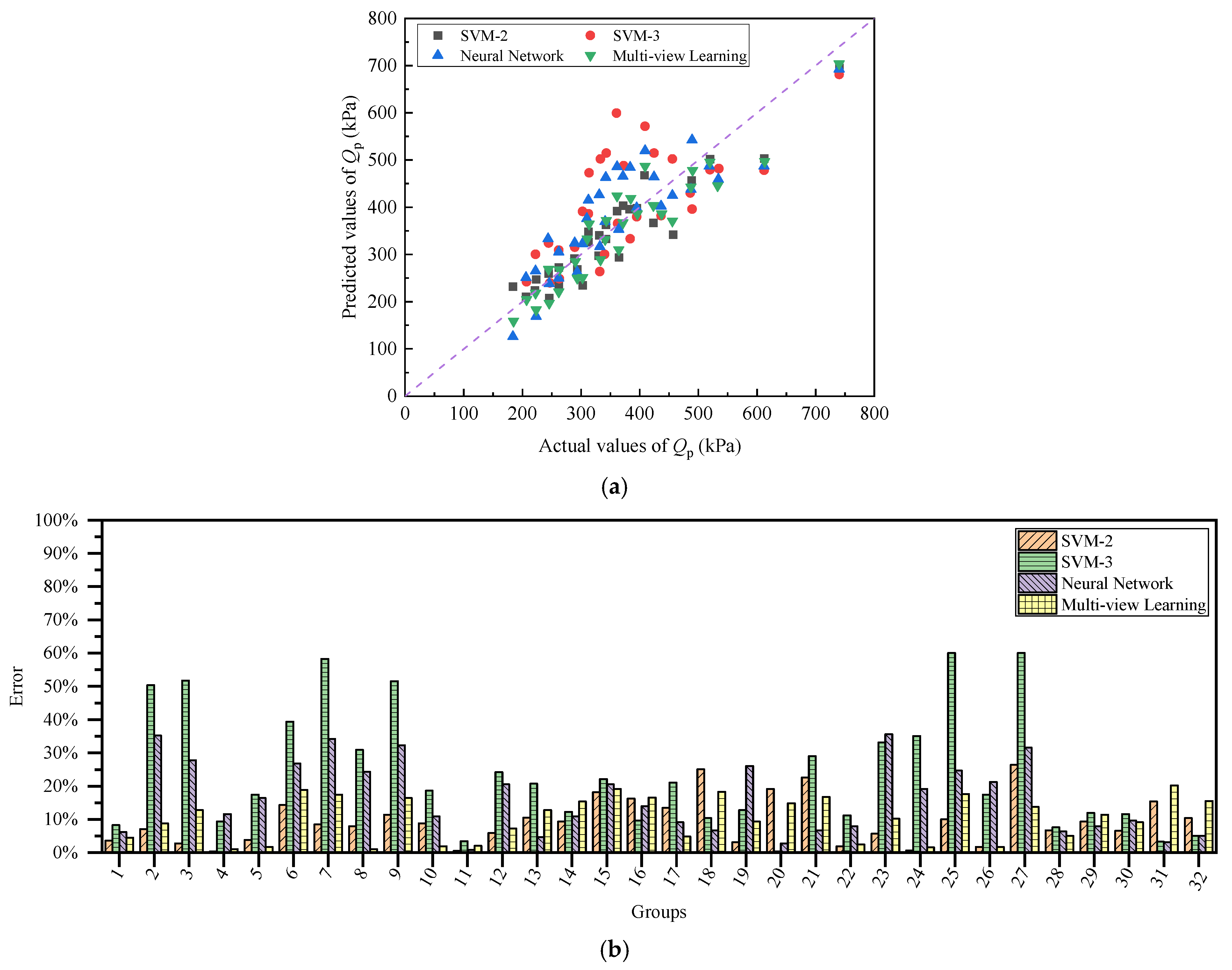
5.3. Prediction Feasibility for Three-Layer Clay

5.3.1. Machine Learning Prediction

The predictive models for the three-layer clay strata (soft-stiff-soft and stiff-soft-stiff) utilize a consistent set of input features: the undrained shear strengths (s_u1, s_u2, s_u3) and thicknesses (t₁, t₂, t₃) of the three layers. Model performance is assessed using a combined dataset of eight samples, comprising four from each stratum type (Samples 1–4: soft-stiff-soft; Samples 5–8: stiff-soft-stiff). The partitioning of this dataset into training and test sets is detailed in

Table 10. Setting of training and test sets for machine learning prediction in three-layer clay strata.

Groups	1	2	3	4	5	6	7	8	9	10	11	12
Training sets (Samples)	1, 2, 3, 4				5, 6,7, 8				1, 3, 5, 7
Test sets (Sample)	5	6	7	8	1	2	3	4	2	4	6	8
Groups	13	14	15	16	17	18	19	20	21	22	23	24
Training sets (Samples)	2, 4, 6, 8				1, 2, 5, 6				3, 4, 7, 8
Test sets (Sample)	1	3	5	7	3	4	7	8	1	2	5	6

Note: Samples 1–4 for soft-stiff-soft clay strata, Samples 5–8 for stiff-soft-stiff clay strata.

.

Analysis of the 24 prediction results (Table 10 and Figure 9) indicates that model performance is deficient when the training set is limited to a single type of three-layer clay stratum, as evidenced by the high relative errors in Groups 1–8. In contrast, predictive accuracy improves substantially when the training set incorporates both soft-stiff-soft and stiff-soft-stiff strata. Models such as the Gauss SVM, SVM-2, and Neural Network achieve an MRE of approximately 15% under this combined training strategy (Groups 9–24, Figure 9). These results confirm that combined training on mixed three-layer clay strata is a viable and effective approach. The Neural Network model, in particular, delivers superior performance, attributed to its inherent capacity for modeling complex, nonlinear relationships. As shown in

Table 11. Comparison of different Q_p prediction models in three-layer clay strata.

Methods	Random Forest	Gauss SVM	SVM-2	SVM-3	Multiple Linear Regression	Neural Network
MRE	58.4%	22.9%	18.7%	39.4%	24.7%	13.5%
RMSE	165.36	93.27	86.70	237.70	77.21	42.71

, the models achieve the best results, with an average MRE of 13.5% and an RMSE of 42.71, representing a significant improvement over the deterministic benchmark.

5.3.2. Multi-View Learning Prediction

To evaluate the efficacy of MVL for three-layer clay strata, data are selected from groups representing both poor (Groups 5–8) and good (Groups 13–16) predictive performance, as identified in Figure 9. The corresponding training and test set configurations for this analysis are detailed in

Table 12. Setting of training and test sets for multi-view learning prediction in three-layer clay strata.

Groups	1	2	3	4	5	6	7	8	9	10	11	12
Training sets (Samples) for machine learning	5, 6,7, 8
Test sets (Sample) for multi-view learning	1, 2	1, 2	1, 3	1, 3	1, 4	1, 4	2, 3	2, 3	2, 4	2, 4	3, 4	3, 4
Test sets (Sample)	3	4	2	4	2	3	1	4	1	3	1	2
Groups	13	14	15	16	17	18	19	20	21	22	23	24
Training sets (Samples) for machine learning	2, 4, 6, 8
Test sets (Sample) for multi-view learning	1, 3	1, 3	1, 5	1, 5	1, 7	1, 7	3, 5	3, 5	3, 7	3, 7	5, 7	5, 7
Test sets (Sample)	5	7	3	7	3	5	1	7	1	5	1	3

. To maintain methodological consistency, the MVL model utilizes the same base models as input features: the SVM-2, SVM-3, and Neural Network.

Figure 10 illustrates the Q_p prediction results, demonstrating that the MVL method delivers high accuracy for both low-performance (Groups 1–12) and high-performance groups (Groups 13–24). This is quantified in

Table 13. Comparison of Q_p prediction in three-layer clay from the combined methods.

Methods	SVM-2	SVM-3	Neural Network	Multi-View Learning
MRE	27.1%	29.2%	30.4%	10.6%
RMSE	129.33	159.14	79.65	43.66

, where the model achieves an MRE of 10.6% and an RMSE of 43.66, confirming its superior predictive capability.

5.4. Summary of Feature and Training Set Influences

The analysis of feature influence confirms the general principle that a more comprehensive set of input parameters enhances prediction accuracy. Regarding training data, while a minimum of 12 sets enables basic model function in data-scarce conditions, the resulting predictive quality is demonstrably inferior to that achieved with larger datasets. Therefore, when data availability permits, it is recommended to utilize more than 20 training sets to ensure robust and reliable predictions. It should be noted that predictions under severe data constraints, particularly for extreme values, remain unreliable.

A key methodological finding concerns three-layer clay strata. While conventional deterministic models for soft-stiff-soft and stiff-soft-stiff clays are developed separately, this study shows that machine learning models trained on a combined dataset yield accurate predictions for both. Although the precise nonlinear mapping within the ML model is not explicitly interpretable, this result provides empirical support for a significant hypothesis: these two three-layer clay profiles may be effectively treated as a single stratigraphic class. This insight offers a feasible pathway for developing a unified deterministic model for Q_p prediction in future research.

6. Conclusions and Limitations

This study employs six ML algorithms and a MVL framework to predict the peak penetration resistance Q_p of spudcan foundations in sand-over-clay and three-layer clay strata. The key findings and study limitations are summarized as follows:

(1)

The trained ML and MVL models generate accurate Q_p predictions for the studied strata, with performance comparable to established deterministic models. Neural networks and MVL showed superior accuracy, confirming the feasibility of data-driven approaches for this geotechnical problem. This performance is comparable to that of established deterministic models, indicating their potential as complementary predictive tools.

(2)

For sand-over-clay strata, both the simplified three-feature and comprehensive six-feature yield satisfactory predictions. However, the model using the six-feature set delivers superior accuracy. Therefore, utilizing the full parameter set is recommended in practice to maximize model performance.

(3)

With sufficient training data, all models achieve an MRE below 20%. Under data-scarce conditions, a training set ratio of 1:2 for MVL to ML can maintain satisfactory accuracy. This offers clear guidance on minimum data requirements.

(4)

This study demonstrates that characterizing soft-stiff-soft and stiff-soft-stiff clay strata as a single stratigraphic class can achieve predictive accuracy for Q_p equivalent to modeling them separately. This finding offers a practical reference for predicting capacity in multi-layered strata where detailed soil parameters are limited.

(5)

A key limitation is the constrained size of the dataset, which is based on the limited pool of reliable, published centrifuge tests. This restricted both model complexity and validation rigor, necessitating a hold-out validation approach rather than more robust cross-validation. Future work should focus on expanding the experimental database to enable more advanced modeling and comprehensive statistical validation.