A Multicomponent OBN Time-Shift Joint Correction Method Based on P-Wave Empirical Green’s Functions

Abstract

To address clock drift arising from the absence of GPS synchronization during ocean-bottom seismic observations, we propose a time-offset correction and quality-control scheme that uses the correlation of P-wave empirical Green’s functions (EGFs) as the metric, and we demonstrate its efficacy in mitigating cross-correlation asymmetry caused by azimuthal noise in shallow-water environments. The method unifies the time delays of the four components into a single objective function, estimates per-node offsets via sparse weighted least squares with component-specific weights, applies spatial second-difference smoothing to suppress high-frequency oscillations, and performs spatiotemporally constrained regularized iterative optimization initialized by the previous day’s inversion to achieve a robust solution. Tests on a real four-component ocean-bottom node (4C-OBN) hydrocarbon exploration dataset show that, after conventional linear clock-drift correction of the OBN system, the proposed method can effectively detect millisecond-scale time jumps on individual nodes; compared with traditional noise cross-correlation time-shift calibration based on surface-wave symmetry, our four-component fusion approach achieves superior robustness and accuracy. The results demonstrate a marked increase in the coherence of the four-component cross-correlations after correction, providing a reliable temporal reference for subsequent multicomponent seismic processing and quality control.

1. Introduction

Ocean-bottom nodes (OBN) and ocean-bottom seismometers (OBS) provide high–signal-to-noise, multicomponent data for marine geophysical exploration and have become a major focus of recent developments in the field [1,2,3,4,5,6,7,8]. Because OBN/OBS systems cannot access GPS timing once deployed on the seafloor, their internal clocks drift by the time the instruments are recovered. The causes of such drift include, among others [9], temperature variations (measurable and correctable), clock aging (temperature dependent and difficult to predict), and thermal hysteresis (difficult to measure or forecast). Clock drift in OBN/OBS deployments is commonly assumed to be linear: instruments are GPS-disciplined prior to deployment, and upon recovery the total drift is estimated by comparison with GPS time and corrected linearly [10,11,12]. However, during extended seafloor observations, clock behavior is not strictly linear; nonlinear drift and abrupt time jumps may still occur. Several studies have reported residual time jumps after linear correction of OBN/OBS data, even when coherent ambient-noise cross-correlations are stacked [13,14].

Time-shift correction is an essential preprocessing step in ocean-bottom seismic data workflows. Wide-azimuth data acquired by OBN/OBS provide rich information for high-resolution imaging; however, any timing inconsistency across receivers and components directly degrades imaging accuracy [15,16]. Time-shift correction for seafloor nodes comprises two distinct approaches: active-source and passive-source methods. The active-source approach exploits direct arrivals from air-gun shots and uses least squares inversion to jointly estimate receiver and shot timing offsets along with spatial location parameters [17]. The passive-source method derives empirical Green’s functions (EGFs) from noise cross-correlation functions (NCCFs) between receiver pairs and then infers inter-receiver relative timing from the temporal symmetry of the EGFs [18,19,20,21,22]. Ideally, with synchronized clocks and a stable medium, noise arriving from all azimuths yields symmetric cross-correlation waveforms; if one instrument’s clock drifts or is biased, the NCCF becomes asymmetric, revealing the magnitude of the time offset [14,23,24,25,26,27].

Noise cross-correlation is a key method for estimating node timing drift, with prior work relying primarily on Scholte and Rayleigh waves. The study by Ref. [28] highlights the role of Scholte waves in OBS time-shift calibration: compared with surface-wave extraction from the vertical component, cross-correlation of the hydrophone component yields Scholte waves with higher signal-to-noise ratios, thereby enabling more precise cross-correlation time shifts and improving OBS timing accuracy from potentially multi-second uncertainties to the 0.1–0.2 s range. Refs. [14,26] made broader use of Rayleigh-wave signals, chiefly via cross-correlations of the vertical or radial components, improving timing-drift correction precision to the ~0.01 s level to meet high-accuracy localization requirements. Overall, the noise cross-correlation method reduces time-shift errors by more than an order of magnitude and, relative to event-based approaches, offers the advantage of continuous monitoring of clock drift; by contrast, event methods typically permit corrections only at discrete time points when phase arrivals are recorded.

Although noise cross-correlation can markedly improve timing-calibration accuracy, in practice it is susceptible to azimuthal inhomogeneity of the noise field, which leads to asymmetry between the causal and acausal branches of the EGFs [29,30,31]. To mitigate these effects, prior studies have (i) extended correlation and stacking durations to smooth the temporal variability of the noise field, (ii) employed joint inversion across multiple receivers to reduce the impact of single-azimuth sources, and (iii) applied robust fits to the cross-correlation results with distance and data-quality weights [27]. Moreover, with respect to waveform and band selection, low-frequency surface waves have long interstation sensitivity but are more vulnerable to azimuthal bias and near-field contamination, whereas high-frequency body waves offer higher SNR yet are constrained by inter-receiver spacing; choices should therefore be data dependent. Furthermore, noise cross-correlation fundamentally provides only interstation relative time offsets; in the absence of an absolute timing reference, one can recover only the relative drift trajectory, and absolute UTC must be imposed using external information [26,28].

The noise cross-correlation method has been used primarily in OBS deployments and is well suited to large interstation spacings and long observation periods. Active-source, event-based approaches are typically employed for short interstation spacing and brief campaigns; however, they require first-arrival picking, which introduces additional uncertainty. Motivated by these considerations, we propose a new technique for clock calibration of shallow-water, four-component OBN data, tailored to estimate time shifts at short receiver spacings under uneven noise-source illumination. Specifically, we use instrument-recorded clock-drift logs and active-source signals as time references, extract body-wave EGFs, and perform time-shift correction.

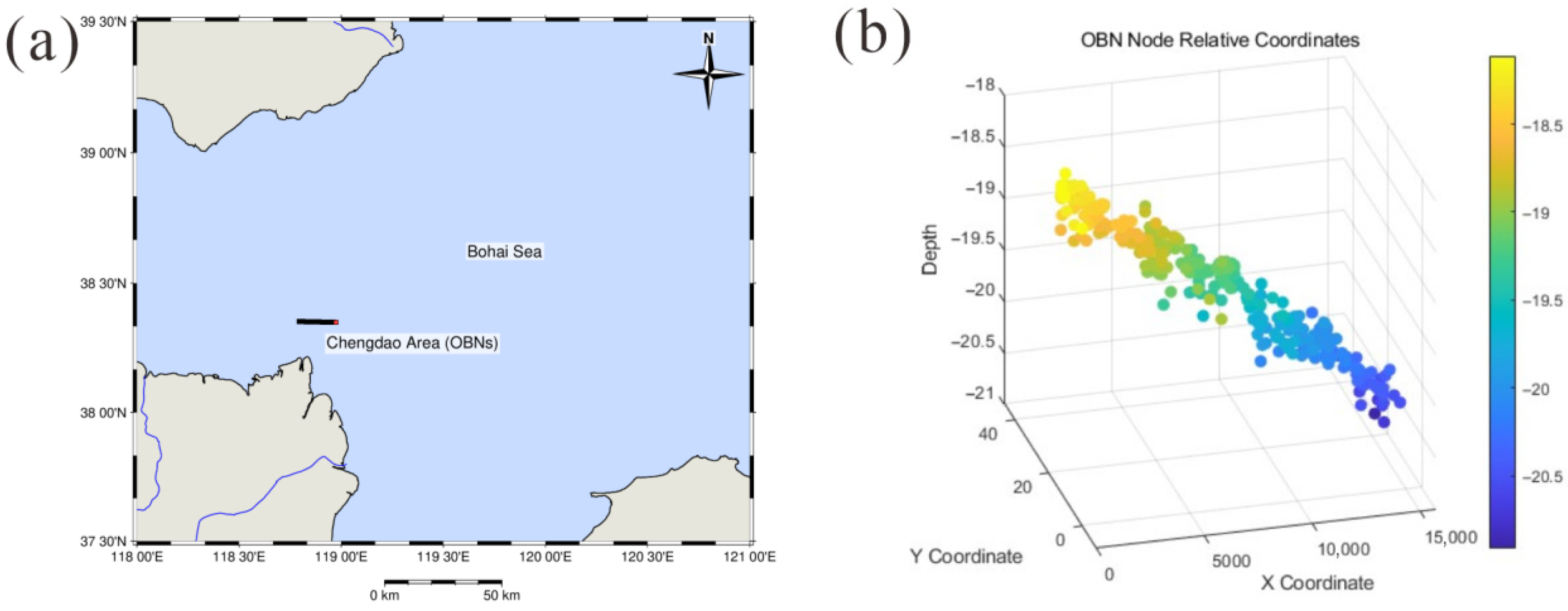
2. Materials

2.1. Data

The Chengdao area of the Bohai Sea is located in the southern Bohai region, bordered to the north by the Yellow River Delta (Figure 1a). It features a distinctive geographic setting and a complex natural environment characterized by prominent estuarine and coastal geomorphology [32]. Four-component ocean-bottom node (OBN) seismic data were acquired in a hydrocarbon field in the Chengdao area by Sinopec Shengli Oilfield Company. The data were recorded with a sampling interval of 1 ms using the GPR300 seabed nodal solution (Sercel, Carquefou, France), comprising three orthogonal ground-motion components and one hydrophone component. All data processing and analysis were performed in Python (Version 3.9.7) using ObsPy (Version 1.3.1), NumPy (Version 1.23.5), SciPy (Version 1.13.1), pandas (Version 2.2.3), Matplotlib (Version 3.4.3), and CuPy (Version 13.4.1) (including cupyx; Version 13.4.1).

The observation period spanned 22–27 September 2023, covering 315 OBN stations spaced 50 m apart. The experimental dataset included 2525 survey lines, with node IDs 6481–7737 (in increments of 4), deployed along an east–west orientation as shown in Figure 1b. Water depths ranged from 18.5 m to 21 m. All nodes were GPS-synchronized prior to deployment and re-aligned with the acquisition vessel’s clock upon recovery, allowing the determination of each instrument’s linear time drift, as illustrated in Figure 2.

2.2. Preprocessing

The raw records contain both active-source acquisition periods and background-noise segments. Two types of noise interference were identified in the raw data. The first type is low-frequency noise with dominant energy between 0 and 3 Hz, while the second type consists of anomalous amplitude signals concentrated in the 30–60 Hz band. To enhance data quality and ensure stable EGF extraction, these anomalous noise components were first attenuated; time-domain comparisons before and after suppression are shown in Figure 3 and Figure 4.

After denoising, daily power spectral densities (PSDs) for Nodes 6481 and 6485 were computed, followed by coherence analysis between the two nodes, as shown in Figure 5. The six-day coherence spectra indicate that effective coherent bands for all components are concentrated in the mid- to high-frequency range of approximately 10–100 Hz, with near-zero coherence below 10 Hz and rapid decay above 100 Hz; distinct differences are observed among components. The P component shows the highest stability and coherence, with a maximum coherence coefficient of 0.5 at 30 Hz. The X component attains a maximum coherence of 0.46 at 62.6 Hz, the vertical Z component 0.31 at 50.2 Hz, and the Y component 0.23 at 59.0 Hz with greater day-to-day fluctuations. These results indicate that EGF computation should focus on the 10–100 Hz band, and they provide component-specific weighting factors for the subsequent joint four-component time-drift inversion.

3. Methods and Technical Workflow

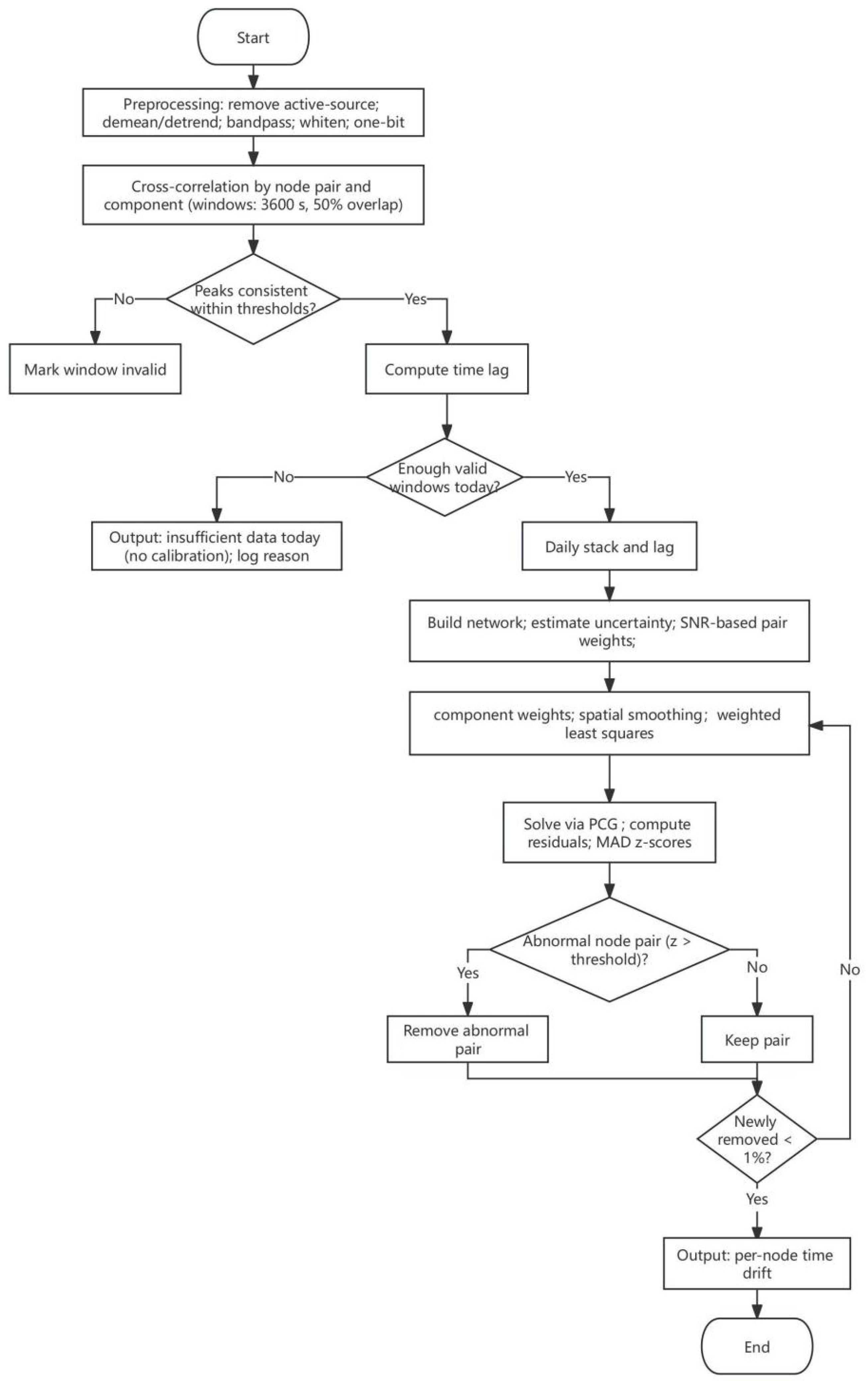
3.1. Technical Workflow

(1)

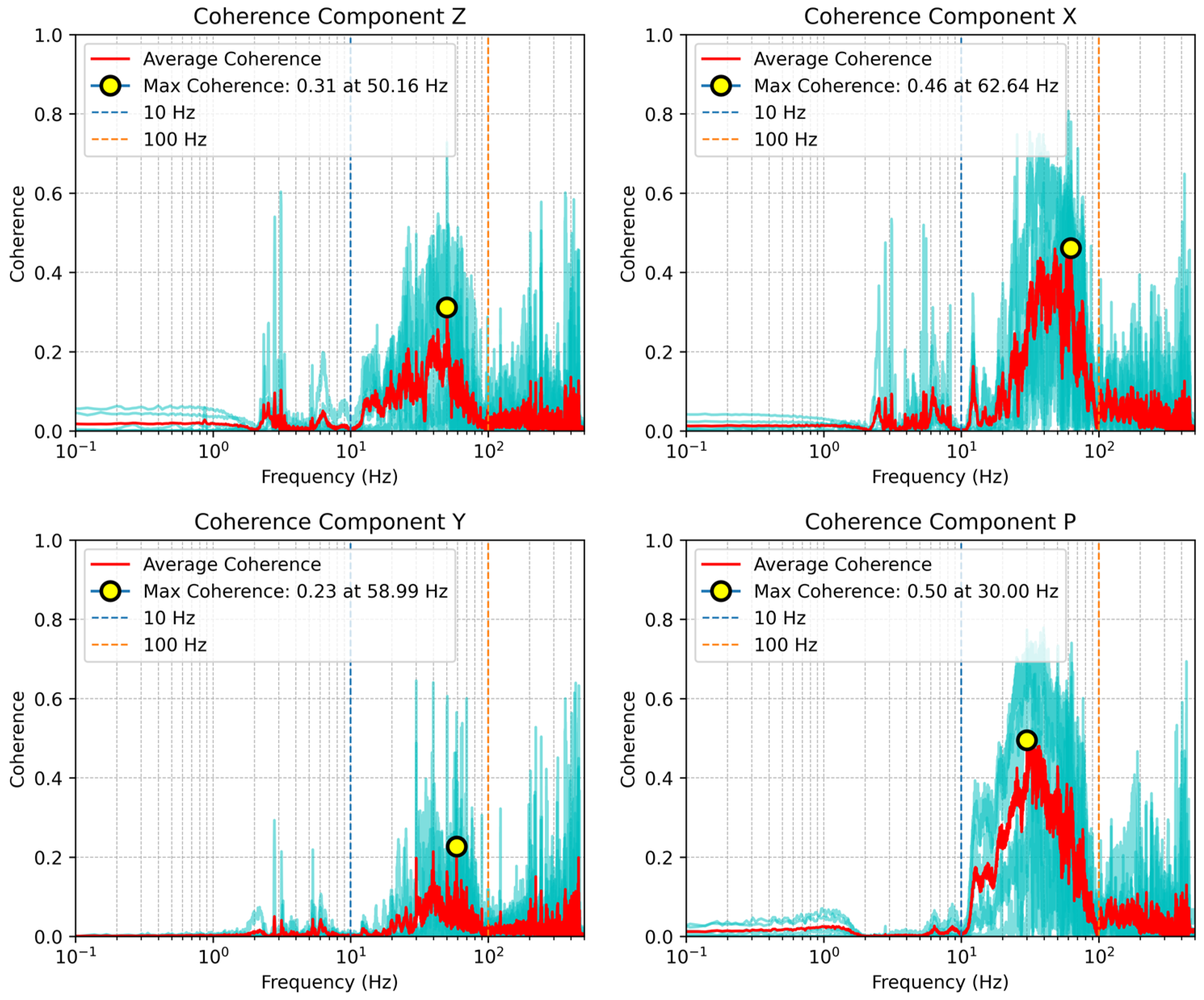
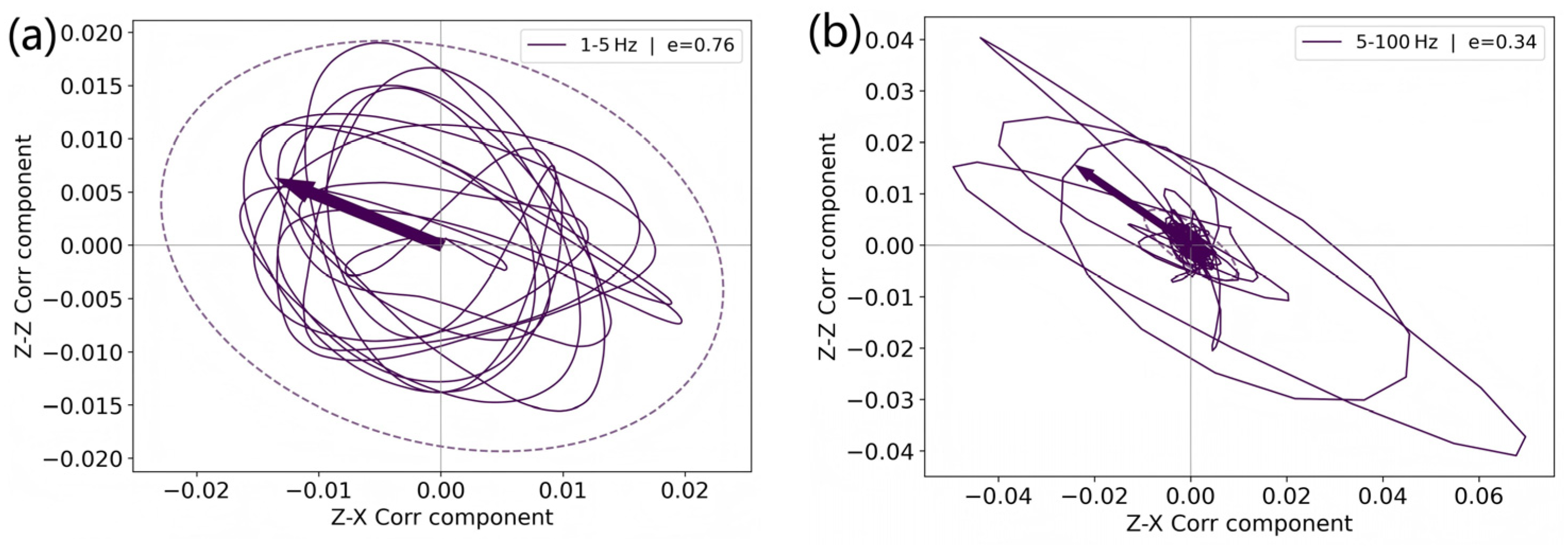
Remove the mean and trend from seismic records; apply band-pass filtering between 10 and 100 Hz (as determined from PSD–coherence analysis); perform spectral whitening and one-bit normalization.

(2)

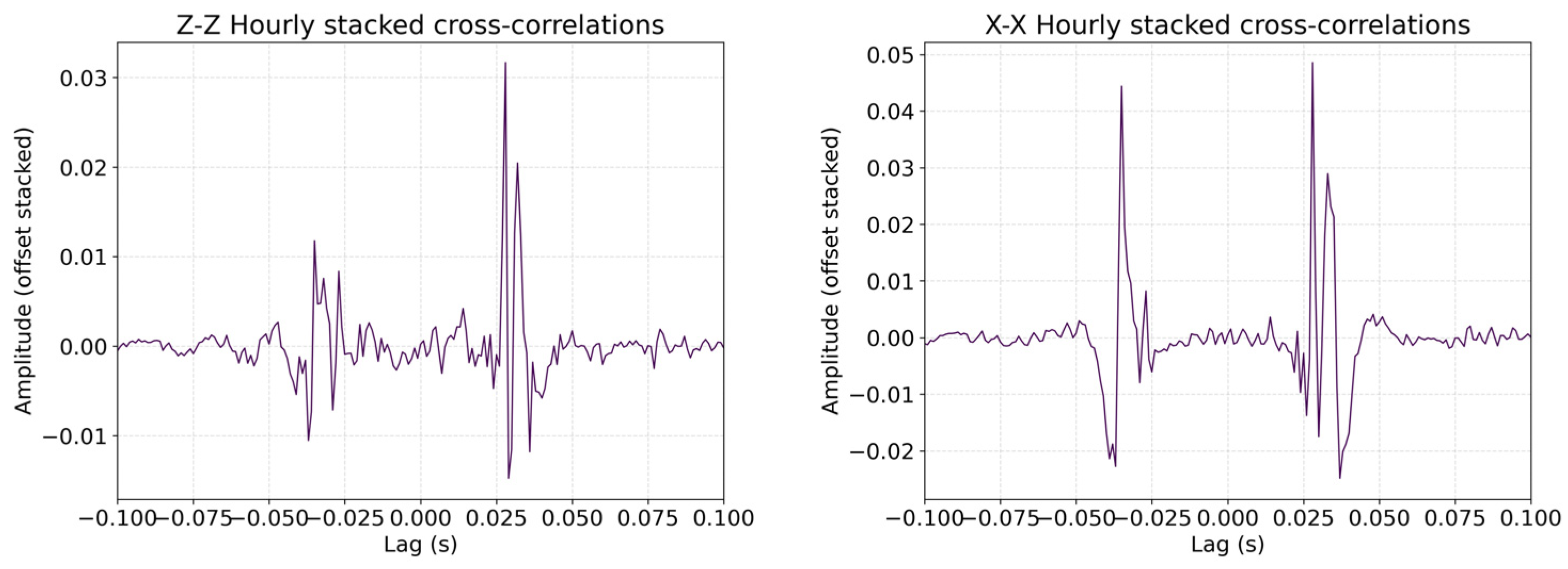
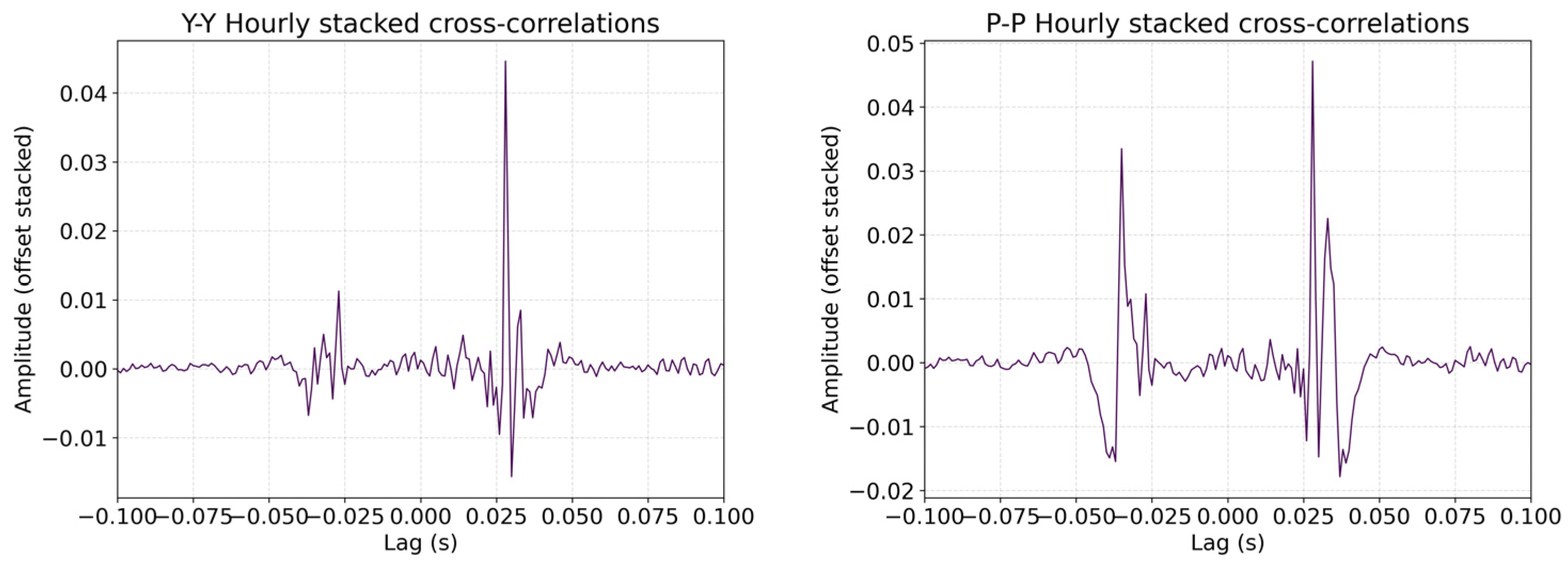
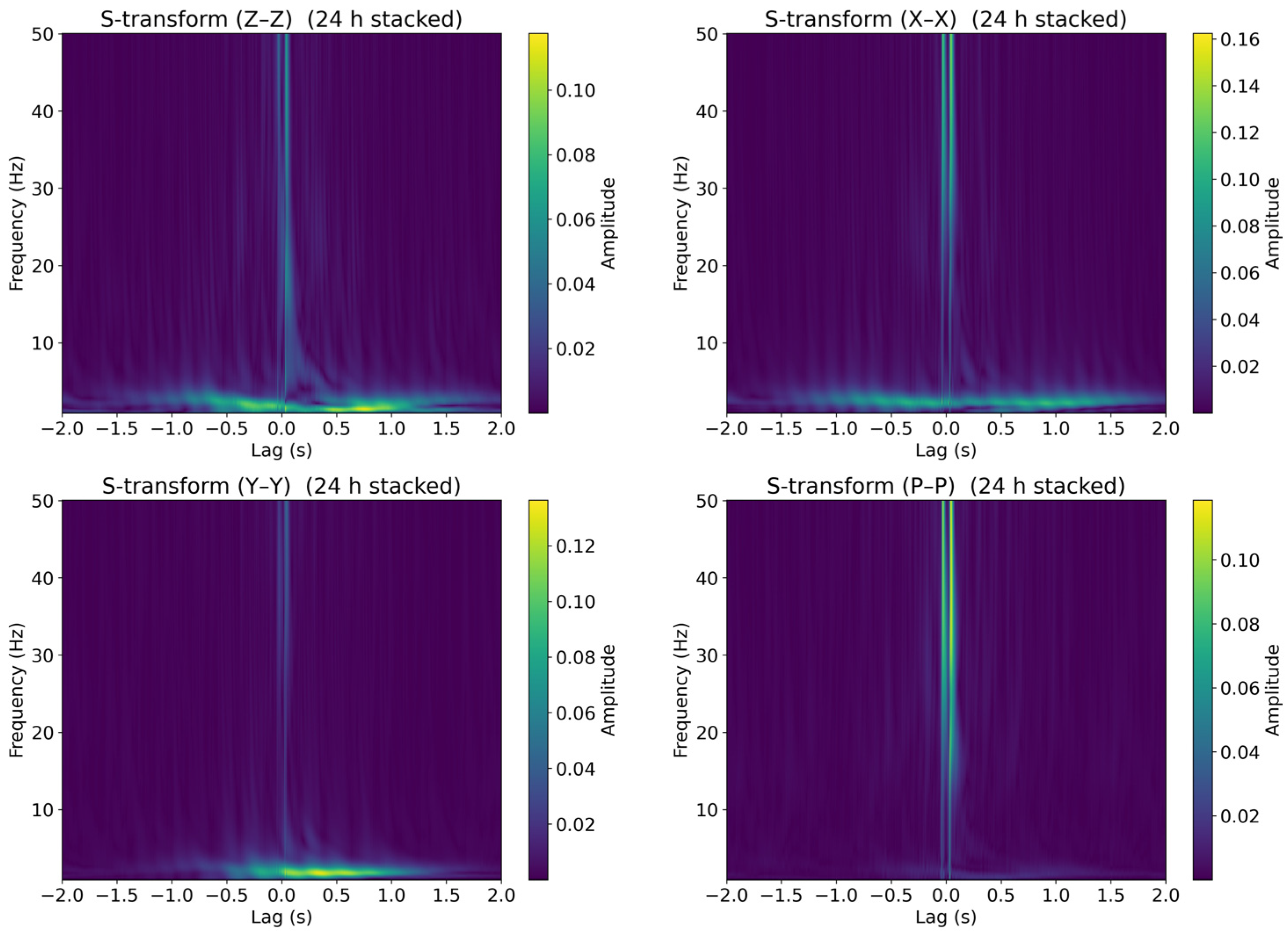
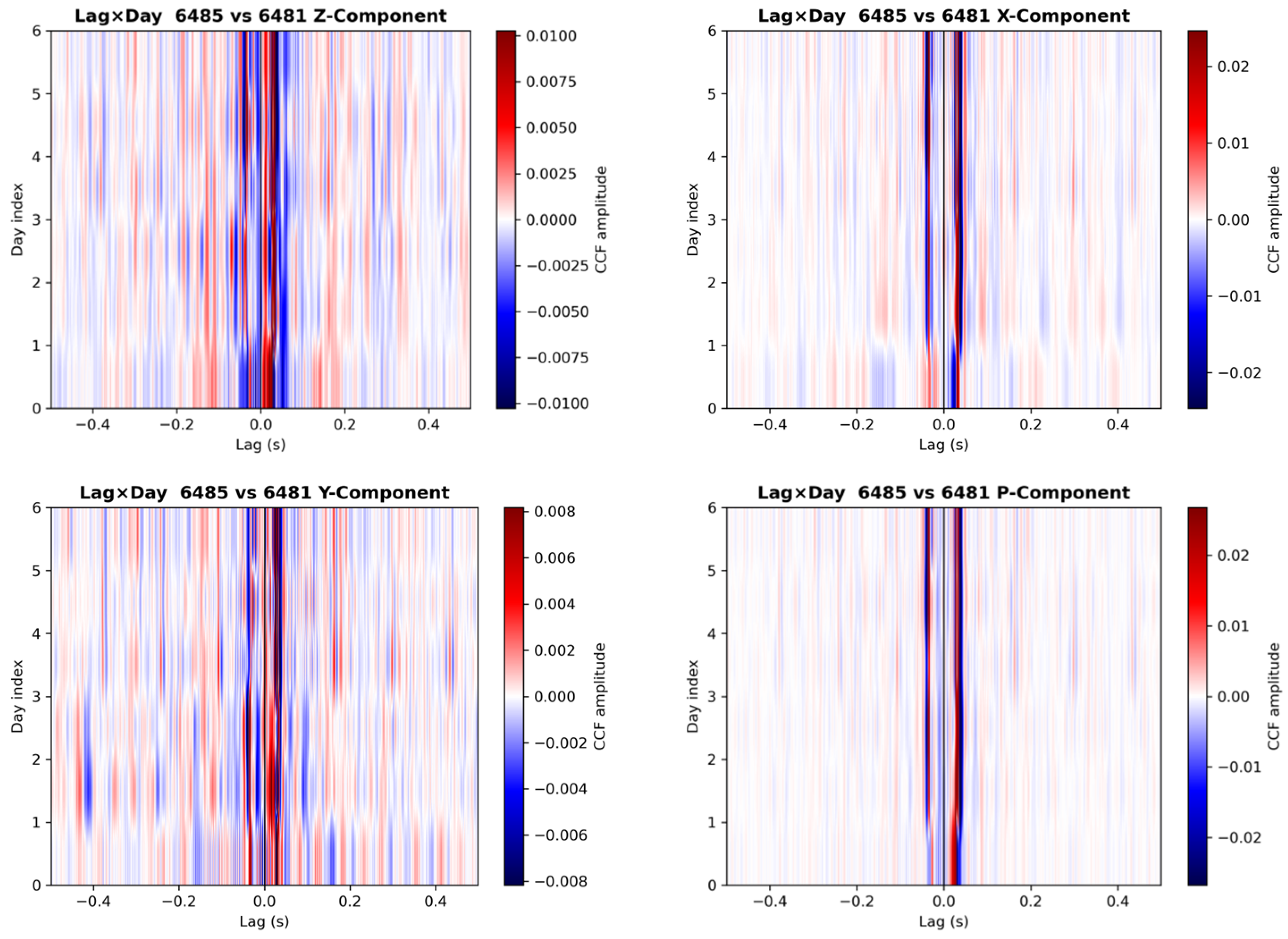
Segment daily data into 3600 s windows with 50% overlap; for each window and each component, compute cross-correlations between adjacent node pairs and extract the time delays of the dominant peaks on both positive and negative branches.

(3)

If the full width at half maximum (FWHM) of the branch peak fails to meet the criterion in Equation (1), that branch is deemed invalid; if the number of valid windows for a given day falls below the threshold, the day is regarded as invalid. The remaining valid windows are stacked to obtain the daily empirical Green’s function (EGF) and the observed P-wave time-delay difference.

(4)

Aggregate all valid adjacent node pairs of the day to form a system of observation equations; assign component weights according to SNR; construct second-order difference operators for each survey segment. Formulate the joint objective function and solve for the daily nodal time shifts using the preconditioned conjugate gradient method.

(5)

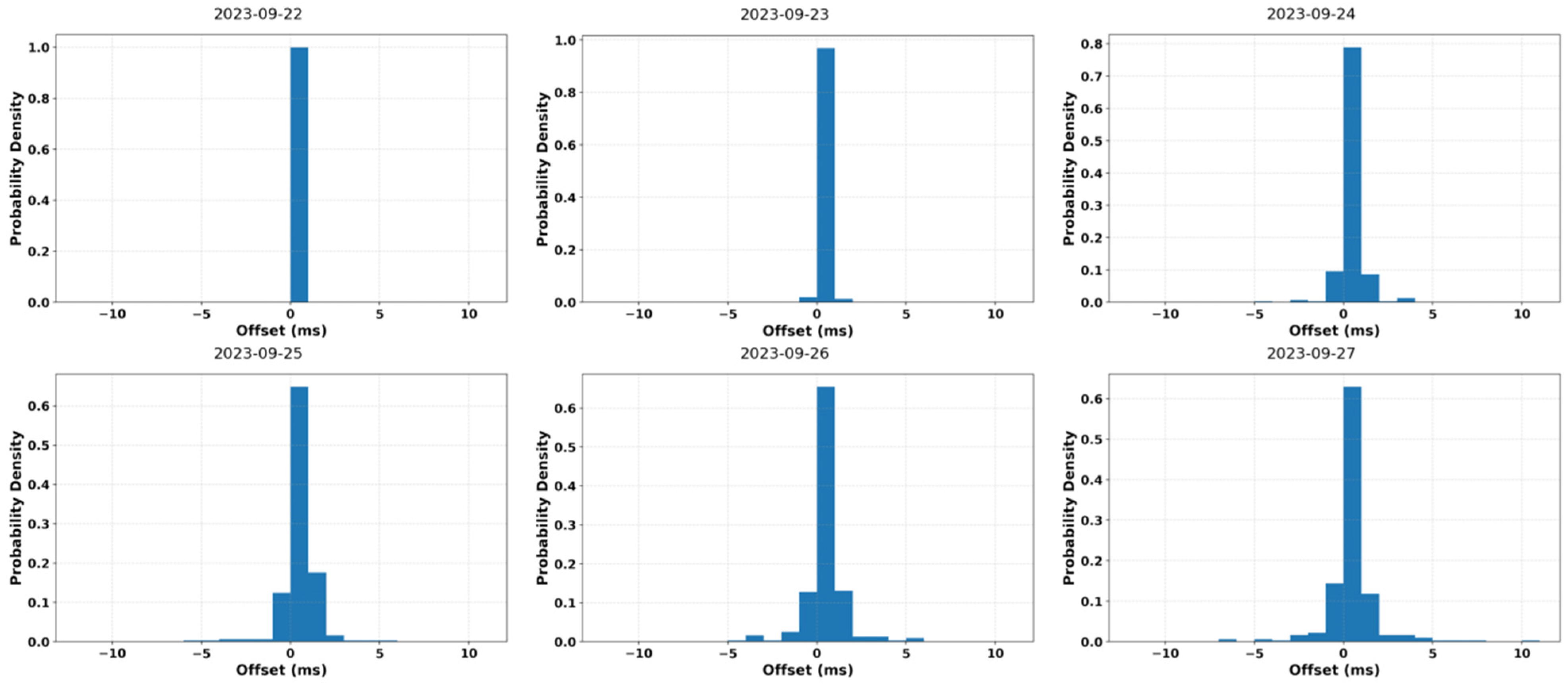
Outlier elimination is performed iteratively using a median-absolute-deviation (MAD)-based scale estimator and a z-score criterion; when the fraction of newly detected abnormal observations remains below 1% for two successive iterations, convergence is considered achieved and the iteration is terminated. If a continuous segment contains k consecutive invalid adjacent node pairs, or if the proportion of valid pairs falls below q%, the temporal continuity regularization term is strengthened to stabilize the solution. The overall technical workflow is illustrated in Figure 6.

3.2. Methods

The method adopted in this study builds upon the time-symmetry analysis framework and empirical Green’s function (EGF) theory proposed by Loviknes and Roux [14,33], incorporating several modifications tailored to the characteristics of the present dataset to perform time-delay correction. After suppressing anomalous noise and analyzing signal coherence, the continuous records were sequentially processed by demeaning and detrending, band-pass filtering, spectral whitening, and one-bit normalization. Each daily record was divided into overlapping time windows of length ${\mathrm{T}}_{\mathrm{w}\mathrm{i}\mathrm{n}}$ (1 h, 3600 s) with 50% overlap to suppress active-source interference. For each window, cross-correlation functions $\mathrm{C}\left(\mathsf{\tau }\right)$ were computed between node signals, and the positive/negative lag peaks ${\tau }^{+},{\tau }^{-}$ were identified; daily EGFs were then obtained by stacking all windows within the day.

To ensure cross-correlation symmetry, given a sampling interval of $∆\mathrm{t}=1 \mathrm{m}\mathrm{s}$, the full width at half maximum (FWHM) of the main correlation peak was denoted as FWHM. The FWHM is computed as the difference between the time lags at which the main peak reaches half of its maximum amplitude on the two sides of the peak. To quantify the consistency of peak-lag estimates across multiple windows within a day, ${\sigma }_{\tau }$ is defined as the standard deviation of the main-peak positions across all windows for that day. To remove unreliable measurements, we first apply a symmetry criterion to assess the consistency between the main peaks on the positive and negative branches, and define

$${\Delta }_{sym}=|{\mathsf{\tau }}^{+}-{\mathsf{\tau }}^{-}|$$

(1)

Here, ${\tau }^{-}$ denotes the absolute time delay (a positive value) of the negative-branch peak. When ${\Delta }_{sym}$ does not exceed the symmetry threshold $T_{\mathrm{s}\mathrm{y}\mathrm{m}}$, the measurement is considered to pass the symmetry test, where

$${\Delta }_{sym}\le T_{sym},\hspace{1em}\hspace{1em}{T}_{sym}=\max \left(10\mathsf{\Delta }t,0.5s,\mathrm{FWHM},3{\sigma }_{\tau }\right)$$

(2)

If Equation (2) is not satisfied, the corresponding branch is deemed invalid for that day; otherwise, we take ${ \tau }_P={\displaystyle \frac{1}{2}}\left({\tau }^{+}-{\tau }^{-}\right)$ as the time shift (ms). In addition, to ensure the stability of the daily estimate, we require each node pair to meet a minimum number of valid windows $N_{min}$ on that day. If the number of valid windows is less than $N_{min}=18$, the drift observation for that day is recorded as missing.

On day $\mathrm{d}$, all OBNs meeting the validity criteria are assembled into node set ${\mathcal{V}}_{\mathrm{d}}$, while valid node pairs for component $\mathrm{c}\in \mathrm{Z},\mathrm{X},\mathrm{Y},\mathrm{P}$ form a separate subset ${\epsilon }_d^c$. Let the time-drift vector of node be denoted as $x_d\in {\mathbb{R}}^{\left|{\mathcal{V}}_d\right|}$. For any node pair $e=\left(i,j\right)\in {\mathcal{E}}_d^c$, the relative time-shift observation $b_{e,c,d}$ (in milliseconds) is obtained through operation ${\tau }_p$, yielding the observation vector ${\mathbf{b}}_{c,d}\in {\mathbb{R}}^{\left|{\mathcal{E}}_d^c\right|}$. The observation model can thus be expressed as

$$b_{e,c,d}\hspace{0.33em}=\hspace{0.33em}{x}_{i,d}-x_{j,d}+{\epsilon }_{e,c,d},\hspace{1em}\hspace{1em}{\epsilon }_{e,c,d}~\mathcal{N}(0,{\sigma }_{\epsilon ,e,c,d}^2)$$

(3)

Let ${\mathbf{B}}_{c,d}\in {\mathbb{R}}^{\left|{\mathcal{E}}_d^c\right|\times \left|{\mathcal{V}}_d\right|}$ denote the incidence matrix between node pairs and nodes, where each row corresponds to a node pair $e=\left(i,j\right)$, with +1 in column $i$ and −1 in column $j$, and zeros elsewhere. To suppress high-frequency spatial noise, a second-order difference smoothing operator ${\mathbf{x}}_d$ is applied to ${\mathbf{D}}_2$.

When data are missing from some nodes along a survey line, the originally continuous line becomes segmented into $s$ continuous subsections. For each continuous subsection, an operator ${\mathbf{D}}_{2,\mathrm{s}\mathrm{u}\mathrm{b}}^{\left(s\right)}$ is constructed; all subsections are then assembled along the diagonal of a large matrix to yield the global second-order difference matrix ${\mathbf{D}}_2$ for the observation network. Accordingly, the single-component objective function is expressed as

$${\min }_{x_d}{\displaystyle \frac{1}{2}}\hspace{0.33em}\Vert B_{c,d}{x}_d-b_{c,d}{\Vert }_{W_d}^2\hspace{0.33em}+\hspace{0.33em}{\displaystyle \frac{{\lambda }_{\mathrm{s}}}{2}}\Vert D_2{x}_d{\Vert }_2^2$$

(4)

Here, $\Vert \mathbf{v}{\Vert }_{\mathbf{W}}^2={\mathbf{v}}^{\mathrm{T}}\mathbf{W}\mathbf{v},{‖\mathbf{u}‖}_2^2={\mathbf{u}}^{\mathbf{T}}\mathbf{u}$ and ${\lambda }_s>0$ denote spatial smoothing parameters. ${\mathbf{W}}_{\mathit{d}}$ is observation weight matrix ${\mathbf{W}}_{\mathit{d}}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(w_d^{snr}\right)$, which is only subject to the signal-to-noise ratio control. The calculation of SNR is based on the cross-correlation function’s RMS ratio between the signal window and the noise window:

$$SN{R}_d={\displaystyle \frac{\mathrm{RMS}\left\{C(\tau )|\tau \in Q_s\right\}}{\mathrm{RMS}\left\{C(\tau )|\tau \in Q_n\right\}}}$$

(5)

where $Q_s$ is the signal window centered around the P-wave peak time $t_p$, and $Q_n$ is the noise window that does not overlap with the signal window. We convert $SN{R}_d$ into a bounded, monotonic scalar weight $w_d^{snr}\in [0,1]$ to suppress unreliable observations while preventing extreme SNR values from dominating the solution. A simple saturating mapping is adopted:

$$w_d^{\mathrm{snr}}=\left\{\begin{array}{ll}0,\hfill & SN{R}_d<SN{R}_{\min }\hfill \\ {\displaystyle \frac{SN{R}_d-SN{R}_{\min }}{SN{R}_{\max }-SN{R}_{\min }}},\hfill & SN{R}_{\min }\le SN{R}_d<SN{R}_{\max }\hfill \\ 1,\hfill & SN{R}_d\ge SN{R}_{\max }\hfill \end{array}\right.$$

(6)

If the calculated ${SNR}_d$ is less than ${SNR}_{min}=2$, it should be discarded. If ${SNR}_d$ is greater than ${SNR}_{max}=10$, the weight defaults to 1 and will not change.

The second-order difference operator on a continuous subsequence is defined as

$$D_{2,sub}^{(s)}\in {ℝ}^{(n_s-2)\times n_s},\hspace{1em}{\left(D_{2,sub}^{(s)}x\right)}_k=x_k-2x_{k+1}+x_{k+2},\hspace{0.33em}\hspace{0.33em}k=1,\dots ,n_s-2$$

(7)

The overall operator is defined as

$$D_2\hspace{0.33em}=\hspace{0.33em}diag (D_{2,sub}^{(1)},D_{2,sub}^{(2)},\dots ,D_{2,sub}^{(S)})$$

(8)

Differentiating objective function (4) with respect to the unknown ${\mathbf{x}}_d$ and setting the derivative to zero yields the linear system in (9):

$$(B_{c,d}^{\mathrm{T}}{W}_d{B}_{c,d}+{\lambda }_s{D}_2^{\mathrm{T}}{D}_2)x_d\hspace{0.33em}=\hspace{0.33em}{B}_{c,d}^{\mathrm{T}}{W}_d{b}_{c,d}$$

(9)

To fuse the four components and enhance estimation robustness, we introduce the component weight ${\alpha }_c\in \left(0,1\right]$, and express it as the product of a component-specific weight and a signal-to-noise ratio (SNR)-based weight. Based on the six-day stacked waveforms and the mean coherence analysis of the four components shown in Figure 5, the component weights were set to fixed values: Z = 0.6, X = 0.8, Y = 0.2, and P = 1.0, defined as

$$w_{c,d}={\alpha }_c\cdot w_d^{snr},W_{c,d}=diag(w_{c,d})$$

(10)

Accordingly, the objective function combining four-component fusion, spatial smoothing, and temporal continuity constraints is

$${\min }_{x_d}\hspace{0.33em}{\displaystyle \frac{1}{2}}{\displaystyle \sum _{c\in \{Z,X,Y,P\}}\Vert B_{c,d}{x}_d-b_{c,d}{\Vert }_{W_{c,d}}^2+\frac{{\lambda }_s}{2}\Vert D_2{x}_d{\Vert }_2^2+\frac{{\lambda }_t}{2}\Vert x_d-x_{d-1}{\Vert }_2^2}$$

(11)

On the first day, set ${\lambda }_t=0$, for $d>1$ use the previous day’s inversion as the initialization; enforce the prior day’s solution ${\mathbf{x}}_{d-1}$ as a constraint. With ${\lambda }_t$ as the weighting coefficient, differentiating objective (11) with respect to the unknown ${\mathbf{x}}_d$ and setting the derivative to zero yields the matrix-form linear system:

$$({\displaystyle \sum _c{B}_{c,d}^{\mathrm{T}}{W}_{c,d}{B}_{c,d}\hspace{0.33em}+\hspace{0.33em}{\lambda }_s{D}_2^{\mathrm{T}}{D}_2\hspace{0.33em}+\hspace{0.33em}{\lambda }_{t}I})x_d\hspace{0.33em}=\hspace{0.33em}{\displaystyle \sum _c{\alpha }_c}{B}_{c,d}^{\mathrm{T}}{W}_{c,d}{b}_{c,d}\hspace{0.33em}+\hspace{0.33em}{\lambda }_t{x}_{d-1}$$

(12)

The resulting matrix is symmetrically positive definite with a sparse banded structure, making it suitable for iterative solvers. We solve it using the preconditioned conjugate gradient (PCG, Preconditioned Conjugate Gradient) method. Define the residuals as

$$r_{c,d}\hspace{0.33em}=\hspace{0.33em}{B}_{c,d}{x}_d-b_{c,d}$$

(13)

Here, ${\mathbf{r}}_{c,d}$ denotes the residual vector for component $c$ over observation period $d$ across node pairs.

To improve robustness, we employ MAD (median absolute deviation)-based standardized statistics; the MAD and the robust scale estimator are given by

$$\left\{\begin{array}{c}MAD(r_{c,d})=median(\left|r_{c,d}-median(r_{c,d})\right|)\\ \stackrel{\wedge }{\sigma }=1.4862MAD(r_{c,d})\\ z_{c,d}={\displaystyle \frac{\left|r_{c,d}\right|}{\stackrel{\wedge }{\sigma }}}\end{array}\right.$$

(14)

Here, $MA{D}_{c,d}$ is computed based on the residuals of all valid node pairs for component $c$ on date $d$. Let $\phi$ be the threshold (default $\phi =3$); if condition $\left|z_{c,d}\right|>\phi$ holds, the adjacent node pair is deemed anomalous and removed. Outlier removal for adjacent node pairs is performed iteratively: we re-estimate and update after each pass until the newly identified outliers fall below 1%, at which point convergence is declared. If, on a given day, a continuous segment exhibits consecutive node-pair failures, or the proportion of valid adjacent node pairs falls below $q\mathrm{\%}$ (baseline $k=3, q=60\mathrm{\%}$), the region is considered observationally interrupted.

4. Results and Discussion

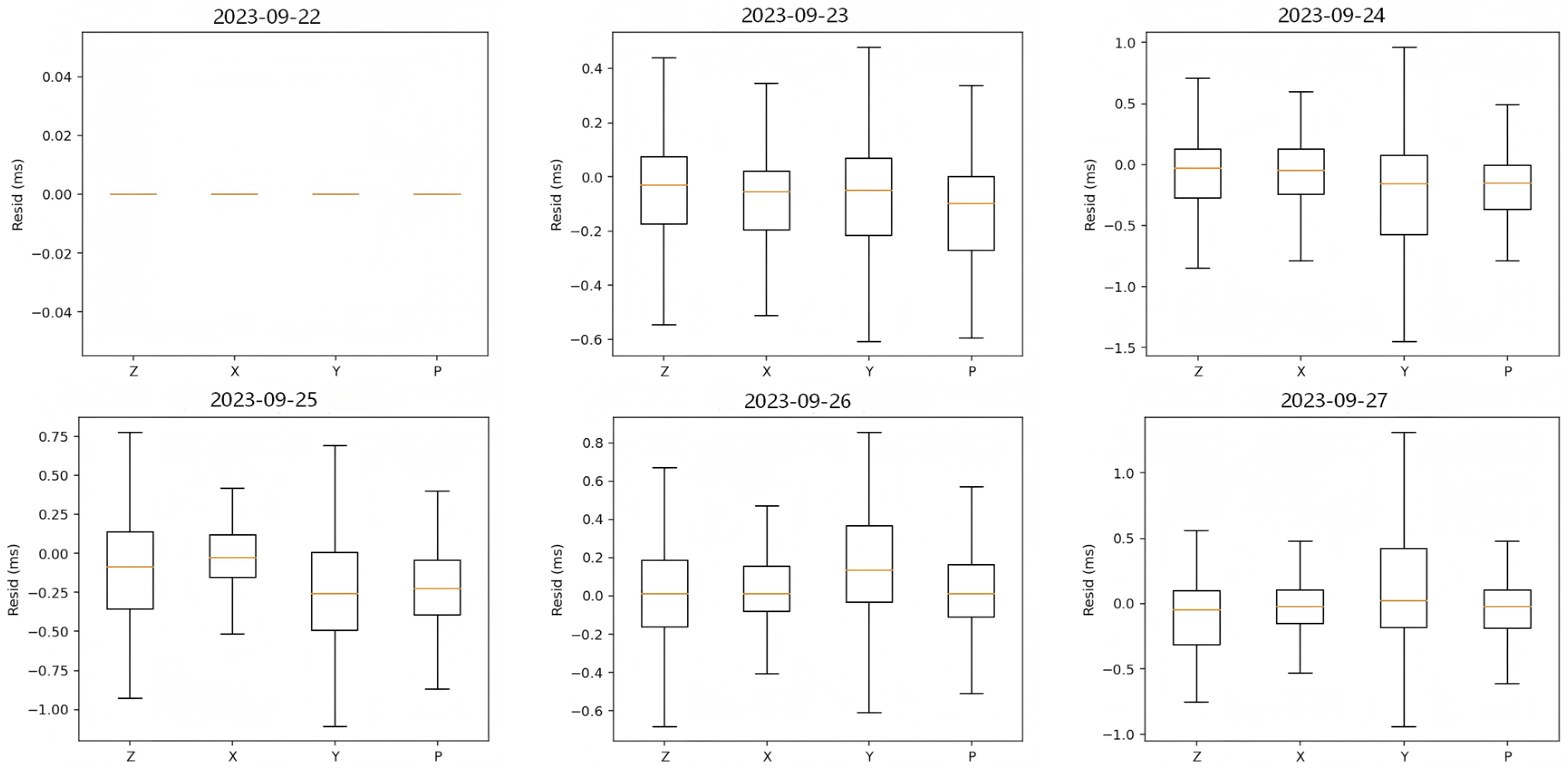
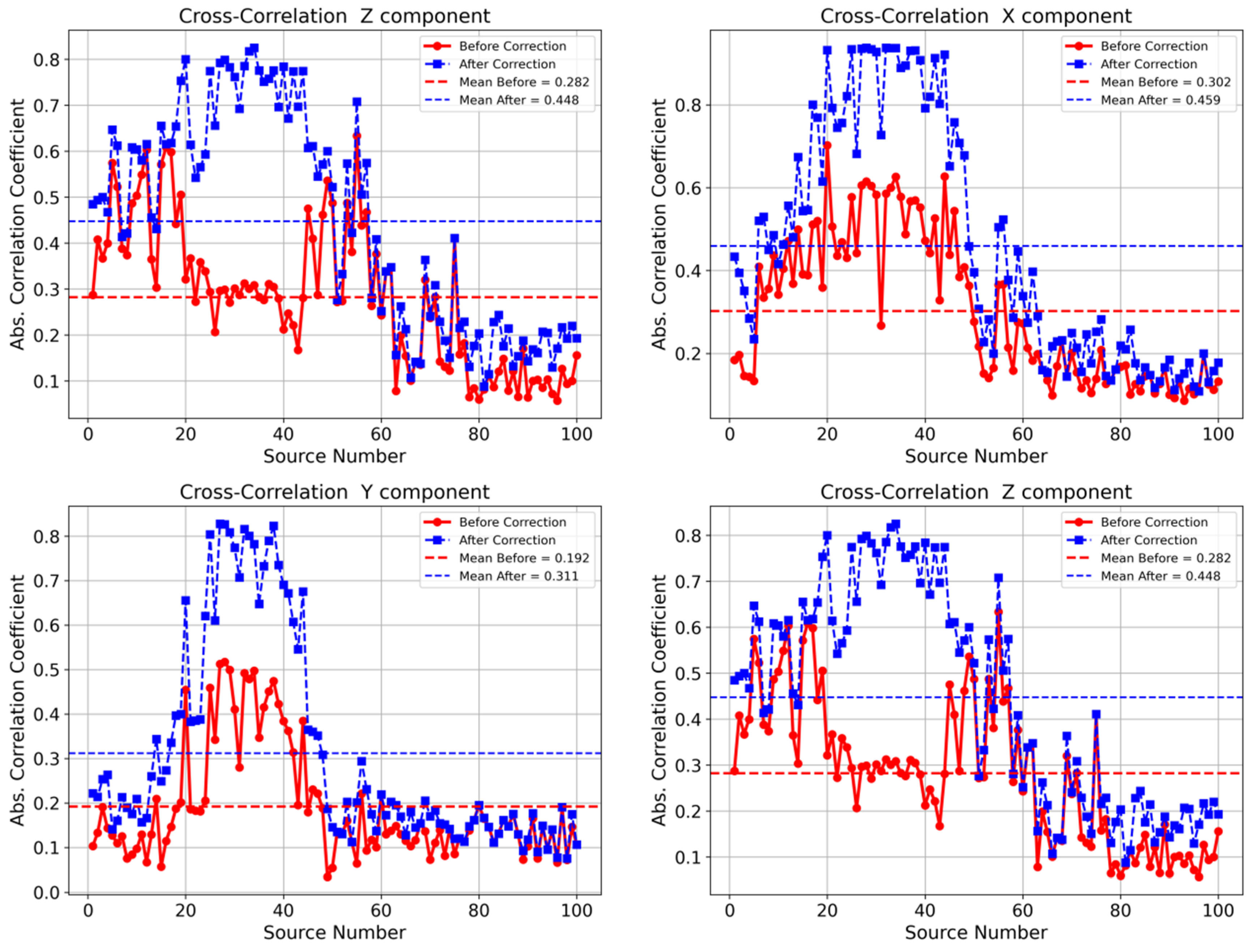
4.1. Results

Following the above methodology and workflow, we first computed the EGF between nodes 6481 and 6485 using 1 h cross-correlation windows with 50% overlap; the 24 h stacked result is shown in Figure 7, and the corresponding time–frequency spectrum is shown in Figure 8.

In Figure 8, a very narrow, broadband high-energy band emerges at t ≈ 0.024 s in the four-component spectra, with P–P and X–X being most prominent and Z–Z and Y–Y slightly weaker; the implied velocity is about 2 km/s. In the 1–5 Hz band, the three-component time–frequency spectra display a V-shaped dispersion cone with EGF amplitude asymmetry, in line with an anisotropic noise source distribution [29,30,31]. From the end of the three-component dispersion cone at t = 0.05 s, the estimated velocity is ~1 km/s [34,35]. The polarization analysis across different bands is shown in Figure 9.

In Figure 9a, the particle-motion trajectory appears knotted, yet the overall envelope forms a counterclockwise ellipse with ellipticity e ≈ 0.76, indicating Scholte waves dominate in this band [31,36,37,38,39,40,41]. The confidence ellipse exceeds the particle-motion locus in area, implying substantial surface-wave phase variability across time windows. The associated time–frequency plot shows a V-shaped dispersion cone at 1–5 Hz, corresponding to velocities of 0.8–1.2 km/s. The computed principal-axis azimuth is 154.9° (mathematical coordinates, 0° = +X to the right, positive counterclockwise).

In Figure 9b, the particle-motion principal axis and solid-line trajectory are spindle-shaped, and the dashed confidence ellipse is highly flattened; the ellipticity e ≈ 0.33 approaches linear polarization, matching the broadband energy at t ≈ 0.024 s and is therefore indicative of body waves [28,42]. The principal-axis azimuth is 147.6°, differing by only ~7° from that of the low-frequency surface waves. These analyses indicate that low-frequency surface waves and high-frequency body waves share the same propagation direction (from 6481 toward 6485), consistent with the positive/negative branch energy asymmetry in Figure 8, confirming a single-sided dominant noise source.

In a marine setting with 50 m node spacing, single-sided noise azimuth, and active-source interference, the P-wave appears in the cross-correlation as a solitary peak only a few milliseconds wide—nearly nondispersive, linearly polarized, and with a peak travel time insensitive to source distribution and band selection—allowing clock drift to be pinpointed within a ±0.05 s window. Accordingly, we adopt the P-wave as the timing-offset reference to enhance robustness and baseline accuracy of clock calibration. Guided by PSD-coherence analysis, we apply a 10–100 Hz band-pass; daily stacked cross-correlations for different components of adjacent nodes (e.g., 6481–6485) are shown in Figure 10. In practice, inter-component timing estimates may differ; component weighting and joint inversion further suppress these discrepancies in Figure 11, yielding the final time drift for each node.

Using 22 September 2023 as the zero reference, node 6481 remained within low-millisecond fluctuations over the subsequent five days. Specifically, the X/Y components stayed within ±2 ms; the P component exhibited a notable −6 ms negative drift on the 27th; and the Z component showed a +6 ms positive drift on the 25th. By contrast, the multi-component combined solution effectively suppresses extremal excursions seen in single-component estimates, demonstrating greater robustness to inter-component differences and thus serving as a superior estimate of node time drift.

For 22–27 September 2023, daily time drifts for all nodes were obtained from EGFs across 315 nodes, as shown in Figure 12.

Figure 12 indicates there are 315 nodes along the profile, with nodes 7061 and 7249 failing (no data over the entire period), partitioning the array into three natural subchains: Chain 1: 6481–7057 (n = 145), Chain 2: 7065–7245 (n = 46), and Chain 3: 7253–7737 (n = 122). Using 22 September 2023 as day-zero, daily drifts remain centered near 0 ms; the histogram in Figure 13 shows that ≥90% of nodes lie within ~±1–2 ms, indicating overall stability after linear correction, though some nodes gradually deviate over time—for example, on 9–27 nodes 6657 and 6733 reach −7 ms, while node 6665 reaches +10 ms.

Figure 14 shows that, except for a few dates, the median of the residuals of each component is close to 0 ms (for example, 23 September 2023, 24 September, 26 September, 27 September), indicating that there is no significant systematic deviation in the overall inversion results, and the diural-scale fitting is relatively stable at the center position. There are significant differences in the degree of dispersion among different components: on most dates, the boxes of the X and P components are narrower and the residuals are more concentrated. The Z portion comes second. However, the Y-component consistently demonstrated significant discreteness, especially on 24 September and 27 September, which proved reasonable to assign a lower weight to the Y-component to mitigate its impact on the final solution.

Using the estimated drifts, we selected an active-source shot on 27 September for validation; for nodes 6481 and 6485, the common-receiver gather cross-correlation coefficients before and after timing-drift correction are compared in Figure 15.

Figure 15 shows that post-correction mean correlation rises significantly for every component (about +0.12–+0.19), and certain single-shot correlations improve by ~0.6. These results indicate a stable millisecond-level relative timing offset between the two nodes; correcting for this offset effectively removes phase biases and substantially improves coherence.

To validate the effectiveness of the time-delay correction, we first computed the expected median direct-arrival travel-time difference from the two shot coordinates ${dt}_{exp}\approx 50.104 \mathrm{m}\mathrm{s}$. We then loaded the drift estimates on 27 September 2023, preprocessed the common-shot gathers, and picked the peak cross-correlation lag $\left(dt\right)$ within the search window to obtain the pre-correction lag $\left(d{t}_{pre}\right)$ and the post-correction lag $\left({dt}_{post}\right)$ after applying Offset as an integer-sample shift. The misfit was defined as $\mathrm{e}\mathrm{r}\mathrm{r}=\left|\left|\mathrm{d}\mathrm{t}\right|-{dt}_{exp}\right|$, and we summarized the median misfit and its change $∆err={err}_{pre}-{err}_{post}$ using only the non-zero-drift nodes (N = 116). As shown in

Table 1. Comparison between expected and measured time lags (median values, ms).

Component	Number of Effective Observations	Median Expected Delay (ms)	Median Error Before Correction (ms)	Median Error After Correction (ms)
P	116	50.103981	3.896019	2.103981
Z	116	50.103981	11.896019	9.896019
X	116	50.103981	7.103981	5.103981
Y	116	50.103981	4.896019	3.896019

, across all four components, the corrected lags became closer to the expected direct-arrival value: the median misfit decreased from 3.896, 11.896, 7.104, and 4.896 ms to 2.104, 9.896, 5.104, and 3.896 ms for P, Z, X, and Y, respectively, corresponding to a median improvement of approximately 1–2 ms. This is consistent with the drift distribution on 27 September 2023, which is concentrated around ~1 ms (Figure 13).

4.2. Discussion

The field site is a challenging, very shallow, short-spacing (50 m) OBN line with one-sided noise azimuth and active-source interference. In these conditions the P–P EGF appears as a narrow, nearly non-dispersive, linearly polarized spike, whose peak time is insensitive to frequency band and noise direction, enabling reliable alignment within a ±0.05 s window. This empirical behavior directly addresses a well-known weakness of conventional surface-wave-based timing (Scholte/Rayleigh), where azimuthal imbalance produces asymmetric cross-correlations and biased time shifts; extending stack length, multi-receiver inversions, and robust weighting are common mitigations in that literature. Here, by pivoting to body-wave EGFs and fusing four components, the method sidesteps the symmetry assumption and capitalizes on a repeatable arrival that is less sensitive to the site’s directional noise and band selection.

Methodologically, the study unifies the four components in a single objective, with SNR- and coherence-based weights, and adds second-order spatial differencing (per sub-chain) plus a time-continuity constraint that ties each day to the previous day’s solution. This stabilizes the inversion when data gaps break the line into sub-chains, preventing spurious extremes in segment endpoints and along gaps. The MAD-z outlier scheme and an adaptive increase in the temporal smoothness term further ensure convergence and robustness during iterative pruning. Collectively, these choices are consistent with the aim of suppressing high-frequency oscillations while preserving true millisecond-scale drifts.

Two levels of evidence support performance:

(1)

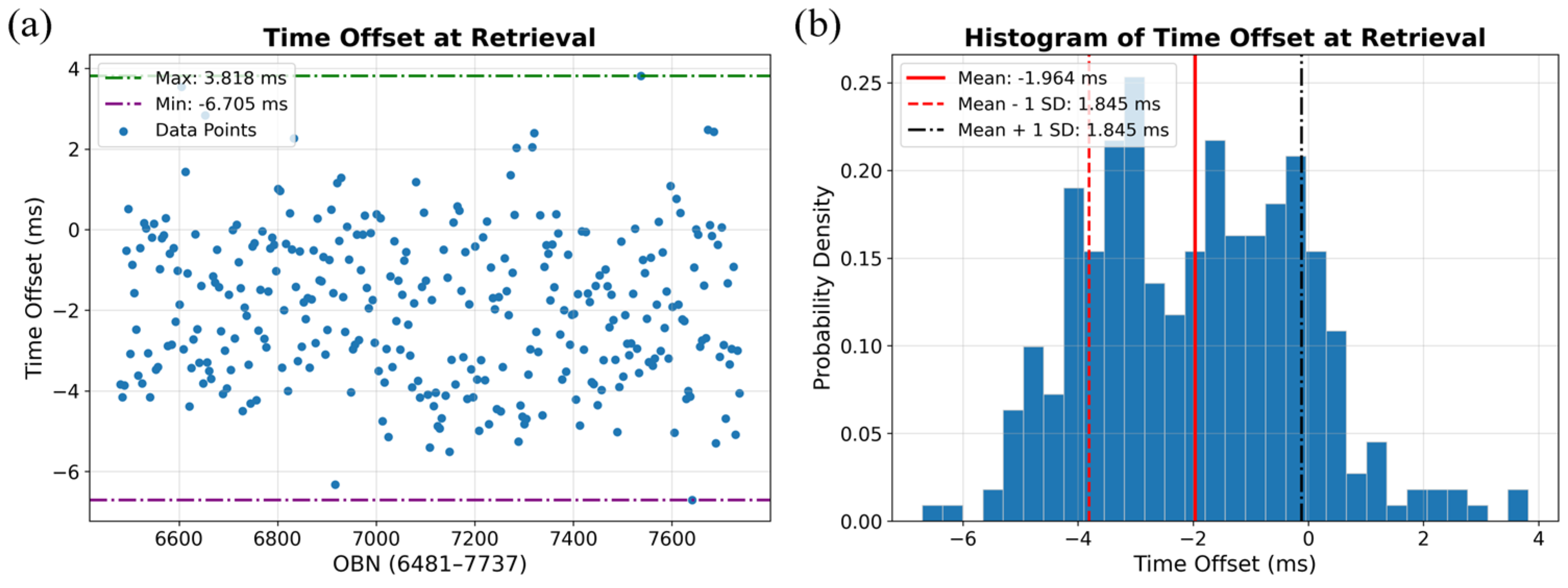
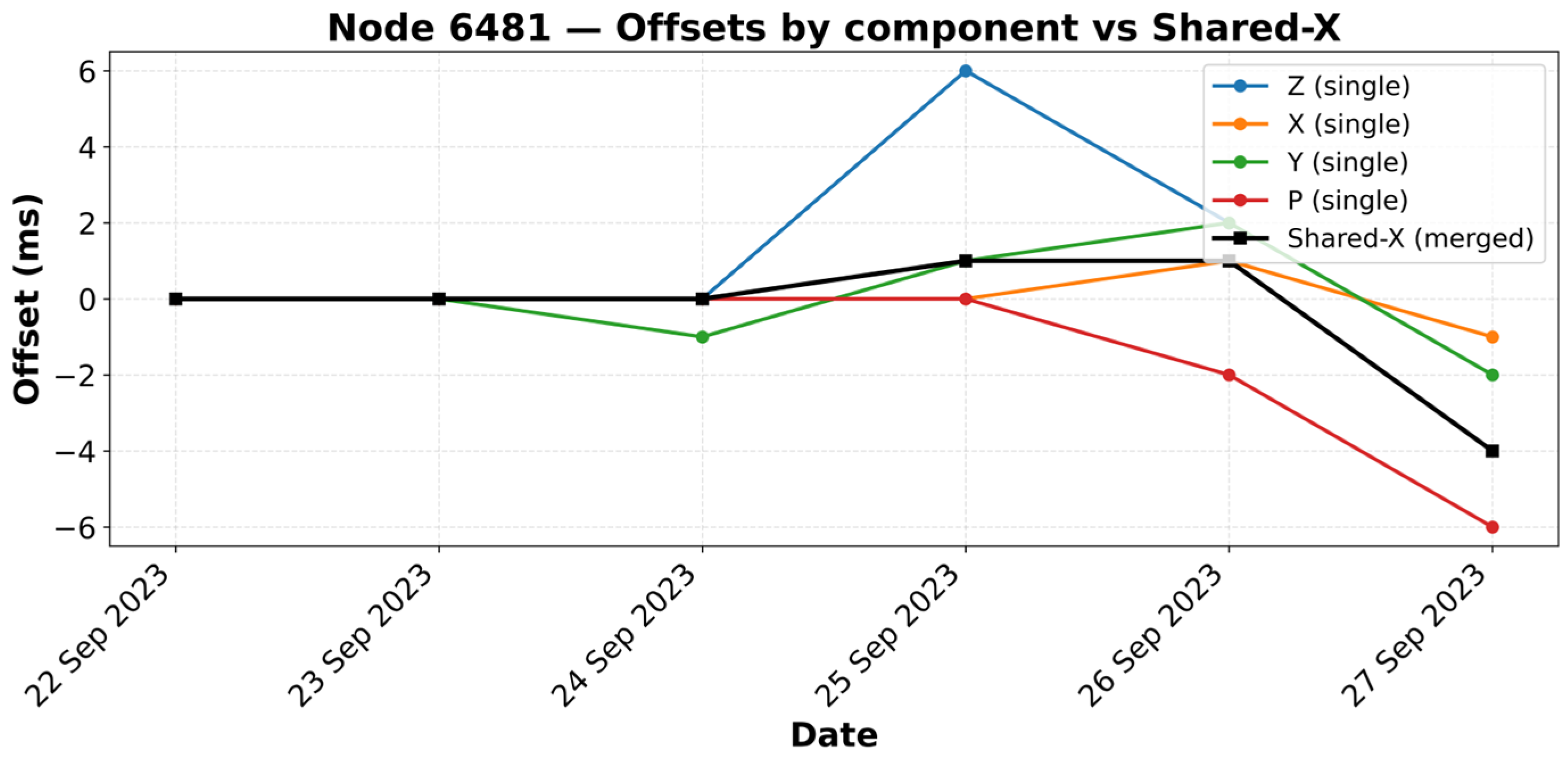
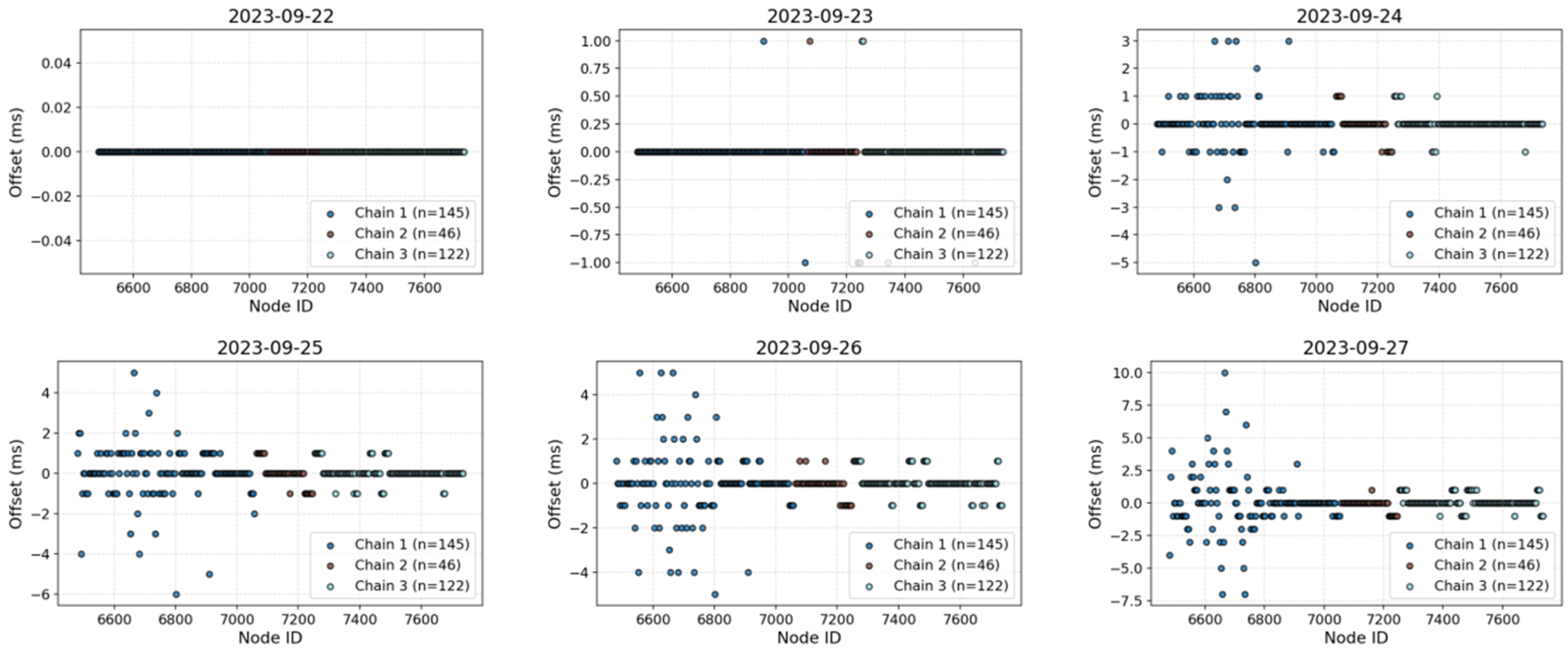
Node-wise and array-wise drift behavior. Across 315 nodes over six days, daily drifts stay centered near 0 ms for ≥90% of nodes (≈±1–2 ms), but a subset shows gradual growth to 7–10 ms by day six—behavior that the method captures without over-smoothing. For a representative node (6481), single-component outliers (e.g., Z: +6 ms, P: −6 ms on particular days) are attenuated in the four-component fused solution, demonstrating the benefit of component fusion for robustness.

(2)

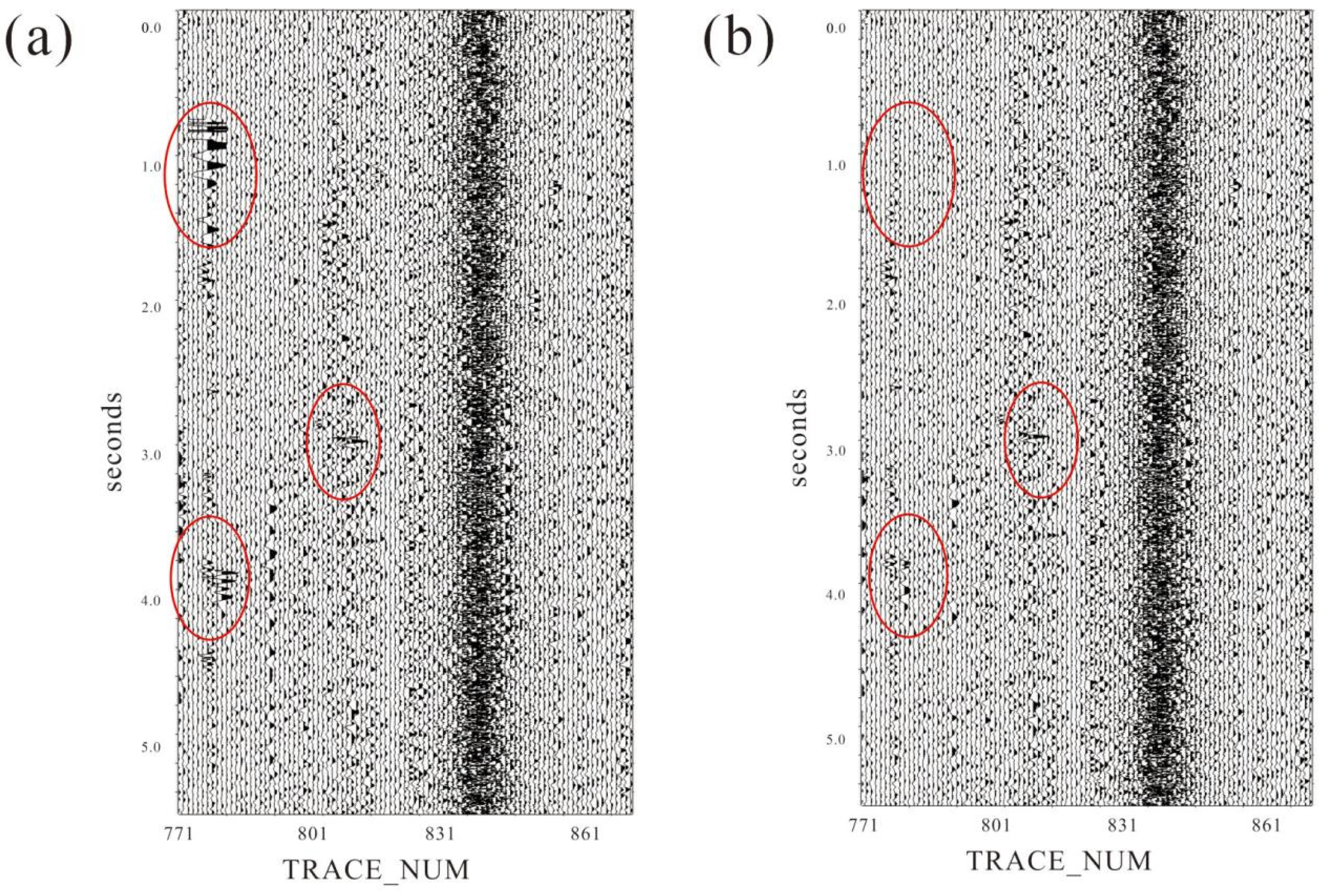
Shot-gather correlation uplift. After applying fixed ms-level timing corrections implied by the inversion, cross-component correlation increases by about +0.12–+0.19 on average, with some shots improving by ≈+0.6, directly linking the time-shift solution to phase-alignment gains in active-source data.

Traditional ambient-noise clock-correction in OBN often relies on surface waves and assumes near-symmetric NCCFs; study-specific issues like directional noise, near-field contamination, and band-dependent dispersion motivate longer stacks, multi-receiver inversions, and quality weighting. This study confirms those challenges at the site (V-shaped dispersion 1–5 Hz, amplitude asymmetry) and justifies the P-wave choice with observed narrow, broadband spikes near |t|≈0.024 s (~2 km/s) and aligned body/surface-wave azimuths. In doing so, it extends ambient-noise timing correction to short-aperture, shallow-water OBN settings where surface-wave symmetry is unreliable, while keeping compatibility with active-source QC via the correlation uplift test.

Although the method demonstrates good stability and consistency, the following two limitations remain:

(1)

Temporal scope. The evaluation covers six consecutive days; longer deployments may exhibit drift nonlinearity and step changes beyond those observed here, even after linear pre-correction.

(2)

Geometry and site specificity. The success of P-wave EGFs hinges on short inter-node spacing and the presence of a repeatable, narrow P arrival in ambient data; larger spacings or different seabed/ambient regimes may reduce P-wave SNR and alter optimal bands (10–100 Hz here).

5. Conclusions

In this study, we employed 315 seabed nodes to collect data from 22 September 2023 to 27 September 2023. The tests showed that in complex scenarios with extremely shallow water, short node spacing (50 m), and a one-sided dominant noise azimuth with active-source interference, using body-wave (P-wave) empirical Green’s functions (EGFs) as the timing reference and performing a four-component joint time-shift inversion is effective. Compared to traditional methods relying on surface-wave symmetry, the P-wave EGFs in the study region exhibit narrow pulses, nearly non-dispersive, and linearly polarized characteristics. Their peak travel time is insensitive to bandwidth and noise azimuth, enabling reliable alignment within a ±0.05 s search window, thereby improving the accuracy and repeatability of time-shift estimates.

In cases where adjacent nodes experience data loss and the survey line is broken into multiple small segments, directly calculating time shifts using the noise cross-correlation method is susceptible to errors caused by these line breaks. To address this, we construct second-order difference smoothing regularization within each smaller survey segment and introduce zero-mean to reduce errors, thereby constraining unreasonable extreme values in time drift and obtaining accurate time drift estimates. In the case of multiple components, we use the same objective function to represent the time shifts in each component, incorporating signal-to-noise ratio weights, coherence coefficient weights, and constraints from the previous day’s inversion results. This approach preserves time-shift information for each component while preventing inconsistencies between components from interfering with the solution, resulting in a multi-component joint time-shift correction method.

In summary, the multi-component joint weighted inversion and time-continuity constrained time-shift correction method based on body-wave EGFs demonstrates good robustness under shallow marine OBN conditions with short spacing, single-sided noise, and active-source interference. The results show that in the early stages of observation, the time drift of each node is close to zero with small fluctuations. Over time, the drifts gradually increase, and accumulation of error produces extreme values of approximately 7–10 ms for some nodes on the final day. The time-shift correction of node data using this method leads to a significant increase in the average cross-correlation coefficients for each component, demonstrating that this method effectively eliminates time jumps and is superior to traditional single-component surface-wave symmetry approaches, offering a high-precision time reference for multi-component data processing.