Analysis on Inner Flow Field and Hydrodynamic Force on Flexible Mining Pipeline Under Bending States
Abstract
1. Introduction
2. Solid–Liquid Two-Phase Flow Numerical Model
2.1. Mathematical Model
- (1)
- Governing equations
- (2)
- Turbulence model
2.2. Validation of Multiphase-Flow Numerical Method
- (1)
- Inlet condition: Velocity inlet at 3 m/s, with turbulent intensity and hydraulic diameter calculated and set;
- (2)
- Wall condition: No-slip wall condition applied;
- (3)
- Outlet condition: Pressure outlet with gauge pressure defined as 0, turbulent intensity, and backflow hydraulic diameter set identical to the inlet.
3. Analysis of Flow Field in the Curved Riser
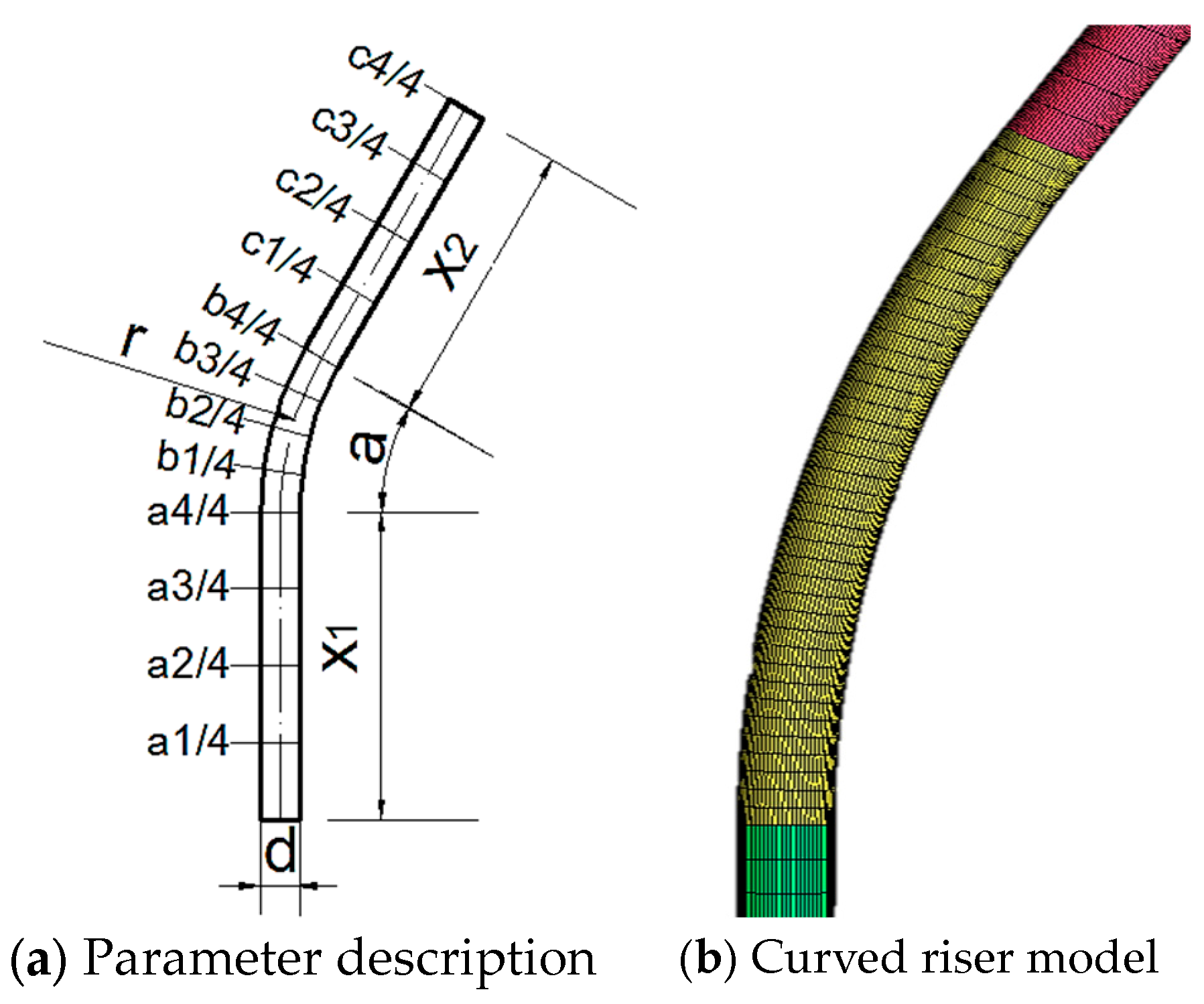
3.1. Establishment of Curved Riser Model
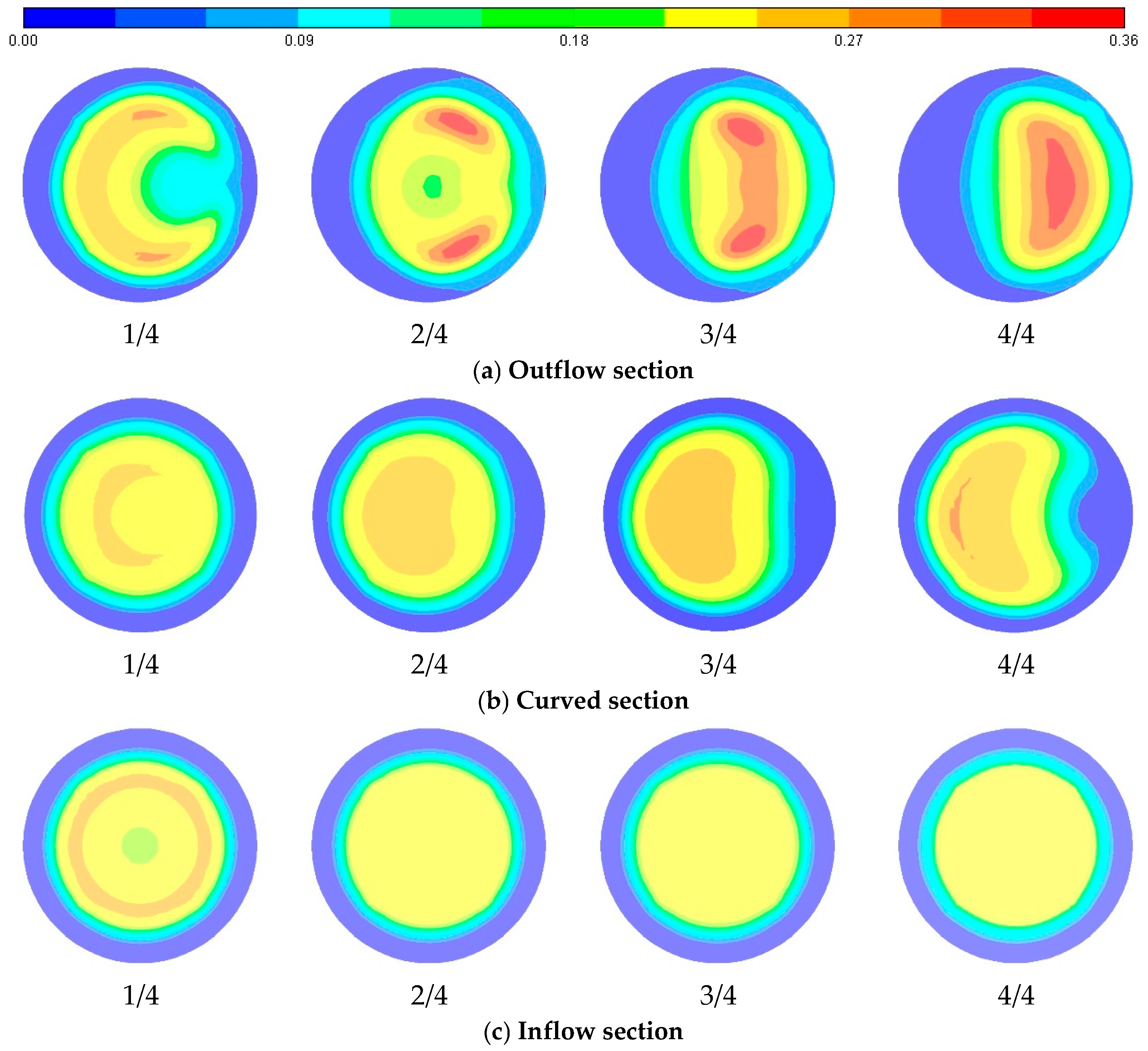
3.2. Distribution of Particle Volume Fraction
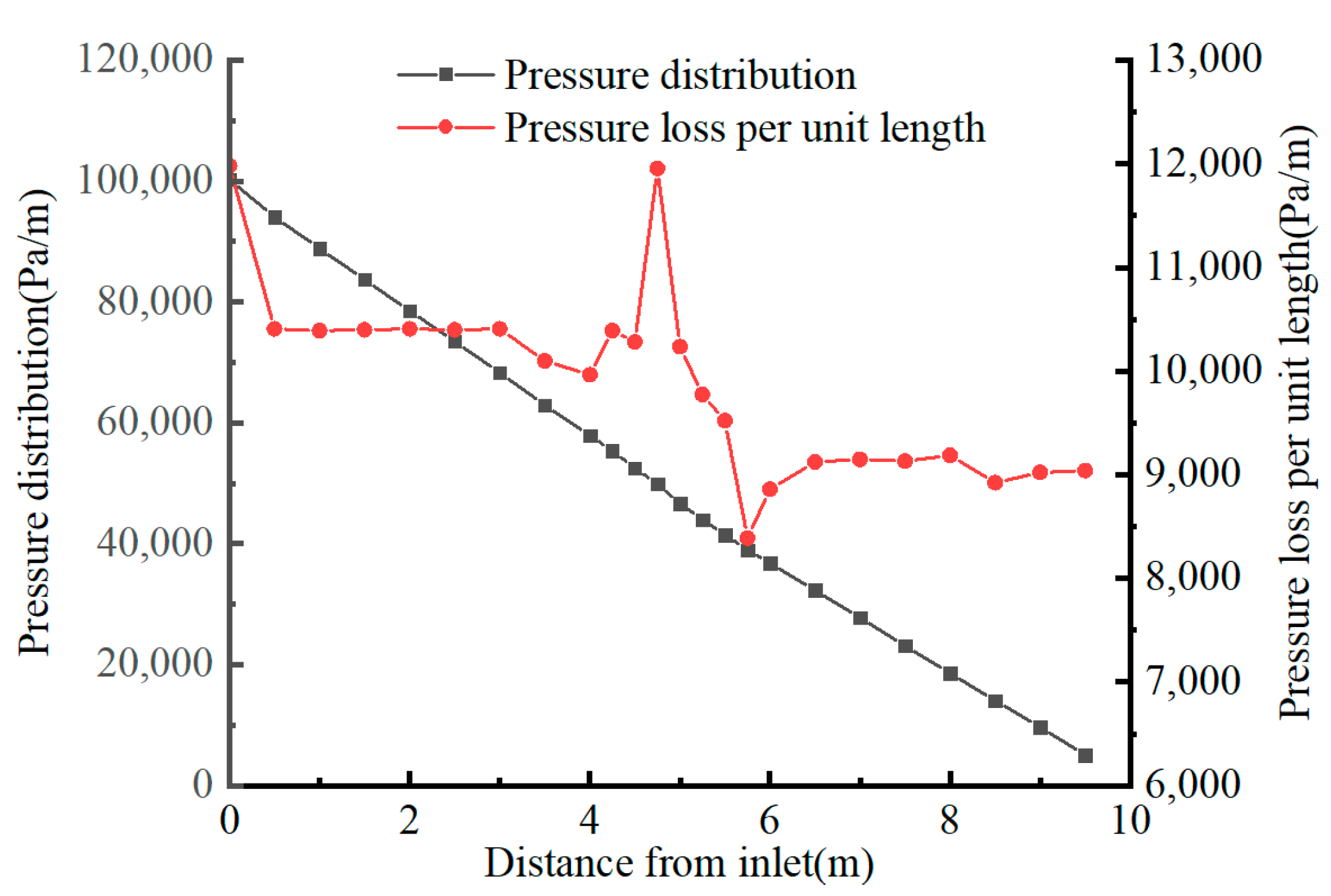
3.3. Pressure Loss
4. Influence of Curvature Radius in Curved Section
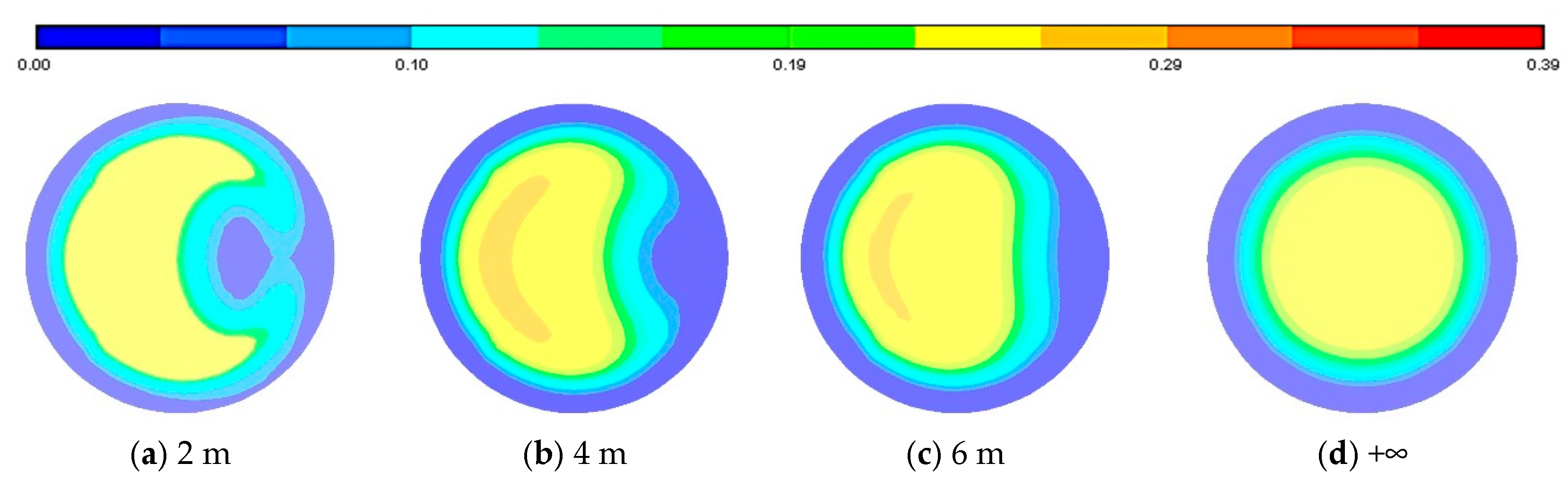
4.1. Impact on Particle Volume Fraction Distribution
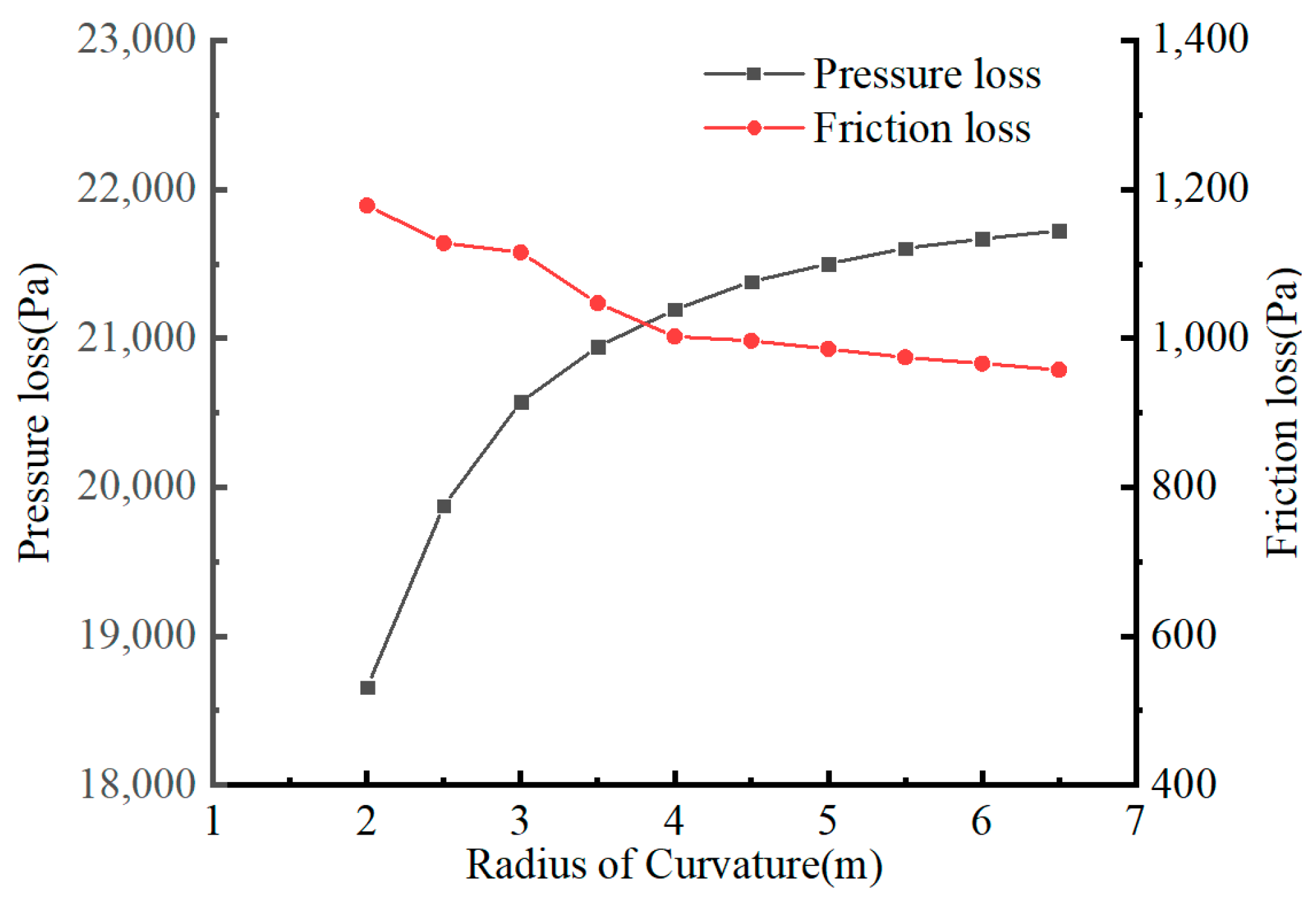
4.2. Influence on Pressure Loss
4.3. Effect on Mechanical Force in Curved Section
5. Conclusions
- (1)
- In vertical risers, particles distribute in a circular pattern. Upon entering curved sections, particles migrate toward the outer bend under centrifugal force. Secondary flows reshape the distribution into a concave circular or crescent profile. At the bend exit, particle concentration peaks at the outer bend. In the outflow section, gravitationally settling particles concentrate toward the bottom, migrating inward from both flanks while forming particle-depleted zones (0% concentration) near the outer flank. Near-wall regions maintain low concentrations due to lift forces throughout curved and outflow sections. Larger curvature radii yield increasingly uniform distributions.
- (2)
- In the inflow and outflow sections of the curved riser, the pressure distribution is mainly influenced by gravity, and the isobars are parallel to the horizontal plane. In the curved sections, combined gravity and centrifugal forces elevate pressure at the outer bend versus the inner bend. The pressure loss per unit length along the pipe direction decreases slightly before flowing into the curved section, increases when entering the curved section, and reaches a maximum at the middle position of the curved section. Then, the pressure loss starts to decrease, drops to the minimum when exiting the curved section, and gradually increases and stabilizes in the inclined riser. Total pressure loss decreases with increasing curvature radius, asymptotically approaching a constant value. Frictional loss reduces with larger radii.
- (3)
- Multiphase flow exerts forces on curved sections that promote realignment to vertical configuration. Smaller curvature radii generate greater restoration forces.
- (4)
- Regarding the influence of curvature radius, we acknowledge that comparing our results with studies using different curvature radii (or conducting an ablation study by varying radius while keeping other parameters constant) would further strengthen the analysis. In the current work, we focused on a representative radius to isolate and clarify the particle distribution and pressure loss mechanisms. As a next step, we plan to extend the model to different curvature radii and include a systematic comparison, which will help generalize the conclusions. As for the study limitations, we recognize that the present simulations adopt simplified particle assumptions (e.g., uniform diameter and density), and the curved riser geometry was considered under idealized boundary conditions. Future work will incorporate polydisperse particle distributions, realistic riser geometries, and varying curvature radii under more complex operational conditions to enhance the applicability of the findings.
- (5)
- The primary objective of this study is to establish an efficient analytical method for solid–liquid two-phase flow in pipes. As such, the model incorporates simplified assumptions such as steady-state flow, uniform particle size, and no heat/mass transfer to highlight the applicability and effectiveness of the proposed method itself. Currently, complex factors in long-distance transportation have not been thoroughly considered, though these factors would indeed influence the results. In subsequent research, we will progressively introduce elements such as unsteady effects, particle size distribution, and energy exchange to further enhance the model’s accuracy and engineering applicability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.J.; Liu, D.H.; Chen, J.J.; Li, C.L.; Yu, Y. Preliminary Assessment of Environmentally Friendly Mining Options Based on Various Mineral Resources—A Case Study of the Clarion-Clipperton Fracture Zone in Pacific. Sustainability 2024, 16, 7872. [Google Scholar] [CrossRef]
- Balaram, V. Rare earth elements: A review of applications, occurrence, exploration, analysis, recycling, and environmental impact. Geosci. Front. 2019, 10, 1285–1303. [Google Scholar] [CrossRef]
- Boschen, R.E.; Rowden, A.A.; Clark, M.R.; Gardner, J.P.A. Mining of deep-sea seafloor massive sulfides: A review of the deposits, their benthic communities, impacts from mining, regulatory frameworks and management strategies. Ocean Coast. Manag. 2013, 84, 54–67. [Google Scholar] [CrossRef]
- Miller, K.A.; Thompson, K.F.; Johnston, P.; Santillo, D. An Overview of Seabed Mining Including the Current State of Development, Environmental Impacts, and Knowledge Gaps. Front. Mar. Sci. 2018, 4, 418. [Google Scholar] [CrossRef]
- Liu, L.; Gai, K.; Yang, J.; Guo, X. Numerical Investigation on the Dynamics of Mixture Transport in Flexible Risers during Deep-Sea Mining. J. Mar. Sci. Eng. 2022, 10, 1842. [Google Scholar] [CrossRef]
- Sun, H.; Wang, Y.; Jia, L.; Lin, Z.; Yu, H. Theoretical and numerical methods for predicting the structural stiffness of unbonded flexible riser for deep-sea mining under axial tension and internal pressure. Ocean Eng. 2024, 310, 118672. [Google Scholar] [CrossRef]
- Tong, Y.; Xia, J. Nonlinear finite element simulation of Flexible riser system in Deep Sea Mining. Chin. J. Comput. Mech. 2022, 39, 129–134. [Google Scholar]
- Xu, W.-H.; Sha, M.; Wang, Y.-Y.; Ma, Y.-X. Review on the Mechanical Properties and Processing Technology of Flexible Pipe in Deep-Sea Mining. Mech. Pract. 2024, 46, 532–547. [Google Scholar]
- Wang, W.-H.; Yang, H.; Wang, L.; Liu, C.; Zhang, K.-D.; Dong, L.-L.; Liu, G.; Wang, Y.-Y.; Sun, H.-B. Configuration characteristics and inversion method of non-metallic unbonded flexible pipeline under typical conditions. Ocean Eng. 2025, 330, 121205. [Google Scholar] [CrossRef]
- Jin, G.; Zong, L.; Zong, Z.; Sun, Z.; Wang, H. Analysis of vortex-induced vibration for a cantilever riser in a deep-sea mining system. Chin. J. Theor. Appl. Mech. 2022, 54, 1741–1754. [Google Scholar]
- Bai, Y.; Bai, Q. Subsea Engineering Handbook; Gulf Professional Publishing: Houston, TX, USA, 2019. [Google Scholar]
- Balachandar, S.; Eaton, J.K. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Elghobashi, S. On Predicting Particle-Laden Turbulent Flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Chen, Q.; Xiong, T.; Zhang, X.; Jiang, P. Study of the hydraulic transport of non-spherical particles in a pipeline based on the CFD-DEM. Eng. Appl. Comput. Fluid Mech. 2020, 14, 53–69. [Google Scholar] [CrossRef]
- Su, T.; Chen, S.; Yuan, H. Research on the Characteristics of Solid-Liquid Two-Phase Flow in the Lifting Pipeline of Seabed Mining. J. Mar. Sci. Eng. 2024, 12, 1409. [Google Scholar] [CrossRef]
- Dai, Y.; Zhang, Y.; Li, X. Numerical and experimental investigations on pipeline internal solid-liquid mixed fluid for deep ocean mining. Ocean Eng. 2021, 220, 108411. [Google Scholar] [CrossRef]
- Wan, C.; Zhu, H.; Xiao, S.; Zhou, D.; Bao, Y.; Liu, X.; Han, Z. Prediction of pressure drop in solid-liquid two-phase pipe flow for deep-sea mining based on machine learning. Ocean Eng. 2024, 304, 117880. [Google Scholar] [CrossRef]
- Ling, Y.; Zhang, H.; Pan, Y.; Wang, Q.; Shang, Z. Numerical Simulation for Phase Volume Fraction of Solid-liquid Multiphase Flows in Horizontal Curved Pipe. Well Logging Technol. 2018, 42, 135–139. [Google Scholar]
- Gao, H.; Guo, L.J.; Zhang, X.M. Liquid-solid separation phenomena of two-phase turbulent flow in curved pipes. Int. J. Heat Mass Transf. 2002, 45, 4995–5005. [Google Scholar] [CrossRef]
- Xie, W.D.; Liang, Z.L.; Jiang, Z.Y.; Zhu, L.X. Dynamic responses of a flexible pipe conveying variable-density fluid and experiencing cross-flow and in-line coupled vortex-induced vibrations. Ocean Eng. 2022, 260, 111811. [Google Scholar] [CrossRef]
- Pickles, D.J.; Hunt, G.; Elliott, A.J.; Cammarano, A.; Falcone, G. An experimental investigation into the effect two-phase flow induced vibrations have on a J-shaped flexible pipe. J. Fluids Struct. 2024, 125, 104057. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, C.; He, C.; Li, L.; Zhou, S. Flow characteristics of hydrate slurry in U-bend pipe. Petrochem. Technol. 2019, 48, 375–380. [Google Scholar]
- Yang, R.; Li, D.; Wang, H. Simulation Study of Hydrate Slurry Flow in Vertical Bend. Contemp. Chem. Ind. 2020, 49, 2597–2601. [Google Scholar]
- Wu, J. Computational Fluid Mechanics, 1st ed.; South China University of Technology Press: Guangzhou, China, 2022; 407p. [Google Scholar]
- Lei, W. Simulation of Liquid-Solid Two-Phase Flow with Particles in Pipes. Master’s Thesis, Hangzhou Dianzi University, Hangzhou, China, 2011. [Google Scholar]






| Particle Size (mm) | 7.5 | 12.5 | 17.5 | 22.5 | 27.5 |
| Solids Content | 4.2% | 18.8% | 16.6% | 31.4% | 29.3% |
| Velocity (m/s) | Frictional Coefficient |
|---|---|
| 2.660 | 0.056 |
| 3.101 | 0.072 |
| 3.549 | 0.090 |
| 4.290 | 0.128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.-H.; Wang, L.; Liu, C.; Wang, L.-J.; Zhao, Z.-H.; Dong, L.-L.; Liu, G.; Wang, Y.-Y.; Sun, H.-B.; Li, K. Analysis on Inner Flow Field and Hydrodynamic Force on Flexible Mining Pipeline Under Bending States. J. Mar. Sci. Eng. 2025, 13, 1599. https://doi.org/10.3390/jmse13081599
Wang W-H, Wang L, Liu C, Wang L-J, Zhao Z-H, Dong L-L, Liu G, Wang Y-Y, Sun H-B, Li K. Analysis on Inner Flow Field and Hydrodynamic Force on Flexible Mining Pipeline Under Bending States. Journal of Marine Science and Engineering. 2025; 13(8):1599. https://doi.org/10.3390/jmse13081599
Chicago/Turabian StyleWang, Wen-Hua, Lei Wang, Chuang Liu, Li-Jian Wang, Zi-Han Zhao, Lei-Lei Dong, Gang Liu, Ying-Ying Wang, Hai-Bo Sun, and Kun Li. 2025. "Analysis on Inner Flow Field and Hydrodynamic Force on Flexible Mining Pipeline Under Bending States" Journal of Marine Science and Engineering 13, no. 8: 1599. https://doi.org/10.3390/jmse13081599
APA StyleWang, W.-H., Wang, L., Liu, C., Wang, L.-J., Zhao, Z.-H., Dong, L.-L., Liu, G., Wang, Y.-Y., Sun, H.-B., & Li, K. (2025). Analysis on Inner Flow Field and Hydrodynamic Force on Flexible Mining Pipeline Under Bending States. Journal of Marine Science and Engineering, 13(8), 1599. https://doi.org/10.3390/jmse13081599







